Combining fMRI with EEG and MEG in order to relate patterns of brain activity to cognition

Abstract

The common factor that underlies several types of functional brain imaging is the electric current of masses of dendrites. The prodigious demands for the energy that is required to drive the dendritic currents are met by hemodynamic and metabolic responses that are visualized with fMRI and PET techniques. The high current densities in parallel dendritic shafts and the broad distributions of the loop currents outside the dendrites generate both the scalp EEG and the magnetic fields seen in the MEG. The. Measurements of image intensities and potential fields provide state variables for modeling. The relationships between the intensities of current density and the electric, magnetic, and hemodynamic state variables are complex and far from proportionate. The state variables are complementary, because the information they convey comes from differing albeit overlapping neural populations, so that efforts to cross-validate localization of neural activity relating to specified cognitive behaviors have not always been successful. We propose an alternative way to use the three methods in combination through studies of hemisphere-wide, high-resolution spatiotemporal patterns of neural activity recorded non-invasively and analyzed with multivariate statistics. Success in this proposed endeavor requires specification of what patterns to look for. At the present level of understanding, an appropriate pattern is any significant departure from random noise in the spectral, temporal and spatial domains that can be scaled into the coarse-graining of time by fMRI/BOLD and the coarse-graining of space by EEG and MEG. Here the requisite patterns are predicted to be large-scale spatial amplitude modulation (AM) of synchronized neuronal signals in the beta and gamma ranges that are coordinated but not correlated with fMRI intensities.

1. Introduction

1A. fMRI, neural activity and brain energetics: statement of the problem

Brains as thermodynamic systems consume energy at rates roughly ten-fold greater than any other organ of comparable mass. The high rates hold whether subjects are at rest or active, leading to the sobriquet “dark energy” (Raichle, 2006) in analogy to the preponderance of inscrutable astronomical mass-energy. This difference in rates of energy dissipation is closely related to that between the metabolic rates of homeotherms vs. poikilotherms. Maintenance of high constant body temperature gives an unequivocal advantage to birds and mammals in the struggle for survival, despite the ten-fold increase in the cost of dissipated metabolic energy. Similarly, the high metabolic rate in brains is necessary to maintain the ionic energy reserves at self-organized criticality (Freeman, 2008), a critical state of readiness to cope with environmental vicissitudes, whatever the metabolic cost.

That readiness is based in the background activity, which has been shown to arise by mutual excitation among cortical excitatory neurons [reviewed in Freeman, 2008]. The intensity of the background activity varies with the degree of arousal, but the stability at every level and in every location is maintained by the refractory periods, not by inhibition or thresholds (Freeman, 2007b). The role of inhibition is to impose spatiotemporal order and structure on the otherwise random noise background activity. The transition from behavioral rest to intentional action invokes reorganization of the background activity that may increase, decrease or not change the mean level of activity. What is expected to change is the emergence of spatiotemporal patterning by local increases and decreases of energy dissipation from the background levels. Obviously in the continuous interactions of excitatory and inhibitory neurons the coincidence of excitatory and inhibitory currents in the same dendritic trees must at least partially cancel the extracellular electric and magnetic fields, but the metabolic demands must still be met for both forms of activation and for all frequency ranges. The resulting dissipation of energy resources, as well as the disparity in manifestations, is likely to be highest in the high frequency ranges, where phase dispersion with fixed axonal delays is maximal, and where the density of neural information is likely to be highest, but where resolution with fMRI is not possible.

This cancellation focuses the problem to be solved for fMRI, which is to relate local cerebral blood flow to local neural activity. The basic relation in the simplistic view is that the capillaries open in brain areas in which CO₂ has accumulated as the by-product of neurons burning glucose. The relation in one respect is simpler than in other organs, because brain arterioles lack the muscular cuff by which neural control can over-ride local control by CO₂, especially in pre-adaptation of blood flow to predicted onset of muscular exercise vs. digestion. However, the CO₂ combines locally with water by the enzyme carbonic anhydrase as carbonic acid, which then dissociates. It is unclear whether the capillaries respond directly to the CO₂ or to the acid (pCO₂ versus pH) or both. Moreover, the astrocytes in cortex hold a substantial reservoir of glycogen (“animal starch”), which is a ready local source of glucose that can be split without oxygen, giving pyruvic and lactic acids without producing CO₂ (anaerobic metabolism), in which instances neural activity might be dissociated from blood flow and blood oxygen level dependent (BOLD) signals for extended time periods until the oxygen debt is repaid.

The homeostatic feedback that regulates the local pCO₂ or pH is likely to be based regionally on the vascular architectures and its coupling to glial circuits (Schummers, Yu, & Sur, 2008) rather than the neural architectures, which varies among cortical regions. Astrocytes, the most abundant glial cells, are not only metabolically coupled to neighboring neurons but also communicate directly with the vasculature. Astrocytic activity affects local blood flow, which can be assessed by noninvasive hemodynamic mapping techniques such as intrinsic signal optical imaging (Arieli & Grinvald, 2002). The relation between neuronal networks, astrocytes, and hemodynamic responses is an important topic of on-going research (Wolf & Kirchhoff, 2008). Resolution of this problem would appear to require detailed comparisons of the vascular and neural architectures of local cortical regions that have been located by simultaneous measurements of glycogen depletion, pO₂, pCO₂ and pH in conjunction with blood flow and, most revealingly, neural activity that has been classified by spatiotemporal neural activity patterns with respect to specific cognitive behaviors.

Further complications ensue from the fact that the activity of inhibitory neurons also requires metabolic energy, and so also does the maintenance of inhibitory synaptic potentials by excitatory neurons (Buzsáki, Kaila, & Raichle, 2007; Logothetis, 2008). Since 95% of cortical energy is expended by dendrites and 5% by axons, the reduction in transmission of action potentials by excitatory neurons cannot compensate for the augmented dissipation necessitated by inhibition. The level of “activity” revealed by hemodynamic imaging alone must inescapably include both excitation and inhibition. However, in the identification of macroscopic spatiotemporal patterns, the localization of peaks and troughs to cortical landmarks is secondary to the classification of the field patterns with respect to intentional behavior, as prelude to correlation with respect to anatomical landmarks. The problem for interpretation of hemodynamic images can then be seen to require coordination not correlation with electric and magnetic measurements of excitation and inhibition in neuron populations across disparate scales of space and time.

1B. Complementarity of EEG, MEG, and fMRI signals

Multivariate approaches for characterizing and decoding local and distributed neuronal activity patterns in fMRI have been receiving increased attention in recent years. Multivoxel pattern analyses of fMRI and BOLD signals are being used to circumvent conceptual and methodological limitations of the localization approach to brain imaging (Logothetis, 2008). Spatial patterns of brain activity can have significantly greater sensitivity and specificity for detecting conscious and unconscious mental processes than activity in individual regions (Haynes & Rees, 2006; Soon, Brass, Heinze, & Haynes, 2008). This newfound emphasis in fMRI research on classification and pattern recognition, which is the focus of our proposed approach, will undoubtedly facilitate a more integrated approach to linking perceptually relevant representations of fMRI, EEG and MEG neuronal signals by highlighting their functional complementarity. The most important insight is that the neural correlates of cognitive load are likely to be found in the large-scale, widely distributed, spatially coherent neural activities at the mesoscopic and macroscopic levels, as defined below. At the systems level the problems encountered in attempts at spatial localization and the precise descriptions of microscopic causal relations are secondary. Our first task is to measure and model these transiently coherent spatiotemporal patterns.

For direct correlation of fMRI with EEG and MEG the limitations of resolution of fMRI must be considered. Only the fMRI images of cortical activity are admissible for the correlation, owing to the limits on the class of neurons that can contribute to signals derived from the EEG and MEG, as discussed below. On the one hand the spatial resolution of fMRI reaches into the mm range, which is appropriate for cortical thickness in humans ranging from 1 to 4 mm. Matching the image of enhanced blood flow to the thickness of the cortical neuropil poses a strict criterion for localization that is not often met by any of the several methods. On the other hand, the temporal resolution of fMRI inherently limits correlations to spatial patterns of EEG and MEG that have been averaged over the several seconds that characterize the time resolution of changes in the metabolic and vascular responses of cortex to metabolic demands for the removal of waste CO₂, acid, and heat. The need for time averaging unavoidably invokes the necessity to deal explicitly with a hierarchy of neural activity in cognition, not only with the microscopic action potentials but also with the macroscopic field potentials of the EEG and MEG.

An optimal way to construct feature vectors for classification of spatial AM patterns would be to combine estimates of analytic power in frames from both EEG and MEG. Feature vectors defined below might then be constructed from all available sources to represent patterns of mean excitation, inhibition, and energy dissipation over the time spans are needed to estimate fMRI images reliably. To accomplish this the data must be spatially coarse-grained to conform to the spatial resolution specified by the spatial intervals of the sensors in the arrays used for EEG and MEG recordings and temporally coarse-grained to conform to the temporal frequencies provided by sequential hemodynamic imaging. The most valuable tool is the spatial power spectral density (PSD_X), which has been calculated for the scalp EEG (Freeman et al., 2003), intracranial human electrocorticogram (ECoG, Freeman et al., 2000) and fMRI (Worsely, 2005) but surprisingly not for MEG.

Temporal summation alone cannot suffice, because spatial images of dissipation given by analytic power from the EEG and MEG are specific for the temporal spectral pass bands, whereas fMRI is indiscriminate in that respect. The obvious remedies are to combine the spatial patterns over the several available temporal pass bands, and to conduct analysis of variance to determine which pass bands of analytic power might correspond to selected components of fMRI from two or more sequential behavioral states. This approach avoids subtracting control and test images in search of localization. As discussed below, in many physical systems the rate of energy dissipation is inversely proportional to the square of the frequency of oscillation. This relation is most clearly seen by graphing the temporal power spectral density (PSD_T) in coordinates of log₁₀ power vs., log₁₀ frequency. Such systems are said to generate “brown noise” with 1/f² power-law PSD (slope of -2). For example, the theta power spectral density at 4 Hz is 100 times the gamma power spectral density at 40 Hz, while the power dissipations at 4 Hz and 40 Hz are equal. The utility of EEG and MEG data might be greatest in helping to decompose fMRI into identifiable frequency ranges of dissipation related to cognitive behaviors. For example, the fMRI might locate cortical areas in which the amplitudes of EEG and MEG oscillations are quite low. If the metabolic demand is low, then the neural activity is low. If the blood flow is high, the relative silence implies active silencing by inhibition. If it is very high, it may signify the furious dissipation of neural energy by the cancellation of strong excitatory and inhibitory synaptic currents in a situation that is metabolically very expensive indeed and perhaps restricted to a narrow pass band, or perhaps not. Then the problem to be solved for fMRI interpretation emerges in predicting the forms of spatiotemporal patterning revealed by EEG and EMG, such that they can be measured and averaged over time and space without loss of the essential features in the process of averaging. That is the problem addressed in the remainder of this essay.

2. The several manifestations of cortical dendritic current in fMRI, EEG and MEG

2A. Foundation of non-invasive brain imaging in neural energy

Human brain activity can be monitored non-invasively at and above the scalp based on the production by intracranial neurons of electric and magnetic fields. The fields accompany the electric current by which dendrites sum and communicate their synaptic input to the trigger zones of the single, often many-branched axon by which each neuron transmits its output to other neurons more or less distant. The frequencies of oscillation in the intensities of the fields are much too low to generate significant electromagnetic radiation (radio waves), and the wavelengths are kilometers long, so the intensities of fields are measured separately as the EEG and MEG.

The energy that drives the electric current is immediately provided by chemical gradients of ions, particularly those for sodium and potassium, which ionic pumps sustain across neural membranes. That chemical energy is held in a vast reservoir that is instantly available at all times like a battery to drive current at the flip of a synaptic switch. After each use that store of energy is replenished by relatively slow metabolic processes, which require the cerebrovascular system to deliver oxygen and glucose and remove carbon dioxide and heat. The modifications in local rates of cerebral blood flow that accompany changes in neural activity are detected and imaged by hemodynamic and metabolic techniques (Logothetis, 2008). The three signals, EEG, MEG, and fMRI, can either increase or decrease in relation to behavioral and cognitive demands, thereby forming spatial patterns in brain images. Because inhibition is an active process that requires expenditure of metabolic energy, “activation” and “deactivation” differ radically from “excitation” and “inhibition”.

2B. Differing sensitivities of electromagnetic and hemodynamic measures

All three types of non-invasive brain imaging methods reveal different aspects of global neural activity. The EEG and MEG manifest the activity of only a limited class of neurons. First, the neurons must have a degree of axial symmetry, meaning that the activated dendrites must lie to one side of the cell body and axon, so that the sites of current outflow (sources) are spatially separated from the sites of current inflow (sinks). Typically these are pyramidal cells, which generate dipole fields that can extend throughout the brain and beyond. Cortical interneurons typically have radial symmetry (stellate cells), so their sources and sinks intermingle, and their distant fields cancel. The local field potentials (LFP) within their dendritic branches are designated as closed; they cannot contribute significantly to the EEG or MEG at or above the scalp, or even to electric fields recorded with electrodes on exposed pial surfaces, the electrocorticogram (ECoG). The syncytia formed by gap junctions also typically generate closed fields. The fields are dendritic in origin; axons clearly mediate the strengths of dendritic currents by the information they transmit, but their action potentials do not contribute directly to the dendritic potentials, certainly not as “envelopes of spikes” except when artificially synchronized by impulse stimuli. Second, the neurons must be aligned in palisades, both the dendrites in cortical columns perpendicular to the pial surface and the cell bodies in layers parallel to the pial surface. The cellular architectures of nuclei and reticular networks that lack the laminar organization of cortex seldom support the spatial summation of multineuronal dipole fields that is required for significant oscillations to appear at the scalp. Third, the contributing neurons must support strong local interactions probably by gap junctions in some areas and certainly by local and distant interactions through axodendritic synapses in all areas, in order to provide the temporal synchrony necessary for sufficiently broad summation for the potential fields to appear at the scalp.

Thus, while fMRI and BOLD can image neural activities in all cortical, nuclear and reticular architectures predominantly containing dendrites, EEG and MEG are largely restricted to imaging activities of cerebral cortex but not cerebellar cortex. Purkinje cells also have a columnar and laminar structure that could, theoretically, permit neuronal sources in the cerebellum to also contribute to scalp EEG. However, the cerebellum does not contribute significantly to EEG signals, because of the extreme curvature of its gyri tending to form closed fields, the sparseness of the Purkinje cells, and the predominance of feedforward inhibition over feedback inhibition. Forward inhibition promotes spatial differentiation, not the integration that gives broad fields of synchronized oscillations provided by feedback inhibition and forward excitation. Likewise, neuronal sources in structures such as the thalamus and basal ganglia have a radial, non-columnar organization, so are less likely to make any significant contributions to the scalp EEG even when intense LFP can be recorded within them (Niedermeyer & Lopes da Silva, 2004). The fMRI signals do not depend on the laminar or the radial neuronal organization, but have more to do with the coupling of metabolic processes to the underlying vascular and glial beds (Fox, Raichle, Mintun, & Dence, 1988; Menon & Crottaz-Herbette, 2005; Herrmann & Debener, 2008).

All three methods give access to wide areas of cortex in a virtual continuum over the calvarium, albeit with differing degrees of spatial and temporal resolution. All three give 2-D images of spatial patterns of neural activity that change with time, some of which are expected to correlate with specific cognitive behaviors. Therefore, the cortical fMRI and EEG and MEG offer opportunities for mutual validation of behavioral correlates. In a simplistic view the rate of energy dissipation that is required to generate dendritic current should rise in proportion to current density and therefore the amplitudes of EEG and MEG potential differences; so likewise on a longer time scale should the rate of tissue perfusion needed to replenish the ionic energy reservoir. Studies reflect that expectation by combining imaging and physiology experiments in monkeys, indicating that the fMRI signals are more closely correlated with EEG, ECoG and LFP than with multiunit and single neuron activity (Logothetis & Pfeuffer, 2004), and that neurometabolic coupling in cerebral cortex reflects dendritic activity more than axonal activity (Viswanathan & Freeman, 2007). LFP in the high gamma band (> 40Hz) are better and more reliable predictors of the BOLD signal (Goense & Logothetis, 2008). However, the mechanisms of the relations between electrical oscillations and the concurrent fMRI signals are not yet known in sufficient detail to integrate reliably. Predictions are needed of what forms the cognitively related activities take, such that the signals can be combined across the differences in time and space scales. This is not a trivial problem. Solution requires a deep understanding of the hierarchical organization of brain activity.

2D. Differences between analyses of neural modules and neural fields

A useful hierarchy of brain signals and levels of organization is based on techniques of observation. The predominant signals that are detected by microelectrodes inserted into cortex are the trains of action potentials from neurons that can be studied individually as components of networks and modules. The signals and the neurons are microscopic. The predominant signals that are recorded from arrays of depth electrodes, the LFP, and from arrays of electrodes on the cortical surface, the ECoG, are sums of potentials generated by cooperative interactions among very large assemblies. The signal from each electrode comes from at least 10,000 neurons and typically many more. These self-organized neural masses are continuous in space, and likewise the signals they generate are spatially continuous. The neural masses are fields that embed the networks and modules forming the primary sensory and motor cortices and components of the limbic system. They constitute the mesoscopic level of brain function. The effects of the fields on the neural networks and modules that they embed are only apparent in statistical averages of the microscopic activity. Lastly, the signals that emerge from the head in the EEG and MEG originate in neural masses that vary structurally and functionally in size and complexity, up to the entire cerebral hemisphere. These signals are from neural fields that are very large indeed, characteristically being difficult to distinguish from referential activity and volume conduction, yet providing insight into the global organization of brain activity. This is the macroscopic level given by EEG and MEG and fMRI from the continuous sheet of neuropil in each cerebral hemisphere in which the microscopic networks and modules are embedded along with the intermediate mesoscopic assemblies. It is apparent that networks and modules are functional entities with variable size and adaptive boundaries being re-defined by the mesoscopic and macroscopic fields of brain activity with each new cognitive task and within tasks from each tenth of a second to the next.

The neocortex provides many specialized areas that provide substrates for locally self-organized modules. The most widely held hypothesis of cortical function is that each module generates its characteristic signal; that these signals intermingle by volume conduction; that separation might be achieved by decomposition with independent component analysis (ICA); and that intermittent transmission among modules is manifested by transient phase-locking of microscopic or mesoscopic oscillations with zero phase lags despite axonal propagation delays on temporary connections (e.g., Singer, 2001; Makeig et al., 2002; Bressler, Richter, Chen, & Ding, 2007). Our thermodynamic hypothesis, which is loosely related to Baars’ (1997) “global workspace”, is that self-organized modules are embedded in the cortical neuropil; that they enter by phase transitions into transient frames of synchronized oscillations having narrow spectral bands and broad spatial distributions; that the oscillation in the pass band of each frame is modulated in amplitude (AM) and phase (PM); that multiple frames coexist in narrow pass bands in the beta and gamma ranges; and that frames can be separated by spectral decomposition. The role of fMRI in this schema is to provide the macroscopic frame for the cortical events occurring in a 4 to 5 s window during a reproducible cognitive task. There is increasing evidence that areas of high and low blood flow form spatial patterns of PET and fMRI (Raichle, et al., 2001; Greicius, et al. 2003; Fransson, 2006; Morcom & Fletcher, 2007; Raichle & Snyder, 2007; Schacter & Addis, 2007; Szpunar, Watson & McDermott, 2008). The roles of EEG and MEG are to provide non-invasive measurements at high spatial and temporal resolution throughout the corresponding spatial and temporal window, and with repetition as often as needed to achieve statistical synthesis and verification in respect to fMRI.

3. Search for control states in fMRI, EEG and MEG

3A. Definitions of “resting” and “ground” states

Many fMRI studies are based on comparison of spatial patterns between an active behavior and the control state without that behavior. Yet brains are always active. The study of the background activity forces this vexing problem (Raichle, et al., 2001; Freeman, 2004a, 2004b, 2995, 2006a). What is the baseline from which changes in activity levels are to be measured? How might a non-cogitative “resting” state or a “ground” state for brain activity best be defined? Must “activation” carry populations above the level of either state, or might “activation” include reductions below either state? If so, how, and with what advantage?

Our path to understanding spatiotemporal patterns in scalp EEG and MEG began with analysis of the spatiotemporal properties of the ECoG in human (Freeman et al., 2006; Panagiotides et al., 2008) and animal (Freeman, 2004 a, b). For the extraction of the relevant AM patterns, the ECoG must be recorded with multielectrode arrays fixed on the flattened pial surface of cortex that provide the necessary window for observation and measurement. Examination of the background spontaneous ECoG in animals and humans has shown that the only unambiguously defined basal level for energy and neural activity is the absence of oscillation and action potentials giving flat EEG. This state is fully reversible when it is induced in some animals by hibernation and in others by very deep surgical anesthesia, therapeutically suppressing neural interactions. It corresponds to the open loop state (Freeman, 1975), in which the mesoscopic time and space constants of the dendrites of neural populations can be measured. From this vacuum state (Freeman & Vitiello, 2006) there is a graded return through slow wave coma and chaotic waking rest to expectant arousal, with culmination in engagement in intentional action (Skarda & Freeman, 1987; Freeman, 2008). The stages of arousal resemble those in waking from slow-wave sleep; they are discriminable with soft criteria.

Of particular interest is the resting state, in which subjects are behaviorally inactive and unchallenged by immediate expectation of a conditioned stimulus (CS) and its attendant conditioned response (CR), eyes closed or open. As observed in humans this state is accompanied with a remarkably reproducible pattern of increased metabolic activity in midline brain structures, notably the ventromedial prefrontal cortex and the posterior cingulate cortex, documented in humans at rest (Shulman, et al., 1997) with closed eyes and presumably empty minds. In view of its reproducibility during task based deactivations Raichle labeled it as a “default mode” (Raichle, et al., 2001); reviewed by (Raichle & Snyder, 2007). These regions are found to be highly correlated with each other and therefore are hypothesized to constitute a default mode network (Greicius, et al., 2003). Embarkation from the default state to overt action is accompanied by increases in neurometabolic demands in some brain regions and decreases in others. The neural mechanisms of the decreases and their functional significance are matters for conjecture and controversy (Morcom & Fletcher, 2007), and likewise the mental contents of subjects at rest in the default mode (Buckner, Andrews-Hanna, & Schacter, 2008). Raichle et al. and Greicius et al. defined their reference state with respect to behavioral and hemodynamic changes (Fig. 1). The uncertainty inherent in this definition is apparent in comparing the pattern with those demonstrated by others (Raichle & Snyder, 2007; Szpunar, Watson & McDermott, 2008) accompanying the cognitive functions of recollection and prediction, showing substantial overlap, which suggests that “resting” may be indistinguishable from “occult cogitating” by these criteria. This holds likewise for imaging correlates of “self-referential processing” (Northoff et al., 2006).

Fig. 1.

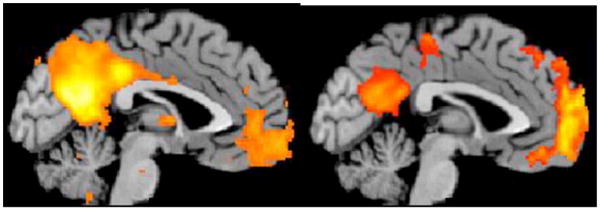
(Left) Independent Components Analysis of “passive” resting-state fMRI scans shows spatially coherent activity in the posterior cingulate cortex, precuneus and medial prefrontal cortex nodes of the default mode network. (Right) Transient fMRI signal reductions are revealed during an auditory “oddball” attention task in these same regions. Unpublished data (Menon).

A complementary approach is to seek in the EEG the characteristic power spectral density (PSD) of the ECoG, EEG or MEG that is recorded from subjects similarly showing no overt or imminent behaviors. The time series from multiple electrodes in this state often yield featureless fluctuations with no periodic waveforms. The PSD_T plotted in coordinates of log₁₀ power vs. log₁₀ frequency often conforms to a straight line with slope ranging from near or below -2 (“brown” noise, 1/f²) in waking rest to near or below -3 (“black” noise, near 1/f³ (Schroeder, 1991)) in deep slow wave sleep (Freeman, Holmes, West, & Vanhatalo, 2006). When subjects become active, and often well before they do, excess power emerges above the straight line particularly in the classic theta (3-7 Hz), alpha (8- 12 Hz), beta (12-25 Hz) and gamma ranges (30-80 Hz) (Fig. 2). These upward deviations manifest the breaking of the symmetry of unstructured random activity in disorder by the emergence of order in the spectral domain, giving the indication that within a collection of “resting” and “occult cogitating” and/or “self-referential processing” states there can be defined a ground state by its lack of spectral peaks reflecting scale-free random noise, which appears to be the form taken by basal brain activity from which order emerges (Freeman, 2006; Freeman and Zhai, 2009).

Fig. 2.

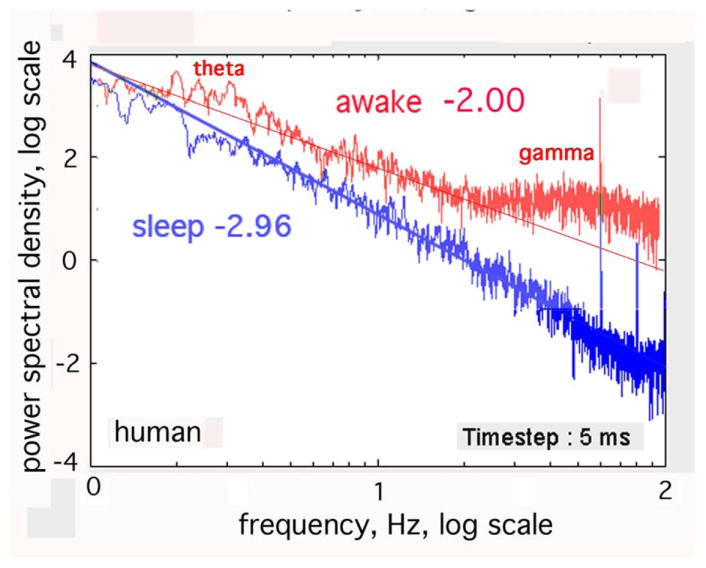
The temporal power spectral density, PSD_T, in this human ECoG tends to a power-law distribution, 1/f^e, with exponent e ~ 3±.25 in slow-wave sleep and e ~ 2±.25 in the awake state (Freeman, et al., 2006). Spectral peaks of excess power in the clinically significant bands (here gamma and low theta) during arousal and task performance. Adapted from (Freeman, et al., 2006).

3B. Deviations from the ground state to an active state by the emergence of order

This conclusion that the ECoG and EEG in the ground state conform to brown noise is consistent with the neural mechanism by which the background activity is maintained (reviewed in Freeman, 2008). The origin is in dense, distributed, mutual excitation among cortical excitatory neurons in positive feedback (Freeman, 1975; Freeman, 2007b; Freeman, 2008). Despite their sparseness, the interconnections are sufficiently dense that an action potential given by each neuron yields a prolonged barrage of action potentials from neighbors; that is, the anatomical connection density supports feedback gain that is potentially greater than unity. It is the refractory period of each neuron that prevents runaway excitation, so that large populations of cortical neurons self-stabilize homeostatically and sustain their activity in steady state at unity gain. This self-stabilized discharge is transmitted also to inhibitory interneurons. It provides the background excitation that inhibitory neurons require to exercise the mutual inhibition that supports spatial and temporal contrast enhancement by positive feedback to each other and the oscillations in the beta and gamma ranges by negative feedback to the excitatory neurons. Local feedback with short delays generates gamma rhythms that in gamma ECoG are synchronized over distances of 1 to 3 cm (Freeman, 2005a). Longer range feedback with greater delays typically gives rise to synchronized beta (Brovelli, et al., 2004) and theta (Rizzuto, et al., 2003) rhythms over larger distances (Freeman, 2005). The inhibitory feedback does not stabilize cortex, nor do neural thresholds stabilize it; the factor that stabilizes the background fluctuations of EEG, MEG and ECoG is the refractory periods.

The level of power is not thereby constrained. Calculation of the probability of neural action potential formation conditional on the amplitude of the ECoG has shown that the background power is maintained in steady state at unity gain (Freeman, 2008) over a broad range of variation in level of arousal, which implicates the role of brain stem nuclei in neurohumoral control of the level of background activity. In the olfactory system the agent of increased background activity with arousal is histamine (Freeman, 2005a). Other systems appear to rely on other neuroamines. In any case the regulation of the ground state admits of two independent degrees of freedom relating to the level of arousal. One is the level of power that is assessed by the intercept of the line fitted to the PSD_T when it approaches the power-law form. The other is the robustness of the background activity, which is manifested as the slope of the PSD_T approaches -2 (Freeman and Zhai, 2009).

There is no a priori reason to suppose that the power level of the ground state should be constant over time and spatially uniform throughout the brain at rest. To the contrary, the brain likely resembles the body, which has “catabolic” musculoskeletal systems that are quiescent during the actions of “anabolic” systems including the intestines, liver and kidneys. In turn the restorative organs shut down during intense muscular activity. Similarly there are likely to be brain regions and networks for which the main functions are anabolic in leisure or down time and others that support catabolic activities during intentional action. It is well known that blood flow is allocated between the two systems in the body largely according to strictly local demand. Similar local controls are known to exist in brains, conceivably giving the observed BOLD patterns (Raichle & Mintun, 2006). The mean level of power dissipation in brains is always high, owing to the necessity for maintaining a high-energy state near criticality (Freeman & Vitiello, 2006), so the question in any particular change of state is whether rate of dissipation necessarily increases with increased order in pattern formation. Indeed it may or may not. The separation between the two degrees of freedom is manifested in the independent variations of the slope and the intercept of the graph of log power versus log frequency (Freeman and Zhai, 2009).

Therefore the 1/f criterion defines the “ground” state as requiring a state of “waking rest” with non-zero activity but without specifying its rate of energy expenditure. Certainly the “open loop” state that supervenes under deep anesthesia serves as a near-equilibrium “vacuum” state with zero background activity, from which the “ground” state emerges with recovery, and then on to the 1/f “waking rest” state as prelude to the “active” state with emergence of spectral structure (Skarda & Freeman, 1987). The “waking rest” state defined behaviorally may include some areas at the “ground” state defined spectrally and other areas in “active” states defined spectrally, so that departures from “waking rest” might incur increases and decreases from prevailing mean levels of activity (Raichle, et al., 2001). A search for EEG and MEG peaks in the temporal PSD_T and spatial PSD_X “resting” state may yield clues to occult neural activity supporting mental activity that is undetected by observers or unreported by subjects because it is not conscious. The pass bands (widths and center frequencies) of the deviations from randomness (1/f irrespective of slope) can give clues to start modeling the activities.

4. Search for spatial structures in EEG and MEG to combine with those in fMRI

Most non-invasive brain imaging studies of field potentials have been devoted to spatial localization of brain activity, including the use of PET/fMRI to guide MEG/EEG source imaging for improved spatiotemporal localization (Heinze, et al., 1994; Menon et al., 1997; Liu, Belliveau, & Dale, 1998; Ahlfors, et al., 1999). Here we propose an alternative way to use the data from the three non-invasive brain imaging methods, namely the detection of spatial patterns of amplitude modulation (AM) and phase modulation (PM) of non-local, transiently phase-locked oscillations in human brains.

4A. Detecting spatial patterns of oscillatory activity in ECoG

The aim of brain imaging is to relate brain state to behavioral state through measurement by which the infinite state spaces is projected into a finite measurement spaces. The high-resolution measurements of the ECoG from arrays of electrodes fixed on the pial surface of cortex serve to sample infinite brain state in a series of spatial patterns of amplitude modulation (AM) and phase modulation (PM) of phase-locked oscillations in the beta and gamma ranges. The behavioral measurements project the infinite behavioral state space into discrete classes of CS and CR. The AM patterns are correlated with CS to which the subjects have been trained to give CR. Multivariate clustering and classification of AM patterns demonstrate the correlations between brain state and behavior state by projection into 2-space, i.e., a graphic display of clusters. Operationally, the amplitude of the signal from each of n spatial points in an array of n electrodes is calculated over a time segment. An n-dimensional feature vector is constructed from the n amplitudes that specify for each AM pattern a point in n-space. Similar AM patterns from repeated trials with the same CS form clusters of points. Differing AM patterns from trials with different CS form separate and partially overlapping clusters (Viana Di Prisco and Freeman, 1985; Ohl, Scheich and Freeman, 2001; Freeman & Burke, 2003; Freeman, 2005b). The trajectories between clusters describe the transitions between states.

The classificatory information in the ECoG is homogeneously distributed over the sensory cortex; no electrode gives a signal that is any more or less effective than any other (Barrie, Freeman and Lenhart, 1996; Ohl, Scheich and Freeman, 2001), showing that the location of the electrodes is not critical, provided that the electrodes are all fixed within the area of spatial coherence of the carrier wave. Both low and high amplitudes of signals have equal value in classification, showing inclusiveness with respect to excitation, disexcitation, inhibition, and disinhibition in activation and de-activation. This generality reflects the distributed nature of the contents of holographic types of memory storage (Pribram, 1975). Each AM pattern is accompanied by a PM pattern, which is imposed by intracortical axonal conduction delays in the formation of each AM pattern. The phase dispersion at the peak frequency is within ±45°; it shows that synchronization is widespread but not strictly at zero lag.

4B. Extrapolation to search for spatiotemporal patterns in scalp EEG

The demonstration of the equal classificatory value of each channel in ECoG is extremely important for image analysis. The geometry of ECoG recording is comparatively simple; that for the EEG and MEG is not. The amplitude of the signal from each scalp sensor depends in part on the intrinsic intensities of the dendritic sources of the local current densities and also on the distances from those sources (Fig. 3), the orientations of the palisade of pyramidal cells as determined by the geometry of the gyri and sulci, and the conductances of the intervening skull and soft tissues. However, after the sensor array has been fixed to the head, the signal from each channel can be normalized to equal variance across the array for the data set that includes all behavioral conditions over which AM patterns are to be compared and classified. Then these several factors can be treated as invariant.

Fig. 3.

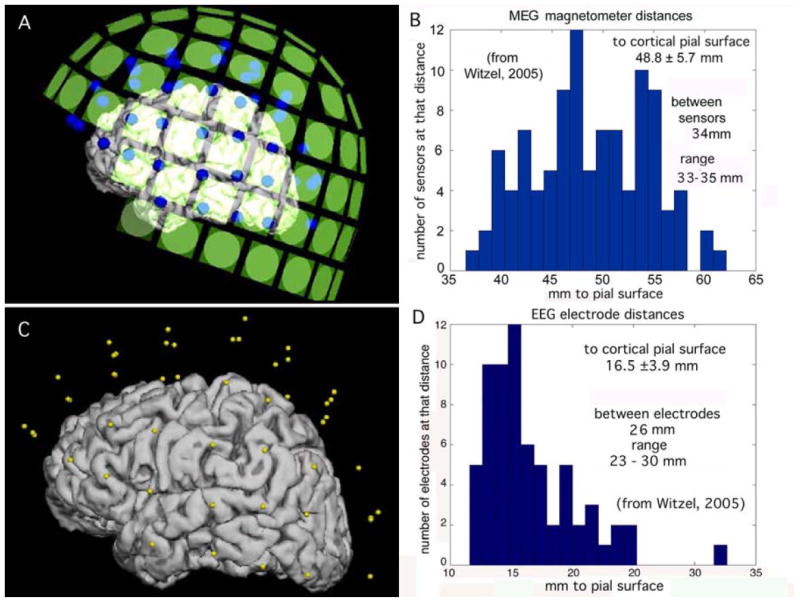
A. Left lateral view of the locations of the MEG sensors (green squares) in relation to the pial surface of the cerebral cortex. The representation for the cortex was reconstructed from MR images. B. Histogram of MEG sensor distances to the nearest point on the pial surface. C. Left lateral view of the locations of EEG electrodes (yellow dots) relative to the cortex. D. Histogram of EEG electrode distances to the pial surface

The AM patterns seen in the ECoG are stationary only for time segments lasting on the order of a tenth of a second. Each has an abrupt onset that is manifested in a temporal discontinuity of the analytic phase. When a jump in phase occurs at any one site, it tends to occur at all sites in the array, constituting what we call coordinated analytic phase differences (CAPD) that mark the onset of an AM pattern. These CAPD are also found in the EEG from 1-D arrays extending for distances up to 19 cm across the scalp (Freeman, Burke and Holmes, 2003). They suggest that comparable AM pattern formation by areas of cortex might simultaneously be manifested in electric, magnetic, and hemodynamic images from extended cortical areas comprising gyri and sulci (Fig. 4). The important lesson here is that time averages must be taken across EEG and MEG data to combine with fMRI data, but not as is commonly done by averaging the time-dependent oscillations, because the variations in frequency and phase degrade the sums. Instead, the requirement is for temporal coarse-graining by identifying the AM patterns at whatever carrier frequencies and phase gradients they might have and saving only the feature vectors as points in n-space within the designated time frame.

Fig. 4.

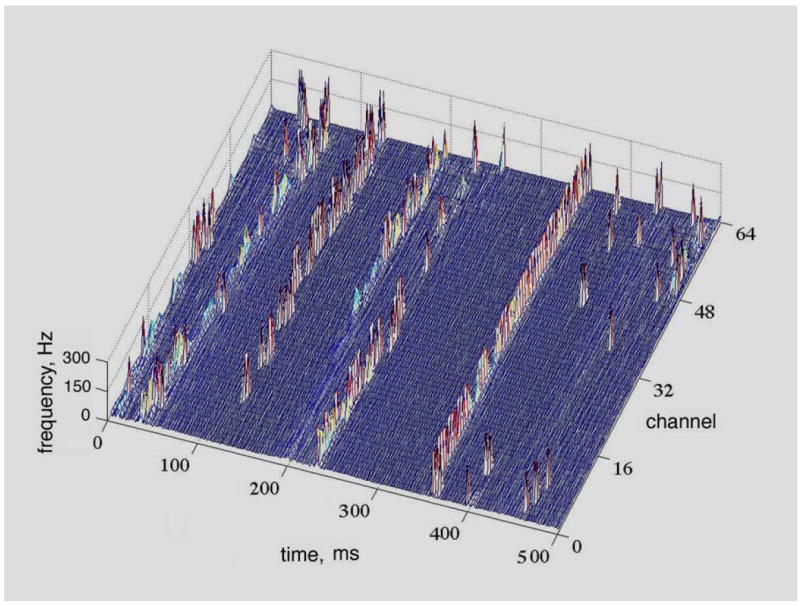
The raster plot shows the CAPD from the scalp EEG of a human volunteer at rest with eyes closed. The array was 1-D across the occipital lobe from right to left in steps of 3 mm (total length: 189 mm). Pass band = 12-30 Hz; spacing = 3 mm. CAPD were calculated at the digitizing step Δt = 5 ms and aligned in rows parallel to the left abscissa. The flat areas show the stationarity of the phase within frames. The spikes aligned in rows parallel to the right abscissa show the spatial coordination of the phase discontinuities, often across both hemispheres (Freeman, 2004a).

4C. Extrapolation to search for spatiotemporal patterns in MEG

Since the electric and magnetic fields of the MEG, EEG and ECoG share the same source in the dendritic currents of cortical pyramidal cells, we expected to find CAPD in the MEG as well. That we did not find them (Fig. 5) is quite instructive. In conformance with the law of charge conservation, dendritic currents flow in closed loops that cross the neural membranes twice. The ionic “battery” at the synapses has a high internal resistance that is matched by the high resistance at trigger zones. Most of the dendritic power is dissipated at these membrane crossings as heat, in proportion to the difference between the intracellular potential measured in millivolts compared with the extracellular potential measured in microvolts, a thousand-fold difference. The internal current is compressed into high density along the dendritic shafts in 1-D. The external current spreads widely in 3-D. A common misconception is that the extracellular current determines the EEG, while the intradendritic current determines the MEG. Actually both parts of the loop current determine the fields of both EEG and MEG, so that variations in extracellular resistance (Pfurtscheller & Cooper, 1975; Zhou & van Oosterom, 1992; Ramon, Schimpf, Haueisen, Holmes, & Ishimaru, 2004) affect both EEG and MEG, and the currents flowing in opposite directions can reduce observed fields of potential by cancellation. Fortunately, although these complex details are critical for researchers who want to localize current sources, they are not needed for multivariate classification of AM patterns of EEG and MEG.

Fig. 5.

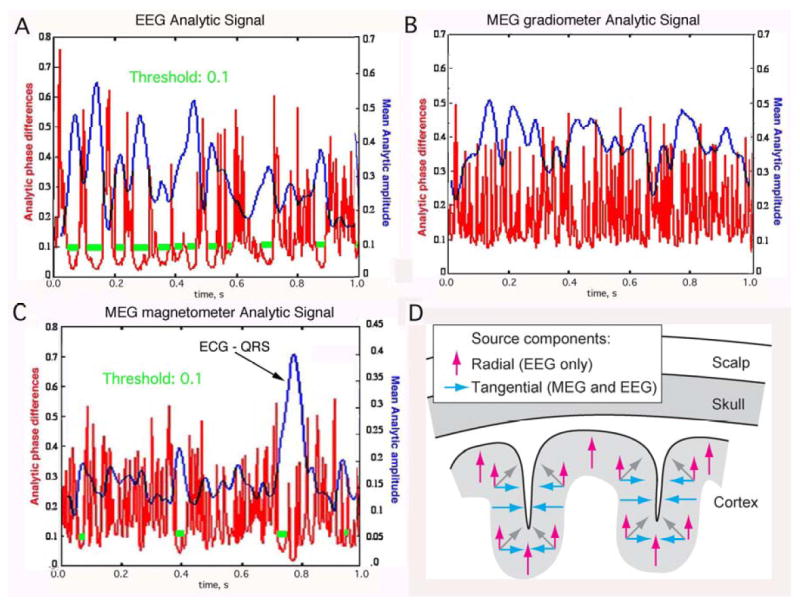
The relationships are shown between analytic amplitude (smooth curves) and phase differences (spikes) in the beta range in non-invasive EEG (A), MEG gradiometers (B) and MEG magnetometers (C). The horizontal bars indicate the segments when the analytic phase difference was below 0.1 for at least 10 msec, suggesting the presence of CAPD. The large amplitude peak in MEG magnetometer data is an artifact due to cardiac magnetic field. D. The orientations of dipoles are schematized with respect to gyri and sulci in widely synchronized oscillatory potentials in the beta and gamma ranges for EEG (vertical arrows) and MEG (horizontal arrows). The signals from tangential source components (blue or black arrows) on opposite walls of sulci tend to cancel; this could explain why CAPD were not observed in the MEG recording.

What is relevant to the missing CAPD is gyrification. The palisades of pyramidal cells are oriented perpendicular to the pial surface in both gyri and sulci. Sources of all orientations contribute to the EEG; however, the strongest contribution comes from the cortex in the crowns of gyri due to their closest distances to the scalp (Fig. 3) as well as the preferred orientation of the source currents. Conversely MEG is insensitive to source currents that are oriented perpendicular to the surface of the skull (radial sources, for example along the crests of the gyri). Therefore the strongest contribution to MEG signals typically originates from the tangentially oriented sources in sulci (Hillebrand & Barnes, 2002; Goldenholz, et al., 2008), provided that the pyramidal cells in the opposing walls are not synchronized, for in the synchronized case the opposing vectors tend to cancel. This may explain the finding that the CAPD do not appear in averaged signals derived from the MEG despite their appearance in averaged signals derived from the simultaneously recorded EEG (Fig. 5). The appearance of CAPD in EEG averages but not in MEG averages means that EEG will be especially important in providing markers for state transitions and frames in the search for AM patterns of analytic power (the maxima in the blue curves in Fig. 5 A) to combine EEG and MEG for inclusion in the construction of global state variables. Power dissipation should be combined over the full spectral range in the steps required for application of the Hilbert transform to compute the analytic power in each frequency band.

5. Conclusion

To reiterate, in the detection and description of mesoscopic AM patterns, the spatial locations on the cortical surface of the peaks and troughs of analytic amplitude and their spatial boundaries are secondary. The identification is made by the locations in n-space of the AM patterns being classified by their Euclidean distances from the centers of gravity of clusters representing the classes. Only after an AM pattern has been correlated with an aspect of cognitive behavior might it then be repeatedly induced and observed. The cortical domain within which it most probably originates can be mapped using a two-dimensional array of local electric and magnetic dipoles at the grain of the arrays, using the gyri and sulci revealed in structural MRI, so that the distributed sources contributing to an AM pattern of analytic power dissipation can be computed for each frequency range. The sum of power over the full frequency range and the time interval needed for reliable fMRI can be compared and coordinated with an fMRI map of power that has been computed with local averages corresponding to the sensor arrays.

The implication is that the brain state in any given time segment has the form of a spatial pattern of the rate of energy dissipation that is manifested in the three forms of imaging. Each state can be expressed in an AM pattern, in which every value, whether high or low, negative or positive, has equal value for purposes of description and classification. The nature of the state variables, whether electric, magnetic, or metabolic, may differ, but the value is independent of the source. The fMRI pattern in each macroscopic time interval at its time resolution provides an arena for analysis. The voxels can be selected to correspond to the neocortex and locally averaged spatially to coarse-grain the data in correspondence to the spatial resolution of the EEG and MEG data, which is determined by the sensor arrays. The high temporal resolution of the EEG and MEG gives repeated samples that cannot be summed as raw oscillations, but the clusters of points of their respective AM patterns can be accumulated over the time intervals dictated by the fMRI, so the basis for combining them is inherent in the spatial layout of the neocortex spread under the scalp and skull. The end result is the reduction of infinite brain state space to a finite measurement space that is determined by the spatial sampling imposed on the EEG and MEG data and the temporal sampling that is imposed on the fMRI data. Multivariate statistics then supports projection of the finite state space into 2-space, a graph, in which each state may appear as a point, similar states as clusters, and state transitions as trajectories between clusters. Such macroscopic patterns are described as metastability (Kelso, 1995; Bressler and Kelso, 2001), itinerant trajectories (Tsuda, 2001), and cinematographic cortical dynamics (Freeman, 2007b).