Critical Role of Substrate Conformational Change in the Proton Transfer Process Catalyzed by 4-Oxalocrotonate Tautomerase

Abstract

4-Oxalocrotonate tautomerase enzyme (4-OT) catalyzes the isomerization of 2-oxo-4-hexenedioate to 2-oxo-3-hexenedioate. The chemical process involves two proton transfers, one from a carbon of the substrate to the nitrogen of Pro1 and another from this nitrogen atom to a different carbon of the substrate. In this paper the isomerization has been studied using the combined quantum mechanical and molecular mechanical (QM/MM) method with a dual-level treatment of the quantum subsystem employing the MPW1BK density functional as the higher level. Exploration of the potential energy surface shows that the process is stepwise, with a stable intermediate state corresponding to the deprotonated substrate and a protonated proline (Pro1). The rate constant of the overall process has been evaluated using ensemble-averaged variational transition state theory, including the quantized vibrational motion of a primary zone of active-site atoms and a transmission coefficient based on an ensemble of optimized reaction coordinates to account for recrossing trajectories and optimized multidimensional tunneling. The two proton transfer steps have similar free energy barriers, but the transition state associated with the first proton transfer is found to be higher in energy. The calculations show that reaction progress is coupled to a conformational change of the substrate, so it is important that the simulation allows this flexibility. The coupled conformational change is promoted by changes in the electron distribution of the substrate that take place as the proton transfers occur.

1. Introduction

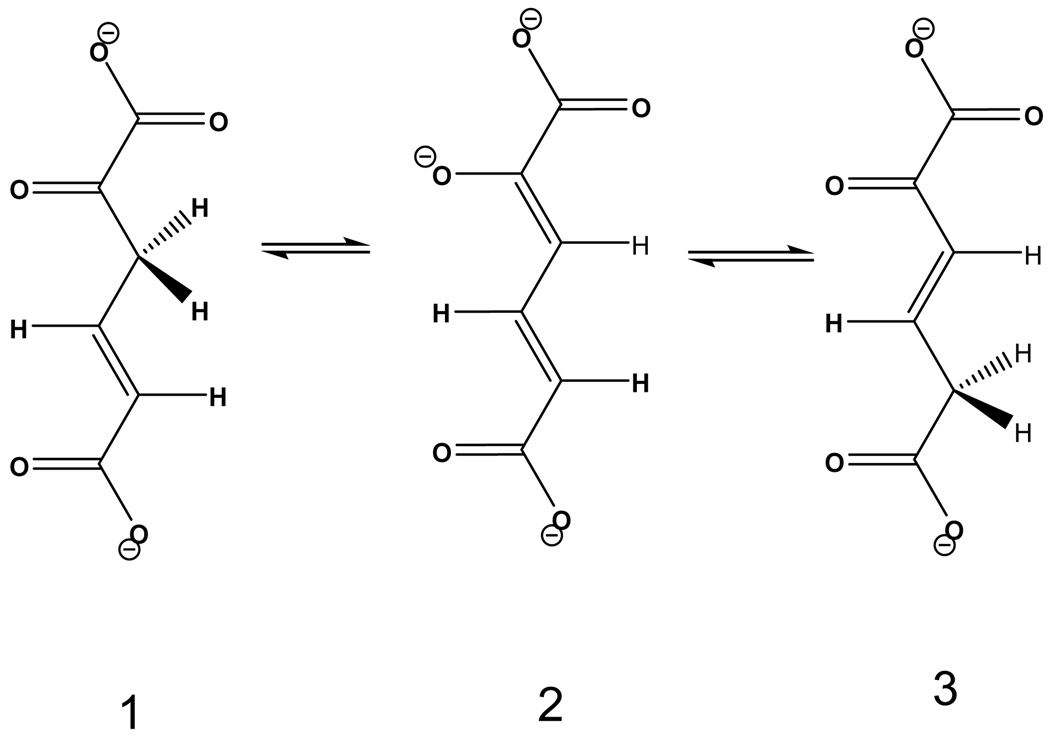
4-Oxalocrotonate tautomerase (4-OT, EC 5.3.2) catalyzes the isomeric conversion of 2-oxo-4-hexenedioate (4-oxalocrotonate, 1) into 2-oxo-3-hexenedioate (3) through the dienolate intermediate (2), which is deprotonated 2-hydroxy-2,4-hexadienedioate, also known as 2-hydroxymuconate (see Scheme I).^1–4 This enzyme is part of a degradative pathway that transforms aromatic hydrocarbons into intermediates in the Krebs cycle.⁵ Kinetic measurements have shown that this enzyme can work using as substrate either 2-oxo-4-hexenedioate or 2-hydroxymuconate.^1,6 The original studies¹ indicated that 1 is a slightly better substrate than the thermodynamically less-stable enol tautomer (2-hydroxymuconate, the protonated form of 2), whereas the newer experimental studies⁶ found the enol to be a substrate that is turned over more rapidly by the enzyme by a mechanism involving 2 as a common intermediate. The difference in the experimental results was explained⁶ by the employment of more modern purification techniques in the more recent work. The phenomenological free energy of activation for the reaction with 2-oxo-4-hexendioate at 303 K is 13.8 kcal·mol⁻¹, as computed from the measured rate constant by transition state theory.⁶

Scheme I.

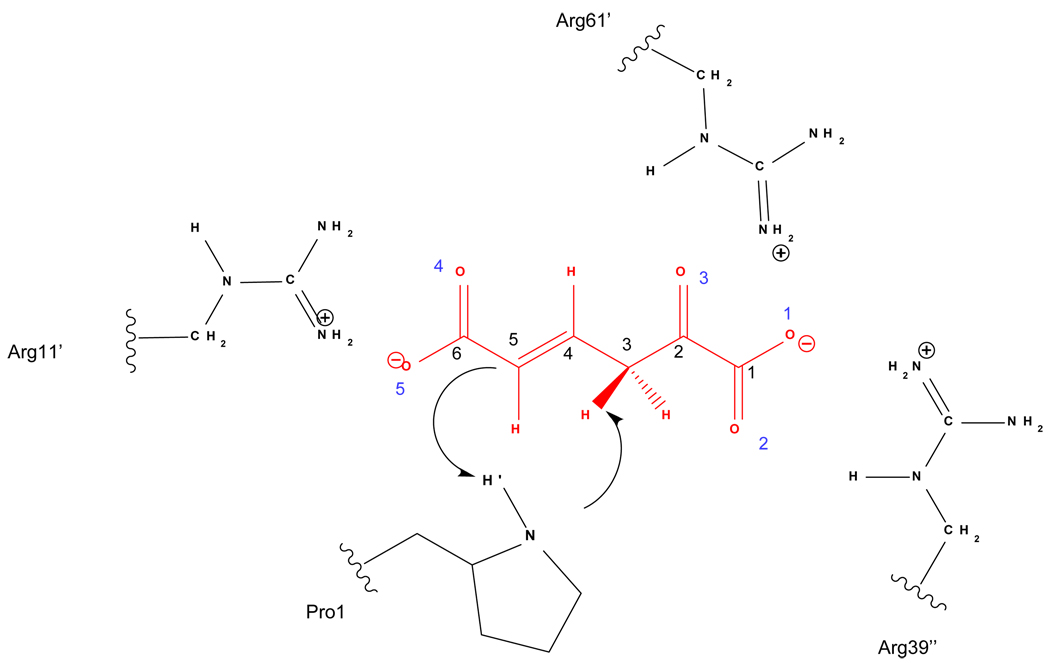
The enzyme 4-OT is a homohexamer composed of a trimer of dimers. Each monomer contains 62 amino acids.⁷ The x-ray structure shows that the active sites are placed at the dimer interfaces.^8,9 Based on experimental kinetics studies it was proposed that the reaction mechanism involves an initial proton abstraction from C3 of the substrate by a terminal proline (Pro1), and the proton is subsequently transferred to the C5 atom of the substrate (see Figure 1).^2,8,10–14 Three arginine residues (Arg11’, Arg39” and Arg61’, where the primes and double primes indicate residues from different subunits) are found in the active site of 4-OT. Mutations of these residues by alanine suggested that Arg11’ and Arg39” play a role in substrate binding and contribute to catalysis.³ In another recent study,¹⁵ mutations of these arginine residues by the isosteric, noncoded, and uncharged amino acid citrulline confirmed the critical role of Arg11’ and Arg39” in catalysis. On the other hand, mutation of Arg61’ produces only minor effects on the kinetic parameters of 4-OT.¹⁵ These studies also showed that Arg11’ has a major effect on substrate binding.¹⁵

Figure 1.

Schematic representation of the active site and the proton transfer steps from C3 to Pro1-N and from Pro1-N to C5. Atom numbering of the substrate (carbon atoms in black, oxygens in blue) is also shown.

Several theoretical studies have been devoted to the chemical steps in 4-OT. In a series of publications Cisneros et al. obtained the minimum energy path for the reaction in the active site and then obtained an energy profile for each of the two steps by an iterative reaction path optimizer.^6,16–19 These investigations corroborated the reaction mechanism proposed in Figure 1 where Pro1 acts as a proton shuttle. The second step to protonate the C5 atom of the enolate species was proposed as the rate-limiting step although the free energy barrier was found to be only 1.5 kcal/mol higher than that for the first proton abstraction step. However, it appears that the pro-S hydrogen on the C3 atom of the substrate was used in those calculations on the first proton transfer reaction,^6,16–19 whereas Whitman and coworkers established that it is the pro-R proton that is abstracted in 4OT (see below).¹⁰ Since the enzymatic process is stereospecific, the good agreement both in computed barrier and in mutation effects with experiments could be due to the use of a fixed reaction path obtained by energy optimization techniques, which does not fully explore the coupled conformational fluctuations between the substrate and the protein environment. Nevertheless, hydrogen bonding interactions with the protein backbone (in particular Leu8’) were proposed to contribute to transition state stabilization.¹⁷ Similar conclusions were reached by Tuttle et al. by means of molecular dynamics simulations, followed by high-level energy calculations with localization of stationary structures.^20,21 The authors concluded that the orientation and conformation of the substrate in the active site are crucial in order to obtain computational results in agreement with experimental findings. In contrast, Sevastik et al.,²² employing a reduced active site model and a significantly higher level of quantum mechanical model, concluded that the first step was the rate-limiting process, whereas the intermediate (2-hydroxymuconate) was much more stable than previously predicted.

Deeper insight can be obtained by considering an ensemble of reaction paths in each of which the dynamics of the protein is coupled to that of the substrate to include the dependence of the substrate conformations and orientations on the progress of reaction. This can be further combined with quantum mechanical treatments of substrate electronic structure, active-site vibrations, and tunneling. The València group has recently presented an efficient way^23,24 of including high-level electronic-structure corrections in the calculation of a reactive free energy profile, which is the potential of mean force (PMF) as a function of the reaction coordinate. The advantage of this strategy is that the flexibility of the full system is incorporated, and configurational changes of the substrate can be coupled to the advance of the reaction. In the present article we employ this method to include a high level of quantum mechanical electronic structure in the description of the active site along with the treatment of the dynamics by ensemble-averaged variational transition state theory (EA-VTST),^25–27 including quantized vibrations and multidimensional tunneling.

In the following, we first present the details of the computational methodology used in the present study; this is followed by results and discussion. Finally, we summarize main findings from this investigation.

2. Metholodogy

2.1. Overview of the method

In this subsection, we discuss some general questions related to the mechanism, the choice of reaction coordinates, the role of the protein rearrangement coordinates or water movement that may be coupled to the reaction path, and statistical averaging over reaction paths. We then review the essential elements that we designed into the present dynamical treatment to provide a reliable treatment of the dynamics when one does not wish to assume that the mechanism and the reaction coordinate are known in advance. Then in Sections 2.2–2.5 we review the details of the method and present its application to the reaction catalyzed by 4-oxalocrotonate tautomerase.

When a reaction involves charge transfer, such as a proton transfer, hydride transfer, or electron transfer, or possibly the transfer of two or more charged particles, the question arises of what is the best reaction coordinate. First we consider the issue of a chemical reaction coordinate (such as a coordinate defined in terms of a transferring proton, or in general some function of the nuclear coordinates of the atoms participating actively in the chemical process) vs. a collective bath coordinate (where the “bath” may be the protein or solvent or both); then we will consider the specific choice of chemical coordinate (for example, a synchronous or sequential motion of two protons).

First consider solvent participation. For example, for a weak-overlap electron transfer in a polar solvent, it is well known that the best reaction coordinate is a solvent polarization coordinate.^28–30 This kind of coordinate is also applicable to some charge transfer processes in proteins.^31–33 Solvent polarization coordinates are often described by using energy gaps computed with non-Born-Oppenheimer diabatic states,³⁴ for example, valence bond configurations.³⁵ However, when the charge transfer is accompanied by nuclear transfer, one can also describe the process by nuclear coordinates,³³ and usually the Born-Oppenheimer approximation is valid, which is a great simplification.

Choosing a reaction coordinate is equivalent to choosing a sequence of generalized transition states, which can be taken as hypersurfaces normal to the reaction coordinate. In principle one can use any reaction coordinate, provided that one uses an accurate transmission coefficient, which depends on the choice of reaction coordinate. The transmission coefficient has two major contributions, one factor (to be called the dynamic recrossing transmission coefficient, or—for short—the recrossing factor) that accounts for systems that reach the transition state without reacting or that reach the transition state more than once in a single reactive event, and another factor to account for quantum effects (primarily tunneling) on the reaction coordinate motion. When the recrossing factor differs greatly from unity, calculating it entails as much work as doing a full dynamics calculation. Thus we seek reaction coordinates that have a transmission coefficient close to one, at least in the absence of large tunneling effects. In some cases, very similar results can be obtained by the two kinds of reaction coordinates (chemical or bath) with the recrossing factor being no smaller than about 0.5.^33,36 We will use a chemical reaction coordinate in the first stage of the present study.

The existence of two possible proton transfers raises new issues, especially if their transfer can be synchronous or sequential. One can determine the mechanism by calculating a two-dimensional potential of mean force^37–39 and comparing the free energy barriers along sequential and synchronous paths from reactants to products. A simpler approach is to calculate a two-dimensional potential energy surface;^24,40 if the energy barriers for different paths differ greatly the extra effort of calculating free energies rather than potential energies along the paths is not required. In the present work we used the latter approach. It turns out that a particular sequential path has a much lower potential energy barrier than either the other sequential path or the synchronous path, so we calculated only a one-dimensional free energy profile along the lower-energy path of the first-stage reaction coordinate. Note though that although the path is one-dimensional, at any value of the progress variable that determines distance along the path, the system samples a canonical ensemble of geometries and conformations for all degrees of freedom except the reaction coordinate, which is locally the same as the progress variable in this work (therefore, as usual, we will call the progress variable the reaction coordinate or distinguished reaction coordinate in the rest of this exposition). Thus there is no bias in the sampling of possible reactive events.

As mentioned above, at a given value of the reaction coordinate, the system samples many conformations, which lie along different reaction valleys on the potential energy surface. In ensemble-averaged variational transition state theory^25–27 (EA-VTST), which is used in the present work (as described further in section 2.5), we sample an ensemble of these paths and their associated reaction valleys. Each reaction valley has an associated reaction coordinate; in stage 2 of the calculation this ensemble of reaction coordinates replaces the earlier single chemical reaction coordinate used in stage 1. Each of these reaction coordinates is associated with the distance along the reaction valley in a particular conformation; but rather than being pre-determined as a chemical reaction coordinate, it is now optimized in 3N₁ degrees of freedom (where N₁, the number of primary atoms, is 51 in the present study). Furthermore, since we consider an ensemble of reaction coordinates, each having a different configuration of the rest of the substrate-enzyme-solvent system, the effective reaction coordinate also depends on all the other coordinates. This allows the whole system to participate in the reaction coordinate so that what started as a purely chemical reaction coordinate now effectively incorporates all the degrees of freedom of the system. For several enzymatic reactions, accurate kinetic isotope effects have been calculated with this scheme,^27,41 thereby validating this approach.

2.2. The system

The initial coordinates were taken from the x-ray crystal structure 1BJP at 2.4 Ǻ resolution.⁹ The structure is a trimer of dimers and we considered one of these dimers for our calculations. In each monomer the crystal structure contains a total of 62 amino acids residues, together with the inhibitor 2-oxo-3-pentynoate, which is replaced manually by 4-oxalocrotonate in our study. The coordinates of the hydrogen atoms of the protein were determined using the HBUILD facility of the charmm package.⁴² All the ionized groups were set to their normal ionization state at pH 7. Thus, all Asp and Glu residues are in anionic form and Lys and Arg residues are positively charged. The protonation states of His residues are set according to neighboring hydrogen bonding interactions; they are kept neutral unless they are directly hydrogen bonded to an Asp or a Glu residue. Once all hydrogen atoms were properly added to the heavy atoms of the X-ray PDB structure, the system was solvated with a sphere of 30 Å containing pre-equilibrated water molecules; water molecules that are within 2.5 Ǻ of any non-hydrogenic atom were deleted. The resulting system was resolvated four more times using different relative orientations between the protein and the water sphere to ensure good solvation of the system. Then, the orientations of the solvent water molecules were optimized by energy minimization, which was followed by geometry optimization of protein within 24 Ǻ to the center of the system, which is defined at the C4 atom of the substrate (following the atom numbering presented in Figure 1). The rest of the system was kept frozen during all the calculations.

After the initial set-up of the solvated protein system, a short molecular dynamics run (10 ps with a time step of 1 fs) was carried out to relax the positions of the water molecules. Then, the system was partitioned into a QM region consisting of the substrate, the Pro1, and part of the Ile2 (33 atoms) and an MM region containing the rest of the system (the enzyme, composed of 1939 atoms in addition to those treated quantum mechanically, and 3689 water molecules, for a total of 13006 molecular mechanical atoms). The QM subsystem was described using the Austin model 1 (AM1) semiempirical molecular-orbital Hamiltonian,⁴³ while the MM part was modeled by using the charmm force field⁴² for the enzyme and the TIP3P potential⁴⁴ for water molecules. The QM and the MM parts were connected by the generalized hybrid orbital (GHO) method.⁴⁵ The AM1/MM energy function may be expressed in the usual way as⁴⁵

$$E_{\mathit{\text{AM}}1/\mathit{\text{MM}}}=E_{\mathit{\text{QM}}}+E_{\mathit{\text{MM}}}+E_{\mathit{\text{QM}}/\mathit{\text{MM}}}$$ (1)

where the three terms correspond to the energies of the quantum mechanical region, the MM region, and their interaction, respectively.

Finally, the full system was heated to 300 K by a series of short dynamic simulations (10 ps), followed by a longer molecular dynamics simulation (200 ps) to ensure the equilibration of the system.

2.3. The energy function

The final structure obtained from the molecular dynamics calculation was employed as the starting point for combined QM/MM simulations, employing the AM1/MM potential energy surface (PES). The CHARMM program⁴² was used to explore the dependence of the potential energy surface on two coordinates (R_i). We considered two elementary chemical steps: a proton transfer from the C3 atom of the substrate to the nitrogen of Pro1 and a proton transfer from this atom to the C5 atom of the substrate. Each of the proton transfers is described by a distinguished coordinate defined as the difference of the distances from the migrating hydrogen atom to the donor (r_D–H) and the acceptor (r_A–H) atoms:

$$R_1=r_{C3-H}-r_{N-H}$$ (2a)

$$R_2=r_{N-H\text{'}}-r_{C5-H\text{'}}$$ (2b)

These coordinates are reasonable reaction coordinates because they change smoothly during the reaction steps.

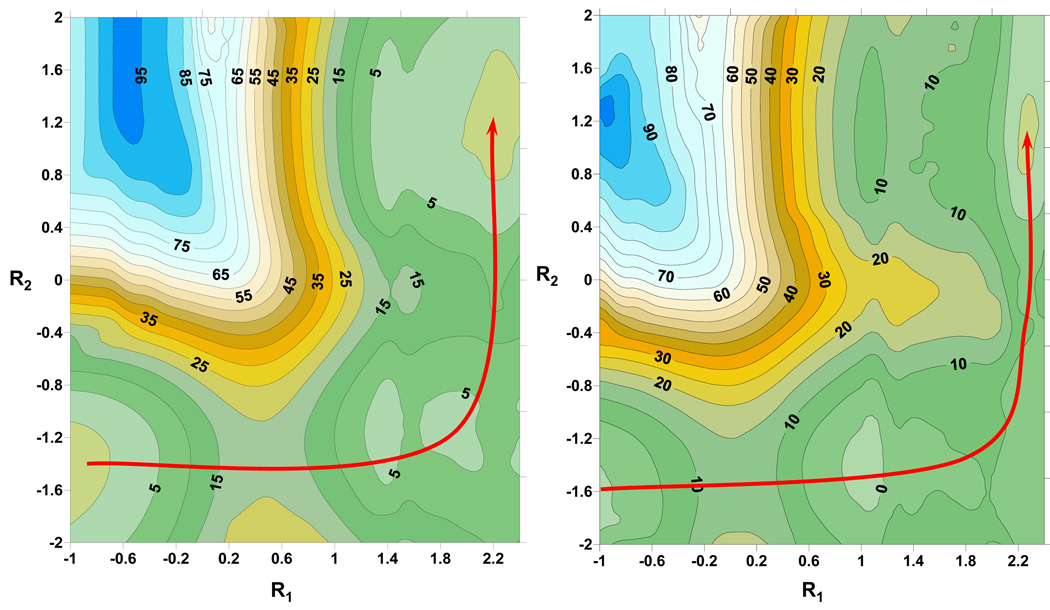
Figure 2 shows the results obtained using the combined AM1/MM potential; in this figure the proton transfer coordinates were kept at a desired reference value by using the RESDISTANCE keyword in charmm to define the reaction coordinates while the rest of coordinates of the flexible region were relaxed. The figure shows that the AM1/MM optimizations yield a stepwise mechanism where the proton is first transferred from the substrate to Pro1 and then transferred back to the substrate. This result is in agreement with all previous calculations on this system.^{6,16,17,20–22}

Figure 2.

Potential Energy Surfaces calculated for the full chemical process at the AM1/MM level (left) and including MPW1BK/6–31+G(d,p) 2-D perturbed interpolated corrections (right). Relative energies in kcal·mol⁻¹ and coordinates in Å. The isopotential lines are shown each 5 kcal/mol.

Although the qualitative features in Figure 2 obtained using the semiempirical AM1/MM method are very good, quantitative results can be further improved using a higher level (HL) of theory. To this end, we used a new energy function defined in terms of interpolated corrections as:

$$E=E_{\mathit{\text{AM}}1/\mathit{\text{MM}}}+S\left[\mathrm{\Delta }{E}_{\mathit{\text{LL}}}^{\mathit{\text{HL}}}(R_1,R_2)\right]$$ (3)

where S denotes a two-dimensional spline function, and its argument $\mathrm{\Delta }{E}_{\mathit{\text{LL}}}^{\mathit{\text{HL}}}(R_1,R_2)$ is a correction term taken as the difference between a high-level (HL) energy of the QM subsystem and the low-level (LL) result (AM1 in this case). Details of the interpolation procedure have been given elsewhere.^23,24 The high level theory was chosen from two density functionals^46,47 that best reproduce the experimental data⁴⁸ (when available) or those from Moller-Plesset second-order perturbation theory,⁴⁹ coupled cluster (CCSD(T)) theory,⁵⁰ and the complete basis set⁵¹ (CBS) and Gaussian-3⁵² composite methods for the reference reactions (see Supplementary Material). We finally selected the MPWB1K/6–31+G(d,p)⁴⁷ density functional as a good compromise between accuracy and computational efficiency.

Structures of the low-level PES were selected to obtain a set of discrete values of the correction energy as the difference of the relative QM energy, in the presence of the MM charges, obtained with the high- and low-level methods. These calculations were carried out using Gaussian03 program.⁵³Figure 2 also shows the corrected PES, and this is qualitatively similar to the AM1/MM PES; both show a stepwise mechanism where the proton is first transferred from C3 to Pro1 and thereafter to C5. Differences are observed in the energetics because the potential energy barriers corresponding to the corrected surface are lower than the ones observed on the uncorrected surface. The intermediate and the product are also stabilized relative to the reactants on the corrected surface

2.4. Potentials of Mean Force

The potential energy surfaces presented in Figure 2 suggest that the isomerization reaction catalyzed by 4-OT takes place by a stepwise mechanism, as shown in earlier investigations. Consequently, the free energy reaction profiles, also called the potentials of mean force (PMF),^54–56 for the two proton transfer reactions can be determined separately by following the respective proton transfer reaction coordinates. We used the umbrella sampling technique to construct each PMF by a series of molecular dynamics simulations in which the reaction coordinate was restrained at a sequence of values of the reaction coordinate, covering the transformation from the reactant state to the intermediate, and from the intermediate to the final product state.⁵⁶ The PMFs are computed using both the spline-corrected and the uncorrected energy functions. To ensure the connectivity between the PMFs for the two reaction steps, umbrella sampling simulations were started in both cases from the reaction intermediate.

Different range of values of the variables (R₁ and R₂ in each of the PMFs) were sampled in a series of biased simulation windows.⁵⁷ For this purpose we used a combination of a harmonic potential, with a force constant of 20 kcal mol⁻¹ Ǻ⁻², and a bias-potential designed to flatten the sampled free energy profile along the reaction coordinate.^58,59 This combination has been shown to be very efficient for obtaining fast convergence in the probability distribution of the reaction coordinate in a sequence of simulation windows. Then, these probability distributions were unified by using the weighted histogram analysis method (WHAM)⁶⁰ to construct the full distribution function from which each PMF was obtained. The simulation windows were run in a consecutive way starting from the intermediate structure towards the reactant or the product state, respectively. Each window was started from the equilibrated configuration of the preceding window and consisted of 10 ps equilibration, which is followed by 80 ps of production. This was long enough to sample a wide range of structures at a reference temperature of 300 K. All molecular dynamics simulations were performed by using an integration time step of 1 fs. The canonical ensemble (NVT) was used for all the simulations, thus yielding estimates of the Helmholtz free energy changes, which for condensed-phase reactions can be considered equivalent to Gibbs free energy variations.

For the PMF associated with the first proton transfer, characterized by the distinguished coordinate R₁, the total number of windows employed to cover the whole range of the reaction coordinate from the intermediate to the reactants was 21, starting at 2.4 Ǻ and finishing at −1.6 Ǻ, with an increment of −0.2 Ǻ. For the PMF associated with the second proton transfer, specified by the distinguished coordinate R₂, the total number of windows employed to cover the whole range of the reaction coordinate from the intermediate to the products was 18, starting ar −1.6 Ǻ and finishing at 1.8 Ǻ, with an increment of 0.2 Ǻ.

The potentials of mean force obtained from molecular dynamics simulations correspond to classical free energy changes. To incorporate the contributions from quantized vibrations for all degrees of freedom except the one corresponding to the distinguished reaction coordinate, we add the difference between the quantum mechanical and classical mechanical (CM) free energies for the 3N₁-7 modes where N₁ is the number of quantized atoms in the primary zone. The resulting PMF is called the quasiclassical (QC) potential of mean force since quantum mechanical tunneling associated with the reaction coordinate is excluded. The relationship between the QC and CM potentials of mean force is given by eq 4:^25,26

$$W_{\text{QC}}(R_i)=W_{\text{CM}}(R_i)+\mathrm{\Delta }{W}_{\mathit{\text{vib}}}(R_i)$$ (4)

where W_QC(R_i) is the QC PMF, W_CM(R_i) is the CM PMF from umbrella sampling simulations, and ΔW_vib(R_i) is the difference between the quantum and classical vibrational free energies for the 3N₁-7 modes orthogonal to the reaction coordinate R_i.

To compute ΔW_vib (R_i) , we first define a quantum primary zone of N₁ atoms, consisting of the atoms that are used in the definition of the reaction coordinate and those that are most strongly coupled to them.^25,26,39 Then, we carry out instantaneous normal-mode analysis within the harmonic approximation for the primary zone atoms.^25,26,39 For the 4-OT reaction, the primary zone atoms include the substrate, the proton acceptor and donor residue Pro1 and the ionizable groups of Arginines 11’, 39” and 61’ in the active site. This yields 51 atoms. The rest of the enzyme-solvent system is called the secondary subsystem or the bath; the number of atoms in the secondary subsystem is 12988. The generalized normal-mode frequencies are averaged over 150 structures obtained from each of the simulation windows corresponding to reactants, the intermediate of the overall reaction, which is the product for the first proton transfer step and the reactant state for the second proton transfer reaction, and transition states for the proton transfer reactions. These frequencies are then used to estimate ΔW_vib(R_i ).⁶¹

The quasiclassical free energy of activation $\mathrm{\Delta }{G}_{\mathit{\text{QC}}}^{\mathit{‡}}$ is:²⁵

$$\Delta G_{\mathit{\text{QC}}}^{\mathit{‡}}=W_{\mathit{\text{QC}}}\mathit{(}{R}_i^{\mathit{‡}}\mathit{)}-\mathit{[}{W}_{\mathit{\text{QC}}}\mathit{(}{R}_i^R\mathit{)}+G_{F,\mathit{\text{QC}}}\mathit{]}+\Delta C\mathit{(}{R}_i\mathit{)}$$ (5)

where $R_i^{‡}$ and $R_i^R$ specify the reaction coordinate at the transition state (the maximum position in W_QC(R_i) ) and at the reactant state for reaction i, respectively, G_F,QC is the quantum mechanical vibrational free energy of the reactant state to account for the mode, F, that correlates with the distinguished coordinate R_i , and ΔC(R_i ) is a Jacobian correction (which is neglected) due to the use of a non-Cartesian reaction coordinate. All calculations were carried out using charmmrate,⁶² which is based on an interface of the programs charmm ⁴² and polyrate.⁶³

2.5. Tunneling and recrossing

Final evaluation of the rate constant is carried out by canonical variational theory^64–66 where quantum effects and recrossing are incorporated through an ensemble-averaged transmission coefficient γ. The first order rate constant is thus obtained as:

$$k^{\mathit{\text{CVT}}}=\gamma \frac{k_{B}T}{h}{e}^{-\Delta G_{\mathit{\text{QC}}}^{\mathit{‡}}/\mathit{\text{RT}}}$$ (6a)

The transmission coefficient γ is obtained as an ensemble average over 21 reaction paths (j = 1, 2, …, 21) of the primary zone corresponding to transition-state configurations obtained during the umbrella sampling calculation. Each individual γ_j consists of two factors, that is,

$${\mathrm{\gamma }}_j={\mathrm{\Gamma }}_j{\mathrm{\kappa }}_j,$$ (6b)

with one factor, Γ_j, being an approximation to the dynamic recrossing transmission coefficient and the other factor, κ_j, resulting from tunneling at energies below the effective barrier and from nonclassical diffractive reflection from the barrier top at energies above the effective barrier.^25,27,39 The ensemble averages of γ_j , κ_j, and Γ_j are denoted by γ, <κ>, and<Γ>, respectively. Each of the Γ_j is a function of the difference in generalized free energy of activation between its maximum on the individual reaction path obtained for a given frozen secondary subsystem and its value at the point corresponding to the maximum of the PMF obtained when the environment is in equilibrium.^25,61,67,68 On the other hand, each κ_j is calculated with the microcanonical optimized multidimensional tunneling method, involving a variational choice between small-curvature and large-curvature tunnelling.^27,69–71 Finally, the phenomenological activation free energy can be obtained including the contribution of the transmission coefficient:

$$\Delta G_{\mathit{\text{phen}}}^{\mathit{‡}}=-\mathit{\text{RT}}\mathit{\text{ln}}\gamma \text{+}\Delta {\text{G}}_{\mathit{\text{QC}}}^{\ne }=\Delta G_{\gamma }+\Delta G_{\mathit{\text{QC}}}^{\mathit{‡}}$$ (7)

3. Results and Discussion

3.1. Substrate Conformation

Extensive biochemical, mutagenesis, and structural studies by Whitman and coworkers established that the enzyme 4-OT catalyzes the isomerization of (E)-2-oxo-4-hexenedioate to (E)-2-oxo-3- hexenedioate by a one-base mechanism through a formally suprafacial 1,3-hydrogen migration, and the specific base has been identified as Pro1, which was confirmed by crystal structures.^9,72 Furthermore, the stereochemistry of the 4-OT catalyzed proton transfer reactions was established by two isotopic labeling experiments carried out in ²H₂O. Specifically, Whitman and coworkers showed that 4-OT converts 2-hydroxymuconate, the enol tautomer of the substrate, into (5S)-[5-²H]-2-oxo-3-hexenedioate, and the dienol compound, 2-hydroxyl-2-pentadienoate (the 6-decarboxy substrate) into (3R)-[3-²H]-2-oxo-4-pentenoate, both in ²H₂O, establishing that the pro-R proton at the C3 position is first abstracted by Pro1 and subsequently delivered to the Re face at the C5 position.¹⁰

The experimental findings provide steric and conformational constraints in the construction of an initial enzyme-substrate Michaelis complex for modeling the enzyme mechanism. A further clue was revealed in the early studies of Whitman et al.¹⁰ who showed that both the unusually stable dienol 2-hydroxymuconate and its keto-tautomer (E)-2-oxo-4-hexenedioate are substrates for 4-OT, but the latter is better than the dienol species. This led to the currently accepted mechanism that 4-OT is an isomerase, catalyzing the conversion of 2-oxo-4-hexenedioate into 2-oxo-3-hexenedioate with the dienolate of 2-hydroxymucoate as the intermediate. Interestingly, the dienolate intermediate can adopt either 2E or 2Z configuration about the C2-C3 double bond, and this difference can have significant consequences on the reaction mechanism. These conformations of the carbon chain of the substrate differ by rotation about the C2-C3 bond, which is a single bond in the reactant state but a double bond in the intermediate. Cisneros et al.^16,17 constructed an enzyme-substrate complex with an all-anti disposition of the carbon chain for the substrate, yielding the 2Z configuration for the dienolate intermediate. They obtained a free energy of activation of 16.5 kcal/mol by optimization of a minimum energy path, in reasonable agreement with experiment (13.9 kcal/mol). Using a similar method and their initial coordinates, Tuttle and Thiel reproduced the calculations of Cisneros et al.^16,17 (model B)^20,21 and also constructed two different Michaelis complex models (A and C) based in part on the enzyme-inhibitor structure containing covalently linked 2-oxo-3-pentynoate, which does not have the 6-carboxylate group. Strcutures A and C were both given a syn conformation of the C2-C3 bond of the carbon chain of the substrate and a 2E configuration for the intermediate. In model A,^20,21 which kept the Arg11' sidechain conformation found in the crystal structure, the computed barrier was 13 kcal/mol greater than the experimental value, but when the Arg11' sidechain orientation was flipped by 180° in model C, the computed barrier are in accord with experiment.^20,21

Examination of the structure of the active site indicates that the substrate is not able to establish strong hydrogen-bonding interactions with Arg11' in an all-anti conformation of the carbon chain, contrary to the experimental finding that Arg11' plays an important role in substrate binding.^3,15 The sidechain conformation change in model C of ref. 21 results in stronger binding interactions with the substrate than that in model B,^20,21 consistent with mutation studies. Both groups used energy minimization techniques to locate a single minimum energy path. Thus, protein and substrate flexibility and entropic contributions were not considered. Furthermore, it appears that in model B^20,21 and in the original work of Cisneros et al.,^16,17 the pro-S proton was abstracted by Pro1 and a proton was transferred to the C5 atom from the Si face of the dienolate intermediate, opposite to the experimental assignment.¹⁰ Remarkably, employing the pro-S reaction, the effects of amino acid mutation on 4-OT kinetics were correctly predicted. In view of the excellent stereoselectivity in enzymatic reactions, the seemingly good agreement between computation and experiment is surprising.

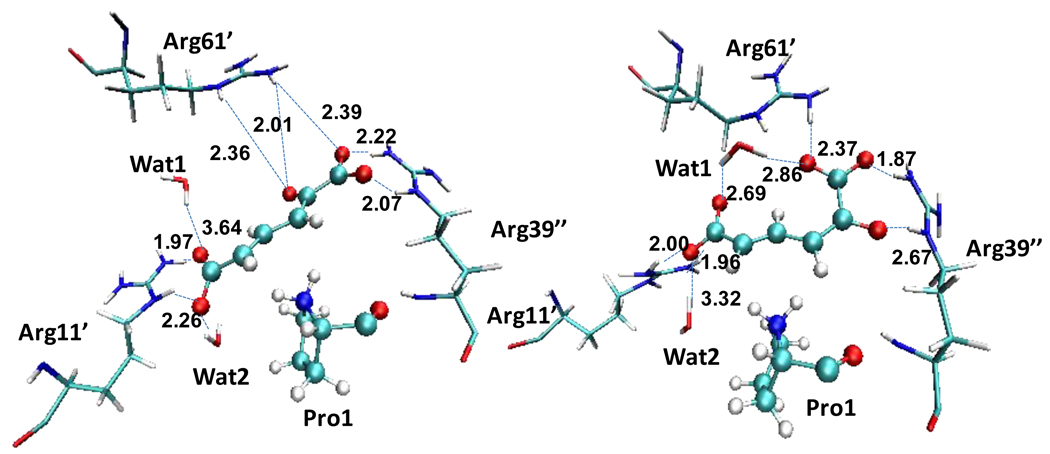
In our preliminary calculations of the potential of mean force for the initial proton abstraction from C3, we noticed that the dienolate intermediate can adopt either a 2Z configuration, similar to that constructed by Cisneros et al., or a 2E configuration, corresponding to the conformation found in the inactive enzyme crystal structure. To explore the conformational flexibility, we further simulated the intermediate state in these two different conformations. MD simulations of these two conformational states showed no transitions between them during 200 ps, indicating that both configurations could be stable forms of the reaction intermediate. Snapshots of these two conformations of the intermediate state are shown in Figure 3, where the average values of the hydrogen bond distances between substrate oxygen atoms and arginines 11’, 61’ and 39” are also provided.

Figure 3.

(2Z,4E) and (2E,4E) configurations of the reaction intermediate. Hydrogen bond distances to the substrate oxygen atoms are given in Å. Carbon atoms: light blue, nitrogen: dark blue, oxygen: red, hydrogen: white.

Starting from the final structures of the initial exploratory simulations of the two intermediate conformational states, we carried out two sets of umbrella sampling simulations to obtain the PMF along the reaction coordinate R₁ in the direction of proton transfer from Pro1 to the C3 carbon of the intermediate, yielding the pro-R hydrogen in the substrate. Analysis of the Michaelis structures at the end of the umbrella sampling calculations shows that both sets of simulations resulted in the same substrate conformation, corresponding to the (4E)-2-syn-2-oxo-4-hexenedioate substrate (where syn refers to the carbon chain). This suggests that starting from the same reactant state and following the reaction coordinate R₁ one could obtain at least two different intermediate conformations. The ratio of the concentrations of the two conformational states is under kinetic control because they cannot be interconverted due to the C2-C3 double bond character of the dienolate intermediate state.

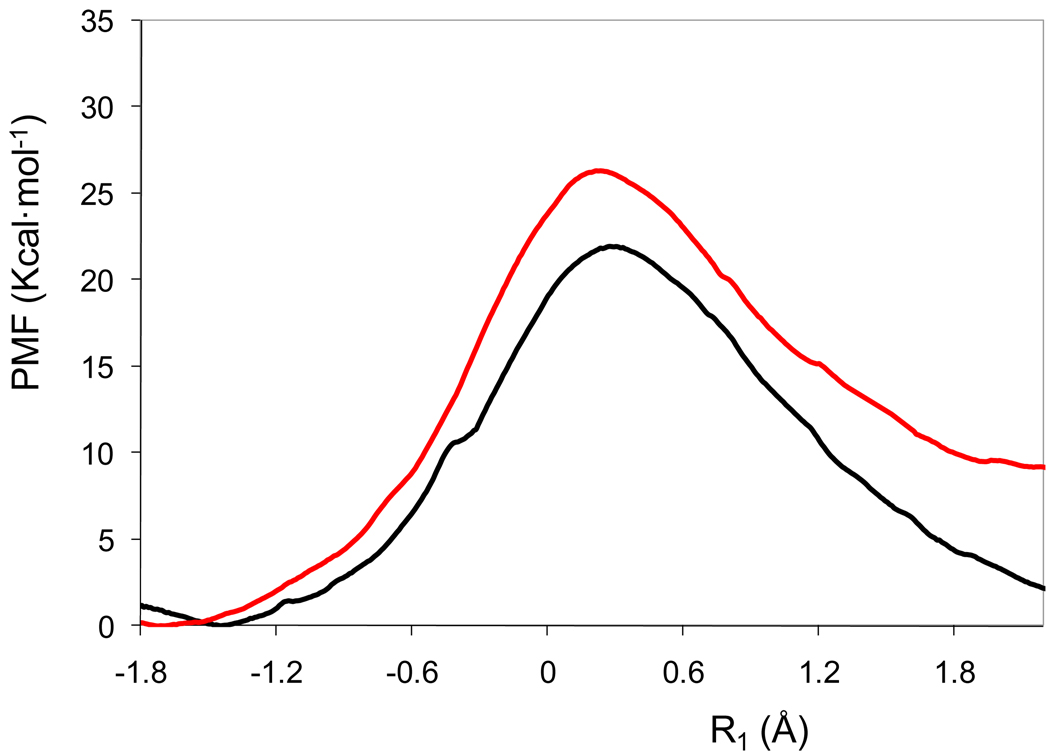
The PMFs for the two reaction paths depicted in Figure 4 show that the (2Z,4E) configuration of the intermediate is more stable by about 6.5 kcal/mol than the (2E,4E) configuration. Furthermore, the free energy barrier is 4.5 kcal/mol smaller for the reaction path leading to the former intermediate than that for the (2E,4E) dienolate species, and this suggests that more than 99.9% of the trajectories produce the more stable (2Z,4E) intermediate in the active site of 4-OT. Significantly, the free energy profiles shown in Figure 4 suggest that the initial (4E)-2-syn conformation of the substrate about the C2-C3 single bond undergoes a conformational change in the course of the proton abstraction reaction to yield an intermediate dominantly in the (2Z,4E) configuration. The driving force for the conformational change may be the development of greater negative charge on the O3 oxygen atom; the oxygen atom of this group is more negatively charged when the pro-R proton on the C3 carbon is transferred to the basic, catalytic residue Pro1. We find that the averaged Mulliken charge on this atom increases from −0.36 a.u. in the reactant state to −0.69 a.u. in the intermediate state. As a result, this oxygen atom in the (2Z,4E) conformation can be better solvated by two strong hydrogen bonds with Arg61’, with averaged distances of 2.01 and 2.36 Å. On the other hand, in the (2E,4E) conformation, the dienolate oxygen atom establishes one hydrogen bond with Arg39”, with an averaged distance of 2.67 Å.

Figure 4.

Potentials of mean force corresponding to the pro-R proton transfer from the C3 atom of the substrate to Pro1, leading from the 2-syn substrate to the (2Z,4E) form of the intermediate (black line) or to the (2E,4E) one (red line). These PMFs do not include the effect of quantizing the vibrations.

This conformational change is already advanced in the simulation window corresponding to the transition state, when R₁ is approximately 0.25 Å, with the proton closer to the nitrogen atom of Pro1 than to the carbon atom of the substrate. The averaged value of the C1-C2-C3-C4 dihedral angle in this simulation window is approximately 150 degrees. As the value of the reaction coordinate further increases, the conformational change is driven to completion, and the substrate is always found in the (2Z,4E) conformation. It is interesting to note that a single simulation started in the reactant state would not be sufficient to detect this hysteresis problem associated with the proton transfer coordinate employed. Simulations in the reactant state show the C1-C2-C3-C4 dihedral angle fluctuates in the range of −60 to +60 degrees. Small differences in this dihedral angle at critical values of the proton transfer coordinate can determine the conformation reached in the intermediate state. We also found that it was possible to reach a different intermediate configuration, namely (2E,4Z), starting from the same (4E)-2-syn conformation of the substrate and using the same reaction coordinate. This path leads to an even less stable intermediate and also presents a higher free energy barrier.

3.2. Potentials of Mean Force

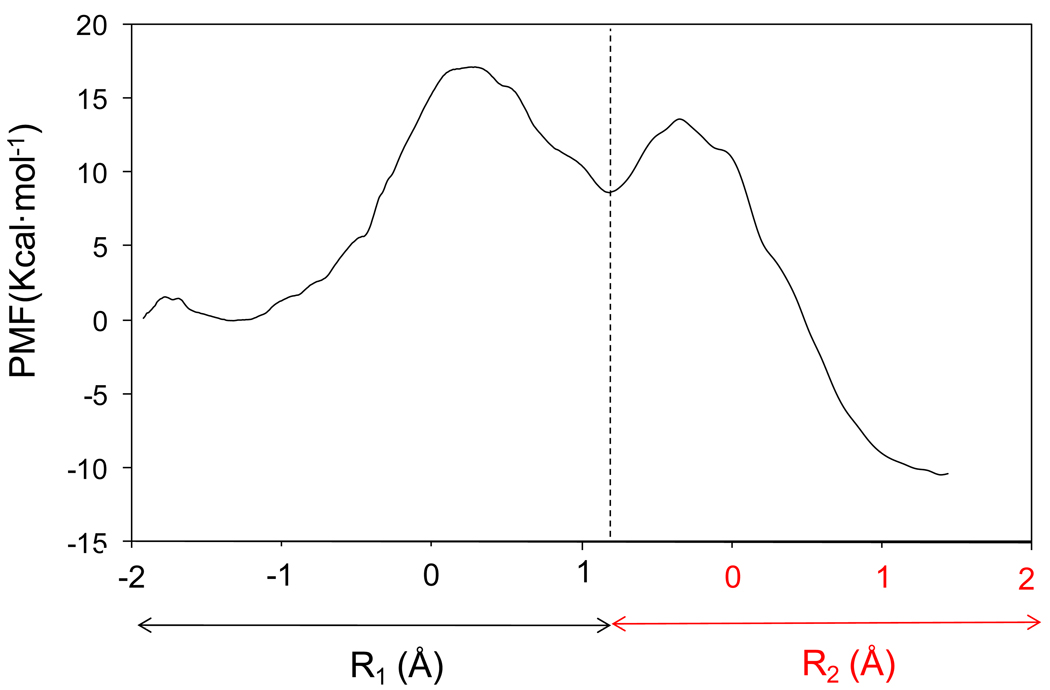
Based on the results described above we decided to trace the PMFs corresponding to the whole reaction starting from the intermediate in the (2Z,4E) configuration. Using R₁ and R₂ we followed the transformations to reactants and to products, respectively. The two PMFs are shown together in Figure 5. These PMFs include the two-dimensional spline corrections evaluated as single-point energy differences between the total energy of the system calculated at the AM1/MM and the MPW1BK/6–31+G(d,p) levels (see Methodology section). This correction term slightly changes the position of the stationary structures on the PES and thus the averaged distances obtained in these simulations do not precisely match the values obtained from uncorrected AM1/MM calculations.

Figure 5.

Potentials of Mean Force obtained for the pro-R proton transfer from the C3 atom of the substrate to Pro1 (R₁) and from Pro1 to C5 (R₂). These PMFs do not include the effect of quantizing the vibrations.

The PMFs in Figure 5 show that the reaction bottleneck is the transition state of the first proton transfer (from C3 atom of the substrate to the nitrogen of Pro1) in agreement with the results of ref. 22. The free energies along key stationary points of the PMFs, including the first transition state (TS1), intermediate (INT), second transition state (TS2) and products (P), relative to that of the Michaelis complex are 17.1, 8.6, 13.6 and −12.7 kcal·mol⁻¹, respectively.

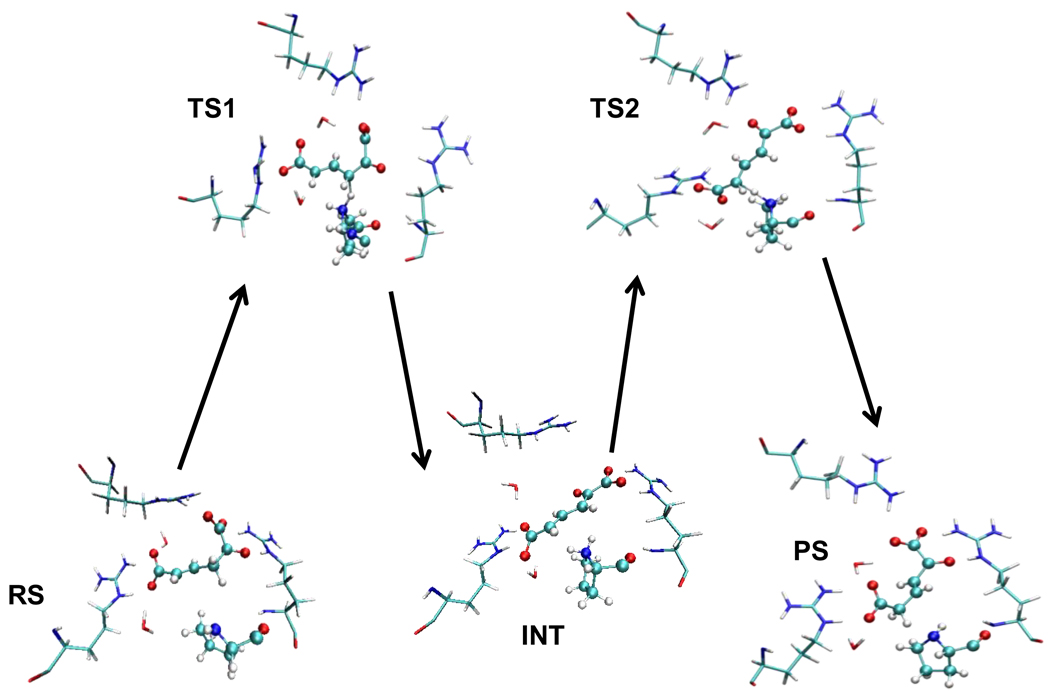
The geometrical changes taking place in the active site during the reaction process are evident in representative snapshots of the stationary structures, which are given in Figure 6. Table I provides averaged values of the distances that define the reaction coordinates (C3-H, Pro1N-H, Pro1N-H’ and C5-H’) and of the shortest hydrogen bond distance established between the substrate oxygen atoms and the arginine residues present in the active site (Arg11’, Arg39”, and Arg61’). These hydrogen bonds can be established either through the NH₂ (H^η atoms) or through the NH groups (H^ε atoms) of the arginine’s side chain.

Figure 6.

Snapshots of the stationary states appearing in the isomerization reaction of 2-oxo-4-hexenedioate (RS) to 2-oxo-3-hexenedioate (PS) through 2-oxo-2,4-hexadienedioate (INT) catalyzed by 4-OT. Colors as in previous figures.

Table I.

Average bond distances for the breaking and forming bonds involved in the two proton transfer reactions, and key hydrogen bond distances between the substrate oxygen atoms and the hydrogen atoms of arginine residues in the active site. The residue and atom type involved in this interaction is also provided. All distances in Å.

	RS	TS1	INT	TS2	PS
C3-H	1.13	1.54	3.33	3.34	3.34
Pro1N-H	2.69	1.24	1.07	1.04	1.01
Pro1N-H’	1.01	1.02	1.04	1.23	2.75
C5-H’	2.63	2.62	2.31	1.56	1.13
O1---H	2.73(Arg61’-Hε)	1.98(Arg39”- Hε)	2.06(Arg39”-Hε)	2.28(Arg39”-Hη)	2.55(Arg61’- Hη)
O2---H	1.90(Arg39”-Hη)	1.99(Arg39”-Hη)	1.99(Arg39”-Hη)	2.13(Arg39”-Hη)	1.84(Arg39”-Hη)
O3---H	2.72(Arg39”-Hε)	2.95(Arg61’- Hε)	1.96(Arg61’-Hη)	2.31(Arg61’-Hε)	2.21(Arg39”-Hε)
O4---H	1.88(Arg11’-Hε)	2.08 (Arg11’-Hε)	2.10(Arg11’-Hη)	1.97(Arg11’-Hε)	1.88(Arg11’-Hε)
O5---H	1.89(Arg11’- Hη)	1.90 (Arg11’-Hη)	1.84(Arg11’-Hη)	1.83(Arg11’- Hη)	2.02(Arg11’- Hη)

The changes in the interaction pattern of each of the oxygen atoms are related to the conformational changes taking place in the substrate as the reaction advances. In the Michaelis complex, the substrate presents a syn disposition of the carbon chain at the C2-C3 single bond, and the C1 carboxylate group forms a strong hydrogen bond with Arg39” at an average distance of 1.9 Å, which is maintained throughout the two proton transfer reaction pathways. In addition, the O1 oxygen of the C1 carboxylate group forms a somewhat longer hydrogen bond with H^ε of Arg61' at 2.73 Å, and the carbonyl O3 atom accepts a weak hydrogen bond from the H^ε atom of Arg39'' with an average distance of 2.72 Å in the Michaelis complex, but these two interactions are swapped at the two proton transfer transition states and the intermediate state. The C6 carboxylate group (O4/O5) interacts with Arg11' through a bidentate coordination, a contact pattern kept throughout the entire reaction path. Using the antisymmetric combination of bond breaking and bond forming distances (R₁) the transition state appears at slightly positive values, which means that the bond distance involving the acceptor atom (1.24 Å) is shorter than the bond distance involving the donor (1.54 Å). At this stage of the reaction, rotation around the C2-C3 bond is partly completed and the O3 atom, now supporting a larger negative charge, interacts with Arg61'. This process is further assisted by concomitant rotation of the C1 carboxylate group that interacts strongly with Arg39” (Table I). The conformational change about the C2-C3 rotation is completed in the intermediate state, where an all-anti carbon chain is found. In this case the negatively charged O3 atom forms a strong hydrogen bond with Arg61', while the C1 carboxylate keeps strong hydrogen bonds with Arg39''. During the motion of the substrate in the active site the hydrogen bonds of C6 carboxylate group with Arg11' are kept within the range 1.8–2.1 Å.

In TS2 the second proton transfer is quite advanced. In terms of the selected reaction coordinate (R₂) the maximum of the free energy profile appears at negative values, indicating that the distance of the proton to the donor atom (1.23 Å) is shorter than the distance to the acceptor atom (1.56 Å). As the proton transfer reaction takes place, the negative charge on the O3 atom of the dienolate species is reduced and the hydrogen bond distance to Arg61' is consequently lengthened. Once the C5 atom receives the proton from Pro1 on the Re face, the negative charge on the O3 atom drops, and the substrate is able to recover its initial syn conformation for the carbon chain. The averaged Mulliken charge on the O3 atom in the product state is reduced to −0.40 a.u. We observed this conformation in our simulations only for advanced values of the R₂ reaction coordinate (beyond 1.2 Å). In this conformation the C1 carboxylate group interacts with Arg39'' and Arg61' and O3 interacts with Arg39''; this represents the same pattern of interactions as that in the reactants state.

We stress that present results show that the conformational change observed in the substrate is coupled to (correlated with) the progress of the reaction coordinate in equilibrium sense, but not necessarily dynamically in real time. As discussed previously,³⁶ one cannot make conclusions about the time scale required for these correlations because of the quasiequilibrium character of umbrella sampling. In our simulation, both the reactant and product are found in a syn conformation about the C2-C3 bond of the carbon chain, but at the transition states TS1 and TS2 as well as in the intermediate state the C2-C3 bond has strong double bond character, corresponding to a dienolate species and adopts the 2Z configuration. As explained before, the negative charge developed on O3 when a proton is lost in the substrate constitutes the driving force by forming stronger hydrogen bonds with Arg61', assisting in the internal rotation of the substrate. These changes, coupled to the reaction advance, are found when the substrate is allowed to fluctuate according to a reference temperature. Previous minimum energy path explorations or simulations which do not incorporate substrate flexibility were not able to locate these conformational changes.^{16,17,20–22} Of course, it is also possible to imagine a scenario where different reaction paths could be feasible, depending, for instance, on particular conformations adopted by the residues of the active site. For example, Tuttle et al. described a sidechain rotation of Arg39'' residue about the C^δ-N^ε bond during a classical molecular dynamics simulation of the initial model A using the charmm force field. This allows the NH₂ group of this residue to directly contact the enolate oxygen atom (O3) of the intermediate.^20,21 Then, conformational changes of the enzyme could favor different reaction paths as a result of the interactions established with the substrate. The existence of conformationally different reaction paths^73–76 (depending on the conformation of the substrate and/or the enzyme) has been already theoretically described in other enzymatic processes.⁷⁷ This behavior has been invoked to explain the kinetic disorder experimentally observed in single-molecule experiments of some enzymatic reactions.^78–82 In some cases each protein conformation can act as an independent enzyme, showing different values of the kinetic constants.^83,84 Changes in average protein conformations and ligand coordination as functions of reaction coordinate progress have been found in several cases, both experimentally and computationally.^{36,68,85–89} This kind of coupling is a key element in the induced fit model of enzyme catalysis.^90,91

The results presented in Table I can be used to interpret the effects of site-directed mutations carried out in the active site, especially chemically modified substitutions of Arg11', Arg39'' and Arg61' by the isosteric but neutral residue, citrulline (Cit).¹⁵ Experimental kinetic results show that mutation of Arg11' has important consequences both on k_cat and K_M, reducing the former and increasing the latter relative to the wild-type enzyme. Our simulations indicate that this residue establishes a salt-bridge with the C6 carboxylate group that is maintained during the reaction process. This is consistent with the experimental finding that substitution of Arg11' affects both substrate binding and the reaction rate. Mutation of Arg39'' to Cit has the largest effect on k_cat.¹⁵ According to our simulations this residue establishes stronger interactions with the C1 carboxylate group in the intermediate and transition states of the reaction, and thus it is expected to contribute to reducing the activation free energy of the reaction. In the case of the mutation of Arg61' to Cit, k_cat is only reduced by a factor of 2.¹⁵ Our simulations indicate that this residue plays an important role in stabilizing the negative charge developed on the O3 atom during the reaction. However, this is true only for the pathway going through the 2Z intermediate. Mutation of Arg61' to a neutral Cit must substantially increase the reaction free energy barrier corresponding to this path, but it would not affect drastically the 2E-intermediate pathway, where the charge on the O3 atoms is stabilized by Arg39''. Thus, in this case, a given mutation can close one of the possible reaction channels without dramatically affecting other reaction possibilities. Interestingly, double mutation of Arg39'' and Arg61' to Cit renders the enzyme completely inactive.¹⁵

3.3. Free energies of activation and kinetic isotope effects

As explained in the methodology section, in order to convert the classical PMF to a quasiclassical one, we have made a quantum correction to the vibrational free energy of the primary zone. This correction includes the zero-point vibrational energy that is not accounted for in the classical simulations of the nuclear motion. This term is especially important when the reaction involves the transfer of a hydrogen atom because the zero-point energy contribution of the stretching motion of this atom in the reactant states makes an important contribution that is greatly decreased in the transition state. Thus, the free energy barrier can be overestimated if one does not properly account for this term. In some hydrogen transfer reactions this term diminishes the free energy of activation by as much as 2–3 kcal·mol⁻¹,^92,93 whereas this contribution is very modest for other reactions.⁹⁴ In the reaction catalyzed by 4-OT the effect is not so large but it is still quantitatively important. The vibrational correction term lowers the free energy of activation associated with the first step by about 1.0 kcal·mol⁻¹ (see Table II). However, the effect on the intermediate and the second proton transfer is very small. This is related to the fact that TS2 is found at a very early stage of the second proton transfer and that the associated free energy barrier is quite small. Zero point energy effects are also noticeable in the product state, where the vibrational correction term increases the free energy by nearly 3.9 kcal·mol⁻¹. We did not observe any appreciable change in the position of the maxima in terms of R₁ and/or R₂ when the vibrational correction term was added to the PMFs.

Table II.

Contributions to the relative free energies (in kcal/mol) of the stationary states for the 4-OT catalyzed reaction employing the substrate with a hydrogen or a deuterium isotope at the pro-R position on the C3 position. Averaged semiclassical tunnelling and recrossing transmission coefficients are also provided.

	C3-1H,1H					C3-2H,1H
	RS	TS1	INT	TS2	PS	RS	TS1	INT	TS2	PS
ΔWCM	0.	17.14	8.65	13.62	12.60	0.	17.14	8.65	13.62	−12.60
ΔΔWvib	0.	−1.10	−0.01	0.04	3.89	0.	−0.36	−0.26	−0.22	3.54
GF,QC	−0.33		−0.54		0.32	−0.31		−0.84		−0.74
$\Delta G_{\mathit{\text{QC}}}^{\mathit{‡}}/\Delta G_{\mathit{\text{QC}}}$	0.	16.37	8.43	13.99	8.70	0.	17.09	7.86	13.71	−9.49
〈κ〉		2.09		1.55			2.01		1.51
〈Γ〉		0.54		0.61			0.86		0.99
γ		1.12		0.93			1.76		1.46

In order to convert from PMF changes to the generalized free energy of activation profiles we need to add the contribution of the reaction coordinate to the free energy minima appearing along the reaction profile.^25,27 This has been estimated as the difference in the free energy obtained from the calculation of vibrational frequencies at the minima of the PMF, first with the reaction coordinate projected out of the Hessian and then without projecting it out. The contribution of this term ranges from approximately −0.3 to −0.5 kcal·mol⁻¹ for the reactants, intermediate, and products states, as reflected in Table II.

According to the relative free energies reported in Table II we evaluated the catalytic rate constant using the following simplified kinetic mechanism:

$$1\underset{k_{-\mathit{1}}}{\overset{k_{\mathit{1}}}{\rightleftarrows }}2\stackrel{k_{\mathit{2}}}{\to }3$$

It has been recently suggested that the O3-protonated form of 2 could also be a substrate of the enzyme⁶ although the reported free energy differences show that the equilibrium population of this substrate in the enzyme relative to 1 should be very small. Moreover, rate constants have been evaluated considering only the contribution of the reaction path with a 2Z configuration of the intermediate. Applying the steady-state approximation in the standard way to the concentration of this intermediate gives

$$k_{\mathit{\text{cat}}}=\frac{k_1{k}_2}{k_{-1}+k_2}$$ (8)

According to the free energy profile obtained from our simulations we cannot assume an equilibrium between 1 and 2 that would correspond to the case in which k₋₁ >> k₂. Using equation (8) we evaluated the catalytic rate constant to be 8.12 s⁻¹ at 300 K, with a phenomenological activation free energy $\Delta G_{\mathit{\text{phen}}}^{\mathit{‡}}$ of 16.3 kcal·mol⁻¹. The experimental values are 498 s⁻¹ and 13.8 kcal mol⁻¹ at 303 K.⁶

To our knowledge, kinetic isotopic effects (KIEs) have been not experimentally determined for this enzyme. KIEs provide an opportunity for the comparison of experimental and theoretical data using variational transition state theory.^70,95–101 This theory has been successfully applied to the interpretation and prediction of enzymatic KIEs, especially when a transferred protium atom is substituted by deuterium and/or tritium.^27,33,36,39 In the present study we decided to evaluate the primary KIE for deuterium substitution of the hydrogen atom transferred from C3 to the Pro1 nitrogen atom (C3-¹H,¹H and C3-²H,¹H substrates in Table II). The present theoretical prediction can be compared with future experiments; this will serve as a test of the present theoretical model. PMFs obtained using Newtonian dynamics are independent of the masses of the nuclei and thus no effect is expected upon substitution. However, other contributions to the rate constant do depend on isotopic substitution. In order to evaluate kinetic isotope effects (KIE) we computed vibrational, tunneling, and recrossing contributions using the same structures selected from the simulations of the protium case but changing the mass of the corresponding atom. The values obtained for this case are presented in Table II. The differences in the rates of the isotopologs are quite moderate and slightly larger for the first reaction step, because in this case the substituted atom is transferred while in the second step this atom does not directly participate in the proton transfer. With these new values we evaluated the rate constant to be $K_{\mathit{\text{cat}}}^{{}^{2}H}$ at 300 K. The ¹H/²H KIE can be now obtained as the ratio of the rate constant obtained with the light and the heavy atom, which has a value of $k_{\mathit{\text{cat}}}^{{}^{1}H}/k_{\mathit{\text{cat}}}^{{}^{2}H}=\mathit{2.09}$. The value obtained neglecting tunneling contributions is in this case very similar: 2.07.

4. Conclusions

We have presented a combined QM/MM free-energy-based simulation of the tautomerization reaction catalyzed by 4-OT. The results obtained are consistent with the proposed mechanism, where a proline residue (Pro1) acts as a proton shuttle, accepting a proton from the C3 atom and transferring another one to the C5 atom. The highly charged intermediate is stabilized by the presence of three arginine residues (Arg11’, Arg39”, and Arg61’) in the active site.

Our molecular dynamic simulations have shown that the system is highly flexible. Previous analysis based on the minimum energy path or free energy perturbations, where only the fluctuations of the environment are included, were unable to identify the possibility of conformational changes of the substrate during the reaction. We point out that some previous work employing a fixed reaction coordinate led to artifacts such as good agreement with experiment for the computed free energy barrier and mutation effects even though the stereochemistry in the proton transfer mechanisms was incorrect. In principle, several reaction paths may be used to examine various possibilities. Molecular dynamics simulations that fully couple protein and substrate conformational fluctuations to the reaction coordinate allow multiple reaction paths to be explored during the free energy calculations. For the 4-OT catalyzed isomerization reaction, we found that the initial proton abstraction from the pro-R position at the C3 atom is the rate limiting step with an estimated free energy barrier of 16.3 kcal/mol, in reasonable agreement with the experimental value (13.8 kcal/mol). This proton transfer leads to a dienolate intermediate species adopts a preferred 2Z-configuration, furthermore, we have predicted the primary ¹H/²H kinetic isotope effect, which can be tested by future experimental measurements.

A key finding of our study is the dynamic coupling between the internal rotation around the C2-C3 single bond of the substrate and the proton transfer. These motions present very different characteristic times. Thus the conformational change can either precede the proton transfer or it can be accomplished during the residence of the substrate in the intermediate state. Our results point to the first scenario. However, it is plausible that conformational changes of the protein affecting the positioning of the arginine residues in the active site could favor different reaction paths where the conformational change could take place after the proton transfer or simply not happen. This should be reflected in the existence of kinetic disorder that could be shown through single-molecule experiments.

Supplementary Material

2. Supporting Information Avalaible.

Calculations carried out to choose the high-level method for correcting AM1/MM results and complete citation of reference 53. This material is available free of charge via Internet at http://pubs.acs.org