Imaging cryosurgery with EIT: tracking the ice front and post-thaw tissue viability

Abstract

Cryosurgery employs freezing for targeted destruction of undesirable tissues such as cancer. Ice front imaging has made controlled treatment of deep body tumors possible. One promising method, recently explored for this task, is EIT, which recovers images of electrical impedance from measurements made at boundary electrodes. However, since frozen tissue near the ice front survives, ice front imaging is insufficient. Monitoring treatment effect would enable iterative cryosurgery, where extents of ablation and need for further treatment are assessed upon thawing. Since lipid bilayers are strong barriers to low frequency electrical current and cell destruction implies impaired membranes, EIT should be able to detect the desired effect of cryosurgery: cell death. Previous work has tested EIT for ice front imaging with tank studies while others have simulated EIT in detecting cryoablation, but in vivo tests have not been reported in either case. To address this, we report 3D images of differential conductivity throughout the freeze-thaw cycle in a rat liver model in vivo with histological validation, first testing our system for ice front imaging in a gel and for viability imaging post-thaw in a raw potato slice.

1. Introduction

Cryosurgery is a minimally-invasive surgical technique which seeks to destroy undesirable tissue through freezing. Counter to resection, tissue is left in situ to be slowly resorbed, preserving blood vessel architecture, incurring minimal bleeding, and generating a local anesthetic effect (Onik 1996). Cryosurgery has been used in treatment of cancer at or near the body surface since the mid-19^th century (Arnott 1850), but treatment of deep-body tumors was impractical until modern insulated cryoprobes (Cooper and Lee 1961) made freezing large volumes of tissue possible.

An important problem emerged due to the minimally-invasive nature of the procedure: the surgeon could not see the extents of the frozen lesion being created and thus when to stop freezing. This led to the much diminished use of the procedure until the adaptation of intra-operative ice front imaging methods such as ultrasonography (Onik et al 1991) and later MRI (Rubinsky et al 1995) allowed the extents of freezing to be visualized. However, there is much room for improvement. An ultrasound transducer can only image the frozen region from one side, and since ice casts a shadow in the images, the ice front position on the back side is not detected. MRI can recover the full position of the ice front with accuracy, but it is comparatively difficult in a surgical setting. Still, image-guided cryosurgery has become an effective weapon against hepatic (Kerkar et al 2004), renal (Jang et al 2005) and prostate (Han and Belldegrun 2004) cancers.

Electrical impedance tomography (EIT) is a developing diagnostic imaging technique which recovers the spatial variation of electrical impedance within an object from electrical measurements made on its periphery (Brown 2003; Bayford 2006). In EIT, electric current is applied across two or more contacting electrodes and the resulting electric potential distribution within the body is sampled at many others. Then the solution is sought to the inverse problem of determining the cause (impedance distribution) of the observed effects (applied current patterns and measured voltages). This yields a spatial image of specific impedance which is then interpreted according to the particular application. Though it often suffers from low resolution, EIT benefits from fast acquisition and reconstruction (especially for linear algorithms) and low cost (in particular when a distributed network is employed (Otten et al 2004)). Specific impedance magnitude of tissue increases by at least two orders of magnitude on freezing over a wide frequency range (Duck 1990). This is the basis upon which EIT can reveal the ice front position, something that applies also for induced-current impedance imaging (Zlochiver et al 2002).

Proof of concept has been established (Otten and Rubinsky 2000) and tank experiments have been reported (Hartov et al 2002), but the implied hypothesis that EIT can detect the ice front in vivo has yet to be tested. In addition to motion artefacts linked to respiration and pulse, cold temperatures affect the conductivity of the unfrozen tissue. Further, since freezing has a nonlinear effect on blood flow, both directly (vascular occlusion) and indirectly (homeostasis), and hypothermia slows the rate of metabolic heat generation in the unfrozen tissue, the temperature field surrounding the frozen tissue is hard to predict. Therefore, after validating the ability of our system to track the ice front in a gel model, we test this hypothesis with the first in vivo trial of ice front imaging with EIT, in a rat liver model.

There is a problem with the use of ice front imaging alone to guide cryosurgery: frozen tissue near the ice front can survive treatment. This results from the wide variety of conditions experienced by the tissue being frozen and the effects that they produce in different tissues. Cells near the cryoprobe tip are completely destroyed by intracellular ice formation (especially below −40 °C), while those closer to the ice front experience a hypertonic environment, resulting from the preferential freezing of extracellular passages when cooling is slow, which causes crenation and can destroy or preserve depending on the detailed conditions experienced by the cell (Mazur 1984; Gage and Baust 1998). This problem has been approached empirically with multiple freeze-thaw cycles that increase the potential for cell damage near the ice front but at the expense of increased side effects and usually the destruction of excess healthy tissue. A better solution would be to assess treatment effect (non-viability) on thawing so that the region of cell death is more precisely sculpted using fewer, more targeted, freeze-thaw cycles.

Currently the gold standard for viability imaging is provided by PET (Vokow et al 2001), but it has not become widely available due to cost (Wu and Lima 2003). Functional MRI also presents a possible solution (Preece et al 2001); however, it also incurs a high cost and long acquisition time. EIT has recently been proposed as a method for detecting tissue viability after cryosurgery (Davalos and Rubinsky 2004; Edd and Rubinsky 2006). This is based on the principle that cell membrane integrity, and hence viability, influences greatly the electrical conductivity at frequencies below the β dielectric dispersion (Grimnes and Martinsen 2000). Specifically, real conductivity of tissue rises sharply with cell membrane disruption due to the opening of the intracellular spaces to current flow.

In order to test the central hypothesis that EIT can recover images of tissue viability in vivo, where other effects could obscure the expected changes, this paper first describes experiments that recover differential EIT images of the cryoablated lesion post-thawing in a raw potato model and then presents conductivity images of the rat liver that was subjected to cryosurgical treatment, taken in vivo at various times after thawing, interpreting them with respect to histological features. These images represent the first time EIT has been used to image the effect of ablative surgery in vivo, a technique which has the potential to become widely used. Other modalities exist to monitor the ice front during cryosurgery; however, EIT could become the only surgically feasible method to monitor tissue viability peroperatively, and as the following experimental results show, it can pick up the changes indicative of cell death (i.e. a loss of membrane integrity).

2. Materials and Methods

2.1. Electrode arrays

To test EIT for a cryosurgical treatment in vivo, an array containing 60 gold-coated copper electrodes (1 mm squares) was generated on two similar printed circuit boards (Sierra Proto Express Inc., Sunnyvale, CA) (see figure 1(a)). These arrays were designed to face each other at a distance prescribed by a 5mm spacer (aligned via three protruding pegs), so that 28 electrodes contacted the top surface and 32 electrodes touched the bottom surface of a lobe of liver in a live rat. The upper array also contained a hole in the center of the electrode array to allow a 3.4 mm diameter cryoprobe tip, electrically insulated with paraffin, to contact the upper surface of tissue, enabling generation of nearly hemispherical frozen regions.

Figure 1.

(a) Electrode arrays (gold electrodes implemented on printed circuit boards) and (b) imaging mesh. Upper array contains a 3.6 mm diameter hole for cryoprobe insertion. White squares in (b) are 1 mm square electrodes, 1 mm cubes are imaging pixels and dark squares show locations of extra four electrodes on bottom array.

To improve four-electrode impedance measurement, the electrode-tissue interface impedance was reduced via electrochemical deposition of platinum on the gold electrodes. This method, called platinization, produces a black sponge-like or dendritic deposit that increases the effective surface area of the electrode, thus dramatically reducing its impedance (Feltham and Spiro 1971; Geddes 1979). Electroplating solution consisted of 7.5 mL distilled water, 0.25 g Cl₄Pt, 3 mg Pb(CH₃COO)₂•3H₂O and 2.5 mL HCl (0.1 M), and the anode was a 2 cm square of silver foil. Electrodes to be platinized (cathodes) were connected to +15 V through a 3.5 kΩ resistor, resulting in direct currents of about 3.5 mA. Electrodes were electroplated individually for 35 seconds divided into 5 second cycles. With this method, the magnitude of the electrode interface impedance in normal saline (0.9 % w/v NaCl) was reduced below 2 × 10^-4 Ωm² at 1 kHz excitation.

2.2. Data acquisition

The architecture of the measurement system is depicted schematically in figure 2. It is simply a computer-controlled four-electrode impedance-measuring circuit that can be connected to any four electrodes in the array by means of a 4:60 analog multiplexer. First, a lock-in amplifier (Signal Recovery, Oak Ridge, TN; 7280BFP) generates a sinewave voltage (1 kHz for all experiments) which is then converted into constant current (100 μA amplitude) within the signal conditioning electronics. This current is then applied across any pair of electrodes. To sample the resulting potential distribution within the body, the voltage difference between two other electrodes is amplified and returned to the lock-in amplifier which demodulates it with respect to applied current to obtain the voltage difference, real and complex. The measurement hardware also measured the impedance between any electrode and a larger reference electrode, indicating electrode contact quality. It provided another way to track the ice front: electrodes covered by ice had higher impedance.

Figure 2.

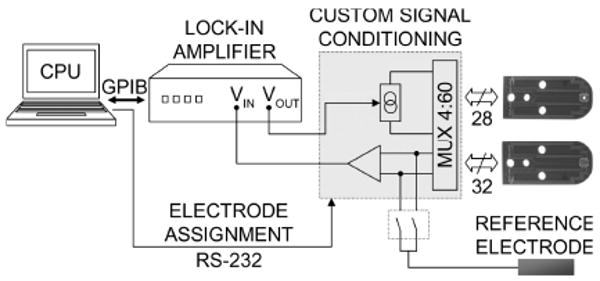
General architecture of EIT system. 60 electrodes are connected four at a time to a 4-electrode impedance measuring circuit. Laptop PC controls the Multiplexing of electrodes as well as the data processing.

Current was always driven between adjacent electrode pairs on the same array, with adjacency being defined along a spiral path. This choice ensured that the electric potential distribution resulting from each bipolar excitation was most dependent on a different region of pixels, but no rigorous attempt was made to determine an optimal choice of current pattern (Demidenko et al 2005; Kao et al 2003). Voltage differences were measured between adjacent electrodes in a similar fashion (skipping current-carrying electrodes). One scan resulted in 30 independent current projections requiring 57 differential voltage measurements each, acquiring a total of 1710 unique four-electrode measurements in about 50 seconds.

2.3. Reconstruction algorithm

Here the finite element method was employed to solve the forward problem for a piecewise-constant and isotropic problem of electrical conduction (∇·(σ∇φ)=0), where (σ) represents conductivity in S/m within a pixel and (φ) is electric potential in Volts, to be recovered at all nodes within the finite element mesh. The electrodes were modeled with the complete electrode model (Somersalo et al 1992), so that non-current carrying electrodes were specified as V_e = φ + z_eσ (∂φ / ∂n), where (V_e) and (z_e) are the voltage and interface impedance (in Ωm²) of electrode (e), and (n) is the outward normal to the body surface in contact with the electrode.

Pixel-based image reconstruction was performed on the mesh in figure 1(b), consisting of five layers of 277 20-node hexahedral elements (1-mm cubes), 1385 unknown conductivities. The iterative reconstruction algorithm started with a guess that conductivity had not changed since the reference scan, then adjusted that guess according to the discrepancy between measured and predicted voltages:

$$\frac{{\sigma }_{\text{n}+\text{1}}}{{\sigma }_{\text{r}}}=\frac{{\sigma }_{\text{n}}}{{\sigma }_{\text{r}}}+{\left({\text{J}}_{\text{n}}^{\text{T}}{\text{J}}_{\text{n}}+\lambda {\text{L}}^{\text{T}}\text{L}\right)}^{-1}{\text{J}}_{\text{n}}^{\text{T}}\left(\frac{{\text{V}}_{\text{0}}}{{\text{V}}_{\text{0r}}}-\frac{{\text{V}}_{\text{n}}}{{\text{V}}_{\text{r}}}\right),$$ (1)

where (σ) is the vector of conductivities, one per pixel, (V) is a vector of voltage differences, (J) is the Jacobian matrix and (L) is the regularization matrix, weighted by the regularization parameter (λ). Subscripts (r) and (0) refer to reference and measured, as opposed to simulated, data respectively and (n) refers to the iteration number so that (V_0r) is the vector of measured voltages during the reference scan and (V₀) is measured during a subsequent scan. Similarly, (V_r) is the set of voltages obtained from solving the forward problem for the starting guess (σ_r), assumed here to be uniform, and (V_n) is computed from the current image iterate (σ_n). The ratio of two vectors denotes an element-by-element division. Each scalar entry of the Jacobian matrix (J_n,ik) represents the perturbation in one voltage measurement (i) resulting from a small increase in conductivity within a pixel (k), and was found as:

$${\text{J}}_{\text{n},\text{ik}}=\frac{\partial ({\text{V}}_{\text{n},\text{i}}/{\text{V}}_{\text{r},\text{i}})}{\partial ({\sigma }_{\text{n},\text{k}}/{\sigma }_{\text{r},\text{k}})}=-\frac{1}{\text{I}}\frac{{\sigma }_{\text{r},\text{k}}}{{\text{V}}_{\text{r},\text{i}}}\underset{{\text{Ω}}_{\text{k}}}{\int }\nabla {\text{φ}}_{\text{d}}\cdot \nabla {\text{φ}}_{\text{m}}\text{d}{\text{Ω}}_{\text{k}},$$ (2)

where (I) is the constant current injected across all driving electrode pairs, (Ω_k) designates integration over pixel (k), and (d) and (m) refer to forward solutions with drive or measurement pairs applying current in accordance with the reciprocity formulation of the Jacobian (Brandstätter 2003). Here, (L) was the inverse of a Gaussian filter with standard deviation of 1 mm, the coding for which is in (Edd 2006). EIT software was implemented in Matlab (www.mathworks.com).

The propagation of measurement errors has been considered. Assuming that the simulated voltages are exact and that the error in each real voltage measurement was random with a Gaussian distribution of mean zero, uniform for all measurements, it can be shown through error analysis that error propagates into the discrepancy between measured and simulated voltages (ΔV = V₀ / V_0r −V_n / V_r):

$$\sum =\left|\frac{\text{η}}{{\text{V}}_{\text{0r}}}\right|\sqrt{{\left(\frac{{\text{V}}_0}{{\text{V}}_{\text{0r}}}-1\right)}^2+1,}$$ (3)

where (Σ_i) is the standard deviation in the measurement discrepancy (ΔV_i) for measurement (i), and (η) is the uniform noise level that is assumed to exist during voltage measurement. With (Σ), it is then possible to define a relative error in each measurement discrepancy (Σ_i / ΔV_i), and then redefine the cost function as:

$$\epsilon =\frac{1}{2}{\Vert \left(\frac{{\text{V}}_{\text{n}}}{{\text{V}}_{\text{r}}}-\frac{{\text{V}}_0}{{\text{V}}_{\text{0r}}}\right)/\sum \Vert }_2^2.$$ (4)

This cost function, whose components have by definition a standard deviation of one, can be minimized by replacing (ΔV_i) with (ΔV_i / Σ_i) in the inverse step, and then dividing each row in the Jacobian matrix (J_i:) by the corresponding error in each measurement (Σ_i). The result is that errors in measurements that have a large effect on (ΔV) will be prevented from skewing images too much, though proper values for (λ) can differ between scans depending on initial discrepancy (ΔV / Σ).

It is important to note that the propagated error (Σ) is constant through each iteration; however, (ΔV) is reduced as the true image is approached, so convergence should be declared when most components of (ΔV) lie below the associated noise levels in (Σ), perhaps stopping when ‖ΔV‖ < ‖Σ‖ (Morozov 1984). Here we instead stop when (ε) stabilizes, usually after a small number of iterations.

2.4. Materials

Uniform gel was prepared by bringing to boil 100 mL DIW holding 1.5 g agar and 10 g NaCl. Raw potatoes were obtained locally. For the in vivo study, the Sprague-Dawley rat (380 g) was obtained from Charles River Labs through the Office of Laboratory Animal Care at the University of California, Berkeley. The animal received humane care from a properly trained professional in accordance with the Animal Care and Use Committee of the University of California, Berkeley and in compliance with both the Principles of Laboratory Animal Care and the Guide for the Care and Use of Laboratory Animals, prepared and formulated by the Institute of Laboratory Animal Resources and published by the NIH.

3. Results

3.1. Ice front imaging in an agar gel

To validate the EIT hardware and software for ice front imaging, a test was first conducted with an agar gel of uniform conductivity (0.208 S/m according to EIT scan) which was cut into a 5 mm thick slab to be placed between the two electrode arrays. After the arrays were fixed in place and the cryoprobe tip was inserted into the hole in the upper array, electrode contact impedances were estimated at 1 kHz (reference electrode was a piece of silver foil attached to the gel), and a reference EIT scan was performed. Immediately thereafter, freezing was initiated by turning on the flow of liquid nitrogen to the cryoprobe. Once the cryoprobe temperature showed that freezing had started (temperature plateau at −1 °C), a second data set was taken, the details for which can be seen in figure 3(a). Cryoprobe temperature was sampled every three seconds via a thermocouple reader (Extech Instruments, Walham, MA; EA15) connected to a type K thermocouple in contact with the cryoprobe shaft just above the upper array, held in place with a paraffin wrap. Further scans (and electrode impedance measurements) were performed at three minute intervals until probe temperature fell below −50 °C.

Figure 3.

Ice front imaging in an agar gel. (a)-(e) Side-photo (with dots along ice front), image of specific impedance (impedivity) magnitude relative to reference scan (|z*|/|z*|_ref − black = 0, white = 5), and electrode impedances (|z*|_elec − black = 0, white = 1.5×10^-3 Ωm²) for intervals of 4 to 28 minutes after starting flow of cryogen. Bar maps grayscale pixel values in linear fashion. In each panel, circular image is upper 1-mm plane of imaging mesh, which contacts cryoprobe, and two orthogonal cross-sections (see dashed lines) are given. Arrow indicates long axis of electrode array, so that lower cross-sections match orientation in the photos, which also include time and cryoprobe temperature. Scale is uniform (pixels are 1-mm cubes, array gap is 5 mm).

The resulting images at six-minute intervals are presented in figure 3(a)-(e) alongside graphic depictions of electrode contact quality across the array and side view photos. Though the transmitted light refracts due to the non-planar surfaces, it is clear that accurate images of the freezing front were obtained. Since the converged image of the previous scan was used as the initial guess for the following reconstruction, gel inside the frozen region in figure 3(e) was erroneously diagnosed as unfrozen. This can be attributed to the fact that there is little current flow in regions encircled with ice and hence no reason for a pixel-based algorithm to keep that impedance high. In practice, measurement of the cryoprobe temperature or simply the knowledge that thawing would proceed from the ice front inward would indicate that these regions were still frozen.

3.2. Viability imaging in a raw potato slice

Freezing in a gel provides a useful test case for ice front imaging; however, the post-thaw conductivity does not resemble that for tissue. To validate the EIT system for detecting cryoablation, we chose first to run a set of similar cryosurgical experiments that captured the essential change expected from freezing-induced cell death, i.e. cell membrane disruption, in a model free of many of the complicating factors inherent with in vivo experiments.

In the aspects that are important here, raw potato tissue is quite similar to liver parenchyma; it contains a relatively isotropic distribution of cells whose plasma membranes restrict low frequency electrical currents to the comparatively narrow extracellular passages. For potato and liver tissues, the low frequency conductivity is hence an indicator of cell membrane integrity. The rigidity of the plant cell wall (enabling turgor pressure), coupled with the mechanical connections between the enclosed plasma membrane and extracellular matrix, makes non-cold-acclimated plant cells less resilient to freezing injury than mammalian cells; they cannot keep pace with the water efflux and then influx demanded by this rapidly changing osmotic micro-environment (Smallwood and Bowles 2002). These factors combine to make potato cell death probable following a rapid and unprepared for freezing event. This will cause the transition zone between complete cell death and healthy tissue to become sharper for potato tissue as compared with rat liver, making possible a clearer analysis of the accuracy of the resulting EIT images.

The EIT images and supporting data presented in figure 4 indicate a large increase in conductivity within the previously frozen zone of potato tissue in each of the four specimens. The observed darkening, or enzymatic browning, in potato tissue after a freeze-thaw cycle is linked to an accelerated oxidation of chemical constituents caused by a decompartmentalization of certain enzymes, substrates, and/or activators (Ashie and Simpson 1996) that occurs in response to cell lysis post-cryoablation. Cell membrane disruption should cause the conductivity at 1 kHz to approach that for frequencies above the β dispersion, where membranes are bypassed (1 MHz conductivity of potato is about 18 times higher than at 1 kHz (Dejmek and Miyawaki 2002)). Independent measurements of the increase in potato tissue conductivity due to freezing, with a simple two electrode impedance cell (two 10-mm diameter electrodes held across a 7.1 mm slab of frozen potato, 30 minutes after thawing), indicate that the 1 kHz conductivity increases by about 16.7 times, where 1 MHz conductivity falls slightly (to 82 % normal), so that post-thaw conductivity at 1 kHz is nearly indistinguishable from that above the β dispersion. In addition we determined by scanning the exposed upper surfaces of the potato slices in figure 4 with a small needle electrode (lower disk electrode completes the circuit) that the transition zone occurs over less than the pixel size of 1 mm, coinciding with the dark-light boundary in the post-thawing photos.

Figure 4.

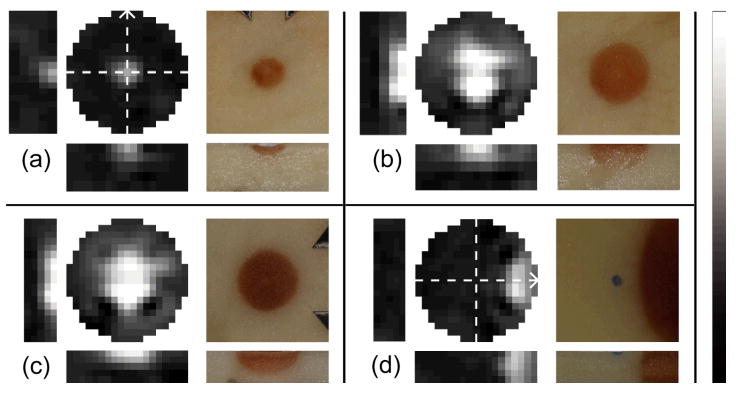
Viability imaging in a raw potato slice. EIT images show fractional changes in conductivity magnitude post-thawing as compared to a reference scan (|σ*|/| σ*|_ref − black = 0, white = 10) for (a)-(c) three central and (d) one non-central cryosurgical lesion. Bar maps grayscale pixel values in linear fashion. Electrode array axis is designated with the arrows in (a) for (a)-(c) and differently in (d). Dark regions in each photo result from freezing-induced cell death (uniform scale).

According to EIT images, post-thaw potato tissue conductivity increased up to 6.7, 13.7, 13.0 and 9.4 times normal levels for figure 4(a)-(d) respectively. Considering the large departure from the reference image, the images capture the approximate shape and size of the ablated regions; smooth regularization prevented full contrast from being built up for the small ablated zone in figure 4(a).

The fourth case (figure 4(d)) was performed with the cryoprobe touching the upper surface of the potato, but outside of the array (i.e. at the distal end of the array). Since this image was reconstructed for a mesh that neglected current flow outside of a roughly 19-mm diameter cylindrical region centered on the electrodes, artefacts may have resulted from the large increase in conductivity incurred outside the mesh. The image seems to match the location of the brown region, but the region of higher conductivity has more curvature than is seen at right. The increase in (σ) is less substantial at the right edge of the mesh, but this could be attributed to a lower sensitivity to changes in this region. Despite the large changes outside of the mesh, there has been no major artefact produced in the image region where no changes would have occurred (the unfrozen zone). These discrepancies are minor and could be eliminated with a larger mesh, the inclusion of a boundary-element-specified free surface, and/or a more accurate meshing of the full tissue geometry.

3.3. In vivo ice front imaging in a rat liver

The procedure for ice front imaging within the lobe of liver of a live rat was similar to that for the gel and the potato; however, the timeline was more complex and freezing proceeded faster in order to ensure a large zone of ablated tissue near the cryoprobe tip. The protocol started with anesthetization via intraperitoneal injection of 0.65 ml Nembutal solution (50 mg/ml sodium pentobarbital, Abbott Labs, North Chicago, IL), or 85.5 mg sodium pentobarbital per kg body mass. Fifty-one minutes later, the liver was exposed via midline incision and the electrode arrays were attached across one lobe of liver (see photo in figure 5) so that a gap of 5 mm was present between arrays. Twenty-seven minutes after incision, a reference scan was taken (with a measurement of contact impedances) followed by three similar scans during freezing (one during cooling to zero, one at the initiation of freezing and one after four minutes of freezing) and four scans during and after thawing, as seen in figure 5. Three minutes after the last scan, the arrays were removed, revealing the macroscopically visible concentration of blood in the treated region (see figure 5(h)). Eleven minutes later, the rat was euthanized by exsanguination and the liver lobe was perfused via the hepatic portal vein with physiological saline followed by a 5 % formalin fixative. The liver lobe was then excised for storage in formalin and thin sections were prepared with Hematoxylin-Eosin (H&E) staining.

Figure 5.

In vivo ice front and viability imaging in a rat liver. Fractional change in (a)-(c) impedivity magnitude during freezing (|z*|/|z*|_ref – black = 0, white = 5) and (d)-(g) its inverse (conductivity magnitude) during thawing (|σ*|/|σ*|_ref – black = 0, white = 2.5) as compared with reference scan, for the in vivo experiment. Bar in (h) maps grayscale pixel values in linear fashion. Scan for (a) was taken 6 min after reference scan, where probe temperature was 12 °C; scans in (b) and (c) were taken during cooling, 4 and 8 minutes later (−2 °C and −25 °C respectively). Scans in (d)-(g) were taken during and after thawing, at times of 15, 21, 28 and 34 min after the reference scan ((d) was partially frozen; 2 °C probe temperature). From initial scan, liver conductivity was normally about 0.08 S/m. (h) Photo of treated liver after perfusion-fixation. * in photo designates 5-mm spacer. Solid white curves in (c) and (g) and dotted curves in (g) are superimposed from histology in figure 6(g).

The resulting images are presented in figure 5(a)-(c). Since the furthest extents of freezing were not apparent from these images, it is useful to look at the histological thin sections that were prepared from the treated liver lobe. The resulting two and three dimensional graphs in figure 6(e)-(h) make it clear that a nearly hemispherical zone of freezing was present, about 11.5 mm wide at the top surface of the liver lobe and penetrating to a depth of 4 mm. It is also apparent that the vasculature in a smaller hemisphere (about 5.5 mm wide and 2 mm deep) inside the ice front was compromised, which can be seen from the failure of the perfusion fixation technique to remove erythrocytes (RBCs) there. This most likely resulted from the well-documented detachment of endothelial cells that occurs when the vessel lumen expands during freezing as water is withdrawn from cells via osmosis (Rubinsky et al 1990), which would have finally resulted in coagulative necrosis.

Figure 6.

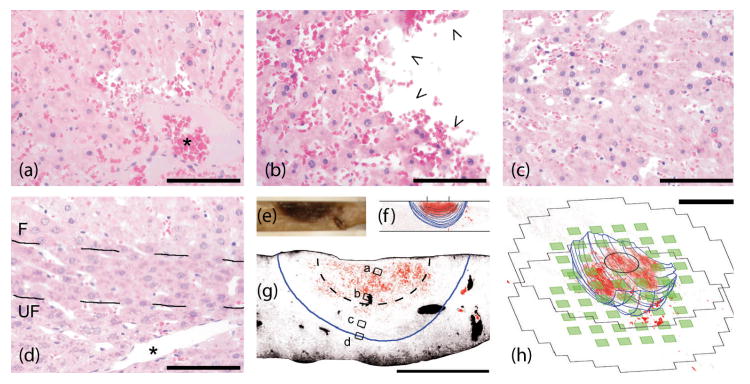
Microscopic pathology along a radial path from cryoprobe tip to the ice front. Small boxes in (g) mark the locations of pictures in (a)-(d) taken from a probe-centric thin section of (e) fixed liver. Dotted line in (g) encloses inner hemisphere of fully ablated tissue as implied from the conductivity image presented in figure 5(g). Scale bar is 100 μm in (a)-(d), 5 mm in (g)-(h). (f)-(h) resulted from image processing of histological thin section photos (see online supplemental figure 1), where RBCs are red, empty space (i.e. sinusoids) is black and the ice front is blue. Electrodes (green) and image mesh extents are superposed with 3D histology in (h). * in (a) marks a fully clotted blood vessel with entrapped RBCs, while * in (d) shows a healthy blood vessel just outside the ice front. Arrows in (b) show endothelial detachment within the region that experienced slower freezing. Ice front designated in (d) as zone between broken lines, where F and UF designate the frozen and unfrozen sides.

3.4. In vivo viability imaging in a rat liver

The conductivity images during thawing, depicted in figure 5(d)-(g), show the emergence of a nearly circular region (about 6 mm diameter) of elevated (2–2.5 times higher) conductivity, centered in the previously frozen zone, primarily in the upper 1 mm of tissue, but penetrating also into the second millimeter.

For frequencies below the β dispersion, cell membranes represent a strong barrier to current flow. Cell death (and subsequent membrane disruption) will therefore increase the bulk conductivity at low frequencies. This expected increase should be similar to the tissue conductivity above the β dispersion, where cell membranes no longer block intracellular current flow. For freshly excised bovine liver, this increase is from about 0.04 S/m at 1 kHz to 0.20 S/m at 1 MHz (Gabriel et al 1996). Similarly, the sub-β-dispersion in vivo porcine liver impedivity magnitude was reported to be 2.4 ± 0.6 times higher than the high frequency limit (β dispersion was at 70.9 +/- 15.9 kHz) (Casas et al 1999). In addition, warm (35 °C) ischemic damage of 505 minutes, at which point the cell membranes had disintegrated, was reported to cause 1 kHz conductivity of excised canine liver tissue to increase to about 7.5 times normal levels (Gersing 1998). We have also recorded that real conductivity of excised rat liver subject to cryogenic freezing in liquid nitrogen and subsequent thawing increases to about 1.6-2.9 times its initial value (Edd 2006). Considering these data, these images suggest EIT has detected a widespread cell membrane disruption, i.e. cryoablation, in the central treated area.

Representative pictures along the central cross-section within the treated zone are shown in figure 6. From these photographs, some of the effects become apparent. First, the macroscopically visible congestion is widespread at points close to the cryoprobe tip (see figure 6(a)-(b)) but conspicuously absent near the ice front and in the unfrozen tissue (see figure 6(d)). Second, though the microscopically visible changes are at an early stage (fixation was 37 minutes after treatment), moderate nuclear pyknosis is present in figure 6(a)-(b) but absent in figure 6(d). In addition, blood vessels near the cryoprobe tip, which have experienced conditions similar to immersion in liquid nitrogen, have clotted (see figure 6(a)). Halfway between the cryoprobe tip and the ice front, conditions appear to have been consistent with a slower freeze; note that the blood vessel depicted in figure 6(b) does not have an intact endothelium. Outside the ice front, as in figure 6(d), vessels appear intact. Figure 6(c) shows tissue exhibiting changes between these extremes.

Moreover, tissue within a hemisphere centered at the cryoprobe tip, approximately half the radius of the ice front, is showing early signs of degeneration and in any case would have died from coagulative necrosis. Varying degrees of damage to the parenchyma are visible between this region and the ice front, at which point the frozen and unfrozen tissues are nearly indistinguishable. As the in vivo results should be more complex than those obtained from excised tissues, the EIT images are consistent with the conductivity profile expected from the observed microscopic pathology. Specifically, a zone of an approximately two-fold increase in 1 kHz real conductivity is present in the frozen region, centered at the cryoprobe tip, which fades gradually to normal at the ice front.

4. Discussion

The EIT system effectively observed the progression of the ice front during freezing in a gel model and generated accurate images indicative of tissue viability post-thawing in a raw potato model; however, the corresponding results for the in vivo study were of a poorer quality. The images of the ice front fall short of the accuracy and resolution possible from ultrasound or MRI; however, the images in figure 5(d)-(g) compare well with competing techniques like PET or functional MRI for tracking tissue viability.

For the advantages of using EIT in monitoring the freezing process of cryosurgery to become realized, these images must approach the quality of ultrasound, which is also comparatively fast and inexpensive. The performance needed to justify the use of EIT for viability imaging in general is considerably lower. For the specific goal of assessing the effect of cryosurgery, a higher resolution is necessary. Here, the goal is to measure the gap between the inner zone of complete cell death and the interface between frozen and unfrozen tissue indicated by ice front imaging. From figure 6(g), this transition zone from ablated tissue to unharmed tissue occurred over about 2 mm, close to the 1 mm pixel size in the images. Ideally, there should be an order of magnitude increase in resolution within this transition zone for the information to become useful to a cryosurgeon.

Though the number of unknowns one can recover (here this is the number of pixels) should not normally exceed the number of independent voltage measurements collected during a scan to ensure stability of the inverse problem, resolution in EIT is more often limited by the accuracy of those measurements and the forward model to which they are compared. It is difficult to obtain an accurate forward model in vivo due to the presence of anisotropic anatomical features, such as the large blood vessels in figure 6(g), but also due to motion artefacts: changes during each 50-second scan will skew the resulting image since each four-electrode measurement will have resulted from a slightly different distribution of properties. We reduce these types of errors by using differential EIT which only requires that relative differences between two scans are known accurately. This can be further improved by direct incorporation of anatomical structures into the forward model based on a preoperative MRI or CT scan, but also with faster acquisition. Even with an accurate forward model, large changes in conductivity within a single pixel cause alterations to electrode voltages that are often too small to resolve accurately. Therefore, to prevent the amplification of any measurement errors into the images, one often reduces the sought-after resolution while making appropriate assumptions about the character of the images that are possible. Here we adjust for the type of measurement noise we expect and enforce smoothness on the conductivity images.

Smoothing does not capture the discontinuity in impedance at the ice front. More specialized methods exist that can recover such a large contrast (Otten and Rubinsky 2005; Soleimani et al 2006a), but only by making the assumption that unfrozen tissue conductivity does not change during cooling. A more robust solution for ice front imaging may be a mixture of a level-set (Soleimani et al 2006b) or boundary element (Otten and Rubinsky 2005) definition of the frozen zone with a pixel-based method in the unfrozen region. This would also prevent the elevated specific impedance magnitude near the ice front from causing the ice front position to be overestimated (Edd et al 2005) while retaining the sharp transition in properties at the ice front. For imaging viability post-thaw, resolution can be enhanced by incorporating the prior knowledge of the ice front position (Edd and Rubinsky 2006) since unfrozen tissue seems little affected by nearby freezing (see figure 6(d)), however care must be taken that changes in conductivity outside of the frozen region are not prevented but that they are assumed to be less likely to occur.

We have improved sensitivity to changes in the previously frozen zone by placing the electrode array close to the target tissue; however, this becomes more difficult when the procedure is to be minimally-invasive. It seems logical to make use of the many cryoprobes used simultaneously in modern cryosurgery as an additional electrode array, something that has been demonstrated for ice front imaging (Hartov et al 2002). This will focus the post-thaw images within the previously frozen zone, more accurately resolving the transition zone.

5. Conclusion

This work has been concerned with using impedance measurements to guide cryosurgery. To that end, it first described a pixel-based differential EIT algorithm and its implementation, then validated the system for ice front imaging in a gel model, for viability imaging post-thaw in raw potato slices, and finally for the first in vivo trial of EIT-monitored cryosurgery, during and after cryoablation, in the liver of a live rat. Although the complexities of using EIT in vivo when compared to the gel and potato models have become apparent, it is clear from the results that EIT can detect frozen tissue and the changes indicative of membrane disruption after thawing in a live animal. Furthermore, as the state of the art in EIT advances, we suggest how the images presented here could be improved to the point that a cryosurgeon will use them as part of a feedback loop during cryoablation. Such a system will allow treatment to exceed current standards of accuracy and reliability, sparing more healthy tissue and reducing occurrences of harmful side effects. In conclusion, EIT should be able to image the result of any ablative procedure whose effect on the low frequency electrical conductivity of tissue is dominated by the disruption of cell membranes, a consideration which argues for increased effort to establish widespread clinical use of the impedance imaging technique.