Abstract
Humans use their arms to engage in a wide variety of motor tasks during everyday life. However, little is known about the statistics of these natural arm movements. Studies of the sensory system have shown that the statistics of sensory inputs are key to determining sensory processing. We hypothesized that the statistics of natural everyday movements may, in a similar way, influence motor performance as measured in laboratory-based tasks. We developed a portable motion-tracking system that could be worn by subjects as they went about their daily routine outside of a laboratory setting. We found that the well-documented symmetry bias is reflected in the relative incidence of movements made during everyday tasks. Specifically, symmetric and antisymmetric movements are predominant at low frequencies, whereas only symmetric movements are predominant at high frequencies. Moreover, the statistics of natural movements, that is, their relative incidence, correlated with subjects' performance on a laboratory-based phase-tracking task. These results provide a link between natural movement statistics and motor performance and confirm that the symmetry bias documented in laboratory studies is a natural feature of human movement.
INTRODUCTION
Studies of sensory systems have shown that their representations are adapted to the statistical structure of natural sensory stimuli (Barlow 1961). For example, the receptive fields of cells in the visual cortex appear to be optimized for the statistical properties of natural scenes (Körding et al. 2004; Olshausen and Field 1996). Although the statistics of natural sensory inputs have received a great deal of attention and detailed characterization (Klein et al. 2003; Ruderman and Bialek 1994; Schwartz et al. 2003), the statistics of natural movements have received little attention (Ingram et al. 2008; Kilbreath and Heard 2005; Slijper et al. 2009). Rather, human movement has been predominantly studied in a laboratory setting using predefined tasks. Just as the study of the sensory system has benefited from analysis of the statistics of natural sensory stimuli, we suggest that the study of the motor system can similarly benefit from an analysis of the statistics of natural movements.
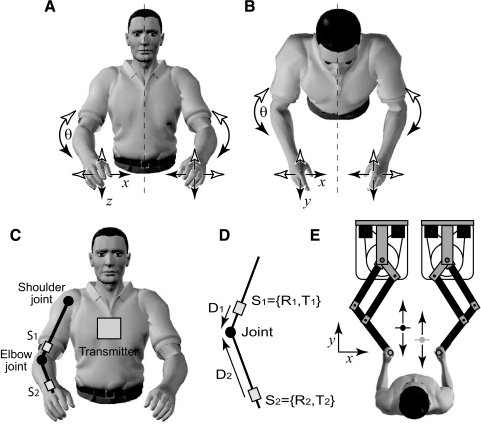
One feature of movement performance, which has been extensively studied in the laboratory, is the phase relation between left and right body parts during rhythmic movements (Kelso 1984, 1995; Li et al. 2005; Mechsner et al. 2001; Schmidt et al. 1993; Swinnen et al. 1998, 2002). In this context, bimanual movements can be described in terms of the phase relation between the left and right arms (see Fig. 1, A and B). In common with previous studies, we use the convention that a 0° phase difference between the two arms corresponds to their moving in a mirror-symmetric way in extrinsic space with respect to the midsagittal plane. In muscle-based definitions of symmetry, such 0° phase differences correspond to the use of homologous muscles (Kelso 1984).
FIG. 1.
A: front view of subject showing movements at the elbow in joint space and at the hands in extrinsic space for the x-axis and z-axis. Dotted line shows the midsagittal plane. The directions of symmetric movements are shown by corresponding pairs of either open arrowheads on both sides or filled arrowheads on both sides. The directions of antisymmetric movements are shown by corresponding pairs of open arrowheads on one side with filled arrowheads on the other. B: top view of subject, as in A, showing movements at the elbow in joint space and at the hands in extrinsic space for the x-axis and y-axis. C: the transmitter and sensor locations shown for the right arm with S1 located on the upper arm and S2 on the lower arm near the wrist. The transmitter is mounted on the chest over the sternum and defines the coordinate system for position and orientation of the sensors. Sensors S3 and S4 (not shown) are similarly located on the left arm. D: details of the joint center analysis showing sensors proximal and distal to the elbow joint with rotations (R1 and R2 for sensors 1 and 2, respectively) and translations (T1 and T2) relative to transmitter. The vectors D1 and D2 describe the location of the joint center relative to the upper and lower sensors, respectively. E: experimental setup for the phase-tracking task. The coordinate system is marked on the figure and the tracking movements were made along the y-axis.
Studies of symmetry bias clearly demonstrate that not all movements are equally easy to perform and highlight two cardinal features. First, at low frequencies both symmetric and antisymmetric movements (phase difference between the two arms of 0 and 180°, respectively) can be performed easily and stably, whereas movements with intermediate phase relations are more difficult to perform. Second, as the frequency of movement increases, only symmetric movements can be performed stably and all other phase relations tend to transition to a symmetric mode (Tuller and Kelso 1989; Wimmers et al. 1992). The properties of this symmetry bias have been extensively documented and modeled using oscillator and nonlinear dynamical systems models. These models can explain not only the two modes of observed stable behaviors but also the discontinuous phase transitions between them (Haken et al. 1985). Here we hypothesize that the symmetry bias will also be present in everyday movements. Moreover, we suggest that the incidence of particular movement phases—that is, how often they occur—will be related to performance. For example, previous laboratory studies have found that measures of performance depend on the logarithm of the number of training trials (Heathcote et al. 2000) and this suggests that the logarithm of the incidence of different phase relations in everyday movements (corresponding to training) may also relate to measures of laboratory performance. This hypothesis would not preclude a dynamic systems model accounting for the empirical data.
To examine whether performance is related to the statistics of natural movements, we developed a wearable motion-tracking system to record the arm movements of human subjects as they went about their daily life. The system allowed our subjects to engage spontaneously in normal everyday tasks while we recorded the kinematics of their right and left arms. Our results suggest that the symmetry bias reported from laboratory-based tasks is present in natural everyday movements. Moreover, when the same subjects performed a laboratory-based tracking task that measured error as a function of different phase relationships between the arms, we found that the incidence of natural movements correlated with subjects performance in the task. Both the form of the phase-related errors on the task and the incidence of particular phase relations in the natural data set replicated the “seagull effect” (Kelso 1995; Tuller and Kelso 1989). Moreover, the relationship between the errors and incidence was well fit using a logarithmic relation, consistent with previous studies (Heathcote et al. 2000). These results represent a novel contribution to the field by, first, documenting the relative phase relations that occur in natural arm movements and, second, demonstrating that the incidence of these phase relations is correlated with performance.
METHODS
Data acquisition
After providing written informed consent, six subjects took part in the experiment. A local ethics committee approved the experimental protocol. Two of the participants were authors (ISH and JNI) and four participants were naïve to the purpose of the experiment. No qualitative differences were observed between the subjects. Liberty sensors (Polhemus, Colchester, VT) were attached to the left and right upper arms, just above the elbow, and also to the wrists (Fig. 1C). Subjects carried a backpack containing the modified Liberty hardware, battery power supply, and a computer logging the data at 120 Hz. The Polhemus transmitter was firmly attached to the participant's chest (Fig. 1C). The initial version of the backpack weighed about 11 kg and allowed subjects to carry out most everyday tasks and move around freely both indoors and outdoors. The design was later improved, reducing its weight to 5.5 kg. In total, >31 h of recording was obtained from the subjects. The first three subjects wore the original backpack design (8.8, 9.1, and 3.9 h recorded in blocks of ∼1 h) and the final three subjects wore the improved design (3.1, 3.1, and 3.0 h also recorded in blocks of ∼1 h). Several of the subjects wore backpacks regularly, rather than using a briefcase, so were accustomed to performing daily tasks in the presence of a backpack. Results were qualitatively the same with both types of backpack and across the subjects, independent of whether they regularly wore a backpack. Subjects were told to avoid close proximity to large metallic objects, which could distort the measurements, and were informed that signal quality could be monitored using a visible status indicator. Subjects were requested to perform typical activities they would do normally; questioning revealed that recording sessions included a wide range of activities such as walking, going shopping, reading, doing jigsaw puzzles, constructing model airplanes, food preparation, and having lunch.
Joint angle analysis
Each sensor provided position and orientation, which was used to calculate the elbow angles and the angular speed of the elbow and shoulder joints of each arm. The Polhemus system records the three-dimensional (3D) position (3 × 1 vectors Tkt) and 3D orientation (3 × 3 matrices Rkt) of each sensor with respect to the transmitter (the subscript k = 1, 2 refers to the upper and lower sensors for a particular arm and the superscript t is the time sample). The center of rotation for the elbow joint can be estimated from the sensors proximal and distal to the joint (Fig. 1D). Each sensor can be considered to represent a coordinate system that translates and rotates with the sensor. Dk is a vector that defines the center of rotation of the elbow joint relative to sensor Sk (Fig. 1D)—that is, using the coordinate system defined by the position and orientation of sensor Sk, vector Dk corresponds to the location of the elbow joint within that coordinate system. Dk is constant because the relative locations of the sensors and elbow joint do not change as the arms move. We used the measurements from each sensor to estimate the location of the center of the elbow joint in the coordinate system of the transmitter: that is, R1tD1 + T1t and R2tD2 + T2t. Because both of these represent the same location—that is, the center of the elbow joint in the coordinate system of the transmitter—they should coincide (subject to noise in the sensor readings and the fact that the elbow joint does not have a single point of rotation). Therefore we can estimate D1 and D2 by finding their values that minimize the error between the two estimates across time samples. Specifically, we seek to minimize the squared error given by
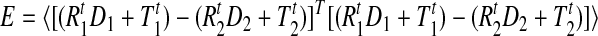 |
where 〈·〉 denotes the average across time samples. For simplicity, we define concatenated matrices and vectors
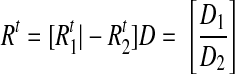 |
and Tt = T1t − T2t.
That is
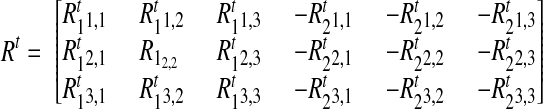 |
which is a 3 × 6 matrix, where the first subscript on each element identifies the original rotation matrix and the second subscript defines its corresponding element. As stated earlier, the superscript t defines time. Similarly
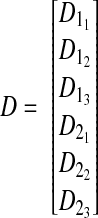 |
which is a 6 × 1 vector where the first subscript on each element identifies the original displacement vector and the second subscript defines its corresponding element.
Thus we can rewrite the expression for error as
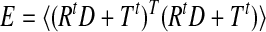 |
To find the minimum we differentiate with respect to D and equate it to zero, that is
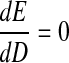 |
which gives
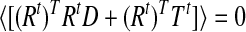 |
and thus
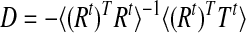 |
To calculate the center of the elbow joint for each time point, we take the average of the estimates derived from the proximal and distal sensors
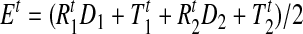 |
where Et is the location of the elbow joint, in the coordinate frame of the transmitter, at time t. The elbow angle was then calculated using the cosine rule as the angle between the vectors linking the proximal sensor to the elbow joint (T1t − Et) and the distal sensor to the elbow joint (T2t − Et). The elbow speed was obtained by computing the difference between elbow angles over consecutive time points and dividing by the sampling interval Δt.
To calculate the angular speed of the shoulder joint we use the fact that rotation of a rigid object, such as the upper arm, can be represented by a single scalar rotation angle about a given axis. This is the basis of the quaternion representation that specifies both the axis of rotation (three parameters defining the vector for the axis of rotation) and the (scalar) angle of rotation. To calculate the shoulder speed we computed the change in rotation angle for the upper arm between consecutive time samples. To do this we first calculated the change in the rotation matrix between time samples ΔRt = (R1t)−1R1t+1. This rotation matrix was used to determine the angular change (Δθt) using standard conversion to quaternion form
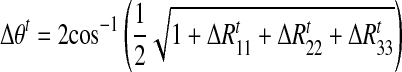 |
where ΔRkkt is the (k, k) element of the matrix. The shoulder rotation speed is then given by Δθt/Δt. We performed these analyses for the left and right arms.
Wavelet phase analysis
Short-term frequency-dependent phase analysis was performed on the two elbow angle time series. Because the elbow angle depends on the relative angle between the two sensors on each arm, it is less sensitive than the raw data to any movements of the transmitter. Moreover, in distinction to the convention needed to define symmetry in terms of movement of the limbs in extrinsic space, there is no ambiguity when defining symmetry in terms of the angular motion of the elbow joints (see Fig. 1, A and B). Position trajectories of point-to-point reaching movements are similar in form to a half cosine and thus have an associated fundamental frequency and phase. An analysis was required that was able to extract the phase of such signals as a function of frequency. Of course, there will also be movements involving oscillations of the arms, especially during activities such as walking, with the arms swinging. Although short-term fast Fourier transform (FFT) analysis can be used to estimate phase, it is not as effective in dealing with localized events such as discrete movements. One way to improve this is to match window length as a function of frequency. In this way, the window length will better fit a discrete event in the signal. This is effectively what wavelet analysis does—the time window of the wavelet is a function of its bandwidth (Mallat 1999). The Hilbert transform is often used to decompose a signal into instantaneous phase and amplitude. However, it is not appropriate here because it does not provide the necessary frequency-dependent phase analysis. Moreover, wavelet analysis is being increasingly applied to biological signals such as electroencephalograms (Selesnick et al. 2005).
We performed a dual-tree complex wavelet transform (DT-CWT) (Kingsbury 2001) on the left and right elbow angles, using eight levels of wavelet decomposition. The complex nature of the subband outputs from this transform produces analytic waveforms that have both amplitude and phase in subbands that are each approximately one octave wide. The DT-CWT has the important property of shift invariance, which ensures that all input signals are analyzed in equivalent ways.
The analysis was repeated several times on resampled input data, to shift the center frequencies of the wavelet analysis, resulting in 30 overlapping bands ranging from a 0.45- to 0.9-Hz band to a 3.2- to 6.4-Hz band. For each band we obtained the time series of phase relations and amplitude in the left and right elbow angle signals. To obtain a relative incidence for each phase relation for a band, we first calculated a weighted incidence using the cross power (i.e., the product of the left and right amplitudes). Because phase is always defined, even when the cross power is close to zero, this ensured the statistics reflected only the phase relations that occurred during significant movements of both arms, thereby excluding periods in which one or both of the arms were stationary. As such, the contributions of unimanual movements to the relative phase distributions are suppressed.
Computation of relative phase incidence
Within a frequency band the relative phase incidences were first allocated to one of 18 bins each 20° wide. The total incidences across all bins in a given frequency band were then normalized to sum to 1. Statistical tests were performed for each subject using a t-test of the relative incidence of phase relations at 0/360° (symmetric) versus 180° (antisymmetric) and at 180° versus the average incidence at 90 and 270°.
Similar phase analyses were performed for movements of the distal sensors for the three Cartesian axes, except that in this case only the low-frequency band of 0.9–1.8 Hz was examined.
Validation of wavelet phase analysis
We validated the wavelet phase analysis on two different data sets. For the first data set, we generated synthetic left and right elbow angle data by simulating two independent random walks. For the second data set, we inserted a set of relative time shifts between the left and right elbow angles from the natural movement data set. In all cases the data were analyzed at low- (0.45–0.9 Hz) and high-frequency bands (3.2–6.4 Hz). Analysis of the random walk data set resulted in uniform phase incidences at both low- and high-frequency bands, as expected. For the time-shifted data sets, analysis resulted in the expected shifts in the relative phase incidences. Full details of these two validations are available in the Supplemental Material.1
Conditioning for similar versus different joints
We also performed a phase analysis of the positions of the distal sensors at the wrists in extrinsic space, for subsets of the data based on whether the arms were moved predominantly by rotations around the same or different joints (see Fig. 5, A and C). If the phase distributions are similar between the two subsets of the data, this would suggest that the symmetry bias (defined in external space) does not occur because we use homologous muscle groups, as previously suggested (Kelso 1984). Elbow and shoulder angular speeds were used to divide the data into either a “similar-joint” subset or “dissimilar-joint” subset. The similar-joint subset included all the data in which, for both arms, either the angular speeds of the shoulders were greater than those of the elbows or the angular speeds of the elbows were greater than those of the shoulders (Fig. 5A). In this case, movement of the distal sensors on both arms was dominated by either both shoulders or by both elbows. In contrast, the dissimilar-joint subset included the complement of the similar-joint subset. Specifically, it included data in which the angular speed of the shoulder in one arm was greater than that of the elbow and in the other arm the converse was true (Fig. 5C). In this case, movement of the distal sensors on both arms was dominated by different joints on each arm.
For both subsets of the data set we calculated the phase relations for each of the three Cartesian axes for movement of the distal sensor using the same methods as described earlier. The phase relations for the three Cartesian axes were then averaged to calculate the relative incidence. We used the convention that a 0° phase difference between the two arms corresponds to their moving in a mirror-symmetric way with respect to the midsagittal plane.
Tracking paradigm
To obtain a quantitative measure of performance at different phase relations for the same subjects who participated in the natural movement data collection, subjects were also required to perform a phase-tracking task. The tracking task was designed to compare phase-tracking performance with the incidence of relative phases between the distal sensors at the wrists in the natural movement data set. The task was similar to that used by previous studies of symmetry bias (Tuller and Kelso 1989). Specifically, subjects were required to track two targets in a virtual reality system, as shown in Fig. 1E (Howard et al. 2009). Each target moved sinusoidally toward and away from the body in the horizontal plane over a range of 16 cm at 0.5 Hz (all subjects) or 1.6 cm at 5.0 Hz (four subjects). Movement amplitude was scaled down for the higher frequency to maintain the same peak movement velocities. We chose the frequencies of 0.5 and 5 Hz because we wanted to use two values that were quite far apart in terms of the distribution of phases from our natural data set to test the logarithmic law hypothesis.
Subjects held the handles of two robotic manipulanda, separated by 13 cm, that were used to record hand movements at 1,000 Hz (Howard et al. 2009). The handles were constrained to move in channels limiting movements to a single degree of freedom (DOF). The position of each handle was represented by its own virtual cursor that was used to track each of the two targets. Although the movement of each hand was constrained to a single DOF in extrinsic space, the arm itself was unconstrained with regard to joint recruitment.
Subjects each performed 20 trials of 15-s duration at each of the 18 relative phases in a pseudorandom order. On each trial the two targets moved with a relative phase that was chosen out of the set (0, 20, …, 340°). The last 13 s of each trial were analyzed using wavelets as described earlier for the distal sensor positions. This allowed us to determine the relative phase between the two hands and thus compute the root-mean-square phase error for the tracking task.
We fit the incidence of relative phases for the distal sensors from the natural movement data set to the performance data from the tracking task. Specifically, we analyzed wrist translation in the y-axis (Fig. 1E), which is the direction used for the tracking task. To estimate incidence at low frequencies, we averaged over several low-frequency bands to achieve a wider bandwidth (0.27–1.2 Hz) than could be achieved from a single wavelet band. This ensured the results included components that covered the low frequencies appropriate for the 0.5-Hz tracking task. For the 5.0-Hz tracking task, a single wavelet band was sufficient (3.4–6.8 Hz).
RESULTS
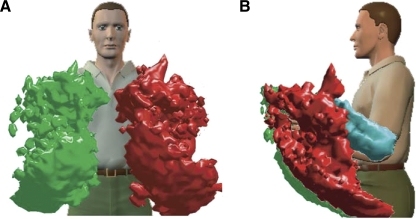
We attached sensors to the elbows and wrists of six volunteers who wore a backpack containing motion-tracking equipment. The sensors recorded the position and orientation of both wrists and elbows over extended periods of time (3.0–9.1 h/subject). The boundary enclosing the 0.9 percentile of the distributions of wrist and elbow positions for one subject is shown in Fig. 2. This shows that the majority of wrist and elbow positions fall within a region close to the body.
FIG. 2.
Distribution of hand and elbow positions. Front and side views (A and B, respectively) showing the outer boundaries of regions that represent 90% of all locations visited by a typical subject's wrists (green and red) and elbows (only left visible, cyan) during 8.8 h of movement. Small isolated regions have been removed for clarity.
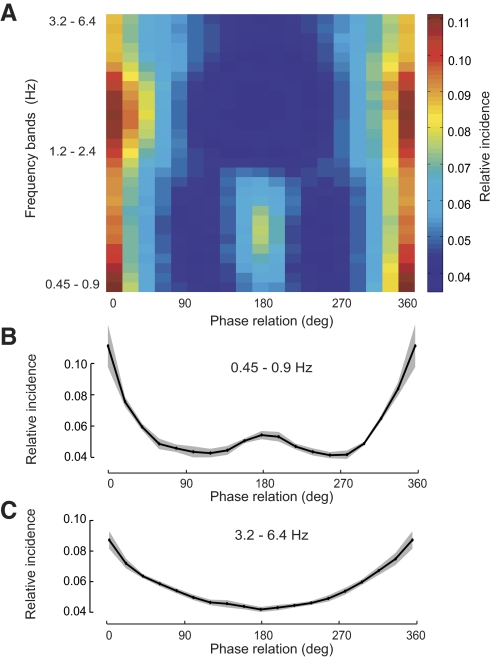
From this natural data set we calculated the phase relations between flexion–extension movements of the right and left elbows for a range of movement frequencies (Fig. 3). For each frequency band we examined how often each phase relation was observed during natural movement, which allowed us to determine the relative incidence of each phase relation. Figure 3A illustrates how this measure of relative incidence changes with increasing frequency, showing a progression from a bimodal to unimodal distribution as the frequency increases.
FIG. 3.
Distributions of the phase differences in the natural movement data set between the elbows averaged over 6 subjects. Phase of 0–180° corresponds to the left elbow leading the right. A: average incidence against frequency. B: average (line) and SE (shading) for the 0.45- to 0.9-Hz frequency band. C: average (line) and SE (shading) for the 3.2- to 6.4-Hz frequency band.
At low movement frequencies (0.45–0.90 Hz, Fig. 3B) each subject's distribution was bimodal with symmetric (phases at 0/360°) movements occurring significantly more often than antisymmetric (phase of 180°) movements (P < 0.01, average ratio of incidence of 2.0 across subjects). Moreover, antisymmetric movements at 180° occurred significantly more often than did the intermediate phase relations of 90° (P < 0.05) and 270° (P < 0.05). At higher movement frequencies (3.2–6.4 Hz, Fig. 3C) the distribution became unimodal, with symmetric movements still occurring significantly more often than antisymmetric movements (P < 0.01, average ratio of incidence of 2.0 across subjects). However, at these higher frequencies the second peak for antisymmetric movements was no longer present and their incidence was significantly less than those of 90° (P < 0.001) and 270° (P < 0.01). Taken together, these results parallel laboratory observations showing that movements with a phase relation other than symmetric and antisymmetric are especially difficult and that antisymmetric movements become unstable as the frequency of movement increases (Kelso 1984).
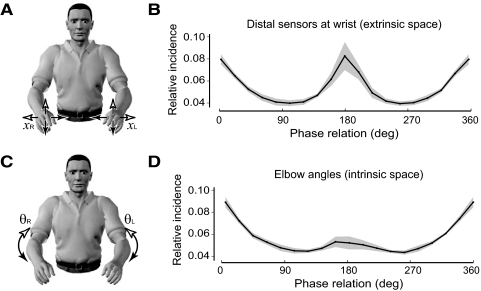
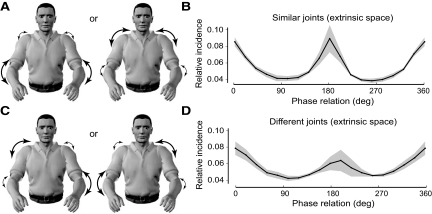
Another fundamental issue that has been addressed in laboratory experiments (Mechsner et al. 2001; Swinnen et al. 1998) relates to the coordinate system for the symmetry bias. Elbow joint angles were used for the preceding phase analysis because these were most precisely measured with our apparatus (see methods). Consequently, such an analysis quantified symmetry bias in joint (intrinsic) space. An important question is whether the symmetry bias is similarly present in extrinsic space. This would be expected if the demands on natural motor tasks are defined in extrinsic space. To examine this, we compared the relative incidence of phase relations for the distal sensors on the wrist moving in extrinsic space (Fig. 4, A and B) with that of the elbow angles in joint space (Fig. 4, C and D). Interestingly, the incidence of 180° phase is significantly higher for the movements defined in extrinsic space than those defined in intrinsic space (P < 0.05 for each subject; averaged incidence ratio = 1.6). Similarly, the incidence of 0° phase was significantly lower (P < 0.01 for each subject; averaged incidence ratio = 0.9). This suggests a stronger component of antisymmetric movement for task-based (extrinsic) coordinates.
FIG. 4.
Comparison of the relative incidence of phase relations in the 0.9- to 1.8-Hz frequency band for movements of the distal wrist sensors in extrinsic space vs. elbow angles in intrinsic space. A: front view of subject showing movements in extrinsic space. Arrowheads indicate the direction of symmetric and antisymmetric movements, as in Fig. 1. B: relative incidence of phase relations for movements of the distal wrist sensors in extrinsic space. Average over subjects (line) and SE (shading). C: front view of subject showing elbow movements in intrinsic space. Arrowheads indicate the direction of symmetric and antisymmetric movements, as in Fig. 1. D: relative incidence on phase relations for movements of the elbows in intrinsic space, plotted as in B.
Another important question is whether the bias favoring symmetric movements arises because they are executed in the same direction in extrinsic space or because they involve movements around the same joints. To address this issue in the natural movement data set, we split the distal sensor data recorded at the wrists into two parts. The first part contained samples in which movement of the left and right arms predominantly resulted from rotations around similar joints (Fig. 5 A). The second part contained samples in which movement of the arms predominantly resulted from rotations around the dissimilar joints (Fig. 5C) (see methods for details). For these two data sets, we analyzed phase relations between the two distal sensors in a midfrequency band (0.9–1.8 Hz). We chose this range so we could examine whether the bimodal peaks in incidence for symmetric and antisymmetric movements were different between the two subsets of the data.
FIG. 5.
Comparison of the relative incidence of phase relations in the 0.9- to 1.8-Hz frequency band for movements of the distal wrist sensors in extrinsic space conditioned on the use of similar or dissimilar joints. A: front view of subject showing movements arising from rotations around similar joints in each arm. B: relative incidence of phase relations for movements of the distal wrist sensors in extrinsic space generated by rotations around similar joints. Average over subjects (line) and SE (shading). C: front view of subject showing movements arising from rotations around dissimilar joints in each arm. D: relative incidence of phase relations for movements of the distal wrist sensors in extrinsic space generated by rotations around dissimilar joints, plotted as in B.
For both the similar- and dissimilar-joint subsets of the natural movement data the distributions were bimodal, preserving the peaks in incidence for symmetric and antisymmetric movements (Fig. 5, B and D, respectively). Moreover, there were no significant differences in the relative incidences between the two data sets at either 0 or 180° phase. Thus the effect of selecting movements on the basis of different joint usage preserves the basic form of the distributions. This finding is in close correspondence with experimental data that show that the symmetry bias is present in extrinsic coordinates, regardless of the joints used (Mechsner et al. 2001; Swinnen et al. 2002).
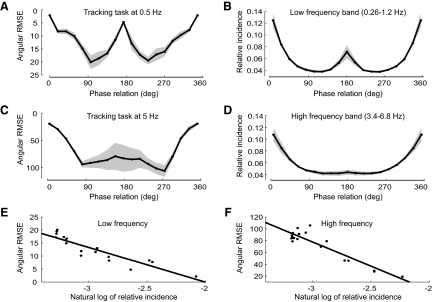
Previous studies have shown a relationship between the amount of training on perceptual tasks and performance (Heathcote et al. 2000). To investigate the relationship between performance and the relative incidence of movement phases in our natural movement data set, subjects performed a bimanual tracking task in a virtual reality environment (Fig. 1E; see methods). This required subjects to track two targets that moved sinusoidally at various phase relations at a low frequency (0.5 Hz) and a high frequency (5.0 Hz). The phase error at 0.5 Hz on the tracking task (Fig. 6A) is small for symmetric (0/360°) and antisymmetric (180°) movements, mirroring the relative incidence of these phases in the natural movement data set (Fig. 6B). Similarly, the phase error at 5 Hz on the tracking task (Fig. 6C) mirrors the relative incidence of these phases in the natural movement data set (Fig. 6D). However, in this case there was a stronger tendency to move symmetrically on the tracking task, as indicated by the almost linear relationship between error and phase between 0 and 90° and 270 and 360° (Fig. 6C). To further quantity the relationship between phase incidence in our natural movement data set and performance on the tracking task, we used linear regression to fit the performance errors to the log incidence of the phases. We found a good fit at both low (r2 = 0.86 P < 0.001, Fig. 6E) and high (r2 = 0.88, P < 0.001, Fig. 6F) frequencies. This demonstrates that the logarithmic law for training is also present between the natural incidence of a movement and motor performance on a laboratory task.
FIG. 6.
Performance on the laboratory-based phase-tracking task compared with incidences of relative phase in the natural movement data set at low frequencies (0.5 Hz, A, B, and E) and high frequencies (5 Hz, C, D, and F). A and C: the root mean squared error (RMSE) of phase in the tracking task is plotted as a function of the phase angle. B and D: the incidence of relative phase along the y-axis in the natural movement data set is plotted as a function of the phase angle. E and F: error in the tracking task plotted as a function of the log incidence of relative phase in the natural movement data set.
DISCUSSION
We recorded >30 h of natural arm movements from six subjects who were free to spontaneously engage in everyday tasks. Despite the large range of possible movements, we found that during most normal everyday tasks the arms are confined to a small volume of space around the body. We also analyzed the phase relations between the movements of the left and right arms and found that the relative occurrence of particular phases supports results from previous studies of symmetry bias in humans. Specifically, we found that at low frequencies both symmetric and antisymmetric movements were prevalent, whereas at higher frequencies symmetric movements became increasingly dominant. At low frequencies, the form of the phase incidence curve reflected the “seagull effect” previously described for finger-tapping experiments (Tuller and Kelso 1989).
The aim of the current study was to acquire data for movements that corresponded to what subjects do during everyday activities. Because there are many laboratory studies that look at only specific movements or tasks, our study was specifically designed to avoid such constraints. To achieve this we let subjects go about their daily routine with only a few instructions, such as avoiding large metallic objects or water. We examined the statistics of the movements and did not try to categorize the specific tasks that subjects were performing. However, it was important that the samples we acquired were representative of normal activities and we therefore collected >30 h of kinematic data. Although subjects may have engaged in different tasks during the recoding period, the statistics across subjects were very similar, as demonstrated by the low SEs (Figs. 3–6). This suggests that we have captured representative statistics in all our subjects.
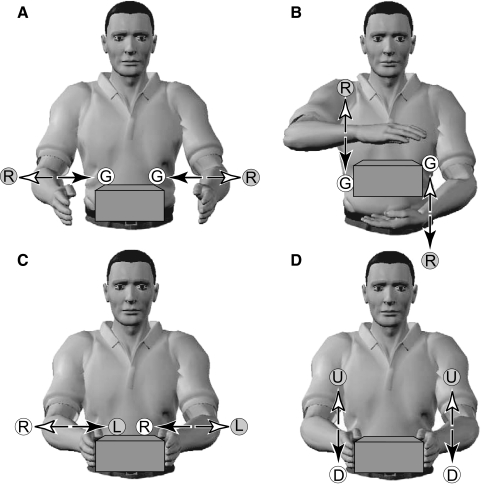
An interesting question arising from the current study is whether the symmetry bias exists because successful interaction with the environment requires both symmetrical movements (such as bimanual grasping of objects) and antisymmetric movements (such as laterally moving a handheld object). Alternatively, the symmetry bias may be an immutable property of the musculoskeletal and nervous systems. As such, it would fundamentally constrain the way we can interact with the world. Previous studies have assumed that fundamental constraints on performance arising from the perceptual (Mechsner et al. 2001) or motor systems (Swinnen et al. 2002) explain the symmetry bias. Indeed Mechsner et al. (2001) reported that symmetry in external space, or visual symmetry, can override this bias. However, as shown here and in laboratory-based experiments, the symmetry bias is present in extrinsic task space. This may be understood in terms of the requirement to interact with the external world. In contrast, constraints on the musculoskeletal and nervous systems would be expected to be manifest in intrinsic (joint space) coordinates. For example, it is intuitively obvious why symmetric and antisymmetric movements may be common in bimanual object manipulation tasks (Fig. 7). If we seek to simultaneously bring both hands together from different positions to pick up an object this requires phases of 0 or 180°, depending on the axis. For example, bringing the hands laterally together to grasp an object from the left and right or moving them apart to release it requires movement phases of 0° (Fig. 7A). In contrast, bringing the hands vertically together to grasp an object from above and below or moving them apart to release it requires movement phases of 180° (Fig. 7B). Once the object is grasped, transporting it then requires movement with phases of either 0 or 180°, depending on the direction of transport. For example, moving a bimanually grasped object left or right requires movement phases of 180° (Fig. 7C). In contrast, moving a bimanually grasped object up or down requires movement phases of 0° (Fig. 7D). Consequently, interaction with objects typically requires movements with phases at 0 and 180° in extrinsic space.
FIG. 7.
Bimanual phase relations during object manipulation. Arrowheads on the left and right indicate the direction of symmetric and antisymmetric movements, as in Fig. 1. A: bringing the hands laterally together to grasp an object (G) from the left and right or moving them apart to release it (R) requires symmetric movements. B: bringing the hands vertically together to grasp an object (G) from above and below or moving them apart to release it (R) requires antisymmetric movements. C: moving a bimanually grasped object left (L) or right (R) requires antisymmetric movements. D: moving a bimanually grasped object up (U) or down (D) requires symmetric movements.
Another interesting question concerns the relationship between the incidence of particular movements and performance. It is well known that training on a task improves performance, but with diminishing returns as training increases (Newell and Rosenbloom 1981). Specifically, relative performance is often related to the log of the number of training trials. This logarithmic dependence of performance on training appears to be a universal law of learning that applies to a wide range of cognitive problems such as multiplication, visual search, movement-sequence learning, rule learning, and mental rotation (Heathcote et al. 2000). In the current study, we found evidence for the existence of the logarithmic relationship between natural movement statistics and performance. This suggests that the log incidence of a movement may be a general predictor of motor performance and may provide a parsimonious explanation for the existence of the symmetry bias.
As previously discussed, the symmetry bias does not appear to be an immutable property of the musculoskeletal and nervous systems. For example, extensive training on the novel phase relation of 90° over the course of several days improves performance at this phase, but leads to a decrement in performance at other phases (Schoner and Kelso 1988; Zanone and Kelso 1992). Such training significantly changes the distribution of phases experienced by subjects and the observed results reflect these novel statistics. Similarly, if subjects are trained at new polyrhythms (Summers et al. 1993), significant improvement is observed (Klaiman and Karniel 2006). Interestingly, improving at one class of movement can come at the expense of a decrease in performance at others (Van Damme et al. 2002). One hypothesis consistent with these results is that there are limited neural resources available and that improvement at one phase necessarily involves a decrement in performance at others. This hypothesis is further supported by the finding that training on a particular task increases the size of its neural representation (Classen et al. 1998; Elbert et al. 1995; Kaas 1991; Karni et al. 1995). Interference between two similar motor tasks that are performed sequentially also suggests competition for finite neural resources (Brashers-Krug et al. 1996; Caithness et al. 2004; Miall et al. 2004; Tong et al. 2002). Taken in the context of the current study, this suggests that neural resources are indeed finite and that the statistics of natural movements will influence their allocation. This view provides a potential link between the occurrence of particular movements and performance.
GRANTS
This research was supported by the Wellcome Trust and European Project Grant SENSOPAC IST-2005-028056. K. Körding was supported by a Deutsche Forschungsgemeinschaft Heisenberg Fellowship.
Supplementary Material
Acknowledgments
We thank N. Kingsbury for advice and assistance with the wavelet analysis and R. Symonds and O. Krömer for technical assistance.
Footnotes
The online version of this article contains supplemental data.
REFERENCES
- Barlow 1961.Barlow HB. Possible principles underlying the transformation of sensory messages. In: Sensory Communication, edited by Rosenblith WA. Cambridge, MA: MIT Press, 1961, p. 217–234.
- Brashers-Krug et al. 1996.Brashers-Krug T, Shadmehr R, Bizzi E. Consolidation in human motor memory. Nature 382: 252–255, 1996. [DOI] [PubMed] [Google Scholar]
- Caithness et al. 2004.Caithness G, Osu R, Bays P, Chase H, Klassen J, Kawato M, Wolpert DM, Flanagan JR. Failure to consolidate the consolidation theory of learning for sensorimotor adaptation tasks. J Neurosci 24: 8662–8671, 2004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Classen et al. 1998.Classen J, Liepert J, Wise SP, Hallett M, Cohen LG. Rapid plasticity of human cortical movement representation induced by practice. J Neurophysiol 79: 1117–1123, 1998. [DOI] [PubMed] [Google Scholar]
- Elbert et al. 1995.Elbert T, Pantev C, Wienbruch C, Rockstroh B, Taub E. Increased cortical representation of the fingers of the left hand in string players. Science 270: 305–307, 1995. [DOI] [PubMed] [Google Scholar]
- Haken et al. 1985.Haken H, Kelso JA, Bunz H. A theoretical model of phase transitions in human hand movements. Biol Cybern 51: 347–356, 1985. [DOI] [PubMed] [Google Scholar]
- Heathcote et al. 2000.Heathcote A, Brown S, Mewhort DJ. The power law repealed: the case for an exponential law of practice. Psychon Bull Rev 7: 185–207, 2000. [DOI] [PubMed] [Google Scholar]
- Howard et al. 2009.Howard IS, Ingram JN, Wolpert DM. A modular planar robotic manipulandum with end-point torque control. J Neurosci Methods 181: 199–211, 2009. [DOI] [PubMed] [Google Scholar]
- Ingram et al. 2008.Ingram JN, Kording KP, Howard IS, Wolpert DM. The statistics of natural hand movements. Exp Brain Res 188: 223–236, 2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kaas 1991.Kaas JH. Plasticity of sensory and motor maps in adult mammals. Annu Rev Neurosci 14: 137–167, 1991. [DOI] [PubMed] [Google Scholar]
- Karni et al. 1995.Karni A, Meyer G, Jezzard P, Adams MM, Turner R, Ungerleider LG. Functional MRI evidence for adult motor cortex plasticity during motor skill learning. Nature 377: 155–158, 1995. [DOI] [PubMed] [Google Scholar]
- Kelso 1984.Kelso JAS. Phase transitions and critical behaviour in human interlimb coordination. Am J Physiol 240: 1000–1004, 1984. [DOI] [PubMed] [Google Scholar]
- Kelso 1995.Kelso JAS. Dynamic Patterns: The Self-Organization of Brain and Behavior. Cambridge, MA: MIT Press, 1995.
- Kilbreath and Heard 2005.Kilbreath SL, Heard RC. Frequency of hand use in healthy older persons. Aust J Physiother 51: 119–122, 2005. [DOI] [PubMed] [Google Scholar]
- Kingsbury 2001.Kingsbury N. Complex wavelets for shift invariant analysis and filtering of signals. Appl Comput Harmonic Anal 10: 234–253, 2001. [Google Scholar]
- Klaiman and Karniel 2006.Klaiman E, Karniel A. Bimanual adaptation: internal representations of bimanual rhythmic movements. Exp Brain Res 171: 204–214, 2006. [DOI] [PubMed] [Google Scholar]
- Klein et al. 2003.Klein DJ, König P, Körding KP. Sparse spectrotemporal coding of sounds. EURASIP J Appl Signal Process 7: 658–667, 2003. [Google Scholar]
- Körding et al. 2004.Körding KP, Kayser C, Einhauser W, Konig P. How are complex cell properties adapted to the statistics of natural stimuli? J Neurophysiol 91: 206–212, 2004. [DOI] [PubMed] [Google Scholar]
- Li et al. 2005.Li Y, Levin O, Forner-Cordero A, Swinnen SP. Interactions between interlimb and intralimb coordination during the performance of bimanual multijoint movements. Exp Brain Res 163: 515–526, 2005. [DOI] [PubMed] [Google Scholar]
- Mallat 1999.Mallat S. A Wavelet Tour of Signal Processing (2nd ed.). San Diego, CA: Academic Press, 1999.
- Mechsner et al. 2001.Mechsner F, Kerzel D, Knoblich G, Prinz W. Perceptual basis of bimanual coordination. Nature 414: 69–73, 2001. [DOI] [PubMed] [Google Scholar]
- Miall et al. 2004.Miall RC, Jenkinson N, Kulkarni K. Adaptation to rotated visual feedback: a re-examination of motor interference. Exp Brain Res 154: 201–210, 2004. [DOI] [PubMed] [Google Scholar]
- Newell and Rosenbloom 1981.Newell A, Rosenbloom PS. Mechanisms of skill acquisition and the law of practice. In: Cognitive Skills and Their Acquisition, edited by Anderson JR. Hillsdale, NJ: Erlbaum, 1981, p. 1–55.
- Olshausen and Field 1996.Olshausen BA, Field DJ. Natural image statistics and efficient coding. Network (Bristol, England) 7: 333–339, 1996. [DOI] [PubMed] [Google Scholar]
- Ruderman and Bialek 1994.Ruderman DL, Bialek W. Statistics of natural images: scaling in the woods. Phys Rev Lett 73: 814–817, 1994. [DOI] [PubMed] [Google Scholar]
- Schmidt et al. 1993.Schmidt RC, Shaw BK, Turvey MT. Coupling dynamics in interlimb coordination. J Exp Psychol Hum Percept Perform 19: 397–415, 1993. [DOI] [PubMed] [Google Scholar]
- Schoner and Kelso 1988.Schoner G, Kelso JAS. Dynamic pattern generation in behavioral and neural systems. Science 239: 1513–1520, 1988. [DOI] [PubMed] [Google Scholar]
- Schwartz et al. 2003.Schwartz DA, Howe CQ, Purves D. The statistical structure of human speech sounds predicts musical universals. J Neurosci 23: 7160–7168, 2003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Selesnick et al. 2005.Selesnick IW, Baraniuk RG, Kingsbury NG. The dual-tree complex wavelet transform. IEEE Signal Process Magazine 22: 123–151, 2005. [Google Scholar]
- Slijper et al. 2009.Slijper H, Richter J, Over E, Smeets J, Frens M. Statistics predict kinematics of hand movements during everyday activity. J Mot Behav 41: 3–9, 2009. [DOI] [PubMed] [Google Scholar]
- Summers et al. 1993.Summers JJ, Rosenbaum DA, Burns BD, Ford SK. Production of polyrhythms. J Exp Psychol 19: 416–428, 1993. [DOI] [PubMed] [Google Scholar]
- Swinnen et al. 2002.Swinnen SP, Dounskaia N, Duysens J. Patterns of bimanual interference reveal movement encoding within a radial egocentric reference frame. J Cogn Neurosci 14: 463–471, 2002. [DOI] [PubMed] [Google Scholar]
- Swinnen et al. 1998.Swinnen SP, Jardin K, Verschueren S, Meulenbroek R, Franz L, Dounskaia N, Walter CB. Exploring interlimb constraints during bimanual graphic performance: effects of muscle grouping and direction. Behav Brain Res 90: 79–87, 1998. [DOI] [PubMed] [Google Scholar]
- Tong et al. 2002.Tong C, Wolpert DM, Flanagan JR. Kinematics and dynamics are not represented independently in motor working memory: evidence from an interference study. J Neurosci 22: 1108–1113, 2002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tuller and Kelso 1989.Tuller B, Kelso JA. Environmentally-specified patterns of movement coordination in normal and split-brain subjects. Exp Brain Res 75: 306–316, 1989. [DOI] [PubMed] [Google Scholar]
- Van Damme et al. 2002.Van Damme R, Wilson RS, Vanhooydonck B, Aerts P. Performance constraints in decathletes. Nature 415: 755–756, 2002. [DOI] [PubMed] [Google Scholar]
- Wimmers et al. 1992.Wimmers RH, Beek PJ, Vanwieringen PCW. Phase-transitions in rhythmic tracking movements: a case of unilateral coupling. Hum Move Sci 11: 217–226, 1992. [Google Scholar]
- Zanone and Kelso 1992.Zanone PG, Kelso JA. Evolution of behavioral attractors with learning: nonequilibrium phase transitions. J Exp Psychol Hum Percept Perform 18: 403–421, 1992. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.