Inhibition and Recurrent Excitation in a Computational Model of Sparse Bursting in Song Nucleus HVC

Abstract

The telencephalic premotor nucleus HVC is situated at a critical point in the pattern-generating premotor circuitry of oscine songbirds. A striking feature of HVC's premotor activity is that its projection neurons burst extremely sparsely. Here we present a computational model of HVC embodying several central hypotheses: 1) sparse bursting is generated in bistable groups of recurrently connected robust nucleus of the arcopallium (RA)–projecting (HVC_RA) neurons; 2) inhibitory interneurons terminate bursts in the HVC_RA groups; and 3) sparse sequences of bursts are generated by the propagation of waves of bursting activity along networks of HVC_RA neurons. Our model of sparse bursting places HVC in the context of central pattern generators and cortical networks using inhibition, recurrent excitation, and bistability. Importantly, the unintuitive result that inhibitory interneurons can precisely terminate the bursts of HVC_RA groups while showing relatively sustained activity throughout the song is made possible by a specific constraint on their connectivity. We use the model to make novel predictions that can be tested experimentally.

INTRODUCTION

In oscine songbirds, the telencephalic nucleus HVC (used as the proper name; Reiner et al. 2004) is a key structure of the premotor pathway, projecting both to the premotor nucleus RA (the robust nucleus of the arcopallium) and to a basal ganglia nucleus, area X, which forms the first step of a basal ganglia–thalamocortical pathway essential for song learning (the anterior forebrain pathway; Abarbanel et al. 2004a,c; Bottjer et al. 1984; Brainard and Doupe 2000; Perkel 2004; Scharff and Nottebohm 1991; Sohrabji et al. 1990).

HVC contains three broad classes of neuron: RA-projecting (HVC_RA), X-projecting (HVC_X), and interneurons (HVC_I) (Dutar et al. 1998; Fortune and Margoliash 1995; Kubota and Taniguchi 1998; Mooney 2000; Nixdorf et al. 1989; Rauske et al. 2003; Shea 2004). Using paired intracellular recordings and antidromic stimulation in slices, Mooney and Prather (2005) found connections between members of all three of these classes and among HVC_RA neurons.

HVC_RA neurons, which are the HVC projection neurons that participate directly in the adult song control pathway, have been shown to exhibit temporally sparse bursting during singing in zebra finches (Hahnloser et al. 2002; Kozhevnikov and Fee 2007): in this study, each neuron bursts at most once per song motif. Each burst consists of 4.3 ± 1.3 spikes and has a duration of 5.1 ± 1.8 ms (Kozhevnikov and Fee 2007). Similar sparse bursting also occurs spontaneously during sleep (Hahnloser and Fee 2007; Hahnloser et al. 2002, 2006). By contrast, HVC_I neurons spike and burst densely throughout the song (Hahnloser et al. 2002; Kozhevnikov and Fee 2007). We and others have previously used this sparse bursting in models of birdsong (Abarbanel et al. 2004b; Fiete et al. 2004, 2007). The basis of sparse bursting in the neuronal circuitry of HVC remains unknown and is the focus of the model that we describe herein. In the following companion paper (Gibb et al. 2009), we present a model of the potential role of neural feedback to HVC in syllable sequencing.

The present study has the goal of developing a numerical model of HVC sparse bursting in which inhibitory interneurons play a central role. In our HVC model, the sparse bursting associated with any syllable is generated by the propagation of a wave of activity along a network of locally excitatory HVC_RA neurons interacting with globally inhibitory HVC_I neurons. We represent this network organization of HVC_RA neurons as a chain of bistable clusters. We see our model as a set of hypotheses, based on experimental data and expressed in quantitative language, from which we can derive predictions to be tested experimentally.

A portion of this work previously appeared in abstract form (Gibb and Abarbanel 2006).

METHODS

We implemented all models in C++ using a neural simulation framework developed by T. Nowotny and extended by L. Gibb, using a Runge–Kutta 6(5) algorithm with a relative error of 10⁻⁶, and we performed analyses of model output in MATLAB. We also tested some of the models in Fortran.

Basic spiking model

All neurons in our model are based on a single-compartment Hodgkin–Huxley-type neuron with just Na⁺, K⁺, and leak currents (Destexhe and Sejnowski 2001; Destexhe et al. 1998a; Traub and Miles 1991). The membrane potential of this basic spiking model follows the equation

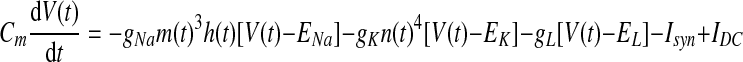where V(t) is the membrane potential; g_Na, g_K, and g_L are the maximal conductances of the Na⁺, K⁺, and leak currents; E_Na, E_K, and E_L are the reversal potentials of the Na⁺, K⁺, and leak currents; I_syn is the sum of synaptic currents; and I_DC is the value of an injected current (I_DC = 0, unless otherwise noted). The gating variables X(t) = {m(t), h(t), n(t)} are taken to satisfy the first-order kinetics

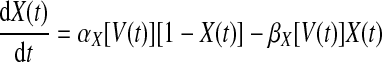where α_X(V) and β_X(V) are given in Table 1.

TABLE 1.

Rate functions of model neurons

Basic spiking model (Traub and Miles 1991)
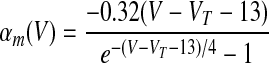
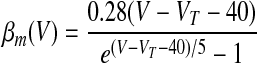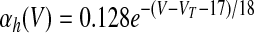
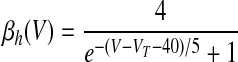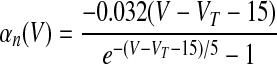
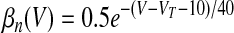IMs and IMf currents of HVCRA neurons
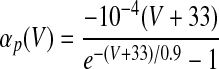
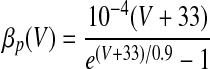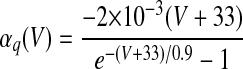
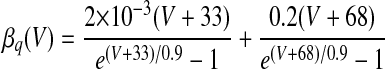Ih current of HVCI neurons

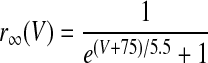
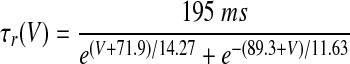V is in millivolts. V_T = −53 mV for HVC_RA neurons; V_T = −63.4 mV for HVC_I neurons.

Although the ionic currents of song system neurons have not yet been well characterized, in many cases the responses of neurons to depolarizing and hyperpolarizing current pulses have been recorded in vitro. To match such data from HVC_RA and HVC_I neurons, we included and modified appropriate currents characterized in mammalian neurons. This level of modeling is appropriate to our long-term goal of spanning cellular, circuit, network, and systems levels of analysis in the song system. As the model develops and new data are obtained, we will replace these neurons with more complex ones where appropriate. We will also explore simplified models to determine which details are essential to the network behavior.

HVC_RA neurons

We assumed in the present work that the HVC_RA neurons that burst sparsely during singing (Hahnloser et al. 2002; Kozhevnikov and Fee 2007) are of the same short dendrite (SD) class that burst sparsely during bird's own song (BOS) playback (Mooney 2000) and (following Shea 2004) that these are the neurons that spike tonically in response to depolarizing current injection. We fit our model to the physiology described in detail by Kubota and Taniguchi (1998) for their type IIa neurons. There is also a “phasic” HVC_RA type, which has been identified with the furry dendrite class (Fortune and Margoliash 1995; Nixdorf et al. 1989; Shea 2004; see discussion). To model Kubota and Taniguchi's HVC_RA neurons, we added two voltage-gated K⁺ currents to the basic spiking model described earlier and modified parameters from those used by Destexhe et al. (1998a) for cortical pyramidal neurons. To better match the in vitro data, we decreased the reversal potential E_L of the leak current from −70 to −83 mV and slightly shifted the voltage-dependent rate functions for the Na⁺ and K⁺ channels (α_m, β_m, α_h, β_h, α_n, and β_n; see Table 1 and the value of V_T) to raise the spike threshold.

The instantaneous spike frequency of these HVC_RA neurons declines rapidly over the first few action potentials and then declines much more gradually thereafter during constant-current injection (Kubota and Taniguchi 1998), which suggests that there are two timescales of spike-rate adaptation. Since the currents underlying this behavior have not been characterized in HVC_RA neurons, we modified the voltage-gated K⁺ current I_M, described by McCormick et al. (1993) and used by Destexhe et al. (1998a) in their model of cortical pyramidal neurons. The modified current I_Ms provides the slow component of adaptation and the modified current I_Mf provides the fast component

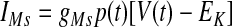and

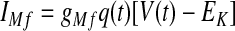where g_Ms and g_Mf are the maximal conductances of I_Ms and I_Mf. For both I_Ms and I_Mf, we shifted the I_M rate functions by −3 mV and sharpened them so that small depolarizing current injections trigger very little spike-frequency adaptation, whereas large injections trigger strong adaptation, in accord with the in vitro data. To generate the rate functions of I_Mf, we multiplied the rate functions of I_M by a constant. To prevent a postburst hyperpolarization that is not observed in the data, we modified β_q so that I_Mf rapidly deactivates below about −68 mV (see Table 1).

We adjusted the parameters to match the resting potential and the instantaneous spike frequency as a function of time for different injected currents described by Kubota and Taniguchi (1998; see Supplemental Fig. S1).1 The parameter values for the HVC_RA neuron model were g_Na = 50 mS/cm², E_Na = 45 mV, g_K = 5 mS/cm², E_K = −88 mV, g_L = 0.1 mS/cm², E_L = −83 mV, C_m = 1 μF/cm², V_T = −53 mV, g_Ms = 0.3 mS/cm², and g_Mf = 0.8 mS/cm².

HVC_I neurons

To model HVC_I neurons, we again built on the basic spiking model described earlier. We modified parameters from those used by Destexhe et al. (1998a) to model cortical interneurons, adjusting the parameters to match the resting potential and the instantaneous spike frequency as a function of time for different injected currents described by Kubota and Taniguchi (1998; see Supplemental Fig. S1). The data reported by Kubota and Taniguchi (1998) and Dutar et al. (1998) demonstrate that HVC_I neurons have a depolarizing sag in response to a hyperpolarizing current injection and show little spike-rate adaptation. We represent this in the membrane voltage equation by including I_h but no special K⁺ currents

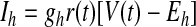where g_h and E_h are the maximal conductance and reversal potential of I_h, and

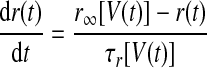where r_∞(V) and τ_r(V) are given in Table 1, based on Huguenard and McCormick (1994). This τ_r(V) is 20 times smaller than that in the model on which it is based. We made this modification solely to improve the match of the model to the data of Kubota and Taniguchi (1998) and Dutar et al. (1998) by speeding up the sag. This modification can be justified by the broad range of I_h time constants reported in different cortical and subcortical neurons, which depend on the subunit composition of I_h channels (Aponte et al. 2006). The parameter values of the HVC_I neuron model were g_Na = 50 mS/cm², E_Na = 45 mV, g_K = 10 mS/cm², E_K = −85 mV, g_L = 0.15 mS/cm², E_L = −64 mV, C_m = 1 μF/cm², V_T = −63.4 mV, g_h = 0.07 mS/cm², and E_h = −40 mV.

Once fit to the in vitro data, the parameters of the neuron models were held fixed; only synaptic strengths and network connectivity were adjusted to achieve the desired network behavior.

Modeling synaptic currents

We modeled both excitatory and inhibitory synaptic currents with the following equations (Destexhe and Sejnowski 2001; Destexhe et al. 1994)

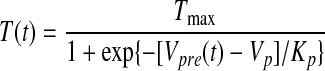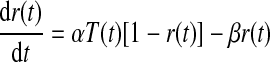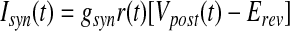where T(t) is the concentration of neurotransmitter in the synaptic cleft, T_max is the maximal neurotransmitter concentration, V_pre(t) and V_post(t) are the membrane potentials of the presynaptic and postsynaptic neurons, r(t) is the fraction of the receptors in the open state, g_syn (g_AMPA or g_GABAA) is the maximal synaptic conductance, and E_rev (E_AMPA or E_GABAA) is the synaptic reversal potential.

The rate constants that we used are based on the time constants of α-amino-3-hydroxy-5-methyl-4-isoxazolepropionic acid (AMPA)–and γ-aminobutyric acid type A (GABA_A)–mediated currents recorded in mammalian neocortical neurons and interneurons in vitro (Destexhe and Sejnowski 2001; Destexhe et al. 1994; Hestrin 1993). AMPA receptors at excitatory synapses onto interneurons are about twice as fast as those onto pyramidal neurons (Destexhe and Sejnowski 2001; Hestrin 1993).

For all synapses in our model, T_max = 1.5 mM, V_p = 2 mV, and K_p = 5 mV. For excitatory synapses, E_rev = 0 mV. For excitatory synapses onto HVC_I neurons, α = 2.2 mM⁻¹ ms⁻¹ and β = 0.38 ms⁻¹ (decay time constant 1/β = 2.6 ms). For excitatory synapses onto all other neuron types, α = 1.1 mM⁻¹ ms⁻¹ and β = 0.19 ms⁻¹ (1/β = 5.3 ms). For inhibitory synapses, α = 5.0 mM⁻¹ ms⁻¹ and β = 0.18 ms⁻¹ (1/β = 5.6 ms). In the reduced cluster model and the chain models based on it, E_rev = −83 mV for inhibitory synapses. In the models with synapses of physiological strength (see the following text), E_rev = −88 mV to give inhibitory postsynaptic potentials (IPSPs) a physiologically correct, nonzero amplitude near the HVC_RA resting potential of −83 mV. Mooney and Prather (2005) did not measure E_rev experimentally; our assumed value of −88 mV is similar to, and slightly less negative than, the mean GABA_A reversal potential measured in neurons of the medial portion of the dorsolateral thalamic nucleus (Person and Perkel 2005). This assumed value is necessarily an informed guess, since Mooney and Prather did not report the resting potentials of the neurons in which they measured IPSP amplitudes. Moreover, in two of the HVC_I → HVC_RA connections that they reported, the PSP was depolarizing rather than hyperpolarizing. However, we do not expect the precise value of E_rev to be critical to the behavior of the model, as long as it is below the spiking threshold.

Modeling temperature dependence of neurons and synapses

In simulations of in vivo activity, as a first approximation of the temperature dependence of neurons and synapses, we scaled all rate functions by a factor of φ(T₁) = Q₁₀^{(T₂−T₁)}/10, assuming a Q₁₀ of 3 for both neuronal and synaptic rates (Collingridge et al. 1984; Hodgkin and Huxley 1952). Here, T₂ is the brain temperature in vivo (assumed to be 40°C) and T₁ is the approximate temperature at which the measurements were made in vitro. T₁ is 32°C for neurons (Kubota and Taniguchi 1998), 31°C for AMPA synapses (Destexhe and Sejnowski 2001; Destexhe et al. 1998b; Xiang et al. 1992), and 34°C for GABA_A synapses (Destexhe et al. 1998b, 2001; Otis and Mody 1992a,b).

Synapses of physiological strength

In some simulations, we used synapses of physiological strength, based on the measurements of Mooney and Prather (2005). The values of α and β for these synapses followed the rules described earlier. We list the other parameter values and postsynaptic potential (PSP) peak amplitudes at 40°C here, together with the peak amplitudes measured by Mooney and Prather (abbreviated MP). HVC_I → HVC_RA: g_GABAA = 0.11 mS/cm², E_GABAA = −88 mV, IPSP amplitude −0.9 mV (MP: −0.9 ± 0.2 mV). HVC_RA → HVC_I: g_AMPA = 0.034 mS/cm², E_AMPA = 0 mV, EPSP amplitude 2.0 mV (MP: 2.0 ± 0.4 mV). HVC_RA → HVC_RA: g_AMPA = 0.018 mS/cm², E_AMPA = 0 mV. EPSP amplitude 2.2 mV (MP: 2.2 ± 1.1 mV).

Poisson synapses

In some simulations, we included Poisson synapses to generate spiking of a particular frequency or to mimic background synaptic activity in vivo in a manner similar to that described by Destexhe et al. (1998a). Each Poisson synapse was an AMPA or GABA_A synapse receiving 1-ms, 1-mM neurotransmitter pulses as Poisson random events. The values of α and β for these synapses again followed the rules described earlier. To mimic background synaptic activity, each HVC_I neuron received 20 Poisson AMPA synapses with a mean rate of 10 Hz and a maximal conductance of 0.02 mS/cm². This resulted in 8.8-Hz spiking (measured over 100 s), which is consistent with the 8 ± 6 Hz spontaneous firing rate measured by Kozhevnikov and Fee (2007). Similarly, each HVC_RA neuron received 20 Poisson AMPA (10 Hz, g_AMPA = 0.02 mS/cm²) and 20 Poisson GABA_A synapses (10 Hz, g_GABAA = 0.1 mS/cm²). This resulted in SD of the membrane potential of 2.8 mV (measured over 100 s). This pattern of Poisson synapses—a combination of AMPA and GABA_A for HVC_RA neurons and just AMPA for HVC_I neurons—mirrors the connectivity of our model: HVC_RA → HVC_RA, HVC_I → HVC_RA, HVC_RA → HVC_I, but no HVC_I → HVC_I synapses. We acknowledge that there may also be a significant number of HVC_I → HVC_I connections, but Mooney and Prather (2005) observed only one example. With appropriate parameter adjustments, we would expect to see similar results if Poisson GABA_A synapses were included on HVC_I neurons.

Sparseness index and spike time

We defined the sparseness of a spike train as S = 1 − D, where D is the fraction of 10-ms bins containing one or more spikes. We defined spike time as the time of the peak depolarization following a crossing of a −15-mV threshold in a positive direction.

Throughout, we report values as means ± SD.

RESULTS

Initial model: dynamic behavior of a single bistable cluster

Our current model has evolved from the simple idea that clusters of HVC_RA neurons could act as bistable units in generating the sparse bursting in HVC. The connectivity of our model clusters (Fig. 1C) is based on the HVC microcircuit described by Mooney and Prather (2005), especially their observations of depolarizing HVC_RA → HVC_RA and HVC_RA → HVC_I and hyperpolarizing HVC_I → HVC_RA connections. The recurrent (feedback) excitation of the HVC_RA neurons is the basis for the bistability: the HVC_RA cluster has two stable states: quiescent and persistently spiking. These states are a fixed point and a stable limit cycle, respectively.

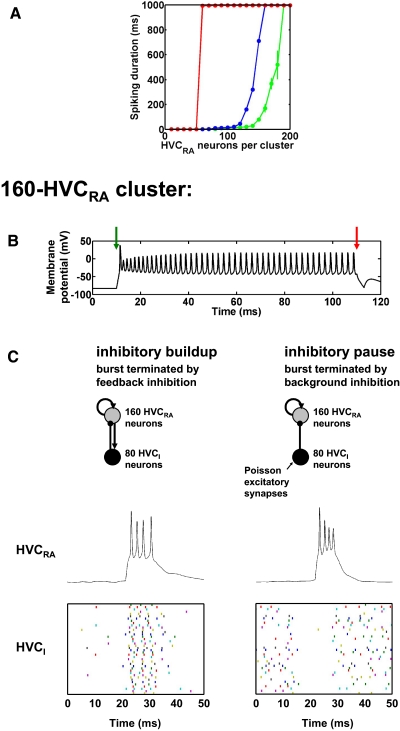
FIG. 1.

Large clusters of HVC neurons with synapses of physiological strength. A: duration of spiking in response to a current pulse injected into 50% of the neurons in clusters of recurrently connected robust nucleus of the arcopallium (RA)–projecting (HVC_RA) neurons with synaptic noise (green), no synaptic noise (blue), and no adaptation currents or noise (red). Spiking is truncated at 1 s by the end of the simulations. Each data point is the mean spiking duration of all the neurons in 3 separate simulations. We show error bars only for points at which SD >20 ms. B: bistability of a 160-HVC_RA cluster without noise. Membrane potential of a representative HVC_RA neuron. Green arrow: time of excitatory current pulse shifting the cluster into its persistently spiking state. Red arrow: time of inhibitory current pulse shifting the cluster back into its quiescent state. C: comparison of 2 distinct modes of inhibition for burst generation in 160-HVC_RA, 80-HVC_I (HVC interneuron) clusters. Top: schematics of the 2 mechanisms. Arrowheads, excitatory connections; dots, inhibitory connections. Middle: representative HVC_RA voltage traces. Bottom: spike time raster plot of 50% of the HVC_I neurons.

Despite the existence of synaptic connections from HVC_X to HVC_RA neurons (Mooney and Prather 2005), we did not give HVC_X neurons a role in HVC_RA sparse burst generation in our model. The observation that adult song production is not affected by targeted ablation of HVC_X neurons, whereas it is often disrupted by ablation of HVC_RA neurons (Scharff et al. 2000), suggests that HVC_X neurons are a less critical part of the premotor pattern-generating circuit (or possibly that there is much greater redundancy in that part of the circuit with respect to premotor pattern generation).

We created clusters in which each HVC_RA neuron sends excitatory synapses of physiological strength (see methods) to a randomly selected set of 50% of the other HVC_RA neurons within the same cluster. We chose this degree of connectivity to provide a high level of mutual excitation without implying an excessively large number of reciprocally connected HVC_RA neurons within each cluster, since reciprocally connected HVC_RA neurons were not observed by Mooney and Prather (2005). We prohibited each HVC_RA neuron from making a synapse onto itself or more than one synapse onto the same postsynaptic neuron.

In Fig. 1A, we show the duration of spiking activity evoked by a 3-ms, 40-μA/cm² DC current pulse injected into 50% of the HVC_RA neurons in clusters without inhibitory HVC_I neurons, plotted as a function of HVC_RA cluster size. The mean spiking duration increases as a function of the number of HVC_RA neurons. For intermediate cluster sizes, with the normal adaptation currents (I_Ms and I_Mf) present (blue and green traces), the repetitively spiking state of the cluster is only transiently stable. The spiking duration reaches ≥1 s at a cluster size of 160 HVC_RA neurons in the absence of synaptic noise (Fig. 1A, blue trace), 190 HVC_RA neurons in the presence of synaptic noise (see methods; Fig. 1A, green trace), and 60 HVC_RA neurons in the absence of the adaptation currents and noise (Fig. 1A, red trace). These sizes are comparable with the number of HVC_RA neurons, about 200, that Fee et al. (2004) estimated are coactive at each time in the song, but we will return to this point in the discussion. Additionally, the spiking duration also increases as a function of the percentage connectivity of the cluster (not shown).

In Fig. 1B, we demonstrate the bistability of a 160-HVC_RA cluster without inhibitory HVC_I neurons or synaptic noise. At t = 10 ms (green arrow), we shift the cluster into its persistently spiking state by exciting 50% of the HVC_RA neurons with a 3-ms, 40-μA/cm² current pulse. This state persists for ≥1 s in the absence of further inputs (not shown). In Fig. 1B, we shift the cluster back into its quiescent state with a 3-ms, −40-μA/cm² current pulse into the same 50% of the HVC_RA neurons at t = 110 ms (red arrow).

Mechanisms of inhibition

As described in the introduction, HVC_I neurons spike and burst densely throughout the song. Given this sustained activity, how could HVC_I neurons contribute to sculpting HVC_RA activity into sparse bursts? Two hypothetical mechanisms stand out as extremes along a spectrum. At one end of the spectrum (an “inhibitory buildup” mechanism), relatively weak feedback inhibition of HVC_RA neurons by HVC_I neurons could exert a hyperpolarizing influence throughout the burst, leading to a reduced spiking frequency followed by a failure of spiking and a termination of the burst after several milliseconds (Fig. 1C, left). In this mechanism, relatively small changes in the strength and timescale of the inhibition strongly influence the duration of the burst.

At the other end of the spectrum, the HVC_RA burst could occur during a pause in inhibition from HVC_I neurons. In this “inhibitory pause” mechanism, HVC_RA neurons are disinhibited during the burst and a strong onset of inhibition after several milliseconds abruptly terminates the burst (Fig. 1C, right). Pauses and periods of low-frequency spiking do in fact occur in the midst of the relatively sustained activity of HVC_I neurons during singing (Hahnloser et al. 2002; Kozhevnikov and Fee 2007). This mechanism is the basis of our model using globally connected HVC_I neurons, described in the following text (Fig. 4). In this mechanism, small changes in the strength and timescale of the inhibition are inconsequential, but the delay between the onset of the burst and the onset of the inhibition controls the duration of the burst. Between the extremes of inhibitory buildup and inhibitory pause is a range of intermediate mechanisms in which the onset of inhibition is delayed but relatively weak, so that a combination of inhibitory strength and inhibitory pause duration controls the duration of the burst.

A second dichotomy between inhibitory mechanisms is that between “local” inhibition, in which each HVC_I neuron connects to a set of HVC_RA neurons in only one part of the HVC_RA network, and “global” inhibition, in which each HVC_I neuron connects to a set of HVC_RA neurons throughout the HVC_RA network.

In the present study, we argue that if inhibition does indeed play a role in HVC_RA burst termination, then global inhibition using the inhibitory pause mechanism is a favored candidate (although the true mechanism may be somewhere between the extremes of inhibitory pause and inhibitory buildup). We make this argument along several lines in the following sections.

Our main goals here are to demonstrate that HVC_I neurons could participate in the HVC_RA burst mechanism, to show a possible mechanism by which they could accomplish this, and to make experimental predictions on the basis of this mechanism.

Computational implementation of inhibitory mechanisms

In this section, we suggest that the inhibitory pause mechanism is a favored candidate for sparse bursting in HVC_RA neurons because it is more robust than the inhibitory buildup mechanism to a variety of parameter changes.

To implement these two basic inhibitory mechanisms, we added HVC_I neurons to the 160-HVC_RA cluster introduced previously, in a proportion based on the literature. Although estimates of the proportions of HVC neuron classes vary substantially (e.g., Alvarez-Buylla et al. 1988; Kirn et al. 1999), one estimate is that 50% of HVC neurons are RA-projecting, 25% are X-projecting, and 25% are interneurons (Nottebohm et al. 1990). Consistent with these proportions, we created a 160-HVC_RA, 80-HVC_I cluster. To verify the robustness of both of these inhibitory models, we included synaptic noise in the HVC_RA and HVC_I neurons as described in methods.

In our implementation of the inhibitory buildup mechanism (Fig. 1C, left), each HVC_RA neuron in the bistable cluster sends a single synapse to each of nine HVC_I neurons and each HVC_I neuron sends a single synapse to each of four HVC_RA neurons. We initiated the burst with a 3-ms, 40-mS/cm² DC current pulse into 50% of the HVC_RA neurons beginning at t = 20 ms (the simulation began at t = −30 ms). For 10 trials with identical parameters but different random connectivity, the number of spikes per burst was 3.6 ± 1.1 and the burst duration was 6.7 ± 2.3 ms.

In our implementation of the inhibitory pause mechanism (Fig. 1C, right), each HVC_I neuron sends a single synapse to each of 70 HVC_RA neurons but does not receive synapses from any HVC_RA neurons. We excite the bistable HVC_RA cluster by a brief current pulse. It is then inhibited by HVC_I neurons that we begin to excite 6.4 ms later; this inhibition terminates the burst. To relate this model to our model using globally connected HVC_I neurons (see the following text; Fig. 4), we also excite the HVC_I neurons until 7 ms before initiating the HVC_RA burst; thus the HVC_RA burst occurs largely during a pause in the high-frequency presynaptic HVC_I spiking. This excitation is a proxy for the input from other HVC_RA neurons in the network, which are included in our model using globally connected HVC_I neurons. We set the pause to begin 7 ms before burst initiation to give the inhibition sufficient time to decay so that it does not interfere with the burst. As in the inhibitory buildup mechanism, we initiated the burst with a 3-ms, 40-mS/cm² current pulse into 50% of the HVC_RA neurons beginning at t = 20 ms (again, the simulation began at t = −30 ms). We elicited the relatively high-frequency spiking of each HVC_I neuron before t = 13 ms and after t = 26.4 ms with a 100-Hz Poisson AMPA synapse with g_AMPA = 0.2 mS/cm² (see methods), together with the synaptic noise. This 89-Hz HVC_I spiking frequency (measured over 100 s) is consistent with the 95 ± 40 Hz firing rate of HVC_I neurons recorded during singing (Kozhevnikov and Fee 2007). For 10 trials with identical parameters but different random connectivity, the number of spikes per burst was 4.0 ± 0.8 and the burst duration was 5.4 ± 1.4 ms. The HVC_I → HVC_RA connections are sufficiently strong that in the absence of the pause in the high-frequency HVC_I spiking, none of the HVC neurons bursts (10 trials).

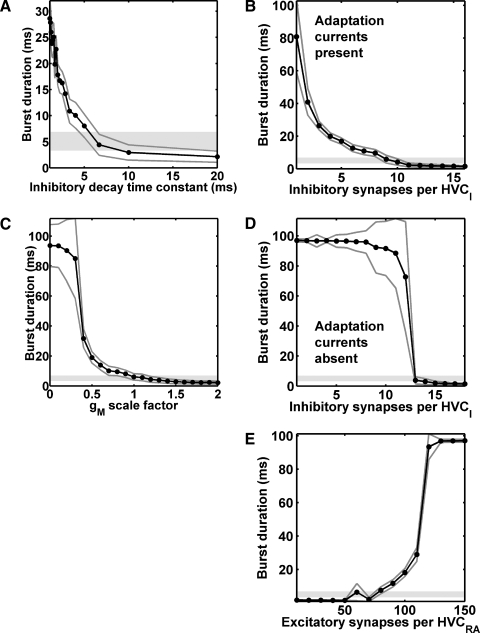
Our implementation of the inhibitory buildup mechanism was more sensitive than the inhibitory pause mechanism to a variety of parameter changes. In the inhibitory buildup mechanism, longer bursts tended to be associated with weaker or more rapidly decaying inhibition (Fig. 2, A, B, and D), consistent with a termination of bursting by the hyperpolarizing influence of inhibition during the burst. The burst duration decreased with the inhibitory synaptic decay time constant, 1/β (Fig. 2A; larger values imply longer inhibitory postsynaptic current decay times). Similarly, the burst duration decreased as the number of inhibitory synapses sent to HVC_RA neurons by each HVC_I neuron increased, either with the normal adaptation currents present (I_Ms and I_Mf; Fig. 2B) or with these currents absent (Fig. 2D). In the absence of the adaptation currents, there was an abrupt transition from long to short bursts (Fig. 2D), suggesting an important contribution of these currents to burst termination. Consistent with this observation, the burst duration decreased with increasing strength of the adaptation currents (Fig. 2C). Additionally, the burst duration increased with the number of excitatory HVC_RA–HVC_RA synapses per HVC_RA neuron (Fig. 2E), consistent with a competition between inhibition and excitation in determining the burst duration.

FIG. 2.

Burst duration for the inhibitory buildup mechanism of Fig. 1C as a function of various parameters. Dark gray lines: mean ± SD. Light gray regions: HVC_RA burst duration (mean ± SD) measured by Kozhevnikov and Fee (2007). A: inhibitory synaptic decay time constant, 1/β (normal value: 5.6 ms). B: inhibitory synapses per HVC_I, normal adaptation currents present (normal number: 9). C: scale factor by which the maximal conductances of both adaptation currents is multiplied (normal value: 1). D: inhibitory synapses per HVC_I, adaptation currents absent. E: excitatory synapses per HVC_RA (normal number: 80).

For our implementation of the inhibitory buildup mechanism, the mean burst durations fell within 1 SD of the mean recorded in vivo (Fig. 2, light gray regions; Kozhevnikov and Fee 2007) only in a narrow range of values (one to four data points). By contrast, in our implementation of the inhibitory pause mechanism, the mean burst durations fell within this range over a much wider range of values (more than eight data points in every case, for the same spacing; Supplemental Fig. S2). This suggests that the inhibitory pause mechanism is the more robust of the two mechanisms.

Reduced cluster models

Network models of HVC with correct numbers of neurons and synapses are very slow and inefficient to simulate. Therefore we created a reduced cluster model that captures the most essential characteristics of the 160-HVC_RA cluster introduced previously, especially its recurrent excitation and bistability. This reduced model contains three HVC_RA neurons recurrently connected in a ring by excitatory synapses (Fig. 3A).

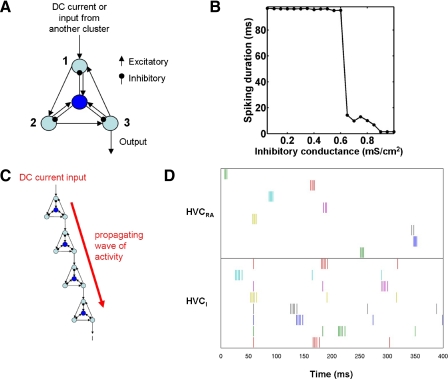
FIG. 3.

Chains of clusters with locally connected HVC_I neurons produce sparse bursting in HVC_RA neurons, but do not produce sustained activity in HVC_I neurons beyond their low-frequency spontaneous spiking. A: schematic of the reduced cluster model used in the sparse bursting chain network, consisting of 3 recurrently excitatory HVC_RA neurons (light blue) and one local HVC_I neuron (dark blue). B: burst duration for the reduced cluster as a function of the inhibitory conductance g_GABAA; GABA_A, γ-aminobutyric acid type A. Because simulations end at t = 110 ms, the maximum possible duration is 100 ms. For every point, SD <2.1 ms. C: schematic of the sparse bursting chain network. Activity of the network is initiated in the first HVC_RA neuron of the first cluster by a DC current pulse. D: raster plot of the spike times of a subset of HVC_RA and HVC_I neurons in a chain of 250 clusters. Each row represents the spike times of one neuron.

We verified that without the HVC_I neuron, the reduced HVC_RA cluster is bistable (Supplemental Fig. S3): by exciting a single neuron of the cluster, we shifted the cluster from its quiescent state into its persistently spiking state. By injecting a hyperpolarizing current into the same neuron, we shifted the cluster back into its quiescent state. The resulting plot (Supplemental Fig. S3A) looks almost identical to the corresponding plot for the 160-HVC_RA cluster (Fig. 1B). We verified that the persistently spiking state persists for ≥1 s in the absence of further inputs.

Like the 160-HVC_RA, 80-HVC_I cluster, the 3-HVC_RA, 1-HVC_I cluster exhibited a burst of appropriate duration for a narrow range of inhibitory coupling. In Fig. 3B, we plot the mean spiking duration of the HVC_RA neurons in this cluster as a function of g_GABAA. At ≤0.6 mS/cm², the HVC_RA neurons showed persistent activity, whereas at ≥0.9 mS/cm², the HVC_RA neurons spiked only zero to two times. In addition, we found that both two- and four-neuron clusters are also capable of generating brief bursts (not shown). The former may have a smaller parameter regime in which bistability is possible.

A model of HVC_RA sparse bursting: the limitations of local inhibition

In this section, we suggest that a chain network using local inhibition and an inhibitory buildup mechanism is not a good model of sparse bursting in HVC_RA neurons because it does not reproduce the sustained HVC_I activity observed experimentally during singing and is very sensitive to parameter changes.

To create such a chain network, we arranged our reduced clusters in a long chain so that they successively excite each other to generate a burst sequence; we illustrate this in Fig. 3, C and D. To initiate the wave of bursting activity, we set I_DC = 30 μA/cm² in the first neuron of the first chain for 5 ms beginning at t = 0 ms. This “begin song” command may correspond to synaptic input from an afferent nucleus or the end of another chain within HVC. The activity then propagates from cluster to cluster until it reaches the end of the chain. Activity in each cluster is evoked by excitatory input to its HVC_RA neuron 1 (Fig. 3A) from the HVC_RA neuron 2 of the previous cluster, and terminated by inhibitory input from the local HVC_I.

Figure 3D is a raster plot of the spike times of a subset of HVC_I neurons from a total of 250 reduced clusters (three HVC_RA neurons each) linked in series. For HVC_RA → HVC_RA synapses within each cluster, g_AMPA = 1.95 mS/cm². For those between clusters, g_AMPA = 1.5 mS/cm². We made the latter weaker to prevent driving the first neuron of each cluster too strongly because it receives a synapse not only from within the cluster but also from the previous cluster (this is an artifact of our reduced model and is not meant to reflect differences in connectivity within HVC). For HVC_RA → HVC_I synapses, g_AMPA = 0.2 mS/cm². For HVC_I → HVC_RA synapses, g_GABAA = 1.45 mS/cm². The burst duration was 5.6 ± 1.5 ms, with 3.3 ± 0.9 spikes per burst. We injected a 0.5-μA/cm² DC current into the HVC_I neurons so that they spiked spontaneously at about 8 Hz, consistent with their spontaneous firing rate in awake, nonsinging zebra finches. The HVC_I neurons had identical initial conditions and DC current, which accounts for the identical timing of the first spike of most of these neurons.

Significantly, in this model, each HVC_I bursts only once as activity propagates along the chain. By contrast, the HVC_I neurons described by Hahnloser et al. (2002) and Kozhevnikov and Fee (2007) show an elevated level of spiking and bursting throughout the song. To correct this discrepancy, we developed the model of global inhibition described in the next section. Additionally, this model required fine parameter tuning and was sensitive to changes in the HVC_I → HVC_RA inhibitory synaptic strength. For example, a decrease from 1.45 to 1.40 mS/cm² destabilized the burst sequence, resulting in a mean burst duration of 27.0 ± 20.9 ms, with 8.9 ± 6.1 spikes per burst.

A model of HVC_RA sparse bursting using global inhibition

In this section, we suggest that a chain network using global inhibition and an inhibitory pause mechanism (i.e., global inhibition with a specific constraint on HVC_I–HVC_RA connectivity) is a favored candidate for sparse bursting in HVC_RA neurons because it generates appropriate HVC_RA bursts and reproduces the sustained HVC_I activity observed experimentally.

Our current model of sparse bursting is depicted in Fig. 4. As in the previous model, HVC_RA neurons are organized into a chain of bistable clusters. However, HVC_I neurons are no longer functionally localized to these clusters; rather, they are permitted to receive excitation from, and send inhibition to, any part of the chain. We initiate the burst sequence by setting I_DC = 20 μA/cm² in the first neuron of the first chain for 5 ms beginning at 0 ms. Again, excitation travels through the network via HVC_RA → HVC_RA synapses. The local excitatory synapses between HVC_RA neurons keep each cluster of neurons in an excited state until a subpopulation of global HVC_I neurons terminates its activity.

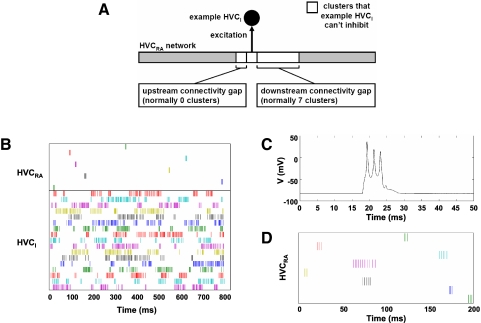
FIG. 4.

Chains of clusters with globally connected HVC_I neurons and constrained HVC_I–HVC_RA connectivity produce sparse bursting in HVC_RA neurons and sustained activity in HVC_I neurons, consistent with experimental observations. A: schematic illustrating the constraint on HVC_I–HVC_RA connectivity that permits normal burst propagation. Because the representative HVC_I receives an excitatory synapse from the cluster shown, it is not permitted to make inhibitory synapses onto the clusters shown in white. The diagram assumes that the wave of activity propagates from left to right along the HVC_RA network. B: raster plot of the spike times of a subset of HVC_RA and HVC_I neurons from a simulation of 300 HVC_I neurons and 200 clusters of 3 HVC_RA neurons. C: portion of voltage trace of HVC_RA neuron 14 from the same simulation. D: subset of HVC_RA neurons in another simulation, in which one of these neurons (magenta) was in a cluster that escaped inhibition to fire a longer burst.

However, without any constraints on HVC_I–HVC_RA connectivity, it is not possible for the inhibition to sculpt the HVC_RA activity into a sequence of appropriate bursts (not shown). With weak inhibition (e.g., g_GABAA = 0 or g_GABAA = 0.01 mS/cm²), HVC_RA bursts failed to terminate, entering a state of persistent activity. With intermediate inhibition (e.g., g_GABAA = 0.02 to 0.04 mS/cm²), HVC_RA neurons showed some combination of variable-duration bursting, persistent activity, and premature termination of the burst sequence. With strong inhibition (g_GABAA = 0.05 to 3.0 mS/cm²), the burst sequence terminated within two clusters of the beginning of the chain: a burst in one cluster caused inhibition in a downstream cluster before that cluster was excited. There was no value of g_GABAA for which HVC_RA neurons showed bursts with a consistent, correct number of spikes.

A solution to this problem is to constrain each HVC_I neuron not to make inhibitory synapses onto any cluster from which it receives an excitatory synapse or onto clusters within some number of clusters downstream of one from which it receives an excitatory synapse (Fig. 4A). We refer to these downstream clusters as an HVC_I “downstream connectivity gap.” A downstream connectivity gap of at least one cluster is necessary to allow enough time for the inhibition on HVC_RA neurons to decay before excitation arrives from an upstream cluster. When the downstream connectivity gap is zero, only the first cluster spikes. To reduce the influence of residual inhibition on burst duration and propagation speed (see Fig. 5), we used a larger, seven-cluster downstream connectivity gap. The HVC_I neuron is constrained not to make excitatory synapses onto any cluster from which it receives an excitatory synapse, so that the HVC_RA neurons have time to burst before the inhibition arrives to terminate the bursts. We generated this synaptic connectivity pattern by the following algorithm.

1. Create a new HVC_I neuron.

2. Select a candidate HVC_RA neuron to make an excitatory synapse onto the HVC_I neuron. If there exists an inhibitory synapse from the HVC_I neuron onto an HVC_RA neuron in the candidate neuron's cluster or onto an HVC_RA neuron that is within seven clusters downstream of the candidate HVC_RA neuron, select a new candidate HVC_RA neuron. Repeat this until an appropriate HVC_RA neuron is found.

3. Select a candidate HVC_RA neuron to receive an inhibitory synapse from the HVC_I neuron. If there exists a synapse onto the HVC_I neuron from an HVC_RA neuron in the candidate neuron's cluster or from an HVC_RA neuron that is within seven clusters downstream of the candidate HVC_RA neuron, select a new candidate HVC_RA neuron. Repeat this until an appropriate HVC_RA neuron is found.

4. Repeat steps 2 and 3 until all of the synapses onto and from the HVC_I have been created.

5. Repeat steps 1–4 until all of the HVC_I neurons have been created.

FIG. 5.

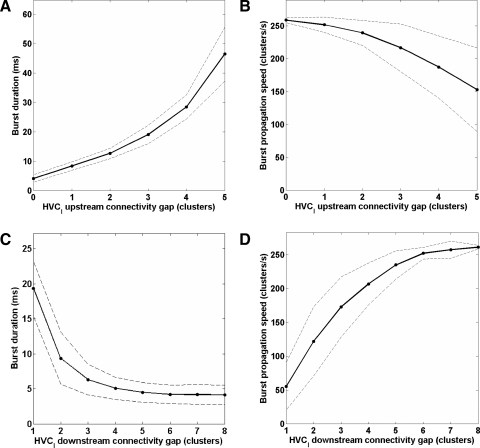
Effects of HVC_I–HVC_RA connectivity on burst duration and propagation speed. Burst duration increases (A) and burst propagation speed decreases (B) as a function of the HVC_I upstream connectivity gap. Burst duration decreases (C) and burst propagation speed increases (D) as a function of the HVC_I downstream connectivity gap. Burst propagation terminated prematurely (293 ms) for the simulation with a downstream connectivity gap of 4.

As a result of this constraint on connectivity, the wave of excitation is preceded and followed by inhibition, but not interrupted by it, despite the sustained activity of the HVC_I population. The HVC_I neurons presynaptic to a given HVC_RA neuron are all silent at about the time of the HVC_RA burst and shortly before; this is functionally equivalent to the pause in HVC_I activity in our implementation of the inhibitory pause mechanism in Fig. 1C.

In addition, we found that neurons in the last cluster of the chain remained persistently active, since there are no clusters downstream of these clusters to inhibit them via the HVC_I neurons. To prevent this persistent activity, we added additional connections from the last two HVC_RA clusters to the HVC_I population.

Figure 4B shows the spike times of a subset of HVC_RA and HVC_I neurons in a simulation containing a total of 300 HVC_I neurons and 200 clusters of 3 HVC_RA neurons (i.e., 33% HVC_I and 67% HVC_RA neurons) with this connectivity pattern. We obtained similar results when the numbers of HVC_RA and HVC_I neurons were the same. We also obtained similar results with 2 or 4 neurons per cluster. HVC_RA2 of each cluster sends an excitatory synapse to HVC_RA1 of the next. Each HVC_I neuron sends 100 synapses to, and receives 100 synapses from, HVC_RA neurons. For HVC_RA → HVC_RA synapses within each cluster, g_AMPA = 1.0 mS/cm². For those between clusters, g_AMPA = 0.5 mS/cm². We made the latter weaker for the reason described in the previous section. For HVC_RA → HVC_I synapses, g_AMPA = 0.1 mS/cm². For HVC_I → HVC_RA synapses, g_GABAA = 3.0 mS/cm².

To prevent persistent activity at the end of the chain, randomly selected HVC_RA neurons from the last two clusters make a total of 300 additional synapses (g_AMPA = 0.1 mS/cm²) onto randomly selected HVC_I neurons. The average burst duration was 4.3 ± 1.4 ms, with 3.2 ± 0.6 spikes per burst. Figure 4C shows a portion of the voltage trace of one of the HVC_RA neurons in this simulation.

Because of the element of randomness in generating HVC_I → HVC_RA connectivity in the model, in some simulations the spiking in one or more HVC_RA clusters was not as rapidly terminated by inhibition. In Fig. 4D, we show an example neuron from such a cluster in a simulation containing 90 HVC_I neurons and 60 clusters of 2 HVC_RA neurons, with 30 synapses to and from each HVC_I neuron. The single HVC_RA neuron that spikes over an unusually long duration in the experiments of Hahnloser et al. (2002; their Fig. 2B) and Kozhevnikov and Fee (2007; their Fig. 2A) has a lower spiking frequency than this. However, it is sufficiently reminiscent that we suggest the possibility that both cases involve a failure of inhibition.

In this model, the duration of an HVC_RA burst is strongly influenced by the timing of inhibition. Most straightforwardly, a larger HVC_I upstream connectivity gap (i.e., the number of clusters that an HVC_I is not permitted to inhibit upstream of one from which it receives excitation; Fig. 4A) leads to a longer delay before a burst is terminated and therefore a longer burst (Fig. 5A). Longer burst durations also result from smaller downstream connectivity gaps (Fig. 5C). This may be related to the fact that smaller downstream connectivity gaps cause slower burst propagation (Fig. 5D): if the downstream cluster bursts later than usual, then its inhibition of the upstream cluster via HVC_I neurons should occur later than usual. The slower burst propagation may be due to residual inhibition delaying the downstream cluster in reaching its spike threshold. Larger upstream connectivity gaps also result in slower burst propagation (Fig. 5B). This may be due to the redistribution of the HVC_I → HVC_RA synapses: when there are fewer HVC_I → upstream HVC_RA synapses, there are more HVC_I → HVC_RA synapses to clusters just downstream of the downstream connectivity gap. This may result in more residual inhibition, which may delay the downstream clusters in reaching their spike threshold.

Sparse bursting without clusters or unidirectional HVC_RA chains

The model does not fundamentally rely on a cluster organization nor on the unidirectionality of the HVC_RA chain to produce a sequence of sparse bursts. For example, in one set of simulations (not shown), we reduced the clusters in our model to 2 reciprocally connected HVC_RA neurons and connected these clusters bidirectionally (g_AMPA = 0.75 mS/cm² for all synapses), effectively creating a chain of 400 bidirectionally connected HVC_RA neurons while retaining the HVC_RA–HVC_I connectivity. Stimulating the first cluster continued to produce a sequence of bursts (burst duration, 3.9 ± 1.3 ms; spikes per burst, 3.0 ± 0.7). Unidirectionality of burst propagation was maintained by the HVC_RA–HVC_I connectivity: stimulating the last neuron of the chain produced a burst in only the last 2 neurons (not shown). This is expected, since there is no gap in the reverse direction to allow the inhibition of the HVC_RA neurons to decay before excitation arrives from an upstream cluster. Thus we expect this unidirectionality of burst propagation to depend on the asymmetry of the upstream and downstream connectivity gaps (Fig. 4A).

Similarly, we created a short chain model of 20 clusters with physiological synaptic strengths, in which the separate identity of the clusters was all but lost by their interconnectivity. Each cluster contained 80 HVC_RA neurons, each of which sent AMPA synapses to a set of 40 other HVC_RA neurons in its cluster, 40 in the previous cluster, and 40 in the next cluster. Thus the connectivity along the chain had no directionality and the connectivity was less one of a chain of clusters and more one of a network of HVC_RA neurons with local random connections. Each of the 1,600 HVC_I neurons sent GABA_A synapses to a set of 80 HVC_RA neurons and received AMPA synapses from a set of 20 HVC_RA neurons. The upstream connectivity gap was one cluster and the downstream connectivity gap was 10 clusters. The connectivity of the clusters in this version of the model allowed us to control the burst duration more finely: setting the upstream connectivity gap to 1 rather than 0 caused the HVC neurons to spike 4.3 ± 0.9 times in 5.3 ± 1.3 ms, longer than the bursts in our previous model. To prevent persistent activity at the end of the chain, each HVC_RA neuron in the last cluster sent AMPA synapses to a set of 30 HVC_I neurons. In every case, we prohibited a neuron from making a synapse onto itself or more than one synapse onto the same postsynaptic neuron. We initiated activity in the first cluster with a 4-ms, 40-μA/cm² current pulse in 50% of the HVC_RA neurons, beginning at t = 0 ms.

Experimental predictions of the sparse bursting model

In Fig. 6, we show experimental predictions of the sparse bursting model. Since GABA_A synapses play a critical role in the model, the model predicts that manipulations that influence GABA_A synaptic transmission can profoundly affect HVC's behavior. When we blocked inhibitory synapses (i.e., set g_GABAA = 0), the bursts of HVC_RA neurons began normally but failed to terminate, entering a state of persistent activity. The prediction of normal burst onset will hold only if blocking GABA_A synapses does not in itself lead to runaway excitation in HVC before the onset of singing.

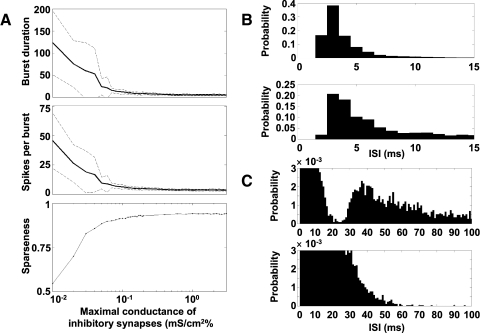
FIG. 6.

Sparse bursting model predictions: A: burst duration (top), spikes per burst (middle), and sparseness (bottom) as a function of g_GABAA. Solid lines: mean. Dashed lines: mean ± SD. At g_GABAA ≥ 0.4 mS/cm², the burst duration is 5.0 ± 0.3 ms and the number of spikes per burst is 3.6 ± 0.1. B and C: HVC_I interspike interval (ISI) distributions may differentiate between connectivity patterns. B, top: ISI distribution of HVC_I neurons in the simulation shown in Fig. 4B, connected according to the rule described herein. Bottom: ISI distribution of HVC_I neurons receiving completely random synapses from the same set of HVC_RA neurons. C: the same ISI distributions, with lower y-axis and higher x-axis limits. Top: ISI distribution of HVC_I neurons connected according to the rule described herein shows a characteristic dip. Bottom: ISI distribution of HVC_I neurons receiving random synapses lacks this dip.

Figure 6A shows the effect of varying g_GABAA on the sparseness of spiking in a version of the model containing 90 HVC_I neurons and 60 clusters of 3 HVC_RA neurons, illustrated with the burst duration, spikes per burst, and the sparseness index defined in methods. We calculated burst duration and spikes per burst over the time interval from the beginning of current injection into the first neuron (0 ms) to approximately the end of the last burst in the chain in the normal case (230 ms). For very low values of g_GABAA, HVC_RA neurons entered a state of persistent activity. However, HVC_RA neurons showed relatively short, consistent bursts over a wide range of g_GABAA values from about 0.1 to ≥3.0 mS/cm². This robustness is due to the HVC_I–HVC_RA connectivity pattern described earlier, which results in an inhibitory pause during which bursting can occur.

We also found that the interspike interval (ISI) distribution may contain a signature of the HVC_RA → HVC_I connectivity pattern, if sufficiently many HVC_I spikes are recorded. Since each HVC_I is constrained not to receive excitation from any cluster to which it sends inhibition, or from clusters within seven clusters upstream of one to which it sends inhibition, we would expect ISIs corresponding to this nearly eight cluster gap in connectivity, and less, to be underrepresented in the ISI distribution. Since the propagation speed along the chain is 0.26 cluster/ms, we would expect a dip in the ISI distribution below 31 ms. Figure 6B (top) shows the ISI distribution for all spike times of all HVC_I neurons in the simulation illustrated in Fig. 4B. Figure 6B (bottom) shows the ISI distribution of another set of HVC_I neurons. Each HVC_I neuron in this second set was driven by exactly the same set of HVC_RA bursts and received exactly the same number of HVC_RA → HVC_I synapses, but the HVC_RA → HVC_I connectivity pattern was completely random. These HVC_I neurons did not send synapses to HVC_RA neurons. Figure 6C shows the same ISI distributions with altered axis limits, to accentuate their differences. Unlike the random case (bottom), the constrained case (top) resulted in a histogram with a prominent dip in ISIs below 30 to 35 ms, corresponding to the gap in HVC_RA → HVC_I connectivity. Experimentally, such a histogram should include ISIs only from the period corresponding to singing and not from periods of spontaneous activity. The model predicts that both the size of the connectivity gap and the propagation speed of the waves will determine which ISIs are underrepresented in the histogram.

Additional predictions of the inhibitory pause mechanism

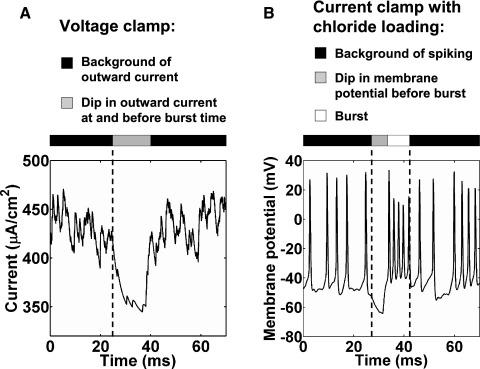
The role of inhibition in the sparse bursting model is similar to that in the inhibitory pause mechanism of Fig. 1C. If sleep replay or BOS playback-evoked activity in HVC_RA neurons is the result of the same mechanism as singing-related bursting (see discussion), then the inhibitory pause mechanism makes two predictions that could be tested in head-fixed or anesthetized birds. First, under voltage clamp at the AMPA reversal potential (0 mV), an HVC_RA neuron will have a background of outward, hyperpolarizing current during the fictive singing, with a dip shortly before and during the time of the burst (Fig. 7A). Second, chloride loading should result in a background of spiking during the fictive singing by making the GABA_A synapses functionally excitatory (Fig. 7B).

FIG. 7.

Experimental predictions from the inhibitory pause mechanism of Fig. 1. A: current in a representative HVC_RA neuron under voltage clamp at the AMPA reversal potential (0 mV). The neuron showed a background of outward, hyperpolarizing current, with a dip during and before the time of the burst. B: membrane potential of a representative HVC_RA neuron from a different simulation, when we set the GABA_A reversal potential to −21 mV to simulate chloride loading. The neuron showed a background of spiking, with a dip in membrane potential before the burst. In both A and B, the HVC_I pause lasted from t = 23 to 36.4 ms, the depolarizing DC current pulse into HVC_RA neurons lasted from t = 30 to 33 ms, and the simulation began at t = −20 ms.

DISCUSSION

We have presented a model of sparse bursting based on inhibition, recurrent excitation, and bistability. This model builds on the observation by Hahnloser et al. (2002) and Kozhevnikov and Fee (2007) of sparse bursting in HVC_RA neurons and on their hypothesis that HVC_RA neurons form a chainlike organization in which neuronal ensembles burst in sequence at every moment of the song, driving RA neurons to burst in sequence (Fee et al. 2004).

The chainlike organization of our bistable clusters is reminiscent of synfire chains, which have been discussed elsewhere (Abeles 1982, 1991; Diesmann et al. 1999; Hermann et al. 1995). Recently, chain models have been proposed for HVC (Fiete et al. 2005; Jin et al. 2007; Li and Greenside 2006), also building on the work of Fee et al. (2004). Although our model includes chainlike networks, we have focused on the role of bistability and inhibition rather than chains. Unlike other chainlike models, our model postulates a central role for inhibitory interneurons in sparsely bursting telencephalic premotor networks, HVC in particular. This mechanism is related to those of central pattern generators and cortical networks, which make use of inhibition, recurrent excitation, and bistability (McCormick 2005; Shu et al. 2003; Yuste et al. 2005).

Inhibitory interneurons also played a key role in the Drew and Abbott (2003) model of song selectivity and sequence generation in HVC, although this role was not in terminating sparse HVC_RA bursts. Their model was limited by its dependence on a long afterhyperpolarization in HVC_RA neurons and by the fact that its HVC_RA neurons were active only during extrinsically generated excitatory pulses applied every 75 to 100 ms.

Our sparse bursting model is distinguished from other chainlike models by a number of key assumptions and predictions.

1. Our model assumes that a large proportion of HVC_RA neurons participate in a local connectivity of recurrent excitation with other HVC_RA neurons that are nearby in the network, which is the basis of the bistability.

2. Our model assumes that each HVC_I neuron is constrained not to make inhibitory synapses onto HVC_RA neurons within some distance upstream and downstream of one from which it receives an excitatory synapse (Fig. 4A). This gives the HVC_RA neurons time to burst before the inhibition arrives and reduces the influence of residual inhibition on burst duration and propagation speed (Fig. 5).

3. Our model assumes that an additional mechanism activates HVC_I neurons at the end of the HVC_RA burst sequence to prevent persistent activity at the end of the chain. In this model, we added additional connections from HVC_RA neurons at the end of the chain to the HVC_I population. In the model presented in our companion paper (Gibb et al. 2009), which includes neural feedback via nucleus uvaeformis (Uva), these connections are replaced by ones from Uva to HVC_I neurons.

4. As a result of the HVC_I–HVC_RA connectivity, our model predicts that every HVC_RA neuron that participates in sparse bursting receives a background of inhibition throughout the song, with a reduction shortly before and during the time that it bursts (Figs. 1C and 7A). If the mechanism of sparse bursting during sleep or BOS playback is sufficiently similar to that during singing (which is not certain, given the involvement of NIf [nucleus interface of the nidopallium] in the former but not the latter; Cardin et al. 2005; Hahnloser and Fee 2007), then voltage-clamp or chloride loading experiments can be used to test this prediction (Fig. 7). During fictive singing, an HVC_RA neuron will have a background of outward current, with a dip shortly before and during the time of the burst (Fig. 7A), and chloride loading of an HVC_RA neuron will result in a background of spiking (Fig. 7B).

5. Our model predicts that, if GABA_A synapses are blocked, excited groups of HVC_RA neurons will enter a state of persistent activity, whether in vitro or in vivo. How long this activity will last depends on the size of the groups (Fig. 1A), the percentage connectivity of the HVC_RA neurons within groups, and the strength of voltage-dependent hyperpolarizing currents (Figs. 1A and 2, B and C) and neurotransmitter-activated hyperpolarizing currents (e.g., GABA_B; Dutar et al. 1998). However, this effect will be seen only if blocking GABA_A synapses does not itself evoke a high level of song-independent activity. To evoke this persistent activity in vitro, it is necessary to excite a sufficiently large fraction of the HVC_RA neurons in a cluster or the functional equivalent of a cluster. In vivo, our model predicts that song-related HVC_RA bursts will be initiated normally but fail to be rapidly terminated.

6. Our model predicts that HVC_I ISIs during song will have a distribution resembling Fig. 6C, top (with a dip in the frequency of occurrence of certain ISIs), more than Fig. 6C, bottom. Which ISIs will be underrepresented in the histogram depends on both the burst propagation speed and the size of the HVC_I connectivity gap. Since spontaneous activity between song bouts may influence the ISI distribution, the ISIs for such a test should be taken from HVC_I neurons only during the period corresponding to singing. Additionally, it is possible that a version of the model could be developed in which the HVC_I → HVC_RA connectivity pattern is constrained but the HVC_RA → HVC_I connectivity pattern is random. In such a model, HVC_I neurons would not be expected to have this ISI distribution.

Potential role for a Ca²⁺ current in HVC_RA bursting

Under normal conditions, injection of depolarizing current into the soma of an HVC_RA neuron does not evoke Ca²⁺ spikes or any evidence of bursting (Dutar et al. 1998; Kubota and Taniguchi 1998; Long and Fee 2006; Mooney and Prather 2005; Shea 2004). Consequently, we formulated a model in which bursting is not intrinsic to HVC_RA neurons but instead arises in the microcircuitry of HVC. However, recent preliminary work shows that Ca²⁺ spikes, which appear to be of the L-type, are elicited by somatic depolarization of HVC_RA neurons in the presence of a Na⁺-channel blocker (Long and Fee 2006). The same study demonstrates that sleep bursts of HVC_RA neurons are augmented by an agonist of the L-type Ca²⁺ current. These results suggest that an L-type Ca²⁺ current is present in HVC_RA neurons and is capable of influencing bursting. If this current proves to be essential to the bursting mechanism of HVC_RA neurons, it may play a complementary role to inhibition and recurrent excitation.

If this current merely serves to enhance the excitation of postsynaptic HVC_RA neurons, then we would expect augmenting it to have a similar effect to increasing the number or strength of excitatory synapses onto HVC_RA neurons in our model. In this case, the presence of the current may not fundamentally alter our predictions. By contrast, if inactivation of a Ca²⁺ current, rather than inhibition mediated by HVC_I neurons, provided the basis for burst termination, then our predictions would have to be revised. In particular, bursts would continue to terminate even in the absence of inhibition (persistent activity would not be observed). However, it is unlikely that inactivation of an L-type Ca²⁺ current is responsible for terminating the bursts, since this type of current inactivates slowly (Catterall et al. 2005).

Even if intrinsic currents are identified that provide the basis for burst termination, our proposed inhibitory mechanism could still play important roles: for example, it could enhance the temporal precision of the bursts and prevent excitatory inputs from evoking activity outside the normal burst time.

Cluster size

Fee et al. (2004) estimated that about 200 HVC_RA neurons may be coactive at each time in the song motif, which is similar to the number of neurons in our large clusters with physiological synaptic strengths. However, this may be an overestimate, since the study on which they based it (Wang et al. 2002) did not use stereological methods for reconstructing total cell number (JR Kirn, personal communication; West 1999). HVC contains an average of about 40,000 to 50,000 neurons per hemisphere (Burek et al. 1991, 1997; Nordeen and Nordeen 1988, 1989; Ward et al. 1998).

Using the estimate that half of HVC neurons are RA-projecting (Nottebohm et al. 1990) and assuming that only half of the HVC_RA neurons participate in syllable networks, we arrive at an estimate of 10,000 to 12,500 participating HVC_RA neurons. Taking the motif duration to be about 0.5 to 1 s (Fee et al. 2004; Immelman 1969; Price 1979) and the average burst duration to be 5 ms (Kozhevnikov and Fee 2007), we calculate that about 50 to 125 HVC_RA neurons may be coactive at each time in the song motif. In a chain framework, the propagation speed implied by these figures is about 10 to 25 HVC_RA neurons per millisecond. Thus if the number of HVC_RA neurons per cluster is 160, cluster activations must be staggered by about 6 to 16 ms to achieve such slow propagation. The result presented in Fig. 5D suggests that a smaller HVC_I downstream connectivity gap may promote slower propagation. Alternatively, clusters could be smaller and the synaptic response of HVC_RA neurons could be enhanced by a dendritic Ca²⁺ current (Jin et al. 2007; Long and Fee 2006) to achieve an equivalent synaptic effect.

Additionally, our chain model with physiological synaptic strengths suggests that the sparse burst mechanism does not fundamentally rely on a cluster organization; the important elements are recurrent local excitation among HVC_RA neurons and patterned inhibition from HVC_I neurons.

A possible role for developmental plasticity in the establishment of HVC_I → HVC_RA connectivity

What developmental mechanism could generate the pattern of HVC_I → HVC_RA connectivity shown in Fig. 4A? We suggest that a novel form of timing-dependent synaptic plasticity at inhibitory synapses could serve this role. In this proposed model, early in development, HVC_RA → HVC_I and HVC_I → HVC_RA synapses are weak or absent and sustained (nonsparse) spiking activity propagates along chains of recurrently excitatory HVC_RA neurons, terminated by slow hyperpolarization. HVC_RA → HVC_I synapses are gradually added and/or strengthened with time. As they strengthen, subsets of them become strong enough that concurrent spiking in the presynaptic HVC_RA neurons can elicit spiking in the postsynaptic HVC_I neuron.

Additionally, HVC_I → HVC_RA synapses begin weak and follow a specific timing-dependent synaptic plasticity rule: if the presynaptic HVC_I neuron spikes within a few tens of milliseconds before or a few milliseconds after the postsynaptic HVC_RA neuron, the inhibitory synapse is weakened. If the HVC_I neuron spikes outside this time window, the synapse is strengthened. For some period of time after the induction of plasticity, the synapse is resistant to further induction, so that only the first spikes of the propagating activity are involved in triggering plasticity. We suggest that over many bouts of propagation, a plasticity mechanism like this could generate the HVC_I → HVC_RA connectivity required by our model. Our proposed plasticity rule is similar to, although distinct from, various forms of timing-dependent plasticity that have been observed at excitatory and inhibitory synapses (Dan and Poo 2006; Haas et al. 2006; Holmgren and Zilberter 2001; Woodin et al. 2003).

GRANTS

This work was partially supported by National Science Foundation (NSF) Grant NSF PHY0097134 and Multidisciplinary University Research Initiative Contract ONR N00014-07-1-0741 to H. D. I. Abarbanel. H. D. I. Abarbanel also acknowledges partial support through the NSF-sponsored Center for Theoretical Biological Physics at University of California, San Diego (UCSD). D. L. Gibb received support from the NSF Integrative Graduate Education and Research Traineeship program through the UCSD Computational Neurobiology Graduate Program and a predoctoral fellowship from the Training Program in Cognitive Neuroscience of the Institute for Neural Computation at UCSD, supported by National Institute of Mental Health Grant 2 T32 MH-20002.