Brain Stem Feedback in a Computational Model of Birdsong Sequencing

Abstract

Uncovering the roles of neural feedback in the brain is an active area of experimental research. In songbirds, the telencephalic premotor nucleus HVC receives neural feedback from both forebrain and brain stem areas. Here we present a computational model of birdsong sequencing that incorporates HVC and associated nuclei and builds on the model of sparse bursting presented in our preceding companion paper. Our model embodies the hypotheses that 1) different networks in HVC control different syllables or notes of birdsong, 2) interneurons in HVC not only participate in sparse bursting but also provide mutual inhibition between networks controlling syllables or notes, and 3) these syllable networks are sequentially excited by neural feedback via the brain stem and the afferent thalamic nucleus Uva, or a similar feedback pathway. We discuss the model's ability to unify physiological, behavioral, and lesion results and we use it to make novel predictions that can be tested experimentally. The model suggests a neural basis for sequence variations, shows that stimulation in the feedback pathway may have different effects depending on the balance of excitation and inhibition at the input to HVC from Uva, and predicts deviations from uniform expansion of syllables and gaps during HVC cooling.

INTRODUCTION

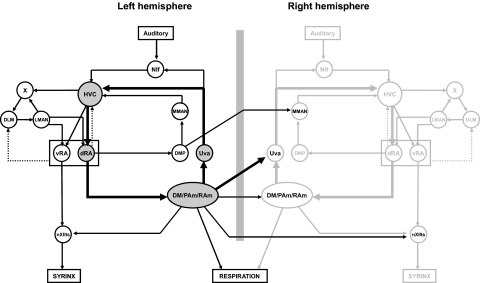
The song system of oscine songbirds is a collection of bilaterally coordinated brain structures, organized into both feedforward and feedback pathways (Fig. 1). As a model system for vocal pattern generation and learning, it has been extensively studied using anatomical, lesion, and electrophysiological approaches, particularly in zebra finches.

FIG. 1.

A: bilateral view of the song system, highlighting the bilateral feedback pathway to HVC via Uva. NIf, interfacial nucleus of the nidopallium; X, area X of the medial striatum; DLM, medial portion of the dorsolateral thalamic nucleus; LMAN, lateral magnocellular nucleus of the anterior nidopallium; MMAN, medial magnocellular nucleus of the anterior nidopallium; dRA and vRA, dorsal and ventral regions of the robust nucleus of the arcopallium; DMP, dorsomedial nucleus of the posterior thalamus; Uva, uvaeform nucleus of the posterodorsal thalamus; RAm, nucleus retroambigualis; PAm, nucleus paraambigualis; DM, dorsomedial nucleus of the intercollicular complex; nXIIts, tracheosyringeal part of the hypoglossal nucleus. Dotted lines indicate the weak projection from RA to DLM described by Wild (1993a) and Vates et al. (1997) and the projection from dorsal RA to HVC described by Roberts et al. (2008). [Based on a figure from Schmidt et al. (2004) and Ashmore et al. (2005), with permission.]

The song of an adult zebra finch consists of a number of introductory notes followed by one or more motifs, each lasting about 0.5 to 1 s (Fee et al. 2004; Immelman 1969; Price 1979) and consisting of several syllables. Syllables are identified as the smallest units of song separated by silent intervals and are a few tens to a few hundreds of milliseconds in duration (Glaze and Troyer 2006; Zevin et al. 2004). Syllables can be further subdivided into notes, which are delimited by sudden changes in the spectrogram (Ashmore et al. 2005).

In the preceding companion paper (Gibb et al. 2009), we presented a model of sparse bursting in the telencephalic premotor nucleus HVC (used as the proper name; Reiner et al. 2004) in which inhibitory interneurons play a key role. Here we incorporate HVC into a larger model of the song system. As Fig. 1 illustrates, HVC projects to another telencephalic premotor nucleus, RA (the robust nucleus of the arcopallium), which in turn projects to respiratory and vocal areas in the brain stem. Following Ashmore et al. (2005), we use the terms dorsal RA (dRA) and ventral RA (vRA) to refer to the dorsal cap area of RA (Reinke and Wild 1998; Vicario 1991) and the rest of RA, respectively. Ventral RA projects to the brain stem nucleus nXIIts (tracheosyringeal part of the hypoglossal nucleus), which controls the syrinx, whereas dorsal RA projects to a brain stem respiratory network consisting of DM (dorsomedial nucleus of the intercollicular complex), PAm (nucleus paraambigualis), and RAm (nucleus retroambigualis) (Fig. 1; Nottebohm et al. 1976, 1982; Reinke and Wild 1998; Sturdy et al. 2003; Suthers et al. 1999; Vicario 1991; Wild 1993a,b, 1997).

No direct bilateral connections exist between any of the telencephalic song nuclei, including HVC. However, two neural feedback pathways to HVC are known to contain bilateral connections, potentially helping to coordinate activity in the two hemispheres: HVC → dRA → brain stem → uvaeform nucleus of the posterodorsal thalamus (Uva) → interfacial nucleus of the nidopallium (NIf) → HVC and HVC → dRA → dorsomedial nucleus of the posterior thalamus (DMP) → medial magnocellular nucleus of the anterior nidopallium (MMAN) → HVC (Fig. 1; Foster et al. 1997; Reinke and Wild 1998; Striedter and Vu 1998; Vates et al. 1997; Wild 1997).

The focus of our model is the potential role of neural feedback to HVC in syllable sequencing. Although the stereotypy of adult zebra finch song motifs might superficially suggest that motifs are monolithic units with a fixed syllable sequence, there are a number of hints that individual syllables are more basic units, which can be rearranged, repeated, or skipped. Many of these hints come from cases of adult syllable-sequence variability (Brainard and Doupe 2001; Leonardo and Konishi 1999; Scharff and Nottebohm 1991; Thompson and Johnson 2006; Williams and Vicario 1993). Two additional pieces of evidence for the idea that syllables constitute basic units are that syllables stretch and compress proportionally less than intersyllable gaps during changes in song tempo (Glaze and Troyer 2006) and birds tend to interrupt their songs during gaps, rather than syllables, when presented with light flashes (Cynx 1990; Franz and Goller 2002).

Schmidt (2003) showed that peaks in the interhemispheric synchronization of HVC lead the onsets of syllables and notes, suggesting a model in which HVC receives bilaterally synchronized timing pulses from an afferent nucleus shortly before the onsets of syllables and notes (Coleman and Vu 2005; Schmidt 2003). In the present work, we asked: What model of HVC input emerges if we make the reasonable assumption that the two HVCs remain coordinated during variable, as well as normal, song sequences? We suggest that if the syllable transitions in the left and right HVCs are to remain coordinated during variable song sequences, then these bilaterally synchronized pulses should specify not just the timing, but also the identity of the next syllable. We refer to this as “syllable-specific input,” in contrast to “syllable-unspecific input.” As a thought experiment, if atypical syllable transitions were instead initiated independently in the two hemispheres, then the two HVCs could make transitions to different syllables. This would violate our assumption of interhemispheric coordination during variable sequences.

Coordination does not necessarily imply that the two hemispheres produce the same commands; it implies only that they are in agreement about what syllable is being sung, irrespective of their relative contributions to the sound produced. A model of input to HVC in songbirds must be flexible enough to explain the bilateral coordination of HVC commands, whether syllables are produced by one side of the syrinx, by both sides in concert, or by switching between sides (Floody and Arnold 1997; Goller and Suthers 1995; Nottebohm 1971, 1977; Nottebohm and Nottebohm 1976; Suthers 1990; Williams et al. 1992).

Because it participates in a bilaterally connected pathway and is necessary for normal song production in adult songbirds (Coleman and Vu 2005), Uva is a good candidate for a nucleus specifying the timing and identity of syllables in the left and right HVC. By contrast, NIf is not necessary for normal adult song production (Cardin et al. 2005) and bilateral adult MMAN lesions affect song only slightly (Foster and Bottjer 2001).

The present study has the goal of integrating the model of HVC sparse bursting developed in our companion paper into a larger song-system model including nuclei of the HVC → dRA → brain stem → Uva → HVC feedback loop, to provide an integrated picture of the dynamics of syllable sequencing in songbirds. In this model, the feedback pathway to HVC via Uva sequentially activates networks controlling different syllables in the model. HVC, dRA, dorsomedial nucleus of the intercollicular complex/nucleus paraambigualis (DM/PAm), and Uva are all assumed to contain syllable-specific populations of neurons. Our model embodies a set of hypotheses and we use it to derive predictions to be tested experimentally.

The model predicts that song-sequence variations can be generated by activating syllable-specific populations of neurons out of sequence, that the balance of excitation and inhibition at the input to HVC from Uva influences whether stimulation of the feedback pathway produces syllable truncations or syllable transitions, and that syllables and gaps expand differentially during HVC cooling.

A portion of this work previously appeared in abstract form (Gibb and Abarbanel 2006).

METHODS

We implemented all models in C++ using a neural-simulation framework developed by T. Nowotny and extended by L. Gibb, using a Runge–Kutta 6(5) algorithm with a relative error of 10⁻⁶, and we performed analyses of model output in MATLAB.

Modeling neurons

We created a simple computational sketch of RA, DM/PAm, Uva, nucleus retroambigualis (Ram), and the tracheosyringeal part of the hypoglossal nucleus (nXIIts) using the basic spiking model described in our companion paper (Gibb et al. 2009; a single-compartment Hodgkin–Huxley-type model with just Na⁺, K⁺, and leak currents). The parameter values of these model neurons were g_Na = 50 mS/cm², E_Na = 45 mV, g_K = 5 mS/cm², E_K = −85 mV, g_L = 0.1 mS/cm², E_L = −70 mV, C_M = 1 μF/cm², and V_T = −55 mV. For HVC_RA and HVC_I neurons, the model equations and parameter values were identical to those in our companion paper: HVC_RA neurons included a fast and a slow voltage-gated K⁺ current, and HVC_I neurons included I_h. The parameters of the neuron models were held fixed; only synaptic strengths and network connectivity were adjusted to achieve the desired network behavior.

Modeling synaptic currents

We modeled synaptic currents using the equations of Destexhe et al. (1994) and Destexhe and Sejnowski (2001), as given in our companion paper. The basic synapse model does not include transmission delays. Where noted, we inserted delays in the feedback pathway by delaying the time of the synaptic current in the postsynaptic neuron. For excitatory synapses onto all neuron types except for HVC_I neurons, α = 1.1 mM⁻¹ ms⁻¹ and β = 0.19 ms⁻¹, as given in our companion paper. All other synaptic parameter values are given in our companion paper, except for the maximal synaptic conductance (g_syn) values, which are given in Table 1.

TABLE 1.

Strengths and numbers of synapses in brain stem feedback model

Synapse	Type	Maximal Conductance, mS/cm2	Number of Synapses
HVCRA → HVCRA within cluster	E	1.0	1 per HVCRA neuron
HVCRA → HVCRA between clusters	E	0.5	1 per cluster (except last cluster)
HVCRA → HVCI	E	0.1	100 per HVCI neuron
HVCI → HVCRA	I	3.0	100 per HVCI neuron
HVCRA → dRADM	E	0.004	1,170 per syllable*
HVCRA → dRARAm	E	0.3	Variable (see text)
HVCRA → vRAnXIIts	E	0.3	Variable (see text)
dRADM/PAm → DM/PAm	E	0.075	5 per dRADM neuron
DM/PAm → Uva	E	0.075	5 per DM neuron
Uva → HVCRA	E	0.04	3 per Uva neuron
Uva → HVCI	E	0.0125	5 per Uva neuron
dRARAm → RAm	E	0.02	15 per dRARAm neuron
vRAnXIIts → nXIIts	E	0.02	15 per vRAnXIIts neuron

E, excitatory; I, inhibitory.

^*Here, 150 synapses per syllable with a maximal conductance of 0.03 mS/cm², and other combinations, produce indistinguishable model spike patterns.

Modeling temperature dependence of neurons and synapses

As in our companion paper, as a first approximation of the temperature dependence of neurons and synapses, we scaled all rate functions by a factor of φ(T₁) = Q₁₀^{(T₂−T₁)/10}, assuming a Q₁₀ of 3 for both neuronal and synaptic rates (Collingridge et al. 1984; Hodgkin and Huxley 1952). Here, T₂ is the brain temperature in vivo (assumed to be 40°C) and T₁ is the approximate temperature at which the measurements were made in vitro. T₁ values were the same as in our companion paper. To produce a uniform slowing of HVC neurons and synapses in the cooling simulation, we scaled not only the rate functions but also the voltage equations of the neurons by a single constant.

Connectivity and neuron numbers for the syllable-sequencing model

Table 1 summarizes the connectivity of the syllable-sequencing model. The neuron numbers are as follows: 3 neurons per cluster, 20 clusters per HVC chain, 90 HVC_I neurons, 10 neurons per subpopulation in the feedback pathway, and 30 neurons each for dRA_RAm, vRA_nXIIts, RAm, and nXIIts. Neurons in the third- and fourth-to-last clusters of each HVC_RA syllable network synapse on a dRA_DM/PAm subpopulation. Uva neurons synapse on HVC_RA neurons in the first cluster of the next syllable network. At each step in the feedback pathway, the postsynaptic neurons were selected randomly from the appropriate subpopulation.

Spike time

We defined spike time as the time of the peak depolarization following a crossing of a −15 mV threshold in a positive direction.

Analysis of stimulation results

For simplicity of analysis, in the stimulation results presented in Fig. 5 and Supplemental Fig. S3,1 we classified a distortion as spiking activity of ≥100 Hz in HVC_RA neurons that lasted for >12 ms. We counted a given result as belonging to only one of the four categories: a syllable transition or song stop that was accompanied by distortion was counted simply as a syllable transition or song stop.

The syllable-sequencing model contained 25% HVC_X neurons (not shown) in addition to 50% HVC_RA neurons and 25% HVC_I neurons (Nottebohm et al. 1990). These HVC_X neurons did not send synapses to any other neurons in the model, but they were included among the neurons stimulated in HVC. This reduced the probability of stimulating HVC_RA and HVC_I neurons.

The syllable-sequencing model contained 25% HVC_X neurons (not shown) in addition to 50% HVC_RA neurons and 25% HVC_I neurons (Nottebohm et al. 1990). These HVC_X neurons did not send synapses to any other neurons in the model, but they were included among the neurons stimulated in HVC. This reduced the probability of stimulating HVC_RA and HVC_I neurons.

Excitatory and inhibitory conductance

In Fig. 6, the excitatory conductance is the α-amino-3-hydroxy-5-methyl-4-isoxazolepropionic acid conductance of the Uva → HVC_RA synapses onto the three HVC_RA neurons in the first cluster of the syllable network (triggered by Uva stimulation; see Fig. 6A), averaged over the three neurons. The inhibitory conductance is the γ-aminobutyric acid type A conductance of the HVC_I → HVC_RA synapses onto the same three HVC_RA neurons, averaged over the three neurons. The integrated conductance is the excitatory or inhibitory conductance integrated over the stimulation interval.

Statistics

We made statistical comparisons using the two-tailed exact test of Liddell (1978) because the sample sizes were small. Throughout, we report values as mean ± SD.

RESULTS

How can our model of sparse bursting, presented in the preceding companion paper (Gibb et al. 2009), be related to syllable sequencing? We propose that each syllable or note is controlled by a dedicated, chainlike network in HVC. During stereotyped song, a brief, syllable-specific signal sent from near the end of one HVC network activates the next HVC network via the feedback pathway through dorsal RA, the brain stem, and Uva. Thus the sequence is stored in the feedback-pathway connections between HVC syllable networks. Inhibition between HVC networks helps to ensure that only one is active at a time and feedforward inhibition by Uva of all but the next HVC network in the sequence also promotes the correct sequence. We frame our model in terms of syllables, but suggest that both syllables and notes may be sequenced in a similar manner. Our model makes predictions concerning the neural basis of sequence variations, the effects of feedback-pathway stimulation, and the effects of HVC cooling, which we describe in this section.

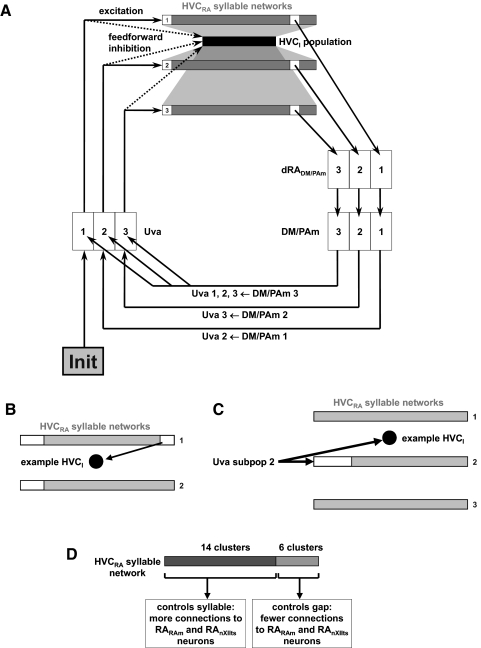
Figure 2 A illustrates our model of syllable sequencing. Each syllable network is a chain of bistable clusters like the one described in our companion paper. HVC activity near the end of syllable network N excites a specific subpopulation of DM/PAm-projecting dRA (dRA_DM/PAm), DM/PAm, and Uva neurons, which then excites syllable network n + 1 in HVC, and so forth, until all the syllables of the motif are completed. Since the differential contributions of the Uva-projecting brain stem structures DM and PAm are unknown, we grouped them together in the model.

FIG. 2.

Model of syllable sequencing via brain stem feedback. A: schematic of model. The motif is initiated by a current pulse into the first subpopulation of Uva (“Init”) and the activity propagates through the network in a spiral in this diagram. Each HVC_RA syllable network (dark gray rectangles) is a chain of 20 clusters of 3 HVC_RA neurons. Each of 90 HVC_I neurons (black rectangle) receives excitation from, and sends inhibition to, 30 HVC_RA neurons. dRA_DM/PAm, DM/PAm, and Uva contain subpopulations dedicated to the transitions between individual syllables. B: schematic illustrating the constraint on HVC_RA–HVC_I connectivity that provides a release of inhibition from the beginnings of all syllable networks when a syllable ends (see text). Because the representative HVC_I neuron receives an excitatory synapse (arrow) from a cluster near the end of an HVC_RA syllable network, it is not permitted to make inhibitory synapses onto the parts of syllable networks shown in white. C: schematic illustrating the constraint on Uva → HVC_I connectivity that prevents feedforward inhibition from blocking the initiation of the new syllable network. Because the representative HVC_I neuron does not make inhibitory synapses onto the first 8 clusters of HVC_RA syllable network 2 (white), it is permitted to receive an excitatory synapse (arrow) from Uva subpopulation 2. D: the first 14 clusters of each HVC_RA network control syllables, whereas the last 6 clusters control gaps.

To prevent persistent activity in the HVC_RA clusters at the end of the last syllable network, and to account for the multiunit “superbursts” observed in Uva by Williams and Vicario (1993) and in HVC by Schmidt (2003), neurons in the final DM/PAm subpopulation in the model synapse on all of the Uva subpopulations (Fig. 2A; see following text).

Roles of HVC_I neurons and constraints on inhibitory connectivity

The population of HVC_I neurons provides inhibition between syllable networks and mediates feedforward inhibition from Uva (i.e., Uva → HVC_I → HVC_RA). We included connections from Uva to HVC_I neurons based on the observation that low-frequency electrical stimulation in Uva elicits excitatory postsynaptic potentials (EPSPs) in HVC_I neurons (Coleman et al. 2007) and the observation that thalamocortical feedforward inhibition is present in mammals (Gabernet et al. 2005). Since it is not clear that HVC_I neurons receive direct connections from Uva, we also created a version of the model in which the feedforward inhibition is absent.

As in our companion paper, the HVC_I neurons play the role of terminating HVC_RA bursts. Each HVC_I neuron is constrained not to make inhibitory synapses onto any cluster from which it receives an excitatory synapse, or onto clusters within seven clusters downstream of one from which it receives an excitatory synapse.

To provide a release of inhibition from the beginnings of all syllable networks when a syllable ends, so that a new syllable network may be excited by input from Uva, we extended the constraint on HVC_I–HVC_RA connectivity as follows: for the purposes of the constraint rule, “7 clusters downstream” extends from the end of a syllable network to the beginnings of all syllable networks (Fig. 2B). For example, an HVC_I neuron that receives excitation from the third cluster from the end of one syllable network cannot send inhibition to either the last three clusters of the same syllable network or the first five clusters of any syllable network.

Additionally, to prevent the feedforward inhibition from blocking the initiation of the new syllable network, we permit each subpopulation of Uva neurons to synapse only on those HVC_I neurons that do not synapse on the first eight clusters of the corresponding HVC syllable network (Fig. 2C). We chose this number of clusters to ensure that the feedforward inhibition has enough time to decay, although we did not fine-tune this parameter.

Control of RAm and nXIIts

The model assumes that there is no difference between the parts of HVC_RA networks controlling syllables and networks aside from their downstream connectivity. Syllable-controlling parts of HVC_RA networks project more strongly to RAm- and nXIIts-projecting regions of RA (dRA_RAm and vRA_nXIIts), whereas gap-controlling parts of HVC_RA networks project less strongly. The summed activity of these RA regions thus reaches a low at gaps. The resulting lows in the activity of RAm and nXIIts correspond to gaps between syllables. Since Leonardo and Fee (2005) reported that the fractions of RA neurons bursting during syllables and gaps are not significantly different, we regard this aspect of our model as an oversimplification designed to convey that some portions of the chains control syllables, whereas others control gaps.

More specifically, the syllable-controlling part of each HVC_RA network consists of the first 14 clusters, whereas the gap-controlling part consists of the last 6 clusters (Fig. 2D). The propagation time for the syllable-controlling part is 56.1 ± 1.7 ms (n = 96) from the first to the last spike; that for the gap-controlling part is 17.7 ± 0.7 ms (n = 96). The activity of the gap-controlling part is truncated by the arrival of input from Uva. Each neuron in dRA_RAm and vRA_nXIIts is twice as likely (P = 0.05) to receive a synapse from a syllable-controlling HVC_RA neuron as from a gap-controlling one (P = 0.025).

Activity of the model

Figure 3 shows the complete spiking activity of the model. A wave of HVC_RA bursting (5.1 ± 2.0-ms burst duration, 3.6 ± 1.0 spikes per burst; 32 trials) is initiated by a brief burst of spikes in the first Uva subpopulation (triggered in the model by a 5-ms, 20-μA/cm² current pulse injected into all Uva neurons of this subpopulation at t = 0 ms). Neurons near the end of a given HVC syllable network trigger a sequence of activations of the appropriate dRA_DM/PAm, DM/PAm, and Uva subpopulations. The Uva subpopulation then excites the next HVC syllable network and, via HVC_I neurons, inhibits the other syllable networks.

FIG. 3.

Spike times of all neurons in the model shown in Fig. 2. The first subpopulation of Uva is excited by a current pulse at t = 0 ms.

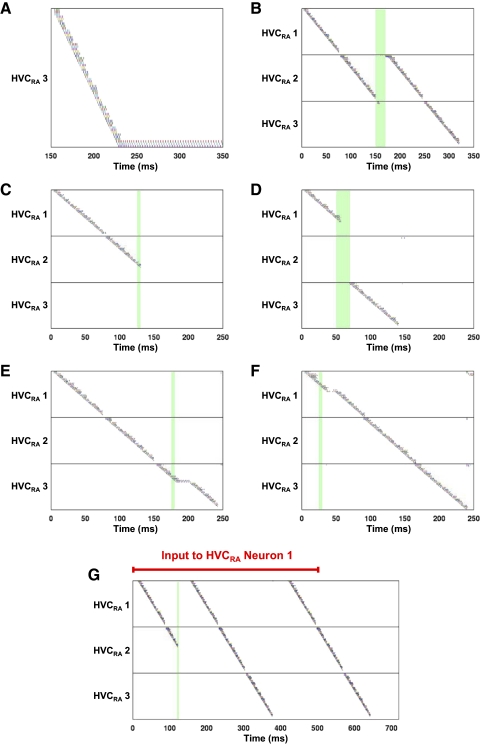
The last DM/PAm subpopulation excites all of the Uva subpopulations, causing both excitation and feedforward inhibition of the first cluster of each chain. The parameters are set so that the inhibition predominates over the excitation and the activity in HVC ends. If we omit synapses from the final DM/PAm subpopulation to all of the Uva subpopulations, then one or two clusters at the end of the last HVC_RA syllable network enter a state of persistent activity (Fig. 4 A).

FIG. 4.

Perturbations of the syllable-sequencing model. Green rectangles indicate stimulation times. All examples except for F are for versions of the model that include Uva → HVC_I connections. A: spike times of the last HVC_RA syllable network when we omit the excitation of all Uva subpopulations by the terminal DM/PAm subpopulation. B: stuttering of the second syllable, generated when a 20-ms current pulse is injected into dRA_DM/PAm subpopulation 2. C: example of truncation and “song stop” caused by a 5-ms current pulse injected into all dRA_DM/PAm neurons. D: example of syllable transition, elicited by a 20-ms current pulse injected into dRA_DM/PAm subpopulation 2. E: example of distortion in the HVC_RA burst sequence caused by a 5-ms current pulse injected into dRA_DM/PAm subpopulation 2. F: example of distortion in the HVC_RA burst sequence caused by a 5-ms current pulse injected into dRA_DM/PAm subpopulation 2. G: motif restart generated after syllable truncation caused by a 5-ms current pulse injected into all DM/PAm neurons. In this version of the model, we stimulate the first neuron of the first syllable network in HVC with a current lasting from t = 0 to t = 500 ms.

Neural basis of sequence variations

What is the neural basis of stutters and other sequence variations? We imagine that in real birds, the neural “tracks” that lead from one syllable representation to another are not strict: under certain circumstances, the bird can leap from one track to another. The model can be made to stutter in two very simple ways. In the first (Supplemental Fig. S1), we rewired the HVC → dRA_DM/PAm connections so that HVC syllable network 3 activates dRA_DM/PAm subpopulation 2 instead of dRA_DM/PAm subpopulation 3. In the second (Fig. 4B), we stimulated all of the neurons in dRA_DM/PAm subpopulation 1 with a timed 20-ms, 20-μA/cm² current pulse, triggering a reactivation of HVC_RA syllable network 2 followed by a normal completion of the sequence. This current injection could represent the synaptic influence of the lateral magnocellular nucleus of the anterior nidopallium (LMAN) on dRA (Johnson et al. 1995; see discussion).

Generation of repeated motifs

As described earlier, the model normally runs through a series of syllables and then stops. However, a slight modification of the model generates repeated motifs. We suggest that a population of initiator neurons in HVC may be activated by input carrying an “intention” to sing from elsewhere in the brain. The model is neutral with regard to the source of this input, although it is plausible that the source is again Uva and the brain stem (perhaps DM). We performed 10 simulations (Supplemental Fig. S2), in which we injected a constant current of 5 μA/cm² into the first neuron of the first HVC_RA cluster. The current initiates each wave of activity in the syllable networks in the usual manner. While the syllable networks are active, they inhibit the initiator neuron via the HVC_I neurons, preventing the initiator neuron from spiking. When the activity reaches the end of the last syllable network, this inhibition is released, allowing the initiator neuron to reach threshold again and trigger a new motif.

Perturbation of the model

Experimentally, electrical microstimulation in the feedback pathway can produce syllable truncations, song stops, and motif restarts (Ashmore et al. 2005). These observations are consistent with a model like ours, in which the feedback pathway forms an integral part of the song pattern generator. To compare the model to the real system and make novel predictions, we performed a set of stimulation experiments on the model. Taking advantage of the flexibility of the computational framework, we stimulated either focally or broadly in HVC and the feedback pathway. Based on the possibility that the syllable-specific subpopulations of the feedback pathway are organized as “syllabotopic” maps (i.e., topographic maps organized by syllable), each focal stimulation of the feedback pathway activates an entire subpopulation, whereas broad stimulation activates all subpopulations in a nucleus. By contrast, we assumed that each focal stimulation of HVC activates only part of a syllable network (a single neuron in this reduced model), rather than an entire syllable network.

Based on the functional connectivity of the model, one might expect to observe three different effects—syllable truncation, syllable transition, and HVC_RA distortion—in response to different types of stimulation. We outline these possibilities below.

Ashmore et al. (2005) observed syllable truncations in response to stimulation in the feedback pathway. In the model, one might expect truncations (premature terminations of the HVC_RA burst sequence) to be produced by feedforward inhibition from Uva to HVC. If the stimulation excites Uva subpopulations during a syllable, the feedforward inhibition of the ongoing HVC_RA activity could truncate the syllable. In the absence of a motif-restart mechanism, this truncation would also result in a song stop.

Under some circumstances, stimulation in the model could result in a syllable transition: termination of the ongoing HVC_RA activity could be followed by initiation of a new syllable network. For example, if the stimulation excites a single syllable-specific subpopulation of Uva neurons, the truncation of the previous syllable (as earlier) could be followed by the initiation of the new syllable network. For this to happen, the stimulation should be long enough so that excitation of the new syllable network predominates over the residual inhibition from the previous syllable.

Relatively minor effects that we collectively refer to as “HVC_RA distortions,” which are characterized by a lengthening of burst duration, are also possible in response to stimulation in the feedback pathway in the model. For example, excitation of a single subpopulation of Uva neurons near the transition time could cause a prolonged burst in the first HVC_RA cluster of the corresponding syllable network. Additionally, Uva-evoked inhibition in HVC that was not strong enough to terminate HVC_RA activity could instead cause a brief pause in a cluster's spiking, thus prolonging its total spiking duration. Finally, because our model uses feedforward inhibition of all but the first eight clusters of a syllable network, excitation of a single subpopulation of Uva neurons could, through feedforward inhibition, temporarily suppress bursting in HVC_RA cluster 9 and thus delay the normal termination of bursting in cluster 8 by cluster 9.

As suggested by the above-cited thought experiments, we observed three effects of perturbing our model: truncation, syllable transition, and HVC_RA distortion (Fig. 4, B–F).

A truncation in the model was a premature termination of the HVC_RA burst sequence. Figure 4C shows a syllable truncation and song stop of the HVC_RA burst sequence caused by injecting a 5-ms, 20-μA/cm² current pulse into all the neurons of all three subpopulations of dRA_DM/PAm. In addition, Ashmore et al. (2005) observed examples of motif restart following syllable truncation. Figure 4G shows that the version of the model in which a constant current into the initiator neuron is maintained can produce a motif restart after truncation.

A syllable transition in the model was a premature termination of the HVC_RA burst sequence followed by a continuation of the burst sequence from the beginning of a different syllable network. In addition to the specific type of syllable transition (stutter) shown in Fig. 4B, Fig. 4D shows an example of a syllable transition evoked by stimulation of the neurons in RA_DM/PAm subpopulation 2 with a 20-ms, 20-μA/cm² current pulse.

Our focus here is on truncations and transitions rather than HVC_RA distortions. We define the latter narrowly as spiking activity of ≥100 Hz in HVC_RA neurons that lasts for >12 ms. Figure 4E shows an HVC_RA distortion caused by injecting a 5-ms, 20-μA/cm² current pulse into all the neurons of dRA_DM/PAm subpopulation 2. Figure 4F shows an HVC_RA distortion in the version of the model without Uva → HVC_I connections, caused by injecting a 5-ms, 20-μA/cm² current pulse into all the neurons of dRA_DM/PAm subpopulation 2. Note the brief pause in spiking.

Exploring the effects of stimulation on the model

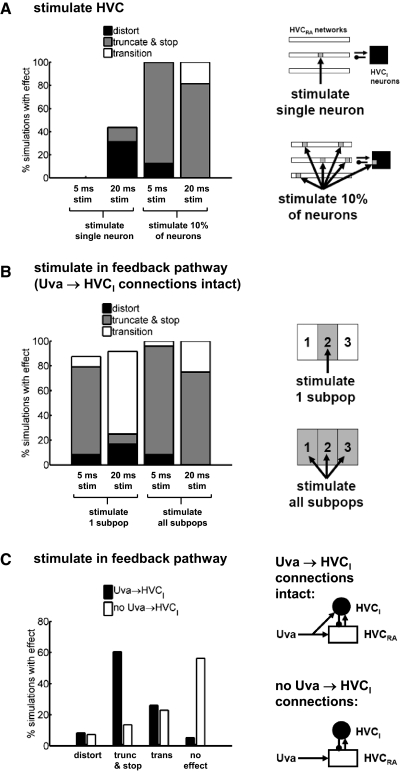
We performed 128 simulations with and 128 simulations without Uva → HVC_I connections, stimulating HVC, dRA_DM/PAm, DM/PAm, or Uva with current pulses of different durations and with greater or lesser numbers of neurons stimulated (Fig. 5; Table 2). The simulations without Uva → HVC_I connections were performed because it is not clear that HVC_I neurons receive direct connections from Uva. In HVC, we stimulated either a single neuron or 10% of the total population. In the feedback pathway, we stimulated either a single subpopulation of 10 neurons (“1 subpop” in Fig. 5B) or the total population of 30 neurons (“all subpops” in Fig. 5B). For each stimulation type (i.e., each combination of nucleus stimulated, extent of stimulation, and duration of stimulation), we stimulated at t = 25, 50, 75, 100, 125, 150, 175, and 200 ms. The current pulses were 20 μA/cm² in amplitude and either 5 ms (“short”) or 20 ms (“long”). For each simulation, the connectivity of the model was recalculated with new random numbers.

FIG. 5.

Exploring the effects of stimulation on the syllable-sequencing model. Percentage of simulations showing HVC_RA distortion (distort), truncation, and song stop (truncate and stop), or syllable transition (transition). A, left: effects of stimulating either a single HVC neuron or 10% of the total HVC population with either 5- or 20-ms current pulses. Right: schematic of the 2 spatial patterns of HVC stimulation. Arrowheads represent excitation and dots represent inhibition. B: effects of stimulating in the neural feedback pathway of the model with Uva → HVC_I connections intact. Left: effects of stimulating dRA_DM/PAm, DM/PAm, or Uva neurons: either a single subpopulation (stimulate 1 subpop) or the total population (stimulate all subpops), and either 5- or 20-ms current pulses. We grouped the data for stimulation of dRA_DM/PAm, DM/PAm, and Uva. Right: schematic of the 2 spatial patterns of feedback-pathway stimulation. C: different effects of stimulating in the feedback pathway of models with or without Uva → HVC_I connections. Left: percentage of simulations showing distortion, truncation, and song stop, syllable transition, or no effect. Right: schematic of the model with and without Uva → HVC_I connections. The white rectangles and black circles represent the HVC_RA and HVC_I populations, respectively.

TABLE 2.

Effects of stimulating brainstem feedback model

Nucleus	Extent of Stimulation	Duration of Stimulation, ms	n Normal	n Truncate and Stop	n Distort	n Syllable Transition
HVC	Single neuron	5	8	0	0	0
		20	4	1	3	0
	10% of neurons	5	0	7	1	0
		20	0	8	0	0
dRA	1 subpop.	5	1*	5	1	1
		20	0	0	2	6
	All subpops.	5	0	7	0	1
		20	0	6	0	2
DM/PAm	1 subpop.	5	1*	6	1	0
		20	1*	1	1	5
	All subpops.	5	0	8	0	0
		20	0	5	0	3
Uva	1 subpop.	5	1*	6	0	1
		20	1*	1	1	5
	All subpops.	5	0	6	2	0
		20	0	7	0	1

1 subpop., single subpopulation of 10 neurons; all subpops., total population of 30 neurons.

^*These are cases in which a subpopulation was stimulated at a time when it was normally active.

Figure 5A summarizes the effects of stimulating HVC. We combined the results with and without Uva → HVC_I connections because the differences between them were not significant (P > 0.1, Liddell's exact test). We observed significantly fewer truncations for single-neuron stimulation (either short or long) than for stimulation of 10% of HVC neurons (either short or long; P < 0.001, Liddell's exact test). The mechanism of this truncation likely involves excitation of HVC_I neurons.

Figure 5B summarizes the combined results of stimulating dRA_DM/PAm, DM/PAm, and Uva when the Uva → HVC_I connections were intact. We observed significantly fewer truncations (P < 10⁻⁵, Liddell's exact test) and significantly more syllable transitions (P < 0.01, Liddell's exact test) for long stimulation of a single subpopulation than for the other three stimulation protocols. This agrees with the thought experiment described earlier, in which long stimulation of a single subpopulation promotes syllable transitions.

The duration of HVC_RA distortions in response to stimulation of HVC was 22.1 ± 6.6 ms (n = 16 neurons; grouping data from the models with and without Uva → HVC_I connections). The duration of HVC_RA distortions in response to stimulation in the feedback pathway was 25.1 ± 8.2 ms (n = 36 neurons) for the model with Uva → HVC_I connections and 18.3 ± 7.8 ms (n = 23 neurons) for the model without these connections. In 19 of 22 trials containing distortions, the distortions were confined to neurons in just one cluster.

Comparison of stimulation effects with and without feedforward inhibition

Figure 5C shows the number of distortions, truncations, transitions, and simulations with no effect for dRA_DM/PAm, DM/PAm, and Uva stimulation either with or without the Uva → HVC_I connections. There was a large decrease in the number of truncations (from 60 to 14%) and a large increase in the number of simulations with no effect (from 5 to 56%) without the Uva → HVC_I connections (P < 10⁻¹⁰ for both, Liddell's exact test). This agrees with the intuitive picture described earlier, in which feedforward inhibition from Uva promotes truncation.

Mechanism of syllable transition versus truncation: balance of excitation and inhibition

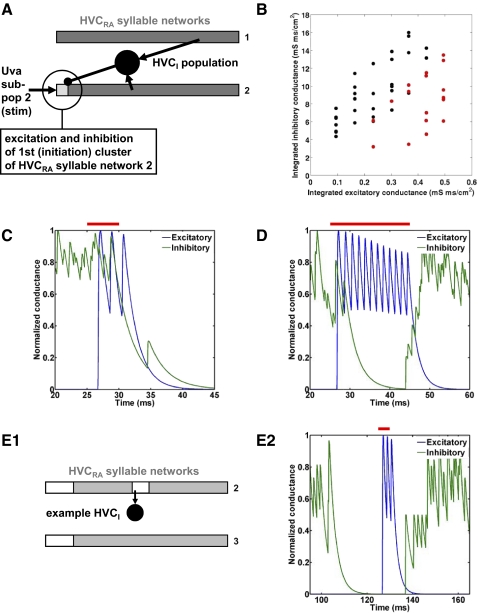
As described earlier, a key finding was that longer (20-ms) stimulation of a single subpopulation increased the likelihood of triggering a syllable transition, whereas shorter (5-ms) stimulation tended to promote truncation and song stop (Fig. 5B). In the thought experiment described earlier, we noted that for syllable transition to occur, the stimulation should be long enough so that excitation of the new syllable network predominates over the residual inhibition from the previous syllable network. From this intuitive picture, it is clear that the balance of excitation and inhibition at the initiation cluster of a syllable network may influence whether truncation or syllable transition occurs. We investigated this effect in the simulations summarized in Fig. 6. We stimulated a single subpopulation of Uva neurons with durations from 5 to 20 ms (2.5-ms increment; stimulation beginning at t = 25 ms in every case) and calculated the integrated excitatory and inhibitory synaptic conductances at synapses onto HVC_RA neurons of the initiation cluster of the corresponding, triggered syllable network (see Fig. 6A). This initiation cluster receives excitatory input from the stimulated Uva subpopulation and inhibition from other clusters via the HVC_I population.

FIG. 6.

Mechanism of truncation vs. syllable transition in the syllable-sequencing model. A: the HVC_RA cluster in which we measured the excitatory and inhibitory conductance (circled; first cluster of syllable network 2 in B–D, first cluster of syllable network 3 in E) receives excitatory input from the stimulated Uva subpopulation and inhibition from other clusters via the HVC_I population. B: Uva stimulation causing truncation (black dots) tended to be associated with higher integrated inhibitory conductance and lower integrated excitatory conductance in the neurons of the first cluster of the corresponding syllable network, whereas Uva stimulation causing transition (red dots) tended to be associated with the converse. C and D: representative time courses of inhibitory and excitatory conductances, normalized, for C a short (5-ms) stimulation of Uva, causing truncation and D a long (20-ms) stimulation of Uva causing syllable transition (mean of 3 neurons). Red bars: time of Uva stimulation. The normal onset time of syllable 2 is 79.2 ± 0.4 ms. E: modifying the HVC_I–HVC_RA connectivity to release inhibition from the first cluster at the time of a short (5-ms) stimulation of Uva permits the inhibitory conductance to decay before the excitatory input arrives, thus favoring transition over truncation. E1: schematic illustrating modified connectivity, providing a release of inhibition from the first cluster at the time of stimulation (cf. Fig. 2B). Because the representative HVC_I neuron receives an excitatory synapse (arrow) from a cluster that spikes near what would be the truncation time, it is not permitted to make inhibitory synapses onto the parts of syllable networks shown in white. E2: representative time courses of inhibitory and excitatory conductances in the first cluster of syllable network 3, normalized, for a simulation with this modified connectivity (mean of 3 neurons). The normal onset time of syllable 3 is 154.1 ± 0.7 ms.

As Fig. 6B shows, truncation tended to be associated with higher inhibitory conductance and lower excitatory conductance values at the initiation cluster of the syllable network, whereas transition tended to be associated with the converse. There is, however, overlap between the two clusters: the integrated excitatory and inhibitory conductances did not completely predict transition and truncation. It is reasonable to suppose that the specific time courses of the excitatory and inhibitory conductances, in interaction with the voltage-dependent currents, are important in determining whether excitation or inhibition predominates. The integrated conductances do not capture these details, which may account for the overlap. To illustrate these two classes of stimulation effect, we show the time course of the mean excitatory and inhibitory conductance of the three neurons of the initiation cluster for stimulation producing truncation (Fig. 6C) and transition (Fig. 6D).

If, as these results suggest, truncation is related to the inhibition of initiation clusters, then artificially removing this inhibition at about the time of stimulation should change truncations into transitions—this is indeed what we find (Fig. 6E). Normally, when we stimulate at t = 125 ms, the 12th cluster in the second syllable network is the second-to-last cluster to spike before the truncation. To artificially release the inhibition of the third syllable network's initiation cluster at the appropriate time, we treated the 12th cluster in the second syllable network like the end of a syllable network: the “7 clusters downstream” rule extended from this cluster to the beginnings of all syllable networks (Fig. 6E1). Figure 6E2 shows that this modification permits the inhibitory conductance to decay before the excitatory input arrives from Uva. With this modification, 10 of 10 trials with 5-ms stimulation showed transition, whereas in the normal case, 10 of 10 trials with 5-ms stimulation showed truncation.

Timing dependence of stimulation effects

Given the nonuniform functional connectivity of the model, one might expect to observe different effects depending on the timing of the stimulation relative to syllable onset. As Supplemental Fig. S3 shows, we did see evidence for such timing dependence.

Compensation for feedback delay

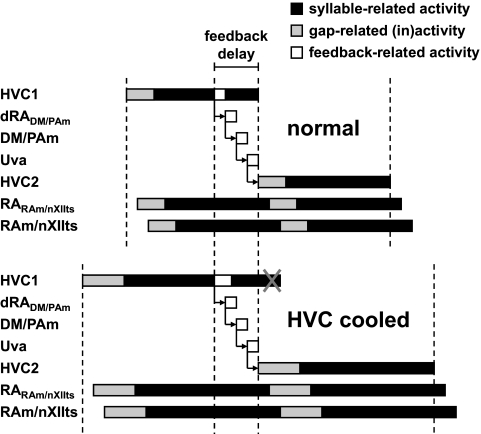
The HVC → dRA_DM/PAm → DM/PAm → Uva → HVC feedback delay in our current model is 14.3 ± 0.5 ms (n = 10). The signal to dRA_DM/PAm is sent by a cluster before the end of each HVC syllable network, so this delay does not result in a pause in HVC_RA activity (Fig. 7, top). This arrangement permits the generation of intersyllable gaps that are shorter than the feedback delay.

FIG. 7.

Effect of HVC cooling. Top, normal: a region of a syllable network sends a signal to the feedback pathway. This region is well before the end of the network, to compensate for the feedback delay. Bottom, HVC cooled: when the activity of HVC is slowed, the feedback delay remains approximately constant while the HVC activity expands in time. Consequently, the end of the syllable network's activity is suppressed by Uva input and/or activation of the next syllable network (gray X). This truncation has different effects depending on whether the gap is controlled by the beginning or the end of the syllable network (see text).

The feedback delay has not been measured directly in birds. The HVC → RA delay is about 4.5 ms (Hahnloser et al. 2002; consistent with Kimpo et al. 2003) and the delay between Uva stimulation and the onset of postsynaptic potentials in HVC is about 5 ms (Coleman et al. 2007). If the other two connections in the feedback loop have similar delays, then the total delay is about 20 ms. Consistent with this estimate, Vu et al. (1998) found that the shortest delay between stimulation of HVC in one hemisphere and full suppression of the other was 24 ms (mean = 36.1 ms). This provides an upper limit on the feedback delay.

In the simulations described so far, the signal to dRA is sent by the third- and fourth-to-last clusters of each HVC syllable network. In 10 simulations, we increased the HVC-to-HVC delay to 36.2 ± 0.2 ms by inserting a total of 24 ms of delays in the pathway from HVC to Uva. We found that having the ninth- and tenth-to-last clusters, rather than the third- and fourth-to-last clusters, project to the feedback pathway compensated for this increased delay.

Differential expansion of syllables and gaps during HVC cooling

If HVC is cooled as in the experiments of Long and Fee (2008), our solution to the problem of feedback delay predicts that syllables and gaps will show differences in expansion. In Fig. 7 (bottom), we show the effect of slowing HVC activity, assuming that input from Uva truncates the previous syllable network while activating the next syllable network. As a result of this truncation, the syllable expands less than the gap.

We observed this phenomenon of truncation, resulting in differential expansion of syllables and gaps, in model simulations. We set the feedback delay to 23.4 ± 0.4 ms (n = 5) and made the fifth- and sixth-to-last clusters project to the feedback pathway. We implemented the slowing in a phenomenological manner by multiplying all of the neuronal and synaptic differential equations in HVC by a constant, 0.67, to produce a uniform 50% slowing of activity within each syllable network in HVC. This is meant to model the functional but not the physiological effects of cooling. This approach is appropriate to the goal of this section, which is to show that our model's feedback architecture itself predicts nonuniformities in the expansion of syllables and gaps, irrespective of physiological details.

As a result of truncation, more clusters were silent at the end of the syllable network in the slowed case (the third-to-last cluster is the last to exhibit spiking; Supplemental Fig. S4) than in the normal case (the last cluster is the last to exhibit spiking).

What effect will this truncation have on syllable and gap durations? The answer depends on whether the truncated part of the syllable networks control syllables or gaps (or some combination of the two). If the last six clusters of each syllable network control the gap, then we calculate from these simulations that gaps lengthen by 14.7 ± 9.6% (n = 5) and syllables by 51.1 ± 2.5% (n = 5). If the first six clusters control the gap, then gaps lengthen by 51.6 ± 2.3% (n = 5) and syllables lengthen by 36.6 ± 4.7% (n = 5).

Slowing HVC slightly increased the measured feedback delay (to 27.3 ± 1.4; n = 5), which can partially be accounted for by the increase in time from the onset of depolarization to the first spike in the HVC_RA initiation neurons (7.4 ± 0.9 vs. 5.1 ± 0.5; n = 5).

We can analytically calculate the degree of expansion of syllables and gaps during cooling in an idealized version of this syllable-sequencing model. In this idealized model, let us assume that a syllable network in HVC sends a brief signal to the feedback loop at a time t_delay before the end of the syllable network. After a delay of t_delay, this signal activates the next syllable network. To accommodate the possibility of a slight change in this delay with HVC cooling, we distinguish the original and final delay, t_delay1 and t_delay2, respectively. If the previous syllable network is still active at this time, it is instantaneously suppressed. Now suppose that HVC activity is stretched in time by the factor f_slow (f_slow = 1.5 implies a 50% lengthening). Let t_syllable1 and t_syllable2 be the original and final duration, respectively, of the network activity controlling a syllable, and t_gap1 and t_gap2 be the original and final duration, respectively, of the network activity controlling a gap. For simplicity, let us consider syllables and gaps that are not at the beginning or the end of the motif and let us assume for now that gaps and syllables are consistently controlled by either the beginnings or the ends of syllable networks throughout the motif.

If gaps are controlled by the ends of syllable networks and t_gap1 ≥ t_delay1 − t_delay2/f_slow, then when HVC is cooled, the activity controlling a gap will be partially truncated and the activity controlling a syllable will not be truncated at all. In this case, t_gap2 = f_slow(t_gap1 − t_delay1) + t_delay2 and t_syllable2 = f_slowt_syllable1. This implies a uniform expansion of the syllable and a competition between expansion and truncation of the gap during cooling. For our simulations, described earlier (using the mean values t_gap1 = 24.4 ms, t_delay1 = 23.4 ms, and t_delay2 = 27.3 ms), this predicts an 18% expansion of the gaps and a 50% expansion of the syllables, which are similar to the values calculated earlier from our model.

If gaps are controlled by the beginnings of the syllable networks, then if, as is reasonable to assume, t_syllable1 ≥ t_delay1 − t_delay2/f_slow, the activity controlling the first gap will not be truncated at all and the activity controlling the first syllable will be partially truncated. In this case, t_gap2 = f_slowt_gap1 and t_syllable2 = f_slow(t_syllable1 − t_delay1) + t_delay2. This implies a uniform expansion of the gap and a competition between expansion and truncation of the syllable during cooling. For our simulations, described earlier (using the mean values t_syllable1 = 55.5, t_delay1 = 23.4 ms, and t_delay2 = 27.3 ms), these equations predict a 50% expansion of the gaps and a 36% expansion of the syllables, which are similar to the values calculated earlier from our model.

DISCUSSION

Our model extends the framework of sparsely bursting networks of HVC_RA neurons presented in the preceding companion paper (Gibb et al. 2009). We propose that each syllable is controlled by such a network and that such networks are activated in sequence by feedback via the brain stem and Uva. The model suggests that activation of syllable-specific populations out of sequence may underlie song-sequence variations, that stimulation of the feedback pathway may produce truncations or syllable transitions depending on the balance of excitation and inhibition at the input to HVC from Uva, and that HVC cooling will result in differential expansion of syllables and gaps. This model makes a number of assumptions and predictions.

First, in its current form, our model predicts that individual Uva, DM/PAm, or dorsal RA neurons are active only near the onsets and/or offsets of particular syllables or notes. Formulated more generally, our model predicts that the summed activity of subpopulations of Uva, DM/PAm, or dorsal RA neurons peaks only near the onsets and/or offsets of particular syllables or notes. Although the RA neurons that have been recorded during song generate an average of 12 bursts per motif (Leonardo and Fee 2005), it may be that the summed activity of subpopulations of these neurons peaks near syllable onsets and/or offsets. Alternatively, it may be that these recordings do not include dRA_DM/PAm neurons.

Second, our model of repeated-motif generation predicts that HVC_RA and HVC_I activity reaches a low between motifs.

Third, our model of syllable sequencing predicts that electrically stimulating Uva, DM/PAm, or dorsal RA neurons may promote syllable truncation, song stop, HVC_RA distortion, or atypical syllable transitions, depending on stimulus parameters and number of neurons stimulated (Fig. 5). We related the increased number of transitions and decreased number of truncations that we observed in response to longer-duration stimulation to the relative excitation and inhibition at syllable initiation zones in HVC (Fig. 6). The modeling result in Fig. 4G suggests that song restart may occur after song stop if the HVC input representing an “intention” to sing continues after the stimulation interrupts the song.

Fourth, our solution to the problem of feedback delay (Fig. 7) results in the prediction that there will be deviations from uniform expansion of syllables and gaps when HVC is cooled, as in the experiments of Long and Fee (2007). Gaps expand less than syllables when they are controlled by the ends of syllable networks and more than syllables when they are controlled by the beginnings of syllable networks. These calculations can also be expanded to cases in which subsyllabic notes and/or gaps are controlled by discrete HVC networks activated by Uva input.

Fifth, atypical syllable transitions in our model can be induced by stimulating a syllable-specific subpopulation of dRA_DM/PAm neurons out of sequence. Input from lateral LMAN to dRA (Johnson et al. 1995) could play this role in juvenile songbirds and in adults during states of sequence plasticity (Brainard and Doupe 2001; Thompson and Johnson 2006). This would predict that neural activity corresponding to an atypical syllable transition would begin in lateral LMAN and spread to dRA, the feedback pathway, HVC, and vRA, in that order. In the model of Troyer and Doupe (2000), input from LMAN to RA biases sequence transitions and plays a role in sequence learning. However, their model does not include the HVC neural feedback pathway and differs fundamentally from ours in the manner in which it represents sequences.

Consistent with this idea, lesions or inactivations of LMAN in juvenile zebra finches decrease the variability of syllable sequences (Bottjer et al. 1984; Olveczky et al. 2005; Scharff and Nottebohm 1991). By contrast, recent experiments by Hampton et al. (2009) show that LMAN lesions in adult Bengalese finches do not affect syllable-sequence variability; in this case, the variability may be due to a different mechanism, such as MMAN or NIf input to HVC (Foster and Bottjer 2001; Hosino and Okanoya 2000).

An additional prediction, which is less specific to our model, is that a repetition of a syllable within a motif (e.g., ABCB) will be accompanied by a repetition of an HVC_RA burst. This feature is not included explicitly in models that describe a single HVC chain (Abarbanel et al. 2004; Fiete et al. 2005; Jin et al. 2007; Li and Greenside 2006), nor in other models that assume a fixed sequence of bursts in HVC (Fiete et al. 2004, 2007). Finally, our model assumes that the two hemispheres of HVC are coordinated even during variable sequences.

Inhibitory connectivity in HVC

Central to our model's behavior is the assumed connectivity of inhibitory interneurons in HVC. First, as in our companion paper, the interneurons are able to participate in the generation of sparse bursting because of a specific constraint on their connectivity. Second, we extended the constraint on their connectivity in a manner that provides a release of inhibition from the beginnings of all syllable chains at the time of syllable transitions. Third, in the version of our model that includes Uva → HVC_I connections, we constrained the connectivity in a manner that ensures that the HVC_RA neurons in the first segment of a newly initiated syllable network are not inhibited by Uva → HVC_I feedforward inhibition.

The results of our stimulation experiments (Fig. 5) are closely tied to the inhibitory connectivity in HVC. Syllable truncations elicited by stimulation of the feedback pathway tended to be associated with higher inhibitory conductance and lower excitatory conductance values at the first cluster of a syllable network, whereas syllable transitions tended to be associated with the converse (Fig. 6B). Additionally, the nonuniform connectivity of the model is reflected in the timing dependence of stimulation effects (Supplemental Fig. S3).

Absence of syllable transitions in experimental data

Importantly, although stimulation of our model can produce jumps to syllables out of sequence, such syllable transitions have not been reported in response to experimental stimulation in the feedback pathway or HVC of songbirds. Syllable truncations, however, have been frequently observed (Ashmore et al. 2005). It is possible that the stimulation protocols that have been reported experimentally correspond functionally to only a subset of our stimulation protocols.

For example, the 5-ms stimulation of all the subpopulations in our model produces only a very small fraction of syllable transitions (Fig. 5B) and, in this respect, is similar to the data of Ashmore at al. (2005). This stimulation may be functionally similar to their experimental stimulation, although theirs consisted of a somewhat longer series of extracellular current pulses. The experimental stimulation may excite neurons broadly throughout a nucleus, rather than within a single putative syllable-specific subpopulation.

Our results suggest that, at a minimum, it would be worthwhile to explore the experimental stimulus parameter space more extensively to see whether syllable transitions can be evoked in singing birds. Can longer stimulus trains (perhaps also at a different frequency or with modified pulse characteristics) evoke syllable transitions? Based on the possibility that syllable-specific subpopulations are arranged “syllabotopically,” can more focal stimulation in the feedback pathway evoke syllable transitions? For example, perhaps a bipolar stimulating electrode with very closely spaced tips—and an appropriate stimulus amplitude—could stimulate neurons primarily within a single subpopulation and thereby evoke a syllable transition.

Which brain stem nucleus (if any) is involved in syllable sequencing?

In an earlier version of this model (Gibb and Abarbanel 2006), we gave PAm the key role of providing syllable-specific feedback to HVC via Uva. Given PAm's role in inspiration (Reinke and Wild 1998), it is reasonable to suppose that its respiratory neurons show activity corresponding to the inspiratory “minibreaths” between syllables (Calder 1970; Hartley and Suthers 1989; Wild et al. 1998). Additionally, recent work shows that bursting in a type of nonrespiratory neuron in PAm is correlated with bursting in the contralateral RA (Ashmore et al. 2008). However, as a medullary nucleus, PAm may convey simple timing signals to Uva, rather than relatively high-level signals concerning syllable identity.

As a midbrain nucleus, DM may be a reasonable candidate for carrying syllable-specific information. DM is commonly believed to be involved in the production of calls rather than song (Simpson and Vicario 1990; Vicario and Simpson 1995; Wild 1997; Wild et al. 1997). Nottebohm et al. (1976) reported small effects of unilateral intercollicular nucleus lesions, including loss of syllables and what they described as “instability.” Vicario and Simpson (1990) found that DM lesions affect the temporal characteristics of song but do not abolish it (Vicario 1991). However, these lesions may have been incomplete (D. S. Vicario, personal communication), so it is possible that a small part of DM is essential for song production.

Thalamic gating and interruption of song at syllable boundaries

Birds tend to interrupt their songs in the silent intervals between syllables, rather than within syllables, when presented with light flashes (Cynx 1990; Franz and Goller 2002). This can be explained within the framework of our model. If a light flash prevents the activation of the next syllable network in HVC, the wave of bursting in the current syllable network must still complete its propagation; thus the current syllable is completed. Uva receives not only visual but also somatosensory, auditory, and neuromodulatory inputs (Akutagawa and Konishi 2005; Coleman et al. 2007; Wild 1994). Our proposed role for Uva makes it an ideal site for rapid thalamic gating of the song on the basis of sensory input, arousal, and attention.

Comparison with recent experimental data

In recently reported work, Coleman et al. (2007) stimulated Uva and recorded from HVC in anesthetized zebra finches. Our model is broadly consistent with their finding that low-frequency Uva stimulation elicits EPSPs in HVC_I neurons and projection neurons, but three of their observations can potentially form the basis for further refinement of our model. First, all of the HVC_RA neurons from which they recorded while stimulating Uva at low frequency showed short-latency EPSPs, whereas in our model, only the HVC_RA neurons at the beginnings of syllable networks receive input directly from Uva. However, these data are consistent with a minor modification of our model in which many or all HVC_RA neurons receive input from Uva, but the input is large enough to initiate a burst sequence only at the beginning of a syllable network. Alternatively, it may be that a large proportion of the HVC_RA neurons recorded by Coleman et al. (2007) are of the class that does not participate in sparse bursting during singing.

Second, the mean delay from Uva stimulation to EPSP onset was somewhat longer in HVC_I neurons than in projection neurons, suggesting the possibility that the HVC_I EPSPs are elicited only indirectly via the projection neurons. The stimulation results of Fig. 5 are substantially different depending on the presence or absence of these connections. Third, Coleman et al. (2007) indicate that high-frequency stimulation of Uva can cause a long-lasting (∼2 s) suppression of auditory responses in HVC. Future work should verify that the inclusion of a mechanism in the model to reproduce this result is compatible with our proposed mechanism of sequence generation.

Hahnloser et al. (2008) recently provided further evidence regarding the influence of Uva on HVC. During sleep, peaks and dips in covariance functions of paired Uva and HVC neurons suggest that Uva bursts mediate HVC excitation, whereas single spikes mediate HVC inhibition. These observations could motivate the inclusion of a new mechanism of Uva → HVC inhibition in the model, but in the absence of such paired recordings during singing, it is not possible to make strong statements. Although HVC-projecting Uva neurons produce mostly single spikes during sleep, the balance of NIf-projecting and HVC-projecting influence may differ in singing birds, since NIf drives HVC activity during sleep (Hahnloser and Fee 2007) but is not necessary for singing (Cardin et al. 2005).

Our HVC cooling calculations were inspired by the preliminary finding (Long and Fee 2007) in zebra finches that selectively cooling HVC causes a uniform expansion of syllables and gaps. While the present paper was under review, the final version of their work was published (Long and Fee 2008), which shows that syllables and gaps do in fact show a difference in expansion, as predicted by our model: median gap stretch was 12% larger than median syllable stretch. This may be related to the finding by Glaze and Troyer (2006) that gaps are more elastic than syllables.

In the model, several factors influence the difference in expansion of syllables and gaps. The shorter the feedback delay and the longer the uncooled duration of syllables, the more similar the expansion of gaps and syllables will be. It can also easily be shown that the difference in expansion is influenced by the degree to which the control of gaps is shared by the beginnings and ends of syllable networks.

Our model assumes that during cooling, input from Uva truncates the previous syllable network while activating the next syllable network. We showed that when the truncated part of the syllable networks controls syllables rather than gaps, syllables stretch less than gaps (as observed by Long and Fee). In this case, the syllables are truncated. Long and Fee did not report such truncations; however, the observed difference in expansion was small, leaving open the possibility that further analysis of the data would reveal small truncations. These truncations would be reduced if the control of gaps were shared by the beginnings and ends of syllable networks, as discussed earlier.

Additionally, Long and Fee showed that cooling a given hemisphere stretches some syllables more than others and showed a significant anticorrelation between stretch during left and right cooling; moreover, Wang et al. (2008) showed that the efficacy of HVC stimulation in perturbing the song alternates rapidly between hemispheres. These results suggest that the degree of song control switches rapidly between hemispheres over the course of a song. Based on these results, a bilateral version of our model could incorporate bilateral asymmetry in the connections from HVC to RA. This asymmetry could include the HVC → dRA connections of the feedback pathway: different transitions (either between or within syllables) could be controlled by syllable networks in either the left or the right HVC.

Some of the experimental facts that we have discussed constitute apparent challenges to our model: in particular, the fact that RA neurons have many bursts per motif (Leonardo and Fee 2005), the fact that syllable transitions have not been observed in stimulation experiments, and the fact that excitatory input from Uva to HVC_RA neurons is more widespread than our model assumes (Coleman et al. 2007). However, as we have discussed, all of these facts can be reconciled with our model. Given the need for interhemispheric coordination, which has now been brought into even sharper focus by the recent evidence for rapid interhemispheric switching (Long and Fee 2008; Wang et al. 2008), our model, first presented in Gibb and Abarbanel (2006), remains plausible in its essential features and useful as a basis for further investigations into the song system.

GRANTS

This work was partially supported by National Science Foundation (NSF) Grant NSF PHY0097134 and Multidisciplinary University Research Initiative Contract ONR N00014-07-1-0741 to H. D. I. Abarbanel. H. D. I. Abarbanel also acknowledges partial support through the NSF-sponsored Center for Theoretical Biological Physics at University of California, San Diego (UCSD). L. Gibb received support from the NSF Integrative Graduate Education and Research Traineeship program through the UCSD Computational Neurobiology Graduate Program and a predoctoral fellowship from the Training Program in Cognitive Neuroscience of the Institute for Neural Computation at UCSD, supported by National Institute of Mental Health Grant 2 T32 MH-20002.