Resolving crossings in the corticospinal tract by two-tensor streamline tractography

Abstract

An inherent drawback of the traditional diffusion tensor model is its limited ability to provide detailed information about multidirectional fiber architecture within a voxel. This leads to erroneous fiber tractography results in locations where fiber bundles cross each other. This may lead to the inability to visualize clinically important tracts such as the lateral projections of the corticospinal tract. In this report, we present a deterministic two-tensor eXtended Streamline Tractography (XST) technique, which successfully traces through regions of crossing fibers. We evaluated the method on simulated and in vivo human brain data, comparing the results with the traditional single-tensor and with a probabilistic tractography technique. By tracing the corticospinal tract and correlating with fMRI-determined motor cortex in both healthy subjects and patients with brain tumors, we demonstrate that two-tensor deterministic streamline tractography can accurately identify fiber bundles consistent with anatomy and previously not detected by conventional single tensor tractography. When compared to the dense connectivity maps generated by probabilistic tractography, the method is computationally efficient and generates discrete geometric pathways that are simple to visualize and clinically useful. Detection of crossing white matter pathways can improve neurosurgical visualization of functionally relevant white matter areas.

Introduction

Diffusion-weighted MRI (DWI) provides a unique way to probe tissue microstructure by characterizing the random motion of water molecules within the tissue. Diffusion tensor imaging (DTI) represents the diffusion with a tensor model, allowing visualization of white matter fiber orientations corresponding to the preferred direction of water diffusion (Basser et al., 2000). The reconstruction of fiber bundles, a process called tractography, is usually carried out by line propagation or streamline techniques using the principal eigenvector of the diffusion tensor (Basser et al., 2000; Conturo et al., 1999). DTI is the first method able to demonstrate white matter architecture in vivo, and thus there has been much enthusiasm for its application to clinical neurosciences.

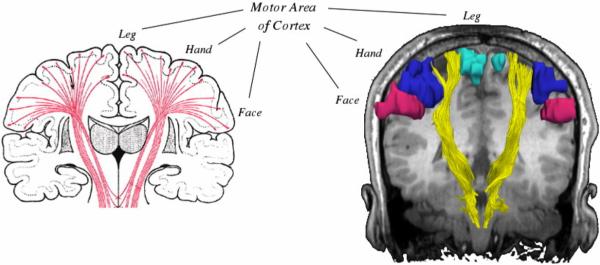
DTI fiber tractography, however, is inaccurate in regions where fiber bundles intersect each other. Due to the orientational heterogeneity in such locations the principal eigenvector does not correspond to the fiber direction (Alexander et al., 2001), and thus the traditional diffusion tensor model fails to estimate the correct fiber orientations. For example, as shown in Fig. 1, corticospinal tract (CST) fibers descending from the upper-extremity and face regions of motor cortex curve inferiorly and medially and intersect the superior longitudinal fasciculus (not shown in the figure), which traces anteroposteriorly through the corona radiata and the centrum semiovale. Thus, traditional tractography techniques depicting the CST actually trace only those fibers going to the leg area of the cortex and are unable to trace fibers going to the upper extremity area or the face area (Fig. 1). Maintaining the continuity of those fibers is critical for preserving motor function for patients. Clinically, the hand is the most important function; so visualization of these fibers is particularly important. Motivated by this clinical need and by disappointing results from single tensor tractography, we investigated approaches to resolving crossing fibers with the particular goal of tracing the lateral projections of the CST fibers to the hand and face area.

FIG. 1.

Anatomic relationship of corticospinal tracts as they connect from the internal capsule to the various motor regions of the cortex. Conventional single tensor tractography is only able to demonstrate the fibers from the motor tracts (shown in yellow) leading to the leg area of the motor cortex (turquoise) and cannot resolve those fibers leading to the hand (blue) or face (magenta) areas.

The limitation of the traditional tensor model in areas of crossing fibers has led to the development of new acquisition techniques along with more complex models of diffusion. One strategy to characterize the underlying complex fiber architecture is to quantify the diffusion function using the Fourier relationship first observed by (Stejskal and Tanner, 1965), between the diffusion function and the diffusion signal attenuation in q-space (Callaghan et al., 1988). Q-space imaging methods are essentially model-independent; they aim to directly measure the 3D probability diffusion function of water molecules. A number of approaches based on the q-space formalism have recently been proposed (Jansons and Alexander, 2003; Tournier et al., 2004; Tuch et al., 2003; Wedeen et al., 2000). These methods, however, require a large number of gradient directions (typically > 100), incurring long acquisition times, which make them impractical in a clinical setting.

Previous work has attempted to explicitly model the complexity of the DWI signal formation in the presence of multiple fibers (Alexander, 2005). A simple model is a mixture of Gaussian densities (Alexander et al., 2001; Blyth et al., 2003), which can be thought of as a generalization of the single tensor model. A similar approach by (Behrens et al., 2003) modeled the underlying diffusion profile using infinite anisotropic components and a single isotropic component. It should be noted, however, that the constraints on the model parameters for the above are non-linear; therefore the optimization is time intensive, along with the problem of robustly yielding a global minimum for the objective function. Another inherent problem is that the model has no knowledge of the actual number of fibers present in a voxel, therefore accuracy may be reduced by representing the voxel with multiple fiber orientations when it can be better represented by a single fiber.

Recently, (Peled et al., 2006) introduced a constrained bi-Gaussian model for analysis of crossing fibers with fewer model parameters, utilizing the information present in the single tensor. This two-tensor approach models a voxel containing two tracts using two cylindrical tensors (with identical eigenvalues), that lie in the plane spanned by the two largest eigenvectors of the single tensor fit. These physically realistic constraints contribute to the robustness of the fit even with a relatively small number of acquired gradient directions.

Attempts have been made to incorporate complex models of diffusion in both deterministic (Blyth et al., 2003; Deriche and Descoteaux, 2007) and probabilistic tractography techniques (Behrens et al., 2007; Parker and Alexander, 2003; Staempfli et al., 2006). Due to the limitations of deterministic algorithms such as lack of a measure describing certainty of the resultant trajectories, probabilistic tractography methods have been developed as an alternative. The majority of the probabilistic techniques differ from their deterministic counterparts by generating multiple streamlines from the seed point with random perturbations to the principal diffusion directions to generate a probability distribution of the fiber orientations.

For some application domains such as neurosurgical planning and guidance, however, deterministic tractography has several advantages over probabilistic tractography. First, deterministic methods are fast and therefore may be used interactively. Second, visualization of the deterministic streamline trajectories is qualitatively similar to the expected white matter fiber tracts, whereas the output of probabilistic methods may be harder to visually interpret. Instead of recognizable and discrete geometric pathways, probabilistic methods generate a dense 3D volume of potential connectivities, which cannot be easily inspected except by further visualization methods (cutting planes, projections, isosurfaces, etc.). Thirdly, the connectivity maps from probabilistic tractography tend to leak into unexpected regions of the brain white matter (Descoteaux et al., 2007), as demonstrated in Fig. 2.

FIG. 2.

Simulated data. (a) The simulated 60° fiber crossing. Inside the brown region (middle), the two fibers are crossing each other. Outside the crossing region there is one anisotropic tensor per fiber and the direction is color-coded. (b) Single tensor tractography when seeded in the region bounded by the yellow box. (c) Connection map from Probabilistic tractography when seeded in the same region (voxels are color coded from 5000 (blue) to 4 (red) samples passing through the voxel). (d) Tractography based on XST.

For these reasons as well as the widespread availability of deterministic methods, single-tensor deterministic streamline tractography has been widely applied for neurosurgery (Nimsky et al., 2005; Talos et al., 2003). In neurosurgery, defining critical white matter tracts has been particularly difficult as white matter tracts are not directly captured by conventional imaging and there is no reliable way to test for their presence, even using invasive intra-operative testing. Therefore tumors located near critical brain areas such as primary motor, sensory or language cortices or functionally significant white matter (WM) fiber tracts are difficult to resect maximally while avoiding postoperative neurological deficits. DTI tractography has been applied for identification of the motor pathway (Coenen et al., 2003; Holodny et al., 2001). However, the fiber crossing problem has been shown to affect single-tensor based fiber-tracking pyramidal tracts for neurosurgery (Kinoshita et al., 2005; Mikuni et al., 2007).

The aim of this paper is to present a two-tensor deterministic tractography method that resolves some of the limitations of the common single-tensor deterministic streamline tractography method. The method presented, eXtended Streamline Tractography (XST), is a new technique based on the constrained two-tensor model estimation proposed in (Peled et al., 2006). We evaluate the performance of XST by comparing the results to those obtained from traditional single tensor tractography, and the probabilistic tractography technique proposed in (Behrens et al., 2007). The methods are compared by seeding in the internal capsule, and determining whether a method successfully reconstructs fiber bundles arising from the major divisions of primary motor cortex (face, hand, and leg), as identified by fMRI activation maps in a healthy subject and in two patients with brain tumors in the region of the motor cortex.

Materials and Methods

Background Theory: Single tensor modeling and tractography

The diffusion of water molecules in time t can be described by a spatial probability density function P_t with a displacement x in time t. For isotropic media the diffusion is the same in all directions and can be described by a single constant ADC. For an anisotropic material, P_t reflects the tissue microstructure as more of the diffusion is parallel to the direction of the fiber than across it. For the traditional single tensor model the probability density function is a zero-mean multivariate Gaussian distribution (Basser et al., 1994).

In a diffusion-weighted MRI experiment extra gradient pulses are introduced, and the amount of signal loss S_q when compared to the original signal S₀ (without diffusion weighting) is modeled by the following equation (Basser, 1995):

$$S_q=S_0{e}^{-b{\widehat{g}}^{t}D\widehat{g}}$$ (1)

where D is the apparent diffusion tensor (ADT). The eigenvalues of D are the apparent diffusion constants in the principal directions, ĝ is a unit vector representing the direction of a diffusion gradient, and b is a factor describing the gradient timing and strength (LeBihan et al., 1986). To estimate the tensor D, Eq. [1] is usually solved by the linear least squares method.

Based on the single tensor model, the most commonly used streamline tractography algorithm uses the direction of the principal eigenvector as a local fiber orientation (Basser et al., 2000). The method starts from an initial seed point, and the fibers are propagated by solving the following 3D path equation:

$$\frac{ds\left(t\right)}{dt}=r\left(t\right)$$ (2)

where s(t) is the fiber curve path position at time t and r(t) is the local tangent orientation of the path. Eq. [2] can be numerically solved by Euler or Runga-Kutta integration schemes.

Two-tensor Model

Eq. [1] describes the signal attenuation function for a single tensor model, which is described by a Gaussian function. The signal attenuation equation for a generalized two-tensor model can similarly be described by a weighted sum of two Gaussian functions:

$$S=S_0(f{e}^{-b{g}^t{D}_{a}g}+(1-f)e^{-b{g}^t{D}_{b}g})$$ (3)

where S₀ is again the base-line image acquired without diffusion weighting. Eq. [3] has 13 unknowns, compared to six in the single-tensor case (six parameters for each of the two diffusion tensors D_a and D_b plus the fraction factor f). Given the known noise-sensitivity of the single-tensor model (Bastin et al., 1998), the greater number of degrees of freedom is problematic for the two-tensor model. To address this, we use the constrained two-tensor model of (Peled et al., 2006), with only seven degrees of freedom. The model utilizes information from the single tensor fit; it assumes that both fiber tracts are constrained in the plane spanned by the first two principal eigenvectors (ê₁,ê₂). A further assumption of the model is that the apparent diffusion constants parallel and perpendicular are same for both the fiber tracts. With the single tensor fit determining 3 degrees of freedom (orientation of ê₃ and minor eigenvalue λ₃) the remaining free parameters are:

• f: fraction of the first tensor, or the weighting factor,

• ϕ_a and ϕ_b : the angles subtended in the plane by the principal directions of the two diffusion tensors and,

• λ₁ : the principal eigenvalue which is assumed to be same for both the fiber tracts.

Given the above constraints the two tensors are represented in the principal frame of the single tensor fit as:

$$D_a=\left[\begin{array}{ccc}\hfill d_{a1}\hfill & \hfill d_{a3}\hfill & \hfill 0\hfill \\ \hfill d_{a3}\hfill & \hfill d_{a2}\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill {\lambda }_3\hfill \end{array}\right],D_b=\left[\begin{array}{ccc}\hfill d_{b1}\hfill & \hfill d_{b3}\hfill & \hfill 0\hfill \\ \hfill d_{b3}\hfill & \hfill d_{b2}\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill {\lambda }_3\hfill \end{array}\right]$$

where

$$d_{p1}={\cos }^2{\varphi }_p{\lambda }_1+{\sin }^2{\varphi }_p{\lambda }_3,p\in \{a,b\}$$

$$d_{p2}={\sin }^2{\varphi }_p{\lambda }_1+{\cos }^2{\varphi }_p{\lambda }_3$$

$$d_{p3}=\cos {\varphi }_p\sin {\varphi }_p({\lambda }_1-{\lambda }_3)$$

λ₃ is calculated from the single tensor fit. Transforming the gradients into the new coordinate system the signal attenuation equation is then represented as:

$$S_q=S_0(f{e}^{-b{\widehat{G}}^t{D}_a\widehat{G}}+(1-f)e^{-b{\widehat{G}}^t{D}_b\widehat{G}})$$ (4)

In this work, Eq. [4] was solved using Levenberg-Marquardt non-linear optimization. As in the single tensor case, the model can be fitted to every voxel however fitting a more complex model to the data may lead to a poor estimate of the underlying fiber orientation. The method assumes that the two fiber tracts are assumed to lie in the plane spanned by the first two eigenvectors of the single tensor fit. Therefore as suggested in (Peled et al., 2006) only planar voxels were subjected to the more complex two-tensor fit where the degree of “planarity” was determined by C_p, which is Westin’s planar anisotropy index (Westin et al., 2002).

eXtended Streamline Tractography (XST)

To incorporate two principal diffusion directions we need to extend the traditional streamline method proposed in (Basser et al., 2000). To trace a continuous trajectory in the single tensor case, the integration scheme requires repeated tensor interpolation to derive a tensor at an arbitrary position. This is usually done by a weighted sum of neighboring tensors. With two rather than one tensor per sample, however, there is correspondence ambiguity inherent in the interpolation. Between two samples (each with two tensors), there are two ways of establishing correspondence, but the combinatorics become complex with the 2×2×2 sample neighborhood for trilinear interpolation or the 4×4×4 neighborhood for tricubic interpolation. To avoid this complex correspondence problem, the diffusion weighted images (DWIs) were interpolated at each step along the estimated trajectory, and for each step the two tensors were estimated from the interpolated DWIs using Eq. [4]. Thus the model-fitting here is performed after interpolation, which is in contrast to both previous work in single-tensor tractography, and in probabilistic tractography where model fitting is performed first, followed by model interpolation (Behrens et al., 2007).

Although the correspondence problem is removed by performing the two-tensor model fitting after interpolation, one of the two tensors must be chosen when tracing a specific fiber trajectory. For this we choose the tensor whose principal eigenvector has the least deviation from the incoming trajectory direction. The next decision to be made is when to stop tracing the trajectory. For single tensor tractography, the stopping criterion is normally based on detecting low anisotropy, since the direction of the tensor becomes more and more uncertain when the anisotropy is reduced. In two-tensor tractography, defining the stop criterion is more complex, since the methods are designed to trace through low (single-tensor) anisotropy regions. In this work, trajectories are terminated when linear anisotropy (as measured by C_l (Westin et al., 2002)) falls below a given threshold (typically 0.2-0.3), when the radius of curvature becomes too small (2.3mm), or when the fraction of the chosen tensor component is lower than 0.1. Further, if the resultant trajectory is shorter than a predefined length (40mm), it is discarded. These parameters were chosen by testing a range of values in a stepwise fashion, and were optimized for maximal depiction of the fiber tracts on one of the subjects, and then applied to other subjects.

The fiber trajectories were seeded from hand-drawn regions of interest, and to ensure a dense set of trajectories, seed points were placed at nine evenly-spaced points within each voxel. If the seed point was a region of crossing fibers (according to the planar measure threshold described earlier) then two separate trajectories were generated from the seed point, along the two tensor components. In our implementation we used cubic spline interpolation (Pajevic et al., 2002) of the DWIs and fourth-order Runga-Kutta integration to solve Eq. [2].

The method has been implemented as a part of the TEEM toolkit and can be downloaded from: http://teem.sourceforge.net/.

Probabilistic Tractography

In order to better understand the merits of the developed two-tensor stream-line tractography method, it was compared to a recent probabilistic technique proposed by (Behrens et al., 2007). The probabilistic method is a part of FSL (FMRIB’s Software Library: http://www.fmrib.ox.ac.uk/fsl/). All the parameters for the method were the same as in (Behrens et al., 2007), although we recognize that some of the parameters for the probabilistic pre-processing phase can be optimized for different SNR levels.

Synthetic Data Generation

Based on Eq. [4], two anisotropic tensors with eigenvalues 1.7, 0.2, 0.2 × 10^-3 mm²/s were simulated, corresponding to the eigenvalues in the splenium of the corpus callosum (Pierpaoli et al., 1996). The DWI’-s were then estimated for each voxel of the image. The number of gradient directions was 55, with b = 1000 s/mm², and 5 non-diffusion-weighted images. The fraction of signal for the two tensors was kept constant at 0.5. The fibers cross at the center of the image at an angle of 60°. Outside the crossing region the tensors were anisotropic and at the border they were chosen to be isotropic. Additionally, complex Gaussian noise was added to simulate SNRs of 18, 20, and 22. Fig. 2 (a) illustrates a simulated slice with a 60° fiber crossing at an SNR of 18.

Human Brain Data

Three subjects (2 patients) were included in the study. The patients had lesions in the region of the primary motor cortex. The study was approved by the Partner’s Institutional Review Board and informed consent was obtained from all participants. Subjects underwent the following MR imaging protocol on a General Electric (Milwaukee, WI), 3T Signa scanner with Excite 14.0, using an 8-channel head coil and ASSET. High resolution whole brain T1-weighted axial 3D SPGR (TR=7500ms, TE=30ms, matrix=256×256, FOV=25.6cm, FA=20°; imaging 176 slices of 1mm thickness) was acquired. Next, DWI was acquired with a multi-slice single shot diffusion weighted echo-planar-imaging (EPI) sequence (TR=14000ms, TE=76.6ms) consisting of 55 gradient directions with a b-value of 1000 s/mm², and 5 baseline T2 images. The FOV was 25.6cm. Imaging matrix was 128×128 with a slice thickness of 2.6mm.

Functional MRI (fMRI) Data

Whole-brain functional images were acquired using a quadrature coil with a T2*-weighted EPI sequence sensitive to the blood oxygen-level-dependent (BOLD) signal (TR=2000ms, TE=30ms, matrix=128×128, FOV=25.6cm; imaging 27 interleaved slices of 4mm thickness). For mapping motor areas, the tasks were self paced done at each subject’s comfort level. The fMRI activations were recorded for hand, leg, and lip motor areas. Irrespective of the task paradigm four task epochs of 30 seconds duration were interleaved with three 10 second rest epochs for all the three motor tasks. SPM2 was used for reconstruction and analysis of the fMRI. The fMRI was subsequently aligned with the anatomical high resolution 3D-SPGR, and the baseline DWI scan.

Experiments

The performance of the methods was first compared in the synthetic data. Tractography from all methods (probabilistic, deterministic single-tensor, and XST) was generated in the simulated fiber crossing dataset. The performance of XST was then evaluated relative to the other methods in the human brain datasets, using seed regions of interest in the internal capsule. The generated fiber trajectories from the in vivo studies were evaluated by visual inspection based on the subject-specific fMRI activations. The methods were tested on a Pentium 4 processor, with 4GB of RAM.

Results

In this section, we show the results comparing the new two-tensor tractography method to traditional single tensor tractography and to a probabilistic tractography method, when applied to both simulated and in vivo brain data.

Simulated Data

Tracking results in the simulated fiber crossing data show performance differences across tractography methods (Fig. 2). Fig. 2a shows a slice through the data set in which the fibers cross at a 60° angle (brown region). Fig. 2b illustrates the fiber tracts reconstructed from standard single tensor tractography. The tractography was seeded in a region (yellow box) that can be best described by the single tensor fit. Ideally, one would expect the tractography trajectories to continue horizontally along the fiber in which they were seeded; instead as they enter the crossing region the fiber tracts diverge in the wrong direction. Fig. 2c illustrates the connection probability map resulting from probabilistic tractography. The estimated pathways have leaked and are dispersed, which makes the main pathway of connectivity more difficult to comprehend. Fig. 2d illustrates the fiber tracts obtained from the XST method. The tractography correctly follows the horizontal fiber direction through the fiber-crossing region.

In summary, Fig. 2 shows that single tensor deterministic tractography (Fig. 2b) results in erroneous tracts, probabilistic tractography (Fig. 2c) results in too many tracts (i.e. the visualization is hard to comprehend), while XST (Fig. 2d) is able to trace the two individual tracts through the crossing area, without dispersing or terminating early.

In Vivo Fiber Tractography

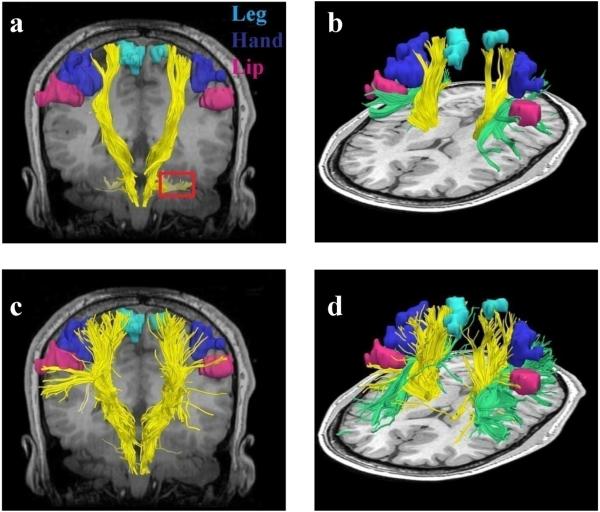
Fig. 3 shows the single tensor and two tensor tractography results with the fMRI activation areas in the healthy subject. Both tractography methods were seeded in the posterior limb of the internal capsule within a manually drawn region of interest. Fig. 3a,b shows the fiber trajectories as reconstructed by single tensor tractography. Fig. 3a,b shows that single tensor tractography can only depict those motor fibers originating from the leg area (running superior-inferior): the hand and the lip fibers are not detected at all. Additionally, Fig. 3a shows that some CST fibers crossing the pons diverge laterally likely due to the large number of crossing horizontal fibers in the pons. In contrast Fig. 3c,d shows that XST is able to reconstruct fibers that are able to propagate to the different motor areas including hand and face.

FIG. 3.

Single tensor vs. XST when seeded in the internal capsule. Fibers from single tensor tractography and the fMRI activation areas are shown in (a) coronal and (b) lateral view. Note that where the CST passes through the pons, single tensor tractography demonstrates divergent fibers leading into the cerebellum (region marked in red). Fibers from the superior longitudinal fasciculus (SLF) (green) are also shown. (c) Fibers traced from XST are shown in (c) coronal and (d) lateral view. The fibers are able to reach all three fMRI activation areas. (d) shows areas of crossing between the SLF and CST.

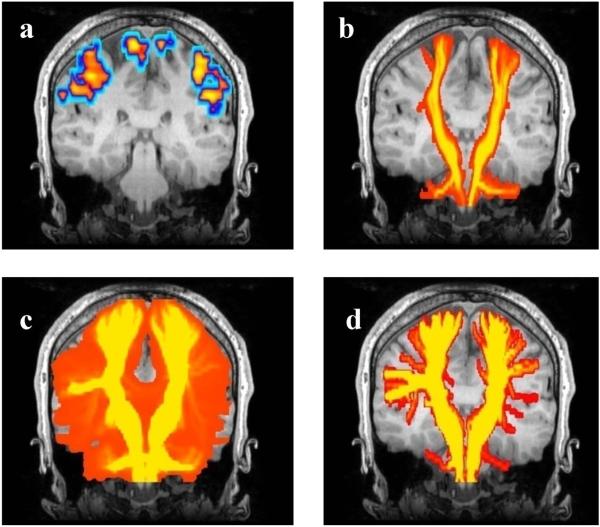
The probabilistic tractography results in a connection map indicating the confidence that each voxel is connected to the seed region. To compare the other methods to probabilistic tractography it was necessary to generate comparable images, therefore we generated maximum intensity projection (MIP) maps of single and XST based tractography. Fig. 4 illustrates these maps for the healthy subject. Probabilistic tractography methods can in principle trace through regions of crossing fibers, but Fig. 4c shows that in this example the method fails to depict the fibers going to the hand and lip areas. The figure depicts widespread dispersion but nevertheless, the majority of the streamlines (shown in yellow) fail to reconstruct the connections to the hand and lip fMRI activations.

FIG. 4.

Tracing the motor tract when seeded from the posterior limb of the internal capsule. To generate a comparable visualization to probabilistic tractography for all methods, a coronal maximum intensity projection (MIP) map is shown for all tractography and fMRI data, overlaid on a representative coronal anatomical image. (a) The FMRI activation areas. (b) Single tensor tractography (voxels are color coded based on the number of trajectories passing through them, followed by the MIP). (c) Probabilistic tractography. (d) two-tensor XST. In (b), (c), and (d) the colored regions show voxels containing at least one fiber trajectory.

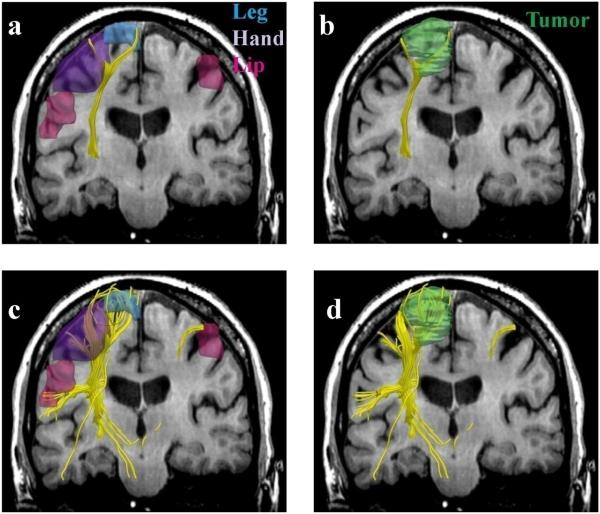
Fig. 5 and Fig. 6 illustrate the behavior of reconstructed fiber tracts in the patients. The figures not only confirm the results from the healthy subject, but additionally also show that two-tensor tractography depicts a higher number of trajectories around the tumor (Fig. 5d and Fig. 6d). This information is particularly of interest for neurosurgical planning. Knowledge of the white matter tracts serving the hand is particularly clinically important in order to avoid a postoperative motor deficit.

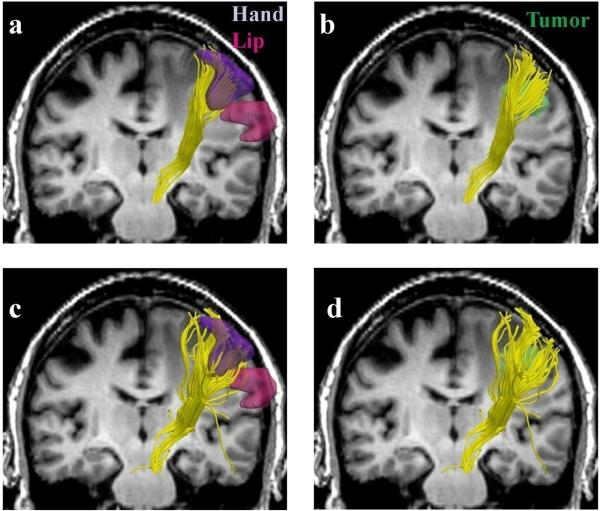
FIG. 5.

Single (a,b) vs. two-tensor XST (c,d) tractography results on a 64-year old caucasian female with left frontoparietal meningioma. Fibers were seeded in the internal capsule and those intersecting fMRI activations were retained. Three-dimensional surface models represent (a, c) fMRI areas for the leg (blue), hand (purple) and the lip (pink) and (b, d) tumor (green).

FIG. 6.

Single (a,b) vs. two-tensor XST (c,d) tractography results on a 64-year old caucasian male with right metastatic melanoma. Fibers were seeded in the internal capsule and those intersecting fMRI activations were retained. Three-dimensional surface models represent (a, c) fMRI areas for the hand (purple) and the lip (pink) and (b, d) tumor (green).

XST took approximately 1s to generate a single trajectory from a seed point. In contrast, the probabilistic tractography was a slower two-step process. A pre-processing step which involved generating various parameters required for tractography was computed once for each subject. This step took approximately 48h, after which the next step of trajectory generation (based on a seed point) took approximately 10s.

Discussion

In this study, we evaluated whether multi-tensor tractography can be used to visualize fiber tracts in areas of multidirectional fiber architecture in the brain. Such areas are problematic for single tensor tractography methods because the single tensor model cannot describe the complexity. As highlighted in this report, areas of multidirectional diffusion are present in clinically important fiber tracts such as the CST. For resection of cerebral tumors, the correct depiction of motor pathways (specifically those that course laterally to the hand and face areas) is critical. If the motor pathway is damaged during the surgery the patient is likely to have a motor deficit (Kinoshita et al., 2005). Subcortical stimulation mapping is the clinical gold standard and the only functional method for identifying the motor pathways (Keles et al., 2004), however, this technique does not reveal the full 3D extent of the motor tract (Duffau et al., 2003). Recently fiber tracking based on the traditional tensor model has been widely applied for neurosurgical planning, specifically for preoperative assessment of functionally relevant white matter anatomy (Chen et al., 2007; Hendler et al., 2003; Niizuma et al., 2006; Wieshmann et al., 2000); however, inability of the method to trace through regions of crossing fibers, resulting in inaccurate depiction of the motor tract, is a major limitation (Berman et al., 2007; Kinoshita et al., 2005; Mikuni et al., 2007). In this report, we have shown that results from a multi-tensor tractography method can visualize motor fibers that could not be seen in the results from single-tensor tractography, and thus may be useful in surgical planning for resection of tumors adjacent to the corticospinal tract.

A criticism for deterministic tractography is the lack of a measure describing confidence or uncertainty of the reconstructed trajectories. This may be a reason for the recent interest in probabilistic tractography techniques, since with those methods it is possible to quantify the degree of uncertainty in the principal diffusion direction. The connectivity maps from probabilistic tractography are no more than an indicator of the number of visitations that a certain trajectory underwent (from the seed point). For regions where there is a single dominant fiber pathway (such as the corpus callosum) the uncertainty in the principal diffusion direction is very small, therefore one would expect minimum dispersion in the connectivity maps. However, the dispersed behavior of tracts shown in Fig. 2c as a result of seeding in a single tensor region (mimicking the corpus callosum) is not what clinicians expect to see based on their neuroanatomical knowledge. The aim of any tractography algorithm is to reconstruct tracts that accurately correlate with the underlying white matter pathways. Given a 3D volume of connectivity maps with a dense map of frequent visitations it is extremely difficult to pick the most probable trajectory. In short, neurosurgeons want to know where the fiber pathways are located, not where they might be probable.

A limitation of our study is that the sensitivity of the results regarding parameter selection (such as C_p, radius of curvature, and ROI for seeding) has not been thoroughly studied. With a different choice of parameters, such as denser seeding we may reconstruct a larger number of trajectories. The use of C_p as a criterion for classifying voxels with crossing fiber tracts is a simplification and more complex models can be considered. Previous works have used statistical methods such as an F-Test to decide whether it makes sense to fit a more complex model when the simpler model is enough to describe the data (Alexander et al., 2002). Our initial experiments with information criterion methods (Akaike, 1974; Schwarz, 1978) for model selection were not very promising. This might be because the two-tensor model (Peled et al., 2006) is constrained and comparing that to an unconstrained single tensor model might not be feasible. When evaluating the model selection criterion we need to formulate the inclusion of these constraints, which might not be trivial. Another limitation of this study is evaluating sensitivity of the method to different noise conditions; however, despite the low SNR on simulated data (Fig. 2), the method is able to trace through successfully, and seems to be robust (in addition, it worked well on the in vivo data).

In summary, a novel tractography method is presented that shows promise in resolving some of the issues with the traditional tractography, however, the method is still in development and more validation is required. Future work will involve a thorough clinical evaluation; a qualitative study on the behavior of the different parameters for XST based tractography, and development of a more robust criterion (to either replace or complement C_p) for quantification of goodness of fit of the underlying model. It would be interesting to carry out a comparison study of probabilistic tractography based on different models of diffusion, such as using the model proposed in (Peled et al., 2006).

Conclusion

Two-tensor deterministic tractography shows promise in resolving white matter pathways in areas of crossing fibers. We have shown that using the XST two-tensor deterministic streamline tractography method, it is possible to visualize white matter fiber tracts that are not obtainable using single tensor tractography approaches. Although probabilistic tractography results detect more connected areas than single tensor stream-line tractography results, they show more dispersion than the results obtained using the presented two-tensor method which is undesirable for neurosurgical planning. By reconstructing fibers traversing the internal capsule and comparing their trajectories to fMRI motor activations, we demonstrated that our approach could successfully trace critical motor pathways and may better delineate neurosurgically critical motor fibers than standard tractography.