Nonlinear temperature effects indicate severe damages to U.S. crop yields under climate change

Abstract

The United States produces 41% of the world's corn and 38% of the world's soybeans. These crops comprise two of the four largest sources of caloric energy produced and are thus critical for world food supply. We pair a panel of county-level yields for these two crops, plus cotton (a warmer-weather crop), with a new fine-scale weather dataset that incorporates the whole distribution of temperatures within each day and across all days in the growing season. We find that yields increase with temperature up to 29° C for corn, 30° C for soybeans, and 32° C for cotton but that temperatures above these thresholds are very harmful. The slope of the decline above the optimum is significantly steeper than the incline below it. The same nonlinear and asymmetric relationship is found when we isolate either time-series or cross-sectional variations in temperatures and yields. This suggests limited historical adaptation of seed varieties or management practices to warmer temperatures because the cross-section includes farmers' adaptations to warmer climates and the time-series does not. Holding current growing regions fixed, area-weighted average yields are predicted to decrease by 30–46% before the end of the century under the slowest (B1) warming scenario and decrease by 63–82% under the most rapid warming scenario (A1FI) under the Hadley III model.

With evidence accumulating that greenhouse gas concentrations are warming the world's climate, research focuses increasingly on estimating impacts that may occur under different warming scenarios and how economies might adapt to changing climatic conditions. Agriculture is a key focus because of its direct connection to climate. Although agriculture comprises a small share of GDP in the United States, the U.S. persists in being the world's largest agricultural producer and exporter of agricultural commodities, so impacts in the U.S. could have broad implications for food supply and prices worldwide. At the same time, debate continues about whether warming will be a net gain or loss for agriculture in currently temperate climates like that of the United States (1–8).

In this paper, we estimate the link between weather and yields for the three crops with the largest production value in the United States: corn, soybeans, and cotton. Corn and soybeans, the nation's most prevalent crops, are the predominant source of feed grains used in cattle, dairy, poultry, and hog production. Corn is also the main source of U.S. ethanol. Cotton is the fourth-largest crop in acres planted, but more valuable on a per-acre basis and more suited to warmer climates than are corn and soybeans. Estimating the correct relationship between weather and yields for these major crops is a critical first step before more elaborate models can be used to examine how crop-planting choices, food and fiber supply, and prices will ultimately shift in response to climate change.

Our data are comprised of new fine-scale weather outcomes merged together with a large panel of crop yields that spans most U.S. counties from 1950 to 2005. The new weather data include the length of time each crop is exposed to each one-degree Celsisus temperature interval in each day, summed across all days of the growing season, all estimated for the specific locations within each county where crops are grown. The new fine-scale weather data facilitate estimation of a flexible model that can detect nonlinearities and breakpoints in the effect of temperature on yield. If the true underlying relationship is nonlinear (e.g., increasing and then decreasing in temperature), averaging over time or space dilutes the true temperature response. For example, similar average temperatures may arise from two very different days, one with little temperature variation and one with wide temperature variation. Holding the average temperature constant, days with more variation will include more exposure to extreme outcomes, which can critically influence yields (9). The empirical challenge is to map an entire season of widely varying temperature outcomes to each year's yield. Accurate estimation of nonlinear effects is particularly important when considering large, nonmarginal changes in temperatures, now expected with climate change.

Results

Regression analyses, which control in various ways for precipitation, technological change, soils, and location-specific unobserved factors, all show a similar nonlinear relationship between temperature and yields. Additional results and sensitivity checks are given in the SI Appendix.

Yield Growth Increases Gradually with Temperature up to 29–32° Celsius, Depending on the Crop, and then Decreases Sharply for All Three Crops.

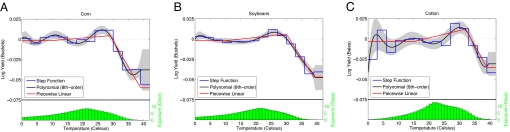
Estimates and standard errors of temperature effects for all three crops are displayed in Fig. 1. The figure has three frames, where each column represents one crop. Different specifications of the link between temperature and yield growth are indicated by the color of the estimated curve. The blue line shows the most flexible specification, a step function that fits a separate growth rate for each three-degree temperature range. The black line shows the specification where yield growth is modeled as an eighth-order polynomial function of temperature and the 95% confidence band after adjusting for spatial correlation is added in gray. The red line shows a piecewise linear specification that follows the agronomic concept of degree days. Each specification shows the same characteristic shape, increasing modestly up to a critical temperature and then decreasing sharply. For corn, the critical threshold temperature is 29° C; for soybeans it is 30° C; and for cotton it is 32° C.

Fig. 1.

Nonlinear relation between temperature and yields. Graphs at the top of each frame display changes in log yield if the crop is exposed for one day to a particular 1° C temperature interval where we sum the fraction of a day during which temperatures fall within each interval. The 95% confidence band, after adjusting for spatial correlation, is added as gray area for the polynomial regression. Curves are centered so that the exposure-weighted impact is zero. Histograms at the bottom of each frame display the average temperature exposure among all counties in the data.

The vertical axis in each figure marks the log of yield (bushels per acre for corn and soybeans and bales per acre for cotton) with the exposure-weighted average predicted yield normalized to zero. The horizontal axis is temperature. In comparing two points on any curve, a vertical difference of 0.01 indicates an approximately 1% difference in average yield for the year. For example, the blue line frame A (the flexible model for corn), substituting a full day (24 h) at 29° C temperature with a full day at 40° C temperature results in a predicted yield decline of ≈7%, holding all else the same. The green histogram shows the average exposure to each one-degree Celsius interval during the growing season (March–August for corn and soybeans and April–October for cotton).

Coefficients on other explanatory variables (precipitation, squared precipitation, county fixed effects, and state-specific quadratic time trends) are not reported here. Precipitation has a statistically significant inverted-U shape with an estimated yield-maximizing level of 25.0 inches for corn and 27.2 inches for soybeans in the flexible step-function specification in Fig. 1. The precipitation variables are not statistically significant for cotton, which is not surprising given that 58% of the crop is irrigated. Fixed effects control for time-invariant heterogeneity (like soil quality) and state-specific quadratic time trends control for technological change. With wide geographic variation in average yields and a three-fold increase in yields over the sample period, these controls have strong statistical significance.

The pattern of temperature effects is quite robust to specification and controls. The same nonlinear temperature effect emerges whether or not any of the controls, or any subset of controls, are included in the regressions. We also find the estimated temperature effects to be very similar if we instead control for technology and time effects by using year-fixed effects rather than state-specific quadratic time trends.

Holding Current Growing Regions Fixed, Area-Weighted Average Yields Are Predicted to Decrease by 30–46% Before the End of the Century Under the Slowest Hadley III Warming Scenario (B1), and Decline by 63–82% Under the Most Rapid Warming Scenario (A1FI).

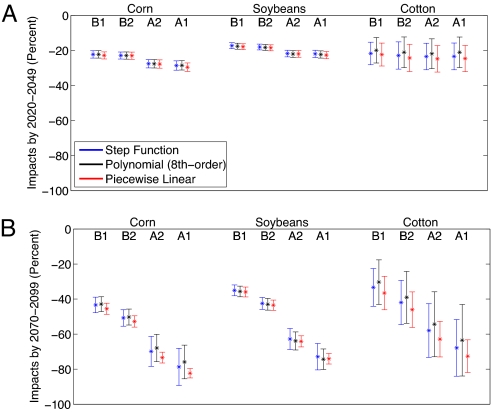
For comparison, a linear model that uses the average growing-season temperature as an explanatory variable gives predicted impacts of −16% to +3% (B1) and −30% to +6% (A1FI) among the three crops. Yield predictions are summarized in Fig. 2. Frame A shows predictions for the medium term (2020–2049) and frame B for the long term (2070–2099). Predictions are for changes in total production under four climate scenarios in the Hadley III climate model. Across all scenarios, model specifications, and crops, the aggregate impacts show marked declines, even though yields in some individual counties are projected to increase. The driving force behind these large and significant predicted impacts is the projected increase in frequency of extremely warm temperatures.

Fig. 2.

Predicted climate-change impacts on crop yields under the Hadley III climate model. Graphs display predicted percentage changes in crop yields under four emissions scenarios. Frame A displays predicted impacts in the medium term (2020–2049) and frame B shows the long term (2070–2099). A star indicates the point estimates, and whiskers show the 95% confidence interval after adjusting for spatial correlation. The color corresponds to the regression models in Fig. 1.

Out-of-Sample Model Predictions Are More Accurate than Previous Statistical Models.

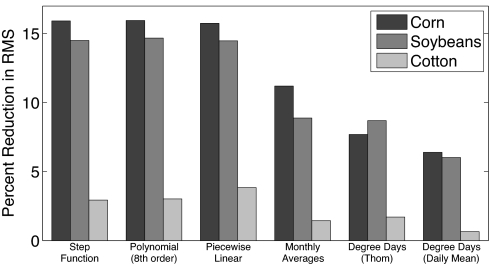
The new regression models were compared with other specifications in the literature by using the root-mean squared error (RMS) of out-of-sample predictions. Each model is estimated 1,000 times, randomly choosing 48 years of our 56-year history of yields. The estimates are then used to predict yield outcomes for the remaining eight years (≈14%) of each sample. We randomly sample whole years and not observations because yields are spatially correlated in any given year. We compare our own three specifications of temperature effects (step function, polynomial, and piecewise linear) with three alternative specifications: (i) a model with average temperatures for each of four months (1); (ii) an approximation of growing-degree days based on monthly average temperatures (Thom's formula) (4); and (iii) a measure of growing-degree days, calculated by using daily mean temperatures (8), that does not include a separate category for extremely warm temperatures.

As a baseline, we consider a model with county-fixed effects and quadratic state-level trends, but no weather variables. Such a model simply forecasts the average yield trend for a county in each year. We derive the percent reduction in the RMS if weather variables are also included. Results are summarized in Fig. 3. A reduction by 100% would imply that the model produces no error and gives a perfect forecast, whereas a percent reduction of 0% implies that the weather variables have no additional explanatory power.

Fig. 3.

Out-of-sample prediction comparison for various model specifications. Bar charts display the percent reduction in the root-mean-squared prediction error (RMS) for each model in comparison with a baseline model with no weather variable. Each model is estimated 1,000 times, where each replication randomly selects 48 of the 56 years in our full sample. Relative performance is measured according to the accuracy of each model's prediction for the omitted eight years of the sample (≈14%). We sample years instead of observations because year-to-year weather fluctuations are random, but there is considerable spatial correlation across counties within each year. Step function, polynomial (eighth order), and piecewise linear are the models developed in this paper; the other models are from the existing literature.

The new models reduce RMS by between 40% and 360% more than other specifications. Welch tests find no significant difference between our three models, but strongly significant differences are found when compared with other specifications in the literature.

The Same Nonlinear Relationship Between Yields and Temperature Is Observed in both the Cross-Section of Counties and the Aggregate Year-to-Year Time Series.

The results described in Yield Growth Increases Gradually with Temperature up to 29–32° Celsius are from regression models with county-fixed effects, which identify temperature effects on yields using within-county time-series weather variation. Although random variation is useful from a statistical standpoint, such analysis accounts only for grower adaptation in response to current-year weather (e.g., additional use of irrigation in a dry year), and not for systematic crop- or variety-switching in anticipation of a different climate. In contrast, a cross-sectional analysis identifies temperature effects by using only variations between counties with different climates. Both the cross-section and the time series give results comparable with the baseline model that pools weather and climate variations. In particular, the cross-sectional and time-series estimates show the same characteristic nonlinear temperature relationship, similar optimal temperatures, and predict nearly equal yield impacts under Hadley III climate-change scenarios.

The Nonlinear Relationship Between Yield and Temperature Observed in Cooler Northern States Is Similar to the One Observed in Warmer Southern States.

To explore how the temperature-yield relationship varies over different regions of the country, we divided our sample into three mutually exclusive geographical regions corresponding to the most northern (and coolest) states, the most southern (and warmest) states, and those in the middle. We focus on corn because it is grown over the widest geographic area and has been by far the most valuable crop grown in the United States. The interesting feature is the relative stability of the estimated temperature relationship across the three subregions.

The Nonlinear Relationship Between Yield and Temperature Observed Between 1950 and 1977 Was the Same as the One Observed Between 1978 and 2005.

To explore how the temperature-yield relationship has changed over time, we split the sample into two time periods of equal length, 1950–1977 and 1978–2005. The critical threshold when temperatures become harmful is rather robust over time. The similarity of the temperature-yield relationship across subsamples is particularly interesting given that, because of technological change, average yields in the more recent sample are about twice those in the earlier sample.

Greater Precipitation Partially Mitigates Damages from Extreme High Temperatures.

We explore interactions between temperature and precipitation outcomes by dividing the sample into quartiles of total precipitation during the months of June and July. These estimates have a shape similar to those of the pooled sample up to the critical temperature threshold. The decline above the threshold, however, is less steep for corn subsamples with greater precipitation.* However, omitting temperature-rainfall interactions will not bias predictions of average effects of temperature and rainfall, as we do not find a significant correlation between temperature outcomes and precipitation outcomes in the raw daily data.

The Estimated Climate-Change Impacts Are Insensitive to the Specified Growing Season and Consistent with Time Separability.

The baseline model uses temperature and precipitation measures for the months of March through August for corn and soybeans. In practice, northern regions tend to plant later than southern regions, and planting dates may vary from year-to-year depending on weather conditions. The SI Appendix shows results from eight alternative specifications of the growing season, all with comparable results. When we limit the growing season to two-month intervals or estimate separate temperature response functions for July (when corn flowers) and other months, we find qualitatively similar temperature-response functions for each subperiod. Although F tests give significantly different coefficient estimates in July compared to the pooled remaining months, the fit (R²) hardly increases at all when breaking the growing season into various subperiods and predicted climate-change impacts that are not significantly different. For example, a corn-yield model with separate temperature coefficients for July only slightly increases the R² from 0.7654 to 0.7698 under the step function and changes overall predicted long-run yield impact from −43% to −44% under the slow-warming scenario (B1) and from −79% to −74% under the fast-warming scenario (A1FI).

Discussion

Many studies, spanning several disciplines and employing different methods, have linked weather and climate to agricultural outcomes such as yields, land values, and farm profits, each with their own set of strengths and weaknesses.

Agronomic studies are the predominant tool used to evaluate potential effects from climate change. Examples include refs.13–17, but there are many others. These studies emphasize the dynamic physiological process of plant growth, seed formation, and yield. The process is understood to be quite complex and dynamic in nature and thus not easily estimated in a regression framework. Instead, these studies use a rich theoretical model to simulate yields given daily and subdaily weather inputs, nutrient applications, and initial soil conditions. In some cases, simulated yields are compared with observed yields with some success. We are not aware of any agronomic study that has tested a simulation model by using data different from what was used to calibrate it. Current versions of models developed for many crops are maintained by the Decision Support System for Agrotechnology Transfer (www.icasa.net/dssat/).

A strength of simulation models is that they fully incorporate plant-growth theory. These models also incorporate the whole distribution of weather outcomes over the growing season. This differs markedly from earlier regression-based approaches that typically use average weather outcomes or averages from particular months and thus give biased estimates of nonlinear temperature effects. Potential weaknesses of simulation approaches are their complexity, uncertainty about the structure of the physiological process, and the large number of parameters. Some agronomists seem to worry about possible misspecification and omitted variables biases (10–12). These models also take production systems and nutrient applications as exogenous: There is no account of farm operators' decisions.

Several earlier economic studies use hedonic models to associate land values to land characteristics, including climate, by using reduced-form linear regression models (e.g., refs. 1, 4, and 6). A strength of this approach is that it accounts for the whole agricultural sector, not just a single crop at a time. It can also account for farm operator behavior and adaptation. Cooler areas are likely to become more like warmer areas, with crop choices, management practices, and land values changing in accordance with current geographic variation in climate.

The overarching concern with the hedonic approach, and with cross-sectional studies generally, is omitted variables bias. Climate variables (e.g., average temperature) and other variables, such as soil types, distance to cities, and irrigation systems, are all spatially correlated. If critical variables correlated with climate are omitted from the regression model, the climate variables may pick up effects of variables besides climate and lead to biased estimates and predictions. Cross-sectional studies may be strongly suggestive, but do not carry the same empirical weight as a physical or natural experiment. Indeed, earlier work shows how omission of heavily subsidized irrigation systems strongly influences predicted climate impacts (18).

Recently, Auffhammer, Ramanathan, and Vincent (7) used a panel of yields and weather outcomes in India to model the role of brown clouds. Similarly, Deschênes and Greenstone (8) linked agricultural profits in the United States to yearly weather variations by using a four-year county-level panel from the Census of Agriculture. Whereas both studies aggregate weather, our model, like simulation models, incorporates the whole distribution of temperature outcomes in a flexible way. Unlike simulation models, it is amenable to estimation by using standard regression analysis. Like refs. 7 and 8, we consider specifications with county-fixed effects to identify parameters by using year-to-year weather variations that serve as a natural experiment. Like ref. 7, but unlike ref. 8, we focus on yields rather than profits. Potential problems with the use of profits are discussed in ref. 19.

Our study aims to combine the strengths of previous approaches. We use fine-scale weather data and combine it with flexible regression models. The findings are notable for the consistency of the estimated nonlinear temperature effects across time, locations, crops, and the many sources of variation in temperature and precipitation considered.

Perhaps most interesting is the consistency of the estimated relationship when comparing estimates based on year-to-year weather variations and cross-sectional climate variations. This finding suggests limited historical adaptation to extreme heat for any given crop. This implication follows from the fact that cross-sectional variations include farmers' adaptations to warmer climates whereas estimates using time-series variations do not. The first approach is akin to hedonic models that link land values to average weather outcomes, except that it does not account for crop switching.

There are, of course, many other possible adaptations that this study cannot address. The simplest form of adaptation would be to change the locations or seasons where and when crops are grown.^† Understanding the scope for this kind of change would require more careful analysis of potential yield effects on a global scale. Furthermore, if climate change were anticipated to induce severe yield impacts on a global scale, then anticipated increases in commodity prices would likely encourage greater investments in new seed varieties, irrigation systems, and other technological changes. Thus, although historical data show the same heat tolerance in the first and second half of our sample, greater heat tolerance still may be possible if greater returns for such innovation arise. Recently, a National Science Foundation-funded study completed a draft sequence of the corn genome, which might make it easier to develop new corn varieties with greater heat tolerance (see http://monsanto.mediaroom.com/index.php?s=43&item=576 for more information).

An important caveat concerns our inability to account for CO₂ concentrations. Plants use CO₂ as an input in the photosynthesis process, so increasing CO₂ levels might spur plant growth and yields. Yield declines stemming from warmer temperatures therefore may be offset by CO₂-fertilization. Although higher CO₂ concentrations may boost yields, the magnitude of the effect is still debated. Long, et al. (12, 20) recently stressed that existing laboratory studies and field experiments might overestimate this effect. We cannot account for CO₂ effects in regression analysis of observed yields because CO₂ concentrations quickly dissipate throughout the atmosphere, leaving only a gently increasing time trend, which is impossible to statistically disentangle from technological change.

Methods

Data.

Yields for corn, soybeans, and cotton for the years 1950–2005 are reported by the U.S. Department of Agriculture's National Agricultural Statistical Service. These yields equal total county-level production divided by acres harvested. We limit the analysis to counties east of the 100° meridian (excluding Florida) for corn and soybeans because cropland in the West often relies on heavily subsidized irrigation systems.^‡ For cotton, we use all counties that report cotton yields because there are fewer observations and a larger share of cotton is grown in the West. In the SI Appendix we report results for all three crops if we split them into Eastern and Western subsets. Results differ substantially for corn and soybeans, but to a lesser degree for cotton, and we hence pool observations from the East and West for the latter. For results reported here, we have 105,981 observations with corn yields, 82,385 observations with soybeans yields, and 31,540 observations with cotton yields.

Construction of the fine-scale weather data are briefly described here and in more detail in ref. 21 and the SI Appendix. The basic steps are as follows. We first develop daily predictions of minimum and maximum temperature on a 2.5 × 2.5-mile grid for the entire United States. We then derive the time at which a crop is exposed to each one-degree Celsius interval in each grid cell in each day. These predictions are merged with a satellite scan that allows us to select only those grid cells with cropland. We then aggregate the whole distribution of outcomes for all days in the growing season in each county. To preserve within-county temperature variation, it is important to derive the time each grid cell is exposed to each one-degree Celsius interval before aggregating to obtain the county-level distribution.^§ The average historical weather distribution and its variability across time and space are summarized in the SI Appendix.

To examine whether corn varieties have been adapted to warmer temperatures, we divide the United States into three regions, the northern, the interior, and the southern, all east of the 100° meridian.^¶

Climate-change predictions are drawn from the Hadley III model (www.metoffice.com/research/hadleycentre/). We obtain a monthly model output for both minimum and maximum temperatures under four major emissions scenarios (A1FI, A2, B1, and B2) for the years 1960–2099. The B1 scenario assumes the slowest rate of warming over the next century and the A1FI scenario assumes continued use of fossil fuels, which results in the largest increase in CO₂-concentrations and temperatures. The B2 and A2 scenarios fall between the B1 and A1F1 scenario. We find the predicted difference in monthly mean temperature for 2020–2049 (medium-term), 2070–2099 (long-term), and historic averages (1960–1989) at each of 216 Hadley grid nodes covering the United States. Predicted changes in monthly minimum and maximum temperature at each 2.5 × 2.5-mile PRISM grid are calculated as the weighted average of the monthly mean change in the four surrounding Hadley grid points, where the weights are proportional to the inverse squared distance and forced to sum to one. In a final step, we add predicted absolute changes in monthly minimum and maximum temperatures at each PRISM grid to the observed daily time series from 1960 to 1989. In other words, we shift the historical distribution by the mean monthly change predicted by each climate scenario. An analogous approach was used for precipitation, except that we use the relative ratio of future predicted rainfall to historic rainfall instead of absolute changes. The predicted changes in temperatures under various scenarios are shown in the SI Appendix.

Regression Models.

We assume temperature effects on yields are cumulative over time and that yield is proportional to total exposure. This implies temperature effects are additively substitutable over time. Specifically, plant growth g(h) depends nonlinearly on heat h. Log yield, y_it, in county i and year t is

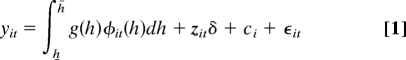where φ_it(h) is the time distribution of heat over the growing season in county i and year t. We fix the growing season to months March through August for corn and soybeans and the months April through October for cotton. Observed temperatures during this time period range between the lower bound h and the upper bound h̄. Other control factors are denoted z_it and include a quadratic in total precipitation as well as quadratic time trends by state to capture technological change. Finally, c_i is a time-invariant county-fixed effect to control for time-invariant heterogeneity, such as soil quality. We allow the error terms ε_it to be spatially correlated by using the nonparametric routine used by ref. 24.

By using data on exposure to each 1° C temperature interval, we approximate the above integral with

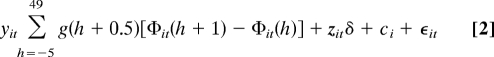where Φ_it(h) is the cumulative distribution function of heat in county i and year t.

We consider three specifications for g(h): A step function with a different growth rate in each 3° C temperature interval; an eighth order Chebychev polynomial; and a piecewise linear function. Details are provided in the SI Appendix.

Perhaps the strongest assumption of the regression models is time separability of temperature effects. This assumption is partly rooted in agronomy. In crop simulation models, however, temperature effects can vary over the life cycle of the plant. In the SI Appendix, we report results from a model that uses various definitions of the growing season and allows the coefficients to be time-varying over the growing season.