Meshless Generalized Finite Difference Method and Human Carotid Atherosclerotic Plaque Progression Simulation Using Multi-Year MRI Patient-Tracking Data

Abstract

Atherosclerotic plaque rupture and progression have been the focus of intensive investigations in recent years. Plaque rupture is closely related to most severe cardiovascular syndromes such as heart attack and stroke. A computational procedure based on meshless generalized finite difference (MGFD) method and serial magnetic resonance imaging (MRI) data was introduced to quantify patient-specific carotid atherosclerotic plaque growth functions and simulate plaque progression. Participating patients were scanned three times (T₁, T₂, and T₃, at intervals of about 18 months) to obtain plaque progression data. Vessel wall thickness (WT) changes were used as the measure for plaque progression. Since there was insufficient data with the current technology to quantify individual plaque component growth, the whole plaque was assumed to be uniform, homogeneous, hyperelastic, isotropic and nearly incompressible. The linear elastic model was used. The 2D plaque model was discretized and solved using a meshless generalized finite difference (GFD) method. Starting from the T₂ plaque geometry, plaque progression was simulated by solving the solid model and adjusting wall thickness using plaque growth functions iteratively until T₃ is reached. Numerically simulated plaque progression agreed very well with actual plaque geometry at T₃ given by MRI data. We believe this is the first time plaque progression simulation based on multi-year patient-tracking data was reported. Serial MRI-based progression simulation adds time dimension to plaque vulnerability assessment and will improve prediction accuracy for potential plaque rupture risk.

1 Introduction

Cardiovascular disease (CVD) has remained the number one cause of death in America since 1902. 36% of 45 year olds and 80% of those 75 and older have CVD to some degree. A large number of the fatal clinical events are caused by rupture of a vulnerable atherosclerotic plaque. [Fuster (1998); Fuster et al. (1990); Naghavi et al. (2003a, 2003b)]. Many victims of the disease who are apparently healthy die suddenly without prior symptoms. While major advancements in the treatment of CVD continue, progress has been very limited in early detection and treatment of at risk individuals. Our long-term goal is to develop non-invasive methods to assess plaque vulnerability and predict possible rupture before the fatal event actually happens.

There has been considerable effort investigating mechanisms governing atherosclerotic plaque progression and rupture [Friedman, Bargeron, Deters, Hutchins and Mark (1987); Friedman and Giddens (2005); Giddens, Zarins, Glagov, S. (1993); Ku, Giddens, Zarins and Glagov (1985); Scotti et al. (2005); Yuan, Mitsumori, Beach, and Maravilla (2001)]. Most efforts were focused on fluid dynamics side since it has been well accepted that atherosclerosis initiation and progression correlate positively with low and oscillating flow wall shear stresses. However, this “low and oscillating shear stress hypothesis” cannot explain why moderate and advanced plaques continue to grow under elevated flow shear stress conditions [Tang et al. (2005)]. Our recent results using serial MRI patient-tracking data and computational models (200–700 data points/patient) indicated that 18 out of 21 patients studied showed significant negative correlation between plaque progression measured by wall thickness increase and plaque wall (structure) stress. However, computational models using patient-specific plaque progression data to simulate plaque growth and predict future plaque rupture risk are lacking in the current literature.

In this paper, a computational procedure based on meshless generalized finite difference (MGFD) method and serial MRI data is introduced to quantify patient-specific carotid atherosclerotic plaque growth functions and simulate plaque progression. By adding time dimension into our play, plaque vulnerability assessment and clinical decisions can be based on multi-time MRI scans and simulated “virtual” plaque progression. Seeing is believing. With validation, our procedure can be implemented in clinical applications and will lead to considerable improvement in prediction accuracy for potential plaque rupture risk and possible prevention of fatal cardiovascular events.

Because of the complexity of plaque geometry and structure, a meshless GFD method is introduced in this paper to avoid frequent mesh updates and adjustments. Computational modeling for engineering applications with meshless methods have made considerable advances in recent years [Ahrem, Beckert and Wendland (2006); Atluri (2004, 2005); Atluri, Yagawa, and Cruse (1995); Bathe (1996, 2002); Ling, Atluri (2006); Shu, Ding, and Yeo (2005); Wu, Shen, Tao (2007)]. A series of meshless local Petrov-Galerkin (MLPG) methods were introduced to solved 3-dimensional elasto-static and dynamical problems [Han and Atluti (2004a, 2004b, 2007); Han, Liu, Rajendran, Atluri (2006)] and nonlinear problems with large deformation and rotations [Han, Rajendran and Atluri (2004)]. A “mixed” approach was introduced to improve the MLPG method using finite volume method [Atluri, Han and Rajendran (2004)] and finite difference method [Atluri, Liu, and Han, (2006a, 2006b); Hu, Young, Fan (2008)]. A new meshless interpolation scheme for MLPG method was developed by Ma [Ma (2008)]. Analysis of structure with material interfaces was performed by Masuda and Noguchi [Masuda, Noguchi (2006)]. Perko and Sarler studied weight function shape parameter optimization in meshless methods for non-uniform grids [Perko and Sarler (2007)]. Remeshing and refining with moving finite elements were investigated by Wacher and Givoli [Wacher, Givoli (2006)]. Numerical methods were also developed to solve problems with free and moving boundaries [Zohouri, Pirooz, and Esmaeily (2005); Mai-Duy and Tran-Cong, (2004)]. GFD methods have been used in many engineering applications and in our previous papers where irregular geometries and free-moving boundaries are involved [Kleiber (1998); Liszka and Orkisz (1980); Tang, Chen, Yang, Kobayashi and Ku (2002); Tang, Yang, Kobayashi and Ku (2001)]. One advantage of using GFD is that generalized finite difference schemes can be derived for user-selected irregular grid points which can be freely adjusted to accommodate plaque deformation and growth. The MGFD method introduced in this paper uses grid points from the local support of each nodal point so that theoretical MLPG framework can be applied [Atluri (2004)]. Details are given in the following sections.

2. Models and methods

Due to the complexity of the problem, we start from 2D models in this paper to get some insight for further full 3D investigations. Patient-specific plaque progression data was acquired by serial MRI (scanning patients multiple times with time span at about 18 months). Corresponding slices were matched using carotid bifurcation as the registration point. 2D models were constructed for selected slices and solved by meshless GFD method to obtain the stress distributions in the plaque. Point-wise plaque growth functions were determined based on three time point stress and vessel wall thickness data. The growth functions were then used to simulate plaque progression starting from Time 2 plaque morphology. The simulated Time 3 plaque morphology was compared with actual Time 3 plaque geometry to validate our modeling method. Details are given below.

2.1 In vivo Serial MRI Data Acquisition

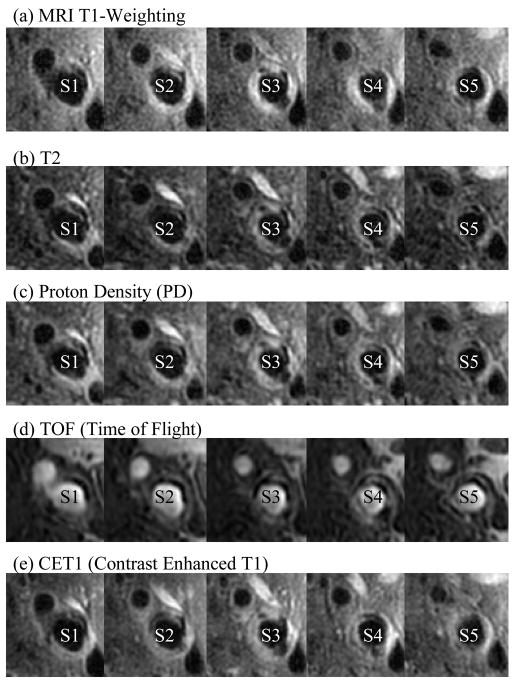
Serial MRI data from one patient was provided by the University of Washington (UW) group using protocols approved by the University of Washington Institutional Review Board with informed consent obtained. Scan time intervals were about 18 months, subject to scheduling variations. MRI scans were conducted on a GE SIGNA 1.5-T whole body scanner using an established protocol outlined in the papers by Yuan and Kerwin et al. [Kerwin, Hooker, Spilker, Vicini, Ferguson, Hatsukami, and Yuan (2003); Yuan and Kerwin (2004)]. Upon completion of a review, an extensive report was generated and segmented contour lines for different plaque components for each slice were sent to Tang’s group for model construction and further computational mechanical analysis. Details of the model construction process can be found from [Yang et al. (2007); Tang et al. (2008)]. Figure 1 shows 5 (selected from 12) MRI slices with 5 different weightings obtained from a human carotid plaque sample. Figure 2 gives the reconstructed 3D geometries of the plaque at three time points showing plaque progression. Figure 3 gives three-time point segmented contour plots of 5 selected slices. These slices were used for model construction, quantification of growth function, and validation of simulated plaque progressions.

Figure 1.

Selected multi-weighting MRI slices (5 of 12 slices) of carotid plaque from a participating patient. Multi-weighting MRI techniques can better differentiate plaque components and provide more accurate plaque vulnerability assessments [Yuan and Kerwin (2004)].

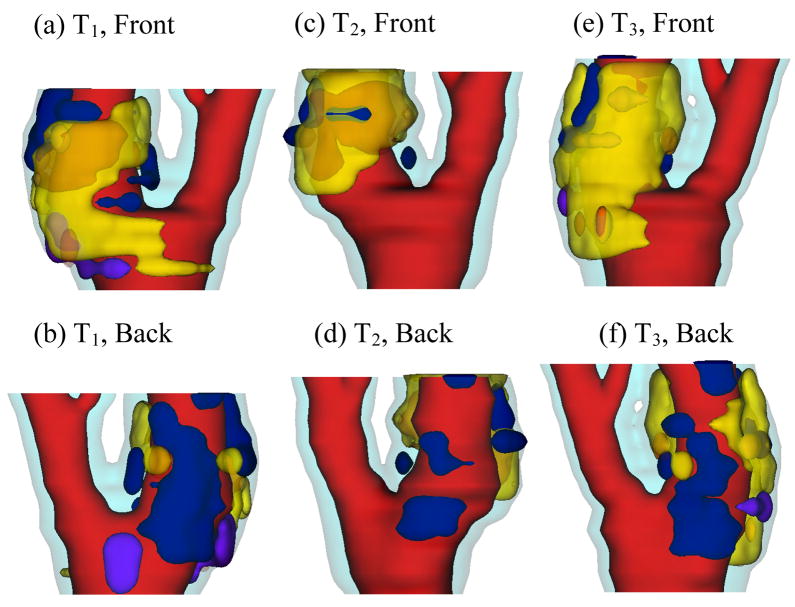
Figure 2.

Re-constructed 3D geometry of a carotid plaque based on in vivo serial MRI data. Three time point data are shown. T₁, T₂ and T₃ refer to time points from here on, unless otherwise indicated. T₁–T₂: 525 days; T₂–T₃: 651 days. Red – lumen; Cyan- outer wall; Yellow - necrotic core; Fresh red - hemorrhage in necrotic core); Purple - loose matrix; Dark blue – calcification; Green - fibrous cap.

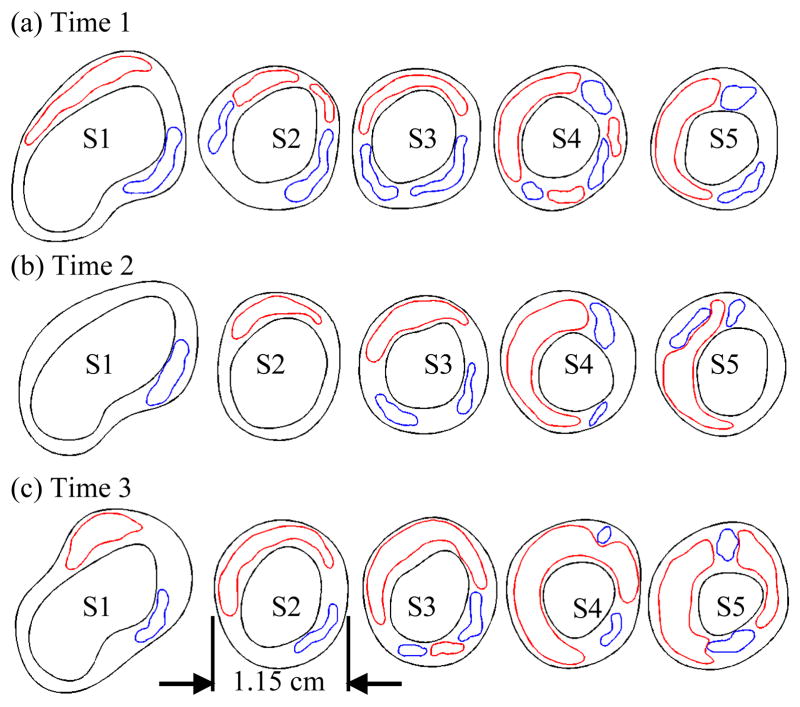
Figure 3.

Segmented contour plots using CASCADE showing plaque components and plaque progression. 5 slices were selected with the bifurcation serving as the registration point. Data from three time points are shown. Red – lipid; blue – calcification (Ca).

2.2 The structure model

Since there was insufficient data to quantify individual plaque component growth, the plaque was treated as a uniform material, which was assumed to be hyperelastic, isotropic, incompressible and homogeneous. The governing equations and corresponding initial and boundary conditions are given below [Fung (1994)]:

$$\rho u_{i,tt}={\sigma }_{ij,j},\text{i},\text{j}=1,2;\text{sum}\text{over}\text{j},$$ (1)

$${\epsilon }_{ij}=(u_{i,j}+u_{j,i})/2,\text{i},\text{j}=1,2,3$$ (2)

$${{\sigma }_{ij}·n_j\mid }_{\text{out}\_\text{wall}}=0,$$ (3)

$${{\sigma }_{ij}·n_j\mid }_{\mathrm{\Gamma }}={p_{in}(t)\mid }_{\mathrm{\Gamma }},$$ (4)

$${u_i\mid }_{t=0}=u_{i0},$$ (5)

$${u_{i,t}\mid }_{t=0}={\stackrel{.}{u}}_{i0},$$ (6)

where ρ is material density, u=(u₁, u₂) is the displacement vector, σ is stress tensor, ε is strain tensor, P_in is the specified lumen pressure, Γ is vessel inner boundary, f _{•, j} stands for derivative of f with respect to the jth variable.

Using a linear model, the strain-stress relationship is [Fung (1994)]:

$$\left(\begin{array}{l}{\sigma }_{11}\hfill \\ {\sigma }_{22}\hfill \\ {\sigma }_{12}\hfill \end{array}\right)=C·\left(\begin{array}{l}{\epsilon }_{11}\hfill \\ {\epsilon }_{22}\hfill \\ {\gamma }_{12}\hfill \end{array}\right)$$ (7)

$$C=\frac{E_0}{1-{\mu }_0^2}·\left(\begin{array}{ccc}1& {\mu }_0& 0\\ {\mu }_0& 1& 0\\ 0& 0& \frac{1-{\mu }_0}{2}\end{array}\right)=·\left(\begin{array}{ccc}{C}_1& C_2& 0\\ C_2& C_1& 0\\ 0& 0& C_3\end{array}\right)$$ (8)

where E₀ is the Young’s Modulus, μ₀ is the Poisson ratio, C₁, C₂, and C₃ are coefficients defined by (8) for convenience. Substituting (2) and (7)–(8) into (1), we have the displacement equations in scalar form:

$$\rho \frac{{\partial }^2{u}_1}{\partial t^2}=C_1\frac{{\partial }^2{u}_1}{\partial x_1^2}+C_3\frac{{\partial }^2{u}_1}{\partial x_2^2}+(C_2+C_3)\frac{{\partial }^2{u}_2}{\partial x_1{x}_2},$$ (9)

$$\rho \frac{{\partial }^2{u}_2}{\partial t^2}=C_3\frac{{\partial }^2{u}_2}{\partial x_1^2}+C_1\frac{{\partial }^2{u}_2}{\partial x_2^2}+(C_2+C_3)\frac{{\partial }^2{u}_1}{\partial x_1{x}_2},$$ (10)

The boundary conditions are:

$$C_1{n}_1\frac{\partial u_1}{\partial x_1}+C_2{n}_1\frac{\partial u_2}{\partial x_2}+C_3{n}_2(\frac{\partial u_1}{\partial x_2}+\frac{\partial u_2}{\partial x_1})={\overline{t}}_1,$$ (11)

$$C_2{n}_2\frac{\partial u_1}{\partial x_1}+C_1{n}_2\frac{\partial u_2}{\partial x_2}+C_3{n}_1(\frac{\partial u_1}{\partial x_2}+\frac{\partial u_2}{\partial x_1})={\overline{t}}_2,$$ (12)

where (n₁,n₂) is the normal direction of the boundary and (t̄₁, t̄₂) = (P_inn₁, P_inn₂) is the fluid force applied at the inner boundary (lumen), and the outer boundary is treated as a free boundary, with (t̄₁, t̄₂) = 0.

2.3 The meshless GFD method

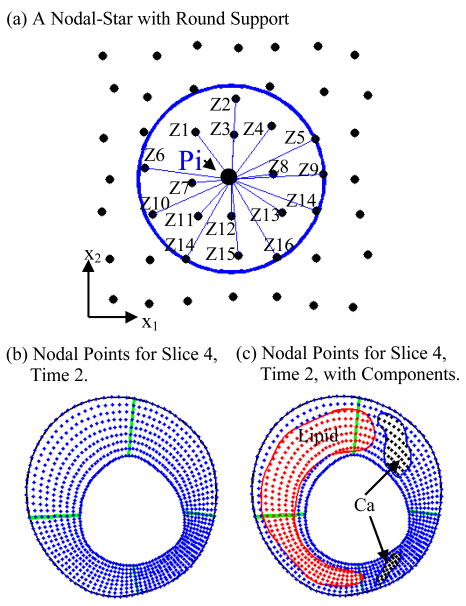
The advantage of MGFD method is that generalized finite difference schemes can be derived using arbitrarily distributed points (see Fig. 4). With MGFD, we will be able to use denser nodal point distributions where plaque has higher stress/strain concentration or critical morphological features. We will also be able to adjust, move, add or drop nodal points as needed. This leads to the desired flexibility in handling the complex geometry and plaque growth where not only the geometry changes, the total plaque area (volume if 3D) also changes. The GFD concept is explained by the following example. Fig. 4(a) gives a selected nodal point Pi, its round support and all surrounding points Zj, j=1, …, Ni, which are used to derive the GFD scheme.

Figure 4.

Meshless GFD scheme derivation and nodal point distributions. (a) A schematic plot illustrating the derivation process of meshless GFD schemes with round support; (b)–(c) Nodal points distributions on Slice 4, Time 2, with and without plaque components.

To derive the second order GFD schemes for the first and second order derivatives of the unknown function f(x₁, x₂), we use the Taylor expansion of f at Pi. Omitting higher order terms, we have,

$$\begin{array}{l}{f_j=f_i+h_j\frac{\partial f}{\partial x_1}|}_i+{k_j\frac{\partial f}{\partial x_2}|}_i\\ +{\frac{h_j^2}{2}\frac{{\partial }^{2}f}{\partial x_1^2}|}_i+{h_j{k}_j\frac{{\partial }^{2}f}{\partial x_1{x}_2}|}_i+{\frac{k_j^2}{2}\frac{{\partial }^{2}f}{\partial x_2^2}|}_i+o(h_j^2+k_j^2)\end{array}$$ (13)

where the subscript i indicates the selected node Pi at which derivative GFD schemes are being derived, j=1…Ni are the other nodes in the Ni-node-star of Pi, f_j is the function value at Zj, Zj are the neighboring points of Pi within the support, h_j=x_1j−x_1i, k_j=x_2j−x_2i. Ignore the higher order terms in (13), we have:

$$\left(\begin{array}{ccccc}{h}_1& k_1& \frac{h_1^2}{2}& h_1{k}_1& \frac{k_1^2}{2}\\ ⋮& ⋮& ⋮& ⋮& ⋮\\ h_{Ni}& k_{Ni}& \frac{h_{Ni}^2}{2}& h_{Ni}{k}_{Ni}& \frac{k_{Ni}^2}{2}\end{array}\right)·{\left(\begin{array}{c}\frac{\partial f}{\partial x_1}\\ \frac{\partial f}{\partial x_2}\\ \frac{{\partial }^{2}f}{\partial x_1^2}\\ \frac{{\partial }^{2}f}{\partial x_1{x}_2}\\ \frac{{\partial }^{2}f}{\partial x_2^2}\end{array}\right)}_i=\left(\begin{array}{c}{f}_1-f_i\\ ⋮\\ f_{Ni}-f_i\end{array}\right)$$ (14)

Rewrite (14) as Af⃗= g⃗, and use the least-squares method to get the formula for f⃗:

$$\overrightarrow{f}={(A^{T}WA)}^{-1}{A}^{T}W\overrightarrow{g}$$ (15)

where W is the weight matrix with

$$W=\left(\begin{array}{ccc}{w}_1& & 0\\ & \ddots & \\ 0& & w_{Ni}\end{array}\right),w_j=\frac{1}{(h_j^2+k_j^2)},\text{j}=1,2,\dots \text{Ni},$$ (16)

Let B = (b_kl)_5×Ni = (A^TWA)⁻¹ A^T W, we have,

$${\left(\begin{array}{c}\frac{\partial f}{\partial x_1}\\ \frac{\partial f}{\partial x_2}\\ \frac{{\partial }^{2}f}{\partial x_1^2}\\ \frac{{\partial }^{2}f}{\partial x_1{x}_2}\\ \frac{{\partial }^{2}f}{\partial x_2^2}\end{array}\right)}_i=\left(\begin{array}{c}\sum _{j=1}^{ni}{b}_{1j}(f_j-f_i)\\ \sum _{j=1}^{ni}{b}_{2j}(f_j-f_i)\\ \sum _{j=1}^{ni}{b}_{3j}(f_j-f_i)\\ \sum _{j=1}^{ni}{b}_{4j}(f_j-f_i)\\ \sum _{j=1}^{ni}{b}_{5j}(f_j-f_i)\end{array}\right)$$ (17)

Substituting (17) into (9)–(10), we get the discrete approximation for inner nodes. For boundary nodes, we do a similar work using 1^st order GFDM method. That is:

$${f_j=f_i+h_j\frac{\partial f}{\partial x_1}|}_i+{k_j\frac{\partial f}{\partial x_2}|}_i+o(h_j+k_j)$$ (18)

$$\left(\begin{array}{cc}{h}_1& k_1\\ ⋮& ⋮\\ h_{Ni}& k_{Ni}\end{array}\right)·{\left(\begin{array}{c}\frac{\partial f}{\partial x_1}\\ \frac{\partial f}{\partial x_2}\end{array}\right)}_i=\left(\begin{array}{c}{f}_1-f_i\\ ⋮\\ f_{Ni}-f_i\end{array}\right)$$ (19)

$${\left(\begin{array}{c}\frac{\partial f}{\partial x_1}\\ \frac{\partial f}{\partial x_2}\end{array}\right)|}_i=\left(\begin{array}{c}\sum _{j=1}^{ni}{b}_{1j}(f_j-f_i)\\ \sum _{j=1}^{ni}{b}_{2j}(f_j-f_i)\end{array}\right)$$ (20)

Substituting (20) into (11)–(12), we get the discrete approximation for boundary nodes. Second order scheme for boundary nodes were also tested. However, it did not give good result. One order lower schemes for boundary nodes are common in computational schemes.

Time derivatives are discretized using the 2^nd order center difference scheme:

$$\frac{{\partial }^{2}f}{\partial t^2}=\frac{f^{n+1}-2f^n+f^{n-1}}{\mathrm{\Delta }{t}^2}+O(\mathrm{\Delta }{t}^2),$$ (21)

Assembling all the discretized equations and boundary conditions, we get the final linear system:

$$K\overrightarrow{u}=\overrightarrow{f},$$ (22)

The vector $\overrightarrow{u}=\left(\begin{array}{c}{\overrightarrow{u}}_1\\ {\overrightarrow{u}}_2\end{array}\right)$ is the displacement solution at time step (n+1). Equation (22) is solved by a sparse solver under Matlab environment.

2.4 The shrink-pressurize process and MGFD model validation

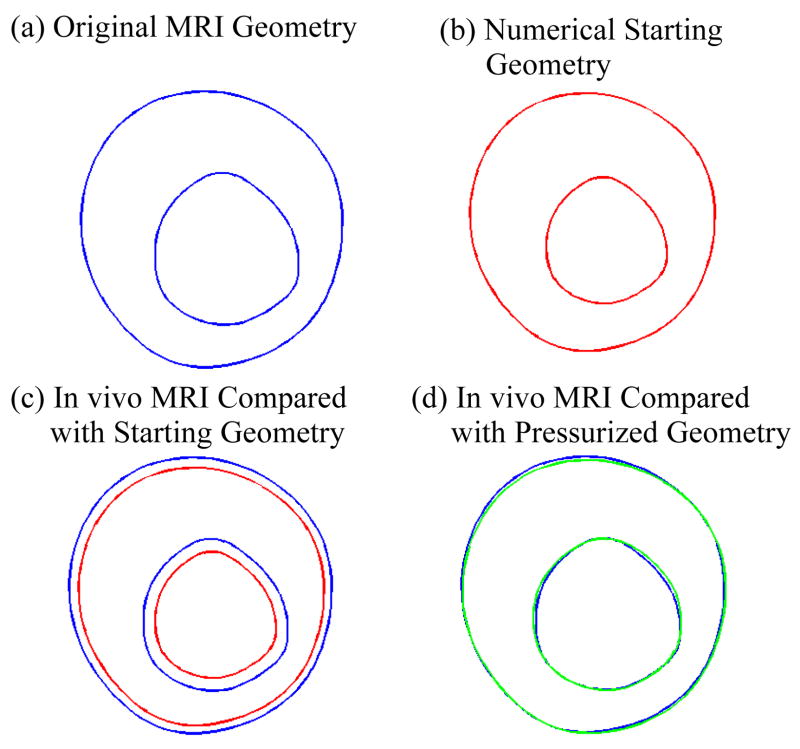
When constructing in vivo MRI-based plaque models, a shrink-pressurize process needs to be used to (a) shrink the original in vivo MRI geometry to get the numerical starting geometry with zero lumen pressure and then (b) pressurize the reduced starting geometry to recover the original in vivo geometry with specified lumen pressure. Using Slice 4 (S4) at Time 2 (T₂) as an example, Fig. 5 shows its original in vivo MRI geometry, the numerical starting geometry with 16.75% inner boundary shrinkage and 6.5% outer-boundary shrinkage, and the pressurized geometry obtained by solving the GFD plaque model. The outer boundary was reduced less so that the conservation law of mass (area for 2D models) is enforced. Young’s modulus was set at E₀=2.3×10⁶ dyn/cm², based on our experimental data [Kobayashi, Tsunoda, Fukuzawa, Morikawa, Tang, Ku (2003); Tang et al. (2008); Tang, Yang, Zheng, Woodard, Saffitz, Petruccelli, Sicard and Yuan (2005)] and current literature [Fung (1993); Humphrey (2002)]. Patient-specific pressure = 136 mmHg (by arm) was used as the lumen pressure.

Figure 5.

Comparison of (a) original in vivo MRI plaque geometry with (b) numerical starting geometry, inner boundary shrinkage, 16.75%, outer-boundary shrinkage 6.5%, and (d) the pressurized geometry obtained by solving the GFD plaque model, Slice 4 at T₂ was used.

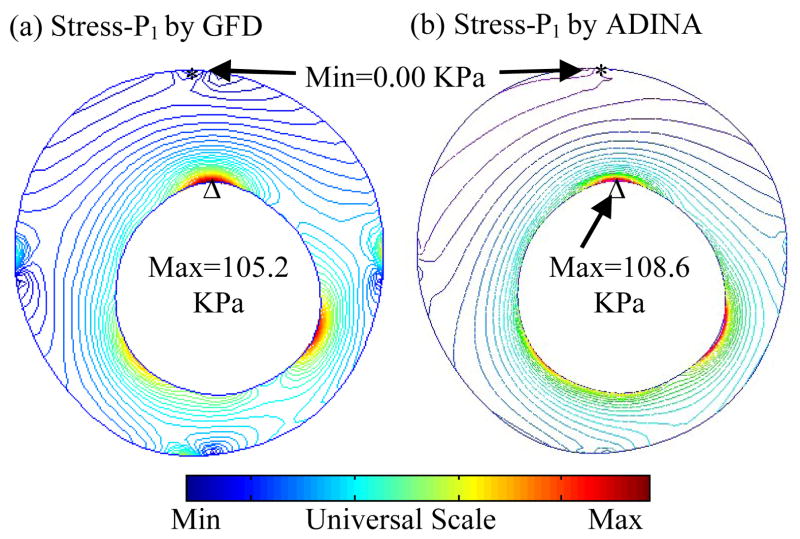
A commercial finite element software package ADINA (ADINA R & D, Inc., Watertown, MA) was used to validate our MGFD model. ADINA has been validated by hundreds of realistic engineering and real life applications and is well accepted in the industry and research communities [Bathe (1996); Bathe (2002)]. We have been using ADINA in the past 10 years to construct and solve 2D/3D artery models which were validated by experimental measurements [Tang et al. (2005,2008)]. A finite element ADINA model was constructed using S4 geometry and following the same procedures using in [Tang et al. (2005)]. Figure 6 compares maximum principal stress (Stress-P₁) from MGFD and ADINA models and shows that results from both models had very good agreement (error < 3%).

Figure 6.

Comparison of maximum principal stress (Stress-P₁) by MGFD and ADINA for model validation.

3. Plaque growth function and progression simulation

With the MGFD model validated, we can use it to derive plaque growth function and simulate plaque progression.

3.1. A piecewise equal-step method to define wall thickness

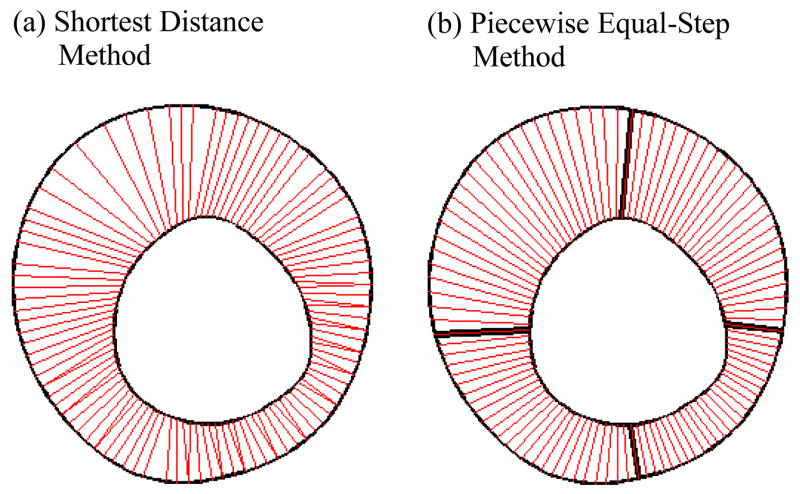
Vessel wall thickness was selected as the measure for plaque progression. In our previous paper, the “shortest distance” method was used to determine vessel thickness, i.e., for a selected nodal point on the inner boundary (lumen), the shortest distance between that point and the out-boundary was defined at the vessel thickness at that lumen point. That led to uneven selection of nodal points from the out boundary as shown by Fig. 7(a). A piecewise equal-step method is introduced to fix the problem. The vessel is divided into several pieces (segments) according to its geometry (4 in the S4 case). For each piece, equal step is used for inner and outer boundaries respectively to choose equal number of nodal points. The corresponding points on the inner and out boundaries are paired and the distance between the paired points are defined as vessel wall thickness at the given lumen point (Fig. 7). This method is sufficient for the cases covered in this paper.

Figure 7.

Piecewise equal-step method for determination of vessel wall thickness. Slice 4 at T2 is used for demonstration. The vessel wall was divided into 4 segments. 25 points were equally distributed on each segment.

3.2. Quantifying plaque growth function (PGF) using serial MRI data

Plaque growth function (PGF) is a function we use to determine the vessel wall thickness or nodal point displacement for every numerical time step based on current and past plaque geometry and mechanical conditions. The following assumptions were made when deriving the plaque growth functions:

1. Plaque growth depends on local plaque morphological and mechanical conditions;

2. For simplicity, a single-point correspondence approach is used, i.e., plaque growth at a given nodal point is determined by information from the past and current time steps at the same point. In reality, influence from neighboring points should already be factored in by the plaque growth at the chosen nodal point;

3. The first order time derivatives of the vessel wall thickness and stress conditions (which are functions of time, for every nodal point under consideration) should be included in PGF;

4. The information at most current time step is most directly related to plaque growth in the nearest “future”. Two different plaque growth function forms were used in our derivation and simulation process.

Three-time-point function

Data from three time steps T₁, T₂ and T₃ are used to fit wall thickness or displacement at T₃. The fitting function is:

$$\begin{array}{l}{f_{T_3-\mathit{fit}}(i)={a_i}^{\ast }{f}_{T_2}(i)+{b_i}^{\ast }\frac{df}{dt}|}_{T_2}(i)+\\ {+{c_i}^{\ast }{\sigma }_{T_2}(i)+{d_i}^{\ast }\frac{d\sigma }{dt}|}_{T_2}(i)\end{array}$$ (23)

where f is the wall-thickness or displacement function, i is the nodal point numbering index (100 points were chosen from the inner boundary), σ is the Stress-P₁ function, a_i, b_i, c_i, and d_i are coefficients determined by the least squares method to fit T₃ wall thickness or displacement data, and the time derivatives are calculated by

$${\frac{dg}{dt}|}_{T_2}(i)=w^{\ast }\frac{g_{T_3}(i)-g_{T_2}(i)}{T_3-T_2}+{(1-w)}^{\ast }\frac{g_{T_2}(i)-g_{T_1}(i)}{T_2-T_1},$$ (24)

where g can be either f or σ, w is a weight function to be adjusted for better agreement when the growth function is used in progression simulation. When the growth function (23) is used in the plaque progression simulation code to adjust the inner and outer boundary at each numerical time step, the time derivatives are evaluated with T3 replaced by the “current” time corresponding to the numerical step:

$${\frac{dg}{dt}|}_{t_n}(i)=w^{\ast }\frac{g_{t_n}(i)-g_{T_2}(i)}{t_n-T_2}+{(1-w)}^{\ast }\frac{g_{T_2}(i)-g_{T_1}(i)}{T_2-T_1},$$ (25)

where t_n indicates the current time in the numerical simulation.

Two-time-point function

Data from two time steps T₁ and T₂ are used to fit wall thickness or displacement at T₂. The fitting function is the same as that given by (23) except that the derivatives are calculated using two time points by:

$${\frac{dg}{dt}|}_{T_2}(i)=\frac{g_{T_2}(i)-g_{T_1}(1)}{T_2-T_1}.$$ (26)

In the simulation code, (25) will be used to calculate time derivatives, the same way as it is done for the three-point growth function. So the main difference between the three-point formula and the two-point formula is that the coefficients a_i, b_i, c_i, and d_i are determined using different time (two or three) data points. The formulas for the two growth functions in the simulation code are almost the same.

3.3. Plaque progression simulation

Using S4 at T₂ and the plaque growth function determined in 3.2, the following procedure is used to simulate plaque progression:

Step 1. Start from the original in vivo MRI geometry (S4 at T₂), use proper shrinkage to get the zero-pressure numerical starting geometry;

Step 2. Discretize the geometry using the meshless GFD method, solve the model to get plaque geometry and stress/strain distributions under specified pressure conditions;

Step 3. Use the growth function to determine the plaque geometry for next numerical time step by adjusting the nodal points on inner and outer boundaries;

Step 4. Adjust internal nodal points as needed;

Step 5. Solve the plaque model using the updated plaque geometry;

Step 6. Repeat Steps 3–5 till numerical time reaches T₃ (MRI scan time).

Results obtained from the simulation code are presented in next section.

4. Results

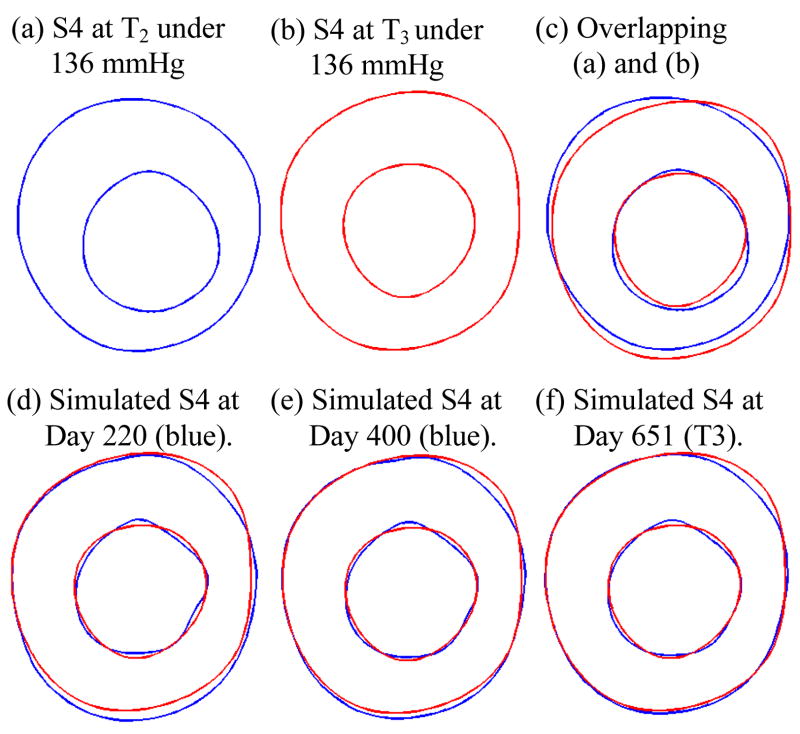
Slice 4 was used as the sample to demonstrate the simulation process. The procedure described in 3.3 was followed. Fig. 8 gives the starting, target and three simulated geometries, showing good agreement between simulated and actual plaque progression. Define the absolute and relative errors as:

$$\text{Absolute}\text{Error}=\mathrm{\sum }(\mid \text{WT}\_\text{num}(\text{i})-\text{WT}\_\text{T}3(\text{i})\mid )/100,$$ (27)

$$\text{Relative}\text{Error}=\mathrm{\sum }[(\mid \text{WT}\_\text{num}(\text{i})-\text{WT}\_\text{T}3(\text{i})\mid )/(\text{WT}\_\text{T}3(\text{i})\mid ]/100,$$ (28)

where 100=total number of nodal points selected from inner boundary, we have:

$$\text{Absolute}\text{Error}=0.0126\text{cm},$$ (29)

$$\text{Relative}\text{Error}=4.52\%,$$ (30)

for the case simulated (S4, 3-point formula).

Figure 8.

Simulated plaque growth has good agreement with MRI data (error = 4.52%). Progression code starting time: T₂; ending time: T₃. S4 was used as the sample slice. The three-point growth function was used. S4 geometry at T₃ determined from MRI data was used as the benchmark data for validation. Lumen pressure: 136 mmHg. T₂–T₃ time span was 651 days.

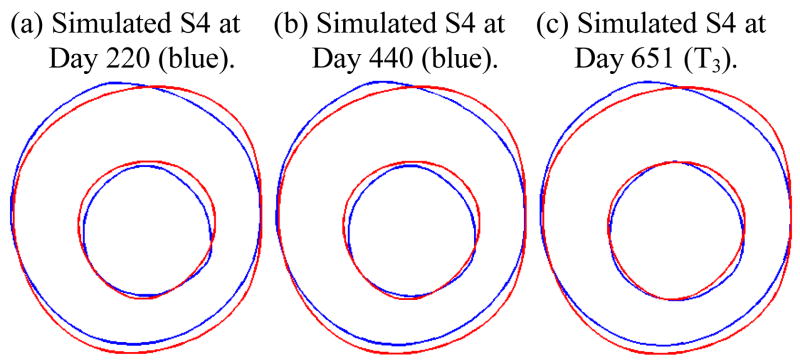
Figure 9 gives the simulated plaque geometries at Days 220, 440, and 651 (ending time, T₃) using the two-point growth function (26). The errors are:

$$\text{Absolute}\text{Error}=0.0329\text{cm},$$ (31)

$$\text{Relative}\text{Error}=11.4\%.$$ (32)

Figure 9.

Simulated plaque geometries at three numerical time steps showing the prediction accuracy (error = 11.4%) using the two-point growth function was not as good as that from the three-point growth function.

It is clear that the three-point growth function gave more accurate predictions.

Simulations were also conducted for S2, S3 and S5. Results from S3 were similar to that of S4. S2 and S5 did not give good results because the original MRI geometries differ too drastically from T₁ to T₂ and from T₂ to T₃ and no clear trend could be quantified.

5. Discussion

5.1. The computational approach

It is well-known that atherosclerotic plaque progression is a multi-faceted process involving not only mechanical factors, but also plaque type, component size and location, cell activities, blood conditions such as cholesterol level, diabetes, changes caused by medication such as statin, and other chemical conditions, inflammation and lumen surface condition. Investigations and findings from all the channels, modalities and disciplines could be integrated together to obtain better and more thorough understanding of the complicated atherosclerotic progression process. In stead of trying to identify the individual factors which contribute to plaque growth, our computational simulation approach takes the actual multi-year plaque progression data to simulate future growth, based on the assumptions that the trend that led to the current state would continue into the future. In other words, the trend would continue; the governing mechanisms (whether we know them or not) would remain the same; the contributing factors would continue to contribute the same way as they did in the past, with the changes taken into consideration by the terms included in the growth function.

Our results from the 4 slices simulated indicated that our model worked well when the trend from T₂ to T₃ was more or less similar to that from T₁ and T₂. And the model did not work very well when T₂ geometry seemed to be “out of place” between T₁ and T₃. Our model was applicable to 50% of the cases considered.

5.2. Model limitations

Clearly the current model is very limited and serves as initial demonstrations of the MGFD method and the potential significant contributions from the progression simulation model. The model needs to be extended to 3D. And the growth functions need to be adjusted to include the proper terms that can represent the plaque growth trend. Better understanding of the biological and mechanical factors will help us to better formulate the growth function. Fluid forces and blood conditions (cholesterol, lipid lowering medication factor) can be included for better accuracy of predictions.

5.3. Progression simulation and plaque vulnerability assessment

The long term goal of the current study is that patient-specific quantitative plaque growth functions can be determined based on multiple annual MRI scans and used to simulate plaque progression. “Future” plaque vulnerability can be assessed based on predicted future plaque morphologies by the progression simulation models. We are adding the “time dimension” into plaque assessment technology to improve the predicting power and accuracy. If our studies are successful, annual MRI scans would be recommended to patients who are in their early-to-middle stages of atherosclerosis. Simulated plaque growth would be generated for their early diagnosis and proper treatment for prevention of serious or even fatal clinical cardiovascular events.

6. Conclusion

We believe that this is the first time that human carotid atherosclerotic plaque progression was simulated based on patient-specific plaque morphology and point-wise plaque growth functions derived from multi-year MRI data. Our results indicated that our proposed progression simulation process was able to accurately predict future plaque morphology if the current progression trend was continued. The meshless GFD method worked well for the progression model. The predicted progression by the three-time-point growth function was considerably more accurate than that given by the two-time-point (4.52% vs. 11.4%). The current 2D model can be extended to 3D model with more terms added to the growth functions for better predictions. More case studies are needed to validate our findings. Accurate plaque progression simulation adds the time dimension to plaque vulnerability assessment strategies and should improve our predicting accuracies.