Selective-Tap Blind Dereverberation for Two-Microphone Enhancement of Reverberant Speech

Abstract

In this letter we propose a novel approach for two-microphone enhancement of speech corrupted by reverberation. Our approach steers computational resources to filter coefficients having the largest impact on the error surface and therefore only updates a subset of coefficients in every iteration. Experimental results carried out in a realistically reverberant setup indicate that the performance of the proposed algorithm is comparable to the performance of its full-update counterpart.

I. Introduction

Acoustic reverberation is caused by multiple reflections and diffractions of sounds on the walls and objects in enclosed spaces. Reverberation is harmful to speech intelligibility since it blurs temporal and spectral cues, flattens formant transitions, reduces amplitude modulations associated with the fundamental frequency of speech and increases low-frequency energy, which in turn results in masking of higher speech frequencies [1]. Blind reverberation cancelation or dereverberation is a well-known technique, based on which we can reconstruct an estimate of a speech signal distorted by reverberation with no prior knowledge of the signal itself or the acoustical properties of the room [2]. To isolate the original or ‘true’ source signal in a multi-path propagation scenario, one needs to rely solely on information that can be collected from the microphones. Gannot and Moonen [3] were the first to propose a multi-microphone dereverberation technique using a generalized singular-value decomposition (GSVD) approach. Nakatani and Miyoshi [4] achieved speech dereverberation by extraction of the harmonic components of clean speech after filtering the reverberant signal through a pre-trained harmonic filter. Wu and Wang [5] proposed to maximize the kurtosis of the linear prediction (LP) residual of the original clean speech and then to use a spectral subtraction algorithm to decrease late reverberation. Lee et al. [6] resorted to a binaural (two-channel) model to reformulate the problem of blind dereverberation as a single-input multiple-output (SIMO) inverse filtering problem. Jointly reducing spectral coloration due to late reverberant energy as well as background noise for speech enhancement in practical applications has also been the focus of other recent single- and multi-channel speech dereverberation strategies (e.g., see [7]–[9]). The aforementioned dereverberation strategies perform well, as long as large amounts of processing power and training data can be made available. However, since most algorithms require a large number of taps to capture room impulse responses and since their computational complexity and processing delays are proportional to the tap length used, they are prohibitively expensive for use in practical applications (e.g., hearing aids).

In this letter, we derive a novel blind single-input two-output reverberant speech enhancement strategy, which stems from the multi-channel least-mean-square (MCLMS) algorithm [10]. The proposed method uses second-order statistics to identify the acoustic paths in the time-domain and relies on a novel selective-tap criterion to update only a subset of the total number of filter coefficients in every iteration. Therefore, it substantially reduces computational requirements with only minimal degradation in dereverberation performance. The potential of the proposed low-complexity algorithm is verified and assessed through numerical simulations in realistic acoustical scenarios.

II. Problem Formulation and Algorithm

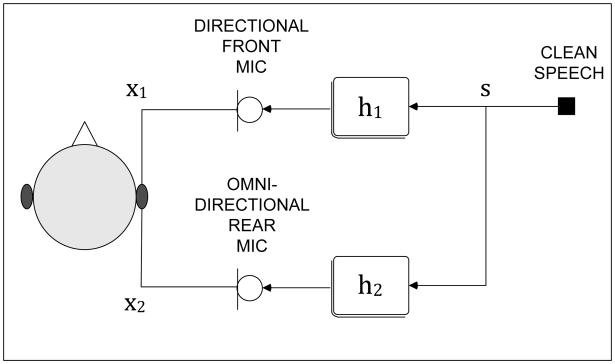
Consider the paradigm shown in Fig. 1 where speech is picked up by the two microphones of a hearing aid device. Let s(k) represent the sound source, h₁(k) and h₂(k) denote the impulse responses of the two acoustic paths modeled using finite impulse response (FIR) filters and x₁(k) and x₂(k) be the reverberant signals captured by the two microphones of the device. In the noiseless two-microphone scenario, we exploit the correlation between the output signals of each microphone

Fig. 1.

A typical SIMO hearing aid setup, in which the two signals picked up by the directional (front) and omni-directional (rear) microphones are used to adaptively cancel the reverberation present in the background.

$$x_i(k)=h_i(k)\ast s(k)\text{and}{x}_j(k)=h_j(k)\ast s(k)$$ (1)

where * denotes linear convolution and i, j = 1, 2. From (1) and for all i ≠ j, it follows that

$$\begin{array}{l}{h}_j(k)\ast x_i(k)=h_j(k)\ast [h_i(k)\ast s(k)]\\ =h_i(k)\ast x_j(k)\end{array}$$ (2)

A. Multi-Channel LMS Algorithm

As shown in [10], an intuitive way to ‘blindly’ calculate the unknown acoustic paths is to minimize a cost function that penalizes correlated output signals between the ith and jth sensors¹, such that

$$J(k+1)=arg\underset{\mathit{h}}{min}\sum _{i=1}^{M-1}\sum _{j=i+1}^M{e}_{ij}^2(k+1)$$ (3)

After re-writing (2) in vector notation, the error function e_ij(k + 1) in (3) can be further expanded to

$$e_{ij}(k+1)={\mathit{x}}_i^T(k+1){\stackrel{\sim }{\mathit{h}}}_j(k)-{\mathit{x}}_j^T(k+1){\stackrel{\sim }{\mathit{h}}}_i(k)$$ (4)

defined for all i, j = 1, 2 and i ≠ j, where (·)^T denotes vector transpose, vector h̃_i (k)=[h_i(0), h_i(1),…, h_i (L−1)]^T represents the estimate of the time-invariant impulse response of the ith microphone at time instant k of order L and

$${\mathit{x}}_i(k)={[x_i(k),x_i(k-1),\dots ,x_i(k-L+1)]}^T$$ (5)

is the corrupted (reverberant) speech picked up by the ith microphone. Accordingly, the update equation of the time-domain multi-channel least-mean-square (MCLMS) algorithm is given by [10]

$$\stackrel{\sim }{\mathit{h}}(k+1)=\stackrel{\sim }{\mathit{h}}(k)-\mu \nabla J(k+1)$$ (6)

$$\nabla J(k+1)=\frac{\partial J(k+1)}{\partial \stackrel{\sim }{\mathit{h}}(k)}$$ (7)

$$=\frac{2[{\stackrel{\sim }{\mathbf{R}}}_x(k+1)\stackrel{\sim }{\mathit{h}}(k)-J(k+1)\stackrel{\sim }{\mathit{h}}(k)]}{{\left|\right|\stackrel{\sim }{\mathit{h}}(k)\left|\right|}^2}$$ (8)

where 0 < μ < 1 is the learning parameter controlling the rate of convergence and speed of adaptation, h̃(k) is the (2L × 1) composite channel response vector formed by the two separate channel coefficient vectors, such that

$$\stackrel{\sim }{\mathit{h}}(k)={[{\stackrel{\sim }{\mathit{h}}}_1^T(k),{\stackrel{\sim }{\mathit{h}}}_2^T(k)]}^T$$ (9)

and R̃_x(k) is the (2L × 2L) autocorrelation matrix of the microphone signals, which is equal to

$${\stackrel{\sim }{\mathbf{R}}}_x(k)=\left(\begin{array}{ll}{\stackrel{\sim }{\mathbf{R}}}_{x_2{x}_2}(k)\hfill & -{\stackrel{\sim }{\mathbf{R}}}_{x_2{x}_1}(k)\hfill \\ -{\stackrel{\sim }{\mathbf{R}}}_{x_1{x}_2}(k)\hfill & {\stackrel{\sim }{\mathbf{R}}}_{x_1{x}_1}(k)\hfill \end{array}\right)$$ (10)

with ${\stackrel{\sim }{\mathbf{R}}}_{x_i{x}_j}(k)=E[{\mathit{x}}_i(k){\mathit{x}}_j^T(k)]$ valid for all i, j = 1, 2.

B. Selective-Tap Two-Channel LMS Algorithm

Below, we formulate the new selective-tap approach based on the two-microphone configuration depicted in Fig. 1. By inspecting (6)–(8) we can see that as the adaptive algorithm approaches convergence, the cost function J(k+1) diminishes and its gradient with respect to h̃(k) becomes

$$\mathrm{\Delta }\stackrel{\sim }{\mathit{h}}(k)\simeq -2\mu {\stackrel{\sim }{\mathbf{R}}}_x(k+1)\stackrel{\sim }{\mathit{h}}(k)$$ (11)

after removing the unit-norm constraint from (8). From the above equation, it readily becomes evident that the convergence behavior of the MCLMS algorithm depends solely on the magnitude (element-wise) of the autocorrelation matrix R̃_x estimated at each iteration k. The computational complexity and slow convergence of the MCLMS algorithm can be therefore reduced substantially by employing a simple tap-selection criterion to update only M out of L coefficients containing the largest values of the autocorrelation matrix [11]. The subset of the filter coefficients updated at iteration k can be determined from the M × M matrix Q(k), which is coined the tap-selection matrix

$$\mathbf{Q}(k)\triangleq \left(\begin{array}{cccc}{\mathit{q}}_{ij}(0)& 0& \dots & 0\\ 0& {\mathit{q}}_{ij}(1)& \ddots & ⋮\\ ⋮& 0& \ddots & 0\\ 0& 0& 0& {\mathit{q}}_{ij}(M-1)\end{array}\right)$$ (12)

where each element is given by

$${\mathit{q}}_{ij}(k)\triangleq {[q_{ij}(k),q_{ij}(k-1),\dots ,q_{ij}(k-M+1)]}^T$$ (13)

such that

$$q_{ij}(k-\ell )=\{\begin{array}{ll}1,\hfill & \mid {\stackrel{\sim }{\mathbf{R}}}_x(k-\ell )\mid \in M\text{maxima}\mid {\stackrel{\sim }{\mathbf{R}}}_x\mid \hfill \\ 0,\hfill & \text{otherwise}\hfill \end{array}$$ (14)

where in a two-channel setup (12)–(14) are defined for i, j = 1, 2 and for all lags l = 0, 1,…, M − 1 and the operator |·| denotes absolute value. In order to calculate the different filter coefficients that are to be updated at different time instants, a fast sorting routine (e.g., see SORTLINE [12]) is executed at every iteration. After sorting, each block of the tap-selection matrix Q(k) contains M coefficients equal to one in the positions (or indices) calculated from (14) and zeros elsewhere, such that M < L with M = tr [Q(k)], where tr [·] denotes the sum of the diagonal elements of matrix Q(k). To update only M taps of the equalizer h̃(k), we write the selective-tap two-channel least-mean-square (SETA-TCLMS) algorithm as follows

$${\stackrel{\sim }{\mathit{h}}}_{\ell }(k+1)={\stackrel{\sim }{\mathit{h}}}_{\ell }(k)-2\lambda {\stackrel{\sim }{\mathbf{R}}}_x(k-\ell +1){\stackrel{\sim }{\mathit{h}}}_{\ell }(k)$$ (15)

where the update is carried out with learning rate λ only if l corresponds to one of the first M maxima of |R̃_x|, whereas when q_ij(k − l) = 0 then (15) becomes

$${\stackrel{\sim }{\mathit{h}}}_{\ell }(k+1)={\stackrel{\sim }{\mathit{h}}}_{\ell }(k)$$ (16)

where h̃_l = [h̃_l(0), h̃_l (1),…, h̃_l(M −1)]^T. Note that for M = L, the SETA-TCLMS reduces to the full-update algorithm described in (6)–(8).

III. Experimental Results

The performance of the SETA-TCLMS algorithm is evaluated using 5 different speakers (3 male and 2 female). The speech sources are approximately 10 s in duration and are recorded at a sampling rate of 8 kHz. All signals are taken from the IEEE database, which consists of phonetically balanced sentences, with each sentence being composed of approximately 7 to 12 words [13]. Reverberant speech is generated by convolving ‘clean’ speech with room impulse responses measured inside a 5 × 9 × 3.5 m office using an experimental two-microphone hearing aid device mounted behind the ear of a KEMAR positioned at 1.5 m above the floor and at ear level [14].

The length of the acoustic impulse responses is ≈ 1,920 sample points and the reverberation time² is equal to T₆₀ = 200 ms in the 20–4000 Hz frequency band, which is a typical value encountered in most daily reverberant environments. All numerical simulations are carried out for a single-source and a two-microphone configuration. The SETA-TCLMS algorithm is executed with L = 2,048, whereas the tap-selection length M is set to 2,048, 1,024 and 512 taps. The learning rates are explicitly tuned to yield the maximum possible steady-state performance. The enhanced speech is obtained by convolving the reverberant speech with the inverse of each estimated impulse response upon convergence.

A. Performance Evaluation

1) NPM

Since, in our experimental setup the acoustic channel impulse responses are known a priori the channel identification accuracy is calculated using the normalized projection misalignment (NPM) metric [10]

$$\text{NPM}(k)\triangleq 20{log}_{10}\frac{\left|\right|\epsilon (k)\left|\right|}{\left|\right|\mathit{h}\left|\right|}$$ (17)

with $\mathit{h}={[{\mathit{h}}_1^T,{\mathit{h}}_2^T]}^T$ and the projection misalignment ε(k)

$$\epsilon (k)=\mathit{h}-\frac{{\mathit{h}}^T\stackrel{\sim }{\mathit{h}}(k)}{{\stackrel{\sim }{\mathit{h}}}^T(k)\stackrel{\sim }{\mathit{h}}(k)}\stackrel{\sim }{\mathit{h}}(k)$$ (18)

where for perfectly identified acoustic paths ε(k) → 0.

2) PESQ

Although the NPM metric can measure channel identification accuracy reasonably well, it might not always reflect the output speech quality. For that reason, we also assess the performance of the proposed algorithm using the perceptual evaluation of speech quality (PESQ) [15]. The PESQ employs a sensory model to compare the original (unprocessed) with the enhanced (processed) signal, which is the output of the dereverberation algorithm, by relying on a perceptual model of the human auditory system. In the context of additive noise suppression, PESQ scores have been shown to exhibit a high Pearson’s correlation coefficient of ρ = 0.92 with subjective listening quality tests [16]. The PESQ measures the subjective assessment quality of the dereverberated speech rated as a value between 1 and 5 according to the five grade mean opinion score (MOS) scale. Here we use a modified PESQ measure [16], referred to as mPESQ, with parameters optimized towards assessing speech signal distortion, calculated as a linear combination of the average disturbance value D_ind and the average asymmetrical disturbance values A_ind [15], [16]

$$m\text{PESQ}=a_0+a_1{D}_{\text{ind}}+a_2{A}_{\text{ind}}$$ (19)

such that

$$a_0=4.959,a_1=-0.191\text{and}{a}_2=-0.006$$ (20)

By definition, a high value of mPESQ indicates low speech signal distortion, whereas a low value suggests high distortion with considerable degradation present. In effect, the mPESQ score is inversely proportional to reverberation time and is expected to increase as reverberant energy decreases.

B. Discussion

Table I contrasts the performance of the SETA-TCLMS algorithm relative to the performance of its full-update counterpart (see Section II-B). As it can be seen in Table I, the full-update TCLMS yields the best NPM performance and the highest mPESQ scores. Still, the degree of dereverberation remains largely unchanged when updating with the SETA-TCLMS using only M = 1,024 filter coefficients. In fact, even when employing just M = 512 taps, which accounts for a 75% reduction in the total equalizer length (with a processing delay of just 64 ms at 8 kHz) the algorithm can estimate the room impulse responses with reasonable accuracy.

TABLE I.

Dereverberation Performance For Five Speakers Averaged Across Both Microphones. All Values Obtained After Convergence.

L|M	SPEAKER	NPM (dB)	OUTPUT PESQ
2,048|2,048	A	−10.97	4.12
	B	−10.83	4.09
	C	−12.62	4.27
	D	−11.01	4.18
	E	−11.24	4.21
2,048|1,024	A	−10.24	3.52
	B	−10.01	3.28
	C	−11.79	3.89
	D	−10.57	3.65
	E	−10.92	3.77
2,048|512	A	−7.18	3.27
	B	−9.67	3.12
	C	−8.52	3.50
	D	−7.31	3.52
	E	−7.98	3.63

In terms of overall speech quality, the mPESQ score for the reverberant (unprocessed) speech signals averaged across all five speakers and in both microphones is equal to 2.72, which suggests that a relatively high amount of degradation is present in the microphone inputs. In contrast, after processing the two-microphone reverberant input signals with the SETA-TCLMS algorithm, the average mPESQ scores increase to 4.17, 3.62 and 3.40 when using M = 2,048, 1,024 and 512 taps, respectively. The estimated mPESQ values suggest that the proposed SETA-TCLMS algorithm can improve the speech quality of the microphone signals considerably, while keeping signal distortion to a minimum.

IV. Conclusions

We have developed a selective-tap blind identification scheme for reverberant speech enhancement using a two-microphone configuration. Numerical experiments carried out with speech signals in a moderately reverberant setup, indicate that the proposed two-channel dereverberation technique is capable of equalizing fairly long acoustic echo paths with sufficient accuracy and nearly no degradation. The proposed adaptive algorithm exhibits a low computational overhead and therefore is amenable to real-time implementation in portable devices (e.g., hearing aids).