Latent-model Robustness in Joint Models for a Primary Endpoint and a Longitudinal Process

Summary

Joint modeling of a primary response and a longitudinal process via shared random effects is widely used in many areas of application. Likelihood-based inference on joint models requires model specification of the random effects. Inappropriate model specification of random effects can compromise inference. We present methods to diagnose random effect model misspecification of the type that leads to biased inference on joint models. The methods are illustrated via application to simulated data, and by application to data from a study of bone mineral density in perimenopausal women and data from an HIV clinical trial.

1. Introduction

It is often of interest to characterize the association between a primary endpoint and a longitudinal process and to also understand the inherent features of the longitudinal process. One popular approach is to link a regression model for the primary endpoint and a mixed effects model for the longitudinal process through joint dependence on latent random effects. It has been demonstrated (e.g., Hsieh, Tseng, and Wang, 2006) that appropriate parametric modeling of the random effects in joint models yields more effcient inference procedures and can also shed light on the underlying features of the longitudinal process. One concern in this approach is the sensitivity of inference to the model assumptions on random effects. In this article, we address the issue of robustness of estimators for the primary regression parameters to such assumptions. We call this aspect of robustness latent-model robustness.

The primary endpoint in the joint model setting can be a simple response such as a binary indicator of the presence of a disease, or more complex such as a possibly censored time-to-event. The Study of Women’s Health Across the Nation (SWAN) (Sowers et al., 2003) provides an example of the former. Two objectives of SWAN are to characterize the association between an indicator of the evidence of osteopenia, a binary endpoint, and the underlying hormone patterns over the menstrual cycle in perimenopausal women, and to understand the underlying hormone patterns in this population. The hormone patterns cannot be observed directly but are observed through longitudinal progesterone levels derived from urine (PDG). AIDS Clinical Trials Group (ACTG) Protocol 175 (Hammer et al., 1996) is a setting where a joint model with time-to-event endpoint is a relevant framework. In this study, more than 2000 HIV-1-infected subjects were followed for their CD4 counts from week 8 post baseline and every 12 weeks thereafter, and the “event” is defined as a composite of ≥50% decline in CD4, progression to AIDS, or death. It is of interest to study the prognostic value of CD4 counts and their inherent trajectories over time in this population. In both studies, the longitudinal measurements, PDG and CD4 counts, are subject to assay error and intra-subject variation.

Assuming multivariate normal random effects, Wulfsohn and Tsiatis (1997) obtained maximum likelihood estimators (MLEs) for the regression parameters in joint models with time-to-event endpoint. Wang, Wang, and Wang (2000) proposed three methods to estimate the primary regression parameters in joint models with simple endpoint. Their methods rely on the assumption that the random effects follow a multivariate normal distribution, and they noted the concern about the sensitivity of inference to the normality assumption. Song, Davidian, and Tsiatis (2002) modeled the random effects using a flexible seminonparametric (SNP) model to avoid the restrictive normal assumption. Li, Zhang, and Davidian (2004) proposed conditional score estimators (CSEs) for the primary regression parameters in joint models with simple endpoint. Tsiatis and Davidian (2001) also derived the CSEs for the regression parameters in joint models with time-to-event endpoint. The CSEs require no assumption on the random effects. However, the latent-model robustness of the CSEs is achieved at the expense of loss of effciency. The effects of model misspecification on random effects in joint models have been investigated by several authors. Through extensive simulation studies, Hsieh et al. (2006) demonstrated robustness of the MLEs against departure from the normal random effect assumption in joint models with time-to-event endpoint. Hsieh et al. (2006) concluded that the MLE is robust to random effect model misspecification when there is rich enough information from the longitudinal data. Also focusing on joint models with time-to-event endpoint, Rizopoulos, Verbeke, and Molenberghs (2008) investigated the effect of misspecifying the random effect model on the parameter estimators and their standard errors. They showed that the difference between the MLE obtained from the joint model with a misspecified random effect model and the MLE based on the correct model converges to zero as the number of repeated measurements per subject increases.

Assuming the two component models in a joint model correct, the MLE is consistent and effcient when the random effect model is correctly specified. Even with the robustness property of the MLE revealed by the aforementioned authors, a relevant question is whether or not the available longitudinal information in a particular data set is rich enough to yield an MLE insensitive to model misspecification. Diagnostic tools that can reveal adverse effects of model misspecification when they do exist are thus desired. Huang, Stefanski, and Davidian (2006) applied a remeasurement method to structural measurement error models to diagnose model misspecification on the unobservable true predictor. In this article, we use an improved remeasurement method to develop diagnostic tools for joint models. In Section 2, we formulate joint models generically. From a viewpoint different from that of Rizopoulos et al. (2008), we provide an explanation in Section 3 for the asymptotic latent-model robustness of the MLE when longitudinal data information is extensive enough. In Section 4, we describe the improved remeasurement method and apply it to joint models to diagnose random effect model misspecification; test statistics are also proposed to assess quantitatively the robustness of parameter estimators. The diagnostic methods are illustrated via simulation in Section 5. In Section 6, the proposed methods are applied to the SWAN and ACTG 175 data sets.

2. Joint Models

For subject i, i = 1,…, n, denote by Y_i the primary endpoint, which is a scalar in joint models with simple endpoint, and is defined as a vector in joint models with time-to-event endpoint. Denote by W_i = (W_i1,…,W_imi)^T the set of longitudinal measurements recorded at times t_i = (t_i1,…,t_imi)^T and by H_i the vector of observed covariates, for i = 1,…, n. Finally, define ${\mathbf{Q}}_i^T={({\mathbf{Y}}_i^T,{\mathbf{W}}_i^T,{\mathbf{H}}_i^T)}^T$ as all the observed data from subject i, for i = 1,…, n.

The two component models in a joint model are the model for the primary response Y_i and the model for the longitudinal process W_i. Define f_Yi|XiHi(y_i|x_i, h_i; θ, ζ) as the density function associated with the first component model, where θ is the vector of primary regression parameters that relate Y_i to (X_i, H_i), ζ is a vector of nuisance parameters, and X_i is the p×1 vector of latent variables. Denote by $f_{{\mathbf{X}}_i\mid {\mathbf{H}}_i}^{(a)}({\mathit{x}}_i\mid {\mathit{h}}_i;{\mathit{\tau }}^{(a)})$ the assumed density of X_i conditional on H_i, where τ^(a)is a vector of model parameters. The second component model is derived from the linear mixed effects model,

$${\mathbf{W}}_i={\mathbf{D}}_i{\mathbf{X}}_i+{\mathbf{U}}_i,$$ (1)

where D_i is an m_i × p (m_i > p) design matrix of rank p, U_i = (U_i1,…, U_imi)^T is the vector of intra-subject errors distributed according to N_mi(0, σ²I_mi), and I_mi is the m_i × m_i identity matrix. The density of W_i given X_i, f_Wi|Xi(w_i|x_i; σ²), is thus N_mi(D_iX_i, σ²I_mi). It is assumed that Y_i and W_i are independent given X_i and H_i (Carroll et al., 2006, Section 2.5).

Let Ω = (θ^T, τ^(a)T, σ², ζ^T)^T be the d × 1 vector of all unknown parameters in the joint model. Inference on θ is of central interest. The MLE for Ω maximizes the observed data likelihood, to which the contribution from subject i is given by, for i = 1,…, n,

$$f_{{\mathbf{Y}}_i,{\mathbf{W}}_i\mid {\mathbf{H}}_i}({\mathit{y}}_i,{\mathit{w}}_i\mid {\mathit{h}}_i;\mathbf{\Omega })=\int f_{{\mathbf{Y}}_i\mid {\mathbf{X}}_i,{\mathbf{H}}_i}({\mathit{y}}_i\mid {\mathit{x}}_i,{\mathit{h}}_i;\mathit{\theta },\mathit{\zeta })f_{{\mathbf{W}}_i\mid {\mathbf{X}}_i}({\mathit{w}}_i\mid {\mathit{x}}_i;{\sigma }^2)f_{{\mathbf{X}}_i\mid {\mathbf{H}}_i}^{(a)}({\mathit{x}}_i\mid {\mathit{h}}_i;{\mathit{\tau }}^{(a)})d{\mathit{x}}_i.$$ (2)

For the SWAN data, the primary response is binary with Y_i = 1 indicating absence of osteopenia (bone mineral density above the 33rd percentile), and Y_i = 0 indicating presence, for i = 1,…, 632. Li et al. (2004) analyzed these data and assumed a logistic model for Y_i,

$$Pr(Y_i=1\mid {\mathbf{X}}_i,{\mathbf{H}}_i)={\{1+exp(-{\beta }_0-{\mathit{\beta }}_1^T{\mathbf{X}}_i-{\mathit{\beta }}_2^T{\mathbf{H}}_i)\}}^{-1},$$ (3)

where H_i includes covariates such as age and ethnicity indicator, and X_i = (X_1i, X_2i)^T is a bivariate latent variable. The observed longitudinal process W_i is the recorded natural log of PDG over one menstrual cycle, the length of which is standardized to a reference of 28 days. Li et al. posited a piecewise linear mixed effects model for W_i given by W_ij = X_1i+X_2i(t_ij−1.4)₊−2X_2j(t_ij−2.1)₊+U_ij, i = 1,…, 632, j = 1,…, m_i, where u₊ = uI(u > 0), I(·) is the indicator function, t_ij is in units of 10 days, and 6 ≤ m_i ≤ 14. Here, then, X_1i denotes the subject-specific natural log PDG up to day 14, and X_2i is the subject-specific “slope” of the symmetric rise (days 14–21) and fall (days 21–28) of natural log PDG over a standardized cycle. In this example, $\mathit{\theta }={({\beta }_0,{\mathit{\beta }}_1^T,{\mathit{\beta }}_2^T)}^T$, and there is no ζ in model (3).

For the ACTG 175 data, the response of interest is a time-to-event T_i, for i = 1,…, 2279. Define Y_i = (V_i, Δ_i)^T, where V_i = min(T_i, C_i), C_i is the censoring time, and Δ_i = I(T_i ≤ C_i). Song et al. (2002), who analyzed these data, assumed that censoring, intra-subject errors, and timing of measurements are noninformative, and specified the first component model as the proportional hazards model (PHM)

$$\begin{array}{ll}{\lambda }_i(u\mid {\mathbf{X}}_i,H_i)& =\underset{du\to 0}{lim}d{u}^{-1}Pr(u\le T_i<u+du\mid T_i\ge u,{\mathbf{X}}_i,H_i)\\ & ={\lambda }_0(u)exp\{\gamma (X_{1i}+X_{2i}u)+\eta H_i\},\end{array}$$ (4)

where λ₀(u) is an unspecified baseline hazard function, H_i is a treatment indicator, and X_i = (X_1i, X_2i)^T is a bivariate latent variable, with (X_1i + X_2iu) representing the true post-12-week log₁₀ CD4 count of subject i at time u. The observed post-12-week log₁₀ CD4 count is given by, for i = 1,…, 2279, j = 1,…, m_i,

$$W_{ij}=X_{1i}+X_{2i}{t}_{ij}+U_{ij}.$$ (5)

The density of Y_i given X_i and H_i is

$$\begin{array}{l}{f}_{{\mathbf{Y}}_i\mid {\mathbf{X}}_i,H_i}({\mathit{y}}_i\mid {\mathit{x}}_i,h_i;\mathit{\theta },{\lambda }_0)={[{\lambda }_0(V_i)exp\{\gamma (x_{1i}+x_{2i}{V}_i)+\eta h_i\}]}^{{\mathrm{\Delta }}_i}\\ exp\left[-{\int }_0^{V_i}{\lambda }_0(u)exp\{\gamma (x_{1i}+x_{2i}u)+\eta h_i\}du\right].\end{array}$$

In this example, θ = (γ, α)^T, and λ₀(u) can be viewed as the nuisance parameter ζ in the first component model.

Throughout the article we assume both component models in the joint models are correctly specified, and we focus on the assumed latent variable model, $f_{{\mathbf{X}}_i\mid {\mathbf{H}}_i}^{(a)}({\mathit{x}}_i\mid {\mathit{h}}_i;{\mathit{\tau }}^{(a)})$.

3. Expected Robustness

Consistency of the MLE is guaranteed when either σ² = 0 or the assumed random effect model is correct. Neither are likely to hold in practice, and thus the relevant issues are sensitivity of the MLE to the random effect model assumption and how to study the effects of model misspecification if they exist. Several authors (Song et al., 2002; Hsieh et al., 2006; and Rizopoulos et al., 2008) reported intriguing latent-model robustness under joint model setting. Hsieh et al. (2006) provided a heuristic explanation for this phenomenon. Rizopoulos et al. (2008) showed for survival models with finite dimensional parameter space that the score vector under the misspecified model is close to the correct score vector when m_i is large enough. In this section, we provide a new explanation for the robustness property of the MLE through the following result.

Theorem 1

Denote the ordinary least squares estimator for X_i by X̂_mi, i.e., ${\widehat{\mathbf{X}}}_{m_i}={({\mathbf{D}}_i^T{\mathbf{D}}_i)}^{-1}{\mathbf{D}}_i^T{\mathbf{W}}_i$. The ratio of the density in (2) and the following expression,

$$f_{{\mathbf{W}}_i\mid {\widehat{\mathbf{X}}}_{m_i}}({\mathit{w}}_i\mid {\widehat{\mathit{x}}}_{m_i};{\sigma }^2)f_{{\mathbf{Y}}_i\mid {\widehat{\mathbf{X}}}_{m_i},{\mathbf{H}}_i}({\mathit{y}}_i\mid {\widehat{\mathit{x}}}_{m_i},{\mathit{h}}_i;\mathit{\theta },\mathit{\zeta })f_{{\mathbf{X}}_i\mid {\mathbf{H}}_i}^{(a)}({\widehat{\mathit{x}}}_{m_i}\mid {\mathit{h}}_i;{\mathit{\tau }}^{(a)}),$$ (6)

approaches one as the longitudinal information increases without bound.

The proof is given in Web Appendix A. The intuition of this result is that, when the longitudinal data information is rich enough, X_i can be well estimated by X̂_mi so that it is as if X_i were observed like fixed effects instead of being latent quantities, and thus the dependence of likelihood inference on the assumed model for X_i weakens. Note in (6) that θ appears only in f_Yi|X̂mi,Hi (·). Consequently, the MLE derived from the likelihood based on (6) does not depend on $f_{{\mathbf{X}}_i\mid {\mathbf{H}}_i}^{(a)}(·)$ and thus neither will the MLE based on (2) as the longitudinal information increases. The key issue in practice is knowing when the longitudinal information is great enough for the MLE to achieve a desired degree of robustness. We next describe an improved remeasurement method for assessing robustness of the MLE in a particular data set.

4. Diagnostic methods

4.1 Remeasurement Method (SIMEX)

The remeasurement method in Huang et al. (2006) is derived from the SIMEX method developed by Cook and Stefanski (1994) and Stefanski and Cook (1995), also described in Carroll et al. (2006, Chapter 5). To motivate our improved remeasurement method, we first review the remeasurement method of Huang et al. (2006) in the joint model context.

The remeasurement method involves further contaminating W_i and reestimating Ω based on the contaminated-enhanced data. Specifically, for each prespecified positive constant λ:

• Step 1. For b = 1,…, B, generate the bth λ-remeasured data set, denoted by ${\{{\mathbf{Q}}_{b,i}(\lambda )\}}_{i=1}^n$, where ${\mathbf{Q}}_{b,i}(\lambda )={\{{\mathbf{Y}}_i^T,{\mathbf{W}}_{b,i}{(\lambda )}^T,{\mathbf{H}}_i^T\}}^T$, by taking

  $${\mathbf{W}}_{b,i}(\lambda )={\mathbf{W}}_i+\sqrt{\lambda }\sigma {\mathbf{Z}}_{b,i},$$ (7)

  where Z_b,i are independent m_i-dimensional standard normal random errors, for i = 1,…, n and b = 1,…, B.

• Step 2. Estimate the parameters based on ${\{{\mathbf{Q}}_{b,i}(\lambda )\}}_{i=1}^n$. Denote by θ̂_b(λ) the estimate for θ, and by Ω̂_b(λ) the entire estimated parameter vector, for b = 1,…, B.

• Step 3. Compute ${\widehat{\mathit{\theta }}}_B(\lambda )=B^{-1}{\sum }_{b=1}^B{\widehat{\mathit{\theta }}}_b(\lambda )$. Similarly define ${\widehat{\mathbf{\Omega }}}_B(\lambda )=B^{-1}{\sum }_{b=1}^B{\widehat{\mathbf{\Omega }}}_b(\lambda )$.

• Step 4. Plot θ̂_B(λ) versus λ ≥ 0, where θ̂_B(0) = θ̂(0) is the estimate based on ${\{{\mathbf{Q}}_i\}}_{i=1}^n$. This plot is referred to as SIMEX plot.

A SIMEX plot where θ̂_B(λ) remains relatively constant across λ indicates robustness.

The above procedure has two drawbacks. First, the remeasured W_b,i(λ) defined in (7) depends on the unknown σ. Second, Ω is estimated B times in step 2 in order to obtain Ω̂_B(λ), which is computationally burdensome. The improved remeasurement method we now propose overcomes both drawbacks.

First, to generate remeasured data free of parameters, we define

$${\mathbf{W}}_{b,i}(\lambda )={\mathbf{W}}_{1,bi}(\lambda )+{\mathbf{W}}_{2,i}(\lambda ),$$ (8)

where

$${\mathbf{W}}_{1,bi}(\lambda )={\mathbf{P}}_{{\mathbf{D}}_i}{\mathbf{W}}_i+\sqrt{\lambda }{\mathbf{D}}_i{({\mathbf{D}}_i^T{\mathbf{D}}_i)}^{-1/2}{\mathbf{T}}_{b,i}^T{\mathbf{W}}_i,$$ (9)

$${\mathbf{W}}_{2,i}(\lambda )=\sqrt{1+\lambda }({\mathbf{I}}_{m_i}-{\mathbf{P}}_{{\mathbf{D}}_i}){\mathbf{W}}_i,$$ (10)

${\mathbf{P}}_{{\mathbf{D}}_i}={\mathbf{D}}_i{({\mathbf{D}}_i^T{\mathbf{D}}_i)}^{-1}{\mathbf{D}}_i^T,{\mathbf{T}}_{b,i}=({\mathbf{I}}_{m_i}-{\mathbf{P}}_{{\mathbf{D}}_i}){\mathbf{Z}}_{b,i}{\{{\mathbf{Z}}_{b,i}^T({\mathbf{I}}_{m_i}-{\mathbf{P}}_{{\mathbf{D}}_i}){\mathbf{Z}}_{b,i}\}}^{-1/2}$, and the elements in the m_i × p matrix Z_b,i are independent standard normal random variables. It can be shown that ${\mathbf{Z}}_{b,i}^T({\mathbf{I}}_{m_i}-{\mathbf{P}}_{{\mathbf{D}}_i}){\mathbf{Z}}_{b,i}$ is positive definite almost surely when m_i ≥ 2p so that ${\{{\mathbf{Z}}_{b,i}^T({\mathbf{I}}_{m_i}-{\mathbf{P}}_{{\mathbf{D}}_i}){\mathbf{Z}}_{b,i}\}}^{-1/2}$ exists almost surely. The construction of the new W_b,i(λ) in (8) is in the spirit of the empirical SIMEX discussed in Section 5.3.1.3 in Carroll et al. (2006). As elaborated in Section 4.2, W_1,bi(λ) is a suboptimal, normally distributed, unbiased estimator for D_iX_i, and W_2,i(λ) is a normal unbiased estimator for zero, with the combined variance-covariance matrix of W_1,bi(λ) and W_2,i(λ) equal to (1 + λ)σ²I_mi, which coincides with the variance-covariance matrix of the old W_b,i(λ) defined in (7).

Second, to avoid repeated estimation of Ω using the remeasured data, we construct a new system of estimating equations at λ > 0. Assume that Ω̂(0) solves the vector estimating equation evaluated at the observed data given by

$$\sum _{i=1}^n\mathit{\psi }({\mathbf{Q}}_i;\mathbf{\Omega })=\mathbf{0},$$ (11)

for some d × 1 vector-valued function ψ(·; Ω). The functional form of ψ (·; Ω) depends on estimation procedure. We defer specification of ψ (·; Ω) until Section 5 where specific joint models and target estimators are considered in simulation. Based on the remeasured data, we solve the following vector estimating equation evaluated at all B sets of λ-remeasured data for an estimator of Ω,

$$\sum _{i=1}^n{\mathit{\psi }}^{(B)}\{{\mathbf{Q}}_i^{(B)}(\lambda );\mathbf{\Omega }\}=\mathbf{0},$$ (12)

where ${\mathbf{Q}}_i^{(B)}(\lambda )={\{{\mathbf{Q}}_{b,i}(\lambda )\}}_{b=1}^B$, and ${\mathit{\psi }}^{(B)}\{{\mathbf{Q}}_i^{(B)}(\lambda );\mathbf{\Omega }\}=B^{-1}{\sum }_{b=1}^B\mathit{\psi }\{{\mathbf{Q}}_{b,i}(\lambda );\mathbf{\Omega }\}$, for i = 1,…, n. Denote by Ω̃_B(λ) the solution to (12) and by θ̃_B(λ) the corresponding estimator for θ. Using Ω̃_B(λ) in place of Ω̂_B(λ) in the remeasurement method is appealing for two reasons. First, while Ω̃_B(λ) is obtained by solving only one vector estimating (12), Ω̂_B(λ) requires solving B vector estimating equations,

$$\sum _{i=1}^n\mathit{\psi }\{{\mathbf{Q}}_{b,i}(\lambda );\mathbf{\Omega }\}=\mathbf{0},b=1,\dots ,B.$$ (13)

Second, the summand in (12) is usually “smoother” than that in (13), thus solving (12) is often easier than solving (13). To be consistent in notation, we define Ω̃(0) as the estimator based on ${\{{\mathbf{Q}}_i\}}_{i=1}^n$, which is the same as Ω̂(0).

4.2 Equivalence Between Two Versions of the Remeasurement Method

The improved remeasurement method is more efficient computationally, and it still retains the key features necessary for diagnosing model misspecification. First, note that, for the old W_b,i(λ) defined in (7), one has W_b,i(λ)|X_i ~ N_mi {D_iX_i, (1 + λ)σ²I_mi}, just like W_i|X_i ~ N_mi {D_iX_i, σ²I_mi} except for the inflated variance, (1 + λ)σ². This feature is important because it implies that the density of Q_b,i(λ) is identical to that of Q_i except for the measurement error variance. Therefore, if the observed data density given in (2) is correct, then replacing σ² with (1 + λ)σ² in (2) gives the correct density of the λ-remeasured data. With the correct likelihood, consistent MLE for all sizes of λ is achieved, resulting in a constant SIMEX plot asymptotically. Conversely, a nonconstant SIMEX plot indicates model misspecification.

We show now that the new W_b,i(λ) defined in (8) has the same feature as that of the old W_b,i(λ). Because W_i|X_i ~ N_mi (D_iX_i, σ²I_mi), it is obvious by (10) that

$${\mathbf{W}}_{2,i}(\lambda )\mid {\mathbf{X}}_i\sim N_{m_i}\{\mathbf{0},(1+\lambda ){\sigma }^2({\mathbf{I}}_{m_i}-{\mathbf{P}}_{{\mathbf{D}}_i})\}.$$ (14)

To derive the distribution of W_1,bi(λ) given X_i, we first consider the distribution of W_1,bi(λ) given T_b,i. By (9), W_1,bi(λ)|T_b,i ~ N_mi[E {W_1,bi(λ)|T_b,i}, var {W_1,bi(λ)|T_b,i}], where, by noting that ${\mathbf{T}}_{b,i}^T{\mathbf{D}}_i=\mathbf{0}$,

$$E\{{\mathbf{W}}_{1,bi}(\lambda )\mid {\mathbf{T}}_{b,i}\}=({\mathbf{P}}_{{\mathbf{D}}_i}+\sqrt{\lambda }{\mathbf{D}}_i{\mathbf{L}}_i{\mathbf{T}}_{b,i}^T){\mathbf{D}}_i{\mathbf{X}}_i={\mathbf{D}}_i{\mathbf{X}}_i,$$

in which ${\mathbf{L}}_i={({\mathbf{D}}_i^T{\mathbf{D}}_i)}^{-1/2}$ such that ${\mathbf{L}}_i{\mathbf{L}}_i^T={({\mathbf{D}}_i^T{\mathbf{D}}_i)}^{-1}$. Then by realizing that ${\mathbf{T}}_{b,i}^T{\mathbf{P}}_{{\mathbf{D}}_i}=\mathbf{0}$, and ${\mathbf{T}}_{b,i}^T{\mathbf{T}}_{b,i}={\mathbf{I}}_p$, we have

$$var\{{\mathbf{W}}_{1,bi}(\lambda )\mid {\mathbf{T}}_{b,i}\}=({\mathbf{P}}_{{\mathbf{D}}_i}+\sqrt{\lambda }{\mathbf{D}}_i{\mathbf{L}}_i{\mathbf{T}}_{b,i}^T){\sigma }^2{\mathbf{I}}_{m_i}({\mathbf{P}}_{{\mathbf{D}}_i}+\sqrt{\lambda }{\mathbf{T}}_{b,i}{\mathbf{L}}_i^T{\mathbf{D}}_i^T)=(1+\lambda ){\sigma }^2{\mathbf{P}}_{D_i}.$$

That is, W_1,bi(λ)|T_b,i ~ N_mi {D_iX_i(1 + λ) σ²P_Di}, and thus

$${\mathbf{W}}_{1,bi}(\lambda )\mid {\mathbf{X}}_i\sim N_{m_i}\{{\mathbf{D}}_i{\mathbf{X}}_i,(1+\lambda ){\sigma }^2{\mathbf{P}}_{{\mathbf{D}}_i}\}.$$ (15)

Lastly, straightforward algebra reveals that, given X_i, cov {W_1,bi(λ), W_2,i(λ)} = 0. Combining (14) and (15), we have W_b,i(λ)|X_i ~ N_mi {D_iX_i, (1 + λ) σ²I_mi}, as desired. The new definition of W_b,i(λ) given in (8) is assumed in the sequel.

Second, we prove that Ω̂_B(λ) and Ω̃_B(λ) defined in Section 4.1 are asymptotically equivalent. Assume that the vector equation

$$E[\mathit{\psi }\{{\mathbf{Q}}_{b,i}(\lambda );\mathbf{\Omega }(\lambda )\}]=\mathbf{0}$$ (16)

uniquely defines Ω(λ), where the expectation is taken with respect to the true density of Ω_b,i(λ). Recall that Ω̂_b(λ) is the solution to (13), for b = 1,…, B. A first-order Taylor expansion of (13) around Ω(λ) and rearrangement of terms gives

$$n^{1/2}\left\{{\widehat{\mathbf{\Omega }}}_b(\lambda )-\mathbf{\Omega }(\lambda )\right\}=n^{-1/2}{\mathbf{A}}_1^{-1}\{\mathbf{\Omega }(\lambda )\}\sum _{i=1}^n\mathit{\psi }\{{\mathbf{Q}}_{b,i}(\lambda );\mathbf{\Omega }(\lambda )\}+{\mathit{o}}_p(1),$$ (17)

for b = 1,…, B, where A₁ {Ω(λ)} is equal to E[− ∂ψ{Q_b,i(λ); Ω}/∂Ω^T] evaluated at Ω(λ), and the expectation is taken with respect to the true density of Q_b,i(λ). Averaging (17) over b = 1,…, B for any finite B gives

$$\begin{array}{ll}{n}^{1/2}\left\{{\widehat{\mathbf{\Omega }}}_B(\lambda )-\mathbf{\Omega }(\lambda )\right\}& =n^{-1/2}{\mathbf{A}}_1^{-1}\{\mathbf{\Omega }(\lambda )\}\sum _{i=1}^n{B}^{-1}\sum _{b=1}^B\mathit{\psi }\{{\mathbf{Q}}_{b,i}(\lambda );\mathbf{\Omega }(\lambda )\}+{\mathit{o}}_p(1)\\ & =n^{-1/2}{\mathbf{A}}_1^{-1}\{\mathbf{\Omega }(\lambda )\}\sum _{i=1}^n{\mathit{\psi }}^{(B)}\{{\mathbf{Q}}_i^{(B)}(\lambda );\mathbf{\Omega }(\lambda )\}+{\mathit{o}}_p(1).\end{array}$$ (18)

Next consider the vector equation that uniquely defines Ω^*(λ),

$$E[\mathit{\psi }\{{\mathbf{Q}}_i^{(B)}(\lambda );{\mathbf{\Omega }}^{\ast }(\lambda )\}]=\mathbf{0},$$ (19)

where the expectation is taken with respect to the true density of ${\mathbf{Q}}_i^{(B)}(\lambda )$. Because

$$E[\mathit{\psi }\{{\mathbf{Q}}_i^{(B)}(\lambda );\mathbf{\Omega }\}]=B^{-1}\sum _{b=1}^{B}E[\mathit{\psi }\{{\mathbf{Q}}_{b,i}(\lambda );\mathbf{\Omega }\}]=E[\mathit{\psi }\{{\mathbf{Q}}_{b,i}(\lambda );\mathbf{\Omega }\}],$$

for any b and i, the solution to (16), Ω(λ), also solves (19). By the uniqueness of the solution to (19), Ω^*(λ) = Ω(λ). A first-order Taylor expansion of (12) around Ω^*(λ)(= Ω(λ)) gives

$$n^{1/2}\left\{{\stackrel{\sim }{\mathbf{\Omega }}}_B(\lambda )-\mathbf{\Omega }(\lambda )\right\}=n^{-1/2}{\mathbf{A}}_2^{-1}\{\mathbf{\Omega }(\lambda )\}\sum _{i=1}^n{\mathit{\psi }}^{(B)}\{{\mathbf{Q}}_i^{(B)}(\lambda );\mathbf{\Omega }(\lambda )\}+{\mathit{o}}_p(1),$$ (20)

where

$$\begin{array}{ll}{\mathbf{A}}_2\{\mathbf{\Omega }(\lambda )\}& ={E[-\partial {\mathit{\psi }}^{(B)}\{{\mathbf{Q}}_i^{(B)}(\lambda );\mathbf{\Omega }\}/\partial {\mathbf{\Omega }}^T]\mid }_{\mathbf{\Omega }=\mathbf{\Omega }(\lambda )}\\ & =B^{-1}\sum _{b=1}^B{E[-\partial \mathit{\psi }\{{\mathbf{Q}}_{b,i}(\lambda );\mathbf{\Omega }\}/\partial {\mathbf{\Omega }}^T]\mid }_{\mathbf{\Omega }={\mathbf{\Omega }}_{(\lambda )}}\\ & ={\mathbf{A}}_1\{\mathbf{\Omega }(\lambda )\}.\end{array}$$

Finally, subtracting (20) from (18) reveals that $n^{1/2}\{{\widehat{\mathbf{\Omega }}}_B(\lambda )-{\stackrel{\sim }{\mathbf{\Omega }}}_B(\lambda )\}\stackrel{p}{\to }\mathbf{0}\text{as}n\to \infty$.

4.3 Test of robustness

The SIMEX plot is a convenient graphical tool to visually assess latent-model robustness. However, due to the variation in the estimators, (non)robustness is not always evident from the SIMEX plot. We now define two test statistics to objectively assess robustness.

For a vector (or a square matrix) Π, denote by [Π]_(k) the kth element (or diagonal element) of Π. Analogous to the test statistic proposed in Huang et al. (2006), we define a test statistic to assess latent-model robustness based on the improved remeasurement method as

$$t_1^{\ast }(\lambda )=n^{1/2}{\left\{{\stackrel{\sim }{\mathbf{\Omega }}}_B(\lambda )-\stackrel{\sim }{\mathbf{\Omega }}(0)\right\}}_{(k)}/\sqrt{{[{\widehat{\mathit{\nu }}}_1]}_{(k)}},$$

for 1 ≤ k ≤ d, where ν̂₁ is an estimator for the variance-covariance matrix of n^1/2{Ω̃_B(λ) − Ω̃(0)}. A second test statistic we propose is defined by

$$t_2^{\ast }(\lambda )=n^{-1/2}{\left[\sum _{i=1}^n{\mathit{\psi }}^{(B)}\left\{{\mathbf{Q}}_i^{(B)}(\lambda );{\stackrel{\sim }{\mathbf{\Omega }}}_{-{\sigma }^2}(0),(1+\lambda ){\stackrel{\sim }{\sigma }}^2(0)\right\}\right]}_{(k)}/\sqrt{{[{\widehat{\mathit{\nu }}}_2]}_{(k)}},$$

where Ω̃_−σ²(0) is Ω̃(0) excluding σ², and ν̂₂ is an estimator for the variance-covariance matrix of $n^{-1/2}{\sum }_{i=1}^n{\mathit{\psi }}^{(B)}\{{\mathbf{Q}}_i^{(B)}(\lambda );{\stackrel{\sim }{\mathbf{\Omega }}}_{-{\sigma }^2}(0),(1+\lambda ){\stackrel{\sim }{\sigma }}^2(0)\}$. Note that, unlike $t_1^{\ast }(\lambda )$, computing $t_2^{\ast }(\lambda )$ does not require estimating Ω at λ > 0.

Define by Ω_−σ² the parameter vector Ω excluding σ². Both test statistics are motivated by the fact that, if the estimators for Ω_−σ² are robust, then Ω_−σ² (λ) = Ω_−σ² (0) for λ> 0, and both test statistics should center at zero. The derivations for ν̂₁ and ν̂₂ are given in Web Appendix B. We also show in Web Appendix C that $t_1^{\ast }(\lambda )$ and $t_2^{\ast }(\lambda )$ are asymptotically equivalent for assessing robustness.

5. Simulation studies

5.1 Joint models with simple endpoint

We first demonstrate the proposed diagnostic methods applied to joint models with simple endpoint. A data set of size n = 500 is generated from a joint model with a binary response. The first component model is a logistic model, Pr(Y_i = 1|X_i) = {1 + exp(−β₀ − β₁X_i)}⁻¹, where X_i = (X_1i, X_2i)^T, and β₁ = (β₁₁, β₁₂)^T. The true values of the primary regression parameters $\mathit{\theta }={({\beta }_0,{\mathit{\beta }}_i^T)}^T$ are (−2, 1, 1)^T. The latent variable X_i is generated from a location mixture bivariate normal (BVN), (1 − p)N₂(δ, I₂) + pN₂(0, I₂), where p = 0.4 and δ = (5, 0)^T. The longitudinal measures W_i are generated according to (1), with m_i = 5, t_ij = j for j = 1, …, 5, D_i 5 × 2 with jth row equal to (1, j), and U_i ~ N₅(0, 0.6I₅), for i = 1, …, 500.

We consider four estimators for θ. One is the CSE derived in Li et al. (2004). The other three are the MLEs when the assumed models for X are a two-component location mixture BVN; a non-mixture BVN; and a model specified by the bivariate second-order SNP density (Zhang and Davidian, 2001) given by $f_{\mathbf{X}}^{(a)}(\mathit{x};{\mathit{\tau }}^{(a)})=P_2^2\{{\mathbf{R}}^{-1}({\mathit{x}}_i-\mathit{\mu })\}\phi \{{\mathbf{R}}^{-1}({\mathit{x}}_i-\mathit{\mu })\}\mid \mathbf{R}{\mid }^{-1}$, where $P_2(\mathit{z})=a_{00}+a_{10}{z}_1+a_{01}{z}_2+a_{20}{z}_1^2+a_{11}{z}_1{z}_2+a_{02}{z}_2^2$ for z = (z₁, z₂)^T, and the polynomial coefficients in P₂(z) are constrained so that $f_{\mathbf{X}}^{(a)}(\mathit{x};{\mathit{\tau }}^{(a)})$ integrates to one. Among the four estimators, the CSE is robust by construction (Li et al., 2004), as is the MLE based on a mixture BVN, the correct model for X. The other two MLEs are suspect, as the assumed random effect models are incorrect. We use the proposed diagnostic devices to evaluate the robustness of the estimators. The function ψ (·;Ω) in (11) associated with the CSE is the conditional score defined in Li et al. (2004); and ψ(·;Ω) associated with the MLE is given by

$$\mathit{\psi }(Y_i,{\mathbf{W}}_i;\mathbf{\Omega })=\left(\begin{array}{c}\frac{1}{m_i-2}{\mathbf{W}}_i^T\{{\mathbf{I}}_{m_i}-{\mathbf{D}}_i{({\mathbf{D}}_i^T{\mathbf{D}}_i)}^{-1}{\mathbf{D}}_i^T\}{\mathbf{W}}_i-{\sigma }^2\\ \frac{\partial log{f}_{{\mathbf{W}}_i}({\mathit{w}}_i;{\mathit{\tau }}^{(a)},{\sigma }^2)}{\partial {\mathit{\tau }}^{(a)}}\\ \frac{\partial log{f}_{Y_i,{\mathbf{W}}_i}(y_i,{\mathit{w}}_i;\mathit{\theta },{\mathit{\tau }}^{(a)},{\sigma }^2)}{\partial \mathit{\theta }}\end{array}\right),$$

where f_Wi(w_i; τ^(a), σ²) is the marginal density of W_i.

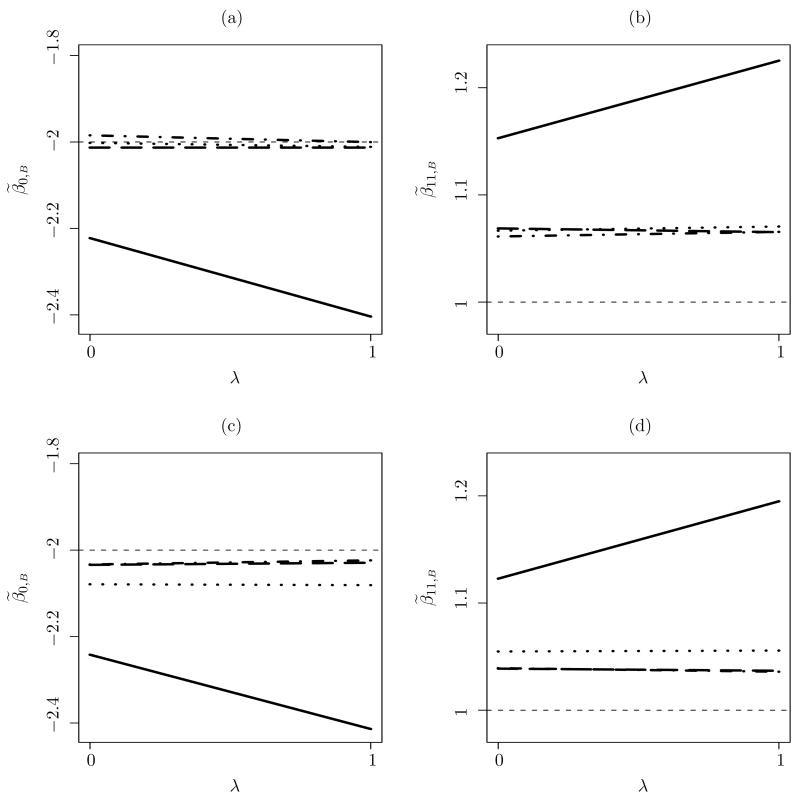
We first implement the improved remeasurement method on one simulated data set with B = 50 and λ ∈ [0, 1] to construct SIMEX plots. Denote the four estimators as ${\stackrel{\sim }{\mathit{\theta }}}_B^{(c)}(\lambda ),{\stackrel{\sim }{\mathit{\theta }}}_B^{(m)}(\lambda ),{\stackrel{\sim }{\mathit{\theta }}}_B^{(n)}(\lambda )$, and ${\stackrel{\sim }{\mathit{\theta }}}_B^{(s)}(\lambda )$, where the superscript identifies the estimator: c, CSE; m, mixture BVN; n, BVN; s, SNP. Figure 1a and b contain the SIMEX plots of the first two elements in θ for each of the four estimates. As expected, ${\stackrel{\sim }{\mathit{\theta }}}_B^{(c)}(\lambda )$ and ${\stackrel{\sim }{\mathit{\theta }}}_B^{(m)}(\lambda )$ appear to be robust as reflected by the nearly constant SIMEX plots. The estimate resulting from the flexible SNP modeling ${\stackrel{\sim }{\mathit{\theta }}}_B^{(s)}(\lambda )$ also has a relatively flat SIMEX plot. However, the SIMEX plot of ${\stackrel{\sim }{\mathit{\theta }}}_B^{(n)}(\lambda )$, which is based on the least flexible assumed model for X among all the considered models, is clearly distinguished from the other three. In order to observe the typical trend in SIMEX plots, we repeat this experiment 30 times and construct the average SIMEX plots. These appear in Figure 1c and d. Note the similarity with Figure 1a and b.

Figure 1.

Plots (a) and (b) are SIMEX plots for the MLEs of the first two elements in each of ${\stackrel{\sim }{\mathit{\theta }}}_B^{(c)}(\lambda ),{\stackrel{\sim }{\mathit{\theta }}}_B^{(m)}(\lambda ),{\stackrel{\sim }{\mathit{\theta }}}_B^{(n)}(\lambda )$, and ${\stackrel{\sim }{\mathit{\theta }}}_B^{(s)}(\lambda )$, computed from one simulated data set. Plots (c) and (d) are the average SIMEX plots from 30 Monte Carlo replicates. The line types are, ${\stackrel{\sim }{\mathit{\theta }}}_B^{(c)}(\lambda )$: long dashed; ${\stackrel{\sim }{\mathit{\theta }}}_B^{(m)}(\lambda )$: dash-dotted; ${\stackrel{\sim }{\mathit{\theta }}}_B^{(n)}(\lambda )$: solid; and ${\stackrel{\sim }{\mathit{\theta }}}_B^{(s)}(\lambda )$: dotted. The short dashed lines are the reference lines at the true values, β₀ = −2 and β₁₁ = 1. The ranges of the vertical axes in (a) and (b) are set to be one estimated standard deviation of θ̃⁽ⁿ⁾ (0) below and above the average of the four types of estimates at λ = 0.

To assess the robustness objectively, we present $t_1^{\ast }(1)$ and $t_2^{\ast }(1)$ in Table 1 for the four types of estimators depicted in Figure 1a and b. In Table 1, the pattern of p-values is consistent with the visual impressions of Figure 1a and b. The operating characteristics of $t_1^{\ast }(\lambda )$ based on the improved remeasurement method are similar to those based on the original remeasurement method of Huang et al. (2006). To examine the operating characteristics of $t_2^{\ast }(\lambda )$, we compute $t_2^{\ast }(1)$ associated with ${\stackrel{\sim }{\mathit{\theta }}}_B^{(c)}(\lambda ),{\stackrel{\sim }{\mathit{\theta }}}_B^{(m)}(\lambda )$, and ${\stackrel{\sim }{\mathit{\theta }}}_B^{(n)}(\lambda )$, respectively, for 500 replicate data sets generated from the same joint model as above. The percentages of | $t_2^{\ast }(1)$| values exceeding t_0.975(n − d) are presented in Table 2. The results of $t_2^{\ast }(1)$ for ${\stackrel{\sim }{\mathit{\theta }}}_B^{(c)}(\lambda )$ and ${\stackrel{\sim }{\mathit{\theta }}}_B^{(m)}(\lambda )$ indicate reasonable size of $t_2^{\ast }(1)$. The results of $t_2^{\ast }(1)$ associated with ${\stackrel{\sim }{\beta }}_{11,B}^{(n)}$ and ${\stackrel{\sim }{\beta }}_{12,B}^{(n)}$ suggest promising power. In combination, these results suggest that $t_2^{\ast }(\lambda )$ provides power for detecting the effects of latent model misspecification, while maintaining reasonable size.

Table 1.

Statistics $t_1^{\ast }(1)$ and $t_2^{\ast }(1)$ associated with ${\stackrel{\sim }{\mathit{\theta }}}_B^{(c)},{\stackrel{\sim }{\mathit{\theta }}}_B^{(m)},{\stackrel{\sim }{\mathit{\theta }}}_B^{(n)}$, and ${\stackrel{\sim }{\mathit{\theta }}}_B^{(s)}$ as depicted in Figure 1a and b from the simulation in Section 5.1. The numbers in parentheses are the p-values associated with the statistics.

Statistic	Parameter	CSE	Mixture BVN-MLE	BVN-MLE	SNP-MLE
$t_1^{\ast }(1)$	β0,B	0.001 (0.999)	0.80 (0.42)	3.53 (< 0.001)	0.43 (0.67)
	β11,B	0.46 (0.64)	−0.51 (0.61)	−3.37 (< 0.001)	−0.42 (0.67)
	β12,B	0.73 (0.47)	1.00 (0.32)	−0.26 (0.80)	1.83 (0.07)
$t_2^{\ast }(1)$	β0,B	−0.95 (0.34)	−0.53 (0.59)	−0.70 (0.48)	0.01 (0.99)
	β11,B	−0.59 (0.56)	0.54 (0.59)	3.24 (0.001)	0.11 (0.91)
	β12,B	−0.33 (0.74)	−1.47 (0.14)	−2.74 (0.006)	−0.21 (0.83)

Table 2.

Percentage of $t_2^{\ast }(1)$ that exceed t_0.975(n − d) in absolute value among the 500 replicate data sets from the simulation in Section 5.1.

Parameter	CSE	Mixture BVN-MLE	BVN-MLE
β0	0.06	0.04	0.06
β11	0.05	0.04	0.95
β12	0.03	0.05	0.56

5.2 Joint models with time-to-event endpoint

We now study the diagnostic methods on a joint model with possibly censored time-to-event endpoint. Each simulated data set has n = 500 subjects. The time-to-event is generated according to a PHM given by λ_i(u|X_i) = λ₀(u) exp{γ(X_1i + X_2iu)}, with γ = −1 and λ₀(u) = I(u ≥ 16). The bivariate latent variable X_i = (X_1i, X_2i)^T is generated from a truncated BVN obtained by first generating X_i from a BVN with E(X_i) = (4.173, −0.0103)^T, and {var(X_1i), cov(X_1i, X_2i), var(X_1i)} = (4.96, −0.0456, 0.012), then discarding the realizations with negative γX_2i. This causes around 46% truncation of the original BVN. The censoring distribution is exponential with mean 110, resulting in a censoring rate of around 25%. The longitudinal measures W_ij are generated according to (5) at times t_ij = (0, 2, 4, 8, 16, 24, 32, 40, 48, 56, 64, 72, 80), with a 10% missingness rate at times u ≥ 16. On average there are around six repeated measures for each subject under this configuration. The intra-subject error variance is σ² = 0.15.

Using the superscript convention introduced in Section 5.1, we consider three MLEs in this simulation, ${\stackrel{\sim }{\gamma }}_B^{(m)},{\stackrel{\sim }{\gamma }}_B^{(n)}$, and ${\stackrel{\sim }{\gamma }}_B^{(s)}$, where the assumed SNP model is of first order; and the MLEs are obtained via the EM algorithm as described in Wulfsohn and Tsiatis (1997) and Song et al. (2002). The function ψ(·; Ω) in (11) is the likelihood score in this case. Because it is often very time-consuming to estimate the parameters in the setting of joint models with time-to-event endpoint, we only compute $t_2^{\ast }(\lambda )$ to assess robustness. For a data set generated from the current joint model, the values of $t_2^{\ast }(1)$, with the associated p-values in the following parentheses, are found to be: ${\stackrel{\sim }{\gamma }}_B^{(m)}$, −1.56 (0.12); ${\stackrel{\sim }{\gamma }}_B^{(n)}$, −1.81 (0.07); and ${\stackrel{\sim }{\gamma }}_B^{(s)}$, −1.15 (0.25). As in the previous simulation, ${\stackrel{\sim }{\gamma }}_B^{(n)}$ exhibits the greatest evidence of non-robustness, although falling short of 0.05 level of significance. These results agree with the observations in Song et al. (2002) and Hsieh et al. (2006) under similar simulation settings. This is an example where the longitudinal information is great enough to yield the MLEs relatively insensitive to random effect model assumptions. Among 100 Monte Carlo (MC) replicates, the proportions of data sets that yield significant $t_2^{\ast }(1)$ are, 0.08, 0.12, and 0.06 for ${\stackrel{\sim }{\gamma }}_B^{(m)},{\stackrel{\sim }{\gamma }}_B^{(n)}$, and ${\stackrel{\sim }{\gamma }}_B^{(s)}$, respectively, which suggests some gain in robustness from flexible modeling on X when the true model deviates from normal.

One complication arises when computing the proposed test statistics for joint models with time-to-event endpoint due to the dimensionality of Ω. Strictly speaking, the nuisance parameter ζ in the first component model is the baseline hazard function, λ₀(u), which is infinite dimensional. Because the observed data likelihood is maximized when λ₀(u) = 0 at non-event time u (Song et al., 2002), we define ζ= {λ₀(u₁), …, λ ₀(u_L)}^T, where (u₁,…, u_L) is the set of observed times-to-event, and L is the number of distinct times-to-event in the data set. This treatment of ζ yields a finite yet large dimension of Ω, since L is usually large. As shown in Web Appendix B, computing $t_1^{\ast }(\lambda )$ and $t_2^{\ast }(\lambda )$ involves the d × 1 score vector and d × d Hessian matrix. It is formidable to implement the computation when d is large. Our current solution to this computational obstacle is to drop ζ from the parameter space when computing the score or Hessian. The tradeoff is that the variance estimators, ν̂₁ and ν̂₂, may be biased downward. The extent of underestimation depends on model configuration. For instance, in the foregoing simulation with 100 MC replicates, the ratio of the average of $\sqrt{{\widehat{\nu }}_2}$ over the empirical standard deviation of the numerator of $t_2^{\ast }(1)$ are 0.94, 0.97, and 1.00 associated with ${\stackrel{\sim }{\gamma }}_B^{(m)},{\stackrel{\sim }{\gamma }}_B^{(n)}$, and ${\stackrel{\sim }{\gamma }}_B^{(s)}$, respectively, with standard error (estimated via the jackknife method) around 0.07 for each ratio. To compare with the variance estimators when there is no such complication, we summarize in Table 3 the ratio of the mean of $\sqrt{{\widehat{\nu }}_l}$ averaging across 100 MC replicates over the empirical standard deviation of the numerator of $t_l^{\ast }(1)$ from the simulation in Section 5.1, for l = 1, 2. The results in Table 3 indicate that ν̂₁ and ν̂₂ are reasonably reliable variance estimator in the setting of joint models with simple endpoint.

Table 3.

Ratio of the average of $\sqrt{{\widehat{\nu }}_l}$ over the empirical standard deviation of the numerator of $t_l^{\ast }(1)$ from 100 MC replicates, for l = 1, 2, associated with ${\stackrel{\sim }{\mathit{\theta }}}_B^{(c)},{\stackrel{\sim }{\mathit{\theta }}}_B^{(m)}$, and ${\stackrel{\sim }{\mathit{\theta }}}_B^{(n)}$ from the simulation in Section 5.1. The numbers in parentheses are the jackknife estimates for the standard errors of the ratios.

Statistic	Parameter	CSE	Mixture BVN-MLE	BVN-MLE
$\sqrt{{\widehat{\nu }}_1}$	β0	1.00 (0.07)	1.02 (0.08)	1.00 (0.09)
	β11	0.99 (0.07)	1.04 (0.07)	1.00 (0.09)
	β12	0.98 (0.06)	1.00 (0.07)	1.00 (0.07)
$\sqrt{{\widehat{\nu }}_2}$	β0	1.07 (0.07)	1.03 (0.06)	0.99 (0.06)
	β11	1.02 (0.07)	1.05 (0.07)	1.01 (0.06)
	β12	1.07 (0.08)	1.04 (0.07)	1.01 (0.07)

Due to the complication in variance estimators in joint models with time-to-event end-point, even though an insignificant value of $t_1^{\ast }(\lambda )$ or $t_2^{\ast }(\lambda )$ still indicates lack of evidence for nonrobustness, one should be cautious when interpreting significant values of the test statistics. In that case, one needs to explore further whether or not the significant results are caused by overoptimistic variance estimators. For instance, one can use the bootstrap procedure to obtain a more reliable variance estimator, as outlined in Hsieh et al. (2006).

6. Application to SWAN and ACTG 175

6.1 SWAN

We now apply the diagnostic methods to the SWAN data. For simplicity, we exclude the observable covariates H_i from the first component model for the simple endpoint in (3) and posit the logistic model given by Pr(Y_i = 1|X_i) = {1 + exp(−β₀ − β₁X_i)}⁻¹. Three estimators for the primary regression parameter $\mathit{\theta }={({\beta }_0,{\mathit{\beta }}_1^T)}^T$ are considered, including the CSE, the MLE when assuming X_i follows a two-component location mixture BVN, and the MLE resulting from a BVN assumed model for X_i. We compute $t_1^{\ast }(1)$ and $t_2^{\ast }(1)$ with B = 100 to assess the robustness of these three estimators. The resulting test statistics are presented in Table 4. The SIMEX plots for these three sets of estimates are given in Web Appendix D.

Table 4.

Statistics $t_1^{\ast }(1)$ and $t_2^{\ast }(1)$ associated with ${\stackrel{\sim }{\mathit{\theta }}}_B^{(c)},{\stackrel{\sim }{\mathit{\theta }}}_B^{(m)}$, and ${\stackrel{\sim }{\mathit{\theta }}}_B^{(n)}$ for the SWAN data. The numbers in parentheses are the p-values associated with the statistics.

Statistic	Parameter	CSE	Mixture BVN-MLE	BVN-MLE
$t_1^{\ast }(1)$	β0	−0.18 (0.86)	−0.70 (0.48)	0.64 (0.52)
	β11	−0.12 (0.90)	−0.67 (0.50)	0.57 (0.57)
	β12	0.17 (0.87)	0.68 (0.50)	−0.82 (0.41)
$t_2^{\ast }(1)$	β0	0.42 (0.67)	0.87 (0.38)	1.64 (0.10)
	β11	0.03 (0.98)	0.49 (0.62)	−0.83 (0.41)
	β12	−0.02 (0.98)	−0.35 (0.73)	1.63 (0.10)

The statistics $t_1^{\ast }(1)$ indicate little evidence of nonrobustness for any of the three estimators for θ, which is also reflected by the SIMEX plots in Web Appendix D. The statistics $t_2^{\ast }(1)$ do not suggest strong evidence of nonrobustness either, but the values of $t_2^{\ast }(1)$ associated with ${\stackrel{\sim }{\beta }}_{0,B}^{(n)}$ and ${\stackrel{\sim }{\beta }}_{12,B}^{(n)}$ are much closer to being significant than those for the counterpart estimates in ${\stackrel{\sim }{\mathit{\theta }}}_B^{(c)}$ and ${\stackrel{\sim }{\mathit{\theta }}}_B^{(m)}$. Li et al. (2004) found that the estimated density for X_i “does not deviate considerably from multivariate normality.” Their finding may explain why our diagnostic tools do not find strong evidence that ${\stackrel{\sim }{\mathit{\theta }}}_B^{(n)}$ is not robust.

6.2 ACTG 175

We now consider the ACTG 175 data with 2279 subjects and 350 events. This clinical trial found zidovudine alone to be an inferior treatment compared to the other three therapies, zidovudine plus didanosine, zidovudine plus zalcitabine, and didanosine alone. We assume the PHM in (4) where H_i = I(treatment ≠ zidovudine for subject i). There is an average of 8.28 CD4 measurements per subject in this data set.

We compute $t_2^{\ast }(1)$ with B = 30 associated with three MLEs for θ = (γ,α)^T, with assumed models for X_i as a two-component location mixture BVN, BVN, and the first-order SNP, respectively. The resulting statistics $t_2^{\ast }(1)$ are, for γ: γ̃^(m), 1.37 (0.17); γ̃⁽ⁿ⁾, 1.73 (0.08); and γ̃^(s), 1.77 (0.08); for α: α̃^(m), 0.98 (0.32); α̃⁽ⁿ⁾, 1.32 (0.19); and α̃^(s) 0.42 (0.67). Therefore, there is not suficient evidence to imply nonrobustness of the MLEs for θ under any of the three assumed random effect models. This reconciles with the findings in Song et al. (2002).

7. Discussion

We have presented a graphical method and two test statistics for diagnosing latent-model robustness in joint models for a primary endpoint and a longitudinal process. The methods are designed to reveal sensitivity of the target estimator to model assumptions on the random effects in joint models. With these diagnostic tools, it is hopeful to find an appropriate and parsimonious random effect model to implement parametric inference as opposed to semipara-metric inference as in Li et al. (2004) and Song et al. (2002), which can be less eficient. Our diagnostic methods are closely related to the SIMEX method. Many authors (e.g., Li and Lin, 2003;Greene and Cai, 2007; He, Yi, and Xiong, 2007) used SIMEX for estimating regression parameters when covariates in survival models are measured with error, which is in line with the initial motivation of SIMEX developed in the framework of structural measurement error models. Our use of SIMEX is a new application of it as we do not use it for parameter estimation per se but mainly for assessing latent-model robustness.

As noted in Section 5.2, the variance estimators in the test statistics for joint models with time-to-event endpoint can be overly optimistic. More refined variance estimators for constructing the test statistics to assess latent-model robustness in these complicated joint models call for further investigation.

Supplementary Material

supplementary. Supplementary Materials.

Web Appendices referenced in Sections 3, 4.3, 5.2, and 6.1 are available under the Paper Information link at the Biometrics website http://www.biometrics.tibs.org.