Predicting the Thirty-year Risk of Cardiovascular Disease: The Framingham Heart Study

Abstract

Background

Present cardiovascular disease (CVD) risk prediction algorithms were developed for the 10-year or shorter period. Clustering of risk factors at younger ages and increasing life expectancy suggest the need for longer term risk prediction tools.

Methods and Results

We prospectively followed 4506 participants (2333 women) of the Framingham Offspring cohort aged 20–59 and free of CVD and cancer at baseline examination in 1971–1974 for the development of `hard' CVD (coronary death, myocardial infarction, stroke). We used modified Cox model that allows adjustment for competing risk of non-cardiovascular death to construct prediction algorithm for 30-year risk of hard CVD. Cross-validated survival c statistic and calibration chi-square were used to assess model performance. The 30-year hard CVD event rates adjusted for the competing risk of death were 7.6% for women and 18.3% for men. Standard risk factors (male sex, blood pressure and antihypertensive treatment, total and HDL cholesterol, smoking, diabetes) measured at baseline, were significantly related to the incidence of hard CVD and remained significant when regularly updated on follow-up. Body mass index was associated with 30-year risk of hard CVD only in models which did not update risk factors. Model performance was excellent as indicated by cross-validated discrimination c = 0.803 and calibration chi-square = 4.25 (p-value=0.894). In contrast, thirty-year risk predictions based on different applications of 10-year functions proved inadequate.

Conclusions

Standard risk factors remain strong predictors of hard CVD over extended follow-up. 30-year functions offer additional risk burden information that complements that of 10-year functions.

INTRODUCTION

Identification of risk factors contributing to the incidence of cardiovascular disease (CVD) is among one of the major accomplishments of the 20^th century epidemiology. Going a step further, researchers were able to construct multivariable risk prediction algorithms intended to aid clinicians in risk assessment. The importance of these algorithms was underscored by their incorporation into the Third Adult Treatment Panel's (ATP III) treatment recommendations¹. Multiple risk scores have been proposed in the literature in the last 20 years^2–13. These have all been developed for risk assessment in a 10-year or shorter horizon. Some experts articulated the need to know the longer term risk in order to better understand the public health burden and the true need for intervention¹⁴. As an answer to this need, several reports presented the lifetime or long-term risks of CVD, coronary heart disease (CHD), stroke and their risk factors^15–23. Some investigators attempted to calculate lifetime and long-term risks within specific risk factors' categories or their clusters^{15, 24, 25 26}. Their findings emphasized the importance of risk factors levels in early adulthood on the long-term risks of CVD as well as the substantial impact of CVD risk factors on all-cause mortality. They also suggested that 10-year functions may underestimate the true risk burden, particularly in younger individuals and women. These results underscore the need for long-term CVD risk prediction models applicable to younger adults that account for the competing cause of non-CVD mortality. The need for long-term CVD risk prediction models was recently articulated by Blumenthal et al.²⁷ and Sniderman and Furberg²⁸. However, to the best of our knowledge, no algorithm has been proposed to quantify 30-year risk of CVD as a direct function of risk factors (allowing risk assessment for any combination of risk factors). This can be partially explained by the difficulty of finding a cohort with a sufficiently long and rigorous follow-up and also by the methodological complexities associated with incorporating the competing risk of death due to other causes into the multivariable risk estimation.

In this report, we develop a tool for estimating 30-year risk of hard CVD events among individuals free of the condition at baseline. Our risk estimates allow for an adjustment for the competing risk of non-CVD death, and utilize the standard risk factors that can be collected during a physician office visit. The tool is based on the Framingham Offspring cohort that has contributed to the creation of several successful risk score algorithms^{2–5, 29} and offers 35 years of rigorous surveillance for CVD occurrence. Its performance is contrasted with methods based on long-term applications of 10-year risks.

METHODS

The Framingham Heart Study started in 1948 with the enrollment of the `original' cohort of 5209 individuals. In 1971, some 5,124 offspring of the original cohort and their spouses were enrolled into the Framingham Offspring Study ³⁰. Constant monitoring of CVD events and mortality has been carried out and was available through the end of 2007 for this investigation. Attendees of the first Offspring examination were eligible for this investigation if they were at least 20 and below 60 years of age (N=4828), free of CVD (N=4758) and cancer at baseline (N=4723), were not lost to follow-up (N=4680) and had complete risk factor profile yielding a final sample of 4506 individuals (2333 women, mean age 37). All participants gave written informed consent and the study protocol was approved by the Institutional Review Board of the Boston Medical Center.

A detailed physical examination, anthropometry, blood pressure determination, and phlebotomy for vascular risk factors were conducted at each Heart Study examination as described in D'Agostino et al.¹² Body mass index (BMI) was calculated as the weight in kilograms divided by the square of height in meters. Antihypertensive medication use was ascertained by the physician examiner at the Heart Study and based on self report. Serum total and high-density lipoprotein (HDL) cholesterol and triglycerides levels were determined using standardized enzymatic methods. Low-density lipoprotein (LDL) cholesterol was calculated using Friedwald's formula³¹. Cigarette smoking in the year preceding the examination was ascertained by self-report. Diabetes was defined as fasting glucose at or above 126 mg/dL or use of insulin or oral hypoglycemic medications.

Participants were followed for a maximum of 35 years (median 32 years). We focused on a `hard' CVD as the primary outcome of interest and defined it as a composite of hard CHD (coronary death, myocardial infarction) and stroke (fatal and non-fatal). Full CVD defined as in D'Agostino et al.¹² (hard CHD plus coronary insufficiency and angina pectoris, stroke plus transient ischemic attack, intermittent claudication and congestive heart failure) was used as a secondary outcome. Medical histories, physical examinations at the study clinic, hospitalization records and communication with personal physicians were all used to obtain information about CVD events on follow up.

Statistical Analysis

In our primary model we assessed the effect of risk factors measured at baseline on the long-term (30-year) risk of hard CVD using Cox regression³². In secondary model we used full CVD as outcome. Considering the extensive length of follow-up and the potential bias due to the competing risk of non-cardiovascular mortality in the prediction of long-term risk, we employed the model given by Andersen et al.^33–36 to adjust the risk estimates for the competing risk of non-CVD mortality. Standard Cox model, similarly to standard Kaplan-Meier estimator, may provide biased estimates of absolute long-term risk as it fails to treat those who die of non-cardiovascular causes as ineligible for development of CVD events³⁷. The competing risk model corrects this shortcoming calculating the cumulative incidence of CVD in the following manner:

$${\widehat{I}}_{CVD}\left(30\right)=\sum _{t_i<30}{\widehat{\lambda }}_{CVD}\left(t_i\right)\widehat{S}\left(t_{i-1}\right).$$

The quantities under summation denote the instantaneous hazard of CVD at event time t_i and survival rate from both CVD and non-cardiovascular death past event time t_i-1. Further statistical details including estimation techniques are presented in the online supplement's Technical Appendix. The assumption of linearity for all predictors was verified using cumulative sums of martingale residuals as described by Lin et al.³⁸. Given no significant interactions with sex, the final model was sex-pooled but adjusted for sex. Likewise, no effect modification by baseline age was detected. We also verified that the choice of time scale (time-on-study vs. age of onset^{39, 40}) did not impact the results. In addition to standard factors (systolic blood pressure (SBP) and antihypertensive treatment, total and HDL cholesterol, smoking and diabetes) used in CVD risk prediction (cf. D'Agostino et al.¹²), we considered diastolic blood pressure (DBP), triglycerides and LDL as a replacement for total cholesterol (cf. Wilson et al.³). Moreover, given recent reports underscoring the usefulness of BMI in cardiovascular risk prediction models we included it as a candidate risk factor (cf. ^{12 41 42}). Continuous variables were log-transformed to decrease the impact of extreme observations.

To assess model performance we used discrimination c statistic which takes into account the timing of events as proposed by Harrell et al.⁴³ and Pencina and D'Agostino⁴⁴ and Nam and D'Agostino's modification of the Hosmer-Lemeshow calibration chi-square⁴⁵ with survival estimates adjusted for the competing risk of non-cardiovascular death³⁷. Five-fold cross-validation⁴⁶ was used to account for the fact that we evaluated the model on the same data on which it was developed: this way we were able to utilize all data available while correcting for potential over-optimism in the assessment of model performance. Additionally, we performed internal validation by randomly splitting the sample 2:1 and developing the function on the first two thirds and evaluating its performance on the remaining third. Net reclassification improvement (NRI), as proposed by Pencina and D'Agostino⁴⁷, was used to assess clinical utility of additional variables and different ways of estimating 30-year risk (see below). ATP III-based¹ cut-off points determining categories of low, intermediate and high risk were adjusted proportionally to the increased duration of follow-up and incidence (from 6% and 20% to 12% and 40%).

An Excel risk score calculator was constructed to facilitate application by clinicians and is available as online supplement. All p-values reported were two-sided, and a conservative 0.01 level of significance was adopted to avoid inclusion of weak effects. SAS version 9.1 was used to perform all analyses⁴⁸.

Time-dependent analysis

Given the long-term follow-up and the fact that all risk factors were re-assessed regularly approximately every 4 years between 1970s and early 2000s, we performed additional analysis updating all variables as soon as the new values became available. This resulted in a Cox regression with time-dependent covariates which corresponds to a short-term risk assessment. The results were contrasted with those obtained for the 30-year model developed without updating.

Comparison with alternative approaches for 30-year risk prediction

The following approaches were considered:

1. Naïve. This method calculated the 30-year risk as a three times the 10-year risk from the model that did not account for the competing risks. It ignores aging as a key determinant of CVD risk so we know a priori that it cannot be correct. However, given its simplicity it might seem attractive, so we wanted to assess the amount of bias that it would introduce;

2. Combined. This approach utilized an application of 10-year CVD risk calculators. For fairness of comparison, we estimated 10-year probabilities of survival based on our data. Three probabilities were calculated for each person: the first using baseline age, second using baseline age plus 10 years and third using baseline age plus 20 years, with all other risk factors based on the baseline values. The 30-year risk was calculated as the difference of 1 minus the product of these three 10-year probabilities;

3. Unadjusted. Here we applied the standard Cox model to our data with full follow-up ignoring competing risk of death;

4. Adjusted. This is our main approach following the model described earlier above. The above four methods were applied to individuals with different combinations of risk factors for hard CVD events.

The authors had full access to the data and take responsibility for its integrity. All authors have read and agree to the manuscript as written.

RESULTS

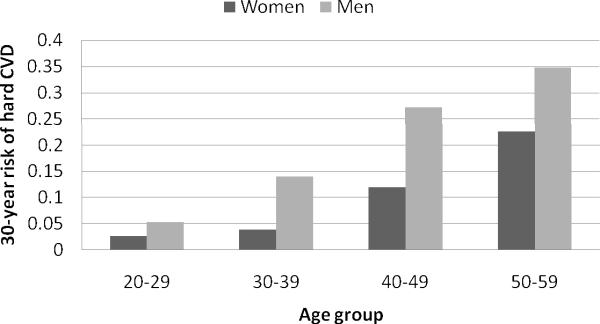
The sex-specific risk factor profile of our sample at baseline as well as number and type of hard CVD events are given in Table 1. In our baseline cohort at least 20 but below 60 years of age, men had numerically higher levels of all risk factors except HDL cholesterol. The three younger age decades (20–29, 30–39, 40–49) had similar representation between sexes with the fewest people in the oldest age group (50–59). Over a maximum of 35 years of follow-up, 671 participants (219 women) experienced a first hard CVD event and 622 (267 women) died of non-CVD causes. Of note, strokes constituted almost 40% of events experienced by women but less than 25% of events experienced by men. The 30-year Kaplan-Meier rate of hard CVD adjusted for the competing risk of non-CVD death (using the adjustment of Gaynor et al. ³⁷) was 7.6% for women and 18.3% for men. These are lower than the long-term and lifetime risks reported previously from the Framingham data²³. This can be explained by substantially younger ages of our cohort and different definition of the endpoint of interest (only `hard' events considered in our analysis). Event rates by sex and age decade are presented in Figure 1.

Table 1.

Baseline Characteristics^* and Incident Events

Clinical Features	Women (n=2333)	Men (n=2173)
Age, years	36.3±9.3	37.3±9.2
Age group, %
20–29 years	28.0	23.9
30–39 years	33.9	34.9
40–49 years	28.9	29.7
50–59 years	9.2	11.5
Systolic BP, mm Hg	118±16	126±15
Diastolic BP, mm Hg	76±10	82±11
Antihypertensive Treatment, %	2.7	3.1
Total Cholesterol, mg/dL	192±38	202±39
HDL Cholesterol, mg/dL	57±15	44±12
LDL Cholesterol, mg/dL	120±35	135±35
Triglycerides, mg/dL	77±73	115±97
Body Mass Index, kg/m2	23.9±4.5	26.5±3.6
Smoking, %	45.0	46.2
Diabetes, %	0.9	2.6
Incident Events (n)
Cardiovascular death	22	67
Myocardial infarction	111	281
Fatal and nonfatal stroke	86	104

^*Values are means ± standard deviations for continuous variables or percents for categorical variables.

Figure 1.

Average 30-year risk of hard CVD and corresponding Kaplan-Meier rates; both adjusted for the competing risk of non-cardiovascular death

Standard CVD risk factors (male sex, age, SBP, antihypertensive treatment, total and HDL cholesterol, smoking and diabetes) were highly significant (0.01 level) in the multivariable model. DBP and triglycerides were not statistically significant and inclusion of LDL in place of total cholesterol did not improve model performance. BMI was weakly significant in the final model (p-value = 0.04); it did not increase the c statistic and had a non-significant NRI of less than 1%. Hence we decided not to include it in the main risk prediction model. However, following the example of D'Agostino et al.¹² we constructed a simplified office-based risk model in which BMI replaced the lipids. It was highly significant in the simple model along with all other risk factors (p-value ≤ 0.01). Hazard ratios with confidence intervals for both models are presented in Table 2. Corresponding results for the secondary endpoint of full CVD are given in the online supplement table.

Table 2.

Hazard ratios^* with 95% confidence intervals for 30-year risk of hard CVD

Variables	Main Model	Simple Model
Male Sex	1.73 (1.45, 2.07)	2.08 (1.77, 2.46)
Age	2.09 (1.88, 2.31)	2.22 (2.01, 2.45)
Systolic Blood Pressure	1.29 (1.19, 1.39)	1.26 (1.16, 1.36)
Antihypertensive Treatment	1.48 (1.10, 2.00)	1.48 (1.09, 2.00)
Smoking	2.01 (1.72, 2.35)	2.21 (1.90, 2.58)
Diabetes	2.49 (1.82, 3.41)	2.82 (2.07, 3.84)
Total cholesterol	1.33 (1.23, 1.44)	-
HDL cholesterol	0.78 (0.72, 0.84)	-
Body Mass Index	-	1.20 (1.10, 1.30)

^*Hazard ratios for continuous risk factors are given per 1 standard deviation increase in the natural logarithm. All p-values ≤ 0.01.

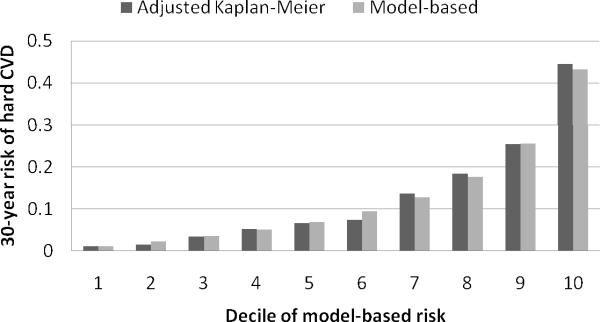
The 30-year risk model offered excellent discrimination (cross-validated c statistic 0.803, 95% CI 0.786–0.820, internally validated c statistic 0.802, 95% CI 0.772–0.832) and calibration (cross-validated Nam-D'Agostino chi-square 4.25, p-value 0.894; Figure 2; internally validated chi-square 3.98, p-value 0.913). It is important to note that our model, which adjusted for the competing risk of non-cardiovascular death, improved the model calibration as compared to the model which ignored the competing risk (cross-validated Nam-D'Agostino chi-square for the model which ignored the competing risk was 18.7, p-value 0.027).

Figure 2.

Average 30-year risk of hard CVD and corresponding Kaplan-Meier rates; both adjusted for the competing risk of non-cardiovascular death

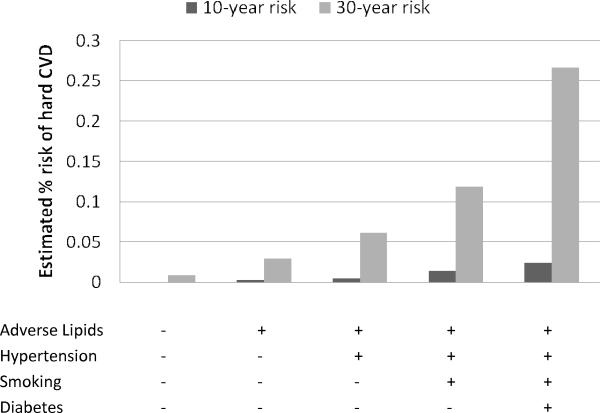
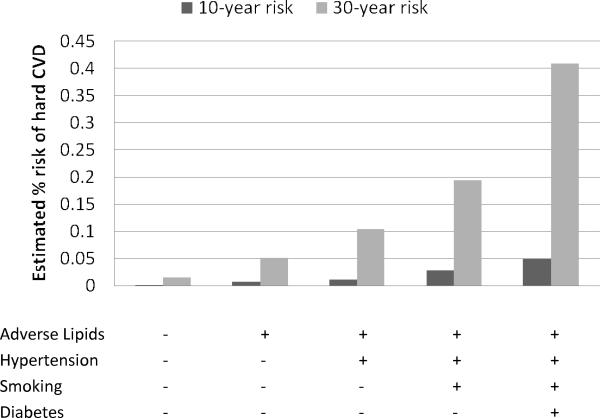
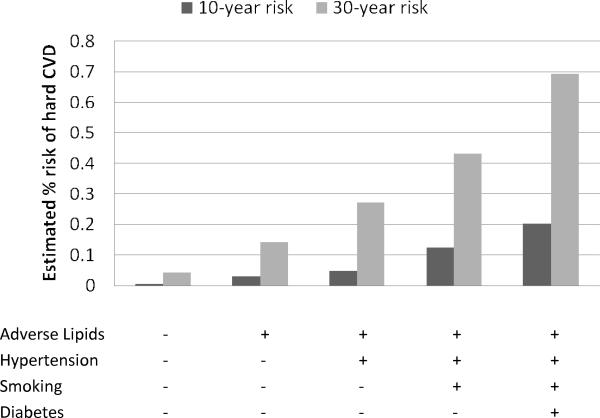
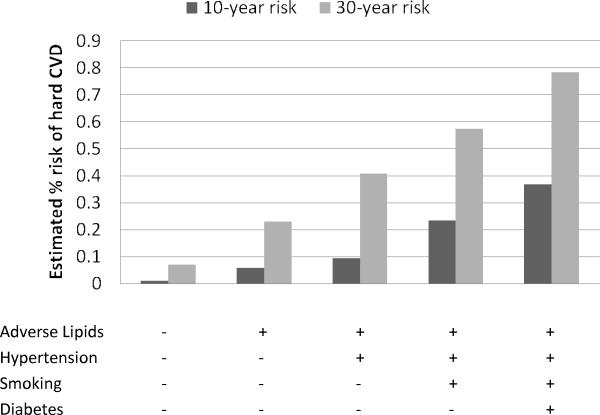
Figures 3 and 4 contrast the estimated 30-year risks of hard CVD adjusted for the competing risk of non-cardiovascular death with 10-year risks, calculated for 25-year-old women and men, respectively. The corresponding estimates for 45-year-olds are given in Figures 5 and 6. These ages were selected to illustrate CVD risk burden in young adults with varied combinations of risk factors as well as in middle age adults. The results for 25-year-olds are striking, especially for women. The 10-year models suggest negligible risk levels (below 2.5% in women and 5% in men) whereas the 30-year models give estimates that are almost 10 times higher. For example, 10-year risk for a 25-year old smoking woman with adverse lipid profile and hypertension is only 1.4% but the corresponding 30-year risk reaches 12%.

Figure 3.

No risk factors profile: total cholesterol = 150 mg/dL, HDL cholesterol = 60 mg/dL, non-treated systolic blood pressure = 110 mmHg, non-smoker, non-diabetic; Adverse lipids: total cholesterol = 260 mg/dL, HDL cholesterol = 35 mg/dL; Hypertension: systolic blood pressure = 160 mmHg, non-treated;

Figure 4.

No risk factors profile: total cholesterol = 150 mg/dL, HDL cholesterol = 60 mg/dL, non-treated systolic blood pressure = 110 mmHg, non-smoker, non-diabetic; Adverse lipids: total cholesterol = 260 mg/dL, HDL cholesterol = 35 mg/dL; Hypertension: systolic blood pressure = 160 mmHg, non-treated;

Figure 5.

No risk factors profile: total cholesterol = 150 mg/dL, HDL cholesterol = 60 mg/dL, non-treated systolic blood pressure = 110 mmHg, non-smoker, non-diabetic; Adverse lipids: total cholesterol = 260 mg/dL, HDL cholesterol = 35 mg/dL; Hypertension: systolic blood pressure = 160 mmHg, non-treated;

Figure 6.

No risk factors profile: total cholesterol = 150 mg/dL, HDL cholesterol = 60 mg/dL, non-treated systolic blood pressure = 110 mmHg, non-smoker, non-diabetic; Adverse lipids: total cholesterol = 260 mg/dL, HDL cholesterol = 35 mg/dL; Hypertension: systolic blood pressure = 160 mmHg, non-treated;

Results of time-dependent analysis

In time-dependent analysis updating all variables approximately every 4 years, all standard risk factors remained significantly related to the hard CVD outcome with hazard ratios similar to those obtained in 30-year risk models (Table 3). Smoking had the biggest numerical change: hazard ratio increased by about one third in the time-dependent model. This can be explained by the fact that time-updated models focus on a shorter event follow-up and can account for changes in risk factor levels – smoking cessation in this case.

Table 3.

Hazard ratios^* with 95% confidence intervals for 30-year risk of hard CVD vs. model with time-dependent risk factors updated every 4 years

Variables	30-year risk model	Time-updated model
Male Sex	1.72 (1.44, 2.05)	2.05 (1.72, 2.44)
Age	2.08 (1.88, 2.31)	2.18 (1.97, 2.42)
Systolic Blood Pressure	1.26 (1.16, 1.37)	1.28 (1.19, 1.39)
Antihypertensive Treatment	1.48 (1.10, 2.00)	1.36 (1.14, 1.62)
Smoking	2.04 (1.74, 2.38)	2.74 (2.32, 3.24)
Diabetes	2.42 (1.77, 3.31)	2.30 (1.89, 2.81)
Total cholesterol	1.32 (1.22, 1.43)	1.23 (1.14, 1.33)
HDL cholesterol	0.80 (0.73, 0.87)	0.75 (0.68, 0.81)
Body Mass Index	1.10† (1.00, 1.20)	0.99‡ (0.91, 1.08)

^*Hazard ratios for continuous risk factors are given per 1 standard deviation increase in the natural logarithm. All p-values ≤ 0.01 except as noted:

^†p-value = 0.04

^‡p-value = 0.82

The most interesting change occurred in the impact of BMI on the risk of hard CVD. Body mass index was weakly significant in the long-term, 30-year model (hazard ratio 1.10 per one standard deviation, p-value 0.04) but lost its entire impact in time-dependent model (hazard ratio 0.99, p-value 0.82). This finding illustrates how the effect of BMI is mediated through other risk factors: it is present in 30-year risk model when the follow-up is extended for a long period from the baseline but then it impacts the individual risk factors, and after we control for this impact in time-updated models, BMI loses its significance.

Comparison with alternative approaches for 30-year risk prediction

The mean estimated 30-year risks based on our model (the “Adjusted” approach) were 7.9% for women and 18.0% for men (as expected, very close to the incidence rates given above). As expected, the “Naïve” approach consistently underestimated the true risk – the mean risks were 4.1% for women and 13.3% for men. If we ignored the competing risk of non-cardiovascular death (“Unadjusted” approach) the mean risks increased to 8.6% and 20.4%, respectively. The risks based on the “Combined” approach averaged across our cohort were even higher, however, the relationship varied across individuals with different levels of risk factors. When we applied these approaches to calculate 30-year risks for individuals with different combinations of risk factors, the “Unadjusted” approach consistently over-estimated the correct predictions based on the “Adjusted” model. The “Combined” approach underestimated the true risk for people with lower risk (younger and with fewer risk factors) and overestimated the risk in people with higher risk (older with several risk factors). Differences were more pronounced for higher risk levels (above 20%). There was a 10% (95% CI: 6%, 14%) net reclassification improvement resulting from using the adjusted 30-year risk estimates over the tripled 10-year risks (“Naïve” approach) but no improvement when compared to the “Unadjusted” or “Combined” approaches.

DISCUSSION

In this report we present a simple way to estimate 30-year risk of hard CVD based on risk factors routinely measured during an office visit. The results are based on over 30 years of rigorous follow-up and ascertainment of CVD incidence and death. Our algorithm allows for risk assessment for individuals with any combination of continuous and categorical risk factors. It also accounts for the competing risk of non-cardiovascular death.

Our approach is based on advanced statistical techniques that allow avoiding bias in the assessment of true absolute risk. Ignoring the competing risk of death inflates the estimates by an average of 1–2% on the absolute scale (or 10% on the relative scale), which leads to inferior calibration as demonstrated in the chi-square statistics. On the other hand, simpler approaches which try to make 30-year inference on the basis of a 10-year risk model are inadequate and may lead to under- or overestimation of the true risk burden.

The need for long-term risk prediction tools has been articulated for many years¹⁴ as a complement for the shorter-term calculators. There are several reasons why it is necessary. As Sniderman and Furberg²⁸ point out, studies with shorter follow-up miss cases that would come out if the duration was extended and thus “restrict our appreciation of the true importance of the modifiable factors that cause vascular disease”. As seen here, 30-year risk cannot be adequately replaced by different combinations of 10-year risks. Blumenthal et al.²⁷ raise the issue of high lifetime risk of CVD in women to underscore the need for long-term risk prediction algorithms. This point finds a striking illustration in our data, where adverse risk factor profile leads to high 30-year risk despite young age, an effect that is entirely missed by 10-year risk model. Moreover, most contemporary cohorts are confounded by treatment effects which significantly influence short-term prediction. The use of 30-year instruments might partially overcome this problem with its long-term focus. Effective risk communication is another reason why 30-year risk might be helpful. Individuals might be more likely to adopt necessary lifestyle changes upon hearing that their 30-year risk of CVD is 1 in 8 (75^th percentile of the 30-year risk in men below age 40) than when they are told it is 1 in 50 in 10 years (75^th percentile of the 10-year risk in men below age 40). Moreover, the potent impact of accumulation of risk factors as presented in Figures 3–6 may serve as an effective risk communication tool.

We have shown that established CVD risk factors which are significant in models based on shorter follow-up duration^{3, 4, 12} are also significantly related to hard CVD incidence in 30 years. The impact of risk factors measured only at baseline is similar to that of risk factors regularly updated at follow-up. The same is not true for BMI which loses its independent impact when other covariates are time-updated. No significant effect modifications by sex were detected, despite differences in hard CVD composition with strokes comprising 40% of all first events in women and 25% in men.

As indicated earlier, this is the first report to our knowledge that presents a risk score for incidence of hard CVD in the 30-year horizon. In their recent publications researchers from the Chicago Heart Association Detection Project in Industry calculate the remaining lifetime risk until age 85 adjusted for the competing risk of death for participants aged 40–59 with 0–5 elevated CVD risk factors²⁴ and quantify the effect of these standard risk factors on the 30-year risk of CVD, coronary and all-cause mortality in women aged 18–39²⁵. While their reports offer valuable insights into the effect of risk factors on the long-term risk of cardiovascular disease they were not designed for individual-specific risk prediction in a clinical setting.

The analysis of changes in impact on the risk of coronary heart disease and death of baseline risk factors during long-term follow-up undertaken by the Chicago Heart Association authors^{24, 25, 26} as well as Menotti and Lanti⁴⁹ revealed that single-occasion measurement risk factors remain strong predictors even in the long-term models. This finding has been confirmed in our setting.

A few limitations of our study need to be acknowledged. First, our results and the risk score were derived based on a Caucasian cohort, which potentially limits the generalizability to other ethnic groups. Appropriate recalibration (cf. ²⁹) may correct differences in baseline survival between ethnicities but further investigation is warranted to determine the impact of relative risks for CVD and the competing risk of non-CVD mortality differing between ethnicities. Second, in the assessment of model performance we accounted for over-optimism introduced by evaluating the model on the same data on which it was developed using five-fold cross-validation and internal validation. While these techniques are well suited for this purpose, they cannot be equated with the preferred method of validation in an outside cohort. Third, we considered only standard risk factors and did not investigate the effect of novel biomarkers on the risk of hard CVD as they were not available at the baseline examination in the early 1970s. Wilson et al.⁵⁰ have shown recently that c-reactive protein measured on the Framingham cohort between late 1970s and early 1980s might contribute to improvement in risk reclassification, a finding postulated before by Ridker et al.^{10, 13} based on other cohorts. It is plausible that the use of novel biomarkers could help reduce the amount of risk underestimation with 10-year models as compared to 30-year models. Further research is needed to investigate this issue. Fourth, the effect and interplay of risk factors might be different now than it was 30 years ago. However, no other way of constructing a 30-year risk score is possible given the length of time horizon. Fifth, the nature of our design did not account for changes in risk factor levels that can take place during the course follow-up. For example, smoking cessation between early 1970s and the present time period might have reduced the true absolute risk leading to an underestimation of the effect of continued smoking. However, we have shown that regardless of the absence or presence of risk factor adjustment on follow-up, they remain strong independent predictors of hard CVD. Finally, we did not attempt to predict the 30-year risk of death from non-cardiovascular causes; however this risk was implicitly factored into the calculations as the competing cause. Further research is needed to provide estimators of long-term risks of all-cause and non-cardiovascular mortality that would complement the predictions available in this report and allow for patient-specific treatment strategies.

We hope that the simple way of quantifying 30-year risk of hard CVD based on a combination of standard risk factors and additional insights to the nature of their effect presented in this report will complement the currently available 10-year risk algorithms and serve as useful tools in the clinical and public health settings and provide a useful framework for future research.

Clinical Perspective.

The impact of standard risk factors (male sex, age, blood pressure and antihypertensive treatment, cholesterol levels, smoking and diabetes) on 10-year risk of coronary or cardiovascular disease (CVD) has been extensively studied and reliable algorithms exist for risk prediction. In the present investigation, we evaluated the impact of standard risk factors on CVD incidence on long-term follow-up, i.e, over 30 years. Our observations suggest that standard risk factors remain highly predictive of CVD risk over a 30-year follow-up period and their impact is substantial even if levels are not updated. We also quantified the impact of body mass index on 30-year risk of CVD and observed that its association with increased CVD risk is mediated partly through promoting higher levels of standard risk factors over a long-term follow-up. Additionally, we have formulated a 30-year CVD risk prediction algorithm that adjusts for the competing risk of death on long-term follow-up. Our observations suggest that different applications of 10-year risk prediction functions for estimating 30-year CVD risk may be suboptimal, especially when applied to younger women and men who have an adverse risk factor profile(over 10% for women and almost 20% in men who smoke, have hypertension and adverse lipid profile). We also have constructed a simple calculator for estimating 30-year risk of CVD that is based on standard risk factors (with and without knowledge of laboratory values) and which could be easily implemented in primary care settings.