Enhancing Realism of Wet Surfaces in Temporal Bone Surgical Simulation

Abstract

We present techniques to improve visual realism in an interactive surgical simulation application: a mastoidectomy simulator that offers a training environment for medical residents as a complement to using a cadaver. As well as displaying the mastoid bone through volume rendering, the simulation allows users to experience haptic feedback and appropriate sound cues while controlling a virtual bone drill and suction/irrigation device. The techniques employed to improve realism consist of a fluid simulator and a shading model. The former allows for deformable boundaries based on volumetric bone data, while the latter gives a wet look to the rendered bone to emulate more closely the appearance of the bone in a surgical environment. The fluid rendering includes bleeding effects, meniscus rendering, and refraction. We incorporate a planar computational fluid dynamics simulation into our three-dimensional rendering to effect realistic blood diffusion. Maintaining real-time performance while drilling away bone in the simulation is critical for engagement with the system.

1 Introduction

As the capacity of computer graphics to present realistic, interactive scenes in real time increases, techniques for refining representations in order to emulate specific real-world applications become feasible. In the biomedical field, surgical simulation provides a broad array of applications which benefit directly from the advanced capabilities of modern graphics hardware. More convincing interactions with simulated environments provide the possibility of increased engagement between the user and the simulation. This, in turn, has the potential to facilitate learning.

Our targeted application is a mastoidectomy: the removal of portions of the mastoid bone. This surgical technique is the initial step for surgical interventions to eliminate infection, as well as the treatment of middle and inner ear pathologies. These techniques are traditionally learned by performing them in a dissection lab, utilizing excised cadaveric specimens. In this manner, residents integrate knowledge of regional anatomy with surgical procedural technique.

In these procedures, the skin behind the ear is retracted, exposing the mastoid bone. The surgeon uses a bone drill to remove a portion of the skull behind the patient's ear to get access to structures such as the ossicles (the bones of the middle ear) and the auditory nerve that lie deep in the otic capsule. Since traditional methods require destruction of physical material during training, a virtual system provides an excellent method for increasing residents' total training time and exposing them to increased variance through a wider array of specimens.

During temporal bone surgery, the wound is irrigated in order to remove debris and to cool areas near the nerves, which are susceptible to heat damage. The drill is employed by the user's dominant hand, and the suction/irrigation device is controlled by the nondominant hand. Proper irrigation technique is critical to the success of the surgery. Blood pooling in the drilled-out cavity can interfere with the visibility of the bone. The suction/irrigation tool must often be held close to the drill to work effectively, but care must be taken not to make contact with the burr while the drill is activated.

The specific simulation of the irrigation process within the larger context of a temporal bone simulator is not present in any current application. Current temporal bone surgery simulators such as those described by Morris et al. [1], Agus et al. [2], Zirkle et al. [3] and others do not incorporate water rendering or effects.

The addition of a blood and fluid component to this type of simulation can enhance the user's experience and aid in learning the procedures and the anatomy. There are several important blood vessels in the temporal bone area, and care must be taken not to drill into them. In the surgery, drilling into a major blood vessel causes a great deal of bleeding, and steps must be taken immediately to correct the error. This does not happen through the current teaching techniques using cadaveric bones, but can be replicated using computer simulation.

In this paper, we describe techniques that have been used to provide a more realistic experience for the users of our surgical simulation system. A real-time fluid flow algorithm has been integrated with our volume rendering in order to simulate the movement of blood and the irrigation that happens during a surgery (see Fig. 1). We provide the details of a deferred shading model that has been developed to give the bone a glossy look, mimicking the appearance of a thin layer of fluid on the bone's surface. In addition, we replicate details of the appearance of the fluid such as refraction and the meniscus, since these give important cues to the user about the position of the fluid. We will also discuss the results of a small user trial where surgeons with experience in performing mastoidectomies tested these additions to the simulation system (see Fig. 2).

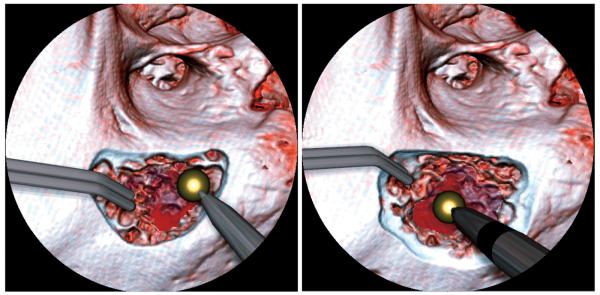
Fig. 1.

Fluid rendering during a mastoidectomy simulation. Notice the blood from the drilled area. The dark circular mask replicates the field of view a surgeon would have under the microscope used for this type of surgery. The fluid ripple effect and blood animation can be seen better in the accompanying movie.

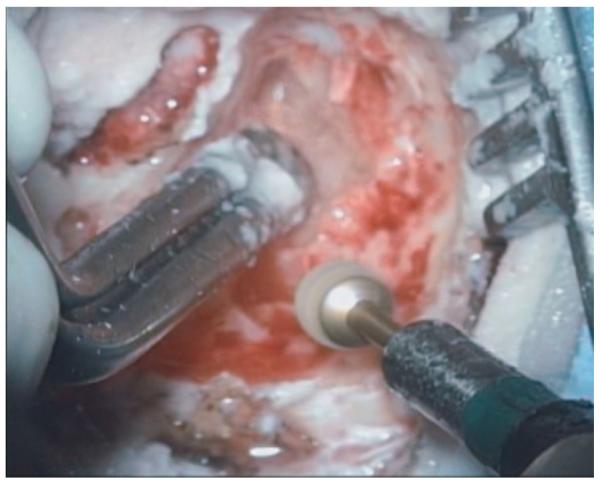
Fig. 2.

A still image taken from a mastoidectomy operation shows a typical view that a surgeon would have during the procedure.

The simulation environment we have created is intended to emulate aspects of the temporal bone dissection lab, and ultimately, surgical techniques. In the dissection lab, bone is removed to expose and identify deeper structures within the skull. A simulation designed to provide structural identification and deliberate practice of technique must seamlessly integrate visual, sound, and haptic feedback to maintain the sense of causality needed for engagement.

Performance is the most important factor across these modes of data transmission for creating the sense of causality that engages the user. Low performance will lead to frustration and lack of engagement with the system, thus, hindering learning. Second in importance to performance is the level of realism, but because real-time procedural techniques are being learned, performance cannot be sacrificed for increased realism. However, as the capabilities of graphics hardware increase, new techniques which create higher levels of realism while maintaining a high rate of performance can be used to improve the overall quality of surgical simulation environments.

The work described in this paper is part of a multi-institutional study funded by the National Institutes of Health (NIH) to develop a temporal bone surgical simulation system and to validate that system for the transfer of skills from the simulation to real performance. The current study is an ongoing research from an earlier exploratory grant given by NIH. Through local trials, we have already received feedback from both surgical instructors and residents who have used earlier versions of the simulator. While they felt the surgical simulation useful, the users provided us with expert advice on how to improve the system to create a better learning environment.

2 Related Work

Much has been written on algorithms for computational fluid dynamics. Jos Stam has described an algorithm [4] for a fast Navier-Stokes equation solver that provides stable results suitable for graphics applications. This solver has been further developed by many seeking to enhance both quality and performance. We base our solver on the system developed by Mark Harris [5], who provides a modification of the Stam algorithm that uses NVIDIA's shading language Cg and framebuffer objects in OpenGL to run the solver using programmable graphics hardware.

3D fluid simulations running in real time have been demonstrated. Work by Liu et al. [6] shows that simulation and rendering of smoke is possible in real time. Smoke requires somewhat smaller grid sizes to get acceptable visual results as opposed to liquid fluids. However, given the constraint of real-time performance, the resolution of these simulations in three dimensions is smaller than that which can be achieved by 2D simulations. For our purposes of simulating shallow water for purely visual effect, rather than physical accuracy, the 2D approach is deemed sufficient. (This is discussed further in Section 4.)

Another grid-based fluid simulation approach is the lattice Boltzmann method (LBM). This method also maps easily to GPUs. An LBM approach to real-time fluid simulation and rendering was demonstrated by Li et al. [7], resulting in satisfactory frame rates for 2D simulations and low performance for 3D ones. The 3D performance is fast enough to be used for visualization alone, but the frame rate could be less than that required for an interactive volume-based surgical simulation due to the additional load on the GPU from the volume rendering.

The Navier-Stokes equation solver we use is a grid-based approach for simulating fluids. Other nongrid-based approaches, such as smoothed particle hydrodynamics (SPH), can be used. In the work by Müller et al. [8], SPH is used to simulate blood in a vessel and generate plausible results for an injured blood vessel with frame rates below 10 FPS. This approach can also be accelerated on graphics hardware. In the work by Harada et al. [9], a GPU accelerated SPH system achieves speeds of around 17 FPS. However, it is not clear how to integrate such a system with dynamic boundaries, a feature which is required for our application.

Another approach for simulating bleeding within the context of a surgical simulation is the use of a dedicated hardware solution. In the work by Kalicki et al. [10], the authors use a commercial physics add-on card to offload the computational work of the physics simulation. In their system they simulate blood only by particle effects and do not perform any fluid dynamics calculations.

Zátonyia et al. [11] have shown an application for fluid flow in enhancing realism in a virtual hysteroscopy simulation. They use a multithreaded CPU based fluid simulation with small grid sizes to achieve performance of up to 60 FPS with a 2D model and up to 7 fps with their high-quality 3D model.

Our refraction effect is similar to previous work involving real-time shading of transparent geometric models. Chris Wyman [12] uses a background image of the local scene to provide an estimate of the contributions from refracted rays. In a recent extension to that work, Oliveira and Brauwers [13] described modifications to the algorithm which allow the incorporation of deformable models into the scene.

Dealing with meniscus effects in computer graphics is not a new idea, but it has been under utilized in real-time rendering. Bourque et al. [14] explore how physically accurate menisci can create more realistic caustics, but their work focuses on high-quality images generated by a non-interactive raytracer.

There is a host of work on rendering wet materials using polygonal models. Jensen et al. [15] use a subsurface scattering model with a raytracer to achieve good results. ElHelw et al. [16] describe their method in improving realism with polygonal models in a surgical simulation, which highlights the importance of using specular variation with multitexturing to provide a more natural looking wet surface, which in their case is tissue with a thin, transparent mucus as seen through a bronchoscope.

As mentioned earlier, the primary requirement of a fluid simulation and rendering extension to our current system (based on the work of Bryan et al. [17]) is that it must not adversely affect the frame rate. Stredney et al. [18] found in 1998 that although volume rendering gave better visuals than a surface-based model, the refresh rate of 4-12 frames per second (FPS) caused user errors during the simulation, such as over-compensation. With current technology, realtime performance with volume rendering is common, but care must be taken to maintain real-time performance throughout the application.

We have found from testing earlier versions of the temporal bone dissection simulator that a perceived lag between the input and the visual output due to decreased frame rate affects the ability of people training with the system to attentively engage withit. Work by Meehan et al. [19]shows that users in a virtual reality environment are very sensitive to latency in the graphics display. The users in the low latency simulation (equivalent to 20 FPS) showed a higher heart rate change and a higher sense of presence compared to the users in the high latency simulation (equivalent to 11 FPS). Therefore, maintaining high frame rates during interaction is critical. Increased realism is important, but the impact on real-time performance must be weighted carefully. By using graphics hardware and modifying existing graphics algorithms for our purposes, realism can be increased while maintaining frame rates of above 20 FPS, thereby increasing engagement with the system.

Fortunately, the surgical techniques themselves provide us with assumptions that can be used to control the frame rate. Because the surgery is performed looking down on the patient under a microscope, fluid pools in the simulation have surfaces perpendicular to the viewing direction. This simplifies our calculations and thus allows us to maintain the high frame rates that are critical to any successful interactive simulation.

3 Simulation System

To display the image of the mastoid bone during the simulation, we use a slice-based volume renderer. The user can select any of the available data sets: We have multiple left and right temporal bone data sets that have been acquired by means of a clinical CT scanner. The user rotates the bone into the appropriate surgical position, analogous to positioning the specimen in the lab bone stand. The user then selects an appropriate drill burr and drills away the bone. During drilling, voxels close to the burr's surface are lowered in opacity and the volume is rerendered. This causes the visual contribution from those voxels to diminish and simulates removal of bone. The degree to which the voxels are affected is dependent on both their proximity to the burr and the type of burr used. A short drop-off is used as opposed to a binary mask in order to improve visual quality and simulate subvoxel accuracy in removal. Different burrs provide different rates of removal (e.g., the diamond burr removes bone more slowly than a tungsten carbide burr), providing options that add to the realism of the system.

The rendering is output to a binocular visor display, of which there are several available in the market. The binocular display is affixed to a stand as shown in Fig. 3. This more closely replicates the physical display that is used in the real surgery, which is done through a binocular microscope held by an arm above the patient. The rendering is also output to a traditional monitor to allow for multiple viewers of the procedure.

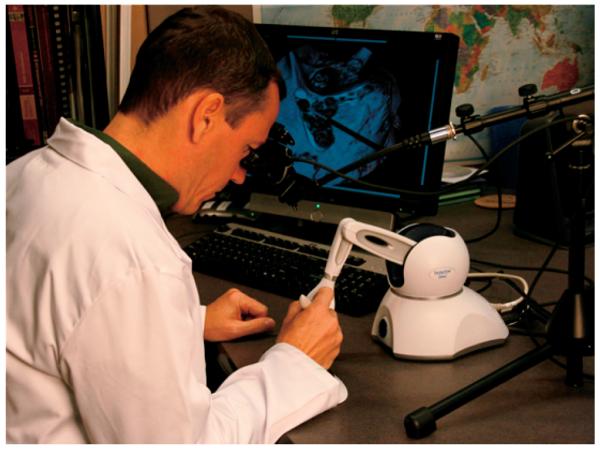
Fig. 3.

A user running the full system, with a binocular display, haptic device, and speaker bar for outputting the sound of the drill.

The user positions both the drill and the suction/irrigation tool using a 3D force feedback joystick (a PHANTOM Omni® manufactured by SensAble Technologies) that allows six degrees of freedom for positioning and three degrees of freedom for force feedback. The system delivers forces to simulate the tools touching the surface of the bone. Other SensAble PHANTOMs are compatible with our system as well, but as we plan to distribute copies of the system, we targeted our system to use the lowest cost haptic feedback device in their product line. The Omni model fits our requirements for the system to be portable and affordable.

In addition to the visual and haptic feedback delivered by the system, sound is used to increase engagement with the software. We recorded samples from real drill and suction/irrigation systems and play back those samples during the simulation. The drill sound is modulated in pitch based on the pressure being applied to it: higher pressure results in a higher pitched noise. All of the sounds are processed using the OpenAL three-dimensional audio positioning library, which gives the user audio positioning cues as they move the tools around the simulation space.

4 Fluid Integration with Volume Rendering

In order to simulate the visual effects of fluid during a mastoidectomy, a grid-based computational fluid simulation was required. Particle system methods can be used to simulate falling water, but in the case of the surgery, pools of water collect in the bone cavity. Simulating such pools with a pure particle system method would require many particle-particle collisions. Another method often used to duplicate the behavior of water is to sum the effects of waves propagating across the surface of the water, such as in work by Loviscach [20]. This can work well for distant water where there is no mixing of fluids. However, in our case we need to simulate both the surface of the water and the diffusion of blood into the water due to bleeding during the surgery. Similarly, the use of any purely procedural techniques to simulate fluid motion would not give realistic enough results when blood was added into the simulation.

As we have seen in the review above, there are many approaches to simulating the behavior of fluids computationally. In our case, however, we have very specific requirements due to our targeted application. The most important of these is high frame rate. From our informal tests, we have found that frame rates below 20 FPS will dramatically reduce the users' willingness to engage with the system. Frustration caused by latency between the time a command is given and the time a result is seen is impossible to completely overcome with high quality renderings.

Although the fluids in the simulation are three-dimensional volumes, filling the cavity of the bone left after drilling, a two-dimensional simulation can be used instead. The water is viewed from above during the surgery. Therefore, due to gravity, the water can be thought of as a height field, representable as a two-dimensional grid. The density of the blood in the water could be defined in three-dimensional space, but when observing recordings of the procedure being performed, we found it very difficult to visually identify the depth of the blood in the fluid. Furthermore, identifying errors in blood flow and dispersion is not important to the educational goals of the simulation. Therefore, using a three-dimensional representation for the blood would not add dramatically to the potential of the rendering to deliver a realistic image.

The use of the drill to remove bone is a vital part of our simulation. Therefore, the ability to have dynamic boundaries is an important requirement for a fluid dynamics system to be integrated into the application. The size and the shape of the bone cavity changes in real time during drilling, and no dramatic reduction in frame rates can be tolerated while the drilling is being performed. We discuss how we use the information from our scene to bound the computational space in Section 4.1.

Because of the requirements discussed above, we chose a two-dimensional, grid based fluid dynamics approach. To shorten development time, we based our system on Mark Harris's publicly available code [21]. We integrate his computational fluid dynamics simulation with our volume rendering by a per pixel test determining if the fluid is visible. This is discussed in Section 5.1.

4.1 Dynamic Boundary Adjustment for the Drilled Cavity

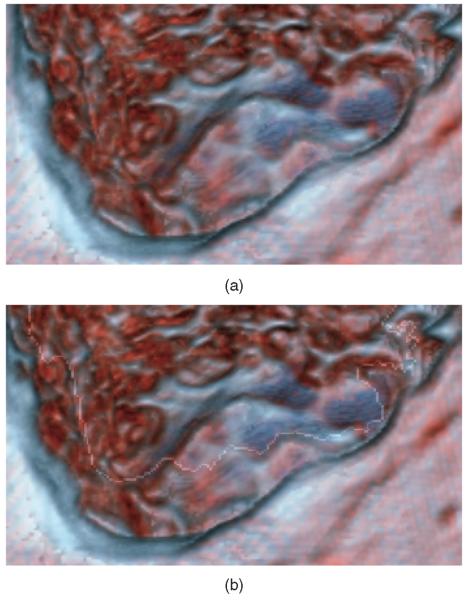
If the flow of the fluid is to appear realistic, it should not seem to penetrate the solid bone. Therefore, we need to construct a boundary region to impede the flow. The boundary is determined by the amount of bone cut away and the nominal fluid level. This fluid level is the same for all pixels and is not determined by the fluid simulation but is given a value based on user selection. We have two different, but related data sets in texture memory: the original volume and the cut volume. The cut volume is modified while the simulation is running by users drilling away parts of the bone. Based on this available data, we construct the fluid boundary mask (see Fig. 4).

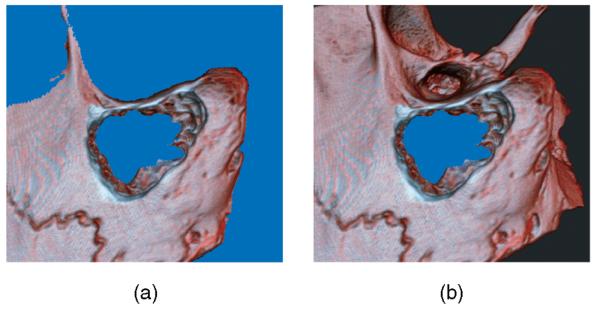
Fig. 4.

In these two images, areas determined to be nonboundary regions are colored blue. These are the areas where fluid would be updated and rendered. The image (a) shows the outcome with only a static depth value. The image (b) shows the final mask results from our method.

The mask containing all areas into which the fluid can flow is the projection to the screen of the removed voxels underneath the fluid level. To generate this mask, we render the original volume into a framebuffer object (FBO), storing both the color and depth buffers. The depth buffer is used in subsequent steps for testing only. All pixels that are rendered that pass the depth test (set to GL_LESS) write the original opacity of the volume to the mask buffer. To complete the mask, we clip it based on the current global fluid level and the depth buffer. Any pixel that has a value greater than zero and that has a depth value farther away from the camera than the fluid level is counted as a nonboundary pixel. Without this mask, the fluid simulation would only be constrained by the edges of the computational space and blood flow within the area rendered would not behave realistically.

This mask could be alternatively calculated by projecting only the cut away voxels to the screen that fall above the fluid level. However, for our system, that would require an extra step. Since we keep track of the lowered opacity, we would need to subtract the cut volume with the original data to find those cut away voxels. In our case, rendering the original volume first allows us to skip this step for a large quantity of voxels that will be discarded due to early depth testing, thereby improving performance.

From our tests, we have found that due to imprecision both in the depth buffer and the scanning artifacts in the original data, the mask often has some salt-and-pepper noise in it. To alleviate artifacts caused by such noise, we implemented a morphological operation which runs on the GPU. Performing this operation on the GPU avoids the latency associated with data transfer across the PCI-E bus.

The morphological operation we use is similar to that described by Hopf and Ertl [22]. They use a multipass technique to sum pixels, while we directly access them in one pass using multiple texture lookups. This is easy to implement in GLSL (or any pixel shader language). We check the four-connected neighborhood of each pixel, plus the pixel itself, for occupancy. We assign the pixel a value according to the number of occupied pixels in the neighborhood: above or equal to the threshold it is assigned one and below it is assigned zero. We call it once with a threshold value of four to remove isolated pixels caused by noise, and then call it with a threshold of one to expand the boundaries of the main cavity, countering the reduction caused by the denoising operation. These two operations combined are similar to the classic binary open operation.

4.2 GPU-Based Fluid Dynamics

The GPU-based fluid solver follows the steps outlined in Algorithm 1. It follows the general framework of Navier-Stokes solvers that have been described in numerous books and papers. Information about how this particular solver was optimized for the GPU can be found in work by Harris [5].

Algorithm 1. Navier-Stokes fluid solver

1. procedure Update

2. Advect blood density and velocity based on current velocity

3. Compute divergence of the velocity (∇ · ν)

4. Compute pressure by Jacobian iteration using Δp = ∇ · ν

5. Compute new velocity by ν ← Δp

6. end procedure

All of the fluid dynamics steps are performed using render-to-texture in Cg. The pressure, velocity, and density are stored in separate texture maps. A derivation from the Bernoulli equations, assuming that the 2D simulation plane height is constant and that the air pressure is equal to the fluid pressure at the boundary, shows that the real height of the fluid is proportional to the pressure. In this way, we can use the pressure term as a height field of the surface of the fluid. Using this height field, we can calculate normals per pixel using central differences. Details of this result can be found in work by Chen et al. [23]. For our fluid rendering, we require only the blood density and pressure: the velocity term is only used for the dynamics and not for rendering.

The fluid solver is run after the boundary is defined. The steps rendering the volume and determining the mask (statements 3 and 4 in Algorithm 2) need to be performed only when either the global water level or the volume image changes. Unless the volume or water level moves in reference to the eye point, the old depth buffer and boundary calculations are reused. Since calculating the mask is expensive due to the two stage volume rendering, this small optimization generates a significant increase in frame rate.

4.3 Real-Time Surgical Interaction and Blood Generation

The key element of the system is the ability of the user to interact with the fluid in real time. To mimic the effects of a surgical drill making contact with the water, we change the velocities of the fluid by adding a velocity from a texture containing Perlin noise. This texture is pregenerated and can be switched out for different effects, such as a drill that creates less vibration. The texture we use is a two-channel Perlin noise: one channel for the x-component of the velocity and one for the y-component. To mimic the effects of a disturbance, we multiply the noise texture with a Gaussian function centered at the location of the disturbance. This creates large changes to areas of the fluid near the contact point of the disturbance and fewer changes farther away. We do not directly incorporate the tools into the boundary definition of the fluid domain, only the volume of the bone and the view direction defines the fluid plane boundary.

Temporal bone surgery, like many surgical procedures, involves blood. In our case, the blood is from vessels inside bony structures that are drilled during the procedure. In traditional training methods, either through a cadaver bone or physical synthetic bone substitute, there is no blood in the training sample and therefore no blood flow is caused by drilling. In our simulation, blood is introduced into the fluid during drilling.

The amount of blood introduced into the fluid varies linearly with the number of voxels that are drilled away in the last frame. This is based on the composition of cancellous bone, which contains red blood marrow and many small blood vessels. Since these blood vessels are small and run throughout the bone, we base the amount of blood purely on the voxels removed. This is a very simplified model, since the structure of bone is complex. We discuss improvements to this model that incorporate greater anatomical details in the conclusion.

The blood released by drilling into the bone is added as an ink density into the fluid simulation and is dispersed by the turbulence caused by the drill bit interaction with the fluid and also the basic dispersion of the ink. As the blood density decreases, the contribution of the blood to the final image color is reduced.

Blood introduced into the water disperses outward from the introduction point and is influenced by both the turbulence in the water from the burr and the boundaries set by the mask. The quality of the fluid simulation can be changed by altering the number of Jacobi iterations used to solve for the pressure term in the Navier-Stokes fluid solver. More iterations will give more physically accurate results, at the expense of frame rate. We found 5-10 iterations to be sufficient, providing realistic animations for this application. The resolutionofthe fluid simulationis equaltothe size of the rendering window. The stability of the fluid solver is excellent, and the noise injections have not caused any dramatic nonrealistic behavior caused by error accumulation.

By including the simulation of blood, we intend the following:

1. Increase engagement with the simulation.

2. Move the simulation closer to the emulation of surgery.

3. Provide a mechanism for easily observing errors, allowing users to make mistakes which lead to immediate and plausible consequences, which is an essential component in maximizing transfer from simulation to actual practice.

With the addition of simulated consequences during training, users can see immediately what behaviors can lead to undesirable results. This is a potential benefit of our system over training with cadaver bones, where instructors evaluate the complete dissection from the finished product after the student has drilled out the bone.

5 Simulation Rendering Pipeline

The entire rendering pipeline takes several steps. The generation of the boundary mask was explained earlier in Section 4.1.

Algorithm 2. Rendering loop

1. procedure RENDER

2. if Volume needs to be redrawn then

3. Render current cut volume scene

4. Generate fluid boundary mask

5. end if

6. Process fluid solver iterations

7. Composite fluid solver output with volume scene

8. Render tools and compute tool shadows

9. Render shadow maps into scene

10. end procedure

The volume renderer we use is slice-based, using 3D texturing hardware through OpenGL. The current volume scene is rendered into an off-screen render target using the FBO OpenGL extension. The color buffer, depth buffer, and normal buffer are saved for later use. The depth buffer is used for creating the mask and the compositing while the color and normal buffers are used later in shading and compositing.

Using GPU raycasting for volume rendering is another common approach and much of the rendering pipeline covered here can be used with such a volume solution. For our application, several other modules not discussed here, such as an anatomical tutor, have been implemented using a slice-based renderer and we use that same renderer to ensure consistent renderings throughout the application.

5.1 Compositing Bone and Fluid

Compositing the water height with the volume image is performed with GLSL. We use alpha compositing, but only for the case where the water is visible (i.e., above the surface of the rendered scene). Where the water is not visible, we do only the deferred shading on the bone color buffer as described in Section 5.4.

$$\begin{array}{cc}\hfill {\text{Composite}}_{\mathit{rgb}}\leftarrow & {\text{Water}}_a{\text{Water}}_{\mathit{rgb}}\hfill \\ \hfill & +(1-{\text{Water}}_a){\text{Volume}}_{\mathit{rgb}}.\hfill \end{array}$$ (1)

To decide whether a pixel rendered is above or below the water, we compare the pressure at that pixel with the information from the depth buffer. Since the depth buffer cannot be directly read during a fragment program operation, it must be passed in as a texture. Due to the nonlinear storage of depth values in OpenGL, the raw depth values must be converted to scene depth values. We can then test whether the water height (pressure value) is above or below the volume depth.

The surgical environment is a well-lit room with a strong annular light at the end of the surgeon's microscope. Because of this, instead of using the standard Phong lighting model with discrete light sources, we perform all the lighting on the water surface by simulating environmental lighting using a cubemap. We estimate the normal of the water's surface by applying the central differences method to the pressure term of the fluid dynamics results. The reason behind our use of the pressure term is covered in Section 4.2.

Using the GLSL reflect function and cube map lookups, we find the color from the environment that will be reflected to the eye:

$$E\leftarrow \text{CubeMap}\left[\mathit{reflect}(I,N)\right].$$ (2)

The opacity of the water is based on the amount of opaque matter in it (i.e., blood). The amount of blood changes over time; blood is added to the environment due to drilling, diluted by irrigation and removed by the suction device. To determine the color of the water, the percentage of blood in the water is multiplied by the blood color

$${\text{Water}}_a\leftarrow {\text{Water}}_{\mathit{blood}},$$ (3)

$${\text{Water}}_{\mathit{rgb}}\leftarrow {\text{Water}}_{\mathit{blood}}\ast B_{\mathit{rgb}}.$$ (4)

The effect of the specular reflection off the water is determined by the percentage of light that is reflected by the water's surface and the percentage that is transmitted through the surface, often referred to as the Fresnel reflectance. We estimate the Fresnel reflectance by:

$$F\leftarrow {(1-\cos \theta )}^2,$$ (5)

and compute the final pixel color by

$${\text{Final}}_{\mathit{rgb}}\leftarrow (1-F)\left({\text{PostWater}}_{\mathit{rgb}}\right)+\left(F\right)\left(E_{\mathit{rgb}}\right).$$ (6)

5.2 Meniscus around the Fluid Filled Cavity

The meniscus is the curve of a fluid's surface near the edges of a container, creating a bright highlight. The visual effect of water tension on comparatively large bodies such as ponds and bathtubs is small and as such is often ignored in real-time rendering. However, with microscopic visual environments such as in temporal bone surgery, the effect of the meniscus is more prominent.

As shown in Fig. 5, rendering the meniscus provides important cues to the boundary of the fluid. While the fluid is in motion, specular and refractive effects can be used to visually determine the location of the fluid. However, when the fluid is calm, these effects tend to be small and imperceptible. We use an edge detection approach to simulate the visual effects of the meniscus.

Fig. 5.

Image (b) is an enlarged rendering with the meniscus effect; image (a) does not have the effect. The boundary of the fluid is nearly imperceptible without rendering the meniscus.

During the compositing pass, surrounding pixels are depth tested. We use a neighborhood of four—the immediate pixels in directions up, down, left, and right. With the addition of the current pixel, this gives five binary variables indicating whether the water level is above or below the bone for the neighborhood. These are summed to produce a value indicating the properties of the boundary for that pixel, according to the procedure in Algorithm 3.

Algorithm 3. Meniscus effect based on a pixel neighborhood of four plus the center pixel

1. procedure MENISCUS

2. EdgeTable ← [0:0, 0:08, 0:05, 0:02, 0:01, 0:0]

3. for all pixels P in the image do

4. a ← 0

5. for all pixels n in the neighborhood of P do

6. if pixel n is above water then

7. a ← a + 1

8. end if

9. end for

10. Meniscus effect for P ← EdgeTable[a]

11. end for

12. end procedure

A six element lookup table is used to determine the strength of the meniscus effect. The first value corresponds to no pixels in the neighborhood being above water, which gives no meniscus effect. The next value corresponds to one pixel being above water, which will generate a high local meniscus effect. The values decrease through the rest of the table, ending with zero effect again for the last element, which corresponds to all pixels below the water. The lookup table can be changed to give more physically accurate appearances for other fluid-surface interfaces. We add the meniscus effect value to the Fresnel reflectivity approximation described in Section 5.1. This gives the edges around the water surface more reflectivity, resulting in the desired bright highlight, shown in Fig. 5.

5.3 Fast Refraction

The effects of refraction are an important component in rendering a transparent fluid. Even though refraction effects could be ignored in some parts of our rendering, due to the thin layers of fluid, with larger fluid amounts the refraction effects become noticeable and the absence of refraction could be a significant drawback to the realism of the rendering.

Generating physically accurate refractions could be done with a raytracing system, but the cost would be substantial. Furthermore, since the fluid is in continuous motion, specific errors in the refraction effect are imperceptible to most users. Therefore, we do not compute physically accurate raytraced refraction, but do generate an effect that gives the appearance of refraction.

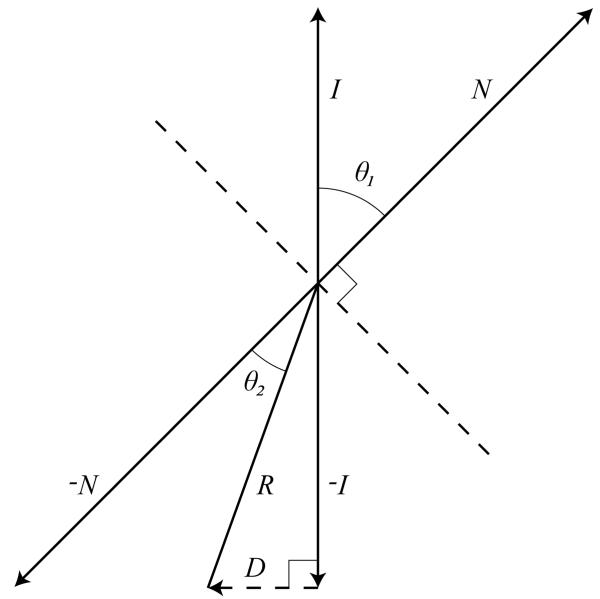
Although we do not compute the true intersection points of the refraction ray with the surface of the bone, the general method of our refraction effect can be thought of as a simplified raytracing approach. Foreach pixelthat represents a location on the surface of the water, we construct a refraction ray based on the normal of the water at that point (see Fig. 6). We then estimate the intersection of the refraction ray with the boundary between the water and the bone.

Fig. 6.

D is the optical displacement due to refraction. I and R are the incident and refractive rays. N is the normal to the water surface.

We assume that all rays entering the water are parallel to the viewing vector and, therefore, perpendicular to the nominal water surface. The normal of the water surface controls the bend of the ray upon crossing the air-water interface according to Snell's law:

$$\frac{\sin {\theta }_1}{\sin {\theta }_2}=\frac{{\eta }_2}{{\eta }_1}.$$ (7)

Since we only consider rays going from air into the fluid, ${\eta }_2{\eta }_1^{-1}$ can be derived purely by considering the refractive index of the fluid. Water has a refractive index of 1.33. Although the refractive index for blood can vary from person to person, we use a value of 1.39, relying on the study done by Xu et al. [24]. We determine the refractive index per pixel, interpolating linearly between these two values based on the amount of blood present in that cell of the simulation.

For each pixel rendered that is determined to be above the surface of the water, we calculate a normal based on central differences, as described above. The vector from the surface of the water down to the surface of the bone is calculated using the GLSL library function refract. This function returns a normalized vector R⃗ in the direction of the refracted ray.

The refraction effect is performed by modifying the texture coordinate used to look up the value from the color buffer holding the volume rendering of the scene. We call the difference between the point on the surface of the bone hit by the ray due to refraction and the point on the surface of the bone hit by the ray assuming no refraction as the optical displacement. Assuming that the local depth of the fluid is constant, the optical displacement is the third side of the triangle made by the refraction ray and the incident ray. We calculate the displacement D⃗ by

$$\overrightarrow{D}=\frac{\overrightarrow{R}S}{\overrightarrow{R}\cdot -\overrightarrow{I}},$$ (8)

where S is the local depth of the fluid. S is determined by a texture lookup into the depth buffer. In our case, since all incident rays are parallel to the viewing vector:

$$\overrightarrow{R}\cdot -\overrightarrow{I}=\left|R_Z\right|\text{when}\overrightarrow{I}=[00-1],$$ (9)

which can be calculated very quickly.

After finding the optical displacement D⃗ for each fragment, we add it to the fragment position and use that result to query the color buffer that holds the volume rendering. This gives us our Volume_rgb used in the compositing operation.

5.4 Bone Volume Rendering with Deferred Shading

Since we are striving to provide a similar experience to the one students have in the bone dissection lab, in order to maximize the knowledge transfer from the simulator to the real world, realistic representations of the temporal bone are of high importance. The shading model we use (see Fig. 7) to render the bone must be able to replicate specific visual elements present in the real environment. However, as stated earlier, high frame rates are of even higher importance: graphical stuttering causes an immediate loss of engagement between the user and the application.

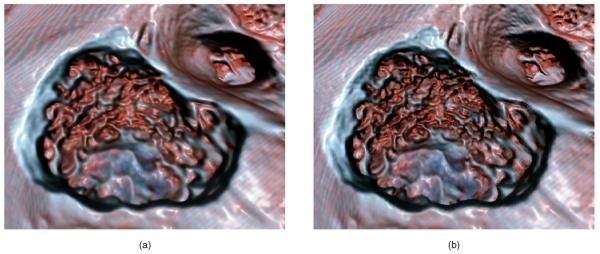
Fig. 7.

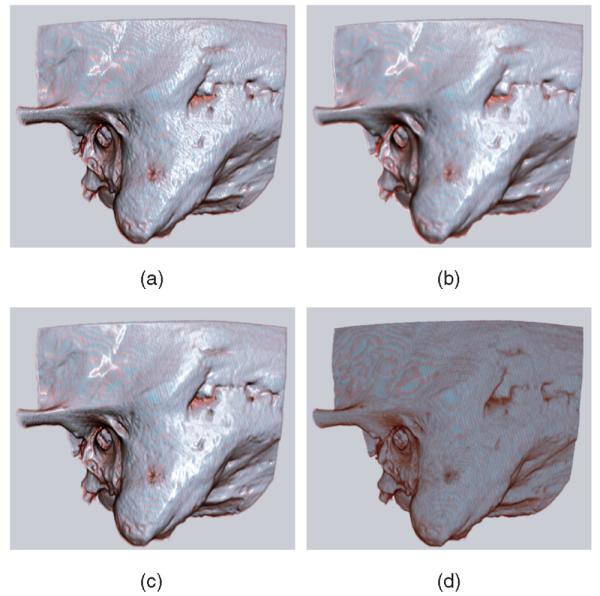
Normal shaded rendering is depicted in (a). (b) shows the results when the smoothed normals are used for both the diffuse and specular parts of the lighting calculation. We use the smoothed normals only for the specular calculation, as shown in (c). This retains details lost in (b) while maintaining a glossy appearance. This gives the visual effect of an object coated with a thin fluid. An unshaded rendering (d) is provided for reference. See Fig. 8 for a close-up comparison of methods (b) and (c). (a) Unsmoothed normals; (b) Smoothed normals; (c) Smoothed specular only; (d) Unshaded.

Along with the pools of water simulated using techniques in the earlier sections, we render the entire bone to make it look as if it is covered with a thin layer of fluid. This closely replicates the environment in the dissection lab and operating room, which are quite different from the appearance of an anatomical model or dry cadaver bone.

To achieve the wet look, the specular highlights should appear smooth and the artifacts caused by normals from a voxelized source should be minimized. We cannot afford to perform a high-order gradient algorithm for high-quality normals in every rendering frame and we cannot process the data before rendering since the volume is modified during the simulation. This leads us to a deferred shader model, where an elementary normal generation algorithm (central differences) is calculated per pixel. Since the volume data we use in the simulation are mostly opaque, we composite the normals to a buffer back to front during volume rendering and keep a contribution based on the opacity of the voxel. This ensures that low opacity voxels do not contribute very much to the final shading of the volume.

The normal buffer is then smoothed. Multiple passes over the normal buffer are performed, each time considering the nine-connected region around each pixel. This smoothing is anisotropic, considering the depth of the neighboring pixels. The contribution from each neighbor is scaled linearly based on the difference between the neighboring pixel and the pixel being smoothed. This provides two benefits: it reduces artifacts, since our data often has scattered low opacity voxels outside the bone due to scanning noise, and it avoids oversmoothing in areas with sharp edges.

These smoothed normals are used only for determining a pixel's specular color. We use the original normals to calculate the diffuse component of the color. This maintains detail and fine edge definition, which is important in determining the texture and location of the bone as the outer edge is drilled away. The resulting color is calculated using a modified version of the Phong shading equation, replacing the diffuse normal with our smoothed normal.

5.5 Shadows

We implemented a simple shadowmap algorithm to give shadows to the tools in the simulation. However, shadows in the operating room tend to be soft, since there are many lights coming from all directions to provide full illumination of the surgical field. A bright light is at the end of the microscope used in surgery, but this does not generate a strong shadow effect, since the light direction is parallel to the view direction. Based on the environment, we use percentage closer filtering to soften the shadows based on multiple jittered lookups to the shadowmap. Since we can calculate the shadows on the volume in screen space using the buffers saved from the deferred shading, the shadows have little effect on frame rates.

6 Performance

For our tests, we ran the software on a quad-core Core 2 PC running at 2.4 GHz with a GeForce 8,800 GTX graphics card. This system is our target machine specification. We used a framebuffer object of size 800×600 pixels to store our volume rendering. This screen size is our target since it is the maximum for our binocular display device. Our fluid simulation is run at the same grid size. The fluid interaction and rendering alone is very fast: frame rates range from 70 to 100 FPS. In our full application, with volume rendering, volume removal, and fluid interaction and bleeding, we achieve frame rates from 25 to 30 FPS (see Table 1), exceeding our lower limit for interactivity of 20 FPS for our target resolution. Each separate run was performed on a different data set. Reducing the simulation grid size has little impact on actual frame rates. We use 256³ voxel, four channel volumes acquired from CT scans on cadaveric skulls which have been processed to add more realistic coloring. We have tested the system on multiple scanned bones and the frame rates are similar for all of the data sets.

TABLE 1.

FPS Statistics for Multiple Runs of the Simulator

	Size 800×600			Size 1024×768
Run	Min	Max	Average	Min	Max	Average
1	25	31	28.5	23	27	24.9
2	28	31	29.5	24	26	24.5
3	28	31	29.7	24	28	25.7
4	28	31	29.6	23	27	25.2

7 User Study

We asked three surgeons, considered experts (with more than 200 surgeries performed), to evaluate our simulator and give us feedback. During the simulation, we toggled the blood, shadows, and lighting model on and off. They rated the effects on a short paper survey and we discussed at length about the simulation.

The answers to the paper survey are shown in Table 2. The surgeons were asked about the features added: They rated them on a scale from distracting (0) to appealing (5) and also answered the following questions on a zero to five scale:

1. How well do the visual updates keep up with your interaction with the software?

2. How does the lighting model affect the appearance of wetness on the surface of the bone?

3. Does the appearance of wetness added by the lighting model match the appearance of wetness you have in the actual surgery?

4. How much do you think the addition of fluid and blood aids in learning irrigation techniques?

TABLE 2.

Ratings of Features by Three Experts (A, B, and C) on a Scale from 0 to 5, and Numerical Answers to Specific Questions

Feature	A	B	C
Lighting	5	5	5
Shadows	3	4	5
Fluid	3	4	0*
Blood	4	4	4
Question	A	B	C
I	4	5	3
II	3	3	3
III	3	3	3
IV	3	4	4

^*Please see detailed explanation in text

All of them thought that the new lighting model used was a large improvement over the standard volume rendering and provided a better sense of form and depth within the bone. All three gave a top score to the lighting model on a scale of zero to five. They did not think that it entirely captured the specular effect of wetness seen in the operating room but they did feel it to be quite appealing and engaging. They thought the shadows were at times helpful for additional depth cues but gave only a minor benefit, since shadows during the surgery tended to be very soft. All the experts were satisfied with the frame rate of the simulator and had no complaints about the interactive latency.

The experts were generally satisfied with the realism in the appearance of the blood mixing with the irrigation fluid. They commented that the fact that blood comes from all voxels removed during drilling rather than from discrete location based on anatomy was only true for diseased bones. We outline a possible solution to this problem in the next section. In addition, in our system the suction effect was the default and irrigation was triggered by a switch, while in the operating room, the device delivers constant irrigation and selective suction. This user interface error was reported as a significant contributor to the low score given to the fluid feature by expert C.

The experts also commented that the simulation environment gives a much more accessible form of training for residents than does drilling cadaver specimens. A resident could use the simulator during a 20 minute break without the preparation and cleanup that is required when working with physical specimens.

Overall, they found the graphical improvements helpful and believed they would help not only with training on the simulator, but also with exploring alternate surgical approaches in preoperative assessment.

8 Future Work and Conclusion

There are some limitations to the system due to the planar fluid approach. One is that gushes or splashes of fluid are impossible to display properly . Since we represent the fluid level graphically as a height field, situations where the water has multiple intersection points along the path to the eye cannot be simulated.

We would like to explore the integration of a fully 3D fluid simulation, such as the one developed very recently by Crane et al. [25], into our system. We would also like to incorporate foaming effects that occur because of the high speed of the drill bit in the water. In addition, bone dust is generated by drilling away the bone and quickly mixes with the fluid to form a paste. This paste could eventually be incorporated into the simulation as well.

An extension we are currently working on introduces bleeding based on expert segmentation of the original volume data. Bleeding should be varied based on the specific qualities of the bone and a large amount of blood should be introduced if the user drills into one of the larger blood vessels that pass close to the temporal bone. Certain voxels can be labeled as “bleeder” voxels and when cut away by the drill they can increase the concentration of blood in the local area.

We have demonstrated that through the use of 2D fluid dynamics routines, realistic renderings of fluid flow can be added to complex volumetric surgical simulations while maintaining high frame rates needed for effective user interaction. By using the GPU, real-time fluid dynamics computations can be performed efficiently enough to provide rendering speeds consistently exceeding our target of 20 FPS. In addition, by using fragment shaders to render visual effects critical to the look of fluid in the surgery—such as blood diffusion, refraction and edge effects—we can deliver a more realistic experience to the user, increasing engagement and potentially increasing the transfer of knowledge from simulation training to the operating room.

To see a movie of our simulation, go to: http://www.cse.ohio-state.edu/~kerwin/.

Fig. 8.

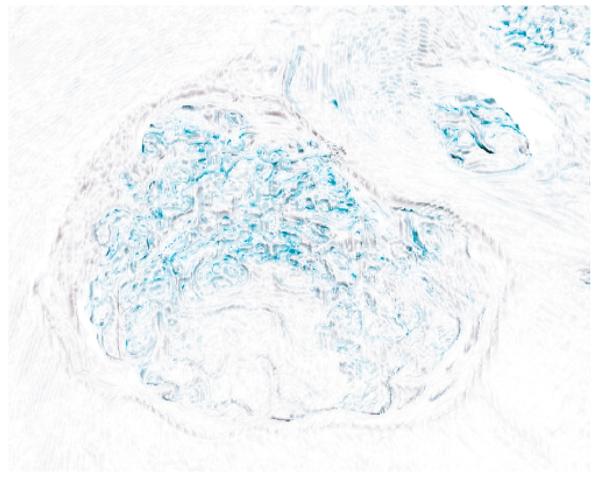
A close-up comparison of shading of a drilled bone: (a) smoothed diffuse and specular normals; (b) with smoothed specular normals only. Image (b) shows how smoothing only the specular preserves more of the detail texture of the bone. See also Fig. 9.

Fig. 9.

This image is a subtraction of the two images in Fig. 8, inverted to provide a white background. This shows the areas where high detail is lost by smoothing the normals used for diffuse shading.

Biographies

Thomas Kerwin received the BS degree in computer science in 2004 from The Ohio State University where he is currently a PhD student in computer science. He works on surgical simulation and medical visualization projects at the Ohio Supercomputer Center. He is a student member of the IEEE and the IEEE Computer Society.

Han-Wei Shen received the BS degree from the National Taiwan University in 1988, the MS degree in computer science from the State University of New York at Stony Brook in 1992, and the PhD degree in computer science from the University of Utah in 1998. From 1996 to 1999, he was a research scientist with MRJ Technology Solutions at NASA Ames Research Center. He is currently an associate professor at The Ohio State University. His primary research interests are scientific visualization and computer graphics.

Don Stredney received the BS degree in medical illustration in 1979 and the MA degree in computer visualization in 1982 both from The Ohio State University. He is currently a research scientist for the Biomedical Sciences and Visualization Group and the director of the Interface Lab at the Ohio Supercomputer Center. He holds adjunct instructor positions in the Departments of Biomedical Informatics and Otolaryngology at The Ohio State University. In addition, he is a member of the Experimental Therapeutics Program at the Comprehensive Cancer Center, and an associate member of the Head and Neck Oncology Program at the Arthur G. James Cancer Hospital and Solove Research Institute in Columbus, Ohio.