Systematic Computational Study of the Effect of Silver Nanoparticle Dimers on the Coupled Emission from Nearby Fluorophores

Abstract

We use the finite-difference time-domain method to predict how fluorescence is modified if the fluorophore is located between two silver nanoparticles of a dimer system. The fluorophore is modeled as a radiating point dipole with orientation defined by its polarization. When a fluorophore is oriented perpendicular to the metal surface, there is a large increase in total power radiated through a closed surface containing the dimer system, in comparison to the isolated fluorophore and the case of a fluorophore near a single nanoparticle. The increase in radiated power indicates increases in the relative radiative decay rates of the emission near the nanoparticles. The angle-resolved far-field distributions of the emission in a single plane are also computed. This is informative as many experimental conditions involve collection optics and detectors that collect the emission along a single plane. For fluorophores oriented perpendicular to the metal surfaces, the dimer systems lead to significant enhancements in the fluorescence emission intensity in the plane. In contrast, significant emission quenching occurs if the fluorophores are oriented parallel to the metal surfaces. We also examine the effect of the fluorophore on the near-field around the nanoparticles and correlate our results with surface plasmon excitations.

1. Introduction

Measurements of the binding interactions between biological molecules are a central component of the biosciences and chemical testing. A wide variety of interactions occur, such as protein-protein binding, nucleic acid hybridization, and association of membrane-bound proteins. In clinical testing, association reactions are routinely used to detect biomarkers in genetics and oncology. Many of these binding interactions are measured using fluorescence-based methods. Many of the clinical assays rely on surface-bound chemistry, such as enzyme-linked immunosorbent assays and DNA arrays, which are multistep and heterogeneous assays. In many cases, it is desirable to have single-step or homogeneous assays. Currently, these measurements typically rely on changes in fluorescence polarization, fluorescence resonance energy transfer (FRET), or both.^1-6

It is interesting to consider why polarization and energy transfer are so widely used in bioassays. The basic reason behind this is that the most widely used probes (fluorophores) do not display useful spectral changes when the labeled molecules interact. Of course there are a number of fluorophores that are sensitive to their local environment and display spectral changes that can be used to detect binding.^7,8 However, these spectral changes are usually specific for the system being investigated and do not provide a general approach to the detection of a target antigen or DNA sequence. These problems are avoided by using fluorophore polarization, which depends on predictable decreases in rotational diffusion when two biomolecules bind together. These problems can also avoided by the use of FRET.⁶ This through-space interaction occurs when a donor and acceptor are within the Forster distance, and the energy transfer does not depend on the detailed molecular structures of the biomolecules.⁶

While polarization and FRET assays are generally applicable and widely used, they do have their limitations. In the case of polarization, the assays are most useful when the target molecule is small. This small size allows rapid rotational diffusion and depolarization during the excited-state lifetimes. Upon binding to a larger biomolecule, the rate of rotational diffusion is decreased and the polarization is increased. However, polarization assays are less useful for the detection of larger molecular weight species because the polarization of the labeled molecule is already high and the extent of depolarization is usually dominated by segmental motions of the probe rather than rotational diffusion.^1-3 FRET assays also have limitations. The distances over which FRET occurs is typically no larger than 5 nm, and energy transfer over 8 nm would be an exceptional case.⁶ Many biomolecules are larger than Forster distances, one example being an IgG molecule, which is ∼10 nm in size. As a result, the extents of energy transfer are often low, which hinders the use of FRET for sandwich assays.

In this report, we study the feasibility of an alternative way to detect biomolecule affinity reactions, which is based on the effect of binding a fluorophore between two metal nanoparticles. This localization could occur for an antigen between antibody-coated particles or for a DNA sequence with particles coated with cDNA. We used finite-difference time-domain (FDTD) calculations to study the effects on the emission of fluorophores located between noble metal nanoparticles (MNPs). In particular, we are interested in the possibility of using fluorophores located within MNP dimers to increase emission that can potentially be used to measure biomolecule association. This approach was motivated by the well-known increases in the electric fields between particles when illuminated from the far field.^9,10 Additionally, we were aware of the growing body of information on enhanced fluorescence near MNPs. Hence, we used the FDTD simulations to predict increases in emission intensity that may occur for a fluorophore localized between two MNPs as compared to an isolated flurophore and a fluorophore near a single MNP. One can readily imagine the use of MNPs, which are brought into proximity by an association reaction, and the use of the increases in fluorescence intensity to detect the binding reaction. The increase in intensity will be due to both an increase in the excitation field and the increased radiation from the fluorophore. Because of the many publications on the fields between particles (due to excitation by incident light), this paper is focused on the effects of silver nanoparticle dimers on fluorophores that are located between the particles. In this study, the radiating fluorophore is modeled as a point dipole source in the near field of the nanoparticles. A realistic model for silver is used that allows for plasmon excitations. The resulting angular distributions of the emission in the x-y plane for the fluorophore in two orientations relative to the nanoparticles are examined. This angular distribution of the emission is then integrated to obtain the total fluorescence emission intensity in the x-y plane. The integrated emission intensity for the system (where the system is the fluorophore-nanoparticle complex) is divided by the corresponding emission intensity of an isolated dipole to obtain the enhancement or quenching of the emission in the x-y plane. We also compute changes in the total radiated power by the system (inferred by integrating the normal flux passing through a closed surface containing the system) in comparison to an isolated fluorophore. This change in total radiated power is indicative of a change in the relative radiative decay rates of the system. We consider several different nanoparticle sizes, multiple spacing of the fluorophore from single nanoparticles, and multiple distances between the nanoparticle dimers. In the case of the dimer systems studied, the fluorophore is located exactly midway between the individual nanoparticles. Both parallel and perpendicular orientations of the fluorophore’s radiating dipole moment relative to the nanoparticle surface are examined. In the case of the parallel fluorophore orientation, we observe only modest enhancements in the emission intensity of the fluorophore near larger nanoparticles. Interestingly, for all of the dimer systems with the parallel fluorophore orientation, we see a dramatic quenching of fluorescence when compared to the isolated fluorophore. Quenching of dipoles oriented parallel to the surface of metals is expected as the tangential electric field components are zero at an ideal metal surface. The normal components however are not zero. Hence, in contrast, for the case of the perpendicular fluorophore orientation, we observe appreciable enhancements in the fluorescence intensity for the fluorophore in proximity to single nanoparticles (up to 1 order of magnitude). For the dimer systems, we observe significant enhancements in the fluorescence intensity (up to 3 orders of magnitude). We also observe that the change in total radiated power by the systems studied was in excellent agreement with the change in the intensity of the scattered emission along the x-y plane for the systems.

It is important to note that our main goal is to elucidate the effect of single nanoparticles and nanoparticle dimers on fluorophores in their proximity. To this end, we deliberately performed separate calculations for various fixed orientations of the fluorophore relative to the nanoparticles and considered a variety of different system parameters. Of course, in some actual experimental conditions, orientational averaging effects can arise that might prevent observation of some of the features seen here.

Section 2 below gives further details of the calculations and section 3 presents our results. Section 4 summarizes our conclusions.

2. Computational Details

Three-dimensional FDTD simulations were performed using the program FDTD Solutions (version 5.0) from Lumerical Solutions, Inc. (Vancouver, Canada).^11-20 The calculations were performed with the parallel FDTD option on a Dell Precision PWS690 workstation with the following components: Dual Quad-Core Intel Xeon E5320 processors at 1.86 GHz and 8 GB RAM. Additional postprocessing of the FDTD Solutions data was performed using MATLAB (version 7.0) from Math-works (Natick, MA), and OriginPro 7 from Originlab Corp. (Northampton, MA). A time-windowed dipole source, radiating at a fixed wavelength of 420 nm was used to mimic the emission of a commercially available fluorophore, Alexa Fluor 405 (AF 405), from Invitrogen (Carlsbad, CA). This is a soft source, that allows backscattered radiation to pass through it.¹³ In order to maintain the accuracy and stability of the FDTD calculations, the smallest grid size to accurately model the prescribed system without being computationally prohibitive was obtained in an iterative fashion (convergence testing). In our implementation of FDTD, convergence testing was done by starting the first calculation with a grid size of λ₀/20, where λ₀ is the smallest wavelength expected in the simulation, and then reducing the grid size by half in sequential simulations and comparing the results of the calculations. The reduction of the grid size was stopped when we approached a grid size (Δ) where results closely match with the set of results that are obtained from half that particular grid size (Δ/2) and that is also computationally feasible.^11,12,20 For our calculations, we employed a grid size of 0.5 nm for the d = 20 nm sphere and a grid spacing of 1 nm for the d = 40-, 80-, 100-, and 140-nm spheres.

The numerical implementation of Maxwell’s equations in the FDTD algorithm requires that the time increment Δt have a specific bound relative to the spatial discretization Δ (as mentioned above) to ensure the stability of the time stepping algorithm.^11,12,20 Typically, the durations of our simulations were 400 fs, corresponding to an excess of 100 000 time propagation steps for each calculation. The FDTD package employed has frequency-domain monitors that perform discrete Fourier transforms of the time-domain fields while the simulation is running. In this manner, continuous wave information is obtained at any prespecified wavelengths for the various electric and magnetic field components. These fields can then be projected onto the far field to obtain the angular distributions.

All of the calculations were done by assuming a background relative dielectric constant of 1.0. The auxiliary differential equations method was used to implement a realistic, frequency-dependent, and lossy dielectric model for the silver nanoparticle.¹¹ At 420 nm, the main wavelength of interest, it is equivalent to a metallic dielectric constant of ∼-5.5 + 0.22i, in good agreement with an interpolation of the empirical results of Johnson and Christy.²¹

Figure 1 is a schematic illustration of the system studied, where d is the diameter of the silver nanoparticle, s is the surface-surface distance between dimers (and in the case of single particles or monomers-the spacing between the fluorophore to the surface of the particle), θ is the polar angle from the z-axis where 0 ≤ θ ≤ π, and Φ is the azimuthal angle in the x-y plane from the x-axis with 0 ≤ Φ < 2π. The fluorophore is placed at the origin, and a spherical silver nanoparticle or nanoparticle dimer is placed near the fluorophore along the x-axis. In our calculations, the spacing of the metal particles from the fluorophore and the distance between the nanoparticle dimers is varied. It is assumed the excitation stage of fluorescence has occurred and the fluorophore is now emitting dipole radiation. We consider x and y dipole polarizations and examine the resulting angle-resolved scattered emission intensity in the x-y plane. The x orientation of the dipole is perpendicular to the metal nanoparticle surface, and the y orientation of the dipole is parallel to the metal nanoparticle surface. The angle-resolved emission intensity was integrated to compute the total emission intensity in the x-y plane for both the isolated dipole and the dipole in the proximity of the nanoparticles. The fluorescence emission enhancement factor along the x-y plane is computed as

$$\frac{{\int }_0^{2\pi }\mathrm{d}\varphi I\left(\varphi \right)}{{\int }_0^{2\pi }\mathrm{d}\varphi I_0\left(\varphi \right)}$$ (1)

where the integral is carried out in the x-y plane (θ = π/2) at a fixed radius that encompasses the dimer/dipole system. In eq 1, I refers to the intensity or time-averaged Poynting vector of the dimer/dipole system and the intensity associated with the isolated dipole is I₀. The majority of the fluorescence-based experiments involve collection optics (optical fibers and objective lenses) and detectors (CCD cameras and photomultiplier tubes) that collect signal either along a plane or a cone in a plane defined by the numerical aperture of the optics. Hence, it is instructive to calculate the profile of the angular distribution of the emission in a plane and also the emission intensity enhancements in a plane (we chose the x-y plane).

Figure 1.

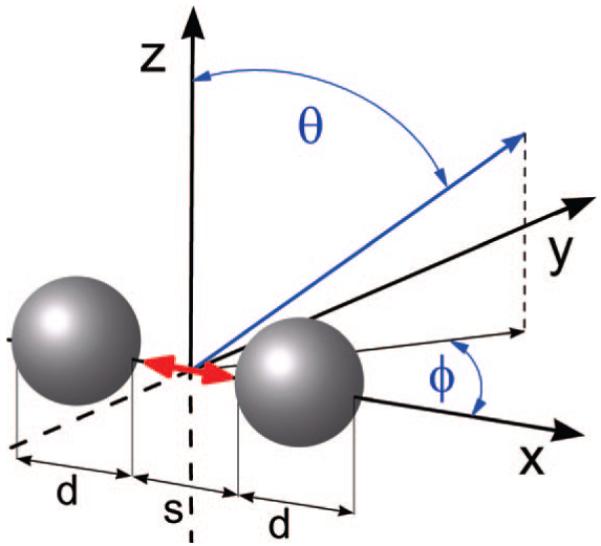
Schematic diagram of the model radiating fluorophore/metal nanoparticle system studied. The red arrow represents the fluorophore, in the systems investigated, the fluorophores will be oriented along either the x or y axes, d is the diameter of the silver nanoparticle, s is the surface to surface distance between dimers (and in the case of the monomerssthe space between the fluorophore and the surface of the particle), θ is the polar angle from the z-axis, where 0 ≤ θ ≤ π, and Φ is the azimuthal angle in the x-y plane from the x-axis with 0 ≤ Φ < 2π.

The enhancement in the total radiated power inferred by integrating the normal flux passing through a closed surface containing the system is given by

$$P_{\mathrm{rad}}∕P_0$$ (2)

where P₀ is the radiated power of a classical dipole in a homogeneous background, which in our case is air/vacuum, and P_rad is radiated power of the dipole in the proximity of the metal nanoparticles. Equation 2 represents the full three-dimensional analogue of eq 1, i.e., it is inferred from integrals of the Poynting vector over a surface enclosing the system or equivalent volume integrals.²² Note that when eq 1 or 2 is less than one it represents quenching as opposed to enhancement.

An enhancement in the total radiated power by a system (system = dipole-nanoparticle complex) when compared to an isolated dipole is indicative of a corresponding increase in the relative radiative decay rate of the system and vice versa.²² This correspondence between quantum and classical theory is valid if normalized quantities are considered and is given by²²

$$\frac{{\gamma }_{\mathrm{rad}}}{{\gamma }_{{\mathrm{rad}}^0}}=\frac{P_{\mathrm{rad}}}{P_0}$$ (3)

where γ_rad⁰ and γ_rad are respectively the radiative decay rate of an isolated classical dipole in a homogeneous background (which in our case is air/vacuum), and the radiative decay rate of the dipole in proximity of the metal nanoparticles.²² In our calculations, since we use a radiating dipole source to model the excited fluorophore, P₀ is well-known.²³ In our implementation of FDTD, we used a set of six frequency-domain surface monitors to create a box around the system and measured the total power radiated by the system by integrating the real part of the Poynting vector over all six surfaces. The power was normalized to the analytic expression for the power radiated by a dipole in a homogeneous dielectric (in this case, air) to get the relative change in power radiated as described in eq 2. The method can be easily verified by calculating the ratio of P_rad to P₀ in the absence of nanoparticles where the expected result is 1, and this gives an estimate of the numerical error. This numerical error is influenced by a variety of factors, including the FDTD mesh size, but is typically on the order of 1% or less. Since we simulate relative changes in decay rates of several orders of magnitude, this numerical error is insignificant. Once the values of P_rad/P₀ are computed, we can make inferences on changes in the radiative decay rate of the Ag-dipole system when compared to the isolated dipole according to eq 3.

3. Results and Discussion

In addition to the isolated dipole, the systems studied in the paper consist of the following: (a) d = 20-nm Ag nanoparticle separated from the dipole by s = 2, 5, and 10 nm. (b) d = 40-nm Ag nanoparticle separated from the dipole by s = 2, 5, and 10 nm. (c) d = 80-nm Ag nanoparticle separated from the dipole by s = 2, 5, and 10 nm. (d) d = 100-nm Ag nanoparticle separated from the dipole by s = 2, 5, and 10 nm. (e) d = 140-nm Ag nanoparticle separated from the dipole by s = 2, 5, and 10 nm. (f) d = 20-nm Ag nanoparticle dimer with surface-surface distance s = 4, 10, and 20 nm. (g) d = 40-nm Ag nanoparticle dimer with surface-surface distance s = 4, 10, and 20 nm. (h) d = 80-nm Ag nanoparticle dimer with surface-surface distance s = 4, 10, and 20 nm. (i) d = 100-nm Ag nanoparticle dimer with surface-surface distance s = 4, 10, and 20 nm. (j) d = 140-nm Ag nanoparticle dimer with surface-surface distance s = 4, 10, and 20 nm.

For all the dimer systems, the fluorophore is located midway between the nanoparticles. For example, in a dimer with a surface-surface distance of 20 nm, the fluorophore is located 10 nm from the surface of each individual nanoparticle. All the calculations were done for both perpendicular (along x-axis) and parallel (along y-axis) orientations of the dipole.

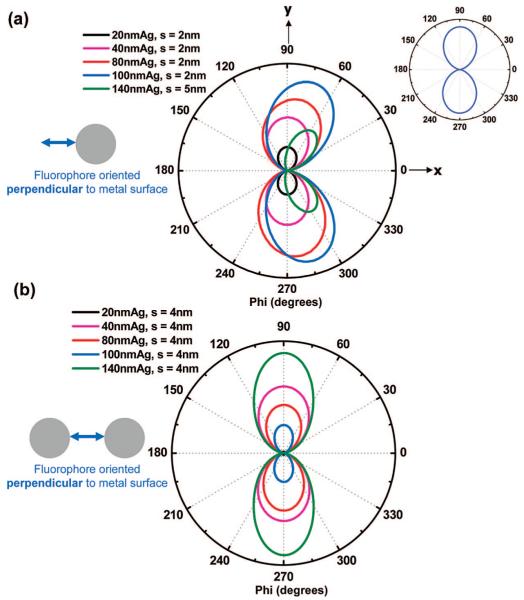
Figure 2 gives polar plots of the emission intensity associated with a circle encompassing the system (system = dipole or Ag-dipole complex). Figure 2a shows for a perpendicular dipole (oriented along x-axis), the angle-resolved intensity in the x-y plane of the far-field scattered emission from the various-sized single nanoparticles at the metal-fluorophore distance s that showed the maximum intensity. The inset in Figure 2a shows the angle-resolved intensity in the x-y plane of the fluorescence emission from an isolated dipole oriented along the x-axis. The scattered emission from the smaller nanoparticles (d ≤ 40 nm) show spatial distribution profiles similar to that of the isolated dipole with peaks near Φ = 90° and 270°, and zero emission near Φ = 0° and 180°, which is expected as the dipole does not radiate along its optical axis. We see that, with an increase in particle size (d > 40 nm), the emission is directed toward the nanoparticle or away from the fluorophore (forward scattering) with the degree of the change in directionality strongly correlated to particle size. This is seen as the scattered emission from the 140-nm Ag nanoparticle has peaks at approximately Φ = 60° and Φ = 300° instead of Φ = 90° and Φ = 270°. These results are related to recently published results from our laboratory that show differences in scattering by silver nanoparticles of incident plane waves and near-field fluorescence.²⁴ One conclusion in that report shows that silver nanoparticles of a certain size (d = 80 nm) scatter the coupled emission back toward the fluorophore for a fluorophore oriented parallel to the metal surface. This was in contrast to the manner in which the particle interacts with plane waves of identical wavelength, where we saw a typical dipole scattering profile around the induced dipole axis in the particle.²⁴ The format of scattered fluorescence emission shown in Figure 2a focused on the angular resolved spatial distribution where the intensity of the emission is in arbitrary units. All the FDTD calculations were done in a similar manner so that the magnitudes of the intensities within a given polar plot can be compared. However, these intensities do not reflect the quantum yield of the system. Due to large-scale enhancements and quenching resulting from the interaction of dimers with fluorophores, the intensities of the spatial distributions of the emission are not comparable between separate FDTD polar plots. The fluorescence enhancement in the x-y plane was calculated by computing the area under the angular-resolved scattered emission curves for all the systems studied and then dividing them with the area under the curve for the emission of the isolated fluorophore. Table 1 (second column) shows the enhancement values from each of the samples studied with the perpendicular dipole orientation. It is clear from these results that we consistently observe a strong enhancement in the intensity of the scattered emission from the different nanoparticles when compared to the isolated dipole. This enhanced intensity of the perpendicular dipole in the proximity of metal nanoparticles can be explained from the perspective of the addition of the fluorophore’s dipole and the induced dipole in the nanoparticles: this configuration allows the dipoles to align along the x-axis head-to-tail, leading to a much larger effective radiating dipole than in case of the isolated dipole. Although only the maximum scattered intensity at a particular distance s for each nanoparticle size is shown in Figure 2a, all the nanoparticles showed consistent enhancements at all the different distances studied, with the 100-nm Ag nanoparticle spaced 2 nm from the fluorophore showing a maximum enhancement of ∼33-fold. Due to the large values of the computed enhancements, plotting the angle-resolved intensity in the x-y plane of the fluorescence emission from the isolated dipole on the same scale with that of the patterns obtained from the nanoparticle-based systems is not convenient. Hence, we have included an inset in Figure 2a that shows the pattern obtained from an isolated fluorophore.

Figure 2.

For a perpendicular dipole (along x-axis), (a) the angle-resolved intensity distribution of the scattered emission in the x-y plane from selected single nanoparticles of a particular size at the metal-fluorophore distance s that showed the maximum intensity. Inset: angle-resolved intensity distribution of an isolated fluorophore. (b) Angle-resolved intensity distribution of the scattered emission in the x-y plane from selected dimers of a particular size at the dimer spacing s that showed the maximum intensity.

TABLE 1. Computed Enhancement/Quenching of the Emission Intensity in the x-y Plane, and the Enhancement/Quenching of the Total Power Radiated (Integrated around a Closed Surface Containing the System) by the Various Nanoparticle Systems Studied with the Dipoles Oriented Perpendicular to the Metal Surface (Along the x Axis)^a.

perpendicular dipole (along x-axis)	enhancement/quenching of emission intensity in the x-y plane	enhancement/quenching of total radiated power
20-nm Ag monomer, s = 2 nm	9.3	9.3
20-nm Ag monomer, s = 5 nm	5.2	4.9
20-nm Ag monomer, s = 10 nm	2.3	2.4
20-nm Ag dimer, s = 4 nm	107	162
20-nm Ag dimer, s = 10 nm	10.1	18.5
20-nm Ag dimer, s = 20 nm	4.5	4.8
40-nm Ag monomer, s = 2 nm	21.1	13.65
40-nm Ag monomer, s = 5 nm	9.78	10.24
40-nm Ag monomer, s = 10 nm	5.52	5.91
40-nm Ag dimer, s = 4 nm	4612	5207
40-nmAg dimer, s = 10 nm	129	139.87
40-nm Ag dimer, s = 20 nm	24	25.38
80-nm Ag monomer, s = 2 nm	31.2	31.2
80-nm Ag monomer, s = 5 nm	31.4	26.5
80-nm Ag monomer, s = 10 nm	18.5	18.3
80-nm Ag dimer, s = 4 nm	3475	3214
80-nm Ag dimer, s = 10 nm	593	572
80-nm Ag dimer, s = 20 nm	140	132
100-nm Ag monomer, s = 2 nm	33	30.1
100-nm Ag monomer, s = 5 nm	29.4	26.5
100-nm Ag monomer, s = 10 nm	21.9	19.4
100-nm Ag dimer, s = 4 nm	4755	5349
100-nm Ag dimer, s = 10 nm	287	355
100-nm Ag dimer, s = 20 nm	98	84.8
140-nm Ag monomer, s = 2 nm	11.9	10.6
140-nm Ag monomer, s = 5 nm	12.3	10.9
140-nm Ag monomer, s = 10 nm	9.9	8.2
140-nm Ag dimer, s = 4 nm	5950	5336
140-nm Ag dimer, s = 10 nm	385.6	361
140-nm Ag dimer, s = 20 nm	68.3	59.6

^aThe enhancement or quenching of the total power radiated indicates changes in the relative radiative decay rates of the Ag-dipole system when compared to the isolated dipole.

Figure 2b shows, for a perpendicular dipole (oriented along the x-axis), the angle-resolved intensity in the x-y plane of the far-field scattered emission from the various-sized nanoparticle dimers at the dimer surface-surface distances s that showed the maximum intensity. Table 1 shows the enhancement values from each of the systems studied with the perpendicular dipole orientation. The most striking feature of the dimer system is the extremely large enhancement factors that are observed when compared to the isolated fluorophore. The enhancements for most cases regularly run into several orders of magnitude with the maximum enhancement of over 5000-fold for the 140-nm dimer spaced at 4 nm from each other (surface-surface). In this case, the fluorophore is located 2 nm from the surface of each of the nanoparticles. Interestingly Figure 2b shows that the angle-resolved scattered emission from the dimer systems of all sizes show spatial distribution profiles similar to that of the isolated dipole with peaks near Φ = 90° and 270°, and zero emission near Φ = 0° and 180°. This is in contrast with the single-particle case in Figure 2a, where large particles tend to display scattered emission that is directed toward the nanoparticle or away from the fluorophore (forward scattering). Another salient aspect of the nanoparticle systems with the perpendicular dipole orientation is that (a) none of the systems leads to a quenching of fluorescence when compared to the isolated fluorophore, and (b) in all cases, the dimer systems always lead to a significantly larger enhancement than the corresponding single-particle (monomer) systems. This can be expected as the fluorophore’s dipole induces two dipoles, one in each of the nanoparticles in the dimer system: this configuration allows all the three dipoles to align along the x-axis head-to-tail, leading to a much larger effective radiating dipole than in case of the isolated dipole and the single-nanoparticle system.

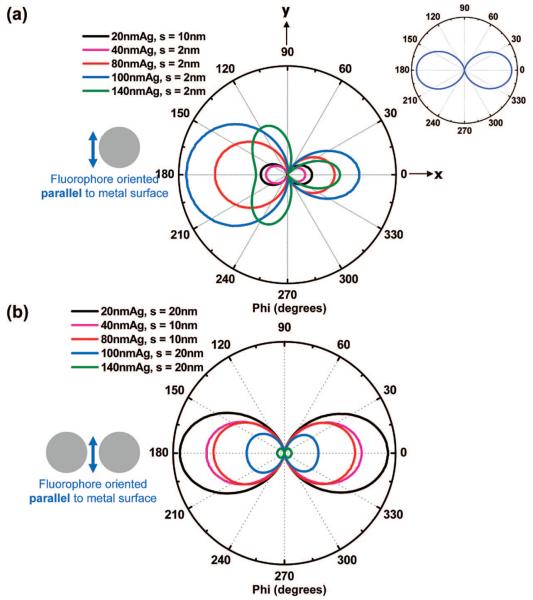
Figure 3, like Figure 2, gives polar plots of the emission intensity associated with a circle encompassing the system (system = dipole or Ag-dipole complex). Figure 3a shows, for a parallel dipole (oriented along y-axis), the angle-resolved intensity in the x-y plane of the far-field scattered emission from the various-sized single nanoparticles at the metal-fluorophore distance s that showed the maximum intensity. The inset in Figure 3a shows the angle-resolved intensity in the x-y plane of the fluorescence emission from an isolated dipole oriented along the y-axis. The scattered emissions from the smaller nanoparticles (d ≤ 40 nm) show spatial distribution profiles similar to that of the isolated dipole with peaks near Φ = 0° and 180° and zero emission near Φ = 90° and 270°, which is expected as the dipole does not radiate along its optical axis. For larger particles however (d > 40 nm), we observe a change in the directionality of the angle-resolved scattered emission profile, with the degree of the change in directionality strongly correlated to particle size. This is seen as the scattered emission from the 140-nm Ag nanoparticle has three peaks at approximately Φ = 0°, 120°, and 240° instead of the two peaks that are seen for smaller particles. This could be due to higher order multipolar contributions to the scattered emission. Another important feature that is seen for the larger particles (d > 40 nm) is that the majority of the emission is directed toward the fluorophore or away from the nanoparticle (back scattering), with the degree of back-scattered emission strongly correlated to particle size. Due to reasons already discussed, the magnitudes of the intensities within a given FDTD polar plot can be compared but are not comparable between separate FDTD polar plots. Table 2 shows the enhancement/quenching values from each of the samples studied with the parallel dipole orientation that were computed in a manner identical to the perpendicular dipole case. The results show that we observe quenching of the intensity of the scattered emission from the small particles (d = 20 and 40 nm) at all separation distances s from the dipole when compared to the isolated fluorophore. The quenching of the parallel dipole orientation is understood from the perspective of the fluorophore’s dipole inducing a dipole in the nanoparticle of the opposite polarity: this configuration cause the dipoles to counteract each other, thus leading to a smaller effective radiating dipole than in the isolated case. Additionally, another reason that might contribute to the quenching is the highly absorbing nature of the smaller particles. Interestingly, for larger particles (d > 40 nm), we observe incremental enhancements for most of the separation distances s between the dipole and particle. The modest nature of this enhancement is manifested by a maximum of ∼2-fold enhancement for the 100-nm Ag nanoparticle spaced 2 nm from the dipole. It is possible that the highly scattering nature of the larger particles might be contributing to the modest enhancements despite the fact that the induced dipoles in the particles are of a polarity opposite to the fluorophore’s dipole moment. Apparently, this cancelation of dipoles does not always occur, and at present, we are investigating the exact factors that result in quenching or enhancement of a fluorophore oriented parallel to the surface of the particles.

Figure 3.

For a parallel dipole (along y-axis), (a) the angle-resolved intensity distribution of the scattered emission in the x-y plane from selected single nanoparticles of a particular size at the metal-fluorophore distance s that showed the maximum intensity Inset: angle-resolved intensity distribution of an isolated fluorophore. (b) Angle-resolved intensity distribution of the scattered emission in the x-y plane from selected dimers of a particular size at the dimer spacing s that showed the maximum intensity.

TABLE 2. Computed Enhancement/Quenching of the Emission Intensity in the x-y Plane, and the Enhancement/Quenching of the Total Power Radiated (Integrated around a Closed Surface Containing the System) by the Various Nanoparticle Systems Studied with the Dipoles Oriented Parallel to the Metal Surface (Along the y Axis)^a.

parallel dipole (along y-axis)	enhancement/quenching of emission intensity in the x-y plane	enhancement/quenching of total radiated power
20-nm Ag monomer, s = 2 nm	0.051	0.042
20-nm Ag monomer, s = 5 nm	0.200	0.180
20-nm Ag monomer, s = 10 nm	0.620	0.590
20-nm Ag dimer, s = 4 nm	0.240	0.280
20-nm Ag dimer, s = 10 nm	0.021	0.029
20-nm Ag dimer, s = 20 nm	0.333	0.280
40-nm Ag monomer, s = 2 nm	0.510	0.300
40-nm Ag monomer, s = 5 nm	0.110	0.058
40-nm Ag monomer, s = 10 nm	0.210	0.180
40-nm Ag dimer, s = 4 nm	0.220	0.240
40-nm Ag dimer, s = 10 nm	0.260	0.280
40-nm Ag dimer, s = 20 nm	0.025	0.029
80-nm Ag monomer, s = 2 nm	1.590	1.410
80-nm Ag monomer, s = 5 nm	1.210	0.860
80-nm Ag monomer, s = 10 nm	0.500	0.360
80-nm Ag dimer, s = 4 nm	0.210	0.244
80-nm Ag dimer, s = 10 nm	0.250	0.304
80-nm Ag dimer, s = 20 nm	0.180	0.248
100-nm Ag monomer, s = 2 nm	2.330	1.758
100-nm Ag monomer, s = 5 nm	1.780	1.275
100-nm Ag monomer, s = 10 nm	1.180	0.765
100-nm Ag dimer, s = 4 nm	0.093	0.137
100-nm Ag dimer, s = 10 nm	0.128	0.175
100-nm Ag dimer, s = 20 nm	0.143	0.203
140-nm Ag monomer, s = 2 nm	1.580	1.166
140-nm Ag monomer, s = 5 nm	1.240	0.904
140-nm Ag monomer, s = 10 nm	0.990	0.721
140-nm Ag dimer, s = 4 nm	0.018	0.031
140-nmAg dimer, s = 10 nm	0.023	0.042
140-nmAg dimer, s = 20 nm	0.032	0.066

^aThe enhancement or quenching of the total power radiated indicates changes in the relative radiative decay rates of the Ag-dipole syste when compared to the isolated dipole.

Figure 3b shows, for a parallel dipole (oriented along y-axis), the angle-resolved intensity in the x-y plane of the far-field scattered emission from the various-sized nanoparticle dimers at the dimer surface-surface distances s that showed the maximum intensity. Table 2 shows the enhancement/quenching values from each of the samples studied with the parallel dipole orientation. The most striking feature of the dimer system is the large quenching that is observed when compared to the isolated fluorophore. The quenching for most cases is quite significant with the maximum quenching of ∼56-fold for the 140-nm dimer spaced at 4 nm from each other (surface-surface). In this case, the fluorophore is located 2 nm from the surface of each of the nanoparticles. Interestingly, Figure 3b shows that the angle-resolved scattered emission from the dimer systems of all sizes show spatial distribution profiles similar to that of the isolated dipole with peaks near near Φ = 0° and 180°and zero emission near Φ = 90° and 270°. This is in contrast with the single-particle case of Figure 3a, where large particles tend to display scattered emission that is directed toward the fluorophore (back scattering). A salient feature of the nanoparticle systems with the parallel dipole orientation is that (a) the great majority of the systems studied lead to a quenching of fluorescence when compared to the isolated fluorophore, and (b) in case of the large particles (d > 40 nm) although there are modest enhancements for the single-particle case at certain metal-fluorophore distances, the corresponding dimer systems always lead to a significantly large quenching than the single-particle (monomer) systems. This can be expected as the fluorophore’s dipole induces two dipoles, one in each of the nanoparticles in the dimer system that is of opposite polarity to the fluorophore’s dipole: this configuration apparently causes the dipoles to counteract each other even more strongly, leading to a smaller effective radiating dipole than in case of the isolated dipole and the single-nanoparticle system.

Thus far, we have presented calculations showing the angle-resolved fluorescence emission for the various systems in one plane of observation, i.e., the x-y plane, and calculated the fluorescence enhancement or quenching in that plane. We believe it is informative to do the calculations along a single plane, since in the majority of experiments dealing with fluorescence-based assays or imaging systems, the collection optics (such as optical fibers and objective lenses) and detectors used (such as CCD cameras and photomultiplier tubes) are planar entities that collect signal either along a plane or a cone in a plane defined by the numerical aperture of the optics. Given these conditions and the ubiquitous use of oriented metal-fluorophore systems, a useful understanding of the profile of the angular distribution of the emission along a plane might aid in maximizing signal collection efficiency.

It is also important to calculate the enhancement or quenching of the total power radiated (in a volume, and not a single plane) around the Ag-dipole systems when compared to the isolated dipole. This was done by calculating the total radiated power inferred by integrating the flux normal to the six sides of a closed box containing the fluorophore-nanoparticle system and then dividing it by the corresponding power radiated by an isolated fluorophore. An enhancement or quenching in the total radiated power by a system is related to relative changes in the radiative decay rate of the system in comparison to an isolated dipole.²² This correspondence between quantum and classical theory is valid if normalized quantities are considered.²² Recently, several groups using both FDTD and other numerical techniques have used changes in the power radiated by a system to compute changes in its relative radiative decay rates.^22,25,26 These findings help to validate our approach. In our simulations, we compute changes in the total power radiated by an Ag-dipole system when compared to that of an isolated dipole (P_rad/P₀). Hence, an enhancement in the power radiated (P_rad/P₀ > 1) by an Ag-dipole system indicates a relative increase in the radiative decay rate of the system when compared to an isolated dipole. The reverse is true in the case of quenching of the power radiated (P_rad/P₀ < 1) by an Ag-dipole system. The fluorescence enhancement or quenching of the emission intensity in the x-y plane, and the enhancement or quenching of the power radiated (in a volume) around each of the systems studied for the perpendicular and parallel dipole orientations is documented in detail in Tables 1 and 2, respectively.

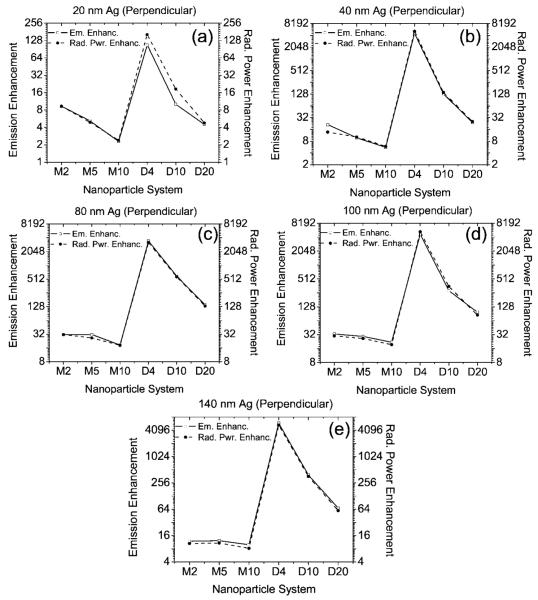
Figure 4 shows, for the perpendicular fluorophore orientation, the computed fluorescence emission intensity enhancement in the x-y plane, and the enhancement in the total power radiated by a system comprising (a) 20-nm Ag nanoparticles, (b) 40-nm Ag nanoparticles, (c) 80-nm Ag nanoparticles, (d) 100-nm Ag nanoparticles, and (e) 140-nm Ag nanoparticles. The x-axis of every figure denotes the nanoparticle system where “M” denotes a single particle or monomer and “D” denotes a dimer. The number after the M represents the space between the fluorophore and the surface of the nanoparticle (in nm), and the number after D denotes the surface-surface distance between the dimer particles (nm). The fluorophore is located midway between the gap in the dimer particles. For example M4 denotes a system comprising a single particle or monomer that is located 4 nm from the fluorophore, and D20 denotes a system comprising a dimer that is 20 nm apart (surface-surface) with the fluorophore in the middle, i.e., 10 nm from the surface of each individual particle. The high enhancements observed for a particular system in each particle size makes it inconvenient to read the data from the other systems in the same scale. Hence, the graphs of Figure 4 were plotted in a semilogarithmic scale (log base 2 along the y-axis) for convenience of observation. Figure 4 clearly shows that the enhancements in the total power radiated by a system closely follow the enhancements in the emission intensity in the x-y plane. Hence, we can use the calculated fluorescence enhancements or the enhancements in the radiated power (Table 1) to estimate the relative changes in the radiative decay rates of the various systems. Figure 4 shows the following: for the (i) 20-nm Ag systems, the highest fluorescence enhancement of over 100-fold and highest enhancements in the total power radiated (highest increase in radiative decay rate) occurs for the D4 sample, i.e., the dimer with a gap space of 4 nm (surface-surface spacing), Figure 4a; (ii) 40-nm Ag systems, the highest fluorescence enhancement of over 4500-fold and highest enhancements in the total power radiated (highest increase in radiative decay rate) occurs for the D4 sample, Figure 4b; (iii) 80-nm Ag systems, the highest fluorescence enhancement of over 3200-fold and highest enhancements in the total power radiated (highest increase in radiative decay rate) occurs for the D4 sample, Figure 4c; (iv) 100-nm Ag systems, the highest fluorescence enhancement of over 4700-fold and highest enhancements in the total power radiated (highest increase in radiative decay rate) occurs for the D4 sample, Figure 4 (d); and (v) 140-nm Ag systems, the highest fluorescence enhancement of over 5300-fold and highest enhancements in the total power radiated (highest increase in radiative decay rate) occurs for the D4 sample, Figure 4e. Figure 4 and Table 1 clearly show that, for the perpendicular oriented dipole (along x-axis), all the monomer and dimer systems show enhanced fluorescence emission and enhanced total radiated power (increased relative radiative decay rates) when compared to the isolated fluorophore. In addition, the results also indicate that the dimers are much more effective than monomers in creating conditions that lead to higher emission enhancements.

Figure 4.

Computed fluorescence emission enhancement along the x-y plane and total radiated power enhancement (integrated around a closed surface containing the system) for the following: (a) 20-nm Ag nanoparticles; (b) 40-nm Ag nanoparticles; (c) 80-nm Ag nanoparticles; (d) 100-nm Ag nanoparticles; (e) 140-nm Ag nanoparticles with the perpendicular fluorophore orientation (along x-axis). The x-axis of every figure denotes the nanoparticle system where M denotes a single particle or monomer and D denotes a dimer. The number after the M represents the spacing of the fluorophore from the surface of the monomer (in nm), and the number after D denotes the surface-surface distance between the dimer particles (in nm). The fluorophore is located midway between the dimer particles.

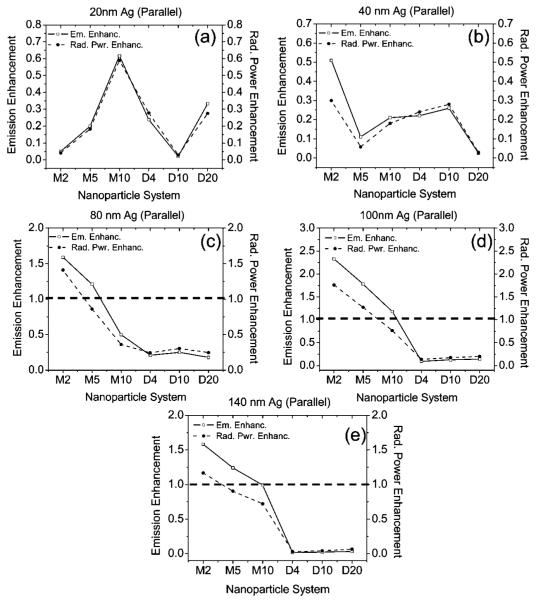
Figure 5 shows for the parallel fluorophore orientation, the computed fluorescence emission intensity enhancement/quenching in the x-y plane, and the enhancement/quenching in the total power radiated by a system comprising the following: (a) 20-nm Ag nanoparticles; (b) 40-nm Ag nanoparticles; (c) 80-nm Ag nanoparticles; (d) 100-nm Ag nanoparticles; (e) 140-nm Ag nanoparticles. The x-axis of Figure 5 is named in an identical manner to Figure 4. The dashed line along 1.0 in Figure 5c-e represents the boundary between fluorescence enhancement and quenching. Values of the emission enhancement (or enhancements in the total power radiated) larger than 1.0 represent enhancements and values lower than 1.0 represent quenching. All such values calculated for the small-particle case in Figure 5a, b showed quenching, and hence, there are no dashed lines. Since all the enhancement values for this dipole orientation were only modest, the need for using a logarithmic scale in the y-axis of Figure 5a-e did not arise (y-axis is in a linear scale). We observe a case similar to that of the perpendicular dipole, where we see changes in the total power radiated by a system (indicative of changes in the radiative decay rate) closely following the computed emission intensity enhancement or quenching in the x-y plane. However, the agreement between the changes in the power radiated and changes in the emission intensity is not as precise as in the perpendicular dipole case. Figure 5 reveals a very interesting phenomenon. It can be clearly seen that, for the parallel case of the dipole, none of the systems studied showed pronounced emission enhancements like we see for the case of the perpendicular dipole orientation. Another important observation is the majority of the systems studied showed quenching of emission when compared to the isolated dipole. We also see that for particle sizes d ≥ 80 nm, the dimer systems lead to a very high degree of fluorescence quenching when compared to the respective monomer systems (as well as the isolated fluorophores). These results indicate that the parallel dipole orientation is not conducive for fluorescence emission enhancements. It is extremely interesting to observe that the orientation of the dipole has such a drastic effect on the emission enhancement conditions. Similar results were observed by Liaw on 2D numerical calculations using the boundary-element method on metallic dimers containing a radiating dipole within the dimer gap space.²⁶ Liaw showed that the system quantum yields (which is the ratio of the radiative decay rate to the total decay rate) is maximum for a dipole oriented along the dimer axis (which in our case is the x-axis), and approaches zero when the dipole oriented normal to the dimer axis (which in our case is the y-axis).²⁶ Such observations are in strong agreement with our FDTD calculations on monomers and dimers and supports our approach.

Figure 5.

Computed fluorescence emission enhancement/quenching along the x-y plane and total radiated power enhancement/quenching (integrated around a closed surface containing the system) of the following: (a) 20-nm Ag nanoparticles; (b) 40-nm Ag nanoparticles; (c) 80-nm Ag nanoparticles; (d) 100-nm Ag nanoparticles; (e) 140-nm Ag nanoparticles with the parallel fluorophore orientation (along y-axis). The x-axis of every figure denotes the nanoparticle system where M denotes a single particle or monomer and D denotes a dimer. The number after the M represents the spacing of the fluorophore from the surface of the monomer (in nm), and the number after D denotes the surface-surface distance between the dimer particles (in nm). The fluorophore is located midway between the dimer particles. The dashed line along 1.0 represent the boundary between fluorescence enhancement and quenching.

It is natural to suspect that surface plasmon behavior is playing a role in our results. For example, we calculated optical spectra of the 80-nm monomer and dimer systems, finding broad plasmon resonances in the 350-500-nm range, consistent with the wavelength (420 nm) of our radiating dipole. In order to verify this possibility, we repeated all our calculations for 80-nm-diameter nanoparticles, treating them as perfect electrical conductors (PECs). A PEC is a loss-less, very high conductivity material that cannot have any surface plasmon excitations. For the case of PEC dimers separated by 4 nm, for example, P_rad/P₀ is reduced to 419 compared to the value of 3475 when the dimers are treated as silver nanoparticles that can support plasmon excitations. In the case of the dipole oriented parallel to the metal surface, P_rad/P₀ for the PEC case is reduced by several orders of magnitude compared to the silver case (which is already small), indicating much more significant quenching presumably due to image dipole cancelation effects.

In all the calculations presented thus far, the dipole is located at the center of the dimer axis, which is also the origin of the coordinate axes used in the calculations (location x = y = z = 0). It is logical to inquire what would be the effect of having the dipole “off center”. In order to answer this question, we performed several calculations where we moved the dipole: (a) 2 nm along the positive y-axis, (b) 20 nm along the positive y-axis, and (c) 40 nm along the positive y-axis. These calculations were done for the 140-nm dimer system spaced 4 nm from each other (control dimer system) for both the dipole orientations. These new movements of the dipole are perpendicular to the symmetry axis. When moving the dipole 2 nm along the y-axis, there was no change in power radiated by either the perpendicular or parallel dipole oriented systems. All changes in power radiated mentioned in this paragraph are with respect to the control dimer case, which had the dipole centrally located along the dimer axis. When moving the dipole 20 nm along the y-axis, the power radiated in the perpendicular dipole orientation dropped by 85% of that of the control dimer case, but was still enhanced compared to the isolated dipole. For the parallel dipole orientation case, the power radiated increased by 205% (2-fold increase) to that of the control dimer case, but was still quenched compared to the isolated dipole. When moving the dipole 40 nm along the y-axis, the power radiated in the perpendicular dipole orientation dropped by 99% of that of the control dimer case, but was still enhanced compared to the isolated dipole. For the parallel orientation, the power radiated increased by 1250% (12-fold increase) compared to that of the control dimer case, but was still quenched compared to the isolated dipole. From these calculations, we can conclude that moving the dipole along the y-axis significantly decreases the enhancement in the power radiated for the perpendicular case. We believe this is because when the dipole is at y = 0, it is capable of efficiently exciting both metal nanoparticle dipolar excitations that leads to a strong additive effect, where the MNP induced dipoles adds to the point dipole source to yield one large dipole that radiates strongly. As the dipole is moved away from the metal along the y-axis, this effect begins to disappear and the dipole becomes less capable of efficiently exciting both the particles. In the parallel case, moving the dipole up along the y-axis dramatically decreases the quenching of the power radiated. We believe that this may be related to image charge effects. When oriented parallel and at y = 0, charge oscillations of a sign opposite to that of the dipole are efficiently set up in the metals that tend to cancel the central dipole and lead to quenching of the radiating power. As the dipole is moved away from the metal along the y-axis, this effect begins to disappear and the dipole becomes more capable of “positively” exciting both particles, and perhaps this might even lead to some enhanced radiating power at large enough displacements along the y-axis.

We should note that seminal calculations on the effect of metals on the fluorophore emission were carried out by Drexhage²⁷ and Chance et al. ²⁸ These calculations involved approximate²⁷ and exact analytical²⁸ solutions for the fluorescence properties of a radiating dipole as a function of its distance from a flat metal surface. It is interesting to note that Kamiski et al. ²² applied an FDTD approach similar to ours to the problem of a dipole near a flat metal surface and found reasonable agreement with the analytical solutions, which feature oscillatory dependences in the radiated power owing to interference effects from reflected waves.²² Our present results dealing with the fluorescence of a radiating dipole in proximity to two metal nanoparticles cannot be directly compared to these results. For example, the role of reflected waves may be diminished in our case owing to the particles being relatively small and their surfaces being curved. Also, in the flat film case traveling surface plasmon polaritons are created whereas in our case localized surface plasmons occur. Nonetheless, it would be an interesting future project to investigate more extensively the distance dependence of the fluorescence in our case, which we only touched on in the above paragraph, and contrast it with the flat film case.

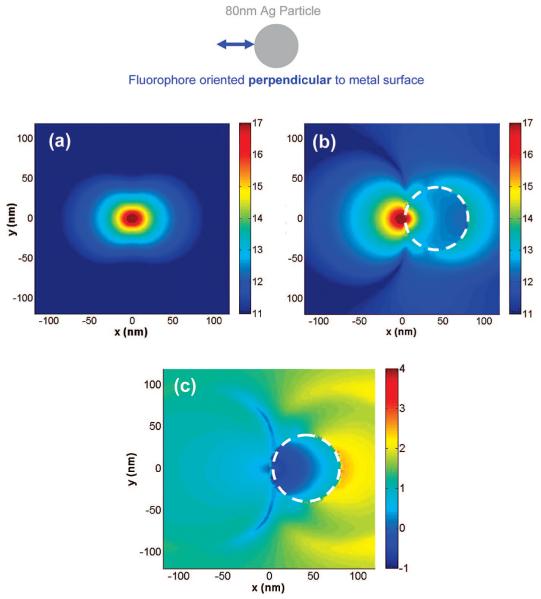
The results of the emission enhancement or quenching in the x-y plane shown thus far have been for far-field scattering of the fluorescence from the nanoparticles. It is also instructive to examine the electromagnetic near-field distributions. Figure 6a shows the electric field intensity in the x-y plane around an isolated perpendicular fluorophore (dipole axis is along the x-axis). It is interesting to note that the isolated dipole has near fields along both the x- and y-axes but, for this orientation, do not create far-field radiation along the x-axis. We have verified, as might be expected, that the intensity of Figure 6a is very similar to the near field of a Hertz dipole.²⁹ Figure 6b shows the near fields around a d = 80-nm silver nanoparticle with the dipole located 2 nm from its surface. Figure 6c is an image of the near-field enhancement and quenching that is generated by dividing the data in Figure 6b by the data in Figure 6a. The images are displayed in the logarithmic scale (base 10) for clarity of presentation. The areas in Figure 6c that correspond in the color map to negative values are areas where we see quenching of the near field around the particle, and areas that correspond to positive values are areas where we see enhancements in the near field. The nanoparticle system studied in Figure 6 shows considerable emission enhancements in the x-y plane (far-field) and increases in total radiated power (increase in relative radiative decay rate) on the order of ∼30-fold when compared to the isolated fluorophore (Table 1). The near fields around the 80-nm Ag particle also show enhancements as seen in Figure 6c. It is interesting to observe that the near field is not enhanced between the particle and the dipole and, while somewhat complex, still shows the largest enhancement for the far or distal side of the particle relative to the dipole.

Figure 6.

Near-field intensity distribution around (a) isolated perpendicular oriented dipole (along x-axis), (b) an 80-nm silver nanoparticle monomer with the dipole located 2 nm from its surface calculated using FDTD, and (c) near-field enhancement and quenching. The white circle denotes the boundary of the nanoparticles. Note all images are displayed in the log scale.

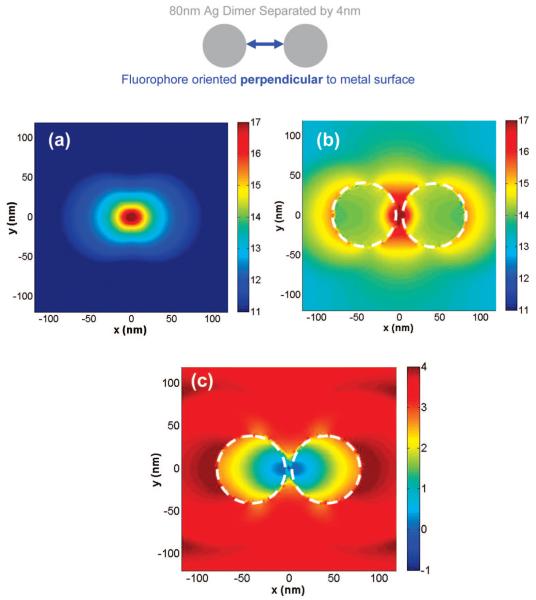
Figure 7a-c show respectively the electric field intensity in the x-y plane around an isolated perpendicular fluorophore (dipole axis is along the x-axis), the near fields around a d = 80-nm silver nanoparticle dimer with a surface-to-surface distance of 4 nm having the dipole is located halfway in between the particles (i.e., 2 nm from the surface of each particle), and the near-field enhancement and quenching image that was calculated in an identical manner to Figure 6c. It is interesting to observe in Figure 7c that the near field is not enhanced in the gap between the particles, but there are intense field enhancements observed around all other areas of the particles. The intense near-field enhancement also extends tens of nanometers from the edge of the particles into the free space as observed by the extent of the red areas in the image. On the side of the nanoparticle dimer that includes the fluorophore, we do not see significant enhancements of the field. The system studied in Figure 7 is the dimer version of the system in Figure 6; i.e., it has identical-sized silver nanoparticles spaced equally from the fluorophore. The results of Figure 7 are very interesting because it shows that for a perpendicular oriented dipole in proximity to silver nanoparticles, the presence of a dimer leads to much larger near-field enhancements than that of a monomer (and of course the isolated dipole). Figure 7c shows large regions in bright and dark red that extend tens of nanometers away from the surface of the dimers in all directions. This is in contrast with the monomer case of Figure 6c where any significant enhancements were both lower in magnitude compared to the dimer case and limited to the side of the nanoparticle distal to the fluorophore. This nanoparticle dimer system displays a high degree of scattered emission enhancement in the x-y plane (far field) and increase in total radiated power (increased relative radiative decay rates) of over 3000-fold when compared to the isolated fluorophore (Table 1). Hence, we see that nanoparticle systems displaying high far-field emission enhancements also show very strong near-field enhancements. In addition, we can also conclude the set of near-field results for monomers and dimers for perpendicular oriented dipoles are in qualitative agreement with the results dealing with changes in the far-field emission intensity and total power radiated of Table 1.

Figure 7.

Near-field intensity distribution around (a) isolated perpendicular oriented dipole (along x-axis), (b) an 80-nm silver nanoparticle dimer with a gap space of 4 nm with the dipole in the middle of the dimer axis calculated using FDTD, and (c) near-field enhancement and quenching. The white circle denotes the boundary of the nanoparticles. Note all images are displayed in the log scale.

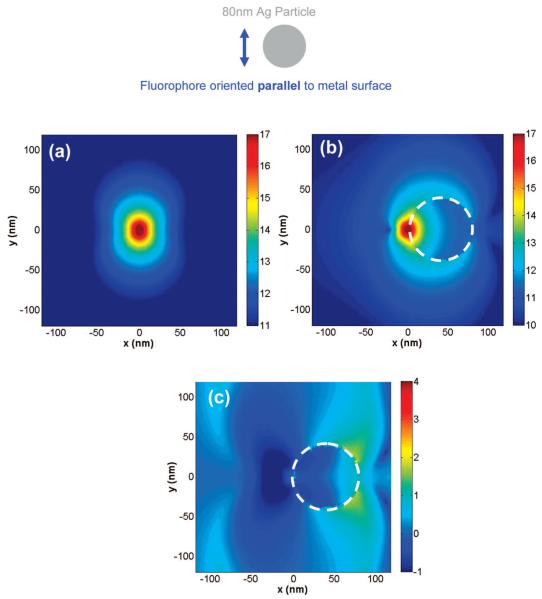
Figure 8a-c show the electric field intensity in the x-y plane around an isolated parallel fluorophore (dipole axis is along the y-axis), the near fields around a d = 80-nm silver nanoparticle with the dipole located 2 nm from its surface, and the near-field enhancement and quenching image respectively. The nanoparticle system studied in Figure 8c shows only very modest emission enhancements primarily in limited “wing-shaped” areas around the side of the nanoparticle distal to the fluorophore. It is interesting to note that there are additional small regions that show slight enhanced near fields in Figure 8c on the side of the location of the fluorophore (far left side of the image), but these regions do not border the nanoparticle. A comparison of Figures 6c and 8c reveals that the near-field enhancements induced around the silver nanoparticles are larger in magnitude for the perpendicular dipoles than for the parallel case. This agrees with our calculations of the changes in both the far-field emission intensity and total power radiated by these systems.

Figure 8.

Near-field intensity distribution around (a) isolated parallel oriented dipole (along y-axis), (b) an 80-nm silver nanoparticle monomer with the dipole located 2 nm from its surface calculated using FDTD, and (c) near-field enhancement and quenching. The white circle denotes the boundary of the nanoparticles. Note all images are displayed in the log scale.

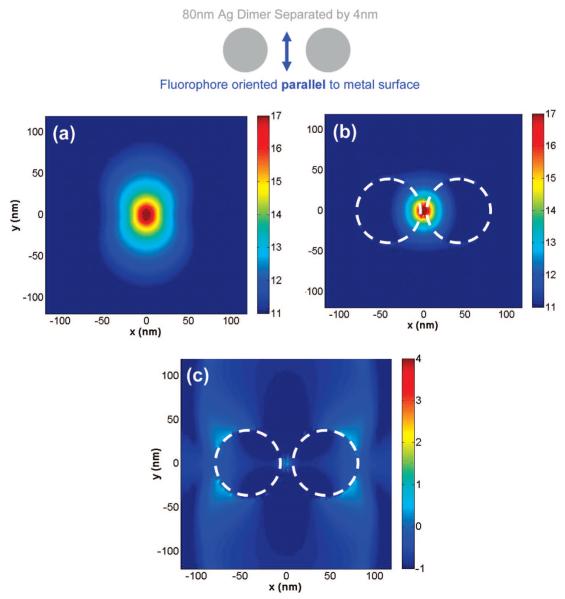
Figures 9a-c show the electric field intensity in the x-y plane around an isolated parallel fluorophore (dipole axis is along the y-axis), the near fields around a d = 80 nm silver nanoparticle dimer with a surface-to-surface distance of 4 nm having the dipole located halfway in between the particles (i.e., 2 nm from the surface of each particle), and the near-field enhancement and quenching image, respectively. The system studied in Figure 9 is the dimer version of the system in Figure 8; i.e., it has identical-sized silver nanoparticles spaced equally from the fluorophore. The results of Figure 9 are very interesting because they show, for a parallel oriented dipole in proximity to silver nanoparticles of large sizes (where d ≥ 80 nm), the presence of a dimer leads to quenching of the emission compared to that of a monomer (and the isolated dipole). In most areas of Figure 9c, we observe a strong degree of quenching of the near fields around the dimer as seen by the large regions in dark blue (representing quenching in the color map) that extends tens of nanometers away from the surface of the dimer in all directions. This is in contrast with the monomer case of Figure 8c where there were areas of modest enhancements around the nanoparticle. Hence, the set of near-field results for monomers and dimers for parallel dipoles are in qualitative agreement with the results dealing with changes in the far-field emission intensity in the x-y plane and total power radiated of Table 2. Figures 6c, 7c, 8c, and 9c show that, for a given system comprising of a fluorophore at a fixed distance away from a metal nanoparticle surface, the extent of emission enhancements in the near field are highly dependent on fluorophore orientation and the presence of a single particle or a dimer. Such spatial variations in the near-field enhancements are not easily inferred from far-field information such as the angular distribution of the emission intensity or even calculations involving changes in the total radiated power (radiative decay rate changes). Thus, they provide additional insight into the nature of metal-enhanced fluorescence that is interesting from the perspective of applications involving molecular spectroscopy.

Figure 9.

Near-field intensity distribution around (a) isolated parallel oriented dipole (along y-axis), (b) an 80-nm silver nanoparticle dimer with a gap space of 4 nm with the dipole located in the middle of the dimer axis calculated using FDTD, and (c) near-field enhancement and quenching. The white circle denotes the boundary of the nanoparticles. Note all images are displayed in the log scale.

4. Conclusions

We presented a detailed computational study of the effect on the emission of an excited fluorophore when it is between nanoparticle dimers and contrasted our results with an isolated fluorophore and fluorophore-monomer cases. The FDTD method was used and a realistic model for silver, allowing for surface plasmon excitations, was employed. The excited fluorophore was modeled as a radiating dipole source, and a variety of particle sizes and fluorophore-particle distances were studied. To the best of our knowledge, this is the first such FDTD study that addresses metal-enhanced fluorescence between silver nanoparticle dimers.

Several interesting results emerged from our work. First, the far-field emission intensity computed in the x-y plane for the dimer systems shows significant variation with the direction of fluorophore orientation. When the fluorophore is oriented perpendicular to the metal surface, we observe significant enhancements in the emission intensity, up to a maximum of an excess of 4500-fold compared to the isolated fluorophore. For this orientation, all the monomer (single nanoparticle) and dimer systems investigated showed enhancements in emission when compared to an isolated fluorophore. In addition, we also observe that the dimer systems display a greater enhancement with respect to the corresponding monomer system. The change in the total power radiated through a closed surface containing the fluorophore in the proximity of various metallic nanoparticles is computed with respect to an isolated fluorophore. This change in the radiated power is indicative of changes in the radiative decay rates of the fluorophore-nanoparticle system. It is seen that there are strong agreements between changes in the total power radiated (or relative radiative decay rates) with changes in the fluorescence emission intensity calculated in the x-y plane. When the fluorophore is oriented parallel to the metal surface, we observe that the dimer systems studied showed significant quenching of the emission when compared to the isolated fluorphore. For larger particle sizes (where d ≥ 80 nm), the dimer systems studied showed quenching of the emission when compared to both the isolated fluorphore and their corresponding monomer systems. Strong agreements between changes in the total power radiated (or changes in the relative radiative decay rates) with fluorescence emission enhancements/quenching in the x-y plane are also observed for the parallel dipole orientation. Our results clearly indicate vast differences in the mode of interaction between perpendicular and parallel oriented dipoles with metal nanoparticles. It is also shown that the exact location of the dipole in between the nanoparticle dimers greatly affects the degree of enhancement or quenching of the radiated power that is observed. It is found that the maximum amount of enhancement or quenching is obtained for a dipole located perfectly in the center of the dimer axis. It is important to note that the calculated increases in total power radiated or emission enhancements in the x-y plane may not represent actual experimentally observed increases in fluorescence intensity. This is because our calculations do not take into account the localized high fields in the vicinity of the nanoparticles that are created by their interaction with the incident light. This results in increased rates of excitation for a fluorophore located in these regions of high localized excitation fields. In this study, we focus only on the emission side of fluorescence. Finally, inspection of intensity patterns reveals how, in the near field, very specific regions around the nanoparticles experience field enhancements and quenching. This type of result is not easily inferred from far-field observations and is relevant to potential applications that would involve spatially resolved molecular spectroscopy or detection using fluorescence. We understand that our computations are only the first step in understanding the nature of the interaction between excited-state fluorophores and metal nanoparticles and believe our results give us a reason for optimism for eventually implementing fluorophore-metal dimer-based systems in the detection of biologically relevant binding events.

In the future, we plan to study the interaction of more complex metallic nanostructures with fluorophores using the computational modeling approach presented here. This should enable the rational design of nanostructures and devices, which can make use of the metal-enhanced fluorescence and related phenomena.