Top-down laminar organization of the excitatory network in motor cortex

Abstract

Cortical layering is a hallmark of the mammalian neocortex and a major determinant of local synaptic circuit organization in sensory systems. In motor cortex, the laminar organization of cortical circuits has not been resolved, yet their input-output operations are crucial for motor control. Here, we developed a general approach for estimating layer-specific connectivity in cortical circuits, and applied it to mouse motor cortex. From these data we computed a laminar presynaptic→postsynaptic connectivity matrix, W_post,pre, revealing a complement of stereotypic pathways dominated by layer 2 outflow to deeper layers. Network modeling predicted, and experiments with disinhibited slices confirmed, that stimuli targeting upper but not lower cortical layers effectively evoked network-wide events. Thus, in motor cortex, descending excitation from a preamplifier-like network of upper-layer neurons drives output neurons in lower layers. Our analysis provides a quantitative wiring diagram framework for further investigation of the excitatory networks mediating cortical mechanisms of motor control.

Motor cortex is centrally involved in mammalian motor behavior and the cortical control of movement. Motor cortex has long been studied in terms of its motor output, and much is known about how corticospinal neuron activity correlates with movement. The large-scale networks linking motor cortex with other cortical and subcortical motor systems are also well characterized. Multiple long-range excitatory input pathways converge on primary somatic motor cortex (M1). These include corticocortical projections (carrying ipsi- and contralateral sensorimotor information), thalamocortical projections (carrying cerebellar and basal ganglionic information via the thalamic ventrolateral nucleus, as well as sensory and other information via multiple additional thalamocortical pathways), and neuromodulatory projections from brainstem and other areas (reviewed in ¹). Major outputs from M1 include projections to spinal/bulbar motor centers, striatum, thalamus, subthalamus, red nucleus, and pons. All excitatory neurons in M1 are pyramidal neurons projecting to one or several of these long-distance targets. Corticofugal outflow to the pyramidal/extrapyramidal motor systems and thalamus originates primarily from cells in middle and deeper layers, while corticocortical connections arise from cells in both upper and deeper layers.

Compared to the relatively well characterized long-range input-output connectivity of motor cortex, far less is known about the intrinsic organization of M1 ^{2, 3}. A cardinal difference between motor and sensory cortex at the local circuit level is the presence of spiny stellate cells in thalamorecipient layers (L4) in sensory areas, which distinguishes granular (sensory) from agranular (motor/frontal) cortex. Because stellate cells densely innervate superficial layers (L2/3), these ascending intracortical projections (L4→2/3) figure prominently in most wiring diagrams for sensory cortex (for reviews, see 4-11). Several additional ascending projections identified in sensory cortex appear to contribute importantly to its local circuit organization - for instance, L5A→2/3 projections in barrel cortex ^{12, 13}, or L6→4 projections in visual cortex (reviewed in ^{4, 5}). These ascending pathways have not been investigated in detail in M1. A prevailing view of the local circuit organization of M1 has been that it is dominated by horizontal pathways in upper and lower layers that provide the structural substrates for motor map organization and plasticity (for reviews, see 2, 3). However, descending inputs from L3 cells to corticospinal neurons have also been identified ^{14, 15}, and the relative contributions of intra- and interlaminar excitatory pathways to the basic excitatory circuit in M1 are unknown.

Local circuits in M1 are critically involved in mediating motor-based behavior, as they receive and integrate convergent inputs from sensory and motor systems, and their collective and coordinated output carries the corticofugal signals generating movement. The neural operations performed in M1 are accomplished not by corticospinal neurons acting alone but as an active local network of projection neurons connecting and interacting in highly specific ways. Determining the local circuit organization of motor cortex is therefore an essential step towards a detailed understanding of cortical mechanisms underlying motor control. This could also illuminate whether local circuits in M1 are functionally specialized, like the long-distance circuits they interact with, or whether they share the cortical circuit design seen in sensory areas.

Here, we developed a connectivity matrix approach for estimating a layer-specific wiring diagram for cortical circuits. Our strategy was to map the functional layout of the pyramidal neuron network across layers in motor cortex by recording from neurons located in all layers, and, for each one, sampling the strength of connections from presynaptic neurons located in all layers. This provided a broad yet detailed survey of excitatory circuits in motor cortex, revealing pyramidal-pyramidal pathways as a function of the laminar locations of the pre- and postsynaptic neurons. Analysis of the connectivity matrix, together with additional investigations of excitatory flow within the network, revealed a strong directionality in the flow of excitation, from upper to lower layers.

RESULTS

For this analysis, we used laser scanning photostimulation (LSPS) based on glutamate uncaging. Among the advantages of LSPS for this study are that it allows rapid electrophysiologically based imaging of local synaptic pathways, by recording synaptic responses from a single (postsynaptic) neuron while stimulating small clusters of (presynaptic) neurons with high spatial resolution, avoiding axons of passage. In mouse brain slices containing the forelimb representation area of somatic motor cortex (M1) (Fig. 1a, Supplementary Fig. 1), calibration experiments indicated that in all cortical layers photostimulation caused approximately ~100 neurons within ~70 μm of the beam to fire ~1 spike per neuron per stimulus (see Methods, Supplementary Methods, and Supplementary Fig. 2). Only monosynaptic activity was evoked under the recording conditions, which included elevated divalent cation concentrations and NMDA receptor blockade to dampen excitability. Inhibitory circuits were left intact, and excitatory currents were isolated by holding at -70 mV, the measured reversal potential for GABAergic inhibitory conductances.

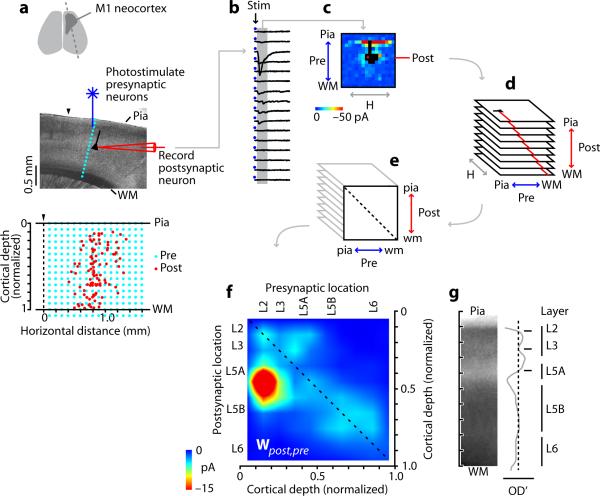
Figure 1.

Experimental approach. a, Slice preparation and recording arrangement. Dashed line (top), slice orientation; (▼), posterior border of M1. Bottom plot: locations of the recorded (postsynaptic) neurons (red), and of the (presynaptic) stimulation sites in the mapping grid (blue), which for each neuron was centered horizontally over the soma. b, Traces from one column of stimulation (Stim) sites. c, One neuron's synaptic input map. Black pixels: traces excluded due to direct dendritic stimulation. d, Maps from all postsynaptic neurons were sorted by postsynaptic laminar location, and binned and averaged. e, Maps in d were projected onto a single plane by averaging along map rows; i.e., collapsing the horizontal (H) dimension. f, The resulting map (interpolated for display) is a laminar connectivity matrix, W_post,pre, representing presynaptic→postsynaptic pathway strengths. Intralaminar pathways are on the main diagonal (dashed line). Color scale compressed by ~50% to show weaker pathways. g, Average of 15 brightfield images of M1, showing cortical lamination pattern. OD', first derivative of image intensity (relative optical density); zero crossings correspond approximately to layers as labeled.

We recorded from 102 pyramidal neurons in cortical layers (L) 2 through 6 (L1 lacks pyramidal neurons) (Fig. 1a). For each neuron, a square stimulus grid was oriented to span all layers, horizontally centered on the soma. The mapped area covered 2.25 mm², extending 0.75 mm to either side of the soma. LSPS responses were analyzed to map the neuron's local sources of excitatory input (Fig. 1b,c). Direct somatodendritic stimulation sites were excluded; thus, the maps underestimate the contribution of very local (<100 μm) pathways to the overall circuit. Each neuron's laminar position was noted as the normalized distance along the radial axis of the cortex; that is, along the pia-white matter axis (pia = 0 and white matter = 1); for convenience, we use `laminar position' throughout this study as shorthand referring to the normalized position of the soma location along this radial axis. Maps were sorted by laminar position and binned (10 bins, 140 μm each, n ≥ 11 neurons per bin except bin 1, which had zero neurons because it spanned L1) (Fig. 1d), and an average map was calculated for each bin. This stack of 9 average maps (Fig. 1d) was then projected onto one plane by averaging along the map rows; i.e., collapsing the horizontal dimension (Fig. 1e). This projected image constitutes a laminar connectivity matrix, W_post,pre, representing the weights of synaptic pathways in the pyramidal neuron network in terms of presynaptic and postsynaptic locations along the radial (laminar) dimension (Fig. 1f).

To relate this matrix to specific layers, we analyzed brightfield images of M1 slices, identifying a laminar pattern similar to adjacent somatosensory (S1) barrel cortex, but with no L4 and an expanded L5B (Fig. 1g). In M1, L5A occupied a zone similar to L4 in somatosensory cortex, consistent with the notion of rodent M1 as an agranular cortex lacking stellate cells ^{1, 16, 17}.

Pathway strengths (matrix values; pixels in W_post,pre) were distributed non-exponentially with clusters at intermediate and high values (Fig. 2a) ¹⁸. Major pathways appeared as hotspots in the connectivity matrix, as illustrated by thresholding near these intermediate values (Fig. 2b). The strongest pathway and largest hotspot was L2/3→5A/B (Fig. 1f), which reached a peak corresponding presynaptically to L2 and postsynaptically to the L5A/B border. This L2/3→5A/B descending pathway accounted for one-third (34%) of total synaptic current in the circuit. Multiple weaker pathways were also evident. The main ascending interlaminar pathway was L5A→2/3, which resembled L4/5A→2/3 pathways in rodent sensory cortex ^{12, 13, 19, 20}. Horizontal (intralaminar) pathways - along the main diagonal of W_post,pre - were strongest in L2, dipped in L3/5A (ratio 0.32; P < 0.01) before returning to higher levels across L5A/B through L5B/6, and falling in L6 (ratio 0.22; P < 0.01) (Fig. 2c). In the lower layers, a network of short-range ascending, descending, and horizontal pathways spanned L5B/6. Examples of average synaptic input maps corresponding to particular rows in W_post,pre, are shown in Fig. 2d. Plotting total synaptic input (calculated by summing along rows in W_post,pre) as a function of cortical layer revealed a sharp peak at the L5A/B border, exceeding the total input to L2/3 and L6 by factors of ~3 and ~10 (P < 0.01), respectively. Total input was similar across upper layers (P > 0.5). The overall form of W_post,pre remained similar even when the middle (i.e., perisomatic) columns of input map data were excluded from the analysis (Supplementary Fig. 3), indicating that the strong descending excitation that was observed was not simply a slice-related artifact - for instance, differential preservation of radially aligned axonal pathways in the home column - but instead was a general property of the network pertaining to laterally offset (i.e., oblique) as well as vertically aligned input pathways.

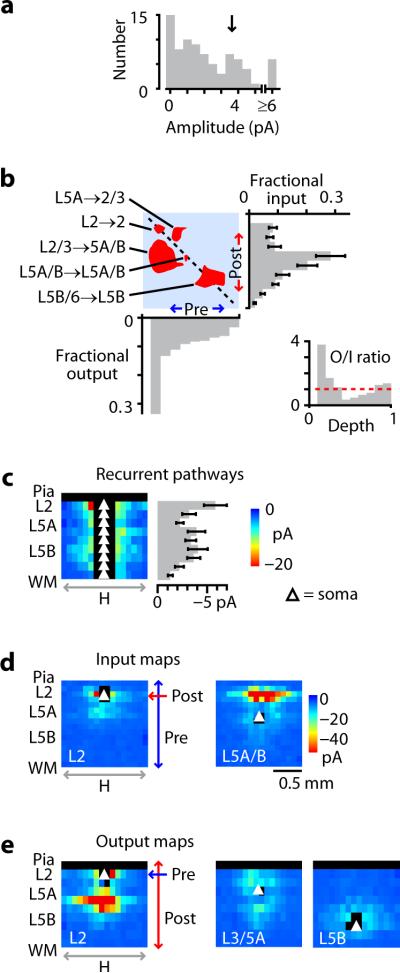
Figure 2.

Synaptic input and output in the local circuit. a, Distribution of pathway strengths, showing peak at intermediate values (arrow). b, Binarized version of the connectivity matrix, thresholded (at arrow in a) to illustrate major pathways (red areas), with plots showing input (right; error bars: s.e.m.), output (bottom), and ratio of output to input (inset) as a function of cortical depth. Horizontal dashed line in inset indicates ratio of 1. Fractional input and output were calculated by summing along rows and columns, respectively, and normalizing by the overall total. c, Recurrent pathways. Each row in the image corresponds to data in the original averaged input maps indexed by level as indicated by the red lines in Fig. 1d. Error bars: s.e.m. d, Input maps, corresponding to rows in W_post,pre, for L2 neurons (left) and L5A/B neurons (right). e, Output maps, corresponding to columns in W_post,pre, for L2 (left), L3/5A (center), and lower L5B (right) neurons. See Fig. 2d for color scale.

Synaptic output maps could also be extracted from this same data set simply by viewing the data in the dimension orthogonal to the input maps. Since rows in W_post,pre represent synaptic `input' - one postsynaptic location, all presynaptic locations (Fig. 2d) - then conversely, columns represent synaptic `output' - one presynaptic location, all postsynaptic locations (Fig. 2e). That is, whereas input maps show local `synaptic receptive fields' (fan-in), output maps show local `synaptic projective fields' (fan-out) ²¹. The output map for L2 neurons showed broadly distributed, strong outputs across middle layers, plus local outputs in L2, whereas output maps for neurons at other laminar levels were weaker and topographically different, extending bidirectionally upward and downward for L3/5A neurons but remaining local for L5B neurons (Fig. 2e). Summing W_post,pre along columns to plot total output as a function of cortical layer revealed an unexpected relationship: total synaptic current varied essentially monotonically as a function of presynaptic depth, from a sharp peak in L2 to a minimum in L6 (Fig. 2b, right). Accordingly, local output/input ratios were high in upper layers, low in middle layers, and balanced in the deepest layers (Fig. 2b, inset).

The matrix represents the relative average strength of pathways connecting small clusters of pre- and postsynaptic neurons (approximately ~100 presynaptic and ~10 postsynaptic neurons). These data were recorded under excitation-dampening conditions designed to restrict feedforward excitation to monosynaptic connections. To explore how information might propagate further forward across multiple synapses in the M1 local circuit, we used the laminar connectivity matrix data directly in a neural network simulation (Fig. 3a), where the vector p is a laminar profile of initial input values, on which the network (c W_post,pre) operates to produce an output vector a, which is then fed back into the network. `Gain' in the network is globally scaled by c. The nodes in this simulated network can be interpreted as representing the average activity of small clusters of pyramidal neurons located along the radial axis of the cortex in M1.

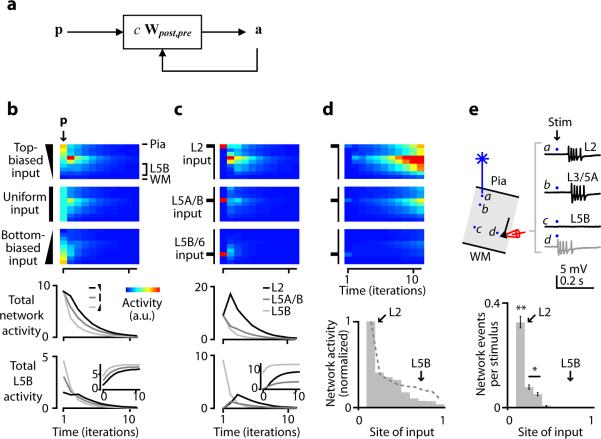
Figure 3.

Network activity in simulated circuits and disinhibited slices. a, Network model. b, Flow of excitatory activity in the network model. Images show simulated network activity over time, for biased patterns of input (p) as indicated. Plots show instantaneous activity summed over all layers (upper plot) or only L5B (lower plot; inset, cumulative plot of same data). c, Flow of excitatory activity in the network model for inputs targeted to different layers. d, Network model as in b, but scaled to induce runaway excitation. Lower plot shows network activity as a function of laminar level of input. For comparison, total output per layer is also plotted (dashed line, data from summed output plot in Fig. 2b). e, Network-wide events were evoked by photostimulation under conditions of mild disinhibition (1 μM SR95531) and recorded in L5B neurons at a variety of horizontal locations in M1. Schematic illustrates recording arrangement. Traces show epileptiform events induced by photostimulation in different layers, recorded from a L5B neuron in cell-attached mode. Direct local stimulation of the neuron caused local short latency events (gray trace). Upper-layer stimulation evoked longer latency network-wide events (black traces). Plot shows average probability (± s.e.m.) of evoking network events as a function of laminar level of input. The likelihood of a stimulus evoking an event was greatest for L2 stimuli (**, P < 0.01 compared to deeper layers), intermediate for other upper-layer stimuli (*, P < 0.05 compared to deeper layers), and at or near zero for lower-layer stimuli.

We first evaluated network dynamics for small c, an overdamped regime in which activity always decays (Fig. 3b). For inputs distributed across layers, those biased towards upper layers were most effective at driving total network activity (Fig. 3b). However, over time the activity in the lower layers reached comparable levels for any laminar pattern of input, due to the downward flow of excitation: inputs directed to L5B caused large, transient (`phasic') activity in L5B, whereas inputs directed to upper layers caused weaker but prolonged (`tonic') activity in L5B (Fig. 3b). Similar results were obtained for inputs focused at different laminar levels (Fig. 3c).

Next we explored network dynamics with large c, an underdamped regime characterized by exploding activity (Fig. 3d). Focusing the inputs at different laminar levels showed that network activity exploded much faster for inputs to upper than for lower layers, and fastest with L2 stimulation. The model also predicted substantially more activity for inputs to the other upper layers (L3/5A) as compared to inputs to the deeper layers (L5B/6), a degree of directionality beyond that expected on the basis of output strength alone (Fig. 3d).

If inhibitory circuits in motor cortex provide broadly tuned gain control for feedforward excitatory activity, as they do in sensory cortex ^{5, 22}, then blocking inhibition could offer a way to evaluate experimentally the predicted effects of changing the global scale c. The data for Wpost,pre were recorded under `low-gain' (small c) conditions, with inhibition present and excitatory activity dampened to allow only monosynaptic events and to prevent feedforward excitation. The dampening role of inhibitory circuits was in fact essential to prevent runaway excitation (epileptiform events); indeed, disinhibition is used to study epilepsy in cortical slices <sup>23</sup>. Therefore, to mimic the `high-gain' (large c) conditions investigated in the model, we promoted feedforward excitation by partially blocking inhibitory circuits with 1 μM SR95531, a GABA_A receptor antagonist. Network-wide events did not occur spontaneously (as they did at 2-10 μM) but could be evoked by photostimulation (Fig. 3e), and could be recorded from neurons located anywhere in the slice, reflecting their global, propagating nature. We recorded from L5B/6 neurons (n = 11 neurons, 11 slices) and mapped the laminar distribution of sites evoking these network events (Fig. 3e). Epileptogenicity, expressed as the likelihood of evoking an event per stimulus, was strongly layer-dependent with a maximum for L2 stimuli, lower values for other upper-layer stimuli, and values at or near zero for lower-layer stimuli. Even under fully disinhibited (10 μM SR95531), strongly excitable conditions (high stimulus intensities, low divalent concentrations, NMDA receptors unblocked), although the epileptogenicity of L3/5A increased, L5B stimuli remained non-epileptogenic (n = 10 neurons, 10 slices). This was not because L5B neurons were inexcitable; they reliably responded to perisomatic stimuli in L5B with strong, event-like responses, but this locally evoked activity failed to spread through the network. The measured laminar profile of hyper- and hypoexcitability (Fig. 3e) closely resembled that obtained by simulation (Fig. 3d). This result, which contrasts with prior observations of middle-layer epileptogenicity in somatosensory cortex ²³, does not preclude the possibility that additional intrinsic and circuit level mechanisms also contribute to epileptogenicity ²⁴, but does demonstrate the presence in M1 L2 of two key circuit-level requirements for an epileptogenic source ²³ - strong feedforward outflow, and recurrent excitation (Fig. 2c,e). More generally, our results indicate that our experimental and theoretical analysis at the circuit level captured major features of the functional structure of the excitatory network.

DISCUSSION

Using a photostimulation-based strategy, we mapped the strengths of local pathways interconnecting pyramidal neurons across and within layers in motor cortex. This allowed us to estimate a laminar connectivity matrix, representing the functional organization of the excitatory local circuit in this neocortical area centrally involved in the cortical control of movement. Our results provide several lines of evidence for top-down organization in the local excitatory network within M1: total excitatory output showed a top-down gradient (Fig. 2b), interlaminar synaptic connectivity was dominated by descending pathways from L2 (Fig. 1f, 2e), the flow of excitatory activity in network simulations was downwardly biased (Fig. 3b-d), and, runaway excitation in disinhibited slices was readily triggered in top-most but not bottom-most layers (Fig. 3d,e).

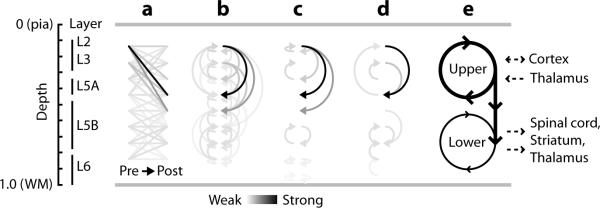
To visualize the circuit as a quantitative wiring diagram, we plotted W_post,pre as a network of pathway arrows (Fig. 4a-d). A schematic diagram summarizing our findings (Fig. 4e) depicts the M1 excitatory circuit as a two-loop system, with strong L2/3→5A/B pathways driving recurrent excitation in a preamplifier-like upper-layer circuit, which also supplies feedforward excitation to lower-layer circuits containing corticospinal, corticothalamic, corticostriatal, and other subcortically projecting output neurons. Interestingly, the M1 wiring diagram with a single dominant outflow pathway obeys at this intra-areal level a `no-strong-loops' rule proposed to govern inter-areal connectivity in sensory cortex ²⁵.

Figure 4.

Wiring diagrams. a, Quantitative representation of the strongest 95% of pathways in W_post,pre. Matrix values were used to color-code lines connecting presynaptic locations (left) to postsynaptic locations (right). b, Same data, but with matrix values color-coded as arrows; ascending pathways are on the left, descending pathways on the right, and horizontal pathways are shown as small arrows on both sides. c, Wiring diagram showing only the strongest input pathways for each postsynaptic layer (W_post,pre row maxima). d, Wiring diagram showing only the strongest output pathways for each presynaptic layer (W_post,pre column maxima). e, Qualitative interpretation. Strong L2 outflow drives both a strong upper loop and a weak lower loop. In M1, corticocortical and thalamocortical inputs target upper layers, and corticospinal and corticothalamic outputs arise primarily from lower layers.

Notably, the upper loop spans levels at which external excitatory inputs enter M1 via corticocortical and thalamocortical channels targeting L3 in particular ^{1, 26, 27}. Prior observations have indicated strong connections between L3 pyramidal neurons and L5 corticospinal neurons ¹⁵. Our findings show that M1 L2/3 neurons converge powerfully onto L5 pyramidal neurons in general, not just corticospinal neurons, which are sparsely distributed and therefore underrepresented in our sample ².

The question of how the excitatory local circuit in M1 compares to sensory cortex is a challenging one, as direct comparison would require a comparable data set for sensory cortex, and indirect comparisons are confounded by differences in cell types, species, and techniques. Moreover, the issue of whether local circuit organization is fundamentally conserved or highly differentiated across cortical areas remains controversial (see ^{5, 28-30}). At the structural level, sensory circuits have been quantitatively estimated using computational neurogeometry approaches in cat V1 ^{31, 32} and rat S1 ^{20, 33, 34}. However, pathways computed from axon-dendrite overlap (Peters' rule; see 31, 35, 36) do not necessarily predict functional connection strengths. For example, in ascending pathways in barrel cortex, the ratio of functional (LSPS) to structural pathway strength (neurogeometry) varies more than 10-fold in a pathway-specific manner, implying considerable functional tuning within the structural layout ²⁰. At the functional level, consensus has emerged both for V1 and S1 that the flow of excitation within the local circuit is radially bidirectional, with a strong upward component ^{5, 8, 37}. Multiple feedforward pathways ascend in parallel to converge on L2/3 pyramidal neurons, which project to higher-order cortical areas; descending pathways converge on infragranular neurons, connecting with various cortical and subcortical targets.

In contrast, our results suggest that the local excitatory circuit in M1 comprises a restricted subset of these pathways, with a predominantly top-down excitatory organization. Of course, absence or weakness of any pathways in our data set must be qualified by considerations of detection efficiency and the possibility of undersampling, especially on the postsynaptic side. Our sample of ~100 postsynaptic neurons was a very small fraction of the total number of neurons in the slice in mapping region (~10⁵). On the other hand, presynaptic sites were densely sampled: for each postsynaptic neuron we tested inputs from >200 local sites, and with ~100 neurons stimulated per site, a lower estimate for the overall total number of presynaptic neurons tested in this study is large (100 • 200 • 100 = 2 • 10⁶). Also, our stimulus parameters (0.1 mm grid spacing) together with the resolution of photostimulation in our system (~0.07 mm) were sufficient to image circuits with sub-laminar resolution. We emphasize that extensive averaging in the connectivity matrix analysis will cause under-representation of rare, sparse, or functionally weak pathways in W_post,pre (for discussion of related technical issues see Supplementary Methods).

The interlaminar pathway most conspicuously weak in M1, compared to sensory cortex, was the ascending lower→middle layer pathway corresponding to L6→4. This pathway is anatomically strong in V1 of rodents and other mammals (reviewed in ^{4, 5}). Its weakness in M1 is hard to ascribe to technical factors, because L6 cells were as photoexcitable as other neurons (Supplementary Fig. 2), and individual middle-layer neurons in our sample did in some cases receive inputs from L6 (data not shown). As a similar paucity of L6→4 inputs has been observed using LSPS in S1 ³⁸, its absence in M1 is not necessarily related to a lack of stellate cell targets in this agranular area. It could reflect sparse axonal projections from L6 ³⁹, preferential targeting of L6 axons to interneurons ^{40, 41}, or functionally weak connections ⁴².

The strongest excitatory pathway we identified, L2/3→5, is a core pathway in sensory cortex (for reviews, see 4-11). Strong L2/3→5 inputs have been reported for a subclass of pyramidal neurons in primate V1 ⁴³, but although L2/3→5 inputs are stronger than L2/3→2/3 in mouse S1 ⁴⁴, this supragranular→infragranular pathway is a relatively weak source of input to L5 in rat S1 ⁴⁵. Our findings show that in M1, L2/3→5 conveys a large fraction of the excitatory drive within the local network. This descending pathway is focused onto the border of L5A and L5B (Fig. 1f,g; Fig. 2e); whether it similarly straddles this boundary in sensory areas is unknown.

The main ascending interlaminar pathway we identified, L5A→2/3, is particularly interesting in light of the agranularity of M1 and the presence of this pathway in sensory cortex. Thus, while M1 (by definition) lacks the canonical L4 stellate→L2/3 projection, its local circuit does include this ascending projection from middle to upper layers. In S1, L5A→2/3 has recently been identified as a prominent ascending pathway parallel to L4→2/3 ^{12, 13}. In rodents, thalamocortical projections from the posterior nucleus (POm) carry paralemniscal sensory information to M1 and S1, which interconnect via paralemniscal-related pathways (reviewed in ⁷), implying that L5A could be a paralemniscal-related thalamorecipient layer in rodent M1 as well. The identification of L5A→2/3 in M1 (this study), S1 ^{12, 13}, and V1 ¹⁹ suggests that this, too, is a core pathway in local circuits across rodent neocortex.

Intralaminar pathways (i.e., recurrent, or horizontal, connections) were present at all levels, with one peak in L2 and a second broader peak over middle/deeper layers (Fig. 2c), consistent with numerous previous studies of horizontal pathways in L2/3 and L5 (for reviews, see 2, 3). These horizontal pathways are already considered a core feature of local circuits across mammalian neocortex. We clearly underestimated the contribution of more distant horizontal inputs due to slicing of connections. However, although horizontal and oblique connections both diminished with distance, even at the largest horizontal distances (within the mapping region-of-interest) the oblique L2/3→5 connections remained much stronger than either L2/3 or L5 horizontal connections (Supplementary Fig. 3). We did not investigate other slice angles in this study, but if we assume that horizontal connections are approximately radially symmetric and extrapolate from a two- to a three-dimensional picture of these circuits, the oblique (L2/3→5) pathways will still predominate over horizontal (L2/3→2/3 and L5→5) pathways in the intact brain.

Our overall impression is that in M1, the major pathways topographically resemble their counterparts in sensory cortex, but the particular ensemble of pathways and the top-down laminar organization of the excitatory are distinct features. As the present study focused only on one M1 subregion, an open question is whether this circuit phenotype is generally characteristic of agranular cortex ⁴⁶. It can be argued that the circuits for motor execution and motor planning are likely to be highly conserved, representing the evolutionary internalization of motor control ⁴⁷. Of note, in S1, sparse optical stimulation of L2/3 pyramidal neurons has been shown to drive perceptual learning and decision making ⁴⁸. In agranular areas, similar strategies could potentially illuminate how top-down laminar excitation within local circuits relates to top-down behavioral control of movement.

It will be important to explore dynamic aspects of information processing in specific nodes in this network under more physiological conditions. In vivo evidence for downward excitation corresponding to the L2/3→5A/B pathways identified here can be gleaned from recordings in disinhibited M1 showing thalamus→upper layer→middle layer activity sequences ⁴⁹. The hypothesis should be tested that inhibitory circuits in L2/3, in addition to providing broadly tuned gain control, mediate the selective gating of top-down excitation through dynamic routing mechanisms ^{5, 22, 50}. The connectivity matrix approach developed here offers a quantitative road map to guide further such investigations of cortical circuit mechanisms underlying motor control.

METHODS

Slice preparation

Experiments followed Northwestern University's Animal Care and Use Committee's guidelines. Brain slices (300 μm) were cut in chilled medium, transferred to artificial cerebrospinal fluid (ACSF) at 34 °C for 30 minutes, then maintained at 22 °C, as described ¹². The slice angle was ~15° off the parasagittal plane (Fig. 1a, top). In separate experiments, we used intracortical microstimulation followed by fluorescent bead injections in vivo to verify that these slices contained the forelimb representation area of M1 (Supplementary Methods).

Electrophysiology

Slices were transferred to the recording chamber and bathed with ACSF containing 4 mM MgCl₂ and CaCl₂ to dampen neuronal excitability. NMDA currents were blocked with 5 μM CPP. Pyramidal neurons were visualized using a 60× objective and video-enhanced infrared gradient contrast optics, and patched with pipets containing potassium-based intracellular solution ¹², composed of (in mM): 128 KCH₃SO₃, 4 MgCl₂, 10 HEPES, 10 phosphocreatine, 4 ATP, 0.4 GTP, 3 ascorbate. Input maps were recorded in voltage clamp at -70 mV, the reversal potential for GABAergic conductances determined separately by GABA uncaging (Supplementary Methods). In the disinhibition experiments, whole-cell recordings were made in current-clamp with cells held near -70 mV. For cell-attached (loose-seal) recordings, voltage follower mode was employed. Traces were filtered at 4 KHz and sampled at 10 KHz.

LSPS data acquisition and analysis

After establishing a patch recording, the lens was switched to a 4× objective, giving a field of view of 2.6-by-2.0 mm. An image of the slice was acquired prior to mapping each cell, and used for precise registration of the mapping grid. For connectivity matrix experiments, a 16-by-16 grid with 100 μm was was rotated and offset to bring it into standard alignment: zero was defined on the vertical axis as the pia, and on the horizontal axis as the center of the grid, which was aligned with the recorded neuron's soma. With 0.2 mM MNI-glutamate (Tocris) in the recirculating ACSF, grid locations were sequentially sampled (every 0.4 sec) with a 1.0-msec stimulus from an ultraviolet laser (DPSS Lasers, Inc.). Synaptic input maps were generated by calculating the mean current at each location, using a post-stimulus time window from ~7 msec to 50 msec post-stimulus. Direct responses (short-latency glutamatergic responses due to direct stimulation of the postsynaptic neuron's dendrites) were detected by temporal windowing ⁴⁵, excluded from analysis, and rendered as black pixels in displayed maps. Each neuron's set of map trials (usually 3) was averaged to yield a single map for the cell.

LSPS calibration

To characterize the photoexcitability of M1 pyramidal neurons under our recording conditions, we recorded excitation profiles (loose-seal recorded maps of LSPS-evoked spikes) from neurons located in the presynaptic fields of interest (for detailed methods, see Supplementary Methods and Supplementary Fig. 2). Briefly, analysis of excitation profile data obtained from neurons distributed across all layers indicated that the resolution of photostimulation averaged ~70 μm across layers, and the average number of spikes per spike-generating site was ~1. The resolution and intensity of photostimulation together with the neuronal density imply that ~100 neurons fired per stimulus. Excitation profile experiments failed to detect evidence for stimulus-evoked synaptic driving (feedforward excitation, due to synaptically generated spikes) under our recording conditions, indicating that the LSPS maps represent monosynaptic input.

Connectivity matrix analysis

We recorded from 102 neurons distributed across all M1 layers. Each cell's soma location was measured in the video image both as an absolute distance from the pia and as the normalized distance from pia to white matter. For averaging, we sorted the cells into bins that were one-tenth of the pia-to-white-matter distance. The morphometric data were similarly used to re-bin each cell's map rows into ten bins spanning the pia-to-white-matter distance. The 2D map representing the connectivity matrix was made by averaging along (projecting) the rows of the average input maps. Because L1 lacks excitatory neurons, and the uppermost bin therefore had no cells, values in the first row and column of the matrix were accordingly set to null values. Error bars (s.e.m.) for summed input per postsynaptic location (Fig. 2b) were obtained based on the standard deviation of the sample in each bin. Error estimates for summed output per presynaptic location (Fig. 2b) could not be obtained because the sampling density of presynaptic locations was insufficient for binning.

Output maps

We obtained another view of the synaptic input maps by viewing the sorted stack of maps in the dimension orthogonal to both the input maps and the connectivity matrix. We refer to these as inferred synaptic `output' maps because, whereas the originally measured synaptic input maps are maps of the pathways from many locations to a single location, these orthogonal views of the map data set represent the pathways from a single location to many locations. (The same data set was used to obtain the average input and output maps, the connectivity matrix, and the summed input and output, and that the data in all cases are expressed in units of current, picoamperes.) A potential source of confusion is that synaptic `input' and `output' can be considered synonyms for the same concept of a connection from A→B. Because the term `synaptic input map' (i.e., topographic map of convergent functional connectivity, A^n=many→Bⁿ⁼¹) is widely used, for consistency and convenience we use the complementary term `synaptic output maps' (i.e., topographic map of divergent functional connectivity, Aⁿ⁼¹→B^n=many). Displayed output maps were reflected horizontally. Vectors obtained by averaging along the horizontal dimension of the output maps correspond to the columns of the connectivity matrix.

Network simulations

The laminar connectivity matrix data, W_post,pre, was used as a neural network model. The matrix was normalized to its maximum value and multiplied by a global scaling constant, c, corresponding to the network `gain'. The input vector p = a_o is a column vector representing a laminar profile of starting input values, on which the network (c W_post,pre) operates to produce an output vector that feeds back into the network with every iteration. The effect of the t^th iteration is described by

$${\mathbf{a}}_t=c{\mathbf{W}}_{\mathrm{post},\mathrm{pre}}{\mathbf{a}}_{t-1}.$$

In the examples shown, we excluded the first row and column of the original 10-by-10 matrix, because they corresponded to layer 1, for which we lacked postsynaptic recordings as this layer lacks excitatory neurons. Thus, the displayed simulations are based on a 9-by-9 version of the matrix. However, essentially identical results were obtained using values of zero for the L1 data.

The network operated in two regimes depending on the value of the gain factor c. For 0 < c < ~1.5, activity always collapsed towards zero, and for c > ~1.5, activity always exploded. As expected in a linear system, different values of c within these two ranges gave essentially equivalent results, differing only in the rate of collapse or explosion. In the examples shown, c was 1 for the low-gain simulations, and 2 for the high-gain simulations.

Disinhibition experiments

SR95531 (gabazine; Tocris) was added to the bath solution at 1-10 μM as indicated. Although network events could be recorded from neurons located anywhere in the slice, for the experiments in Fig. 3 we only used deeper-layer neurons (L5B/6) because this also provided a control for their photoexcitability. Cells were recorded in either whole-cell current-clamp or cell-attached voltage-follower mode. We vertically aligned the top of photostimulation grid to the pia as in the synaptic mapping experiments, and horizontally aligned its left edge with the M1/S1 border, so that we could record from neurons located over a wider horizontal range within M1 while stimulating across M1. An interstimulus interval of 1.5 sec was used, allowing events to settle. Maps were acquired 1-4 times per neuron and averaged. With SR95531 concentrations of 1 μM no spontaneous events occurred. With SR95531 concentrations of 2-10 μM, prior to mapping, events occurred spontaneously at a low rate of up to several events per minute; mapping caused all events to become stimulus locked. For analysis, for each cell, several of the perisomatic columns in the maps were blanked due to contamination by strong local direct responses, including short-latency spikes (Fig. 3e, site d). Traces were analyzed using automated spike-detection routines, and events scored as 0 (absent) or 1 (present). Maps were pooled across cells to compute an overall average map. For plotting, data were re-binned as described above for the input maps and averaged along rows to obtain the plot in Fig. 3e.

Statistical analyses

Group comparisons were performed using Student's t-tests, unless otherwise indicated. Error bars in plots represent s.e.m.