Effects of Salts of the Hofmeister Series on the Hydrogen Bond Network of Water

Abstract

The effect of salts on water behavior has been a topic of interest for many years; however, some recent reports have suggested that ions do not influence the hydrogen bonding behavior of water. Using an effective two-state hydrogen bonding model to interpret the temperature excursion infrared response of the O-H stretch of aqueous salt solutions, we show a strong correlation between salt effects on water hydrogen bonding and the Hofmeister order. These data clearly show that salts do have a measurable impact on the equilibrium hydrogen bonding behavior of water and support models which explain Hofmeister effects on the basis of solute charge density.

1. INTRODUCTION

Late in the nineteenth century, Franz Hofmeister published a series of papers (recently translated to English [1]) describing the effects of common salts on a variety of physiological samples. Since Hofmeister’s original work, Hofmeister effects have been noted in countless systems [2], including salting proteins in and out of solution [1,3,4], water retention in macroscopic systems such as wool [5,6], molecular ordering of surfactants [7], and modulation of membrane protein conformations [8,9]. The most commonly studied phenomena have been the effects of salts on protein stability and solubility [2]. A ranking according to the ability to precipitate proteins yields the following order for the anions and cations used in the present study [1]:

$$\begin{array}{c}\text{Most}\text{Precipitating}\text{Least}\text{precipitating}\\ {{\text{PO}}_4}^{3-}>{{\text{SO}}_4}^{2-}>{{\text{HPO}}_4}^{2-}>{\text{Cl}}^{-}>{\text{Br}}^{-}>{\text{NO}}^{3-}\\ {\text{Ca}}^{2+}>{\text{Mg}}^{2+}>{\text{Li}}^{+}>{\text{Na}}^{+}\ge {\text{K}}^{+}>{{\text{NH}}_4}^{+}\end{array}$$

The relative positions of phosphate vs. sulfate, of sodium vs. potassium, and of calcium vs. magnesium may switch depending on the nature of the system being studied, but otherwise this ordering is highly reproducible in a wide array of systems.

The mechanism of Hofmeister effects has been extensively investigated and widely debated. Such studies have led to detailed theories of aqueous electrolyte solutions which can explain many physicochemical properties of these solutions but still fail to fully explain the mechanism of salt effects on macromolecules or why these effects follow the Hofmeister series [10–16]. Particular attention has been paid recently to the role of dispersion forces [17], but historically the most difficult aspect of explaining salt effects in solution has been consideration of how the ions change the nature of water hydrogen bonding [15].

There is extensive data supporting the idea that ions have significant impact on local water hydrogen bonding behavior [2,18–26]. In fact, one theoretical model, developed by Marcus, has been able to account fairly well for several thermodynamic parameters of a wide variety of ions in solution purely through modeling ion effects on the first hydration layer [20]. Salt effects on water have been most commonly described in terms of the chaotropicity or kosmotropicity of the solutes. Perhaps the best description of the chaotrope/kosmotrope designation is that offered by Collins [26]: binding of chaotropes to water molecules is weaker than binding of water molecules to each other; binding of kosmotropes to water is stronger than binding of water molecules to each other. Chaotropicity seems to correlate with a low charge density, thus large singly-charged ions tend to be chaotropic. Their low charge density means that they have smaller effects on the local hydrogen bonding. Kosmotropicity correlates with a high charge density, thus small or multiply-charged ions tend to be kosmotropic. Their high charge density means that they interfere strongly with local water hydrogen bonding.

The position of ions in the Hofmeister order has been shown to correlate with the Jones-Dole viscosity B coefficient. The Jones-Dole viscosity B coefficient is determined by

$$\frac{\eta }{{\eta }_0}=1+A{c}^{\frac{1}{2}}+Bc$$ (1)

where η is the viscosity of an aqueous solution of ions, η₀ is the viscosity of water at the same temperature, c is the salt concentration, A is an electrostatic term, and B is a measure of the strength of ion-water interactions [26]. The viscosity B coefficient, like chaotropicity/kosmotropicity, has been shown to correlate with charge density. The correlation between viscosity effects, charge density, and Hofmeister order suggests a causal relationship between the character of ions and their effect on solvation properties through impact on water hydrogen bonding.

Recently, a variety of sources have argued that salts have little or no impact on water hydrogen bonding orientations [27]. Dielectric spectroscopy has shown no difference in relaxation times between bulk water and a variety of aqueous salt solutions [28]. Ultrafast IR studies have argued that ions have some effect on water dynamics, but not on equilibrium water-water hydrogen bond geometries [29–33]. Some studies have offered alternative mechanistic explanations for Hofmeister effects, including formation of salt bridges which stabilize or destabilize protein structure [34], and salt-induced changes in solvent surface tension at the protein-solvent interface [35,36]. Several studies have found both specific ion effects and Hofmeister trends, arguing for the presence of both specific ion interactions with proteins and bulk solvation effects mediated by ion-induced changes in water [4,37].

In light of the debate over the effects of salts on water hydrogen bonding, the present study examined the temperature excursion IR (TEIR) spectra of aqueous solutions of 30 salts of the Hofmeister series in an attempt to answer this question. The O-H stretch of these aqueous salt solutions was quantitatively analyzed using an effective two-state hydrogen bonding model for water. This model is based on modeling studies of water by Sharp and coworkers, as well as on the extensive ultrafast IR investigations of water performed over the past decade. Detailed explanation and justification for this model is given in Results. The present data demonstrated a clear correlation between the effects of the various salts on the water hydrogen bond network and the Hofmeister series.

2. MATERIALS AND METHODS

2.1 Spectroscopy

D₂O and ¹⁵N ammonium salts were purchased from Cambridge Isotope Laboratories, Inc. (Andover, MA). Water was deionized and distilled. Salts were purchased from Sigma-Aldrich (St. Louis, MO). The following 30 salts were tested: Li₃PO₄, Li₂SO₄, LiNO₃, LiCl, LiBr, K₂HPO₄, K₂SO₄, KNO₃, KCl, KBr, Na₂HPO₄, Na₂SO₄, NaNO₃, NaCl, NaBr, (NH₄)₂HPO₄, (NH₄)₂SO₄, NH₄NO₃, NH₄Cl, NH₄Br, MgHPO₄, MgSO₄, Mg(NO₃)₂, MgCl₂, MgBr₂, CaHPO₄, CaSO₄, Ca(NO₃)₂, CaCl₂, and CaBr₂. Ammonium salts and other salt hydrates were deuterium exchanged by recrystallization or by lyophilization. Each salt was mixed with D₂O/H₂O to produce a final ratio of 12.5 waters/ion (corresponding to 4.4 molal ions) with 4% H/96% D content. H/D ratio was confirmed for all samples by comparing the absorbance of the D-O-D bend to that of the H-O-D bend (data not shown). Each sample was mixed well and briefly centrifuged to sediment any undissolved salt. The following samples were not soluble at 12.5 waters/ion: CaCl₂, CaBr₂, CaSO₄, Li₃PO₄, Na₂HPO₄, MgHPO₄, CaHPO₄; these samples were heated to 50 °C, mixed, centrifuged and allowed to cool to room temperature. They were mixed again, centrifuged, and the supernatants were then used for IR measurements with the samples considered at saturation. For ammonium salts, ¹⁵NH₄NO₃, ¹⁵NH₄Cl, and (¹⁵NH₄)₂SO₃ were also tested at 12.5 waters/ion in order to examine the effects of the overlap of the N-H stretch on interpretation of the O-H stretch. Infrared spectra of 98% D₂O/2% H₂O (v/v) and of salt solutions were recorded between CaF₂ windows with a 12 μm mylar spacer using a Bruker IFS 66 Fourier transform infrared spectrometer (Bruker, Brookline, MA) at 5 °C intervals from 5 °C to 80 °C. Temperature was maintained with a circulating water bath with temperature measurement at the sample using a FisherBrand Type-K thermocouple (Fisher Scientific, Pittsburgh, PA).

The concentration-dependent effect of salts on the O-H stretch was also investigated. IR spectra were recorded at room temperature with a 12 μm Mylar spacer for all salts (except CaHPO₄, CaSO₄, Li₃PO₄, and MgHPO₄ due to their low solubility) at 800, 400, 200, 100, 50, and 25 waters/ion with final H/D ratio of 4%/96%. These water/ion ratios correspond to dissociated ion concentrations of 0.07, 0.14, 0.28, 0.55, 1.1, and 2.2 molal, respectively. These data are reported in the Appendix.

2.2 Data Analysis: Application of a Two-State Hydrogen Bond Model for Interpretation of the O-H Stretch Bandshape of Water

Spectra were processed using OPUS 5.0 (Bruker). Spectra were corrected for water vapor, cut from 3032 cm⁻¹ to 3728 cm⁻¹, converted from transmission to absorption, smoothed using 25-point Savitsky-Golay smoothing, normalized to 2.0 and finally baseline corrected using a rubberband correction with 10 points.

The spectra were fit to the sum of two Voigt functions representing two populations of hydrogen bond orientations: linear and bent. This model of water approximates the water hydrogen bond network as a continuous network of hydrogen bond distances and angles which naturally exhibits a roughly bimodal distribution with respect to hydrogen bond angle. The lineshape of the O-H stretch is interpreted to be representative of this angular distribution. This simplified view of the water hydrogen bond network models the primary effects of solutes on water as a change in the relative populations of water molecules in the linear vs. bent hydrogen bond conformation. The background for this model is described in Results.

OriginPro 8.0 (OriginLab Corp., Northhampton, MA) was used for all fitting. A Voigt lineshape was chosen for both components to allow inclusion of lifetime broadening, thereby permitting extraction of the Gaussian inhomogeneous broadening contribution to each component. The formulation of the Voigt function used for fitting (as included in OriginPro 8.0) is given in equation 2:

$$y=y_0+A_V\frac{2ln2}{{\pi }^{3/2}}\frac{W_L}{W_G^2}\int \frac{e^{-t^2}}{{\left(\sqrt{ln2}\frac{W_L}{W_G}\right)}^2+{\left(\sqrt{4ln2}\frac{x-x_c}{W_G}-t\right)}^2}dt$$ (2)

where y₀ is the baseline, A_V is the area under the Voigt function, W_L is the Lorentzian width, W_G is the Gaussian width, x is the frequency, and x_c is the peak center frequency. The baseline value was fixed at zero for all functions because baseline correction was performed prior to fitting.

In order to account for the significant lifetime broadening known to contribute to the O-H stretch bandshape, W_L was fixed for both components in all fits. W_L corresponds to the lifetime broadening portion of the lineshape, so there is extensive experimental evidence supporting the choice of a fixed value for this parameter. Though several lifetimes have been reported ranging from 700 fs [38] to 100 fs [39] for the linear population (lower frequency component), 100 fs was used in order to ensure inclusion of the maximum possible lifetime broadening. The lifetime of the bent population (higher frequency component) has been reported consistently between 1 ps and 2 ps [38–51]. Again, the maximum broadening option, 1 ps, was selected. These lifetimes predict a Lorentzian width contribution according to: W_L = 1/2πτ, where τ is the lifetime. The chosen lifetimes of 100 fs and 1 ps correspond to homogeneous broadenings (W_L) of 50 cm⁻¹ and 5 cm⁻¹, respectively. These selections have implications in the final analysis of the data that will be addressed in the Discussion. Inherent in the fixing of the Lorentzian widths of both components is the assumption that the vibrational lifetimes do not vary significantly with temperature. Ultrafast IR measurements have shown that the lifetime temperature dependence is small enough (<10%) to be ignored in the present experimental temperature range [46].

Optimization of the fitting procedure was performed by fitting all TEIR spectra of 98%D₂O/2% H₂O simultaneously. The optimum fitting parameters determined from fitting these spectra were used to analyze the spectra of all salt solutions. Initially, fits with only y₀ and W_L fixed were calculated for the 98%D₂O/2% H₂O spectra. As expected, this process resulted in ambiguous fits of the data in which the peak frequencies of the two Voigt components were unrealistic for application of the two-state model to water.

A great deal is known about the relationship between hydrogen bond geometry and O-H stretching frequencies from the various forms of ice, thus the relationship between O-H stretch frequency and hydrogen bond geometry is well characterized for crystalline forms of water [52–64]. Based on such data and on additional spectral analysis and ab initio calculations, Walrafen assigned specific frequencies for the two structural components of the water O-H stretch: 3350 cm⁻¹ and 3440 cm⁻¹ for linear and bent hydrogen bonds, respectively [65]. Rather than simply using these values, however, an appropriate frequency range was selected to use as bounds for the linear and bent component peak centers based on the literature regarding ice IR spectra and ultrafast IR investigations of the liquid water O-H stretch [38–65]. Bounds of 3300 – 3350 cm⁻¹ and 3450 – 3500 cm⁻¹ were chosen for x_c of the linear and bent populations, respectively, and fitting was repeated for all spectra simultaneously with these bounds and with y₀ and W_L fixed. This method of fitting produced fits that failed to quantitatively represent the variance of the spectra with temperature. Further restriction of the fit was required in order to apply the model to the data in a way that would accurately represent the temperature-dependent spectral shifts.

In order to determine the best set of frequencies at which to fix the peak centers, combinations of fixed frequencies were tested. The fitting process was repeated at fixed 5 cm⁻¹ steps for every combination of peak frequencies within the chosen bounded range. The set of frequencies which provided the best R² value for the worst fit in the temperature range was selected as appropriate for application of the model to subsequent IR data. Peak frequencies of 3350 cm⁻¹ and 3450 cm⁻¹ provided a worst fit R² of 0.996 and produced area and width values whose variance with temperature was representative of the temperature-dependent spectral changes. As a result, fixed values of 3350 cm⁻¹ and 3450 cm⁻¹ were used for x_c of the linear and bent components, respectively. These values agree well with the values proposed by Walrafen as well as with values from ultrafast IR measurements of the O-H stretch dynamic properties [38–51,65].

All salt solution spectra were fit using these water-optimized parameters. As Bakker and colleagues have shown [29–33], the lifetime of the linear hydrogen bond population is independent of ion presence or species. The bent hydrogen bond lifetime is quite dependent on ion character, but the measured changes in lifetime (from 1 ps up to 12 ps) produce reductions in homogeneous broadening from 5 cm⁻¹ to ~0.5 cm⁻¹. This change should not produce significant differences in the fits, so it was ignored for the present samples in order to maintain consistency in the application of the two state hydrogen bonding model to the O-H stretch spectra.

From the fit values for W_G and A_V, the amplitude of each component was calculated by solving equation 12 for x = x_c. The calculated amplitude and W_G were used to compute the area under the Gaussian portion of each component. These areas (linear hydrogen bond area = A_l and bent hydrogen bond area = A_b) were used as the relative populations of hydrogen bonds in each angular orientation. The ratio of these areas was used to calculate the effective equilibrium constant, K_b→l, for transition of an O-H oscillator from a bent hydrogen bond conformation to a linear conformation: K_(b→l) = A_l/A_b. This effective equilibrium constant was then used to calculate an effective energy difference between bent and linear hydrogen bonds in the hydrogen bond network using a simple Boltzmann relationship to free energy:ΔG_b→l = −kTlnK_b→l, where k is the Boltzmann constant and T is the temperature in Kelvin. Comparison of K_b→l. versus reciprocal temperature allowed van’t Hoff analysis and extraction of relative enthalpic and entropic contributions to the solute effect on water-water hydrogen bonding. This approach has been used previously to describe water behavior under nanoconfinement [66]. The van’t Hoff analysis showed non-linear behavior at high temperature. This is indicative of temperature dependence in the heat capacity of the solution. Of course, the temperature dependence of water’s heat capacity is a well-known property, so this non-linearity is not unexpected and has been cited as a common source of error in van’t Hoff analyses [67].

In order to calculate effective values for ΔS_b→l and ΔH_b→l, a linear fit to the van’t Hoff data was performed for all samples, many of which showed substantial curvature above 50 °C. It would be possible to correct for the heat capacity change with temperature for the 98% D₂O/2% H₂O sample, but this was not performed because measurement of the temperature dependence of the heat capacity for all samples was prohibitive, thus the portion of the van’t Hoff data that couple be reasonably approximated as linear was used for all samples without correction. The linear fits to all data sets for 5 °C to 50 °C achieved R² ≥ 0.99. The slope and intercept values for fits to the data for this temperature range were used to estimate effective entropic and enthalpic contributions to the transition from bent to linear water hydrogen bonds.

3. RESULTS

3.1 Temperature Excursion Infrared Spectroscopy (TEIR) of O-H in D₂O

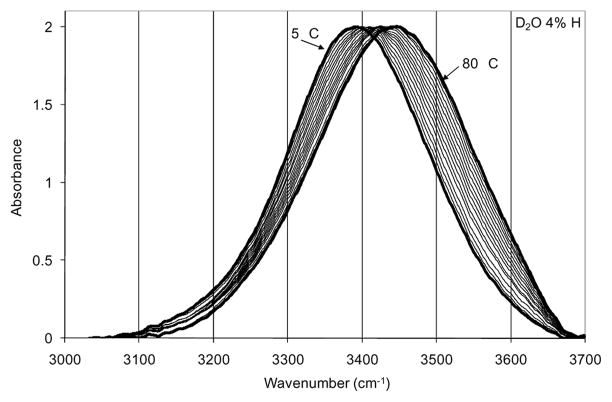
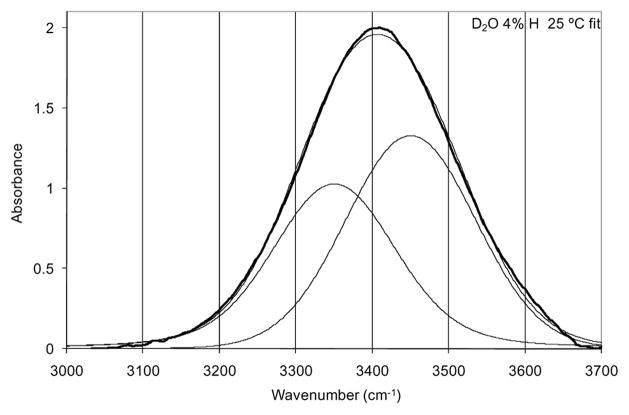
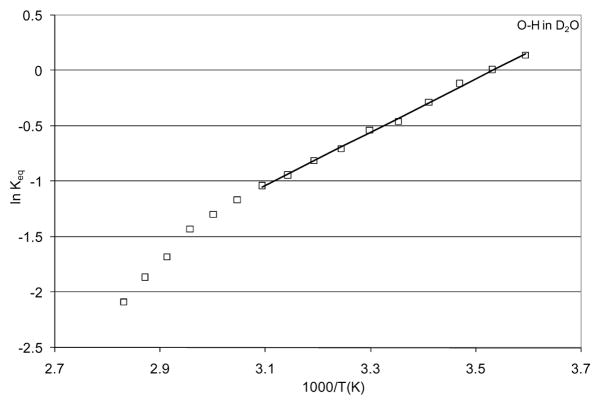
TEIR [68] spectra of the O-H stretch of an isolated O-H oscillator (D₂O with 4% H) are shown in Figure 1. Spectra were recorded at 5 °C intervals from 5 °C to 80 °C. The fit for the 25 °C spectrum is provided showing the respective components in Figure 2. The fit functions were used to calculate the Gaussian area of each component which was then used to calculate an effective equilibrium constant for the transition of bent hydrogen bonds to linear hydrogen bonds. This equilibrium constant was used to perform a van’t Hoff analysis in order to determine effective enthalpic and entropic contributions to the free energy difference between bent and linear hydrogen bonds for the isolated O-H oscillator. The van’t Hoff plot is shown in Figure 3.

Figure 1.

Temperature excursion infrared spectra of O-H in D₂O. Spectra were taken at 5 °C intervals from 5 °C to 80 °C. Extreme temperature spectra are indicated.

Figure 2.

Fit of two Voigt functions to the 25 °C O-H stretch spectrum. The heavy line is the spectral data with the fine lines showing the fit functions and their sum.

Figure 3.

Van’t Hoff analysis of the calculated effective equilibrium constants for the transition from bent to linear hydrogen bonds of an isolated O-H oscillator in D₂O. The linear least squares fit to the data from 5 °C to 80 °C is shown.

The linear fit to the van’t Hoff data from 5 °C to 50 °C gave a slope of 2.41 and an intercept of −8.51, which correspond to values for ΔH_b→l and ΔS_b→l of −4.78 kcal/mol and −16.9 cal/mol K, respectively. These values yield a calculated ΔG_b→l of 252 cal/mol for the transition of the isolated O-H oscillator in D₂O from a bent hydrogen bond configuration to a linear hydrogen bond configuration at 25 °C.

3.2 TEIR of Salt Solutions

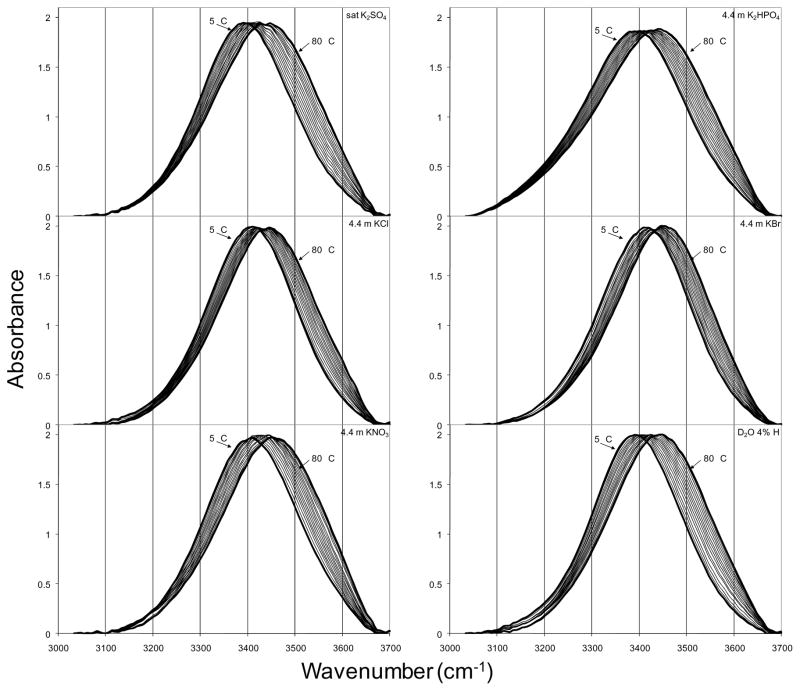
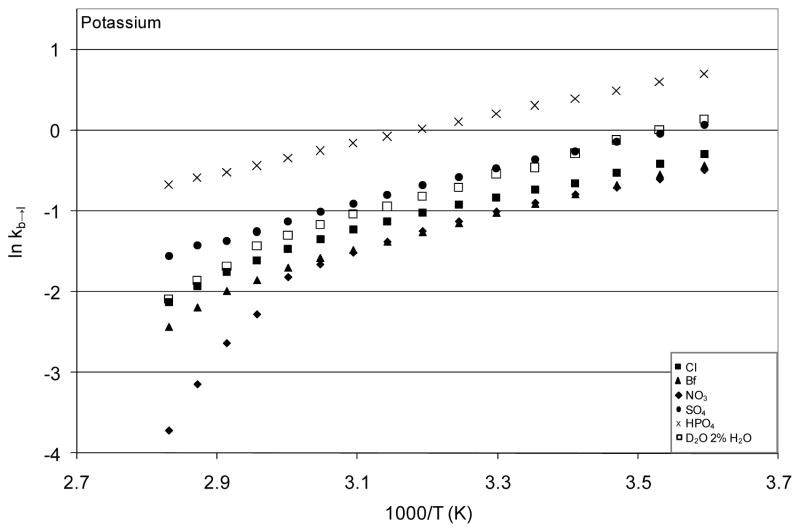
Temperature excursion infrared spectra of the potassium salt solutions, which are typical of the results for all salt solutions, are shown in Figure 4. All other salt solution spectra are included in the Appendix. In all cases, increasing temperature shifted the O-H stretch to higher frequency as expected. The extent of this shift, as well as temperature-dependent changes in bandshape, varied with salt. Quantitative comparison of these spectra was performed by fitting each spectrum using the fitting parameters from the optimized fits to the isolated O-H oscillator spectra. The results of the fitting procedure yielded effective equilibrium constants, permitting van’t Hoff analysis for each solution. The van’t Hoff plot for the potassium salts is shown in Figure 5 with the plots for all other solutions provided in the Appendix. Linear fits to the van’t Hoff plots for temperatures 5 °C – 50 °C were used to estimate effective values for ΔH_b→l and ΔS_b→l in the presence of the various salts. This temperature range was selected because it was the largest range over which the van’t Hoff data of all samples could be approximated as linear (with R² > 0.99). The non-linearity of the van’t Hoff data arises from the temperature dependence of the heat capacity of the solution. Correction for this temperature dependence is possible, but requires measurement of the temperature dependence of the heat capacity for each solution. The heat capacity differences for these salt solutions are very small, and efforts to measure these differences yielded inconsistent results (not shown), so the linear approximation over the lower half of the temperature range was used without correction.

Figure 4.

Temperature excursion infrared O-H stretch spectra of aqueous salt solutions with potassium cation at 5 °C intervals from 5 °C to 80 °C. The TEIR spectra of isolated O-H oscillator in D2O are included for comparison.

Figure 5.

Van’t Hoff plots from the fit analysis of the temperature excursion O-H stretch spectra for all potassium salts. These data are representative of those obtained for each group of salts.

The calculated ΔH_b→l and ΔS_b→l values were then used to calculate an effective ΔG_b→l in the presence of various salts at 25 °C. The ΔH_b→l, ΔS_b→l, and ΔG_b→l values for all salts that were soluble to 4.4 molal ion concentration are reported in Table I. The values for ΔG_b→l are given in Table II grouped by cation and by anion in order to compare each respective set of salts, thereby facilitating comparison of the order of cations or anions to the Hofmeister order. As described in the discussion, the expected Hofmeister order is seen for all anions and for all cations except calcium and ammonium. In the case of calcium, the low solubility of the calcium salts made the position of calcium in the order of cations difficult to determine reliably based on the present methods. Deviation of the ammonium salts from the Hofmeister order with respect to their effects on the water O-H stretch is likely due to vibrational mixing effects or to the ammonium salts engaging in more specific interactions with proteins, as explored further in the Appendix, but from the present data no firm conclusion can be reached with respect to ammonium effects. As a result, both calcium and ammonium are omitted from the remainder of the present discussion.

Table I.

Thermodynamic values from van’t Hoff analysis for all salts soluble to 4.4 molal ions.

	Δ Hb→l cal/mol	ΔΔ Hb→l cal/mol		Δ Sb→l cal/mol K	Δ ΔSb→l cal/mol K		Δ Gb→l @ 25 °C cal/mol	ΔΔ Gb→l cal/mol
MgCl2	−2590.41	2193.88	MgSO4	−7.24	9.65	MgSO4	−542.12	−794.38
(NH4)2SO4	−2612.31	2171.98	(NH4)2SO4	−8.75	8.14	(NH4)2HPO4	−336.50	−588.76
MgSO4	−2700.17	2084.12	MgCl2	−8.87	8.02	K2HPO4	−175.67	−427.93
MgBr2	−2878.50	1905.79	MgBr2	−10.15	6.74	(NH4)2SO4	−3.41	−255.67
NH4Br	−2889.94	1894.35	(NH4)2HPO4	−10.53	6.36	Li2SO4	22.92	−229.34
Mg(NO3)2	−2974.14	1810.15	Mg(NO3)2	−10.60	6.29	MgCl2	55.31	−196.95
Na2SO4	−2988.16	1796.13	NH4Br	−10.68	6.21	MgBr2	147.50	−104.76
NH4Cl	−3067.72	1716.57	Na2SO4	−10.73	6.16	Mg(NO3)2	185.57	−66.70
LiCl	−3383.18	1401.11	K2HPO4	−10.87	6.03	Na2SO4	210.97	−41.29
K2HPO4	−3415.15	1369.14	NH4Cl	−11.11	5.79	K2SO4	226.11	−26.15
Li2SO4	−3466.05	1318.24	Li2SO4	−11.70	5.19	NH4Cl	243.68	−8.58
(NH4)2HPO4	−3475.80	1308.49	LiCl	−12.28	4.61	D2O 2% H2O	252.26	0.00
NH4NO3	−3495.98	1288.31	NH4NO3	−12.77	4.12	LiCl	277.92	25.66
NaBr	−3586.99	1197.30	LiBr	−13.53	3.37	NH4Br	294.56	42.30
KCl	−3615.43	1168.86	KCl	−13.59	3.30	NH4NO3	312.43	60.16
LiBr	−3689.41	1094.89	NaBr	−13.71	3.18	LiBr	343.79	91.53
NaCl	−3718.08	1066.21	K2SO4	−13.71	3.18	LiNO3	399.40	147.14
K2SO4	−3862.22	922.07	NaCl	−13.97	2.92	KCl	437.49	185.22
Ca(NO3)2	−3942.91	841.39	Ca(NO3)2	−14.98	1.91	NaCl	447.84	195.58
KNO3	−3984.33	799.96	LiNO3	−15.10	1.79	NaBr	500.72	248.46
LiNO3	−4103.50	680.79	KNO3	−15.22	1.67	Ca(NO3)2	524.11	271.85
KBr	−4200.42	583.87	KBr	−15.92	0.97	KBr	547.55	295.29
D2O 2% H2O	−4784.29	0.00	D2O 2% H2O	−16.89	0.00	KNO3	554.87	302.61
NaNO3	−4805.58	−21.29	NaNO3	−18.20	−1.31	NaNO3	621.21	368.95

Table II.

Δ G_b→l for all salts grouped by cation and by anion

Salt	Δ Gb→l @ 25 °C cal/mol	Salt	Δ Gb→l @ 25 °C cal/mol
(NH4)2HPO4	−336.50	MgSO4	−542.12
(NH4)2SO4	−3.41	(NH4)2SO4	−3.41
NH4Cl	243.68	Li2SO4	22.92
NH4Br	294.56	Na2SO4	210.97
NH4NO3	312.43	K2SO4	226.11
		CaSO4	229.01
K2HPO4	−175.67
K2SO4	226.11	(NH4)2HPO4	−336.50
KCl	437.49	K2HPO4	−175.67
KBr	547.55	Na2HPO4	54.11
KNO3	554.87	MgHPO4	234.63
		Li3PO4	236.19
Na2HPO4	54.11	CaHPO4	236.39
Na2SO4	210.97
NaCl	447.84	MgCl2	55.31
NaBr	500.72	NH4Cl	243.68
NaNO3	621.21	CaCl2	249.98
		LiCl	277.92
Li2SO4	22.92	KCl	437.49
Li3PO4	236.19	NaCl	447.84
LiCl	277.92
LiBr	343.79	MgBr2	147.50
LiNO3	399.40	NH4Br	294.56
		LiBr	343.79
MgSO4	−542.12	CaBr2	372.21
MgCl2	55.31	NaBr	500.72
MgBr2	147.50	KBr	547.55
Mg(NO3)2	185.57
MgHPO4	234.63	Mg(NO3)2	185.57
		NH4NO3	312.43
CaSO4	229.01	LiNO3	399.40
CaHPO4	236.39	Ca(NO3)2	524.11
CaCl2	249.98	KNO3	554.87
CaBr2	372.21	NaNO3	621.21
Ca(NO3)2	524.11

Note for Table II: * Salts that were measured at saturation are shown in gray. All black values are at 4.4 molal ion concentration.

4. DISCUSSION

4.1 An effective two-state hydrogen bond model for interpreting the O-H stretch bandshape

The temperature dependent changes in the O-H stretch bandshape of water have been interpreted to explain the molecular organization of water for many decades [65,69–72]. Such interpretations of the O-H stretch have relied on models of water as a mixture of short-lived ice-like clusters of water molecules in a sea of non-hydrogen-bonded water molecules. The low frequency component has been attributed to the ice-like population of water molecules, while the high frequency component has been assigned to non-hydrogen-bonded waters. Such mixture models have been quite controversial and have suffered from the lack of experimental evidence to support the existence of locally heterogeneous molecular organization in liquid water. The present interpretation of the O-H stretch in terms of an effective two-state mixture of linear and bent hydrogen bonds is not based on a model requiring local heterogeneity, but rather on a model of water as a random, continuous network of hydrogen bond distances and angles which gives rise to an effectively bimodal distribution of hydrogen bond angles. This model has been established using results from computer simulations and nonlinear IR spectroscopy in the literature.

Sharp and colleagues have performed detailed studies on the nature of water-water hydrogen bonding in molecular dynamics simulations of TIP3P and TIP4P water [73–80]. They used the RNM [81–84] to analyze the water hydrogen bond network. Using the two parameters of the RNM, hydrogen bond angle and O-O distance, they developed a theoretical route from the structural parameters of the water hydrogen bond network to the heat capacity of hydration for small solutes. During the course of this analysis, they noted that both TIP3P and TIP4P [85] water models produced a distinctly bimodal distribution when analyzed according to hydrogen bond angle, despite the fact that both models reliably reproduce the O-O radial distribution function of water, which shows no signs of heterogeneity. The bimodality of the angular distribution of water-water hydrogen bonds was composed roughly of two populations centered at a ~12 degree (roughly linear) and at a ~50 degree (bent) O^···O-H angle.

Sharp and coworkers analyzed a variety of solutes including monovalent ions, small hydrocarbons, nucleic acids, and amphiphilic molecules to show that the general effect of solute on water is a change in the relative distribution of water molecules in these two angular populations with little change in the population centers or widths [73–80]. Since this work, other groups have analyzed the effects of water structure on the O-H stretch of water using simulations. Corcelli and Skinner have produced simulated IR and Raman O-H stretch spectra from ab initio calculations that agree well qualitatively with experiment [86]. Using ab initio-based approximations to calculate infrared spectra from molecular dynamics simulations (Instantaneous Normal Mode Analysis), infrared spectra of aqueous solutions have been simulated with surprising accuracy for a variety of systems [87–89]. Calculations of spectra from molecular dynamics simulations of TIP3P, TIP4P, and SPC/E [90] models have all produced simulated spectra that agree well with experiment for both linear IR O-H stretch spectra as well as nonlinear IR measurements [91–93].

The relationship between water structure and O-H stretch bandshape was further investigated with both non-linear IR and simulations by Fecko, et al. [94]. By comparing the local electric field calculated from the water structure to the O-H stretch frequency, they identified local electric field effects as the most important determinant of the dependence of the O-H stretch on water structure. This analysis was supported by Smith, et al., who calculated the electric field dependence on the O-O distance from simulations of SPC/E water. They showed that the distribution of O-O distances in their simulation varied in a continuous way with temperature and yet gave rise to an O-H stretch shape that appears bimodal [95]. They argued that this was evidence that that the bimodality of the O-H stretch was not representative of any mixture of components, but they failed to analyze the electric field as a function of hydrogen bond angle. A more extensive analysis of the local electric field from simulations of SPC/E water was recently reported by Skinner [96]. This report showed the same relationship between local electric field and O-O distance as seen by Smith, et al., but it also examined the electric field as a function of hydrogen bond angle. The angular analysis showed the same bimodal distribution as seen in the analyses of Sharp and coworkers.

The sum of these studies demonstrates that various models which reproduce the physical properties of water with good accuracy also exhibit a bimodal distribution of hydrogen bond angles and a continuum of hydrogen bond distances. They also provide a link between the bimodality of hydrogen bond angles and the bimodal nature of the O-H stretch of water: the local electric field. These findings, in conjunction with the recent definition of two distinct dynamic populations in the O-H stretch of water [38–51] justify the interpretation of the linear O-H stretch bandshape in terms of the distribution of strong, linear hydrogen bonds versus bent, weak hydrogen bonds.

It is important to note that the ‘linear’ population of hydrogen bonds is not strictly linear, but rather corresponds to a distribution of nearly linear hydrogen bond angles. There is some debate over whether O-H oscillators in the bent population are really hydrogen bonded or not. Theoretical evidence for the slight covalent character of linear hydrogen bonds and the absence of covalent character for bent hydrogen bonds exists [97]. These analyses have shown that there is a small transfer of electron density from the donating hydrogen of a water-water hydrogen bond to the δ* antibonding orbital of the accepting oxygen and that the presence of this donation is dependent primarily on angle rather than on the length of the hydrogen bond. This finding suggests that the linear hydrogen bonds are ‘true’ hydrogen bonds involving some degree of covalence, while the bent hydrogen bonds are probably better characterized as electrostatic interactions. Despite this distinction, we refer to both types of interactions as hydrogen bonds for simplicity.

4.2 Application of the two-state model to the O-H stretch of water

The first reasonable test for applying a two state hydrogen bonding model to the O-H stretch of water is the simple question of whether the O-H stretch can be reproducibly fit to two components in such a way that the parameters of the fit are consistent with the best current knowledge of water’s behavior and O-H stretching vibration. As shown in Figure 2, the spectra can be fit quite well to the sum of two Voigt functions. In general, the O-H stretch can easily be fit to two Gaussian or Voigt functions using a wide variety of parameters, so obtaining a quality fit using two components is an entirely ambiguous way to analyze the spectra in the absence of further constraints. Unlike previous two-component fits to the O-H stretch of water [65,98–100], however, the present model includes consideration of lifetime broadening contributions to the lineshape and limits to the central frequencies of the components.

Knowledge of the vibrational relaxation times of the two hydrogen bond populations in water allowed constraint of the fitting process using fixed Lorentzian contributions to the lineshape. Because the lifetimes of the two populations and their resulting homogeneous broadening contributions are so different, addition of this constraint severely reduced the ambiguity of the fitting process. Because the low frequency component was required to have a Lorentzian width of 50 cm⁻¹ and the high frequency component was required to have one tenth that degree of homogeneous broadening, a high quality fit (R² > 0.99) of the spectra became much more difficult to achieve. This limitation of the fitting process, when combined with knowledge of the frequency range for hydrogen bonds of varying geometry, permitted unambiguous fitting of the spectral data.

The energetic predictions produced from the spectral fits turn out to be quite reasonable. The van’t Hoff analysis produced values for ΔH_b→l and ΔS_b→l of −4.78 kcal/mol and −16.9 cal/mol K, respectively. Data for estimated values of ΔS for the water hydrogen bond network are not available in the literature, but many estimates for the enthalpy of a strong hydrogen bond in water have been described. These estimates range from ~ −2.5 to −8 kcal/mol with the most common cited values in a range of −2.5 to −5 kcal/mol [95,98,100–105]. Our calculated value of −4.78 kcal/mol is in close agreement with these estimates.

Estimates of −5 to −8 kcal/mol come from experimental or theoretical calculations of the hydrogen bond strength of the water dimer or of strong hydrogen bonds in bulk water as compared to the isolated water molecule in vacuum [102,103,105]. These calculations offer an absolute enthalpy of the hydrogen bond, whereas our method calculates the enthalpic favorability of a strong hydrogen bond conformation over a bent conformation in bulk water. As the bent hydrogen bond conformation is certainly a lower enthalpy state than the isolated water molecule in vacuum with respect to a potential hydrogen bond, it would be expected that our value should be smaller. Estimates in the range of −2.5 to −5 kcal/mol come largely from other van’t Hoff analyses of the O-H stretch or from dielectric measurements [95,98,100,101,104]. Our estimate for the enthalpy difference between linear and bent hydrogen bonds falls well in line with the findings of these studies.

Another aspect of our analysis that deserves comparison to the currently accepted view of water is an analysis of the nearest neighbor hydrogen bonding. The present van’t Hoff analysis predicts a room temperature ΔG_b→l of 252 cal/mol for the transition from a bent to a linear hydrogen bond. The K_eq at room temperature from the fit data for the 25 °C spectrum is 0.631. The currently accepted view of bulk water is that a single water molecule has an average of ~5 nearest neighbors with which it participates in ~3 strong hydrogen bonds and ~2 weak hydrogen bonds, predicting a K_eq of ~1.5 [106]. Our calculated K_eq would predict 1.93 strong hydrogen bonds and 3.07 weak hydrogen bonds given, on average, 5 nearest neighbors. This seems a large discrepancy; our model basically seems to get the answer backwards. There are two potential explanations for this apparent error.

The present data are an examination of an isolated O-H oscillator in D₂O. As Scheraga first discovered [107], hydrogen bonds mediated by deuterium are stronger than hydrogen bonds mediated by protium. Scheiner and Cuma [105] performed a detailed ab initio study of this difference for water-water hydrogen bonds. They showed that a DOH…OD₂ bond has a smaller enthalpic favorability than a DOD…OD₂ bond by ~ 0.25 kcal/mol. If we consider the ΔS value from the current analysis to be fairly accurate and correct the enthalpy by the difference between protium and deuterium hydrogen bond mediation, such that the enthalpy is −5.03 kcal/mol rather than −4.78 kcal/mol, the calculated ΔG becomes 2.00 cal/mol at 25 °C. This hypothetical value for ΔG corresponds to a K_eq at 25 °C of ~1.0 and would predict ~2.5 strong hydrogen bonds and ~2.5 weak hydrogen bonds per 5 hydrogen bonds for bulk D₂O. This is closer to what is expected, but still represents a likely overestimate of the favorability of bent hydrogen bonds. It is not unreasonable to expect, however, that an isolated O-H oscillator in bulk D₂O would tend more toward bent hydrogen bonds than it would in bulk H₂O due to the difference in strength of deuterium-mediated hydrogen bonds.

A second potential reason for discrepancies between the predictions of the present analysis and the accepted view of water behavior is the inherent uncertainty of the O-H stretch. The inclusion of vibrational lifetimes in our model strengthens both the reproducibility of the fits and the physical accuracy of the model, but the homogeneous broadening due to the ultrafast relaxation processes in water also creates an unavoidable source of inaccuracy. Because measurements of relaxation processes on the femtosecond scale suffer unavoidable uncertainty broadening themselves, the accuracy with which femtosecond relaxation processes can be measured is limited. The result of the limitations to the accuracy of these measurements is the reporting of vibrational lifetimes ranging from 700 fs [38] to 100 fs [39]. In the present analysis, the fastest lifetime was chosen for inclusion in the model because this value is the most recent measurement with the most advanced technology and creates the maximum lifetime broadening. At such short lifetimes, the degree of homogeneous broadening is large, such that the use of 200 fs for the lifetime would produce a Lorentzian width of 25 cm⁻¹, which is half the homogeneous broadening as that for 100 fs. Considering that the width of the linear hydrogen bond component in the present fits is roughly 100 cm⁻¹, the difference in the Gaussian area calculated from the fit Voigt functions changes considerably when the homogeneous broadening contribution changes only slightly on the femtosecond timescale. Also, our choice to use the maximum lifetime broadening suggested from ultrafast IR measurements would tend to produce analyses that err on the side of overestimating the favorability of bent hydrogen bonds. This source of inaccuracy is currently unavoidable.

The inherent uncertainty imposed on the linear population lineshape by its ultrafast relaxation time severely limits the ability of the two state hydrogen bonding model to produce reliable absolute thermodynamic values for the behavior of the water hydrogen bond network. The purpose of this model, however, is not to measure absolute thermodynamic values for the hydrogen bond network, but rather to facilitate quantitative interpretation of solute effects on the hydrogen bond network of water. In this, the two state hydrogen bonding model succeeds. Consistent application of the model to spectra from samples with varying solutes or solution conditions allows quantitative comparison of the water hydrogen bond network behavior.

4.3 Effects of salts of the Hofmeister series on water hydrogen bonding

The present temperature excursion infrared spectroscopy of aqueous solutions of a wide variety of salts commonly shown to produce Hofmeister effects in biological systems showed correlation between the effects of these salts on the water hydrogen bond network and their position in the Hofmeister series. The salts and their ΔG_b→l values are shown grouped by anion and by cation in Table II. Table II includes all salts, regardless of solubility (though salts at 4.4 molal are shown in black while salts at saturation are shown in gray), and lists each grouping in order of increasing ΔG_b→l.

If there is correlation between salt effect on ΔG_b→l and position in the Hofmeister order, it should appear in these groupings. When comparing the salts that have the same cation, it is clear that a reproducible order appears as a function of anion character for all salts that were soluble to 4.4 molal ion concentration: phosphate/sulfate < chloride < bromide < nitrate. This is the same order seen in the Hofmeister series and when these ions are ranked according to Jones-Dole viscosity B values or charge density, which are known to correlate with each other as discussed in the Introduction. What emerges from the data is a clear picture of anions of the Hofmeister series such that high charge density leads to stronger promotion of linear hydrogen bonding in solvating water, whereas lower charge density leads to less promotion of linear hydrogen bonding and eventually, at low enough charge density, to inhibition of linear hydrogen bonding.

Comparison of the cations when the salts are grouped by anion shows a less obvious pattern. The prevailing order of cations with respect to ΔG_b→l, for the salts which are soluble to 4.4 molal ion concentration, appears to be: magnesium < ammonium < lithium < sodium ≤ potassium. This order is shown for all anions with the exception of phosphate, for which low solubility made the observed trends unreliable. The only calcium salt that was soluble to 4.4 molal ions was calcium nitrate, which formed a highly viscous solution and was difficult to obtain at the necessary H concentration, thus the reliability of this value is somewhat suspect. The position of this salt among the other nitrate salts fails to group the calcium cation near magnesium as the Jones-Dole viscosity B coefficient, charge density, and Hofmeister series would predict. The stoichiometric contribution of the nitrate anion, which strongly promotes bent hydrogen bonding, also makes the relative position of calcium versus lithium difficult to compare reliably. As a result, the position of calcium in the order of the cations is difficult to argue based on these data. The other cations fall in the Hofmeister order with the exception of the ammonium cation, potential explanations for which are addressed in the Appendix. For the remaining four cations, the trend observed for the anions is reproduced, with magnesium most strongly promoting linear hydrogen bonding followed by lithium, sodium, and potassium, respectively. This result is consistent with the prevailing theories relating ionic charge density to Hofmeister effects.

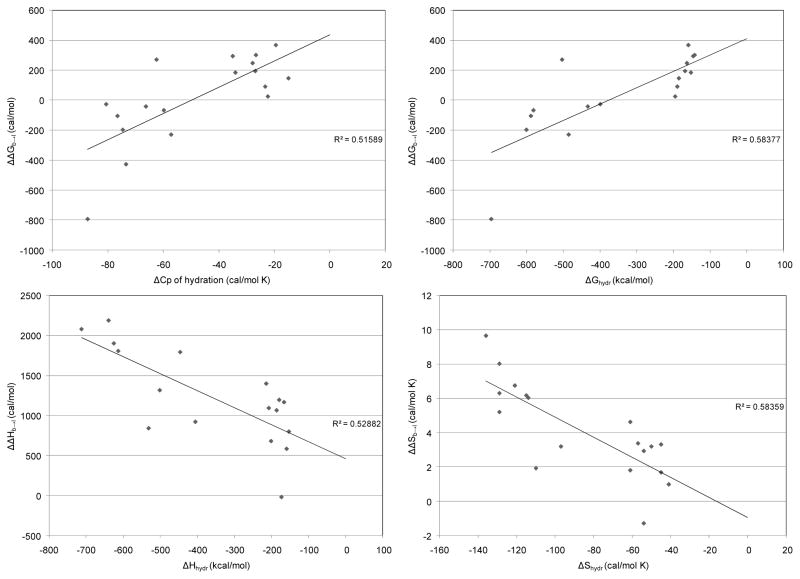
Just as the energetic predictions of the two state model for the isolated O-H oscillator were compared to previous estimates of thermodynamic parameters for water above, it is a useful test of the salt solution results to compare the predicted thermodynamic values for the various salts tested here to known thermodynamic properties. Convenient parameters for comparison are the thermodynamic values of hydration for these salts. It is reasonable to expect that an effect of a given salt on the thermodynamics of the water hydrogen bond network would be correlated to some extent with the measured thermodynamics of hydration for that salt. Marcus has provided hydration thermodynamic values for a wide array of ions, such that the corresponding thermodynamic property of the salt can be calculated from a stoichiometric addition of the values for the substituent ions [20]. Figure 14 shows scatter plots of the thermodynamic values from the present van’t Hoff analysis of aqueous salt solutions versus corresponding thermodynamic values of hydration for the respective salts, as calculated from reference 20. Linear least-squares fits to these data were performed to examine whether a correlation is seen. Comparisons of ΔΔG_b→l to ΔG_hydr and to ΔCp_hydr show evident, though somewhat weak, correlations. Comparisons of ΔΔH_b→l to ΔH_hydr and of ΔΔS_b→l to ΔS_hydr show similarly clear, yet weak, correlations. All salts that were soluble to 4.4 molal ion concentration except the ammonium salts were included in this analysis.

Analysis of variance was performed for the linear regression fit of each data set, and the results of the F-tests gave at least a 0.001 confidence interval for each fit. Thus, though these correlations are weak when measured in terms of the goodness of fit (adjusted R² shown in Figure 6), the statistical significance of the correlations is strong. Such strong statistical correlations lend credence to the validity of the present interpretation of the O-H stretch spectra.

Figure 6.

Correlations of thermodynamic parameters for the transition of a water network hydrogen bond from bent to linear in the presence of various salts calculated from van’t Hoff analysis of TEIR spectra versus experimental thermodynamic parameters of hydration for salts from Marcus [20]. Adjusted R² values are shown for the linear least-squares fit to each set of data.

The weakness of the correlation is unsurprising for several reasons. The thermodynamic values of hydration are considered valid for extremely dilute solutions; whereas the solutions tested in the present study are at quite high concentration. There are also many additional energetic factors that contribute to the thermodynamics of hydration beyond ion effects on the water hydrogen bond network. Naturally, such additional contributions are not included in this analysis. The inherent error in the O-H stretch fitting process that results from homogeneous broadening must also cause some inaccuracy in determining the absolute energy values for the behavior of the water hydrogen bond network, though this error will be reduced by examining the energetic values with salt versus without, as was done for the analysis in Figure 14. Still, the values from the van’t Hoff analysis of the spectral fits will contain some inherent variability due to the nature of this spectral interpretation strategy.

Despite the semi-quantitative nature of the present spectral interpretation, the conclusion remains clear. The effects of salts on the water hydrogen bond network clearly correlate with the Hofmeister series. The extent to which ions promote linear hydrogen bonding of the water network seems to be dependent on the ionic charge density. This trend is readily observable for both anions and cations, though it is clearer for anions. Stronger Hofmeister ordering for anions than for cations has been observed for many other Hofmeister effects [22,26]. This difference between anions and cations has been attributed to their differences in surface charge density; anions have higher surface charge density than cations for equal ionic radii, thus their effects on water are stronger. The present data support a view of ions of the Hofmeister series exerting their effects on biological systems, at least in part, through alteration of the hydrating environment.

5. Conclusions

The present study shows that ions alter the hydrogen bond network of water. Correlation between the nature of ion effects on water hydrogen bonding and the Hofmeister series has been shown. Ammonium is a notable exception to the general trends shown here for several anions and cations. Overall, the present analysis suggests that at least a portion of the physical basis for Hofmeister effects of salts on proteins is a modification of the solvation environment. These data offer no evidence against the possibility of specific ion-protein interactions playing a role, but if specific interactions do occur, it is in conjunction with changes in bulk solvation properties.

Supplementary Material

01

Figure A.1 Temperature excursion infrared O-H stretch spectra of aqueous salt solutions with ammonium cation at 5 °C intervals from 5 °C to 80 °C. The TEIR spectra of isolated O-H oscillator in D2O are included for comparison.

02

Figure A.2 Temperature excursion infrared O-H stretch spectra of aqueous salt solutions with sodium cation at 5 °C intervals from 5 °C to 80 °C. The TEIR spectra of isolated O-H oscillator in D2O are included for comparison.

03

Figure A.3 Temperature excursion infrared O-H stretch spectra of aqueous salt solutions with lithium cation at 5 °C intervals from 5 °C to 80 °C. The TEIR spectra of isolated O-H oscillator in D2O are included for comparison.

04

Figure A.4 Temperature excursion infrared O-H stretch spectra of aqueous salt solutions with magnesium cation at 5 °C intervals from 5 °C to 80 °C. The TEIR spectra of isolated O-H oscillator in D2O are included for comparison.

05

Figure A.5 Temperature excursion infrared O-H stretch spectra of aqueous salt solutions with calcium cation at 5 °C intervals from 5 °C to 80 °C. The TEIR spectra of isolated O-H oscillator in D2O are included for comparison.

06

Figure A.6 Van’t Hoff plots from the fit analysis of the temperature excursion O-H stretch spectra for all salts grouped by anion. The trends seen for the varied cations clearly show correlation with the Hofmeister series for each anion except those that were only slightly soluble in water. The van’t Hoff analysis for the isolated O-H oscillator in D2O is included for comparison.

07

Figure A.7 Van’t Hoff plots from the fit analysis of the temperature excursion O-H stretch spectra for all salts grouped by cation. The trends seen for the varied anions clearly show correlation with the Hofmeister series for each anion except those that were only slightly soluble in water. The van’t Hoff analysis for the isolated O-H oscillator in D2O is included for comparison.

08

Figure A.8 TEIR of 15N-labeled ammonium salts. Spectra are shown at 5 °C intervals from 5 °C to 80 °C.

09

Figure A.9 Difference spectra of 15N-labeled salts versus unlabeled salts. These difference spectra represent the changes to the O-H stretch bandshape as a result of 15N substitution. Clear contribution can be seen at the low-frequency end of the spectrum and to the high-frequency side of the peak, as well.

10

Figure A.10 Concentration-dependent O-H stretch spectra of lithium salts. Concentrations are for total ion content. Spectra are shown for 2.2, 1.1, 0.55, 0.28, 0.14, and 0.07 molal. The highest concentration for each salt is shown as the heavy spectrum. Arrows indicate shift of the spectrum from high concentration to low.

11

Figure A.11 Concentration-dependent O-H stretch spectra of sodium salts. Concentrations are for total ion content. Spectra are shown for 2.2, 1.1, 0.55, 0.28, 0.14, and 0.07 molal. The highest concentration for each salt is shown as the heavy spectrum. Arrows indicate shift of the spectrum from high concentration to low.

12

Figure A.12 Concentration-dependent O-H stretch spectra of potassium salts. Concentrations are for total ion content. Spectra are shown for 2.2, 1.1, 0.55, 0.28, 0.14, and 0.07 molal. The highest concentration for each salt is shown as the heavy spectrum. Arrows indicate shift of the spectrum from high concentration to low.

13

Figure A.13 Concentration-dependent O-H stretch spectra of ammonium salts. Concentrations are for total ion content. Spectra are shown for 2.2, 1.1, 0.55, 0.28, 0.14, and 0.07 molal. The highest concentration for each salt is shown as the heavy spectrum. Arrows indicate shift of the spectrum from high concentration to low.

14

Figure A.14 Concentration-dependent O-H stretch spectra of magnesium salts. Concentrations are for total ion content. Spectra are shown for 2.2, 1.1, 0.55, 0.28, 0.14, and 0.07 molal. The highest concentration for each salt is shown as the heavy spectrum. Arrows indicate shift of the spectrum from high concentration to low.

15

Figure A.15 Concentration-dependent O-H stretch spectra of calcium salts. Concentrations are for total ion content. Spectra are shown for 2.2, 1.1, 0.55, 0.28, 0.14, and 0.07 molal. The highest concentration for each salt is shown as the heavy spectrum. Arrows indicate shift of the spectrum from high concentration to low.

16

Figure A.16 Concentration dependence of ΔG_b→l for all salts grouped by anion. For all salts that show significant effect on ΔG_b→l, concentration dependent response can be approximated as linear. ΔG_b→l for the isolated O-H oscillator in D₂O at 25 °C is ~250 cal/mol ± 25 cal/mol.

17

Figure A.17 Concentration dependence of ΔG_b→l for all salts grouped by cation. For all salts that show significant effect on ΔG_b→l, concentration dependent response can be approximated as linear. ΔG_b→l for the isolated O-H oscillator in D₂O at 25 °C is ~250 cal/mol ± 25 cal/mol.

7. APPENDIX

7.1 Spectra and Van’t Hoff plots for all salts

TEIR of the O-H stretch of the various salt solutions are shown in figures A.1 – A.5. Van’t Hoff plots from the fit data of each set of salt spectra are shown in figures A.6 and A.7. These data consistently show the trends described in the main text.

7.2 Deviation of ammonium salts from Hofmeister order with respect to effects on the water O-H stretch

Deviation of the thermodynamic values of the ammonium salts was thought to be due to the overlap of the N-H stretch with the O-H stretch. As a result, TEIR of ¹⁵NH₄Cl, ¹⁵NH₄NO₃, and (¹⁵NH₄)₂SO₄ were measured with the expectation that isotopic substitution of nitrogen would shift the N-H stretch to low frequency enough to prevent contamination of the O-H stretch. These spectra are shown in Figure A.8. Difference spectra were calculated between the ¹⁵N-labeled salts and the non-labeled salts are shown in Figure A.9. Both the labeled and unlabeled ammonium salt spectra were fit with the two-state hydrogen bonding model in order examine the effect of isotopic substitution on the N-H contamination of the O-H stretch. The resulting energy values are compared in Table A-I.

The difference spectra in Figure A.9 show contributions to the lineshape in both the low-frequency side and the high-frequency side of the O-H stretch, though the low-frequency contribution is clearly larger for all three salts. If the contamination of the O-H stretch by the ammonium ion were due simply to an overlap of the N-H stretch, contribution should only be seen in the low-frequency portion of the spectrum because the N-H stretch of ammonium is centered at 3200 cm⁻¹ – 3250 cm⁻¹. Contribution to the high-frequency side is most likely the result of vibrational mixing from coupling of N-H oscillators with O-H oscillators through hydrogen bonds. Such coupling has been directly measured for nitrogenous ions in aqueous solution [108], so evidence of vibrational mixing is not surprising. The magnitude of contribution from N-H seen in the difference spectra was considerably smaller than expected. At 4.4 molal ion concentration, there was one N-H oscillator for every 6.25 O-H oscillators. Though the extinction of the N-H stretch is smaller than that of the O-H stretch, the absorption difference for the ¹⁵N-labeled salt was expected to be much higher than shown in Figure 13. As the values reported in Table III show, use of ¹⁵N-labeled salt had very small effect on the results of the energy analysis.

The ¹⁵N-labeled salts produced values for ΔG_b→l that were only 50–100 cal/mol higher than those for the unlabeled salts. If the effects of the ammonium salts on the water hydrogen bond network correlated with their position in the Hofmeister series, these energy values would have to be 500 cal/mol or more higher than they are for the ¹⁵N-labeled salts.

The Hofmeister series would predict that ammonium, as the least charge-dense of the cations tested, should fall to the extreme opposite of magnesium. Based on these data, it does not. As Table II in the main text shows, the ordering of the anions of the various ammonium salts clearly correlates with the Hofmeister order, so the discrepancy of ammonium’s position in the present analysis is a result of its comparison to other cations. There are two possible explanations for the deviation of the energetic values of the ammonium salts from the trends seen for the other salts of the Hofmeister series.

Based on comparison between isotopically substituted and unsubstituted salts (Figures A.8 and A.9), it is clear that the N-H stretch causes some contamination of the O-H stretch bandshape. Isotopic substitution clearly removes some of this contamination. However, substitution with ¹⁵N shifts the N-H stretch to a position overlapping the O-D stretch. It is possible that some contamination of the O-H stretch may remain even in the presence of ¹⁵N substitution. Such contamination would distort the O-H stretch in a fashion that is impossible to account for in our analysis.

Another potential reason for ammonium behaving differently in our analysis is the possibility of specific interactions being an important component of the physical basis of ammonium-induced effects on proteins. Nitrogen-based molecules have been shown to engage in vibrational coupling with proteins and with water through hydrogen bonds. Hochstrasser and coworkers have measured such coupling for multiple systems [108–110], demonstrating the potential for ammonium effects on protein structure and stability to occur through specific interactions rather than through bulk changes to the water hydrogen bond network. The present data can offer no insight into which of these two potential explanations is correct. They are certainly not mutually exclusive, so the true explanation for the deviations of the ammonium salts in our data may be the result of some combination of both.

Whatever the reason, the present analysis suggests that ammonium does not show the strong favoring of bent hydrogen bonds that its position in the Hofmeister series, its charge density, and its Jones-Dole viscosity B coefficient would predict. This evidence, however, is certainly not conclusive.

7.3 Concentration dependent IR

The concentration dependence of the O-H stretching vibration was measured for all salts that were soluble to 0.55 m or higher. All given concentrations are ion concentrations, not salt concentrations. These spectra are shown in Figures A.10–A.15. All spectra were fit according to the same procedure used for the temperature excursion spectra. The fitting procedure yielded values for the effective ΔG for the transition from a bent to linear hydrogen bond conformation at each concentration. The ΔG_b→l values are shown as a function of concentration in Figures A.16 and A.17. The ΔG_b→l for the isolated O-H oscillator in D₂O is ~250 cal/mol ± 25 cal/mol using this analysis. All salt solutions show essentially the same ΔG_b→l as salt-free water below 0.14 m. The concentration dependence of all salts that show a significant change to ΔG_b→l at high concentration can be approximated as linear.

These data support the model of salt effects on water structure occurring primarily in the few water layers nearest the dissolved ions. If extensive cooperative effects were occurring, non-linear concentration response would be expected, thus these data are indicative of minimal cooperativity in the salt-induced changes to water hydrogen bonding.