Conformational Entropy of an Ideal Cross-Linking Polymer Chain

Abstract

We present a novel analytical method to calculate conformational entropy of ideal cross-linking polymers from the configuration integral by employing a Mayer series expansion. Mayer-functions describing chemical bonds within the chain and for cross-links are sharply peaked over the temperature range of interest, and, are well approximated as statistically weighted Dirac delta-functions that enforce distance constraints. All geometrical deformations consistent with a set of distance constraints are integrated over. Exact results for a contiguous series of connected loops are employed to substantiate the validity of a previous phenomenological distance constraint model that describes protein thermodynamics successfully based on network rigidity.

1. Introduction

The thermodynamic state of a physical system in equilibrium with a thermal bath is determined by the minimum of its free energy. This minimum would be trivially obtained if the energy (or enthalpy) of the system is a minimum while the entropy is a maximum. Usually, these two conditions cannot be simultaneously satisfied. Typically, there are few low energy microstates compared to the large number of high energy microstates. Thus, systems usually exhibit characteristics of low energy and low entropy at low temperatures, whereas the same systems exhibit characteristics of high energy and high entropy at high temperatures. Interesting behavior in change of state (i.e. phase transitions) occur because these two conditions are in competition. To understand polymer conformations in solution, it is common to identify a variety of mechanisms involving changes in enthalpy and entropy, and to interpret quasi-static equilibrium processes in terms of these mechanisms. One such mechanism is cross-linking of covalent bonded chains. As more cross-links are added, conformational entropy and energy will decrease. Conversely, with the cost of adding energy to the system, cross-links will break, and there will be an increase in conformational entropy. From synthetic polymers to biomacromolecules (i.e., peptides, proteins, and nucleic acids), conformational entropy is an important factor governing the thermodynamic response.

We now turn our attention to globular proteins in aqueous solution, which has motivated this work. Proteins are macromolecules consisting of many noncovalent interactions that determine their three-dimensional structure and stability [1]. Solvation mechanisms such as hydration or the hydrophobic effect contribute to enthalpy-entropy compensation. It is commonly stated that the entropic nature of the hydrophobic effect is the dominant force of protein folding [2]. That is, entropy due to solvation of a folded protein increases because water is transferred from the buried core into bulk water. Interestingly, the hydrophobic effect increases as the temperature increases. Therefore, without other entropic factors a protein would never thermally denature, since the folded state would simultaneously minimize the energy and maximize entropy. Of course, proteins do unfold at high temperatures, and this is because the total entropy of the unfolded state is much greater than that of the folded state. This gain in entropy is from the conformational entropy, which must compensate for the higher energy and overcome a decrease in solvation entropy once the protein opens up to aqueous solution in the unfolded state.

Conformational entropy is related to the change in mechanical nature of the folded (more rigid) and unfolded (more flexible) states. Direct measurements of conformational entropy can be done using neutron spectroscopy [3] or from order parameters obtained from Nuclear Magnetic Resonance (NMR) experiments [4]. Moreover, conformational entropy is invariably a critical factor to protein function [4], either because the protein must be rigid in specific regions, or have intrinsic flexibility in other specific regions to facilitate molecular recognition. Thus, conformational entropy is of central importance to protein stability and function. A convenient way to proceed is to divide entropy contributions into two categories; solvent related mechanisms that deal with solvent degrees of freedom given the polymer conformation, and mechanical mechanisms that deal explicitly with the degrees of freedom within the polymer. Fundamentally, nonadditivity of entropy components are noticeable when there is nonnegligible coupling between polymer degrees of freedom [5, 6]. In constrast, solvent degrees of freedom define the detail-free thermodynamic reservoir, and therefore they can be treated as additive [7].

There is no question that solvation entropy and conformational entropy are both important factors that govern thermodynamic stability in proteins and other polymers. However, the enthalpy-entropy mechanism related to cross-linking of covalent bonded chains must play a dominant role based on the following two findings: (1) Although it is impossible to explain the protein folding transition without accounting for conformational entropy, essential aspects of protein folding are readily explained only in terms of hydrogen bond cross-linking without invoking the hydrophobic effect [8]. (2) Moreover, it has been demonstrated that the process of intramolecular hydrogen bond formation is concomitant with the formation of hydrophobic contacts [9]. We have distilled these two findings into a working hypothesis: The essential mechanism controlling the thermodynamic stability of biopolymers is that of chemical cross-linking covalent bonded chains. Actually, it is the mechanical aspects of cross-linking that plays a significant role.

Cross-links act as mechanical distance constraints between pairs of atoms. Intuitively, it makes sense that as more cross-links form, more atomic motion becomes restricted. The covalent bonded chain augmented by cross-links (say from hydrogen bonding) together form a constraint network. Conformational entropy is related to the accessible atomic motions of the macromolecule. Therefore, a flexible polymer will have greater conformational entropy than a rigid polymer. A polymer with many rigid parts interspersed with few flexible connecting regions will have (more, less) conformational entropy than if it was completely (rigid, flexible). The relationships between where the cross-links are located, the resulting flexibility and rigidity throughout the network (polymer) and the associated increase or decrease of conformational entropy is easy to understand conceptually. Unfortunately, direct calculation of conformational entropy for a large polymer, such as a protein, remains an open problem.

The major source of difficulty in calculating conformational entropy is from nonadditive effects that derive from the mechanical response of fluctuating cross-linking [10]. In previous work on calculating the stability of peptides and proteins (see Ref. [11] for a review) the main source of cross-links come from the hydrogen bond network. Appreciation for the role hydrogen bonds play in stabilizing protein structure has been steadfast [12]. Moreover, it has been recently argued [13] that backbone hydrogen bonds give rise to the dominant force for protein folding, which bolsters our hypothesis. The breaking and forming of hydrogen bonds give rise to an ensemble of constraint networks with varying amount of cross-linking, each having different flexibility and rigidity characteristics. The mechanical characteristic responsible for flexible and rigid regions is called network rigidity, which is intimately related to thermodynamics [14]. The increase in rigidity and loss of conformational entropy as the number of cross-linking constraints increase was calculated using a semi-empirical Distance Constraint Model (DCM) [10, 15]. The conformational entropy was efficiently calculated as a function of independent constraints that were identified by a graph rigidity algorithm [16], which only depends on the topology of the constraint network. Several successful comparisons between DCM predictions and experiment [15, 17–21] provide further evidence in support of our working hypothesis.

To go beyond the phenomenological DCM that requires fitting parameters, a careful mathematical analysis for calculating conformational entropy is neccesary. By focusing on this single aspect, we present novel results that progress toward this goal. In particular, we lay out the groundwork for a general approach applicable to polymers of all types, which is surprisingly tractable and it is expected to be scalable to large systems. As our first step, we consider elementary structures, and purposely keep the model simplified by not considering self-avoidance. Consideration of self-avoidance would result in considerable amount of mathematical complexity. We defer these technically involved calculations because much merit follows from the ideal polymer chains. Chan and Dill give a good discussion of how polymer principles apply to proteins, where they thoroughly describe the role of self-avoidance [22]. By considering ideal polymer chains, we over-estimate conformational flexibility, but these results can be used to gain understanding of the approximations made in the phenomenological DCM [10, 15, 20]. It is worth mentioning that the phenomenological DCM is topologically based, and also neglects self-avoidance. It is common to neglect self-avoidance in topology-based Ising-like models [23–25]. Overall, Ising-like models have proven themselves to be very useful, despite the fact that self-avoidance is neglected.

In this report, a microscopic foundation for the DCM is presented for the first time. We discuss a new analytical technique that, starting from first principles, evaluates the conformational entropy of a given network. The network is composed of ideal cross-linking chains. The new method is based on direct integration of the atomic coordinates in configuration space, explicitly taking into account the restrictions imposed by the chemical bonds. Our results highlight the essential role of the cross-linking mechanism to enthalpy-entropy compensation.

The model considered here involves a collection of atoms, each having three degrees of freedom. Pairwise interactions between certain neighboring atoms can form. These interactions are very strong, and are referred to as chemical bonds. When a chemical bond forms between a pair of atoms, the energy of the system is lowered, and the distance between the atoms remains fixed during all allowed dynamics. Despite the simplicity of the model, all essential aspects of conformational entropy, and enthalpy-entropy compensation related to the cross-linking mechanism is fully contained. Moreover, the mathematical steps and procedures that we present here will remain the same for much larger complex constraint networks that model proteins. In view of our long-term goals of applying the method to proteins, the model presented here deals with two types of chemical bonds. The first type is covalent bonds, which are quenched and do not fluctuate. The second type is hydrogen bonds that provide cross-linking within the network, and readily form and break due to thermal energy.

In section 2, we discuss the general method of a Mayer’s series to evaluate the conformational entropy of a molecular network using the distance constraint approximation. In section 3, we develop the equations for calculating the conformational entropies of different types of networks, ranging from tree topologies to loops, to complex multi-connected loop topologies. The approach effectively involves factorizing the network into additive configuration space volumes; however, this factorization process becomes more complicated in highly cross-linked networks. In these cases, a spanning tree over quenched constraints (the covalent bonded backbone structure) is used to define an internal coordinate system to evaluate the configuration integral. This analytical method accounts for geometrical details. In section 4, the results for a contiguously connected set of flexible loops in series are used to obtain an upper bound error estimate for the semi-empirical DCM, which neglects geometrical details. We find that with suitable rescaling of parameters, the errors are not only small and tolerable, but also explain why the DCM parameters are robust across a diverse set of proteins. This latter result provides an explanation for why the DCM has been successful in describing protein thermodynamics despite its simplicity.

2. Mayer expansion using distance constraints

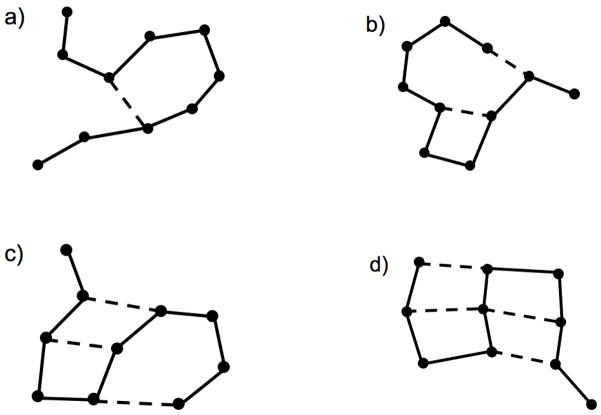
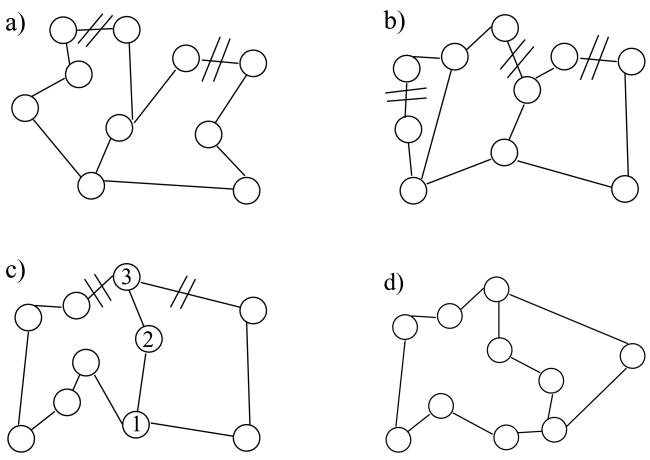
To develop the procedure to calculate the conformational entropy, we start from the classical partition function of N distinguishable atoms. The partition function for a classical system factors into a momentum contribution, and the configuration integral, Q, which is of primary importance [26]. Assuming pairwise interactions only, a cluster expansion for Q can be performed in terms of Mayer f-functions [26] given by f_ij = e^−u(rij)/kT −1 where u(r_ij) is the potential energy between atoms i and j due to a central force, k is the Boltzmann constant, and T is temperature in Kelvin. The displacement vector between these two atoms is given by r_ij = r_i − r_j, and r_ij is its magnitude. Following the standard procedure of expanding the partition function in powers of dimensionless Mayer f-functions results in many terms at different orders (i.e. 1, f, f², … fⁿ). In applications of simple liquids the central force pairwise interactions do not correspond to chemical bonds. However, in the application to polymers with cross-linking, the most important terms in the Mayer expansion are from the f-functions that correspond to chemical bonds. The chemical bonds are modeled as central forces. Therefore, atoms within the polymer are represented as vertices in a graph and chemical bonds are represented as edges in the graph. The graph defines a constraint network as Fig. 1 depicts. Many topologically distinct constraint networks are possible, and all those that are accessible are uniquely labeled using ν as an index.

Figure 1.

Typical constraint networks are shown. Atoms are represented as vertices. Edges represent central force chemical bond interactions between atomic pairs. Solid lines represent covalent bonding, and dashed lines represent hydrogen bonding. The four panels show some examples of how the constraint network can fluctuate as hydrogen bonds break and form. Each panel represents a fixed constraint topology, and the constraint network is labeled with the ν index, as explained in the text.

The partition function, Q, for the system is given by:

$$Q=\sum _{\nu }{Q}_{\nu },Q_{\nu }=\int d^3{\mathbf{r}}_1\dots d^3{\mathbf{r}}_N\prod _{{\langle ij\rangle }_{\nu }}{f}_{ij}.$$ (1)

where Q_ν is the contribution to the partition function from network ν in the Mayer expansion. Note that Q_ν is not itself a partition function as is suggested by the notation. However, the use of the Q_ν notation will become clear below. For a given ν, the topology of the constraint network is fixed. That is, the set of all edges (atomic pairwise interactions) are conserved, where the identified pairs of atoms that chemical bond are labeled as 〈ij〉_ν to specify which atom pairs interact within the ν-th network. Note that subject to preserving the network topology (i.e. keeping the same distribution of f-functions within the graph) all atomic coordinates are integrated over. During this integration, note that all atoms and edges may pass through each other because self-avoidance between atoms is neglected for simplicity.

In principle, we could consider all central force interactions, such as weak van der Waal interactions, and include them in the Mayer expansion. The advantage of including van der Waal forces is that self-avoidance will be maintained. However, the largest and most important f-function contributions are those from chemical bonding. Therefore, the origin of our model that focuses on chemical bonding is based on the awareness that the contributions from the chemical bonding alone describes the essential physics. Also worth mentioning is that covalent bonding is more complicated than a central force interaction; rather, it is also associated with bond-bending interactions dealing with constraining the angles that form between nearest neighbor atoms. If this molecular detail is desired, then these bond-bending interactions can be modeled as next nearest neighbor atomic pairwise central force interactions. Consequently, the approach described here using only central forces is markedly general. These additional considerations of enforcing self-avoidance by keeping track of van der Waal interactions, and modeling bond-bending forces would, however, lead to complicated mathematics. Therefore, unless stated otherwise, we consider the ideal model situation that consists of non-interacting atoms (no self-avoidance just like an ideal gas) except through local central force chemical bonding.

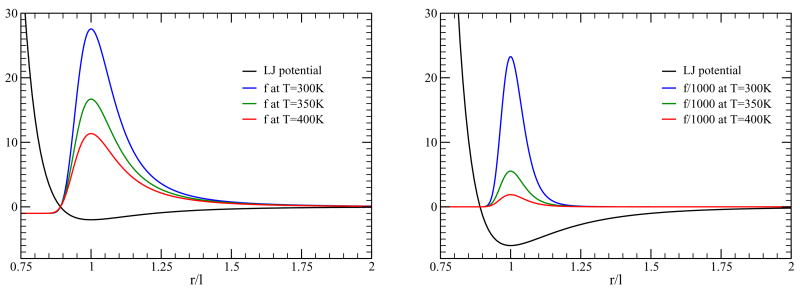
As shown in Fig. 2, f-functions are sharply peaked functions whenever there is a deep minimum in the potential compared to thermal energy. For chemical bonds and for temperatures of interest in projected applications (i.e. protein stability in aqueous solvent over the temperature range 250K ≤ T ≤ 400K), the Mayer f-function is well approximated by a Dirac delta-function given as

Figure 2.

Left panel: A 12-6 Lennard-Jones potential energy function with a minimum energy of −2 kcal/mol is shown, and its corresponding Mayer f-function for temperatures 300K, 350K and 400K. The y-axis has units of kcal/mol with respect to the potential energy function, and is dimensionless for the Mayer f-functions. As temperature is lowered, the Mayer f-function sharpens dramatically. In all cases, the Mayer f-function equals -1 for r/l → 0, which is clearly visible. Right panel: The minimum energy of a 12-6 Lennard-Jones potential is now −6 kcal/mol. The Mayer f-functions are so tall that they are divided by a factor of 1000. After this scaling, it is easy to see that the width of the Mayer f-function decreases as the depth of the well increases. In this case, it is clear the −1 is negligible.

$$f_{ij}\approx C_{ij}\delta (\mid {\mathbf{r}}_i-{\mathbf{r}}_j\mid -l_{ij})\text{with}{C}_{ij}=\underset{0}{\overset{\infty }{\int }}{f}_{ij}(r)dr$$ (2)

where l_ij is a fixed distance that locates the minimum of the potential energy function. The replacement of the Mayer f-function with a Dirac delta function is the distance constraint approximation. As long as the f-function is sharply peaked, this is a good approximation in spite of the fact that the f-function equals −1 as r → 0 [cf. Fig. 2]. The prefactor C_ij provides the appropriate weighting, which is the total area under the f-function.

The distance constraint approximation given in Eq. (2) is checked by constructing an austere test using an ensemble of random test functions {φ_n(r)}. The distance constraint approximation is justified if for any test function,

$$\underset{0}{\overset{\infty }{\int }}{f}_{ij}(r){\phi }_n(r)dr={\phi }_n(l)\underset{0}{\overset{\infty }{\int }}{f}_{ij}(r)dr$$ (3)

can be satisfied within tolerable amount of error. A 12-6 Lennard-Jones potential

$$u(r)=-u(l)\left[{\left(\frac{l}{r}\right)}^{12}-2{\left(\frac{l}{r}\right)}^6\right]$$ (4)

is used as a representative potential energy function. The form of the Lennard-Jones potential makes the calculation of the left and right sides of Eq. (3) independent of the location of the minimum, l. This is because the definite integrals that range from 0 to infinity allow the length l to be scaled out, and then canceled out, on both sides. We construct random polynomials of degree 4 for the set of test functions, {φ_n(r)}. With these choices, both the left and right hand sides of Eq. (3) can be evaluated analytically. This fact allows us to explore an enormous number of samplings while avoiding difficulties with numerical integration of nearly discontinuous functions.

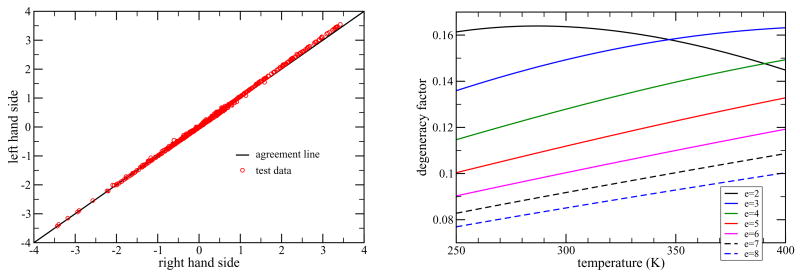
Typical results are shown in Fig. 3(a), where it is seen that the distance constraint approximation is very good. In particular, the test is quite severe because immediately outside the range of the bottom of the well, many of the polynomials grow very fast. Overall, we find that the accuracy of the distance constraint approximation is excellent whenever e^−u(l)=kT ≫ 1 (i.e. existence of a tall peak), and remains reasonable even when −u(l)/kT = 2.5. Certainly all covalent bonds satisfy this criteria far beyond requirements, and nearly all hydrogen bonds satisfy this criteria to make the approximation excellent, except for the most feeble ones. In passing, it is worth noting that the initial −1 in the f-function starting out from r = 0 is the major reason for errors using the distance constraint approximation, and corrections for this part of the f-function can be included if desired (unpublished results). Moreover, the same formalism can be followed with finite width distribution functions, or even the Mayer f-function itself for the cases where the distance constraint approximation breaks down. However, by considering only chemical bonds as an interaction, the distance constraint approximation is always excellent for covalent bonds and very good for hydrogen bonds with binding energy as low as 3 kcal/mol. The distance constraint approximation captures the essential physics, and greatly simplifies the mathematics because we can take advantage of certain orthogonal functions used to represent the Dirac delta function, described in the next section.

Figure 3.

(a) Left Panel: The corresponding left and right hand sides of Eq. (3) in arbitrary units are plotted on the y and x-axis respectively to form the scatter plot shown as red circles. The black straight line shows the agreement line. These are typical results for 3000 random polynomials at room temperature, T = 300K, and a binding energy of |u(l)| = 6 kcal/mol. (b) Right Panel: The degeneracy factor, ω, given in Eq. (5) to parameterize the weighting prefactor C, is plotted as a function of temperature. A series of curves are shown corresponding to the case of using a 12-6 Lennard-Jones potential with binding energies ranging from 2 kcal/mol to 8 kcal/mol. Note that by time the binding energy is 2 kcal/mol, the temperature dependence of ω becomes distinctly different from all the rest of the cases.

The prefactor C for an f-function is adjusted so that the integral over the actual Mayer f-function is by construction identical to the Dirac delta function approximation. It is seen from Fig. 2 that the area under the f-function is strongly temperature dependent. Thus, the prefactor, C, being this area, is temperature dependent. However, for all cases that the distance constraint approximation is reasonable, or better, it turns out that the prefactor C depends on temperature (over the temperature range of interest) in a natural way, given by

$$C=\underset{0}{\overset{\infty }{\int }}f(r)dr\approx (\omega l)e^{-\frac{\epsilon }{kT}}$$ (5)

where ε is the binding energy (a positive number). Note that u(l) is the energy minimum of the potential function, which is less than zero. We take the binding energy to be equal to the value of −u(l). The parameter ω is a dimensionless quantity that is temperature independent. This parameterization has a physical interpretation. The interaction is coarse-grained into an effective interaction that has three attributes: (1) The interaction fixes the distance, l, between the pair of atoms, (2) the interaction is assigned a binding energy, ε, and when binding occurs the energy of the system lowers, and (3) the wiggle room associated with the bottom of the well (which accounts for general atomic motion other than harmonic vibration) is kept track of through a degeneracy factor given by ω > 0. Since the binding energy is defined as the negative of the well depth, which is temperature independent, it follows that Eq. (5) is exact provided the degeneracy factor ω is allowed to be temperature dependent. We show in Fig. 3(b) that the temperature dependence is weak. For the purpose of maintaining a minimal model that retains the essential properties of the cross-linking mechanism, treating ω as independent of temperature is an excellent approximation. We note in passing, that if more detailed effects are added to the model, then treating the weak temperature dependence of ω creates no difficulty in the calculations.

Within the distance constraint approximation of Eq. (2), each term, Q_ν, that appears in the Mayer expansion has a pleasing physical interpretation of being a genuine partition function. The reason why this is true is a consequence of the operational procedure that cleanly separates the problem into energy and entropy contributions. This construction is obtained by inspection, now described. Each Dirac delta function operationally fixes the distance between all interacting pairs of atoms. As depicted in Fig. 1, the collection of all such Dirac delta functions are used to enforce a specified constraint network (labeled with ν). Consequently, each constraint network has a fixed energy. Within the distance constraint approximation, we have a literal and rigorous way to account for the accessible motion of all atoms within configuration space while maintaining a constant energy.

The total conformational degeneracy at fixed energy is given by Ω_ν, and can be calculated by the multi-dimensional configuration integral

$${\mathrm{\Omega }}_{\nu }=\frac{1}{b^{3N}}\int d^3{\mathbf{r}}_1\dots d^3{\mathbf{r}}_N\prod _{{\langle ij\rangle }_{\nu }}{\omega }_{ij}\delta \left(\frac{\mid {\mathbf{r}}_{ij}\mid }{l_{ij}}-1\right).$$ (6)

where b is an arbitrary length scale. It is worth noting that in classical statistical mechanics, entropies cannot be calculated on an absolute scale. As can be seen from Eq. (6), the total configuration space volume has dimension of length raised to the 3N power. Entropy is obtained through a logarithm of a dimensionless degeneracy factor for the total number of microstates. This is accomplished by dividing configuration space volume by a fixed hyperdimensional volume. (i.e. b^3N). Without quantum mechanics, this normalization factor (i.e. the coarse-grain length scale given by b) is arbitrary. Regardless of this coarse-graining scale, differences in entropies are absolute and measurable quantities because this arbitrary factor always cancels out within ratios inside logarithms. For convenience, we choose the normalization factor such that all lengths shown in the equations should be expressed in units of Angstroms.

The cross-linking mechanism is simple. As constraint i is added, the total energy lowers by ε_i, and there is a corresponding reduction in conformational entropy. Therefore, the contribution to the partition function from a given network can be cast in the form

$$Q_{\nu }=e^{S_{\nu }/k}{e}^{-E_{\nu }/kT}$$ (7)

where E_ν = −Σ_i ε_i is the total energy of the system. The total energy, E_ν is a constant of the motion for fixed constraint topology. The conformational entropy of a network is determined by the logarithm of its total conformational degeneracy given by S_ν = k log Ω_ν. In the applications of interest here, we only need to consider connected networks. Moreover, we are assuming that there is a connected path of covalent bonds that define the macromolecule, which never break over the temperature range of interest (i.e. 250 − 400K). Accordingly, atoms are distinguishable, and no factor N!⁻¹ appears in the partition function Q, or individual terms, Q_ν.

To summarize this section, the partition function for a macromolecule can be written as Q = Σ_ν e ^−Gν/kT where G_ν is the free energy of a particular constraint network, given by G_ν = E_ν − TS_ν. This means that each constraint network has a free energy, and equilibrium fluctuations will occur between a small fraction of networks that have approximately the same free energy equal to or near the global minimum. In proteins, there is usually a global minimum in the free energy landscape at any given thermodynamic condition. The landscape is defined in terms of order parameters that also define the macrostate of a protein. It is convenient to consider the number of cross-links as defining the macrostate of a protein. In prior works, we find that proteins exhibit typical free energy basins, giving rise to a most probable character of statistically significant constraint networks. The main character that we have previously considered [11, 15, 17] has been the number of cross-linking constraints (i.e. number of hydrogen bonds). As constraints are added or removed, the energy and conformational entropy concurrently decreases or increases respectively. Thus, our model for cross-linking builds in a very intuitive enthalpy-entropy compensation mechanism. In this report, we focus on the conformational entropy calculation, which is the non-trivial technical part of the problem, but turns out to be surprisingly straightforward.

3. Calculation of conformational entropy

Simply connected networks

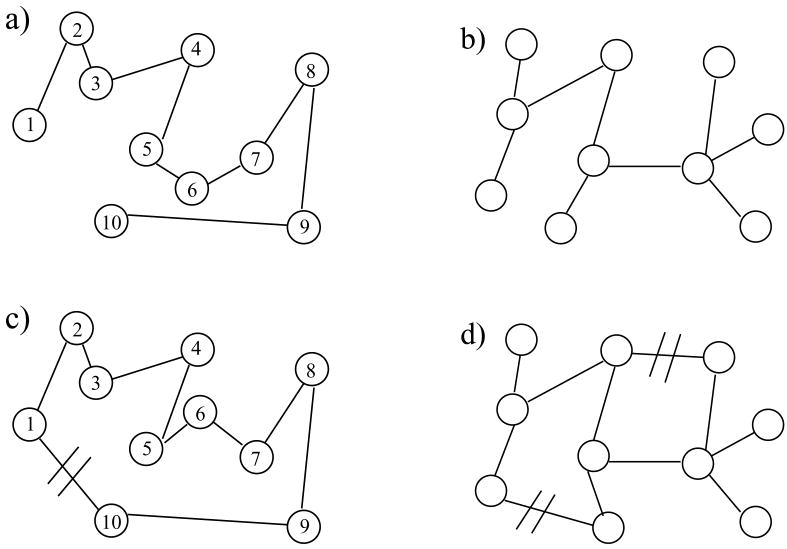
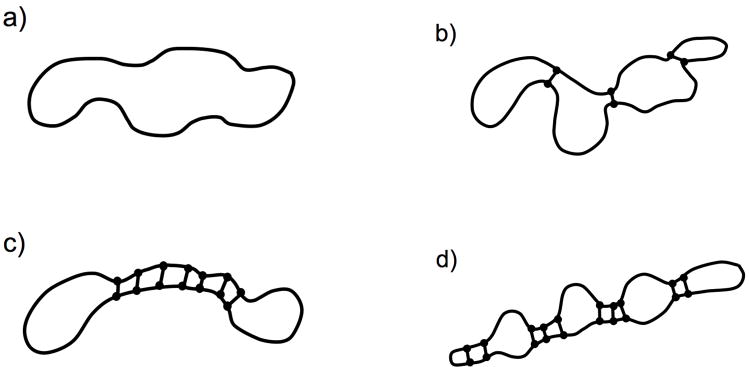
Recall that a constraint network maintains a fixed constraint topology, but there will be a degeneracy over all accessible geometries. Four examples are illustrated in Fig. 4. If distinct parts of a network are connected together only by an atom like that shown in Fig. 4(a,b) or by a hinge like that shown in Fig. 4(d), then the total configuration space volume can be factorized. For example, in Fig. 4(d) there are essentially two loops, with one middle edge shared. The conformational degeneracy can be factored into two distinct parts (right and left loops), which we arbitrarily label A and B. The total conformational degeneracy consists of a product of two terms where Ω = Ω_AΩ_B. Consequently, conformational entropy of the network is additive (i.e. S = S_A + S_B). This property can be employed to simplify calculations of entropy, whenever possible. Unfortunately, factorization generally fails for multiply connected networks, leading to nonadditivity of entropy.

Figure 4.

Examples of molecular networks with different topologies. (a) Random coil - open chain; (b) tree; (c) loop; (d) network with two loops. In panels (c) and (d), doubly crossed bonds (//) denote virtual cuts used in calculations of conformational entropies. Virtual cuts reduce the topology of multiply connected networks (c) and (d) to that of chain (a) and of tree (b), respectively.

Results for a general constraint topology will be developed starting from chain and tree topologies, as illustrated in Fig. 4(a) and Fig. 4(b) respectively. Unless stated otherwise, all bonds are assumed equivalent with l_ij = l and ω_ij = ω for mathematical simplicity. To integrate over r_k in Eq. (6), a set of internal coordinate variables is introduced as r_i,i+1 = r_i+1 − r_i and the center of mass coordinate $\mathbf{R}={\sum }_{i=1}^N{\mathbf{r}}_i/N$ is also employed. Integration over R factors out, giving the volume confining the polymer, ∫ dR = V. Note that in the normal applications that do not deal with polymer confinement, this volume is much greater than the typical volume of a polymer. This piece of the configuration integral reflects the translational motion of the polymer, regardless of its conformational state (i.e. random coil, folded, etc).

Integration over the internal displacements, r_ij, along the chain can be performed in spherical coordinates, dr_ij = dr_ijdr̂_ij. The radial integrals are trivial to carry out because of the δ functions in (6). Integration over the orientations of the unit vector r̂ = r=r that defines the direction of the line of action between a bonded pair of atoms is achieved by the solid angle integration:

$$\int d\widehat{\mathbf{r}}\equiv {\int }_0^{2\pi }d\phi {\int }_0^{\pi }sin\theta d\theta ,$$ (8)

which gives the factor of 4π for each bond. This result follows because in the absence of loops, all bond vectors, r̂_ij, are independent. As expected, for a chain, the multi-dimensional integral factors into separate elementary integrals, and when combined, we obtain for the total conformational degeneracy

$${\mathrm{\Omega }}_0=V{(4\pi \omega l^3)}^{N-1}.$$ (9)

In the more general case of non-identical bonds, we obtain similarly

$${\mathrm{\Omega }}_0=V{(4\pi )}^{N-1}\prod _{i=1}^{N-1}{\omega }_{i,i+1}{l}_{i,i+1}^3.$$ (10)

Since the only requirement to obtain these results was to have bond orientation vectors to act independently of one another, these results (with more general bond indexing) apply to any constraint network of N atoms with a tree topology [cf. Fig. 4(b)].

Entropy of a single loop

For a loop, we make a virtual cut of one of the bonds, as shown in Fig. 4(c). This allows us to benefit from the same integration variables used for the chain. Note that this is a mathematical step, and no physical cut is actually done. For the virtually cut bond, the associated distance constraint contribution, given in Eq. (2) using a Dirac delta function is enforced using the integral representation:

$$\delta \left(\frac{r}{a}-1\right)=\frac{2a^3}{\pi }{\int }_0^{\infty }{x}^{2}dx{j}_0(xr)j_0(xa),$$ (11)

where j₀(x) = sin x/x is a spherical Bessel function. For a single loop [cf. Fig. 4(b)], a single virtual cut gives us a chain, and we must enforce the missing link such that r = |r_1,2 + … + r_N−1,N| and a = l_N−1,N. Integrating out the radial components r_ij of vectors r_ij = r_ijr̂_ij in Eq. (6) yields

$${\mathrm{\Omega }}_{\text{L}}={\omega }^N{l}^{3N-3}{\int }_0^{\infty }{x}^{2}dx{j}_0(xa)\int d{\widehat{\mathbf{r}}}_{12}\dots \int d{\widehat{\mathbf{r}}}_{N-1,N}{j}_0(xr).$$ (12)

To integrate over angular components of r̂_ij according to Eq. (8), we apply successively the identity:

$$j_0(x\mid \mathbf{u}-\mathbf{v}\mid )=4\pi \sum _{\ell =0}^{\infty }\sum _{m=-\ell }^{\ell }{j}_{\ell }(xu)j_{\ell }(xv)Y_{\ell m}(\widehat{\mathbf{u}})Y_{\ell m}^{\ast }(\widehat{\mathbf{v}}),$$ (13)

known as the addition theorem for spherical Bessel functions, where u and v are two vectors. The spherical Bessel functions are defined as

$$j_{\ell }(z)={(-z)}^{\ell }{\left(\frac{d}{\mathit{zdz}}\right)}^{\ell }\frac{sinz}{z},$$ (14)

and the Y_ℓm are spherical harmonics [27]. Integration of products of spherical harmonics is done using the orthogonality relation

$$\int d\widehat{\mathbf{v}}{Y}_{\ell m}(\widehat{\mathbf{v}})Y_{{\ell }^{\prime }{m}^{\prime }}^{\ast }(\widehat{\mathbf{v}})={\delta }_{\ell {\ell }^{\prime }}{\delta }_{m{m}^{\prime }},$$ (15)

where δ_ij is the Kronecker delta. Once these operations are performed, we arrive at the desired result for the total conformational degeneracy of a loop, given as:

$${\mathrm{\Omega }}_{\text{L}}=\omega {\mathrm{\Omega }}_0\frac{2}{\pi }{\int }_0^{\infty }{x}^2{j}_0{(x)}^{N}dx.$$ (16)

The extra ω compared to the chain result given in Eq. (9) appears because of the extra edge that ties the otherwise two ends of the chain together. The remaining integral can be evaluated through the identity

$$I_0^N=\sum _{i=0}^{[\frac{N-1}{2}]}\frac{N!{(N-2i)}^{N-3}{(-1)}^{i+1}}{2^{N-1}(N-3)!i!(N-i)!}$$ (17)

where [a] denotes the integer part of a. For convenience, we introduce shorthand notation for a family of integrals that involve products of powers of spherical Bessel functions. These integrals are denoted as:

$$I_{a,b,\dots ,c}^{A,B,\dots ,C}=\frac{2}{\pi }{\int }_0^{\infty }{x}^{2}dx{[j_a(x)]}^A{[j_b(x)]}^B\dots {[j_c(x)]}^C.$$ (18)

Employing this compact notation, the results for the conformational degeneracy of a single loop of N atoms is given as

$${\mathrm{\Omega }}_{L_1}=\omega {\mathrm{\Omega }}_0{I}_0^N$$ (19)

At this point, we can look at the result and make physical sense of it. As expected, and derived from the above series of equations and mathematical steps, loop closure causes the conformational entropy to be nonadditive. It is interesting to quantify the loss of conformational entropy due to loop formation. Here we have a chain of N atoms, and then we add a single edge between the two atoms at the chain ends to form the loop. From Eq. (9) and Eq. (19) this change in entropy is given by

$$\mathrm{\Delta }S=S_{\mathit{loop}}-S_{\mathit{chain}}=kln(\omega I_0^N).$$ (20)

Notice that for N ≫ 1, $I_0^N\propto N^{-3/2}$. Therefore, Eq. (20) has the form $\mathrm{\Delta }S=\mathit{const}-\frac{3K}{2}lnN$ in the large N limit, which agrees with the well known theory of Flory [28].

Multiply connected networks

Multiply connected networks will generally have many interconnected loops. Some simple examples of multiply connected networks are illustrated in Fig. 5 to facilitate discussions. The approach we use is to construct a spanning tree [29] by virtually cutting one edge out of each loop. The remaining constraint network will be a tree, having no loops. This allows internal integration variables to be defined using the same method discussed above for a chain, tree and loop. Similar to a single loop, for each edge that is virtually cut, the associated distance constraint is enforced using the same integral representation given in Eq. (11) for the Dirac delta function that was used before.

Figure 5.

Multiply connected networks with different types of bridge linkers. (a) A large loop with a single edge bridge linker added to form a double loop; (b) A large loop with two non-crossing single edge bridge linkers added to form a triple loop; (c) A large loop with a double edge bridge linker added to form two non-factorizable neighboring loops; (d) A large loop with a triple edge bridge linker added to form two non-factorizable neighboring loops.

It is prudent to begin by considering some simple cases. As Fig. 5(a) shows, when a dividing edge is added to a single loop, then immediately two smaller loops are defined. Suppose there are N edges in the original loop and the number of edges in these two smaller loops are n₁ and n₂. Because there is one shared edge that is counted twice, it follows that N = n₁ + n₂ −2. Successive application of the addition theorem, i.e. Eq. (13), allows the angular variables in each Bessel function that appears for each virtual cut to be integrated out. Specifically, we have

$$\int d{\widehat{r}}_{12}{j}_0(xl\mid {\widehat{r}}_{12}+{\widehat{r}}_{23}+\dots +{\widehat{r}}_{N-1,N})=4\pi j_0(xl)j_0(xl\mid {\widehat{r}}_{23}+\dots +{\widehat{r}}_{N-1,N}\mid ),$$ (21)

which follows from Eq. (13) while using the orthogonality relation and the identity Y_0,0 = (4π)^−1/2. This procedure, after carried out to completion, yields the result:

$${\mathrm{\Omega }}_{L_2}={\omega }^2{\mathrm{\Omega }}_0{I}_0^{n_1}{I}_0^{n_2}.$$ (22)

Next, we employ Eq. (13) to a single large loop with N edges that is subdivided by k non-crossing edges to form a \ladder” consisting of k + 1 loops in series. In this case, each augmented edge is shared by two and only two loops. Then, the number of edges in the k+1 loops is specified by {n₁, n₂, …, n_k+1}. Similar to what occurred with one dividing edge, each of the k dividing edges is counted twice, since it belongs to two loops. Therefore, we have the sum rule that $N={\sum }_{i=1}^{k+1}{n}_i-2k$. For each of these loops [cf. Fig. 5(b)], one virtual cut is made, and the same procedure is followed, where now there will be a product of integrals of powers of j₀(x_il) where x_i comes from the x_i-th virtual cut. These calculations for a series of k + 1 loops (with k cross-links) returns a final result having the inductive pattern:

$${\mathrm{\Omega }}_{L_{k+1}}={\omega }^{k+1}{\mathrm{\Omega }}_0{I}_0^{n_1}{I}_0^{n_2}\dots I_0^{n_{k+1}}.$$ (23)

The essential ingredient for the pattern is that at each dividing edge, the network can be factored into a “left” and “right” part.

A more complicated case is now considered. Suppose a single loop is subdivided by a bridge consisting of two edges in series, as depicted in Fig. 5(c). The atoms that define this two bond linker are labeled, and is shared by both the “left” and “right” loops. The intermediate atom [cf. Fig. 5(c)] within the linker is labeled 2. Proceeding in similar way as in the case for a one bond linker, the integrations over the angles will give us the product of Bessel functions j₀(xl) times the product of two Bessel functions which involve the “repeated” variables that are mutually shared between the “left” loop and for the “right” loop. These conditions produce a factor in the configuration integral involving two Bessel functions of the form

$$\dots j_0(xl\mid {\widehat{r}}_{12}+{\widehat{r}}_{23}\mid )j_0(yl\mid {\widehat{r}}_{12}+{\widehat{r}}_{23}\mid )\dots$$ (24)

where the variables x and y come from the integral representation of the constraints in the “left” virtual cut and in the “right” virtual cut, respectively (see Fig. 5(c) showing where the two virtual cuts are taken). Expanding both Bessel functions as given in Eq. (24) according to the addition theorem stated in Eq. (13), we form a series involving spherical harmonics Y (r̂₁₂) and Y (r̂₂₃). Integration over the r̂₁₂ and r̂₂₃ is done using the orthogonality relation, Eq. (15), which simplifies the integrals. Once done, we express the remaining integral as a series over a single l, such that

$$\int \int d{\widehat{r}}_{12}d{\widehat{r}}_{23}{j}_0(xl\mid {\widehat{r}}_{12}+{\widehat{r}}_{23}\mid )j_0(yl\mid {\widehat{r}}_{12}+{\widehat{r}}_{23}\mid )={(4\pi )}^2\sum _{\ell =0}^{\infty }(2\ell +1)j_{\ell }^2(xl)j_{\ell }^2(yl).$$ (25)

Here the factor 2ℓ + 1 comes from summation over m [cf. Eq. (13)].

From the above analysis, the conformational degeneracy is given by

$${\mathrm{\Omega }}_{+2}={\omega }^2{\mathrm{\Omega }}_0\sum _{\ell =0}^{\infty }(2\ell +1)I_{0,\ell }^{n_1-2,2}{I}_{0,\ell }^{n_2-2,2},$$ (26)

with the restriction that n₁≠4 or n₂≠4. This expression is reduced to its simplest form as a sum over many terms, which is a consequence that the conformational degeneracy can no longer be factorized into “left” and “right” parts. Instead, a sum over multiple factorized contributions is required. It is worth mentioning, however, that the sum is dominated by the first factorized contributions because the series over ℓ converges rapidly for n_i ≥ 4. This mathematical result makes physical sense because it is not expected that placing a bridging linker consisting of either a single edge or two edges will change the conformational degeneracy by an appreciable amount. Extending this analysis further, consider a loop subdivided by one bridging linker consisting of three or more edges, as depicted in Fig. 5(d). To handle a multi-edge bridge linker, the techniques for angular momentum coupling [30] is used to evaluate the integrals involving multiple spherical harmonics in conjunction with Eq. (13). For such constraint topologies with three edges added, we obtain

$${\mathrm{\Omega }}_{+3}={\omega }^3{\mathrm{\Omega }}_0\sum _{a,c,e=0}^{\infty }(2a+1)(2b+1)(2c+1){\left(\begin{array}{lll}a\hfill & c\hfill & e\hfill \\ 0\hfill & 0\hfill & 0\hfill \end{array}\right)}^2{I}_{0,a,c,e}^{n_1-3,1,1,1}{I}_{0,a,c,e}^{n_2-3,1,1,1},$$ (27)

where (∶∷) is the 3j-symbol [30].

Rigid structures

The above techniques are applicable to rigid structures and rigid regions within networks that are partly flexible and rigid. Consider the smallest possible constraint network that is completely rigid having 6 rigid body motions, namely a triangle. Then, from Eq. (19) with N = 3 (triangle) the conformational entropy is S = k ln(V 8π²ω³l⁶). The conformational entropy derives solely from the rigid body motions. A triangle with unequal lengths has conformational entropy of S = k ln(V 8π²ω₁ω₂ω₃(l₁l₂l₃)²). Moreover, the entropies for a tetrahedron and two face sharing tetrahedra are k ln(V 8π²2^3/2ω⁶l⁹) and k ln(V 8π²0.802ω⁹l¹²) respectively. Interestingly, we find from our analysis that conformational degeneracy is dependent on the overall size and shape of the network. As such, the detailed geometry of a rigid structure is important. It is worth mentioning that the conformational degeneracy for a rigid object is always proportional to 8π², which is the minimal degree of π possible. This minimal factor always appears because it corresponds to global rotations of a rigid body. That is, 4π is the solid angle for locating the rotation axis, and another 2π for the rotation about this axis. Higher degrees of π is an indication for the existence of flexible regions due to bond vectors having unrestricted orientations.

Invariance of the results

For multiply connected networks, the choice of where to place virtual cuts is not unique. Consequently, a different set of internal coordinates will be defined. In addition, the identification of loops is not unique, which means identifying the bridge linkers will also differ. For example, the networks given in Fig. 5 panels (c) and (d) are in fact topologically identical, as can be checked by a careful look. In this case, the same network can be treated using Eq. (26) for a “double edge bridging linker” or according to Eq. (27) for a “triple edge bridging linker”. The starting equations will be different depending on which bridging linker we treat as “internal”, yet the final results are identical. For example, it can be verified that Eq. (26) and Eq. (27) yield the same final answer. Although the starting equations will generally look very different, the physical results are invariant under the mathematical representation. From an algebraic point of view, the invariance in the results is technically a consequence of numerous algebraic identities relating the integrals of spherical Bessel functions $I_{\ell }^n$ and 3j-symbols. Not all of them are quoted in the literature just because of their abundance. While the results are independent on the way the loops are treated, it is a matter of convenience to chose the simplest way for a particular network. However, as the networks get very large, a set algorithm for computer processing must be implemented.

Arbitrary molecular networks

The general scheme of calculations is now complete. Any arbitrary molecular network can be analyzed using the procedures developed above. For a given constraint network, which means the constraint topology is fixed, the conformational entropy can be expressed in terms of the known quantities $I_{a,b,\dots }^{\alpha ,\beta \dots }$ that reflect the changing geometry of accessible atomic motions. Using the techniques introduced above, we have worked out analytical solutions for conformational entropy for more complicated networks, including cases where we consider next nearest neighbor edges to model angle constraints. Self-consistent checks have been performed frequently because the calculations can be worked through algebraically in many different ways, that on the surface look totally different, but lead to the same physical result. As the polymer system gets large, we have developed an algorithm that can handle any type of constraint topology, including those that are rigid or contain rigid regions. The details of how to arrive at these results and how to handle general networks will be published elsewhere.

4. Nonadditivity of entropy from independent constraints

Independent and redundant constraints

There are two sources for nonadditivity found in conformational entropy. As already demonstrated above, adding an extra constraint (edge) to a flexible region that contains loops will reduce the entropy in a non-trivial way that depends on both the formation of additional loops (if any), and their locations relative to all other pre-existing loops in the network. When a distance constraint is added to a flexible region of the network, then the flexibility of the network is said to decrease, meaning that one less degree of freedom is required to specify the atomic configuration. When placing a constraint in a network reduces the number of degrees of freedom (by one), then this constraint is said to be independent. However, there can be regions in the network (group of atoms) that are rigid. If a constraint is placed in a rigid region, the number of degrees of freedom required to specify the atomic configuration does not change. In this latter case, the constraint is said to be redundant.

Distance Constraint Model

In previous work [10, 11, 15] a phenomenological Distance Constraint Model (DCM) was constructed using heuristic arguments, to provide a rapid and accurate estimate of conformational entropy with minimal computational cost. The basic idea is described here in a cursory non-technical way. The first step is to determine whether a constraint is independent or redundant based on network rigidity calculations [16]. If a constraint is identified as redundant, then the conformational entropy of the network is not changed. However, if the constraint is identified to be independent, then it carries a conformational entropy contribution. As such, each constraint is assigned an energy and entropy value. This entropy value is effectively a local quantity as it does not depend on the details of the network beyond establishing whether the constraint is added in a flexible or rigid region. Since methods that test for generic rigidity are topologically based, it is not necessary to know the geometrical details of atomic coordinates.

Meaning of local entropy

From Eq. (5), we identify ω as a degeneracy factor, and rewrite it as ω = e^γ, where γ is dimensionless. Then we associate a physical entropy given by S = k ln ω. As such, γ is interpreted as a pure entropy, and physical entropy is given by S = kγ. Since the value of ω is dependent on an arbitrary length scaling factor, note that ω can be less than unity, resulting in γ possibly being negative. Nevertheless, differences in γ relate to differences in entropy, which enter into the calculations for finding conformational entropy. The local entropy has a physical interpretation; namely, it characterizes the strength of the original interaction. That is, the Mayer f-function has a finite width, and the original interaction allows for some wiggling between the pair of atoms.

Accuracy test of the DCM

The most troublesome part of the DCM assumptions occurs when the constraint is independent, because we know, as demonstrated above, that the change in entropy depends on the entire network. Meaning, entropy is a global, nonadditive quantity, and, strictly speaking, the change in conformational entropy due to the addition of an independent constraint cannot simply be the assigned local entropy. Nevertheless, the DCM does assign local entropy values, and it is found in practice to give markedly good agreement with a large body of experimental data [17–21]. The argument for why the DCM works fine in applications involving peptides and proteins is because deviations from the local entropy assignment is logarithmic in nature [cf. Eq. (20)]. More generally, deviations will depend on the openness of the interconnected loops, and overall geometry of the structure. In the DCM, there are free parameters that are adjusted to scale the entropy. Perhaps on average the use of a local entropy can account for the dominant contributions, and lead to reasonably good results if the errors due to various loop closures cancel out due to self-averaging.

Since we have an exact analytical solution for k-loops connected in series [cf. Eq. (23)], we will use this result to test the assumptions of the DCM, and the accuracy of its estimates for conformational entropy. In the process of making this comparison, we will factorize the conformational degeneracy into a topological part, and a geometrical part. The topological part is given by the DCM, which in this case is nothing more than

$$S_{\nu }^{\mathit{DCM}}=k\sum _i{\gamma }_i$$ (28)

because all the constraints are independent. This is just the leading term in Eq. (23) which is made clear by rewriting it as:

$${\mathrm{\Omega }}_{L_k}=\mathit{const}\left(e^{S_{\nu }^{\mathit{DCM}}/k}\right)I_0^{n_1}{I}_0^{n_2}\dots I_0^{n_{k+1}}.$$ (29)

where const is a constant factor that accounts for arbitrary scaling. In order to give a fair comparison of the importance to the DCM entropy and the geometrical factors that follow, we set const = 1 and adjust γ to be a value that has a typical magnitude reflecting the differences in entropy upon adding or removing an independent hydrogen bond. In other words, we set the entropy scale based on fitting parameters of the DCM that matched experimental data, when const was assumed to be 1.

There are a few factors that prevent an exact comparison to be made. First, the DCM models proteins as constraint networks that are much less flexible than the simplified model introduced here. This is because bond-bending and dihedral angle constraints are included. Second, van der Waal interactions will enforce self-avoidance and reduce conformational entropy as the network tightens up. The more flexible the network, the greater chance the DCM goes wrong because it does not account for the geometrical details of atomic coordinates. Moreover, using ideal chains overestimates the flexibility within a constraint network. Third, because the DCM models a cross-linking hydrogen bond as 5 distance constraints (since angle interactions are included) we must estimate an effective γ to characterize the same hydrogen bond modeled using only 1 central force. Because all the networks we will compare against are flexible in all regions, it is known that all distance constraints are independent. This is the limit where the DCM reduces to an additive model.

Correcting for the differences between modeling a hydrogen bond with multiple constraints (central and bond-bending forces) compared to just using a single distance constraint (central force), we estimate that −10 ≤ γ ≤ −2 is the appropriate range for very strong (i.e. greatest entropy reduction) to medium-weak (i.e. less entropy reduction) hydrogen bonds. These estimates come directly from the implemented DCM parameterization for hydrogen bonds [15, 17] that are transferable between proteins. The simplifying assumption made is that the intrinsic local reduction of conformational entropy of a hydrogen bond is linearly proportional to its energy. Using an energy function that ranges from 0 to −8 kcal/mol, we found by fitting to multiple proteins (while enforcing the assumption of a linear relation), the maximum entropy reduction is 10 when the energy is −8 kcal/mol. When γ = −2, this corresponds to a weak hydrogen bond with energy of $-\frac{8}{5}\text{kcal}/\text{mol}$. These numbers are physically reasonable, consistent with experimental estimates for changes in conformational entropy. From the review given by Pace and co-workers [12] the average change in entropy for a residue to go from a unique native-like conformation to a disordered one, is about 4.2 to 5.6 cal/(K mol). Although this estimated value is derived from heat capacity measurements to obtain total entropy change, and then divided by the number of residues, these values reflect all interactions in the protein.

Typicial DCM parameters that fit to the heat capacity data are about 1.8 kcal/(K mol) per dihedral angle. Noting that there are on average about 4.5 rotatable dihedral angles per residue, the DCM entropy values are about 1.4 to 2 times greater than the experimental estimates. However, the larger entropy values used in the DCM are better reflections of reality, because not all the residues will simultaneously be native in the folded state, nor will they all be simultaneously disordered in the unfolded state. Rather, residue conformations fluctuate between native-like states and disordered states, which is being reflected in heat capacity measurements. Moreover, the DCM accounts for the entropy reduction in the hydrogen bond network forming cross-links, which is why the DCM predictions fit to the experimental heat capacities [17]. Since the DCM parameters account for non-additivity of entropy (i.e. not double counting entropy contributions) and the predicted heat capacity fits well to experimental excess heat capacity, the DCM energy and entropy parameters are all physically reasonable. Furthermore, the adjustable DCM parameters have exhibited marked transferablity in terms of a low overall variance (typically ± 30 %).

Objective test criteria

Since we do not have an exact model-to-model comparison, we wish to argue in terms of worst cases. We consider a single loop of N atoms that can be cross-linked through fluctuating hydrogen bonds as Fig. 6 schematically illustrates. In the case there are no cross-links, as shown in Fig. 6(a) the DCM predicts the loop to have the same entropy as a chain, less that of k|γ|. This part of the exact formula given in Eq. (20) is fine, but as Eq. (30) makes clear, the missing part is the $kln(I_0^N)$ that comes from geometrical considerations when integrating over configuration space. The discrepancy caused by loop closer (starting from a chain) is the worst case. We also monitor the discrepancy as more cross-links are added, which will depend on the details of where the cross-links are located. To do this, we evaluate the entropy formula given by:

$$S_{\nu }^{\mathit{total}}=S_{\nu }^{\mathit{DCM}}+S_{\nu }^g\text{where}{S}_{\nu }^g=kln\left(I_0^{n_1}{I}_0^{n_2}\dots I_0^{n_{k+1}}\right)$$ (30)

for 10,000 randomly generated networks (indexed by ν). We specify the total number of quenched edges in the outer loop. Then we randomly place a certain number of non-crossing dividing edges within the outer loop, making sure the resulting loop sizes are uniformly distributed. This condition is enforced by placing cross-linking edges from left to right starting at one end of the outer loop. A truncated Poisson distribution is used to determine the number of outer edges that need to be skipped. Note that the truncation is a minor perturbation, but is necessary because the outer loop is not infinitely long. The loop size statistics were monitored to verify the uniform distribution of loop sizes was indeed generated.

Figure 6.

Schematic representations of a large loop of N-bonds deforming with fluctuating cross-linking hydrogen bonds. The number of cross-links can range from 0 to ≈ N/4. Note that because all cross-links are independent for these flexible structures, the DCM prediction for the entropy reduction only depends on the number of cross-links. The exact formula for entropy reduction completely accounts for the location of the cross-links and all accessible atomic geometries consistent with the fixed topology.

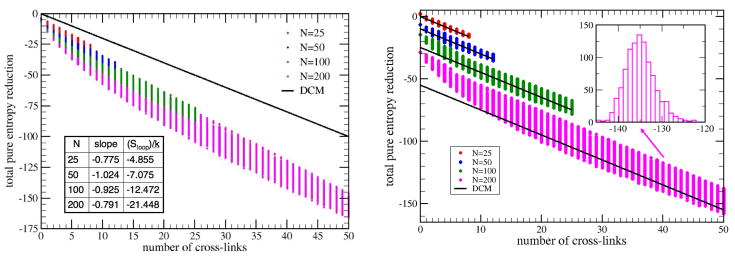
We monitor the total conformational entropy reduction of the fluctuating part of the network as a function of the number of added hydrogen bonds (added edges). Since the quenched constraints on the outer loop do not fluctuate, we use that value as a zero reference, and are effectively not counted in the DCM estimate. The extra edges will never rigidify the network in any part, so that the network will remain everywhere flexible. For various N, Fig. 7(a) shows a scatter plot of the DCM predicted pure entropy reduction (i.e. given by $(S_{\nu }^{\mathit{DCM}})/k$) against the number of added cross-links. The DCM prediction is independent of the loop size, N. We also plot the exact total pure entropy reduction (i.e. given by $(S_{\nu }^{\mathit{total}})/k$) on the same graph for cases N = 25, 50, 100 and 200. It is clear that a straight comparison shows that the DCM calculation underestimates the entropy reduction. This underestimate is directly related to loop creation (ignored by the DCM) that occur as new cross-link bonds are added. At this point, it is clear that the DCM is fundamentally flawed and does not pass as a good approximation. Nevertheless, the DCM works extremely well in practice. What could be the explanation?

Figure 7.

(a) Left panel: Scatter plot showing the pure entropy reduction that occurs when adding 0 to ≈ N/4 cross-links to a single outer loop of N edges, with N = 25, 50, 100 and 200. The DCM prediction is shown as a solid black line, but entropy reduction depends on the details of where the cross-links are placed. The scatter plot provides “error bars” showing a smaller variance for less number of cross-links. (b) Right panel: The systematic errors that are linearly dependent on the number of cross-links have been absorbed into the DCM local entropy parameter. The y-intercepts were arbitrarily shifted for different N to prevent crowding. Note that for N = 200 the black solid line does not pass through the center of the “error bars”, because the density profile of sample points is not uniform. The inlet shows the histogram for 1000 random samples with 40 cross-linkers.

Most of the discrepancies seen in Fig. 7(a) are systematic. The exact entropy reduction is a nearly linear function with respect to the number of cross-links (with some scatter, considered as “error bars”). However, the essential aspect of the DCM reduces to the approximation that entropy reduction is linearly related to the number of cross-links. Technically, the cross-links that act as independent distance constraints. Since the DCM is phenomenological based, the entropy parameters were determined by per system fitting [15, 17]. Therefore, almost all the systematic error is accounted for, as shown in Fig. 7(b). Although the fitting can absorb most of the error, this indicates that the DCM entropy parameters cannot be truely transferable. However, the non-transferability is not dire. The variance in the entropy parameter, γ, for the four loop sizes considered here is less than ±0.15 as seen by comparing the different slopes of the curves shown in Fig. 7(a). Moreover, the variance in the y-intercepts (i.e. (S_loop)/k) are of no concern, as a constant shift never affects any measurable quantity, except absolute entropy. However, we allow ourselves this freedom, since we are working within a classical statistical mechanics problem that cannot determine this anyway.

Employing this ab initio model, we can provide a theoretical upper bound to the error made by the DCM for neglecting the geometrical aspects of loops in flexible regions. In Fig. 7 we used the greatest γ (namely γ = −2) corresponding to the weakest hydrogen bonds considered for which the distance constraint model approximation of Eq. (2) is (barely) valid. For this worst case, the expected deviation in entropy parameters across different systems is about ± 10% (i.e. noting that for a wide range of N we have $\frac{\mathrm{\Delta }\gamma }{\gamma }<\pm 0.2/2$). For a hydrogen bond of average strength (i.e. γ = −6) results in about 3% error, and about 2.3% error for a strong hydrogen bond (i.e. γ = −10). Thus, we see that transferability of hydrogen bond entropies approximately holds for this loop example at least up to N = 200. We also note that the error worsens as N increases. However, we can further minimize the error. In Fig. 7(b) the exact data were not fitted over the entire range from 0 to the maximum possible number of cross-links. Allowing for more error to be made in the cases of very large loops and extremely flexible networks, we dropped the first 20% of the data (starting from no cross-links). This fraction was arrived at because there seemed to be a natural kink near this fraction, which is formed by two approximate straight lines representing the data well. Working only with the bulk of the data (the last 80%), we find the linear regression correlation coefficient to range between −0.895 to −0.936 for the four cases shown. In doing this, Fig. 7(b) clearly shows the linear approximation is very good for about 80% of the data, and poor when the number of cross-links is less than 20% of the loop length.

In the region where the approximate linearity of entropy reduction to the number of cross-links breaks down, the DCM overestimates the entropy reduction

Consequently, the predicted free energy cost of forming a hydrogen bond is higher than reality. In numerous applications to proteins in aqueous solutions, the DCM predicts the unfolded state to have a substantial number of cross-linking hydrogen bonds remaining. In fact, enough cross-links remain in the unfolded state that the troublesome regime involving large loops with less than 5% (i.e. $20\%\times \frac{N}{4}$) of the chemical bonds are cross-links never appear. The most probable constraint topologies of the unfolded free energy basin typically retain many cross-linkers, albeit fluctuating. This latter result markedly agrees with well-known experimental results that observe unfolded proteins in aqueous solution to exhibit structures of a molten globular nature that retains considerable secondary structure that is native-like [31]. Note that the unfolded state has random coil character [32], but the relavent issue is there are enough hydrogen bond cross-links to keep the DCM calculation most accurate. In essence, the greatest error made by the DCM is in a region of the free energy landscape that is both predicted and measured to be essentially of measure zero.

To summarize, we present a geometrically based distance constraint model that overestimates flexibility in polymers. We find that the DCM is based on approximations that are more problematic as the flexibility of the network increases. The analysis presented here yields a theoretical justification showing why DCM entropy parameters are almost transferable. However, this result has only been considered with respect to proteins in aqueous solution. For other polymers and/or solvents, the low density regime of cross-linkers could dominate. Based on these results that assumed a worst case scenario, the DCM as currently formulated may not perform well in the limit where there is a small percentage of cross-links. However, in those cases, the number of cross-links is low, and we can use the ab initio results presented here without difficulty. In other words, we just need to account for large loop entropy reduction carefully when they occur at some appreciable level. Even in these bad cases, the persistence length of the actual polymer will inevitably make the discrepancies highlighted here less of a concern. Fortuitous as it may be, we can assert from these results that the DCM will provide excellent estimates for conformational entropy in proteins.

5. Conclusions

Calculation of conformational entropy in macromolecules has been a long-standing open theoretical problem. We have demonstrated how to accurately calculate conformational entropy within ideal chains that undergo chemical bond cross-linking. An ab initio model based on integrating the configuration integrals using a Mayer series expansion is introduced. The model dramatically simplifies by representing sharply peaked Mayer f-functions as distance constraint Dirac delta functions. In addition, the interaction is assigned an energy and local entropy, which are treated most often as temperature independent. The conditions for when these approximations are valid are also determined. The mathematics involving spherical Bessel functions and spherical harmonics has been developed to handle calculations for general central-force networks, while remaining surprisingly tractable. The ab initio model takes into account geometrical aspects of conformational entropy that includes global nonadditive effects due to loop closers in flexible regions, but neglects self-avoidance. In future work, we plan to extend this method to include self-avoidance.

We present explicit formulas dealing with loops in series that contain varying numbers of cross-links, which are used to test the validity of a previously introduced Distance Constraint Model (DCM). In contrast to the geometical model developed here, the DCM accounts for nonadditivity only through topological properties of network rigidity. We find that with the exception of the unlikely regime of low density of constraints (i.e. when less than 5% of all bonds are cross-linkers) the approximate DCM compares markedly well with the geometrical model. However, for the comparison to be good, the DCM entropy parameters must adjust to account for systematic errors that appear by neglecting geometrical aspects in the DCM. Furthermore, typical changes in the local entropy parameters are found to be small over different systems (less than 10%). Based on the analysis for checking the DCM validity, it was found that the entropy parameters are transferable to an excellent approximation. At least in terms of protein structure, the results presented provide a theoretical justification for why the DCM approach has consistently reproduced experimental results, despite its simplicity. Lastly, the problem of calculating conformational entropy in polymers was separated into a topological and geometrical part for comparison purposes. This natural separation allows the two different approaches to be employed to solve more complicated networks. Applying this complementary division will be explored in future work.