Relation of Frontal Eye Field Activity to Saccade Initiation during a Countermanding Task

Abstract

The countermanding (or stop signal) task probes the control of the initiation of a movement by measuring subjects’ ability to withhold a movement in various degrees of preparation in response to an infrequent stop signal. Previous research found that saccades are initiated when the activity of movement-related neurons reaches a threshold, and saccades are withheld if the growth of activity is interrupted. To extend and evaluate this relationship of frontal eye field (FEF) activity to saccade initiation, two new analyses were performed. First, we fit a neurometric function that describes the proportion of trials with a stop signal in which neural activity exceeded a criterion discharge rate as a function of stop signal delay, to the inhibition function that describes the probability of producing a saccade as a function of stop signal delay. The activity of movement-related but not visual neurons provided the best correspondence between neurometric and inhibition functions. Second, we determined the criterion discharge rate that optimally discriminated between the distributions of discharge rates measured on trials when saccades were produced or withheld. Differential activity of movement-related but not visual neurons could distinguish whether a saccade occurred. The threshold discharge rates determined for individual neurons through these two methods agreed. To investigate how reliably movement-related activity predicted movement initiation; the analyses were carried out with samples of activity from increasing numbers of trials from the same or from different neurons. The reliability of both measures of initiation threshold improved with number of trials and neurons to an asymptote of between 10 to 20 movement-related neurons. Combining the activity of visual neurons did not improve the reliability of predicting saccade initiation. These results demonstrate how the activity of a population of movement-related but not visual neurons in the FEF contributes to the control of saccade initiation. The results also validate these analytical procedures for identifying signals that control saccade initiation in other brain structures.

INTRODUCTION

Studies of the oculomotor system over the last 30 years have found that the production of a saccade depends on the balance of activation of gaze-shifting and gaze-holding neurons distributed in the brainstem (Scudder et al. 2002), superior colliculus (Munoz 2002), basal ganglia (Hikosaka et al., 2000) and frontal eye field (FEF) (Schall et al., 2002). While there is consensus regarding the opponency between gaze-holding and gaze-shifting in the oculomotor system, current models of saccade generation do not explain the preliminary event necessary and sufficient to initiate a saccade (Scudder et al. 2002).

To investigate the neural control of movement initiation, we have used the countermanding or stop signal paradigm (Logan 1994; Logan and Cowan 1984). The countermanding task tests a subject's ability to control the initiation of movements in a speeded response task by infrequently presenting an imperative stop signal. Performance on this task is stochastic but can be accounted for by a race between a process that generates the movement (GO) and a process that interrupts movement preparation (STOP). This race model provides an estimate of the time needed to cancel the planned movement, the stop signal reaction time (SSRT). A new interactive race model of countermanding performance shows that SSRT corresponds to the time when the GO process is inhibited by the STOP process (Boucher et al. 2007).

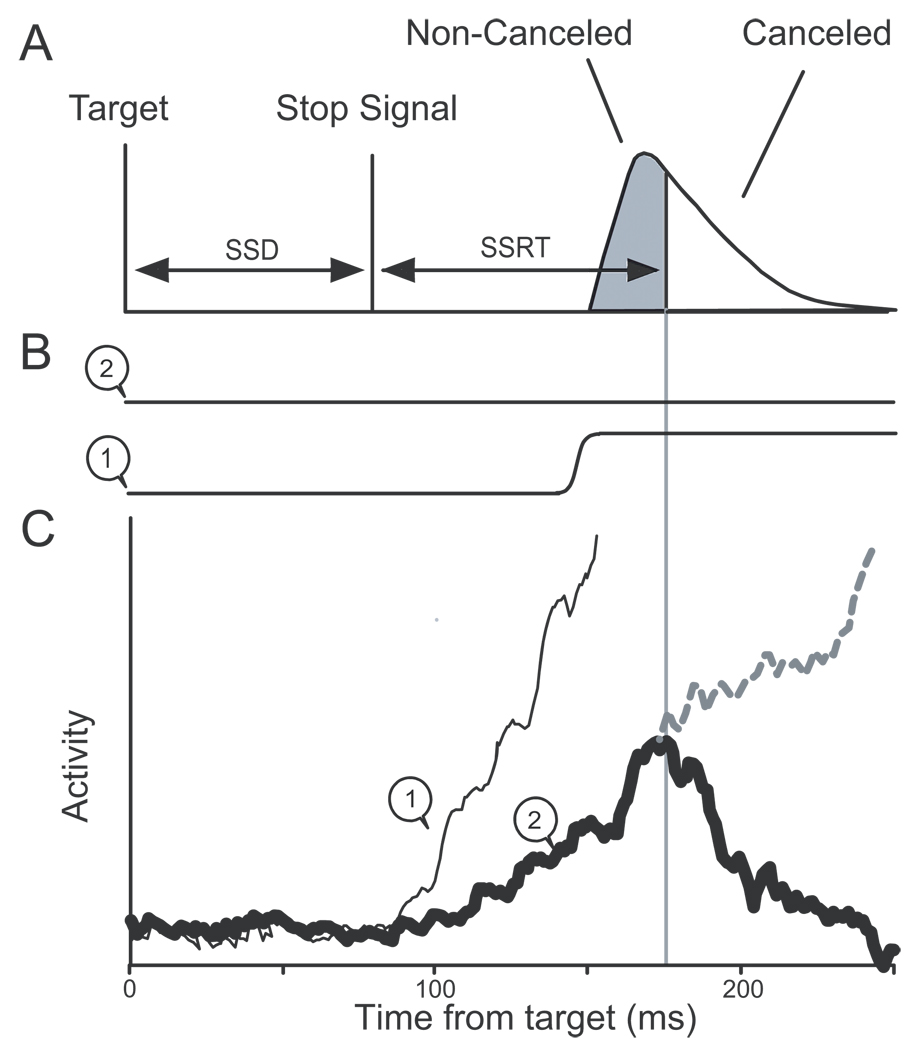
The findings of our previous studies are summarized diagrammatically in Figure 1 (Hanes and Schall 1996; Hanes et al. 1998; see also Paré and Hanes 2003). Saccades were initiated when the discharge rate of single movement-related neurons in FEF reached a particular value. This discharge rate constituted a threshold at which the balance tipped from gaze-holding to gaze-shifting. The variability of saccade latency was accounted for by variability in the rate of increase of the discharge rate of gaze-shifting neurons to the threshold. When movements were canceled in response to the stop signal, the movement-related activity in FEF, which had begun to grow toward the trigger threshold, decreased and so failed to reach the threshold activation level. The modulation of movement-related activity when saccades were canceled occurred within the SSRT. Therefore, according to the logic of the countermanding paradigm, the activity of single FEF movement neurons is sufficient to specify on average whether an eye movement will be produced. This pattern of results was observed consistently in neurons with movement-related activity, and a complementary pattern of activation was observed in fixation neurons but the activity of neurons with only visual responses was modulated not at all or too late to contribute to controlling saccade initiation (Hanes et al. 1998). Effectively identical results have been obtained in the superior colliculus (Paré and Hanes 2003). These findings indicate that the preparation of a saccade is a controlled process that can be canceled if and only if the growth of activation toward the trigger threshold is sufficiently slow to be interrupted.

Figure 1.

Investigating the neural basis of saccade preparation with the countermanding task. A. The race model of countermanding performance. A representative distribution of saccade latencies is illustrated with the characteristic single mode and extended tail. A stop signal presented a particular stop signal delay (SSD) after the target signals the subject to withhold the planned movement. The probabilistic outcome depends on the timing of the stop signal relative to the dynamics of the process that will initiate the saccade. The time needed to cancel the saccade, called stop signal reaction time (SSRT), marks the time when a covert STOP process interrupts preparation of the saccade. Accordingly, SSRT partitions the saccade latency distribution into early values corresponding to non-canceled trials because the saccade was initiated before the STOP process could exert influence and later values corresponding to canceled trials because the saccade was initiated late enough to allow the STOP process to interrupt preparation. B. Eye position for canceled (1) and noncanceled (2) trials. C. Activity of a representative FEF movement neuron in the different types of trials. Saccades are initiated when the activity of these neurons reaches a fixed threshold. If the movement-related activity increases quickly to reach the threshold before the SSRT, a non-canceled trial results (1, thin line). If the activity increases slower so that it would reach the threshold later (2, dashed line), then the STOP process invoked by the stop signal interrupts the growth of activity (thick solid line), preventing it from reaching the threshold so that the saccade is not initiated.

While these findings appear to provide a sensible account of the neural events leading to saccade initiation, some key issues remain unclear. For example, the trigger threshold has been defined simply as the average of the discharge rate in the period immediately before saccade initiation from samples of 10 trials (Hanes and Schall, 1996). This analysis has two shortcomings. First, strictly speaking, all trials with discharge rates less than the average threshold should not have resulted in saccades, which obviously was not the case. Thus, a major goal of the present analysis was to devise a functional formulation of the trigger threshold. Second, averaging across trials probably underestimates the variability of the threshold, but if this variability is too great, the threshold concept may become only a heuristic approximation, in which case the mechanism underlying movement initiation becomes less clear. Thus, the other major goal of this research was to measure the reliability of the trigger threshold in activity pooled across trials and neurons.

The results of inactivation, lesion, and anatomical investigations demonstrate that many (10⁵ – 10⁶) neurons are necessary to produce a saccade¹, but how many single neurons are sufficient to specify whether and when a saccade will be produced? By pooling the activity from a variable number of trials combined within and across neurons, we determined the fewest neurons sufficient to predict reliably when a saccade would be initiated. While the results we describe are consistent with the previous reports and thus are not entirely novel, this work substantiates the theory that saccades are initiated when the total activation among gaze-shifting neurons reaches a threshold and in so doing provides a proof of principle of this analytic approach that empowers it in the companion investigation of the supplementary eye field as well as future studies of other visuomotor structures. Some of these results have been presented in abstract form (Brown et al. 2001; Schall et al. 1999).

MATERIALS AND METHODS

Surgical and Behavioral Procedures

Conventional methods were used. Two male macaque monkeys (Macaca mulatta) were prepared as described previously (Hanes et al. 1998). All experimental procedured conformed to United States Public Health Service guidelines as interpreted by the Vanderbilt University Animal Care and Use Committee. A PDP-11/83 presented stimuli and collected eye position, spike and event data.

The Countermanding Task

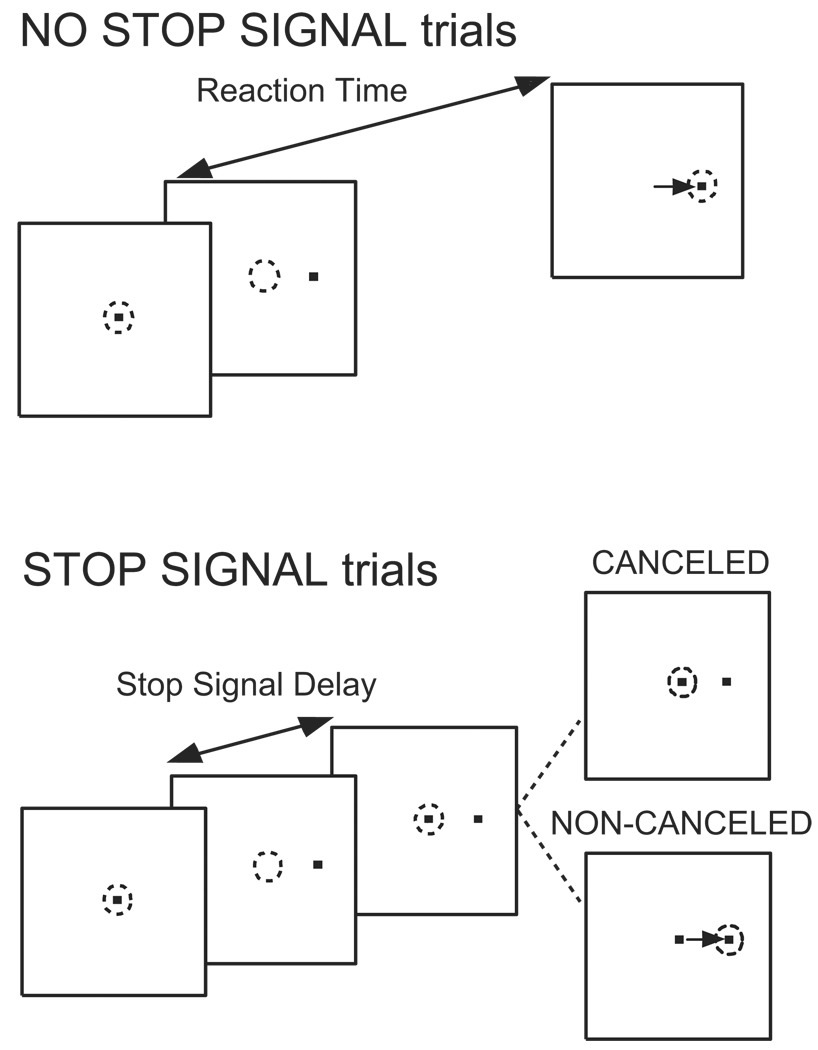
The saccade version of the countermanding task has been described (Hanes et al. 1998; Hanes and Schall 1995) (Figure 2). After fixation of a central spot, it disappeared simultaneously with the presentation of a visual target either in the most sensitive zone of a neuron’s response field or in the opposite hemifield at the same eccentricity. On a fraction of trials after a variable delay, referred to as the stop signal delay, the fixation spot reappeared, instructing monkeys to withhold the movement (stop signal trials). During the trials in which the stop signal was not presented (no stop signal trials) monkeys were rewarded for generating a single saccade to the peripheral target. During stop signal trials monkeys were rewarded for maintaining fixation on the central spot (canceled trials). If the monkeys generated a saccade to the peripheral target during stop signal trials (non-canceled trials), no reward was given. On correct trials juice reward was given on a variable ratio schedule coupled with an acoustic secondary reinforcer given on every correct trial.

Figure 2.

Countermanding task. At the beginning of each trial, monkeys fixate a central spot until it disappears and a peripheral target appears. On most trials monkeys are reinforced for shifting gaze to the target. On less than half of trials at random the fixation spot reappears after a variable stop signal delay. Monkeys are reinforced for canceling the planned saccade to the peripheral target and maintaining fixation. On some trials, though, monkeys shift gaze in error; these non-canceled responses are not reinforced.

Performance in the countermanding task is probabilistic because of the variability in reaction times across trials. The probability of not canceling the movement increases as the delay between the signal to initiate the movement and the signal to inhibit the movement (stop signal delay) increases. Stop signal delays were varied according to the monkeys' performance so that at the shortest stop signal delay monkeys generally inhibited the movement on more than 85% of the stop signal trials and at the longest delay monkeys inhibited the movement on fewer than 15% of the stop signal trials. Movements generated with a short latency tend to be initiated before the stop signal can influence the system. Conversely, movements that would be generated with long latencies tend to be canceled because there is enough time for the stop signal to influence the system. The time needed to cancel the movement, known as stop signal reaction time (SSRT), can be estimated from a model of a stochastic race between a process that produces the movement and a process that cancels the movement (Logan and Cowan 1984; Boucher et al. 2007). The procedures for measuring SSRT have been described in detail previously (Logan and Cowan, 1984; Hanes and Schall, 1995). Saccade stop signal reaction times average around 80–100 ms in monkeys (Hanes et al. 1998; Hanes and Schall 1995; Kornylo et al. 2003).

The goal of this paper is to describe how the activity of FEF neurons relates to performance as a function of stop signal delay. During many but not all recording sessions, stop signal delay was manipulated with a staircase procedure to maintain the error rate on stop trials around 50%. This led to a proliferation of stop signal delays, with as many as 20 per session. Consequently, to achieve sufficient statistical power to estimate discharge probabilities for a given stop signal delay, delays differing by less than 20 ms were combined into 20 ms wide bins, with the mean value used as the stop signal delay for the analysis.

Analysis of Neural Activity

Spike density functions were obtained by convolving the spike train with a function resembling a postsynaptic potential A(t) = [1-exp(-t/τ_g)] ·[exp(-t/τ_d )]. Physiological data from excitatory synapses indicate τ_g ∼ 1 ms and τ_d ∼ 20 ms (Sayer et al. 1990).

Two kinds of analyses were carried out to characterize the relationship between discharge rate and saccade initiation; these will be described in detail below. The neurometric threshold minimized the difference between a neurometric function and a psychometric inhibition function. The optimal discriminant threshold maximized the predictive accuracy that a saccade would occur given the activity level on each stop signal trial.

The value submitted to these analyses from no stop signal and non-canceled trials was the maximum of the spike density function in the 20 ms prior to saccade initiation. This interval (especially between 20 and 10 ms prior to saccade initiation) was used previously to define the threshold for movement initiation (Hanes and Schall 1996) because omnipause neurons release inhibition on the burst neurons at that time before saccade initiation (Scudder et al. 2002) making this the point of no return. In this analysis, we measure the maximimum neural activity until the moment of saccade initiation, as this more directly matches the control condition in the cancelled trials, which extends to the SSRT. However, the main conclusions would not be different if we included values only up to 10–20 ms before saccade initiation. The measure used in canceled trials was the maximum of the spike density function in the interval from target presentation until SSRT + 20 ms; the extra 20 ms was included to account for possible underestimation of the SSRT.

Distributions of maximum activity were obtained from three sets of trials. First, for each neuron, the maximum was measured in the specified interval for each trial. Second, bootstrapped sampling of multiple trials within and across cells was used to obtain an estimate of the variance (and therefore the validity) of the threshold. For the population analysis with bootstrapped sampling, N trials were selected randomly and with replacement either from a single neuron (“pooled within”) or across the sample of neurons (“pooled across”) and combined to generate a virtual trial. The N trials were aligned on the event of interest (target appearance for canceled trials, and saccade initiation for no stop signal and non-canceled trials) and averaged at each point in time. The maximum of this average firing rate in the specified interval pooled among the sample of N trials was determined. When canceled trials with different stop signal delays were combined, the average firing rate at each point in time was calculated from only those trials for which the current time had not exceeded the SSRT + 20 ms. In other words, at each point in time, we excluded from the average those trials for which the SSRT + 20 msec had elapsed, because activity on those trials could not logically provide a causal signal to drive saccade initation. Third, for bootstrap sampling of trials from a single neuron, 1000 virtual trials were generated for each stop signal delay. To avoid bias in the derived thresholds, canceled and non-canceled trials were sampled in proportion to the actual fractions of each trial type that occurred while recording from the neuron. For example, if 60% of stop signal trials were canceled, then 600 virtual canceled trials and 400 virtual non-canceled trials were generated. When pooling trials across neurons, 1000 virtual canceled trials and 1000 virtual non-canceled trials were generated.

Neurometric threshold from best fit of neurometric to inhibition function

The inhibition function plots the fraction of non-canceled trials in which saccade is produced in spite of stop signal as a function of stop signal delay. The fraction of non-canceled trials is an increasing function of stop signal delay, because saccades are less likely to be canceled as preparation progresses through time. If saccades are produced when the activity of movement-related neurons crosses a threshold, then the inhibition function should correspond to the fraction of trials in which the discharge rate exceeded that threshold at each stop signal delay. A neurometric function was defined as the probability of discharge rate exceeding a criterion value as a function of stop signal delay. Therefore, a search was performed for the single criterion discharge rate that provided the best correspondence between the neurometric function and the inhibition function.

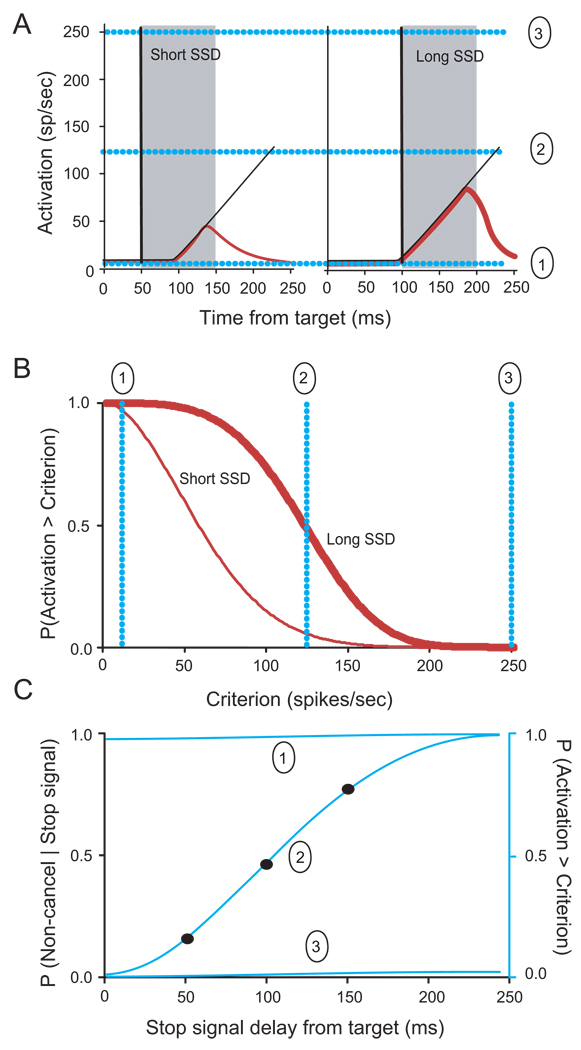
Neurometric functions were constructed as follows (Figure 3). All three sampling methods (individual neurons, bootstrap within and bootstrap across neurons) yielded a set of trials with a measure of maximum activity, grouped by stop signal delay. The fraction of trials that do not exceed a criterion or threshold discharge rate decreases as the criterion increases (Figure 3A). The fraction of canceled and non-canceled stop signal trials in which activity did not exceed the criterion was plotted for each stop signal delay group as a function of criterion value (Figure 3B). Presaccadic movement-related activity increases with time, so the probability of the discharge rate exceeding the criterion will increase with stop signal delay so the neurometric function derived from this relationship will increase with stop signal delay. The neurometric function is parameterized by the criterion discharge rate so that it shifts left or upward for lower criterion values and right or downward for higher values (Figure 3C). In other words, a criterion that is too low would be crossed by minimal discharge rates which would predict many non-canceled saccades, and a criteron that is too high would be crossed only by rare maximal discharge rates which would predict few non-canceled saccades. If a given neuron contributes to controlling saccade initiation, then some criteron discharge rate must exist that produces a neurometric function corresponding closely to the behavioral inhibition function. Therefore, a search was performed for the criterion discharge rate that minimized the least-squares fit of the neurometric function to the inhibition function.

Figure 3.

Neurometric threshold. A. Saccades are more likely to be canceled if the stop signal appears after a shorter delay (left) than after a longer delay (right) because preparation progresses through time. Thin black line plots activity on trials with no stop signal. Red lines plot activity on trials with a stop signal and the saccade was canceled. One can measure the fraction of trials with and without a stop signal on which discharge rate exceeds some criterion. The fraction of 28 trials that do not exceed a criterion discharge rate decreases as the criterion increases. Three representative criteria are illustrated, very low (1), intermediate (2) and very high (3) (light blue lines). Gray fill indicates duration of SSRT within which the activity is modulated on canceled trials. B. The probability that the build-up activity exceeds a criterion discharge rate is plotted as a function of the criterion for short (thin) and long (thick) stop signal delays. Two trends are clear. First, obviously, the probability of the discharge rate exceeding the criterion decreases as the criterion increases. Second, because presaccadic movement-related activity increases with time, the probability of the discharge rate exceeding the criterion increases with SSD C. Inhibition function (solid points) plots probability of not canceling the saccade as a function of stop signal delay. If saccades are initiated when the activity of movement-related neurons reaches a threshold, then the probability of producing a saccade on a stop signal trial should equal the probability that the activity reaches a threshold. In other words, if a neuron contributes to controlling saccade initiation, then a neurometric function should exist that corresponds to the psychometric inhibition function. Neurometric functions for low (1), intermediate (2) and high (3) criterion discharge rates are plotted. Criterion discharge rates that are too low (1) result in a neurometric function falling above the inhibition function because all discharge rates exceed the criterion. Criterion discharge rates that are too high (3) result in a neurometric function falling below the inhibition function because no discharge rate exceeds the criterion. Criterion discharge rates that are just right (2) result in a neurometric function that increases with stop signal delay paralleling the inhibition function.

The goodness-of-fit between the neurometric and inhibition function was measured with the Pearson correlation coefficient. At first glance, the Pearson correlation might appear to be an inappropriate measure of goodness-of-fit, due to insensitivity to scale differences. For example, a range between 1% and 9% saccade probability could correlate highly with a range between 10% and 90% probability of neural activity exceeding threshold, despite scale differences. Nonetheless, this issue is resolved by the fact that the prior best fit of the neurometric threshold requires the actual values of the neurometric and psychometric functions to be as numerically close as possible, i.e. of the same scale. Thus, a high Pearson correlation in this case implies both similar scale and similar functional form, which are the basic elements of a good fit. In principle, a chi-squared test might also be appropriate to test goodness-of-fit. In this case however, a chi-squared test was inappropriate, because it requires an estimate of the variance for the neurometric and inhibition functions, and the variances were not readily known. To obtain reliable estimates of shape parameters, the neurometric function was fit with a Weibull function of the form:

$$\mathrm{W}(\mathrm{t})=\mathrm{\gamma }-(\mathrm{\gamma }-\mathrm{\delta })\cdot \text{exp}(-(\mathrm{t}/\mathrm{\alpha }{)}^{\mathrm{\beta }})$$

where t is time after target presentation, α is the time at which the neurometric function reaches 64% of its full growth, β is the slope, γ is the maximum value of the neurometric function and δ is the minimum value of the neurometric function.

Threshold from optimal discrimination between canceled and non-canceled trial activity

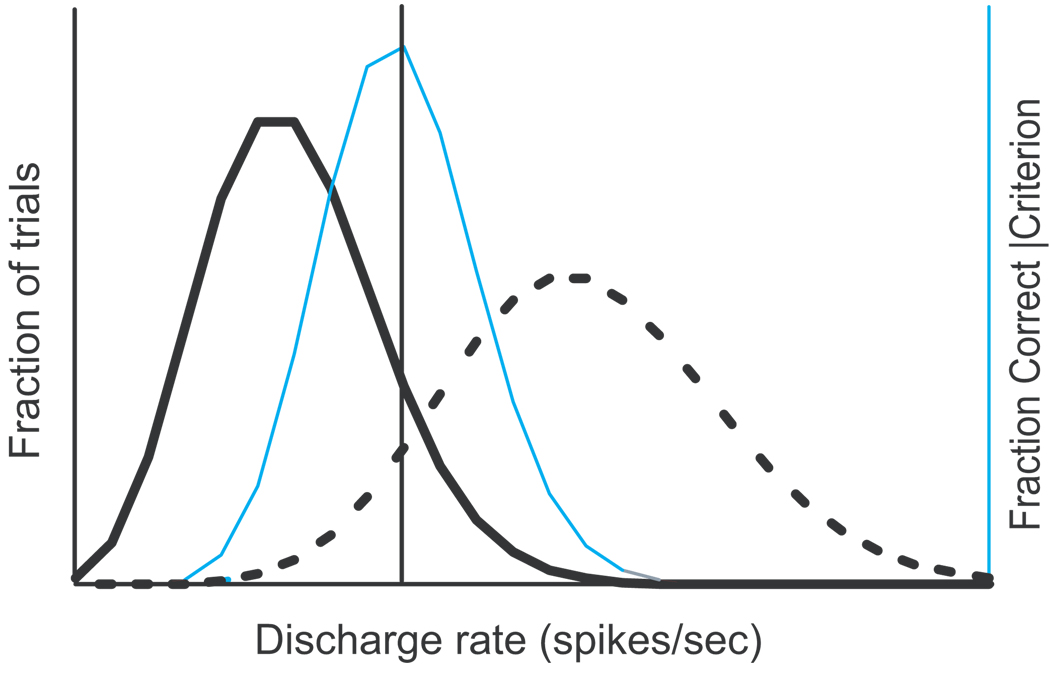
This analysis was based on another defining feature of a trigger threshold. If movements are initiated if and only if the activity of presaccadic neurons exceeds a threshold discharge rate, then the distribution of discharge rates in canceled trials must be less than the distribution of discharge rates in non-canceled trials. Thus, another measure of a putative trigger threshold is the discharge rate that optimally discriminates between the distributions of maximum activity measured in canceled and non-canceled trials (Figure 4). Specifically, this optimal discriminant threshold measurement determined the discharge rate that maximized the number of canceled trials with activity below the criterion threshold and the number of non-canceled trials with activity above the criterion. The quality of the discrimination can be plotted as a function of criterion discharge rate and its value is greatest at the optimal threshold. Trials with no stop signal were not used to calculate the optimal threshold. A measure of this discrimination quality is the fraction of stop signal trials with activity on canceled trials below the criterion and with activity on non-canceled trials above the criterion. The threshold in this case constitutes a classical linear discriminant (Fisher, 1936).

Figure 4.

Optimal discriminant threshold. Theoretical distributions of maximum activity for canceled (thick solid) and non-canceled (thick dashed) trials. If saccades are initiated when activity exceeds a threshold, then the distribution of activity on non-canceled trials should be greater than that on canceled trials. A criterion discharge rate (vertical line) correctly predicts no saccade for all canceled trials with activity less than the criterion, and it correctly predicts saccade initiation for all non-canceled trials with activity greater than the criterion. However, it incorrectly predicts saccade initiation for canceled trials with activity greater than the criterion, and it incorrectly predicts saccade withholding for non-canceled trials with activity less than the criterion. For each criterion discharge rate, the predictive accuracy can be quantified as the percent of stop signal trials whose outcome is correctly predicted. This percentage is plotted as a function of discharge rate (thin gray line). The optimal discriminant threshold is the maximum of this function.

RESULTS

This analysis concentrated on neurons with activity related to the production of saccades. Movement-related and visual activity was distinguished in data collected during performance of memory-guided saccades and the stop signal task. Movement-related activity was identified as pronounced modulation synchronized with saccade initiation, such that movement-aligned activity was greater than stimulus-aligned activity, consistent with our classification in numerous previous studies. We did not require a minimum discharge rate aligned on movement initiation for a cell to be classified as a movement cell. Visual activity was identified as pronounced modulation synchronized on target presentation. The data included 48 neurons with movement-related activity (many of which had visual responses) and a select group of 12 neurons with only visual activity recorded from the frontal eye fields of two monkeys performing the countermanding task (Hanes et al. 1998).

Prediction of Movement Initiation by Individual FEF neurons

Consistent with previous results (Hanes and Schall, 1996), we found that the movement-related activity of most neurons (37/48) exhibited a specific albeit idiosyncratic discharge rate when saccades are initiated. The goal of this study was to explore the reliability of this threshold discharge rate. The analyses presented herein extend the previous analysis that included only trials with no stop signal by determining whether a critical threshold of discharge rate can predict saccade initiation in trials when the stop signal was presented. Movement-related neurons, such as the example shown in Figure 5, generally had greater activity on non-canceled and no stop signal trials than on canceled trials.

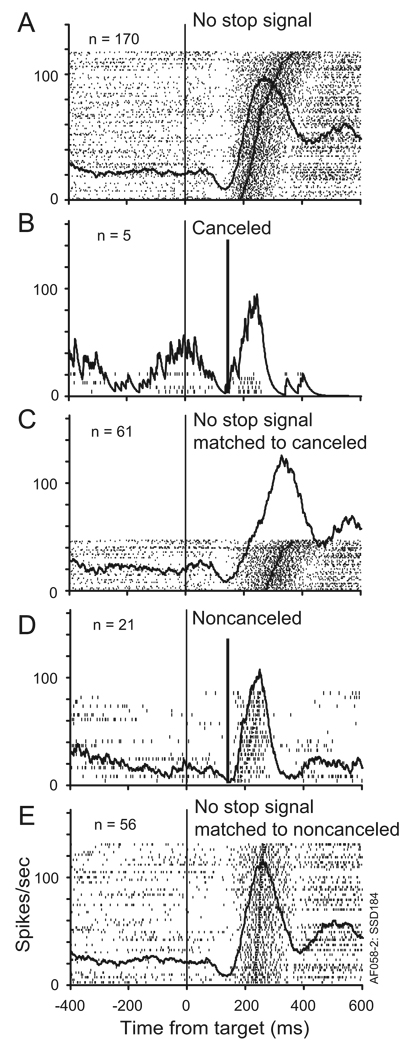
Figure 5.

Activity of a typical movement-related neuron. A. Activity in all trials with no stop signal with the target in the movement field. Activity is shown in rasters for each trial sorted by saccade latency, with saccade initiation time marked by the spot in each raster, and in a plot of the spike density function averaged across the trials. This neuron exhibited a pause in discharging after presentation of the target followed by the characteristic increase of discharge rate before and during saccades. B. Activity in trials with stop signal presented after a particular delay (thick vertical line) and the saccade was canceled. C. Activity in trials with no stop signal with saccade latency equal to or greater than the stop signal delay plus the stop signal reaction time. According to the race model, these trials have latencies long enough that if the stop signal had occurred, the saccade would have been inhibited. These are referred to as latency-matched to the canceled trials. Note the lower peak discharge rate in canceled trials (B) compared to latency-matched no stop signal trials (C). D. Activity in trials with stop signal presented after a particular delay and the saccade was not canceled. E. Activity in trials with no stop signal with saccade latency less than the stop signal delay plus the stop signal reaction time. According to the race model, these trials have latencies short enough that if the stop signal had occurred, the saccade would have initiated anyway. Note that the peak discharge in noncanceled trials (D) is as high as that in latency-matched no stop signal trials (E).

If the fixed trigger threshold hypothesis is correct, then the probability of producing a saccade on a stop signal trial, i.e., the fraction of non-canceled trials, must correspond to the probability of activity exceeding the fixed threshold. This implication of the hypothesis motivates an analysis similar to that performed in studies of sensory discrimination (Britten et al., 1992; Luna et al., 2005) of comparing a neurometric function derived from some measure of neural activity with the psychometric function. Applying the analysis illustrated in Figure 3, we found that in stop signal trials, the probability of the activity of FEF movement neurons exceeding a criterion discharge rate increased with stop signal delay (Figure 6A). This occurs because of the characteristic growth of activity of movement-related neurons in FEF (Figure 1). For a given stop signal delay, the level of peak activity on each stop signal trial was progressively more likely to be less than successively high criterion levels. Figure 6B shows that for this representative movement neuron, one criterion discharge rate existed for which at each stop signal delay, the fraction of trials with activity exceeding the criterion corresponded to the fraction of non-canceled trials produced at that stop signal delay. In other words, a particular discharge rate defined a threshold criterion that provided the best fit between the neurometric and behavioral inhibition functions. This will be referred to as the neurometric threshold.

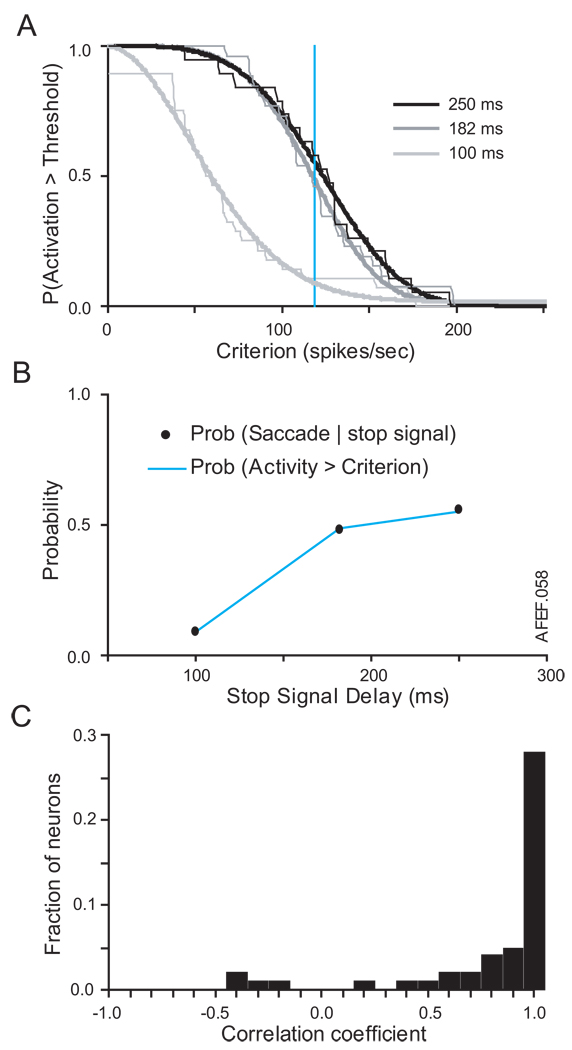
Figure 6.

Fitting neurometric and psychometric functions for neuron shown in Figure 5. A. Probability that activation exceeds a criterion discharge rate decreases with criterion. Thin lines plot actual values. Thick lines plot best fit Weibull function. The curves shift to right for progressively longer stop signal delays (distinguished by grayscale as indicated in legend) because the activation of the neuron builds up with time. The vertical cyan line marks the particular criterion discharge rate at which the probability that the activation exceeds that criterion corresponds to the probability that a saccade was initiated at the respective stop signal delays. B. Inhibition function (solid points) measured while the activity of the neuron was recorded and neurometric function (cyan) derived from the criterion discharge rate that minimized the sum-squared difference between the neurometric and psychometric functions. The Pearson correlation between this neurometric function and the inhibition function was 0.9997, and the neurometric threshold was 117 sp/sec. (C) Distribution of Pearson correlation coefficients across the population of movement-related neurons sampled (median r = 0.92).

The critical step of this analysis was to determine whether any particular discharge rate criterion produced a neurometric function that fit the inhibition function. The neurometric threshold was defined as the criterion discharge rate that minimized the least squares fit between the neurometric and psychometric functions. Figure 6B (cf. Fig. 3B) demonstrates the good agreement between the neurometric and psychometric functions for a threshold of 117 sp/sec for this respective neuron. The goodness of fit was evidenced by a Pearson correlation of r = 0.9997, computed by pairing data points at each stop signal delay from the neurometric and psychometric function.

We determined the Pearson correlation coefficient for neurometric-psychometric functions for all 48 FEF movements, as a measure of goodness-of-fit between the two functions. Figure 6C shows the distribution to be clearly skewed towards values close to 1. The median value was 0.92. The correlation was significant for only a third of neurons (16/48), but this reflects the small sample of stop signal delays providing estimates for each neuron rather than problems with the goodness-of-fit. Unfortunately, it was necessary to use fewer stop signal delays to obtain enough trials at each delay. For example, the Pearson correlation in Figure 6B is close to 1.0 but is based on only three available data points. Nevertheless, the quality of this fit can distinguish neurons with a threshold from those without (see Figure 13 and the companion paper). In summary, for most individual FEF movement neurons, a discharge rate could be determined that provided a unique correspondence between the functionally defined neurometric function and the behavioral inhibition function.

Figure 13.

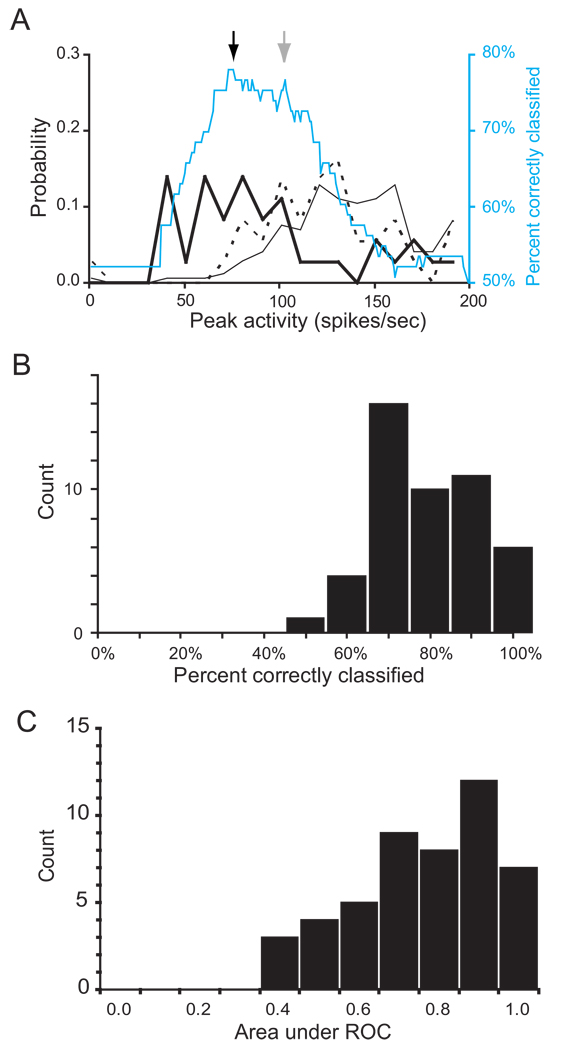
Lack of relation of activity of visual neurons in FEF to movement initiation. A. Raster and average spike density of visually responsive neuron aligned on saccade initiation. Trials are sorted by saccade latency. Target presentation time indicated by red dot in raster. The modulation during the saccade is elicited by the visual image swept across the retina by the saccade. B. Frequency distributions of maximum activity on canceled (thick), non-canceled (dotted), and no-stop signal (thin solid) trials. Note that activity is higher on trials without a saccade than on trials with a saccade, because when a saccade occurs, the activity in the interval measured just before movement initiation is less than the visual activity measured after target onset when no saccade occurs. Percent of trials correctly classified as canceled or noncanceled is plotted as a function of criterion discharge rate (cyan). The optimal discriminant threshold for this cell was 196 sp/sec and yielded a predictive accuracy of 51% which was not different from chance.C. Distribution of percent correctly predicted trials for the visual cells. The distribution is not significantly different from chance of 50%. D. Comparison of inhibition function (solid points) and neurometric function derived from the activity of this neuron (cyan). The neurometric and psychometric functions are negatively correlated (R = −0.99), because with longer SSDs, more non-cancelled trials are generated with activity measured immediately prior to saccade initiation. The presaccadic activity is weaker than the visual activity, which is why the cell fails to reliably predict saccade initiation. Thus, for longer SSDs in visual cells, a smaller proportion of trials show measured activity above the threshold . E. Distribution of correlations between neurometric functions from all visual neurons and inhibition functions while those neurons were recorded. A tendency for negative correlations was evident.

Another clear implication of the fixed threshold hypothesis is that the threshold must be exceeded when saccade is produced on no stop signal or non-canceled trials but not when the saccade is withheld in canceled trials. Figure 7A shows the distributions of maximal presaccadic discharge rates in all non-canceled and canceled stop signal trials and in all trials with no stop signal for this single movement-related neuron. As reported previously (Hanes et al. 1998), across the population, the means of the maximum activity on canceled trials for each cell were less than the means of the maximum activity on non-canceled (t(47) = 6.77 , p < 10⁻⁷) and on no stop signal trials (t(47) = 6.56, p < 10⁻⁷) for each cell. This implication suggests another straightforward estimate of the trigger threshold that can be obtained by determining the discharge rate that optimally discriminated between canceled and non-canceled trials, i.e. minimized the false classification rate of saccade vs. no-saccade given the peak neural activity. This will be referred to as the optimal discriminant threshold.

Figure 7.

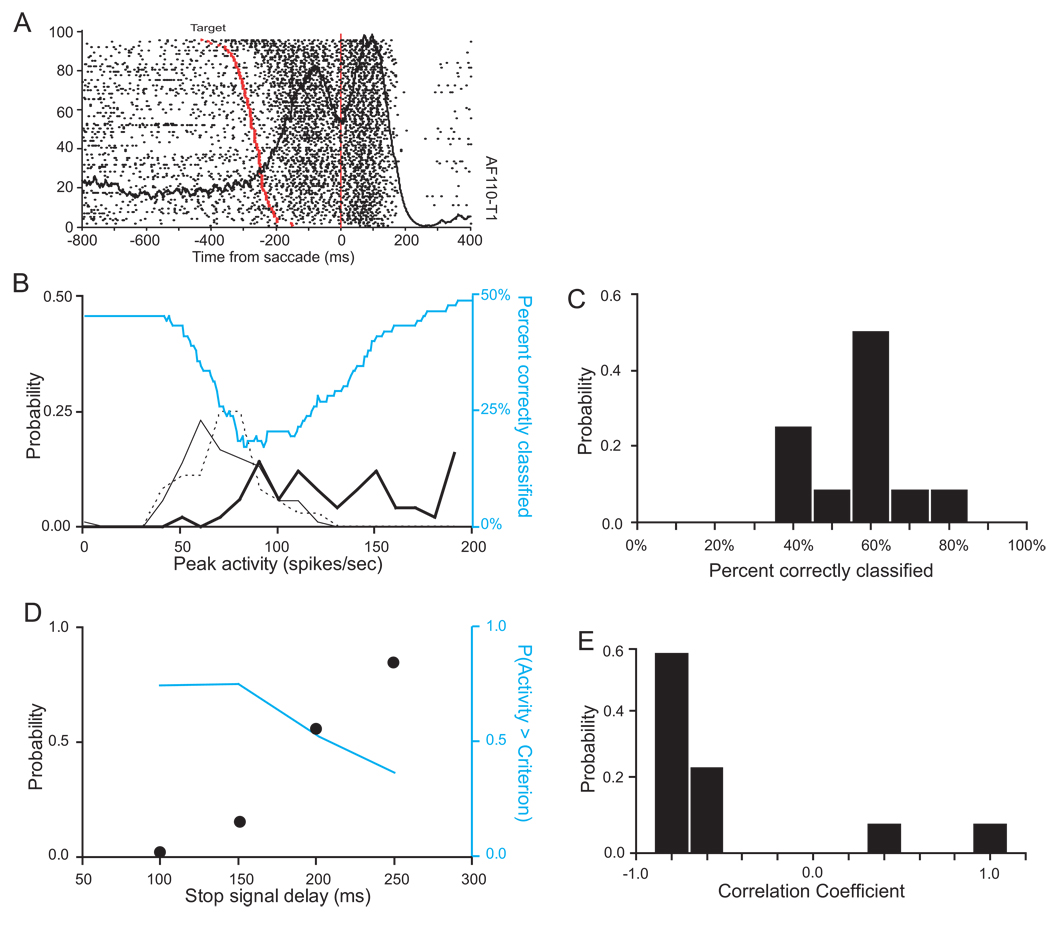
Computing optimal discriminant threshold for neuron shown in Figure 5. A. Probability density distributions of peak discharge rate in trials with no stop signal (thin black), in noncanceled stop signal trials (dashed black) and in canceled stop signal trials (thick black). Percent of trials correctly classified as canceled or noncanceled is plotted as a function of criterion discharge rate (cyan). Threshold was defined as the criterion discharge rate that maximized the number of canceled trials with activity below the criterion and the number of non-canceled trials with maximum activity above the criterion. For this neuron, a threshold of 76 sp/sec provided the maximal discrimination accuracy of 78% (marked by black arrow). The discriminant accuracy function had a plateau around the maximum, so the true threshold value could lie anywhere within this range. A threshold of 103 sp/sec, which agrees more closely with the neurometric threshold, yielded a predictive accuracy of 77% (marked by gray arrow). B. Distribution of values of percent correctly classified by a particular threshold for the 48 movement-related neurons. The median value was 75% correctly classified trials. C. Histogram of areas under the ROC curve for the 48 FEF movement-related cells, using cancelled vs. non-cancelled trials.

The cyan curve in Figure 7A shows the probability that the observed behavior (saccade initiated or not) was correctly classified as a function of criterion discharge rate (cf. Figure 4). Note that the predictive accuracy for extreme discharge rate criteria is chance which is ∼50% because roughly half of the stop signal trials are non-canceled. For example, with a criterion of 0 sp/sec the activity on all trials exceeds the criterion and so should produce a saccade which is what happens by chance on approximately half of the trials. A maximal classification accuracy of 78% was obtained at 76 spike/sec. It should be noted that the discrimination accuracy function for this neuron had a broad peak, so the true threshold value could lie anywhere within this plateau. In fact, a threshold of 103 sp/sec, which agrees more closely with the neurometric threshold, yields a predictive accuracy of 77%.

Figure 7B shows the predictive accuracy distribution based on the optimal discriminant threshold for all 48 FEF movement neurons. The values scatter broadly over a range from 0.5−1 and the median value is 0.75. Clearly, the activity of single movement-related neurons did not predict movement initiation with perfect accuracy, and stronger predictions have been found in superior colliculus cells (Pare and Hanes, 2003). This is due in part to the well-known variability in discharge rates of single neurons, and we show below that combining activity across multiple neurons leads to improved reliability of the relation between fit movement-related activity and saccade initiation. It must also be noted that the activity of other classes of neurons in FEF and other structures relate to saccade initiation much less than these FEF movement-related neurons (see Figure 13 and companion paper).

The validity of the optimal discriminant threshold may be tested by the area under the receiver operating characteristic (ROC) curve. The ROC curve plots the false positive rate against the true positive rate as a function of threshold. The area under the ROC curve provides a measure of how discriminable two distributions are. An ROC area value of 1.0 indicates perfect discriminability, and a value of 0.5 corresponds to chance. The measure is independent of the particular choice of thereshold, which allows it to provide a validity test that is independent of the particular value of optimal threshold. A histogram of the area under the ROC curve for the population of 48 FEF movement neurons is shown in Figure 7C. Each ROC curve calculation was derived from data as shown in Figure 7A. The average ROC curve area was significantly greater than the chance value of 0.5 (t(47) = 8.36, p < 0.00001). In the companion paper, we show that the area under the ROC curve was significantly greater for FEF than SEF movement cells.

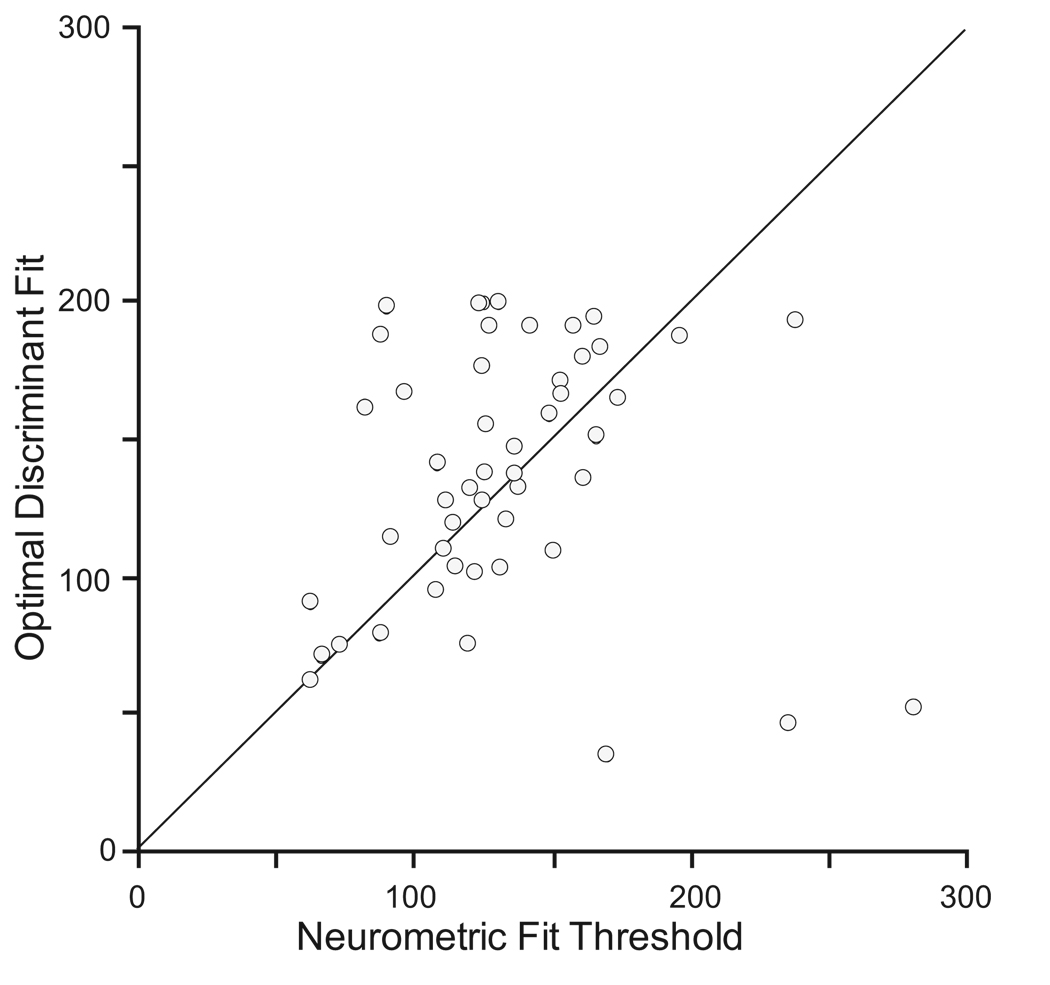
Comparison of Threshold Values

The best-fit neurometric and optimal discriminant thresholds were compared across the FEF movement neuron population. The neurometric and discriminant thresholds found for each neuron generally agreed (Figure 8), except for three obvious outliers. Further investigation revealed that each of these outliers exhibited no significant difference between the distributions of maximum presaccadic activity on canceled and non-canceled trials (t-test, all p’s > 0.05). This violates a key assumption of the optimal discriminant threshold (Figure 4) and therefore makes the test invalid. When we excluded neurons with no significant difference between canceled and non-canceled maximum activity, the correlation between the two threshold measures was significant (r = 0.66, t(25) = 4.44, p < 0.001), and the slope of the regression passing through the origin did not differ from unity (t(26) = 0.32, p = 0.75). Thus, FEF neurons that show significant activity differences between canceled and non-canceled saccades also show strong agreement between the thresholds obtained by the two different methods. This provides converging evidence for both the validity of the concept of a movement initiation threshold and the near-optimality of the best-fit threshold approach.

Figure 8.

Comparison of neurometric and discriminant thresholds for the sample of FEF neurons with movement-related activity. Data points with perfect agreement between the methods would lie along the diagonal.

Timing of threshold crossing for individual trial

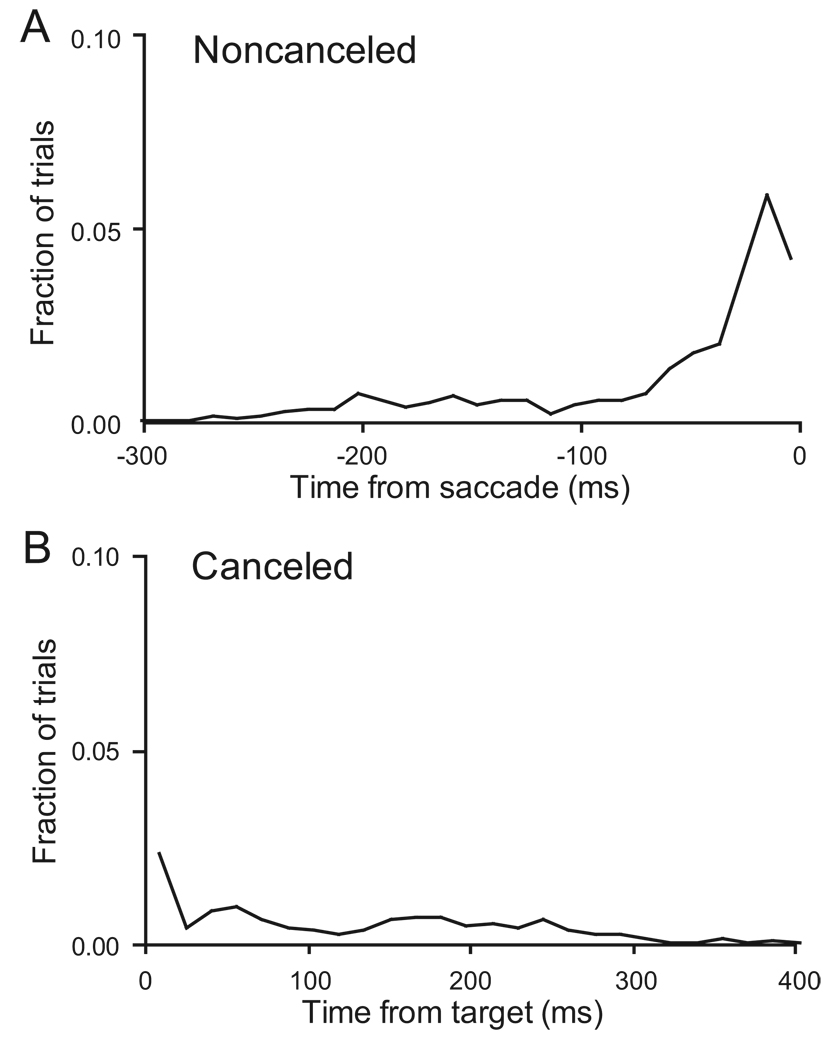
The hypothesis of a fixed threshold trigger of saccade initiation has an implication about timing. If a threshold-crossing triggers a movement, that crossing must happen only once and not too early before the movement is initiated. To this point we have established that whether FEF movement neuron discharge rate reaches a particular value predicts if a saccade is initiated. We will now investigate if the time when the activity first exceeds that threshold predicts when a saccade will be initiated. Figure 9 plots the time when the discharge rate first exceeded the optimal discriminant threshold for all trials of all FEF movement-related neurons. For non-canceled trials (Figure 9A), this event typically occurred most commonly 20 ms prior to saccade initiation, but the distribution spreads broadly around this value. Such dispersion is not unexpected given the well-known variability of neuron discharges, but it should be noted that this temporal relationship does not occur for all neurons in visuomotor structures (see Figure 13 and accompanying paper). The vast majority of values (75%) fell into the range of 100 ms before saccade onset and 70% were within 50 ms of saccade initiation. The modal time of threshold crossing was around 20 ms prior to saccade onset, in agreement with earlier results (Scudder et al. 2002). Figure 9B shows that on canceled trials measure the peak of activity on single trials exceeded threshold occasionally, though much less often and less predictably than in non-canceled trials. This is of course due to the lower level of activity on canceled trials.

Figure 9.

Time of threshold crossing in single trials. A. Distribution of the time when activation first exceeded the threshold measured relative to saccade initiation in non-canceled trials. Activation first exceeded the threshold most commonly 20 ms prior to saccade initiation as expected of a neural event that triggered a saccade. B. Distribution of the time when activation first exceeded the threshold measured relative to target presentation in canceled trials. Overall, activation did not exceed the threshold on canceled trials. However, the distributions of maximum activity for canceled and non-canceled trials overlapped slightly, so even with the optimal discriminant threshold, activity on canceled trials sometimes exceeded the threshold even though no saccade was produced. This occasional threshold crossing in single trials occurred at no particular time, though, suggesting that it constitutes measurement noise.

Population analysis of multiple trials from individual neurons

The results thus far demonstrate that the activity of individual FEF movement neurons accounts reasonably well for whether and when a saccade will be initiated. However, the predictions also showed limitations on both accounts. This is not surprising, because the analysis was based on a single trial from individual noisy neurons. However, it is well known that a population of neurons in a network including FEF, SC, thalamus, basal ganglia, cerebellum and brainstem produces saccades and the activity of pools of neurons is more reliable than that of single neurons. Therefore, we extended the analysis to determine whether a threshold derived from activity averaged from pools of trials and of neurons was more reliable. If so, the results could indicate how many neurons are sufficient to specify whether and when a saccade will be produced. The size of the pool sufficient to account for saccade initiation provides an important perspective on the size of the pool necessary to initiate a saccade. This analysis is similar to that employed by Bichot et al. (2001) to investigate the relation of activity of visually responsive neurons in FEF to saccade target selection during visual search (see also: Krauzlis and Dill 2002; Shadlen et al. 1996; Tolhurst et al. 1983).

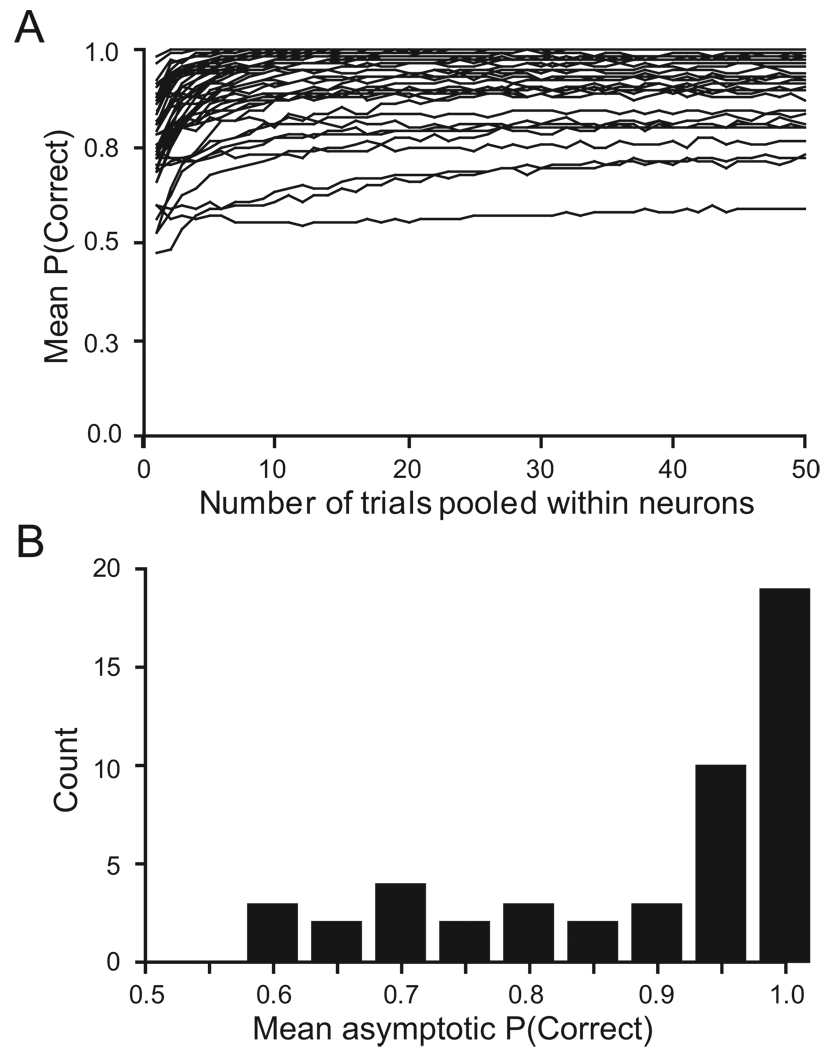
We first tested whether combining multiple trials from an individual neuron yielded greater predictive accuracy for the threshold. We examined trial pools ranging from 1 to 50. For a given trial pool size, we averaged the randomly sampled, individual spike density functions, thus constructing a single virtual canceled and non-canceled trial. We repeated this procedure and created a distribution of virtual pooled trials. We then determined the optimal discriminant threshold between the distributions of activity on pooled canceled and non-canceled trials. As the size of the pool increased, the variance of these distributions decreased, leading to greater resolution between them. Figure 10A shows that the predictive accuracy of the discriminant threshold increases as a function of pool size. For example, the cell in Figure 5 reached 95% accuracy with seven trials pooled and 97 % accuracy with fifty trials pooled. The distribution of asymptotic accuracy is shown in Figure 10B. As a whole, the cells seemed to reach asymptotic accuracy (92%) with 20 trials pooled within a cell, which was just short of the 93% accuracy with 50 trials pooled. However, while most neurons yield an asymptote over 90% accuracy, a few neurons did not carry sufficient information to predict reliably saccade initiation, regardless of how many trials were pooled. The outliers in Figure 8 generally provided less reliable predictive accuracy.

Figure 10.

Effect of pooling trials on accuracy of accounting for saccade initiation A. The accuracy of the optimal discriminant threshold at accounting for saccade initiation is plotted as a function of number of trials pooled for each neuron with movement-related activity. Two trends are evident. First, pooling the activity of a neuron across multiple trials increases the accuracy up to an asymptote. Second, the asymptotic accuracy varies across neurons, but most neurons exhibit asymptotic accuracy exceeding 90%. The optimal discriminant threshold for the neuron illustrated in Figure 5 yielded 97% accuracy. B. Distribution of asymptotic accuracy for neurons plotted in A.

To examine why some cells provided better predictive accuracy than others, we arbitrarily divided the neurons into two subgroups, based on their average accuracy with 40 to 50 trials pooled: a group of “ low predictor” neurons (9/48; 19%) that reach asymptotic fraction correct levels of less than 0.84 (one standard deviation below the mean accuracy) and a larger group of “high predictor” neurons (39/48; 81%) that reach higher fraction correct levels. The average fraction of correctly predicted trials is 0.97 for the high-predictors and 0.76 for the low predictors. We sought to determine whether any other characteristic distinguished these two groups of neurons. The FEF movement neurons change their activity on canceled trials, when the monkey was able to suppress the planned saccade. This time was termed the cancellation time (Hanes et al., 1998). The cancellation times of the low predictor group were not significantly later than the ones of the high predictor group (p = 0.36). Sample size also did not explain the difference. There was no significant difference in either the total number of stop signal trials (p = 0.08) or the smaller number of trials of either canceled or non-canceled trials (p = 0.26). However, the activity profiles of the two groups differed. The low-prediction neurons showed a stronger visual response, while the saccade-related burst was identical. This suggests that the lower prediction results from the stronger visual bursts of these neurons, which lead to maximum activity distributions of canceled trials that show more overlap with the distribution of non-canceled trials. This result emphasizes the point that movement-related neurons are so classified because they respond much more strongly in relation to movement initiation than to visual signals, but this does not necessarily imply the complete absence of a visual response.

Population analysis of multiple trials from multiple neurons

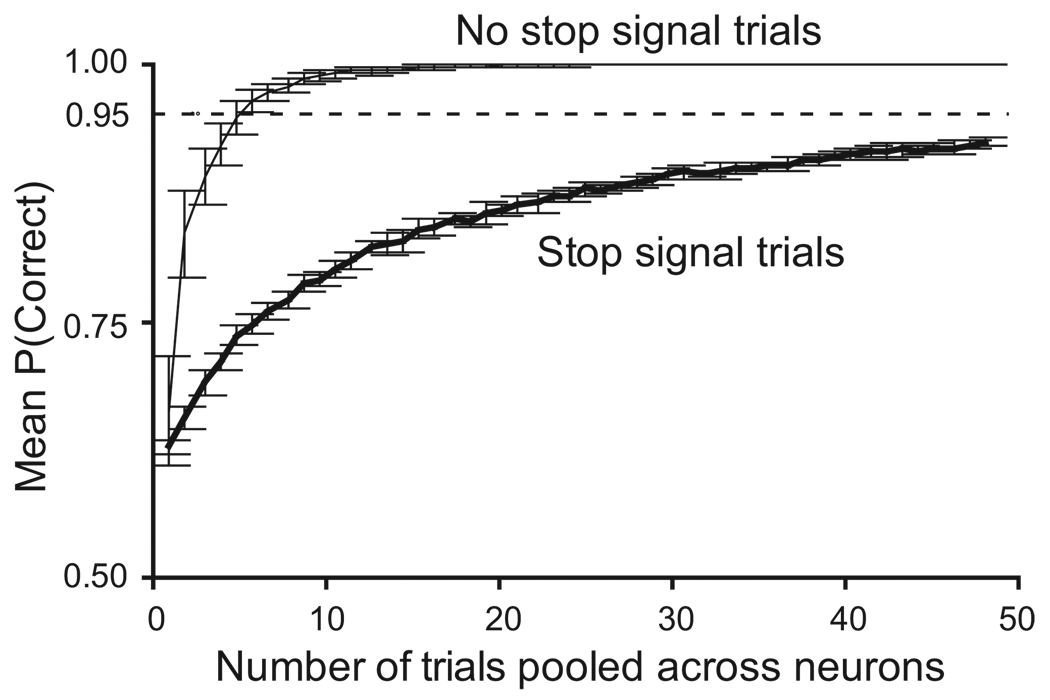
In addition to combining multiple trials from the same neuron, we examined the predictive power of combining multiple trials from different neurons. Figure 11 shows the predictive accuracy for activity recorded in stop trials and in no-stop signal trials, using the discriminant threshold for pools derived from the population of all movement neurons. The error bars represent the standard deviation from 10 random samples. Predictive accuracy reached 95% in no stop signal trials with as few as six neurons and 100% accuracy with 10 neurons. For stop signal trials, the predictive accuracy asymptotically approached 95% accuracy as the pool size approached 50. The reason for the greater predictive accuracy on no-stop signal trials is that the maximum activity across the population on these trials measures on average greater than the maximum activity on non-canceled trials (Figure 5B). Given this fact, the greater average maximum activity on no-stop signal trials is more likely to exceed the threshold than is the maximum activity on non-canceled trials. Furthermore, no stop signal prediction errors consisted entirely of a failure to exceed the threshold, since no stop signal trials resulted in a saccade on effectively all trials. Thus, the maximum activity for these trials essentially always exceeded the threshold for pools of at least 10 trials pooled across neurons, and the threshold derived from stop trials (canceled and non-canceled) applies as well to no-signal trials.

Figure 11.

Effect of pooling trials across neurons on accuracy of accounting for saccade initiation. Average probability that optimal discriminant threshold correctly accounted for saccade initiation as a function of number of no stop signal trials or stop signal trials pooled across neurons. Error bars plot the standard deviation from 10 random samples. On no stop signal trials (thin line) pooling across six neurons yielded 95% accuracy and 100% accuracy with 10 neurons. On stop signal trials (thick line) the accuracy asymptotically approached 95% accuracy as the pool size approached 50.

Pooling across neurons (Figure 11) allows the activation derived from the population to exceed the limitations of the less-predictive individual neurons (Figure 10A). Notably, the predictive accuracy for stop signal trials pooled across neurons did not seem to reach an asymptote, even at a pool size of 50. It may be that pooling more trials across neurons would lead asymptotically to 100% accuracy on stop signal trials as well as no-signal trials.

Timing of threshold crossing for pooled activation

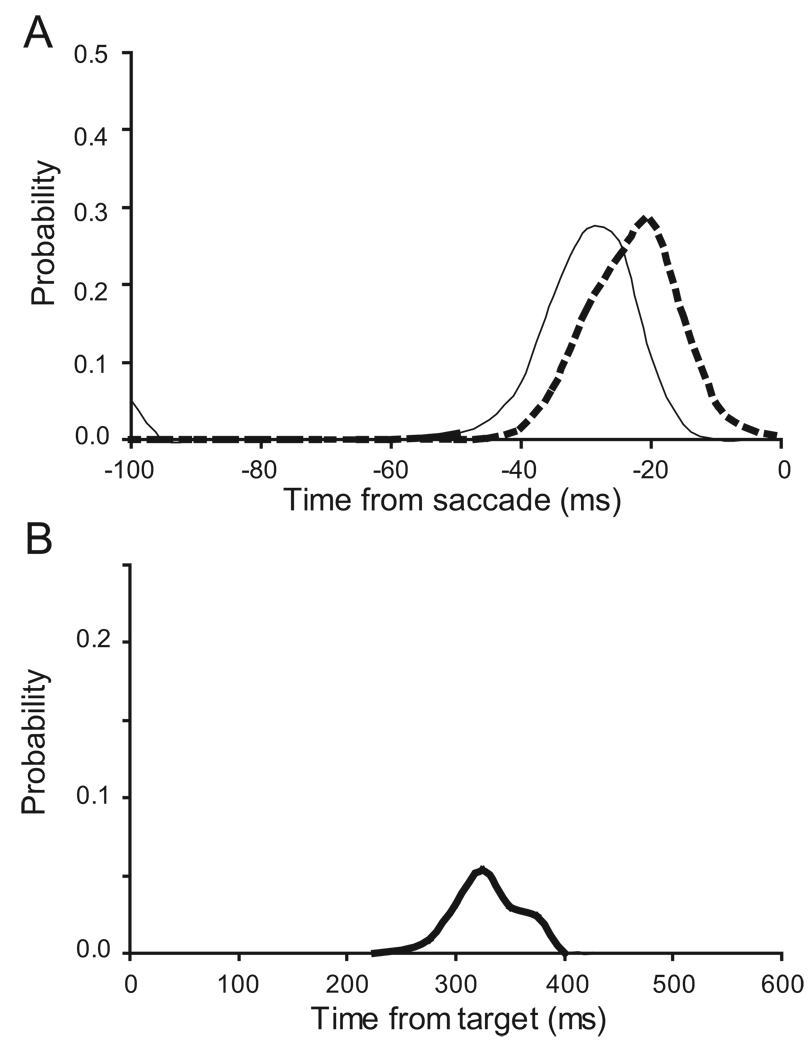
The reliability of accounting for saccade initiation improved if the activity was pooled among multiple FEF movement-related neurons. These data also permit an analysis of the time of threshold crossing. Recall, that a trigger event should be a unique event preceding the saccade by a period corresponding to the ballistic period. Spike density functions were sampled 10,000 times among pooled activity of the 48 movement-related neurons for trials with no stop signal and for stop signal trials. The optimal discriminant threshold was determined for stop signal trials only for each sample and then the time when the spike density function first exceeded the threshold was measured. The distributions of these times for the different trial types are shown in Figure 12. Several features of these plots should be noted. First, the distributions are unimodal with peaks around −20 to −30 ms before saccade initiation. The no-signal trials peak earlier because as noted above, the activity tended to be slightly greater on no signal than on non-cancelled trials, and therefore the activity exceeds the threshold earlier. Second, pooling activity across neurons produces much more reliable estimates of threshold crossing time (compare Figure 9 with Figure 12). The majority of values (75%) occur within 100 ms of saccade initiation, and the earliest time is 50 ms

Figure 12.

Time of threshold crossing of pooled activity. A. Time that pooled spike density functions crossed optimal discriminant threshold for no stop signal (thin) and noncanceled (thick dashed) is plotted as a function of time relative to saccade. The threshold was crossed in 99% of pooled non-canceled trials with a modal value of −21 ms before saccade onset. The threshold was crossed in 100% of pooled no stop signal trials with a modal value of −29 ms before saccade onset. B. Time that pooled spike density functions crossed optimal discriminant threshold for canceled stop signal trials is plotted as a function of time relative to target. The threshold was crossed in 15% of pooled trials with a modal value of 324 ms after target onset which corresponds to the range of saccade latencies. Note the difference in ordinate scale between panels A and B.

In the pooled activation a small number (15%) of predicted saccade initiations were measured during canceled trials (Figure 12B). This is to be expected since even pooling 50 trials across neurons does not result in a perfect predictive power. The distribution of the times of apparent threshold crossing in canceled trials was somewhat tighter than the distribution derived from individual trials (Figure 9B). The times are clustered between 240 to 400 ms (median: 329 ms), a period corresponding to the response times of the monkeys. This change results from the smoothing of the neurons’ activity through the pooling. On a given trial with a single neurons activity, the variance in the activity is larger than the variance of the activity with 50 trials averaged together. Therefore, the activity is more likely to exceed the threshold due to noise, and this can happen at any point in the trial. So the time when it first happens, which is what is shown in the distribution, is likely to be early in the trial. In contrast, when 50 trials are averaged, there is less noise and so the activity is less likely to spuriously exceed threshold. Now, the threshold crossing is most likely around the time when the total neuron activity is close to the threshold and most saccades are initiated.

Threshold analysis applied to visual neurons

Hanes et al. (1998) showed that while movement neuron activity modulated when saccades were canceled early enough to contribute to the control of gaze, visual neurons did not. To explore further whether the activity of visual neurons contributes to saccade initiation, and verify the sensitivity of this analytical approach we applied the same analysis to a set of visual neurons from two monkeys. Figure 13 shows results for a representative neuron in FEF with a pronounced visual response but no presaccadic movement-related modulation. The modulation observed during the saccade is due to the visual environment being swept across the receptive field by the saccade; the peak activity is related to the timing of the target rather than the saccade (Figure 13A). The distribution of activity from canceled trials was higher than those from non-canceled and no stop signal trials (Figure 13B). That is opposite the FEF movement neurons (compare Figure 7A). This was analyzed for the population of neurons using the optimal discriminant analysis. The maximum fraction of correct trials was 51%, corresponding to chance, at a discharge rate of 196 sp/sec, and a minimum of 17% was observed at a discharge rate of 88 sp/sec (Figure 13B). In other words, discharge rates less than 88 sp/sec were more likely to occur when saccades were initiated while discharge rates greater than 88 sp/sec were more likely to occur when saccades were canceled. This is the opposite of what would be predicted if saccades occur when neural activity exceeds a threshold. The activity of most visual neurons, though, was not predictive of whether a saccade would be initiated; the mean value of the fractions of correctly predicted trial outcomes from the optimal discriminant thresholds of all visual neurons was 0.52 (Figure 13C); for comparison, the value for the presaccadic movement neurons was 0.75.

This result sharply contrasts with the results in FEF and was confirmed through the analysis of the neurometric threshold. The neurometric function derived from the activity of the representative visual neuron was almost the perfect inverse of countermanding performance (Pearson correlation = −0.99, t = −8.69, p < 0.02) (Figure 13D), but this is the only visual neuron for which a statistically significant correlation, whether positive or negative, was obtained. The distribution of Pearson correlations between best-fit neurometric functions for visual neurons and inhibition functions had a median value of −0.83 (Figure 13E), which is the opposite of the distribution of the movement neurons (compare Figure 7B). The inverse relationship between neurometric and inhibition functions was due to several trivial factors. First, peak activity in non-canceled trials is measured in the interval immediately preceding the saccade. Second, the visual response tends to decay by the time the saccade is initiated, so it is lower when measured just before the saccade in non-canceled trials. Third, more trials are non-canceled at longer SSDs. Together, this means that in visual cells, the measured probability of maximum activity exceeding a threshold tends to decrease with SSD. To sum up, unlike the activity of movement-related neurons, the activity of visual neurons did not predict saccade initiation.

DISCUSSION

The results of this study demonstrated that whether and when saccades are initiated in a stop signal, countermanding task was predicted by whether and when the discharge rate of movement-related neurons but not of visual neurons in the frontal eye field (FEF) reached a particular threshold. The reliability of this relationship improved by averaging the activity of ∼10–20 trials or neurons. These findings have specific consequences for our understanding of the oculomotor system and demonstrate a method of determining whether any population of neurons contributes to the control of movement initiation.

Threshold as a population phenomenon

The discharge of individual FEF movement related neurons relates reasonably closely to the time of saccade initiation, but pooling trials within or across neurons increased the reliability of this relationship. In other words, FEF movement-related neurons specify not only whether a saccade will be initiated, but also when it will be initiated. The power of single FEF neurons to predict saccade initiation time was significantly higher than by chance but not perfect. The combined activity of ∼20 movement-related neurons in FEF reached its threshold most often in the 20 ms before saccade initiation. This is the time when events in the brainstem reach a point of no return in the inhibition of omnipause neurons and activation of burst neurons. The threshold is therefore the product of the simultaneous activity within a network of neurons. This result complements and extends a similar analysis of the activity of visual neurons in FEF during visual search (Bichot et al. 2001). It might be argued that our analysis of pooling trials across neurons is limited by the fact that the neurons were recorded in separate sessions rather than simultaneously so our values underestimate the actual number because of noise correlation among neurons. Simultaneous recording would provide the most direct test of how many neurons are necessary to predict saccade initiation. Nonetheless, our results still show that both individual neurons and the population as a whole reach a particular threshold of activity to initiate a saccade, and that the timing of the threshold crossing predicts when as well as whether a saccade will be initiated.

The finding that a few (∼10¹) neurons are sufficient to predict behavior contrasts with the observation that many neurons (∼10⁵–10⁶) within the oculomotor network encompassing cortical areas, superior colliculus, basal ganglia, thalamus, the brainstem and most likely cerebellum are necessary to generate a saccade. Since no single neuron is necessary to produce a movement, neurons within and across structures contributing to a given movement seem to have coordinated activity so that each neuron reaches its idiosyncratic threshold at close to the same time. One hypothesis for how this may be achieved is through rapid interactions that coordinate the growth of movement activation between oculomotor structures such that neurons lagging behind are accelerated and those speeding ahead are decelerated. Current evidence already demonstrates that the FEF in opposite hemispheres (Schlag et al. 1998) or the FEF and the SC (Schlag-Rey et al. 1992; Sommer and Wurtz 2000) engage in pronounced interactions during saccade preparation and execution. Transmission times between the FEF and the SC are on the order of 2–3 ms (Sommer and Wurtz 2004), easily fast enough to allow influence within the 80–100 ms interval of movement preparation. Another hypothesis (which is not mutually exclusive) is that a neuromodulatory system may influence the state of activation of the whole system so that on some trials all neurons are more or less active together (Clayton et al., 2004; Aston-Jones and Cohen, 2005). Consistent with this hypothesis, recent work has shown that norepinephrine may modulate synchronized activity in neural oscillators (Viemari and Ramirez, 2006).

Relevance for general models of response time

The evidence that response times in choice tasks are the outcome of at least two successive stages is incontrovertible (reviewed by Sternberg 2001; see also Schall 2003). The first encodes and categorizes stimuli, and the second prepares and initiates responses. Both stages occupy intervals that can be more or less variable depending on stimulus conditions (clarity and number of potential targets) and response complexity (compatibility of stimulus-response mapping and number of alternatives). Hence, overt response time is some combination of these two random intervals. Unfortunately, determining the respective contributions of mixtures of stochastic processes to overall response time is problematic using only overt measures (e.g., Dzhafarov 1993; Luce 1986; Marley and Colonius 1992; Ratcliff et al. 1995; Townsend 1976).

Neurophysiology with behaving monkeys provides a solution to this dilemma if particular cognitive operations can be identified with distinct populations of neurons (Schall 2004). The activity of neurons in monkeys performing response time tasks can reveal the durations of successive stages. Sequential sampling models explain the variability in choice response time as arising from variability in a diffusion or race process that is driven by the quality of evidence derived from the stimuli (Usher and McClelland, 2001; Ratcliff and Smith, 2004; Smith and Ratcliff, 2004; Bogacz et al., 2006). Previous work has characterized the duration of the encoding and categorization stage (Thompson et al., 1996; Sato et al., 2001; Cook and Maunsell, 2002; Krauzlis and Dill, 2002; McPeek and Keller, 2002; Roitman and Shadlen, 2002). Other work has identified the growth of activity of movement-related neurons in the FEF and superior colliculus with the diffusion process described by sequential sampling models (Hanes and Schall, 1996; Ratcliff et al., 2003; Ratcliff, 2006). The variability of response time in this stop signal task can be accounted for almost entirely by the movement-related activity because the stimulus encoding time is so brief due to the presence of a single, suprathreshold target stimulus.

This collection of empirical and theoretical results suggests to us the hypothesis that the modulation of visually-responsive sensorimotor neurons maps onto stimulus encoding and categorization while the modulation of movement-related neurons maps onto response preparation. This hypothesis is consistent with several recent neurophysiological results. First, if encoding is made more difficult, then variability in the time to encode and categorize stimuli will contribute more to variability in response time (Sato et al., 2001; Roitman and Shadlen, 2002); however, the variability of response preparation remains. In fact, new research using a visual search for a target that was easier or harder to locate has found that the beginning of the growth of movement-related activity is delayed by the amount of time needed to encode and categorize the search array (Woodman et al., 2008). Second, stochastic variability in response preparation provides a mechanism by which speeded errors can be produced in choice tasks even though the sensory representation is correct as evidenced by correction of the errors earlier than sensory or error-monitoring feedback would permit (Murthy et al., 2001; Holroyd et al., 2005; Murthy et al., 2007). Accordingly, the particular contribution of response preparation to response time also provides a means by which executive control can influence the trade-off between speed and accuracy (Stuphorn and Schall, 2006). Finally, the flexible relationship between sensory processing and response preparation that is necessary for arbitrary stimulus-response mapping affords an explanation for how transformations within and the transmission between stages can appear to be continuous or discrete (Bichot et al., 2001; Sternberg, 2001; Woodman et al., 2008).

Conclusion

The present study in combination with an earlier study using the countermanding task (Hanes et al. 1998) demonstrates the usefulness of the countermanding paradigm in determining whether neurons or ensembles of neurons control movement initiation. The fact that visual neurons in FEF fail to provide a satisfactory fit to the threshold model and also fail to respond to the countermanding command in sufficient time to drive saccade interruption verifies that this approach can distinguish between neurons that are or are not involved in movement initiation. Accordingly, the stop signal paradigm can be used to explore other areas. For example, this approach can contribute to the debate about the role of parietal cortex in producing saccades (Andersen and Buneo 2002; Colby and Goldberg 1999). In the companion paper we investigated the hypothesis that neurons in the supplementary eye field with saccade-related activity participate in the process of saccade initiation (Stuphorn et al. 2007). We found evidence that this is not the case at least for visually guided saccades.