Nondestructive quantification of leakage at the tooth – composite interface and its correlation with material performance parameters

Abstract

Current methods to determine debonding/leakage at the tooth-composite interface are qualitative or semi-quantitative. Our previous work introduced a 3D imaging technique to determine and visualize leakage and its distribution at the interface of cavity wall and composite restoration in model cavities. In this study, an automated program was developed to quantify leakage in terms of area and volume. 3D leakage distribution obtained via the image analysis program was shown to have excellent agreement with leakage visualized by dye penetration. The relationship between leakage and various material performance parameters including processability, shrinkage, stress, and shrinkage strain-rate were determined using a series of experimental composites containing different filler contents. Results indicate that the magnitude of leakage correlated well with polymerization stress, confirming the validity of the common approach utilizing polymerization stress to predict bonding durability. 3D imaging and image analysis provide insight to help understand the relations between leakage and material properties.

1. Introduction

Visible light cured composites consisting of inorganic fillers and a polydimethacrylate matrix formed by rapid free-radical polymerization in situ are increasingly used as direct restorative materials for tooth cavities[1–3]. The main advantage of composite materials over dental amalgams is their good aesthetics. However, the volume loss during the rapid polymerization of dimethacrylates generates stresses that have been recognized as important factors affecting the marginal integrity of the composites[4;5] and possibly leading to debonding from the surrounding tooth structure[6]. The shrinkage strain-rate also has significant impact on the marginal integrity of composites[7;8], and the resultant gaps could lead to microleakage, marginal staining, and recurrent caries[9]. Penetration of bacteria into the gaps can cause pulp pathology, material degradation, and ultimately failure of the dental composite restoration [5;10].

Tremendous efforts have focused on reducing polymerization shrinkage and the associated stress by incorporating more fillers or introducing new chemical formulations[11;12]. However, a direct connection between the shrinkage, stress, and marginal integrity, such as leakage or gaps at the composite-cavity interface, is still lacking[13]. This missing connection is in part due to a lack of robust methods to quantify leakage at the interface. The prevailing method to analyze leakage is dye penetration, which involves submerging a filled-tooth sample in a dye solution, such as an organic dye or silver nitrate solution. The tooth is then sectioned, and the presence of the dye indicates leakage. However, this method only determines the penetration depth along the plane of one tooth section and depends on how and where the tooth is sectioned[14;15]. In our previous studies, we demonstrated a method to quantify polymerization shrinkage nondestructively using X-ray microcomputed tomography (μCT)[16] and to visualize leakage (gaps along the cavity and composite interface) using 3D image analysis[17]. The leakage pattern was found to be non-uniformly distributed along a model cylindrical cavity, reaffirming the need to obtain complete and quantitative leakage information.

The objective of this study was to develop an automated process to quantify potential leakage in terms of area, volume, and location using data obtained via 3D imaging, and subsequently to correlate leakage parameters with various material performance parameters, including processability, shrinkage, stress, and shrinkage strain-rate, for a series of experimental composites with varying filler content. Polymerization shrinkage and leakage were obtained by 3D imaging via μCT[17] and image analysis, while degree of conversion (DC) was examined using Fourier transform infrared microspectoscopy in reflectance mode (FTIR-RM). The viscosity of each composite paste was characterized using a rheometer, and polymerization induced stress and strain-rate were determined using a tensometer[18;19].

2. Materials and Methods

2.1. Materials^*

Resins, 2,2-Bis(4-(2-hydroxy-3-methacryloxypropoxy)phenyl)propane (BisGMA) and triethyleneglycol dimethacrylate (TEGDMA), were obtained from Esstech Inc. The photoinitiator system of camphorquinone (CQ) and ethyl 4-N, N-dimethylaminobenzoate (4E) was purchased from Aldrich Corp. The fillers, fumed amorphous silica (OX50, 0.04 μm) and silanized glass beads (SP345, 0.4 μm) were provided by L.D. Caulk and Esstech, respectively. All reagents were used as received.

2.2. Composite preparation

BisGMA:TEGDMA (1:1 by mass) was activated for blue light photopolymerization with 0.2 % CQ and 0.8 % 4E (by mass) and stored in the dark until use. SP345 and OX50 fillers were mixed into the activated resin until uniformly distributed, using a SIMENS SpeedMixer (DAC 150FVZ) at a speed of 262 rad/s (2500 rpm) for 1 min three times. Five composites were prepared, each consisting of activated resin with 10 % (by mass) OX50 and varying amounts of SP345. A combination of micro- and nano-sized filler particles was selected to model dual-filled composite systems commonly found in commercial products. The resulting composite series had a total filler content of 55 %, 60 %, 65 %, 70 %, and 75 % by mass.

Model cavities were prepared by assembling a polymethyl methacrylate (PMMA) tube (inner diameter = 4.8 mm, height = 3 mm) with a PMMA base of the same outer diameter (Fig. 1A). For all samples, the cavity surface was sandblasted with 50 μm alumina for 15 s followed by 50 μm silica for 15 s. Fiduciary markers (glass beads, diameter 125 μm to 150 μm) were embedded into the PMMA sample holders.

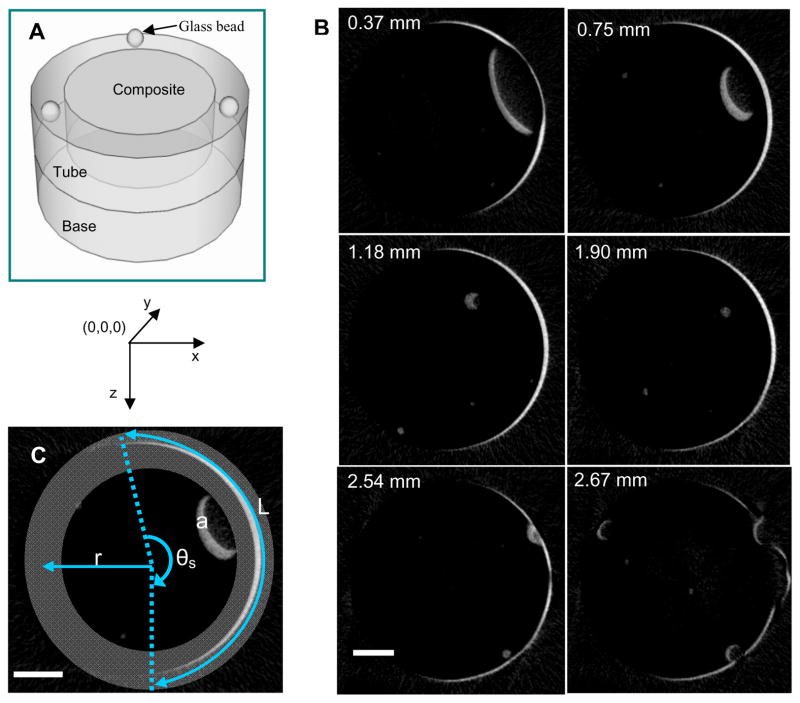
Figure 1.

A: 3D schematic diagram of the model cavity that was assembled and packed with composite paste. Three glass beads were embedded into the top of the tube as fiduciary markers. B: Representative x-y images showing potential leakage (white areas, determined by subtracting the post-polymerization μCT images from the pre-polymerization μCT images) as a function of depth (in mm) for a 55 % filler composite. Scale bar = 1 mm. C: A depiction of the analysis performed by the MATLAB program, where r = cavity radius; θ_s = the summed scan angle; and L = arc length of potential leakage at the composite-cavity wall interface. Region “a” indicates a volume change that was outside of the gray zone and therefore excluded from analysis. Scale bar = 1 mm.

2.3. Viscosity

The viscosity of the five composite pastes was measured using an ARES rheometer (TA Instruments) in the parallel plate configuration (diameter = 19 mm). A nominal gap of 1 mm was used. Dynamic frequency sweep was used to measure the rheological response of composite pastes as a function of frequency (from 0.1 rad/s to 100 rad/s) at room temperature using 10 % strain. The standard uncertainty associated with the rheology measurements is 5 %.

2.4. X-ray microcomputed tomography

A microcomputed tomography scanner (Scanco USA, Inc. Southeaster, PA) was used to image the samples. The micro-focus X-ray source was set at 75 kVp and 114 μA, and the samples were scanned using an 18 μm line resolution with an integration time of 300 s. Composite pastes were filled into the model cavities and covered with a transparent film to reduce oxygen inhibition. The samples were fixed upright using glue at marked positions in the μCT sample holder and scanned. The composites were then irradiated from 1 mm above the top of the composite for 60 s using a 600 mW/cm² Spectrum 200R (Dentsply Caulk) quartz tungsten halogen curing light equipped with an 8 mm 60° light guide. A second μCT scan was performed 60 min after irradiation, enough time to allow the sample to reach its final shrinkage value. 3D images were reconstructed and analyzed using the manufacturer’s complete imaging and evaluation software and ImageJ analysis software. The shrinkage was calculated using procedures described previously[16], which were based on the volume change evaluated using μCT: shrinkage = (V₁ − V₂)/V₁, where V₁ and V₂ were the volume of uncured and cured composite, respectively. Calculated shrinkage is reported as the average of three samples. The standard uncertainty associated with the μCT measurements is 5 %.

2.5. Leakage quantification using ImageJ software and MATLAB

ImageJ software (version 1.39) was downloaded from the National Institutes of Health (NIH) website. Stacks of 2D images of composites before and after polymerization obtained using μCT were imported into ImageJ. Image properties were verified and the dimensions of the images were set according to the voxel size of the μCT data. The post-polymerization 2D images were subtracted from the pre-polymerization images, and the locations of volume changes between the image stacks predicted possible regions of leakage. A macro was written in MATLAB (version 7.3.0.267, R2006b, the Mathworks, Inc.) to quantify the potential leakage area and volume change at the interface between the cavity wall and the composite.

2.6. Dye penetration

After μCT evaluation of the polymerized composites, samples were immersed in a silver nitrate solution (1 % by mass) for 1 h and then exposed to natural light for 1 day. The deposition of silver particles was recorded by taking digital images.

2.7. FTIR microspectroscopy

FTIR microspectroscopy analyses were performed using a Nicolet Magna-IR 550 FTIR spectrophotometer interfaced with a Nic-Plan IR microscope operated in reflectance mode (FTIR-RM). The microscope was equipped with a video camera, a liquid nitrogen-cooled mercury cadmium telluride (MCT) detector and a computer-controlled x-y translation stage. A total of 64 scans were collected from 650 cm⁻¹ to 4000 cm⁻¹ at 8 cm⁻¹ resolution with a beam spot size of 90 μm × 90 μm. Composites were packed into PMMA tubes, sandwiched between 2 glass cover slips, and cured for 60 s. FTIR-RM spectra were obtained from both the top (closest to the curing light) and bottom surfaces at 1 h and 24 h after curing. Each spot was manually focused before data collection. The reflectance spectra were proportioned against a background of an aluminum mirror and transformed to absorbance spectra using the Kramers-Kronig transform algorithm for dispersion correction, which converts the reflectance spectra to absorbance-like spectra[20;21]. The degree of conversion (DC) was calculated as the reduction in the methacrylate peak (1634 cm⁻¹) height using the phenyl absorbance peak (1610 cm⁻¹) as an internal standard. The results are an average of five measurements, and the standard uncertainty associated with the FTIR measurements is 5 %.

2.8. Shrinkage strain-rate and stress

A tensometer[18;19] was used to measure the shrinkage strain-rate and stress during polymerization. Samples confined between two glass rods (diameter = 6 mm) were cured for 60 s using an 800 mW/cm² Spectrum 200R (Dentsply Caulk) quartz tungsten halogen curing light. The shrinkage strain was monitored as the displacement of the upper glass rod (percentage of the initial thickness of the specimen), and the shrinkage strain-rate was calculated from the derivative of the shrinkage strain with respect to the time using numerical differentiation. The polymerization stress was calculated according to the strain at 30 min after light irradiation. The standard uncertainty for these measurements is 3 %.

2.9. Statistical analysis

Data (including DC, shrinkage, stress, and potential leaking area) were analyzed using one-way analysis of variance (ANOVA) and Tukey’s test for post hoc analysis, with a 95 % confidence interval indicating significant differences among the composites.

3. Results and Discussion

Herein, we have demonstrated for the first time that leakage can be quantified nondestructively in terms of area and volume at the interface via 3D imaging and image analysis. This new method was applied to characterize shrinkage and leakage for a series of composites reinforced with an increasing amount of filler. Leakage area and volume determined by 3D image analysis was correlated to various material performance parameters, including shrinkage, stress, and processability.

3.1. Quantification of leakage area and volume

Figure 1 illustrates the model cavity, the x-y 2D images obtained from μCT, and the automated leakage analysis procedure. Fig. 1A shows the model cavity assembly and its geometry, where the large well in the center is the cavity for composite filling. Three small holes were drilled into the outer PMMA wall and embedded with glass beads that were used as reference positions for subsequent image alignment. The analysis procedure involved the following steps: 1) Validating proper alignment between stack of images before and after polymerization; 2) Subtracting post-polymerization images from pre-polymerization images to identify locations where the composite volume changed; 3) Converting gray scale images into binary images; and 4) Applying an automated process to identify the leakage area and its magnitude. The details associated with each step are described below.

First, the images obtained before and after polymerization must be aligned and superimposed upon one another in order to conduct proper image analysis with an accurate determination of volume changes. The composite images were aligned using the positions of the embedded reference glass beads, the relative positions of which do not change upon photopolymerization. Voxel positions in each image were defined in the x- and y- coordinates, and the z-axis represented the sample depth. The positions of the reference beads were calculated in terms of their coordinates before and after polymerization. If the position variation was less than 18 μm (the measurement resolution), no image re-alignment was needed. However, if the sample had shifted more than 18 μm during the μCT measurements, the pre- and post-polymerization images would have been translated and rotated using ImageJ until the coordinates of the reference points were identical. For the current study, none of the samples required image alignment.

After image subtraction (step 2) and binary conversion (step 3), the resultant binary images provided the locations of voxels at which a volume change occurred (indicative of debonding, or gaps between the cavity wall and composite, hence potential leakage). Fig. 1B illustrates representative images of x-y slices from μCT taken at different depths (depth in z-axis is given at the top-left corner of each image in Fig. 1B) where potential leakage sites are indicated in white. The locations of volume change are defined as potential leakage under the following assumptions. As the default, the composite is assumed to be in contact with the cavity wall prior to polymerization; thus the outer boundary of the composite paste can be considered as the composite-cavity interface. The cavity wall position is fixed; therefore, the volume loss (white) at the interface indicates gaps between the cavity wall and composite and is noted as a potential leakage site. These 2D results from μCT (Fig. 1B) can be combined into a 3D object for visualization, as we have previously shown[17], or each image can be further analyzed using our new methods to determine the position and magnitude of leakage.

We developed a macro to automate the process for identifying leakage sites (step 4). This macro has the ability to analyze specified locations within the composite. In this study, this macro was designed to examine the cylindrical interface of the cavity wall and composites, where potential leakage areas had been found. One x-y slice from the μCT imaging (taken at a depth of 0.75 mm) is shown to demonstrate the automated process (Fig. 1C), which ran a 360° angle-by-angle line-scan to detect leakage in a predefined zone covering the entire cavity-composite interface. The origin of the scan was the center of the composite at the top surface. The composite-cavity wall interface was ≈ 2.4 mm from the scan origin for the cavity geometry studied. Since some samples were mounted slightly tilted (< 5 degrees), the actual interfaces fell in a wider range. To account for the sample tilt, the predefined zone was widened to ensure that the potential leakage interface at all depths was within the zone (gray zone in Fig. 1C). The inner and outer radii of this gray zone were 2.04 mm and 2.76 mm, respectively. For counting purposes, only signals that met the following two criteria were recorded as potential leakage. First, signals had to be continuous (≥ 2 voxels); second, the signal position must fall within the gray zone. The first criterion reduced noise and removed questionable gaps that were smaller than or equal to the instrument resolution. The second criterion eliminated the volume changes that were not at the interface. As an example, the region labeled “a” in Fig. 1C indicates a volume change in the center of the composite that was excluded from the counting process. Signals (white voxels) that met both criteria were then further quantified by the macro as a function of scan angle, θ = 1 to 360. The total number of scan angles that encompassed potential leakage in a given image was defined as the summed scan angle (θ_s) and was used to represent the magnitude of leakage area in this image. The automated program read and analyzed each image, and the results were written into two data files. One file recorded sample depth (image number), scan angle, and number of white voxels (indicating potential leakage) at each θ. Results from this file were used to generate 2D leakage maps that showed the position of leakage as a function of depth and scan angle (Fig. 2B). The second file listed image number, θ_s, and the total number of voxels attributed to leakage for each image, from which the leakage area and volume at the interface were calculated.

Figure 2.

Leakage results from the MATLAB program and dye penetration on the same sample (55 % filler content). A: Dye penetration results of the same sample from two angles show the leaking regions as brown areas that are deposits of silver particles. B: A 2D leakage map generated using the output from the MATLAB program. The yellow color illustrates the background, which is the interface of the composite and the cavity wall, and the red color indicates regions of potential leaking. This map successfully captures the curvature of region “b” in the dye penetration images.

After all images were processed, result files were exported into a spreadsheet for calculations. The arc length (L, Fig. 1C) of gaps at the interface of each x-y image was calculated as L = r * θ_s, where r is the radius of the cavity (2.4 mm). L was then converted into interfacial area by multiplying L and the depth of a single image (0.016 mm). For a given composite sample, the potential leakage area (A_L) at the interface was determined by summing the interfacial areas for all x-y images in the stack. The corresponding potential leakage volume (V_L) at the interface was calculated as the volume of a single voxel multiplied by the sum of the number of all the continuous white voxels in the gray zone of the image stack.

3.2. Validation via dye penetration

The validation of the leakage area obtained using the automated program was performed by comparing results obtained by μCT with those from dye penetration. This comparison was possible due to the use of optically clear model PMMA cavities. Dye penetration images (Fig. 2A) and the corresponding 2D leakage map (Fig. 2B) were compared for the same composite sample. The shape of the 2D leakage map agreed well with the dye penetration results. The curvature of the leakage (denoted as “b”) was successfully captured in the 2D map from the image analysis. We note that while the dye penetration showed only interconnected leakage areas, the image analysis method identified small, scattered volume changes or gaps into which the dye could not penetrate and therefore not detect.

3.3. Degree of conversion and material processability

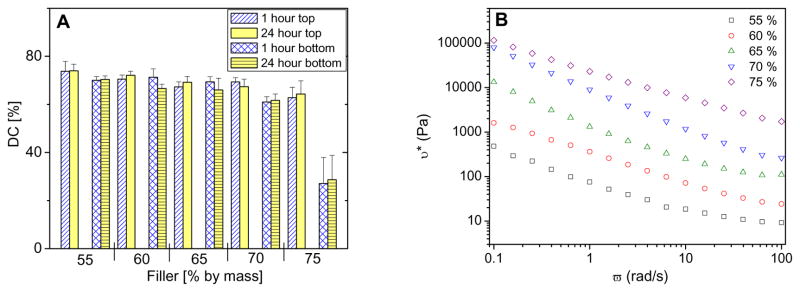
The DC of composites should be comparable in order to obtain meaningful shrinkage and leakage information when evaluating composites placed in cavities. Figure 3A illustrates the DC of the composite series at the top and bottom surfaces, determined by FTIR-RM [22] 1 h and 24 h after irradiation. For composites with filler mass fractions of 55 %, 60 %, and 65 %, DC reached ≈ 70 % regardless of position and time after irradiation. Statistical analysis indicated no significant differences among these composites. The DC of composites with a filler mass fraction of 70 % did not change over time but was lower at the bottom surface as compared to the top surface. Moreover, the DC of composites with 75 % filler (by mass) was significantly lower (p < 0.05) at both the top and the bottom surfaces when compared to the other compositions. The DC of the bottom surface only reached 28 %, likely due to the restricted mobility of the reaction medium and low light transmission at a higher filler content.

Figure 3.

Degree of conversion and material processability. A: Degree of conversion of composites measured using FTIR-RM. Results are an average of five measurements, and error bars represent one standard deviation and are the estimate of standard uncertainty. B: Viscosity of composite pastes as a function of filler content.

The rheology data of composite pastes (Fig. 3B) provided information on viscosity as well as a measure of processability. Results showed that viscosity increased drastically with the addition of more filler. The viscosity increased over 2.5 orders of magnitude in the composition range investigated, indicating the change from relatively more liquid-like properties at lower filler content to a more restricted mobility at higher filler content.

3.4. Relationship between quantified leakage and composite properties

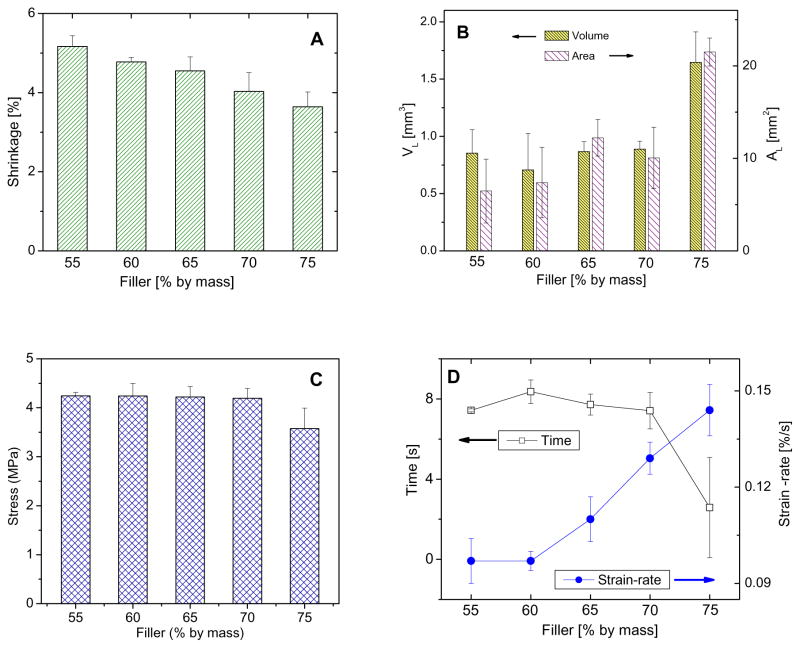
For the first time, leakage has been predicted quantitatively and nondestructively. This quantitative information (A_L and V_L) enriches our ability to understand leakage and its correlation with material performance parameters including processability, shrinkage, stress, and shrinkage strain-rate. As expected, the shrinkage of composites decreased as the filler content increased (Fig. 4A). Fig. 4B illustrates A_L and V_L, representing leakage at the interface only, as a function of filler content. Neither the A_L nor V_L was statistically different (P > 0.05) for composites with 55 % to 70 % filler. However, the 75 % filler composite had a significantly higher A_L and V_L compared to the other compositions. As shrinkage occurs at the top and bottom surface as well as the cylindrical interface non-uniformly, a larger total polymerization shrinkage volume does not necessarily result in a greater leakage area or volume at the interface. The composite with 55 % filler had the largest shrinkage but an average leakage, whereas the largest leakage area and volume came from the composites with the least shrinkage, indicating that shrinkage alone does not dictate the magnitude of leakage in this system.

Figure 4.

Relationships between leakage area and composite properties. A: Polymerization shrinkage of composites with varying filler content. B: Potential leakage area (A_L) and corresponding potential leakage volume (V_L) at the interface of composites with varying filler content. C: Stress in composites as a result of photopolymerization. D: Maximum shrinkage strain-rate and time to reach this maximum value. Lines are drawn to aid the readers’ eyes. Error bars represent one standard deviation and are the estimate of standard uncertainty.

Stress was also studied to understand its correlation with leakage quantification. Stress induced by polymerization shrinkage has been considered to be one of the most important factors leading to interfacial failure. Except for the composite with 75 % filler, total stress generated by polymerization determined by tensometer did not differ significantly (Fig. 4C, p > 0.05). This is reasonable because stress is proportional to shrinkage and modulus. In the current system, the shrinkage decreased but the modulus increased as the filler content was increased. The competing factors of shrinkage and modulus resulted in minimal changes in stress as the filler content increased. Moreover, the polymerization stress data agree well with A_L and V_L for 55 % to 70 % filled composites. But the stress data alone were not sufficient to explain the large A_L and V_L of the composite with 75 % filler content, indicating that other factors affect leakage behavior for this composition.

Besides the total shrinkage and stress development upon polymerization, the large A_L and V_L observed in the 75 % filler composite are likely related to the poor processability, poor initial wetting of the composite paste to the cavity wall, and possibly to the increased shrinkage strain-rate, all of which are results of the increased filler content. Fig. 4D shows the maximum shrinkage strain-rates of each composite and the time needed to achieve this maximum rate of polymerization strain development. Composites with 75 % filler content had a substantially larger maximum shrinkage strain-rate and a shorter time to reach the maximum value as compared to the other compositions. This high shrinkage strain-rate and low mobility may in part account for the high A_L and V_L of the 75 % filler composite.

Polymerization is believed to proceed in two stages, i.e., pre-gelation and post-gelation[2]. At the earlier stage, flow may occur to allow chain rearrangement and alleviate stress; beyond the gel point, chains are “locked” in place and stress develops. The composites with higher filler content have a higher initial viscosity and lower mobility, and reach the gel point faster in the presence of the reactive silane modified fillers. The composite with 75 % filler (by mass) reached its maximum shrinkage strain-rate earlier than the other compositions. Although an increased filler content tends to improve the integrity and performance of the composites, the processability decreases when the filler content becomes too high. In addition to the poor processability, the high shrinkage strain-rate may also contribute to the large leakage at the interface even at a low DC.

4. Conclusions

X-ray microcomputed tomography effectively determined the volume and position of polymeric dental composites in model cavities before and after polymerization, from which polymerization shrinkage and potential leakage area were determined. An automated program was written to quantitatively determine, for the first time, the potential leakage area as indicated by post-polymerization gap formation between the composite and cavity wall. The locations of leakage predicted by the image analysis agreed well with actual leakage sites obtained by dye penetration. Multiple material performance parameters, including processability, polymerization shrinkage, polymerization stress, and shrinkage strain-rate were correlated with leakage area and volume. The magnitude of leakage correlated well with polymerization stress, providing validation to the common approach of utilizing stress to predict the durability at the tooth-composite interface. The addition of excess filler content rendered the composite paste difficult to handle, reduced the overall degree of conversion, and resulted in significantly more leakage, possibly due to poor initial wetting and rapid development of shrinkage strain upon polymerization. Finally, advantages of the methods presented here include the ability to characterize potential leakage area and volume at the composite-cavity wall interface quantitatively and nondestructively, which offers valuable information for optimizing composites while at the same time permitting further evaluation on the intact, unaltered samples.