Checking hazard regression models using pseudo-observations

SUMMARY

Graphical methods for model diagnostics are an essential part of the model fitting procedure. However, in survival analysis, the plotting is always hampered by the presence of censoring. Although model specific solutions do exist and are commonly used, we present a more general approach that covers all the models using the same framework. The pseudo-observations enable us to calculate residuals for each individual at each time point regardless of censoring and provide methods for simultaneously checking all the assumptions of both the Cox and the additive model. We introduce methods for single as well as multiple covariate cases and complement them with corresponding goodness-of-fit tests. The methods are illustrated on simulated as well as real data examples. Copyright © 2008 John Wiley & Sons, Ltd.

1. INTRODUCTION

Hazard regression models provide a convenient way of specifying how covariates affect the survival time distribution. Typical examples include the multiplicative Cox proportional hazards model [1] or the additive hazard model of Lin and Ying [2]. In the former, the hazard function α(t|Z), for given covariates Z, is specified as

$$\alpha (t|Z)={\alpha }_0(t){\mathrm{e}}^{{\beta }^{\mathrm{T}}Z}$$ (1)

while, in the latter, it is given as

$$\alpha (t|Z)={\alpha }_0(t){+}^{{\beta }^{\mathrm{T}}Z}$$ (2)

In both (1) and (2), β is a p-vector of regression coefficients and α₀(t) an unspecified baseline hazard for Z = 0. The choice of the model depends on the data in hand and for that purpose a graphical evaluation of the data can be very helpful. There exists an abundance of methods for plotting in the framework of the classical regression analysis, mainly for quantitative outcomes, but also for categorical data. The plotting of survival data, however, is hindered by its main discerning property, i.e. the presence of censored observations. In the case of right censoring, for example, the survival time of a censored individual will only be known to be greater than a certain value, and therefore, plots mimicking those from the classical regression analysis can be misleading. Instead of plotting individual values, the standard graphical methods for survival data focus on describing the group experience, with the Kaplan–Meier estimate of the survival function S(t)=pr(X>t) being the prime example of such practice. On the other hand, any more specific methods [3–7], providing insight into a particular method fit, are tied to the model specific way of tackling the censoring problems.

In this paper, we explain how assumptions of the different models can be checked within a common framework using pseudo-observations, as introduced for regression modelling in event-history analysis by Andersen et al. [8] and discussed for the analysis of the survival curve in a single point by Klein et al. [9]. For a sample of size n, the pseudo-observation for the survival indicator I(X_i>t), where i is the index running through the individuals, is defined as

$$S_i(t):=n\widehat{S}(t)-(n-1){\widehat{S}}_{-i}(t),t\ge 0$$ (3)

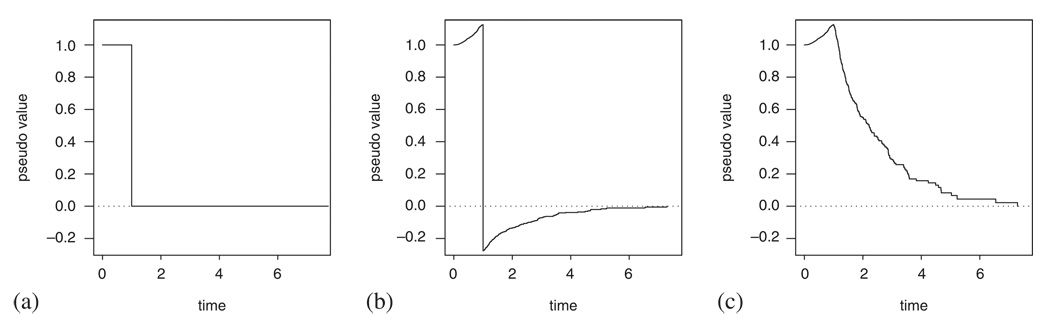
In (3) Ŝ denotes the Kaplan–Meier estimate based on the whole sample and Ŝ_−i denotes the Kaplan–Meier estimate computed by having left out the i th individual (i.e. using n– 1 individuals). In the case of no censoring, this definition simply leaves us with the survival experience of the individual i: S_i (t) = I(X_i>t) is equal to 1 while the subject is still alive and drops down to 0 when he dies (see Figure 1(a)). When censoring is present, the pseudo-observations are still defined for all individuals and at all times; examples for two individuals are given in Figure 1(b) and (c). As the Kaplan–Meier estimates in (3) only change at event times and are constant in between, and the same is true for the pseudo-observations. Therefore, the jump in Figure 1(b) occurs at the time of death and the turning point for the step function in Figure 1(c) is the last event time before censoring.

Figure 1.

The pseudo-observations in time. (a) The pseudo-observations for an individual with X_i=1 in a data set with no censoring; (b) the pseudo-observations for an individual from a censored data set, who experienced an event at time X_i=1; and (c) the pseudo-observations for an individual, censored just after X_i=1.

Without censoring, I (X_i>t) is observed for all combinations of i and t and techniques for binary data [10] could be applied for checking the assumptions of a model for the relation between the survival function P(X_i>t)=EI(X_i>t) and covariates Z_i, e.g. a model specified via the hazard function for X_i. With censoring, I(X_i>t) is not always observed and the idea is then to replace I(X_i>t) by the pseudo-observation S_i(t) given by (3). This makes sense as, on the one hand, the Kaplan–Meier estimator may be written as [11]

$$\widehat{S}(t)=\frac{1}{n}{\displaystyle \sum _{i=1}^n{S}_i(t)}$$ (4)

for t<τ, the last event time, and, on the other hand, when censoring does not depend on covariates

$$E(S_i(t))=EI(X_i>t)$$ (5)

see [8]. Note also that, although individual pseudo-observations do take on quite unusual values and may fall well out of the (0,1) range (see Figure 1), equation (5) implies that they have the right expectation; therefore, we can expect that with smoothing the range problems will become less pronounced.

In this way, by having calculated the pseudo-observations, the main problem of survival analysis, i.e. not having values defined for all cases, is eliminated right at the starting point, and the rest of the graphical analysis can be performed using the same logic regardless of the model in mind.

The purpose of the paper is to review goodness-of-fit examinations for hazard regression models using pseudo-observations and to compare such methods with existing techniques, mostly those for the Cox regression model. This paper is organized as follows: in Section 2, we define pseudo-residuals and illustrate their usefulness for the purpose of initial graphical diagnostics. Section 3 introduces a scatterplot providing a non-parametric estimate of the survival function conditional on a single quantitative covariate and investigates the transformations of this function that help in checking the goodness-of-fit of a chosen model. Section 4 considers the multiple regression setting and proposes corrections that must be applied to discern the effect of the covariate of interest. Any graphical analysis can also be supplemented using formal testing; we describe these methods in Section 5. Some practical considerations are given in Section 6 and a real data example is studied using the proposed methods in Section 7 before the paper is concluded in Section 8.

2. PSEUDO-RESIDUALS

The pseudo-observations are defined for each individual and at each time point and can therefore be used to construct residuals analogous to the residuals in a general linear model: the outcome, in our case S_i(t), is compared with the predicted value for this outcome based on the model, we denote this by Ŝ(t|Zi). A raw residual can, therefore, be defined as S_i(t)−Ŝ(t|Zi). We propose to use

$${\widehat{\epsilon }}_i(t):=\frac{S_i(t)-\widehat{S}(t|Z_i)}{\sqrt{\widehat{S}(t|Z_i)[1-\widehat{S}(t|Z_i)]}}$$

where the raw residual is divided by an estimate of what would be the standard error of S_i (t) without censoring. We shall use these residuals as a graphical diagnostic tool of a model fit. In both, the Cox (1) and the additive model (2), two assumptions are made. The coefficient β is assumed to be constant in time (the proportional hazards assumption in the Cox model and the constant hazards difference assumption in the additive model) and the covariate effect is assumed to be linear. If the model fits the data well, no trends should be seen in the residuals when we plot them with respect to a covariate (or the linear predictor) at any point of time. On the other hand, when the assumptions of the model are not met, we would like to get some insight into the type of departures. We can expect a nonlinear effect of the covariate (we use g(Z) to denote a more general form of the covariate effect) to result in a certain trend when plotting the residuals with respect to a covariate. On the other hand, the effect of changing β in time (we will use the notation β(t) to stress that it might change in time) should be seen in the changes of this trend from time point to time point. In practice, we shall plot the residuals with respect to the covariate at only a few chosen time points; here, we choose four (corresponding to 20th, 40th, 60th and 80th percentile of event times). To make it possible to detect the trends, we shall add a curve representing the smooth average through the residuals.

As an illustration of what we can expect to see, we simulate two data sets following the Cox and the additive model, respectively, and then compare it with three different situations, where the assumptions of the models are violated:

1. the data follow model (1) or (2) with β(t)=δ for t<τ₁ and changing to β(t)=−δ for t≥τ₁, the effect of Z is linear;

2. the data follow either of the models with a quadratic effect of the covariate Z, i.e. g(Z) = Z², the coefficient β is constant in time;

3. both violations are incorporated simultaneously, β(t) and g(Z), as given in the previous two situations.

For simplicity, only one covariate was used in these simulations, it was taken to be uniformly distributed, Z₁ ~ Uni f [−1,1]. The δ was taken to be equal to 2 in the Cox model case and taken to be equal to exp(2) in the additive model case in order to make the effects on the survival scale similar. The change point τ₁ for β was set at the expected 45th percentile of the event times, so that we should see no changes between the first two time points and some effect later on. Note that we can expect the fitted coefficient to be close to 0 for all the three situations. The sample size used was n = 1000 and the censoring was exponentially distributed with the parameter set to give 25 per cent of censored cases. The baseline hazard α₀(t) was constant in time.

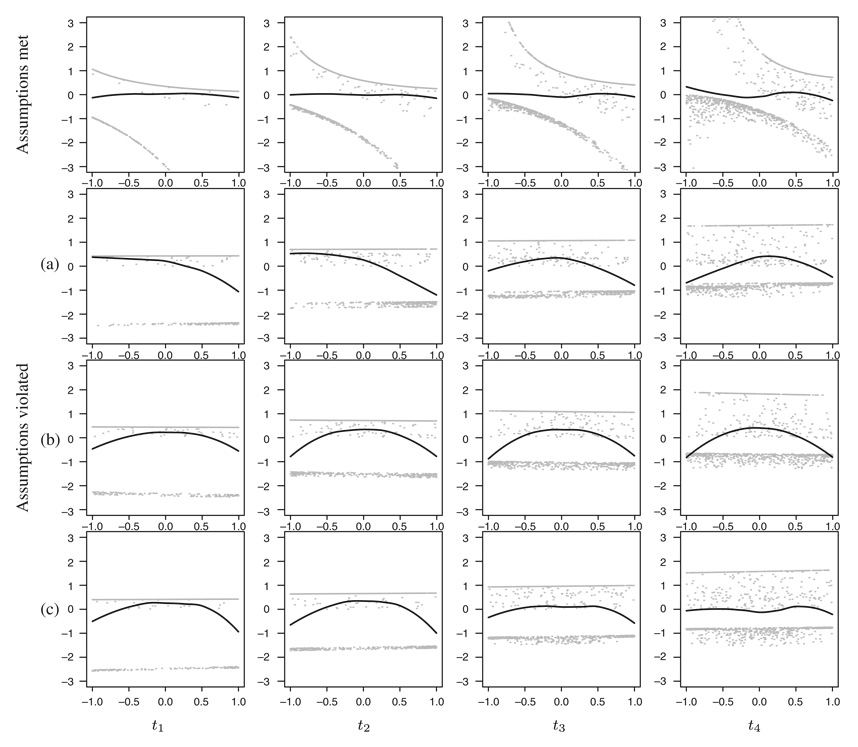
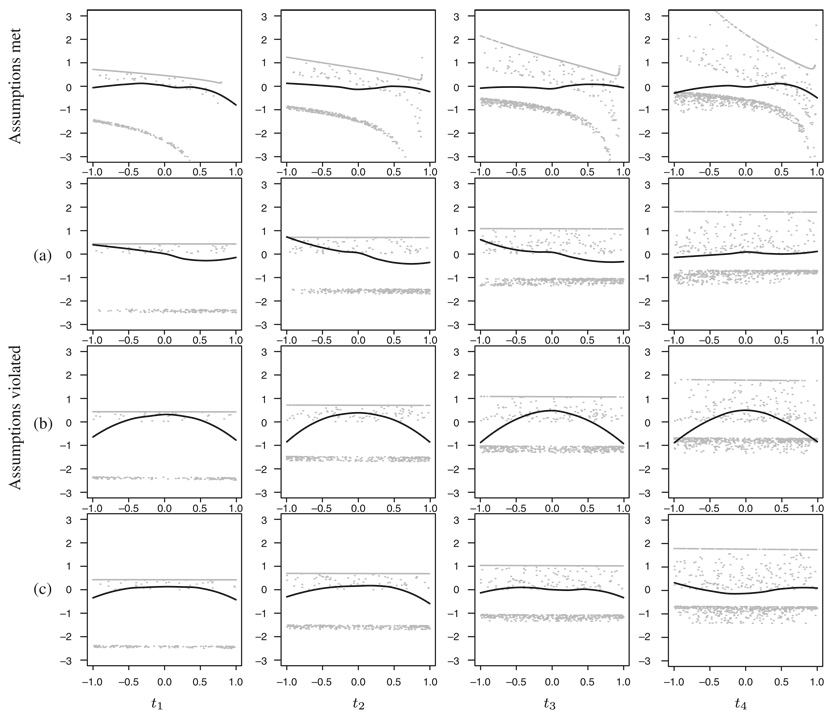
The results are presented in Figure 2 and Figure 3. The residuals (grey points) tend to fall in three different groups. The top group belongs to the individuals that are still at risk. As the pseudo-observations for these individuals at a fixed time are equal (and increase with time, see Figure 1(b)), their residual values seem to form a horizontal line in the rows 2–4, where the predicted values are also very similar for all the individuals (coefficient close to 0). The group of residual values in the middle belongs to the censored individuals—as their pseudo-observations are positive (see Figure 1(c)), their residual values can only be larger than the values corresponding to failures (bottom group), whose pseudo-observations are negative.

Figure 2.

The smoothed average (black curves) through standardized residuals (grey points) with respect to covariate Z evaluated at four different time points: t₁=20th, t₂=40th, t₃=60th and t₄=80th quantile of event times. The four rows of plots represent four different simulated data sets, see text. The data were simulated and fitted using the Cox model

Figure 3.

The smoothed average (black curves) through standardized residuals (grey points) with respect to covariate Z evaluated at four different time points: t₁=20th, t₂=40th, t₃=60th and t₄=80th quantile of event times. The four rows of plots represent four different simulated data sets, see text. The data were simulated and fitted using the additive model.

As so many points are overlapping, it is impossible to judge the trends by looking at the residuals alone; therefore, we focus on their smoothed averages (black curves). In the highest row of the plots, where the same model was used for simulating and fitting the data, no trends can be observed—the four curves all seem to be rather horizontal. In situation (a) the shape of the curves differs in time, and in situation (b), the quadratic effect of the covariate is clearly seen. The curve in (c) implies nonlinearity and changes in time; however, the effect seems somehow less pronounced.

To conclude, the plots seem to give a good initial illustration of the model fit, but the effect may need to be rather large to be observed. Furthermore, as particular deviations from a given model may be difficult to disentangle from graphs in the survival probability scale, it may be advantageous to transform to the assumed scale of the linear predictor. We shall return to the problem of model diagnostics in that scale in the following sections.

3. SCATTERPLOTS FOR A SINGLE COVARIATE

For both quantitative and binary outcome variables, Y_i, a scatterplot of Y_i versus a covariate, Z_i, is very useful for assessment of how E(Y_i|Z_i) varies with Z_i. For binary outcomes, superposition of a scatterplot smoother to such a plot is essential and in order to assess a given link function, such as the logistic link, a transformation of the smooth curve using the corresponding link is usually performed.

For survival data we will introduce a similar scatterplot of the pseudo-observations, S_i(t) versus a covariate Z_i (and versus t) to study how the survival probability S(t|Z_i) = E(I(X_i>t)|Z_i) varies with Z_i.

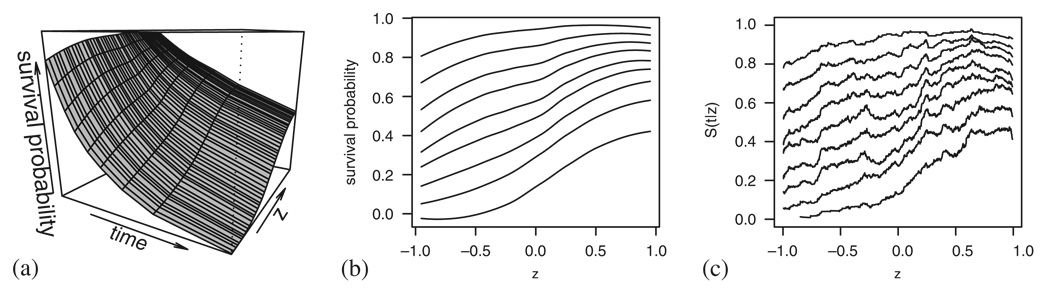
As an illustration we consider again a data set following the Cox model, simulated as described in the previous section (uniform covariate, β=−1). Calculating the pseudo-observations and smoothing them with respect to time and a chosen covariate results in the plot presented in Figure 4(a). As the three-dimensional plots are usually hard to read, we propose that instead only the profile curves, representing S(t_k|Z) at some chosen time points t_k, are plotted against the covariate Z, see Figure 4(b).

Figure 4.

A simulated example with a negative effect (β=−1) of the covariate Z: (a) the pseudo-observations smoothed in time and covariate; (b) the profile curves representing S(t_k|Z) at chosen percentiles of event times; and (c) the profile curves calculated using the Beran estimator.

A plot providing similar information can be attempted using the Beran [12] estimator that calculates a Kaplan–Meier estimate of groups of individuals defined by the nearest neighbours with respect to the covariate. An example is given in Figure 4(c), the neighbourhood for each individual is set to be 10 per cent of the closest values of Z₁ in each direction. The curves are evaluated at each distinct value of Z₁ and can be smoothed if a less jagged impression is preferred. The plots in Figure 4(b) and (c) are very similar, but as the pseudo-observations enable us to have an outcome defined for each individual regardless of the covariate values, we can also use them to derive individual residuals as exemplified in Section 2 and for regression purposes, which is worked out in Section 5.

Turning to checking model specific assumptions, we first consider the Cox model (1). The survival function given the covariates, i.e. S(t|Z)=pr(T>t|Z), equals

$$S(t|Z)={\mathrm{e}}^{-A_0(t)\text{exp}(\beta Z)}$$

Hence, a cloglog transformation of the survival function results in an expression that is linear in the covariates:

$$\text{log}(-\text{log}S(t|Z))=\text{log}{A}_0(t)+\beta Z$$ (6)

This implies that in the single covariate case (p=1), the cloglog transformed estimate of S(t|Z) plotted with respect to Z provides a simple diagnostic tool for checking the Cox model assumptions: if the data follow the Cox model, the resulting profile curves at chosen time points should be parallel straight lines with the slope β. The A₀ term in (6) denotes the cumulative baseline hazard function, $A_0(t)={\displaystyle {\int }_0^t{\alpha }_0(u)}\mathrm{d}u$. As this is a monotonically increasing function of time, the intercept of each next chosen time point is expected to be higher. Figure 5 illustrates two examples, one with no effect of the covariate (a) and the other with an effect of β=−1 (b).

Figure 5.

Two simulated examples following the Cox model with (a) β=0 and (b) β=−1.

The survival function corresponding to the additive hazard model (2) is given by

$$S(t|Z)={\mathrm{e}}^{-[A_0(t)+\beta Zt]}$$

and an expression that is linear in the covariate can be obtained by the logarithmic transformation:

$$\frac{-\text{log}S(t|Z)}{t}=\frac{A_0(t)}{t}+\beta Z$$ (7)

Therefore, the plotting procedure we propose for checking the additive model is to smooth the pseudo-observations, transform them with the logarithm and plot them at chosen time points divided by those chosen time values. If the data follow the additive model this should, as in the Cox model case, result in parallel lines with the slope β. Two examples of data following the additive model, with no effect (β=0) and with a constant negative effect (β=−1), are given in Figure 6(a) and (b), respectively. The reason the lines are now not separated as in the Cox model, but rather overlapping, lies in the different intercept form in (7). The value of A₀(t)/t is not bound to increase with time, but can vary in any direction. In our simulated examples, where the baseline hazard α₀(t) is constant in time, the intercepts are the same for all the time points.

Figure 6.

Data following the additive model with (a) β=0 and (b) β=−1.

If the coefficient β in (6) or (7) changes in time, the slope of the lines can be expected to differ. On the other hand, if the covariate Z is replaced by a more general function g(Z), we shall see curves instead of straight lines.

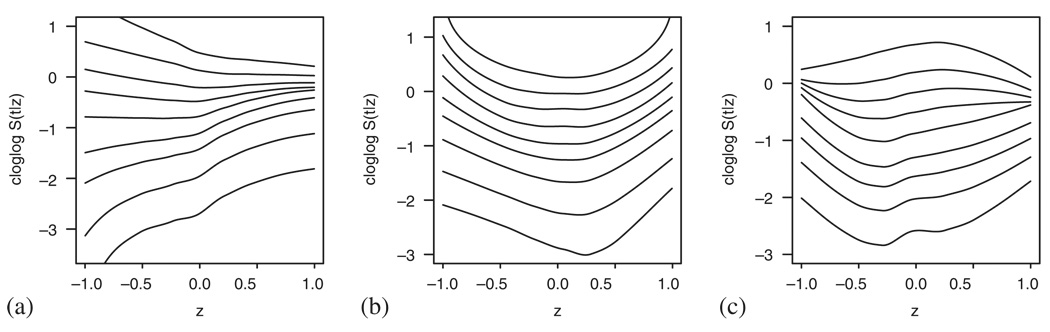
To illustrate the results we are likely to get when the assumptions of either of the models are violated, we simulate the data following the same three situations (a)–(c) described in Section 2, but let the coefficient size be smaller, i.e. δ is equal to 1 in the Cox model case and exp(1) in the additive model case.

Figure 7 and Figure 8 present the results. In situation (a) the curves seem rather straight, but the slope changes in an obvious way thus implying that the effect is linear but changing in time. On the other hand, the curved shape in Figure 7(b) and Figure 8(b) clearly implies the quadratic effect of the covariate that remains the same throughout the time interval. In the last situation (c), the curves again show a positive quadratic effect at the early time points, but we also observe how this effect changes in time and finally becomes negative.

Figure 7.

Examples of violated Cox model assumptions: (a) non-constant β(t); (b) nonlinearity in Z; and (c) nonlinearity in Z and non-constant β(t).

Figure 8.

Examples of violated additive model assumptions: (a) non-constant β(t); (b) nonlinearity in Z; and (c) nonlinearity in Z and non-constant β(t).

The standard methods for checking the Cox model assumptions include Schoenfeld [3] and martingale residuals [4]. Although plotting the smoothed average of the Schoenfeld residuals in time results in a curve that follows the behaviour of β(t) in time, the martingale residuals plotted against the covariate Z give an idea about its true functional form. Either of the methods assumes the other assumption to be met and might be misleading when the opposite is true. To get an idea whether the trends seen in the curves are important, one can add a plot of cumulative sums of these residuals together with some simulated residual patterns [13].

As an example, we look at the same three situations (a)–(c), using the existing functions in R [14] when available (packages survival and timereg). Figure 9(a) illustrates well how β(t) in situation (a) changes in time and Figure 11(b) follows well the true form of the covariate effect. On the other hand, the coefficient in Figure 9(b) seems to stay constant in time, which is in tune with (b), where only nonlinearity is violated, and we could argue similarly in Figure 11(a). However, in situation (c), both the Schoenfeld residuals diagnostics (Figure 9(c)) and the martingale residuals (11c) are misleading. As the best linear fit for the quadratic curve is close to 0 regardless of the true parameter value for the quadratic effect, the Schoenfeld residuals are unable to detect the violations of the assumptions, a similar argument holds also for the martingale residuals case. This is also confirmed on Figure 10; we can see that while the trend is obvious in situation (a), the violations cannot be noticed in situations (b) and (c).

Figure 9.

Examples of violated Cox model assumptions in situations (a)–(c), explored using the Schoenfeld residuals.

Figure 11.

Examples of violated Cox model assumptions in situations (a)–(c), explored using the martingale residuals.

Figure 10.

Examples of violated Cox model assumptions in situations (a)–(c), explored using the supremum-type test with cumulative sums of Schoenfeld residuals.

A method that allows for checking both assumptions simultaneously was introduced by Sasieni and Winnett [5]. They propose using martingale difference residuals, and we use this approach to explore the three situations in Figure 12. Apart from not being bound to having different intercepts, the resulting curves are very similar to those in Figure 7 and the interpretation is the same for both methods in all the presented situations.

Figure 12.

Examples of violated Cox model assumptions in situations (a)–(c), explored using the martingale difference residuals.

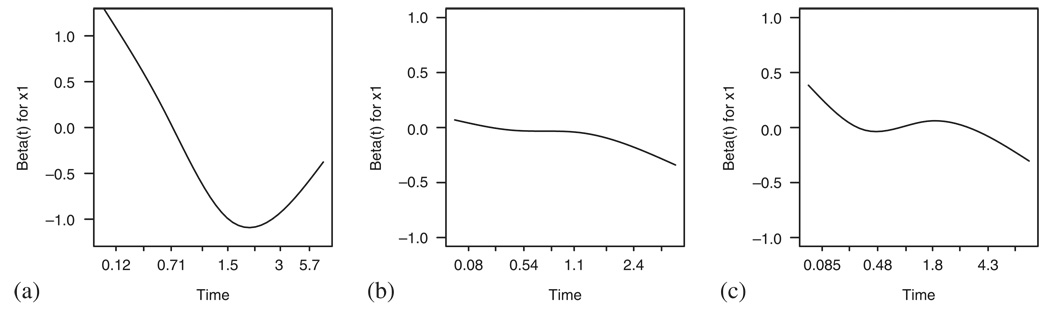
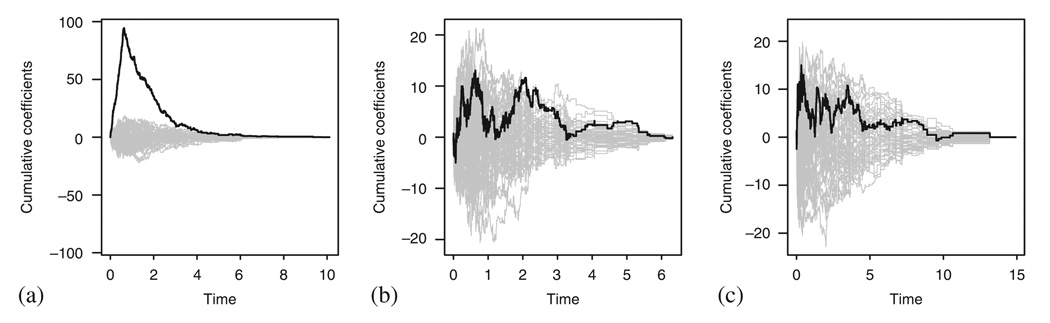
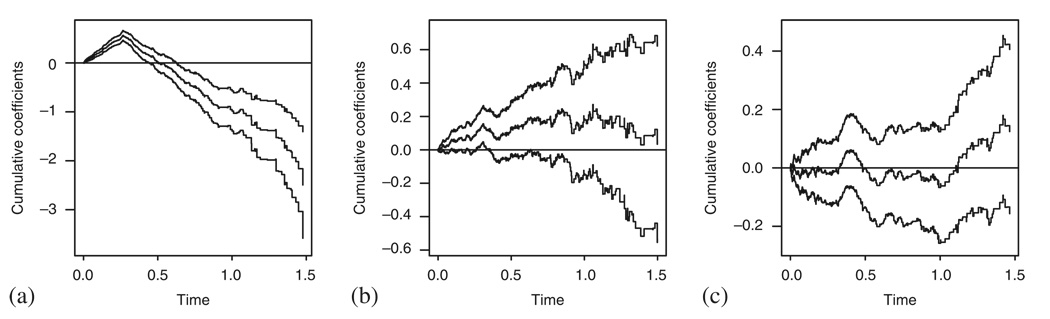
No similar methods are available in the additive model case. However, fitting the non-parametric version of the model and plotting the cumulative B(t)=∫ β(u)du in time can give us a reasonable insight into the constant β(t) assumption [6] provided that the covariate is linear, see Figure 13. Furthermore, using the cumulative martingale residuals, we can check the linearity of the covariate effect [7], Figure 14 presents the results. We can see that the observed cumulative residuals in Figure 14(b) fall out of the area implied by the 50 random realizations of the model and therefore signal problems with the linearity of the covariate effect, although they behave within limits in situation (a). However, in situation (c), where both assumptions fail simultaneously, the plot does not seem to give indications of problems as it should.

Figure 13.

The cumulative coefficient B(t) in the additive model for the situations studied in Figure 8.

Figure 14.

The tests of the linear covariate effect for the situations studied in Figure 8.

To conclude, in the Cox model case, the plots using pseudo-observations can provide us with the same information as the more standard methods using Schoenfeld or martingale residuals.

As it checks for both assumptions simultaneously, this method is more general and the results compare closely with those given by the martingale difference residuals plots. The main advantage of using the pseudo-observations is their generality—we can use the same idea also for checking the additive or any other hazard regression model by specifying a different link function.

However, all of the above only holds in the single covariate case, the case of more covariates is explored in the following section.

4. SCATTERPLOTS FOR MULTIPLE COVARIATES

Let the survival probability be affected by covariates Z₁,…,Z_p, where p>1, and say we are still interested in the effect of the Z₁ covariate. Without loss of generality, let p=2. Ordering in the Z₁ direction and smoothing with respect to Z₁ give a non-parametric estimator of S(t|Z₁)

$$S(t|Z_1)={\displaystyle \int S(t{|Z}_1,Z_2)f(Z_2{|Z}_1)\mathrm{d}{Z}_2}$$

where f(.) denotes the covariate density. In the additive model case with two independent covariates, i.e. f (Z₂|Z₁)=f (Z₂), the term containing Z₁ can be taken out of the integral unaffected by Z₂.

$$\begin{array}{cc}{\displaystyle \int {\mathrm{e}}^{-[A_0(t)+t{\beta }_1{Z}_1+t{\beta }_2{Z}_2]}f(Z_2)\mathrm{d}{Z}_2}\hfill & ={\mathrm{e}}^{-t{\beta }_1{Z}_1}{\displaystyle \int {\mathrm{e}}^{-[A_0(t)+t{\beta }_2{Z}_2]}f(Z_2)\mathrm{d}{Z}_2}\hfill \\ \hfill & ={\mathrm{e}}^{-[A_0^{\prime }(t,Z_2)+t{\beta }_1{Z}_1]}\hfill \end{array}$$ (8)

Therefore, ignoring the Z₂ covariate still leaves us with an additive model in Z₁; all that gets affected is the intercept term. The logarithmic transformation can be expected to be linear in Z₁t and the plots described in the previous section still provide a valid insight into the model fit.

However, when covariates in the additive model are dependent, the term f (Z₂|Z₁) also contains Z₁, and the model is no longer bound to be additive when considering Z₁ only, implying that the logarithmic transformation no longer needs to be linear in Z₁t. Furthermore, in the Cox model case, the term containing the covariate Z₁ cannot be extracted in the same form even when the two covariates are independent [15,16].

The profile curves no longer need to be parallel and linear in order for the model to fit well; instead, we have to predict what they should look like if the model is correct. Therefore, we fit the desired model (using all the covariates) to the data and calculate the predicted survival Ŝ based on the estimated parameters. This leaves us with a predicted value for each individual at each event time. We then smooth these values with respect to time and the Z₁ covariate, perform the desired transformation, and plot the resulting curves against Z₁ at chosen values of event times. Although these curves would be parallel lines in the one covariate case, they might take any other form with more covariates present. The final plot is obtained by subtracting these values from the values of the original observed curves. Any remaining effects observed must be due to the violation of the model assumptions. To make the plots more comparable to those of the martingale difference residuals, the β₁Z₁ term can be added to the resulting curves.

This approach is strongly related to standard graphical techniques for linear regression and can, in fact, be adapted quite easily to generalized linear models. In standard linear regression, residuals Y_i – Ê(Y_i|Z_i1, Z_i2) may be plotted against Z_i1 to see whether any structure, e.g. due to mismodelling of the effect of Z_i1, is present. A scatterplot smoother may be added to the plot. A similar graph may be obtained by plotting Y_i versus Z_i1 and smoothing, plotting Ê(Y_i|Z_i1, Z_i2) versus Z_i1 and smoothing and then subtracting the two smoothers. The latter plot is equivalent to what we suggest here (except for the additional difficulty involved with dealing with time, t) and this can be extended to generalized linear models (with links other than the identity) by adding an extra step in the procedure that transforms the smoothed curves by the link function before subtraction.

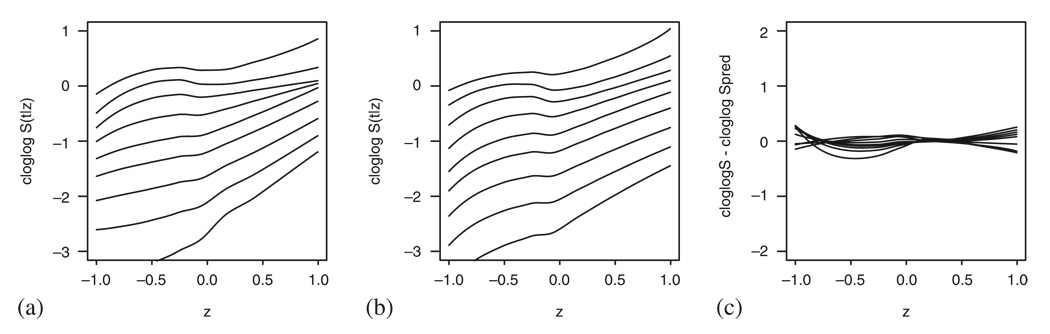
An example of this procedure for the Cox model case is shown in Figure 15. We simulated the data as in previous examples, using a uniformly distributed covariate Z₁ and an additional binary variable Z₂ (Z₂~Bin(0.5)), the coefficients used were β₁=1 and β₂=3. Although the curves in Figure 15(a) correspond to the observed data, Figure 15(b) represents the predicted curves under the model. The difference between the two graphs is given in Figure 15(c).

Figure 15.

Simulated data following the Cox model with two covariates. (a) The cloglog transformed smoothed pseudo-observations; (b) the cloglog transformed smoothed predicted survival (based on the model fit using both covariates); and (c) the remaining effects.

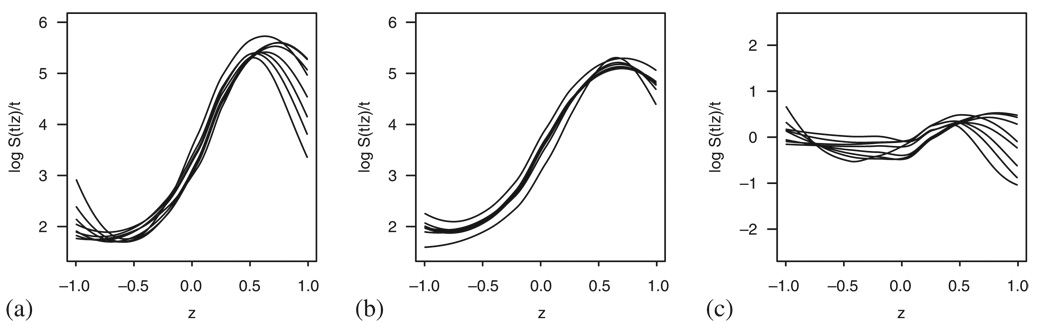
As shown in (8), omitting an independent variable in the additive model presents no problem. As an example for the additive model case, we therefore use the same simulation design as above but let the covariates be dependent with cor(Z₁, Z₂)=0.5. As we can see in Figure 16(b), this causes a nonlinear effect in Z₁. The curves estimated from the observed data (Figure 16(a)) roughly follow the same shape, therefore, no particular effect can be seen in Figure 16(c).

Figure 16.

Simulated data following the additive model with two dependent covariates: (a) the log transformed smoothed pseudo-observations; (b) the log transformed smoothed predicted survival (based on the model fit using both covariates); and (c) the remaining effects.

To conclude, when more than one covariate is suspected to affect survival, the plots described in Section 3 can be insufficient and should be corrected using the predicted values calculated using the desired model. The resulting plots can then be interpreted in the same way as in the previous section.

5. TESTING THE PARAMETERS

All the plotting methods in Section 4 can be supplemented by estimation of the model parameters in (1) or (2). As introduced in [8], this may be done using generalized estimating equation methods modelling

$$\text{log}(-\text{log}E[S_i(t)])=a(t)+\beta Z$$ (9)

and

$$-\text{log}(E[S_i(t)])/t=a(t)+\beta Z$$ (10)

respectively. The purpose of this estimation is not to compete with the standard fitting methods, but rather to obtain parameters that directly correspond to the plotted curves—to this end, the same time points could be chosen for both plotting and fitting.

To get a formal evaluation of the goodness-of-fit supplementing the visual impression implied by the curves, we simply allow more parameters to the model. We study three basic options for testing—we replace the right-hand side of (9) and (10) by

1. a(t)+β(t)Z: By allowing a different coefficient β(t) at each chosen time and testing H₀:β(t₁)=⋯=β(t_k), we are checking the proportional hazards assumption in the Cox model and the constant hazards difference assumption in the additive model case, both under the assumption of linearity. (For simplicity, we refer to this assumption for both models as ‘PH’ in Table I–Table IV.)

2. a(t)+βg(Z): By replacing Z with a more flexible function of the covariate, we can test the linearity assumption assuming proportional hazards or constant hazards difference, respectively. In our examples, we set g(Z₁) to be a restricted cubic spline with three degrees of freedom (i.e. we introduce two new parameters).

3. a(t)+β(t)g(Z): By allowing the functional form of the covariate to be nonlinear and change at each time point, we can test both assumptions simultaneously.

Table I.

Estimated values of β₁ and the p-values for goodness-of-fit tests for a model without and with taking Z₂ into account.

Model	β1	PH assumption	Linearity	Overall
Cox
Z1 only	0.44	<0.01	0.14	<0.01
Z1 and Z2	0.93	0.42	0.81	0.36
Add
Z1 only	2.22	0.34	<0.01	<0.01
Z1 and Z2	1.03	0.91	0.67	0.86

Table IV.

The power of the tests rejecting with the increasing sample size.

		(a)		(b)		(c)
Model	Test	500	1000	500	1000	500	1000
Cox	Linearity (PH assumed)	0.10	0.14	0.98	1.00	0.84	0.98
	PH (linearity assumed)	0.99	1.00	0.12	0.13	0.10	0.10
	Overall	0.98	1.00	0.93	1.00	0.82	0.98
Add	Linearity (PH assumed)	0.05	0.05	0.98	1.00	0.06	0.06
	PH (linearity assumed)	1.00	1.00	0.03	0.04	0.03	0.04
	Overall	0.99	1.00	0.88	1.00	0.63	0.95

As an example, we analyse the data sets presented in Figure 15 and Figure 16. We fit two models for each data set (with and without Z₂) and compare the parameter estimates as well as the p -values for checking the goodness-of-fit assumptions using the three above-described tests (i–iii). The results (evaluated at three time points) are given in Table I. When using both covariates in the model, the estimated coefficient β₁ is close to its true value (β₁=1) and all the tests return high p-values. On the other hand, when the covariate Z₂ is omitted, both the estimate and the goodness of fit are affected.

To investigate the performance of the described tests, we conducted several simulations. First, the size of tests under the null hypothesis was studied. The data were simulated using two covariates following the Cox and the additive model, respectively. In Table II we report the results obtained using either a uniformly (Z₁~Unif[−1,1], β₁=1) or a normally distributed covariate (Z₁~Norm(0,0.5), β₁=1). The covariate Z2 is always simulated as a Bernoulli variable (Z₂~ Ber(0.5), β₂=3) and independent of Z₂. The censoring degree is set to 25 per cent and the baseline hazard is constant, α₀(t)≡1. For each situation 1000 simulation runs were performed.

Table II.

The proportion of tests rejecting under the null hypothesis (nominal size 5 per cent).

		Normal			Uniform
Model	Test	250	500	1000	250	500	1000
Cox	Linearity (PH assumed)	0.07	0.07	0.05	0.05	0.05	0.05
	PH (linearity assumed)	0.06	0.07	0.04	0.05	0.05	0.06
	Overall	0.15	0.12	0.08	0.07	0.04	0.06
Add	Linearity (PH assumed)	0.06	0.06	0.06	0.05	0.04	0.05
	PH (linearity assumed)	0.04	0.04	0.05	0.05	0.04	0.05
	Overall	0.14	0.10	0.08	0.07	0.06	0.05

Although testing for each assumption separately seems to be reliable already at small sample sizes, the size of the overall test (iii) depends not only on the sample size but also on the distribution of the covariates; the more outliers we are likely to get, the larger sample we need for the test to give satisfactory results.

We then considered the performance of the tests, when the assumptions of the two models are violated. In addition to the three situations (a)–(c) described in Section 2, we also look at

• (d) the data that follow the model with two covariates, but Z₂ is omitted when fitting the model;

• (e) the data are simulated to follow the additive model and checked with the Cox model procedure or vice versa.

The Z₁ in all the simulations is uniformly distributed on [−1,1], all the other parameters remain as defined above. The δ in all the situations is set to 1 for the Cox model and to exp(1) in the additive model case. If we used an equal value in both models, this would result in a smaller effect on survival in the additive model, and that would in turn seem as if we had less power in the tests for the additive model case. The results for the sample size 250 are given in Table III. The power is best in situations (a) and (b) that were tailor made for the tests (i) and (ii). As both tests require the other assumption to hold, their power is greater than the power of the overall test. When both violations occur simultaneously (c), the power gets lower. Situations (d) and (e) deal with misspecified models, and the power in such cases is hard to predict. As the two covariates are independent, the power in situation (d) for the additive model must be close to the nominal level of 0.05.

Table III.

The proportion of tests rejecting in the five situations, described in the text.

Model	Test	(a)	(b)	(c)	(d)	(e)
Cox	Linearity (PH assumed)	0.08	0.85	0.43	0.05	0.08
	PH (linearity assumed)	0.96	0.11	0.08	0.29	0.13
	Overall	0.87	0.55	0.45	0.24	0.11
Add	Linearity (PH assumed)	0.06	0.82	0.06	0.06	0.12
	PH (linearity assumed)	0.98	0.03	0.05	0.04	0.84
	Overall	0.92	0.41	0.33	0.06	0.67

The power of any test can of course be expected to increase with the sample size and the size of the covariate effect, situations (a)–(c) are further explored in Table IV. We can see that at sample size 1000 (25 per cent censoring), the power is high also for the overall test.

A somewhat similar general method for testing the goodness of fit for both the Cox and the additive model has been proposed by McKeague and Utikal [17]. They compare the doubly cumulative hazard function (over time and covariate) predicted by each of the models with its non-parametric estimator. They propose formal tests as well as accompanying plots. However, the method is not intended to be informative about the direction of the departures from the model assumptions.

6. SOME PRACTICAL CONSIDERATIONS

When trying out the presented methods in practice, several options arise. In this section, we describe the methods we used in this paper and comment shortly on some other possible options.

The smoothing was performed using local polynomial regression fitting, using the R [14] routine loess [18]. In Section 2, it was performed over the covariate of interest at chosen time points; in all the other sections, it was performed in two steps—first over the time and then over the covariate (at chosen time points). This speeds up the process considerably without any apparent differences to simultaneous smoothing in both directions. The degree of smoothing was left to the defaults of the R function. Changing it, however, can have quite an impact on the visual impression and should be taken into account when interpreting the results. Similarly, one has to be aware of a poorer reliability of the splines in the tails of the covariate distribution.

The positioning of the time points was chosen to follow the percentiles of event times. Most of the examples in this paper include nine points, set at the 10th to 90th percentile of the observed event times. The choice of the number of time points used in plotting seems to be rather unimportant; however, early and late time points can yield smoothed averages that fall out of the (0,1) region. This can be due to either too few or too many events happening in a certain time interval to the individuals within certain ranges of the covariates. Therefore, the stronger the effect of the covariate, the more likely we are to get undefined values (and, because of smoothing, strongly curved lines approaching them) of the log or cloglog transformation; hence, the curves representing early or late percentiles should be either interpreted with caution or avoided altogether.

When interpreting the Cox model plots, one needs to be aware of the fact that the curves cannot cross, as the difference of the intercept from one curve to the next can only be positive. When the effect changes the sign, as, for example, in Figure 7(a), the curves corresponding to later time points, therefore, cannot be expected to show a very strong trend. If we would increase the effect of β in that example, the lines corresponding to later times would get more curved, even though the effect is linear in Z₁.

The choice of the number of time points when fitting seems to be rather more delicate. The performed simulations imply that an increased number of parameters to be tested simultaneously increase the Type I error if the sample size is not sufficient. This seems to depend also on the distribution of the covariate—although the size of the tests for a uniformly distributed covariate seems to be satisfactory already with 200 events, a larger sample is needed in the case of the normal distribution.

The generalized estimating equations in Section 5 were fitted using the geese routine available from the geepack [19] package. This function allows for fitting using either the log or the cloglog link function and encounters no problems with individual values falling out of the (0,1) region. The error structure used was Gaussian and the correlation structure was set to be independent. Choosing other correlation structures seems to have no important effect on either the size or the power of the tests. This is in line with [20].

An R function for hazard models diagnostics using the methods described in this paper is available from the internet,^‡ SAS users can calculate the pseudo-observations using the SAS macros described in [21].

7. AN EXAMPLE FROM PATIENTS WITH PBC

To illustrate our approach, we consider the multi-centre clinical trial conducted on patients with the liver disease primary biliary cirrhosis (PBC). In a randomized study, 349 patients were treated with either Cyclosporin A or placebo and the purpose of the trial was to study the effect of treatment on the survival time, which was defined as time until either death or liver transplant. During the follow-up 88 events occurred, which is less than in all the simulated examples presented so far. Several covariates entered the final Cox model [22], among them the effect of bilirubin will be of interest for this example.

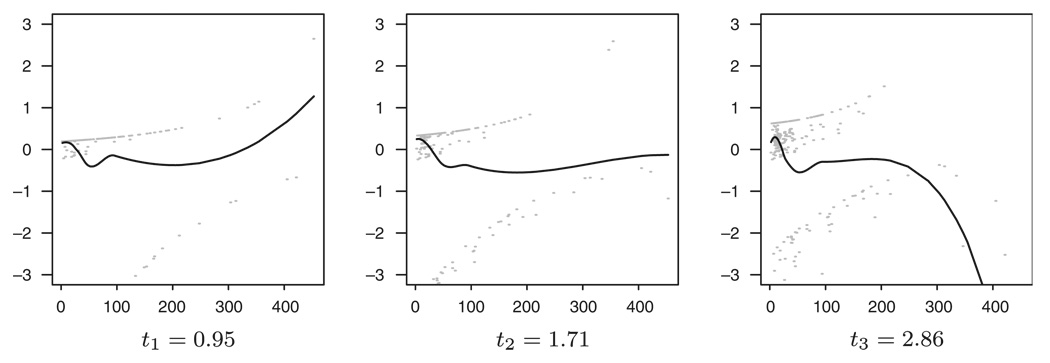
Figure 17 uses the pseudo-residuals to present an initial illustration of the Cox model fit with bilirubin as the only covariate. As the distribution of the bilirubin values is very skewed, the predicted survival of some patients is very close to either 0 or 1 and therefore the standardized residuals get rather large values. The limits of the presented plot were chosen to be [−3,3] and 12–14 residuals fell out of the region of each plot. Judging from Figure 17, the model does not seem to fit well. Although the most obvious feature seems to be the changing of the curve in time, this might not be that important, as there are only few individuals with large values of bilirubin. On the other hand, the part of the curve corresponding to lower values of bilirubin seems to stay rather constant in time but its linearity is more questionable.

Figure 17.

Checking the Cox model fit to the PBC data using the pseudo-residuals. The only covariate used in the model is bilirubin. The three chosen time points are representing the 25th, 50th and 75th quantile of event times.

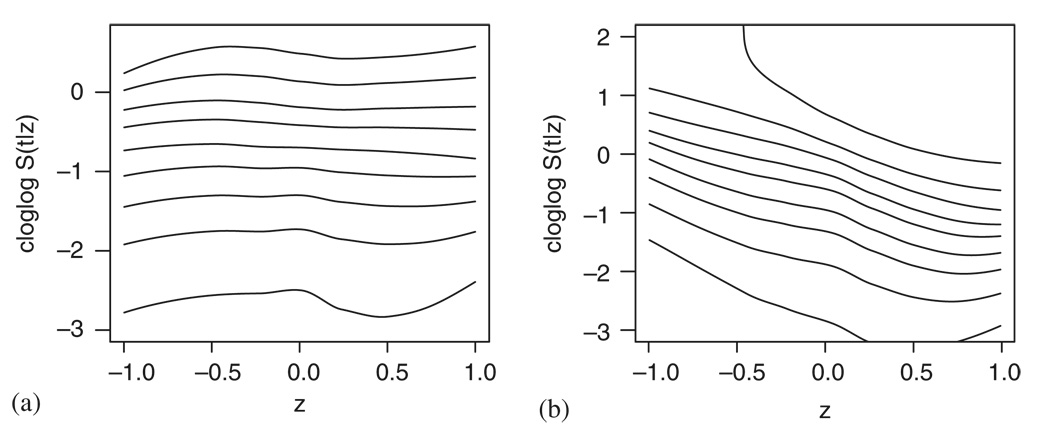
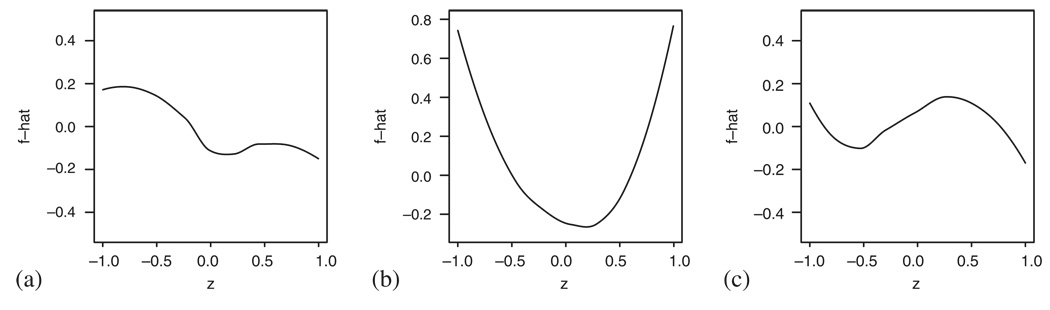
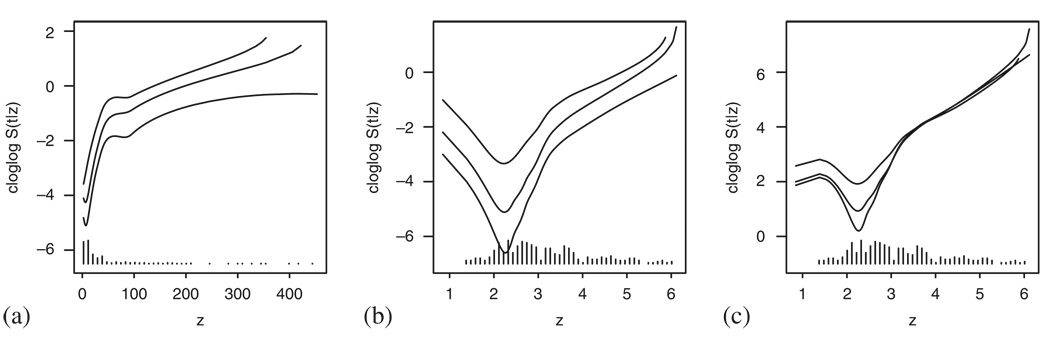
We therefore turn to using the methods described in Sections 3–5 that should provide us with a more detailed information about the Cox model assumptions. Figure 18(a) and (b) explores the Cox model fit when entering bilirubin and log bilirubin, respectively. Owing to the small sample size, three time points, representing the 25th, 50th and 75th percentile of the observed event times, have been chosen for both plotting and testing. Figure 18(a) confirms that the linearity of the covariate seems to be severely violated and all the three tests give significant results (p_lin<0.01, p_PH=0.04 and p_overall=0.02). The logarithmic transformation yields better results and while the curves in Figure 18(b) still seem nonlinear, the goodness-of-fit tests imply that allowing a more general form of the curves does not considerably improve the model fit (p_lin=0.30, p_PH=0.28 and p_overall=0.43)—this disagreement between the graphical impression and the test results can probably be attributed to the small sample size. The final model that was fitted to the data included treatment, age, sex and albumin. Taking these covariates into account and performing a correction as explained in Section 4 result in Figure 18(c). The interpretation of this plot is very similar to the one covariate case and the same is true for the p-values given by the tests: p_lin=0.96, p_PH=0.12 and p_overall=0.25.

Figure 18.

Checking the Cox model fit to the PBC data using smoothed scatterplots of transformed pseudo-observations: (a) bilirubin; (b) log bilirubin; and (c) log bilirubin taking into account the effect of treatment, sex, age and albumin.

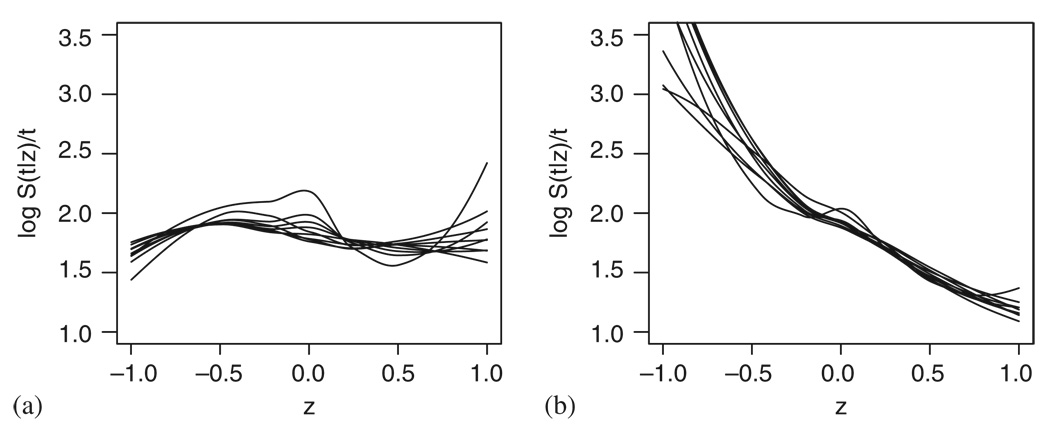
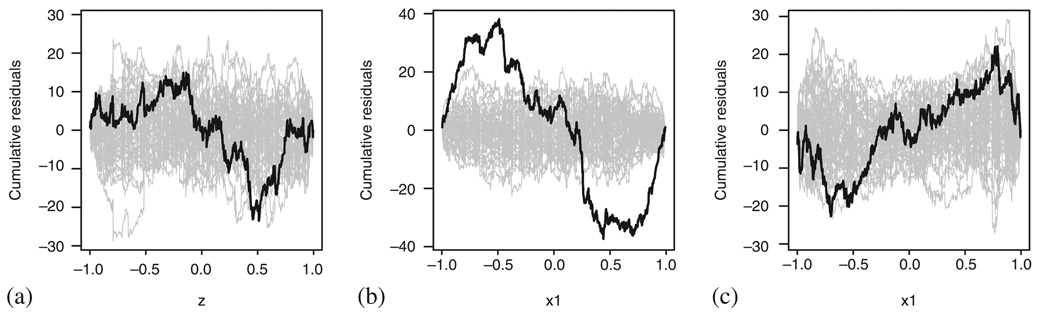
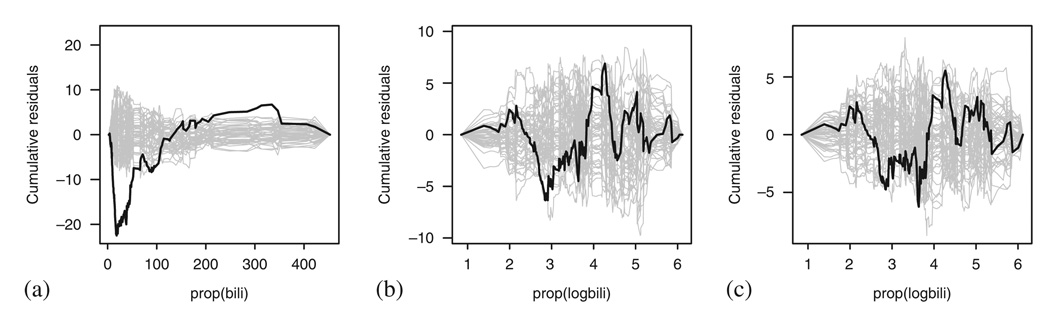
These results compare well with the results of the standard methods. Figure 19 presents the cumulative martingale residuals plots checking the linearity assumption. We can see that while linearity seems severely violated in Figure 19(a), this could not be claimed in Figure 19(b) and (c).

Figure 19.

Checking the Cox model fit to the PBC data using the cumulative sum of martingale residuals: (a) bilirubin; (b) log bilirubin; and (c) log bilirubin taking into account the effect of treatment, sex, age and albumin.

8. CONCLUSIONS

The presence of censoring is the main problem when plotting survival data and the main advantage of using pseudo-observations is that a value can be estimated for each individual at all times regardless of censoring. An initial graphical check can be performed using the pseudo-residuals. The plots are related to those for binary data, with the exception that we have time as an additional dimension. A smoothed average is therefore an essential addition to each plot. This method is very general as any model could be used for calculating the predicted values in the residuals.

Although the pseudo-residuals are useful in signalizing possible departures from the model assumptions, more specific model diagnostics can be performed on the assumed scale of the linear predictor of a chosen model. We have shown that using the proper link function, the assumptions of both the Cox and the additive model can be checked and interpreted in the same way. Similarly, the extensions to multiple covariate case are applied using the same logic. An important feature of this examination that is advantageous to most of the standardly used methods is that the assumptions are checked simultaneously and therefore misspecifying one assumption does not obscure the information about the other.

The main purpose of this paper was to introduce graphical methods for checking the goodness of fit of different hazard regression models using the same framework. However, the fact that we have individual values available, enables simple testing procedures directly corresponding to the plots.

To conclude, the pseudo-observations present a general tool for checking the fit of hazard regression models. Although its generality enables us to apply it to many different problems, we can expect, as with any general tool, that certain specific tests can have a better performance or power. In addition, there will be situations in which the approach should not be used, in our case that would be, for example, the case when censoring depends on covariates. When comparing with the existing methods for the Cox model, we have seen that there are no substantial differences, the important advantage of our approach is that it can be used for a whole range of models.