SUMMARY
The Youden Index is often used as a summary measure of the receiver operating characteristic curve. It measures the effectiveness of a diagnostic marker and permits the selection of an optimal threshold value or cutoff point for the biomarker of interest. Some markers, while basically continuous and positive, have a spike or positive mass of probability at the value zero. We provide a flexible modeling approach for estimating the Youden Index and its associated cutoff point for such spiked data and compare it with the standard empirical approach. We show how this modeling approach can be adjusted to take covariate information into account. This approach is applied to data on the Coronary Calcium Score, a marker for atherosclerosis. Published in 2007 by John Wiley & Sons, Ltd.
Keywords: Box–Cox power transformations, Coronary Calcium Score, diagnostic markers, mixture model, ROC curve, sensitivity, specificity
1. INTRODUCTION
In recent years, the evaluation of the ability of a new diagnostic or screening marker (test) to distinguish a diseased from a non-diseased patient has been widely discussed in the literature [1, 2]. A person is assessed as diseased or healthy depending on whether the corresponding marker value is greater than or less than or equal to a given threshold value. Associated with any threshold value (t) is the probability of a true positive (sensitivity = q(t)) and the probability of a true negative (specificity = 1 − p(t)).
A frequently used summary index of marker accuracy is the Youden Index [2-7], which is defined as
| (1) |
over all threshold values t. The critical threshold value t*, which achieves this maximum, will be referred to as the ‘optimal’ threshold. The optimal threshold is used as a criterion for classifying subjects as healthy (diseased) if their observed marker value is less than or equal to (greater than) t*. Greiner et al. [8] provide a recent discussion of this and other criteria for obtaining the critical threshold value. J and t* are often seen in the applied biomedical literature [9-12].
The Youden Index gives equal weight to sensitivity and specificity. If a researcher thinks that different weights are appropriate (based perhaps on the cost of different types of error), a generalized Youden Index can be used. The generalized J can be motivated from a decision theoretic perspective. The expected loss function in classifying a subject can be written as (1 − κ) p(t) + aκ(1 − q(t)) [5, 8, 13], where ‘a’ denotes the relative loss (cost) of a false negative when compared with a false positive and κ is the proportion of diseased individuals in the population of interest (prevalence). It is easy to see that minimizing this expected loss over all possible threshold values is the same as maximizing r(1 − p(t)) + q(t), where r = (1 − κ)/aκ. For r = 1, this is equivalent to obtaining J. The relative cost and disease prevalence are often difficult to assess (Greiner et al. [8] and the references cited therein). We have, for simplicity, remained with the commonly assumed r = 1 [8], both in the theoretical development and in the example of this paper.
In clinical practice, finding the location of the critical threshold value for discriminating cases and controls with minimal misclassification is of central interest. A recent paper by Fluss et al. [6] discusses the case when marker measurements are continuous and compares several methods of estimation for both the Youden Index and the critical threshold value. In this paper, we extend the presentation to continuous data with mass at zero. Such zero-spiked data were presented by Schisterman et al. [5] in the context of receiver operating characteristic (ROC) curve analysis. The ROC curve is a useful tool for displaying the discriminatory ability of a marker measured through a diagnostic test in distinguishing between diseased and healthy individuals. The ROC curve is a plot of q(t) versus p(t) for all possible threshold values. The accuracy of a diagnostic test is often summarized by the area under the ROC curve (AUC) [1].
As an example of zero-spiked data, consider the Coronary Calcium Score (CCS). Calcium in the coronary arteries indicates the presence of atherosclerotic plaque, and the amount of coronary artery calcification correlates with the amount of atherosclerosis (hard and soft plaque) at autopsy. Electron beam tomography (EBT) is a sensitive, non-invasive modality for the detection of subclinical atherosclerosis by coronary calcium measurement. CCS determined by EBT has been shown to be directly associated with the extent of angiographic coronary artery disease and to be predictive of coronary events [14]. A zero CCS value is interpreted as the tested individual having no calcium in the coronary arteries. Any positive amount of coronary calcium can be quantified continuously by EBT. Furthermore, the discriminatory accuracy of a continuous marker may be influenced by covariate factors such as age, general health status, sex, etc. [15, 16]. Schisterman et al. [16] have shown that the AUC attained from the CCS is a function of age and gender. Based on their findings, it is reasonable to consider that both J and t* should be functions of these covariates. This paper aims at developing a readily applicable methodology for estimating J and t* for zero-spiked data.
To evaluate the critical threshold value and the Youden Index of CCS, we examined a prospective cohort study of 10 377 asymptomatic individuals [14] who were referred by their primary care physicians between 1996 and 2000 for coronary calcium screening with EBT. Patients with a history of coronary disease (i.e. a history that included admission to the hospital for chest pain, acute coronary syndrome, or myocardial infarction (MI), as well as prior coronary angiography and revascularization) were excluded. Patients in our cohort who had an MI within two years from the EBT test were classified as being in the diseased group and otherwise were considered to be in the healthy group.
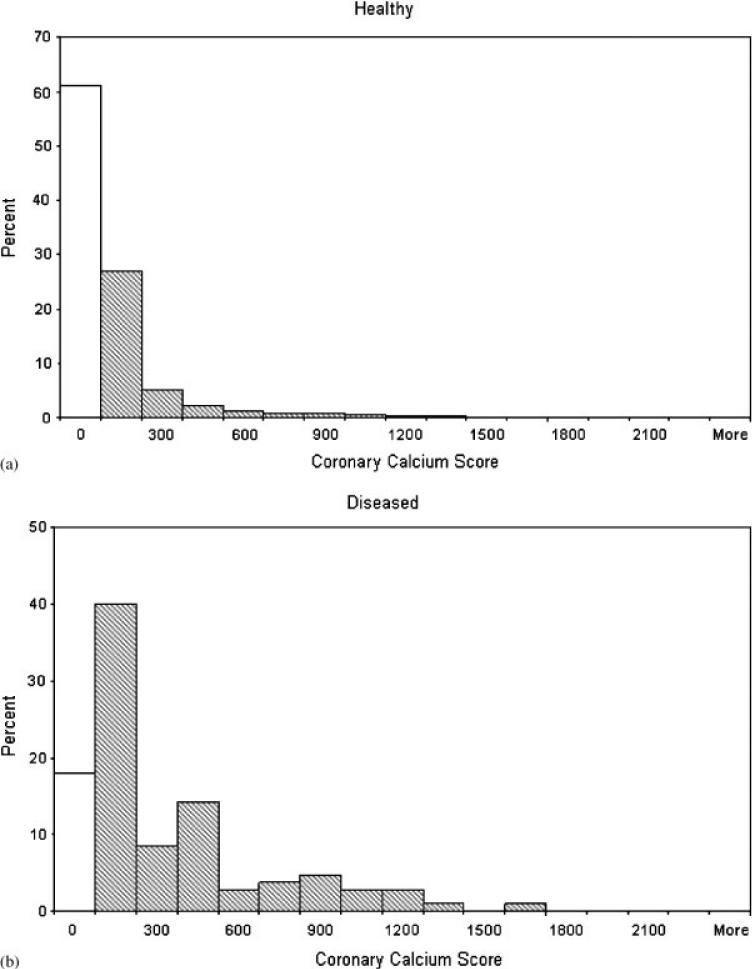
Schisterman et al. [16] showed that this marker has poor discriminatory ability for females. Consequently, in this paper we consider only the 4122 males. Figure 1 provides a histogram for the frequency distribution of CCS by disease status for our sample of males. Note that the CCS has a spike (mass) at zero and the positive CCS marker values have a skewed distribution. The percentages of zeros for the diseased and healthy samples are 18 and 61 per cent, respectively.
Figure 1.
Histograms of CCS data. The first cell in the histograms represents the frequency of just the value zero, while the other cells represent intervals.
Estimation of J and t* follows the estimation of the sensitivity and specificity functions in (1). Both parametric and non-parametric approaches have been suggested for estimating sensitivity and specificity [1]. These procedures differ by using various methods for estimating the cumulative distribution functions (cdfs) of the marker values, based on samples taken from both the healthy and diseased groups. Using these estimated cdfs, the estimation of p(t) and q(t) and consequently J and t* follows. The most common non-parametric method, which we will refer to as the empirical method (EMP), estimates the cdf of the marker with the empirical cdf of the sample. Parametric approaches are based on making distributional assumptions, such as normality on the marker values, and can be quite sensitive to the form of the assumed distributions. A more robust approach (TN) assumes that a monotone transformation exists such that the transformed marker values follow the normal distribution. After estimating the transformation using the Box–Cox power transformation procedure, it is applied to the data and estimation based on normal assumptions is used. This approach has been found useful when dealing with ROC curves [17-20]. Recently, for continuous markers, Fluss et al. [6] compared a number of procedures for estimating J and t* and found that in many cases the TN approach performed well. Schisterman et al. [16] showed how the TN approach could be generalized to estimate the AUC for spiked data. In Section 2, we discuss the TN and EMP approaches for estimating J and t* for spiked data. In Section 3, an extensive simulation study comparing these two approaches is presented. Section 4 shows how the TN approach can be adjusted to account for covariate information. Applications to the CCS data are given in Section 5, while Section 6 provides a concluding discussion.
2. ESTIMATION OF J AND t* FOR SPIKED DATA
2.1. Notation
Following Schisterman et al. [16], let Z and W represent the random variables for the diagnostic test markers on the diseased and healthy populations, respectively. Furthermore, let FZ and GW denote their respective cdfs. Consequently, q(t) = 1 − FZ (t) and p(t) = 1 − GW (t). Suppose the diagnostic test results Z1,..., ZM and W1,..., WN are available with M = m0+m and N = n0 + n, where m0 and n0 represent the number of observations taking the value zero for the diseased and healthy samples, respectively. Let x1,..., xm and y1,..., yn represent the non-zero values in these samples.
2.2. The non-parametric EMP approach
Standard methods [1] provide non-parametric estimations of p(t) and q(t) based on the empirical cdfs for FZ and GW, which are denoted by F̂Z (t) and ĜW (t), respectively. Thus, from (1),
| (2) |
where t ranges over the observed values of Z and W.
Following Fluss et al. [6], we examine two approaches for estimating t*: (a) the observed marker value where the maximum in (2) was found; (b) merge the sampled maker values for both the diseased and healthy groups and sort them in ascending order, denoting the resulting values by d1,..., dm+n. Suppose that J is obtained at dj. Since the value of K̂(t) is constant for the interval [dj, dj+1), any value in this range is a reasonable estimate of t* and we take (dj + dj+1)/2. In our simulation, we found a slight difference between these two methods with a small preference to approach (b). For brevity, we report only on the second approach.
2.3. The TN approach
For completeness, we review the discussion in Schisterman et al. [16] on sensitivity and specificity for zero-spiked data. Consider the random variable Z ≥ 0 to be a mixture having a positive probability πZ at the point Z = 0 and otherwise (with probability 1 − πZ) having a continuous distribution with cdf FC defined over the positive real line. Thus,
Conditional on the marker values being non-zero, x1,..., xm can be considered to be a random sample from FC. We denote the corresponding (non-zero) random variable by X. In parallel, for the healthy population
with y1,..., yn being a random sample on the variable Y having a cdf GC. For any fixed threshold value t, the sensitivity becomes
| (3) |
while 1−specificity is
| (4) |
Schisterman et al. [16] used this spike model to estimate the area under the ROC curve. In the following, we focus on estimating the Youden Index along with the corresponding critical threshold.
Using the above notation, let
| (5) |
while
| (6) |
Following Schisterman et al. [16], we assume that the ‘continuous’ part of the marker distribution can be modeled using the Box–Cox power transformation family. More specifically, we define
| (7) |
and further assume that . Y(λ) is similarly defined with . Note that this transformation is applied only to the non-zero marker values.
Since these transformations are monotonically increasing
| (8) |
where
Φ denotes the standard normal cdf and
| (9) |
Now, K(t) can be written as
| (10) |
where
| (11) |
and
| (12) |
We follow the convention that larger marker values are more associated with disease and would thus generally expect that μD>μH and πW>πZ.
In order to carry out (6), under the assumption that μD − μH>0 and πW − πZ>0, we first compute h′ (k), the first derivative of h(k), set it to zero and solve the resulting quadratic equation. If there is no real solution, then J, the maximum of K(t), is obtained as J = πW − πZ, with t* = 0, where a real solution exists, the root
| (13) |
can be shown to maximize h(k). The corresponding t* will be obtained for any given λ by substituting k* into (12) and solving for t. For the special case of πZ = πW = 0, this reduces to the standard solution for continuous normal data [6]. The maximum of K(t) will then be obtained as either h(k*) or πW − πZ depending on which is greater and t* will be chosen correspondingly.
For the estimation of J and t*, we replace the unknown parameters πW, πZ, λ, μD, μH, σD, and σH with estimates based on sample data from the healthy and diseased populations and carry out the optimization procedure described above.
The probability mass at zero can be estimated immediately from the data as and .
Based on the non-zero sampled observations on the diseased and healthy subjects, the appropriate likelihood function can be constructed [21] and maximized, resulting in , the maximum likelihood estimator of λ. The sample means and standard deviations calculated from the data transformed according to (7) using give , , , and .
2.4. Estimation for the CCS marker
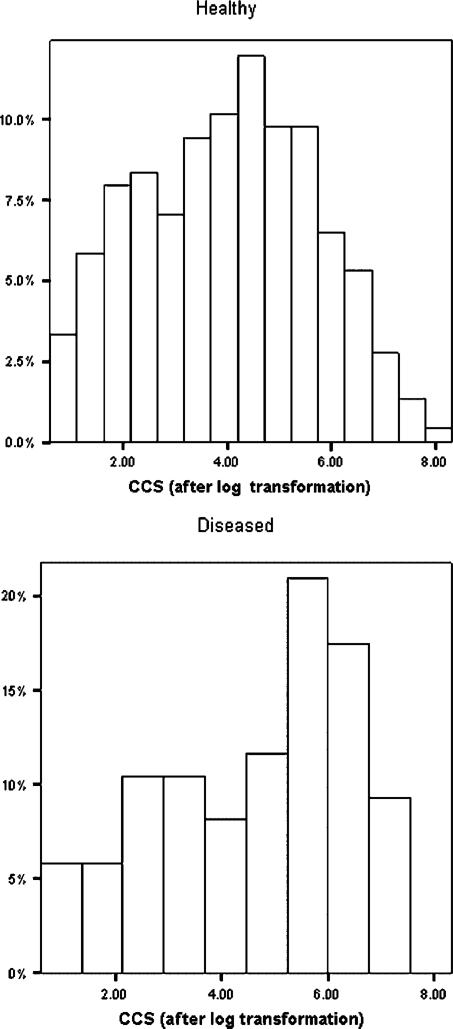
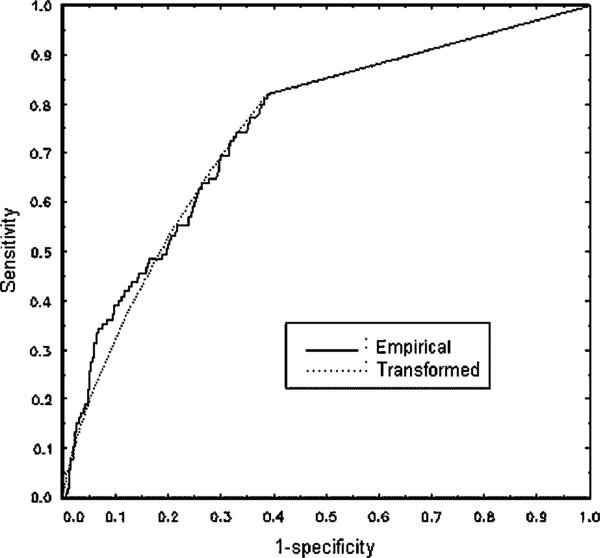
The distribution of the non-zero marker values (see Figure 1) shows considerable skewness for both the healthy and diseased male subjects. This is confirmed by Q–Q plots. The Box–Cox procedure results in , which is quite close to 0, suggesting a log transformation. It needs to be emphasized that this transformation is applied only to the non-zero marker values. Applying it to the zero values would only result in the spike being moved from zero to another value. Since the percentage of zeros is substantial for our data (18 per cent for the diseased and 61 per cent for the healthy), including the zeros in the transformation will necessarily result in strongly non-normal and non-symmetrical distributions. Histograms for the positive marker value after the log transformation are given in Figure 2. These indicate an improvement in symmetry and the data appear more normal like. This is confirmed by Q–Q plots, which are omitted for brevity. As pointed out by a referee, the histogram for the diseased group after transformation is still not symmetric or normal like, although it has certainly improved on the pre-transformed data. Figure 3 shows that the ROC curves estimated by both the EMP and TN approaches are quite similar, indicating some robustness for the TN procedure. In various ROC contexts, using the TN procedure for data generated from distributions that are not in the power family has been found to be effective [6, 19, 22].Hanley [23, 24] has also emphasized the robustness of the binormal model to the normality assumption.
Figure 2.
Histograms of log(CCS) for positive marker values.
Figure 3.
Empirical and TN ROC curves for CCS data.
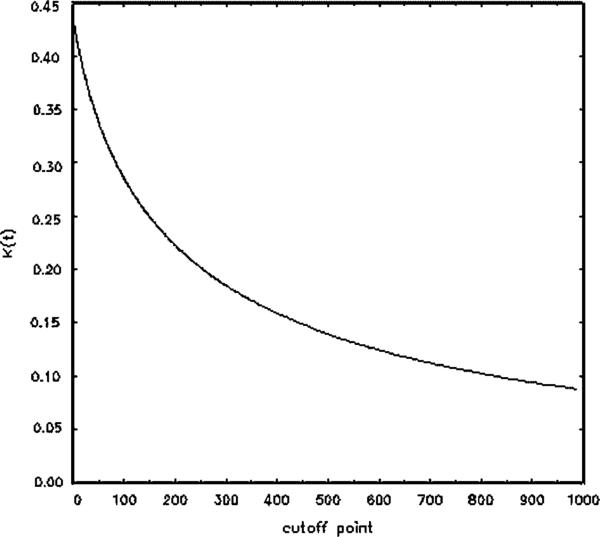
For the CCS data, both the EMP and the TN procedures result in the same estimates of the Youden Index and the optimal threshold, namely Ĵ = 0.431 and t̂* = 0. The estimated specificity and sensitivity at this point are 0.61 and 0.82, respectively. Thes results do not take into account a possible age effect, which will be considered in Section 5. Figure 4 provides a plot of K(t) as estimated by the TN method for various levels of the threshold t. This clearly indicates the peak obtained at t = 0 and the falloff of the curve for larger t values.
Figure 4.
The K function estimated by the TN method.
3. SIMULATION STUDY
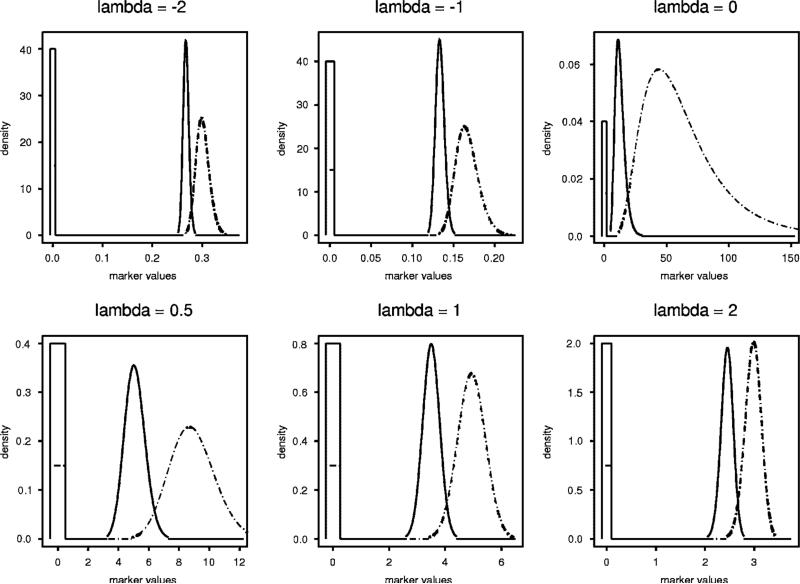
We carried out a simulation study to compare the EMP and TN estimators in terms of bias and root mean-square error (RMSE) for both J and t* via an extensive simulation study. Our simulation considers a variety of distributional shapes and probabilities for observing zero, each for several choices of J and with M = N = 100, 200, 2000. A sampling of these distributions is presented in Figure 5. For a given N, M, πW, and πZ, the number of zero values n0 and m0 was generated from the appropriate binomial distributions. Then, samples of size N − n0 and M − m0 were generated, respectively, for the continuous part of the distribution. In order to obtain various shapes for this continuous part, the Box–Cox model (7) was used to generate data using λ = −2, −1, −0.5, 0, 0.5, 1, and2. The values of μD, μH, σD, and σH were chosen to provide the specified choice of J. The distributions in Figure 5 are standardized to give J = 0.8, πW = 0.4 and πZ = 0.15. The rectangles representing the spikes at zero have been constructed to have areas 0.4, and 0.15. For comparing bias and RMSE, 1000 simulations were carried out for each scenario.
Figure 5.
Distributions used in the simulation study.
Tables I and II summarize the results for J, whereas Tables III and IV provide those for t*. As expected, both bias and RMSE decrease with larger sample sizes. For both J and t* estimation, the TN procedure usually has lower bias and RMSE. For estimating the Youden Index, EMP can have an RMSE as much as 25 per cent larger than that of TN. For the optimal threshold estimation, the RMSE of EMP can be more than double that of TN. Note that for threshold estimation the EMP procedure can exhibit a bias substantially higher than TN even for large sample size. The overall superiority of TN in estimating both J and t* is clear.
Table I.
Simulated bias for the Youden Index estimator.
|
λ = −2 |
λ = −1 |
λ = −0.5 |
λ = 0 |
λ = 0.5 |
λ = 1 |
λ = 2 |
|||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| J | πW | πZ | M = N | EMP | TN | EMP | TN | EMP | TN | EMP | TN | EMP | TN | EMP | TN | EMP | TN |
| 0.4 | 0.2 | 0.1 | 100 | 0.0350 | 0.0026 | 0.0368 | 0.0053 | 0.0377 | 0.0061 | 0.0372 | 0.0048 | 0.0353 | 0.0024 | 0.0369 | 0.0041 | 0.0368 | 0.0037 |
| 200 | 0.0247 | 0.0029 | 0.0240 | 0.0024 | 0.0219 | 0.0012 | 0.0237 | 0.0018 | 0.0245 | 0.0024 | 0.0233 | 0.0010 | 0.0241 | 0.0016 | |||
| 2000 | 0.0053 | −0.0002 | 0.0058 | 0.0006 | 0.0053 | 0.0001 | 0.0052 | −0.0003 | 0.0062 | 0.0005 | 0.0053 | −0.0004 | 0.0064 | 0.0007 | |||
| 0.3 | 0.2 | 100 | 0.0315 | 0.0032 | 0.0334 | 0.0055 | 0.0340 | 0.0058 | 0.0318 | 0.0033 | 0.0332 | 0.0032 | 0.0346 | 0.0051 | 0.0332 | 0.0037 | |
| 200 | 0.0225 | 0.0032 | 0.0220 | 0.0025 | 0.0200 | 0.0012 | 0.0208 | 0.0016 | 0.0222 | 0.0025 | 0.0213 | 0.0013 | 0.0224 | 0.0025 | |||
| 2000 | 0.0049 | −0.0001 | 0.0057 | 0.0010 | 0.0049 | 0.0003 | 0.0052 | 0.0005 | 0.0057 | 0.0006 | 0.0047 | −0.0003 | 0.0056 | 0.0005 | |||
| 0.4 | 0.15 | 100 | 0.0355 | 0.0038 | 0.0375 | 0.0059 | 0.0380 | 0.0068 | 0.0381 | 0.0054 | 0.0365 | 0.0034 | 0.0386 | 0.0060 | 0.0377 | 0.0050 | |
| 200 | 0.0254 | 0.0041 | 0.0241 | 0.0026 | 0.0220 | 0.0013 | 0.0242 | 0.0021 | 0.0249 | 0.0029 | 0.0241 | 0.0020 | 0.0247 | 0.0026 | |||
| 2000 | 0.0056 | 0.0000 | 0.0062 | 0.0008 | 0.0054 | 0.0001 | 0.0055 | 0.0001 | 0.0064 | 0.0008 | 0.0054 | −0.0003 | 0.0065 | 0.0008 | |||
| 0.6 | 0.2 | 0.1 | 100 | 0.0270 | 0.0024 | 0.0286 | 0.0046 | 0.0289 | 0.0054 | 0.0288 | 0.0039 | 0.0275 | 0.0026 | 0.0293 | 0.0043 | 0.0282 | 0.0036 |
| 200 | 0.0195 | 0.0028 | 0.0185 | 0.0021 | 0.0175 | 0.0007 | 0.0177 | 0.0019 | 0.0188 | 0.0023 | 0.0182 | 0.0010 | 0.0185 | 0.0016 | |||
| 2000 | 0.0039 | −0.0001 | 0.0046 | 0.0005 | 0.0041 | 0.0000 | 0.0042 | 0.0002 | 0.0047 | 0.0005 | 0.0037 | −0.0004 | 0.0047 | 0.0006 | |||
| 0.3 | 0.2 | 100 | 0.0231 | 0.0023 | 0.0240 | 0.0038 | 0.0246 | 0.0042 | 0.0222 | 0.0016 | 0.0234 | 0.0028 | 0.0250 | 0.0045 | 0.0233 | 0.0031 | |
| 200 | 0.0164 | 0.0026 | 0.0159 | 0.0020 | 0.0146 | 0.0003 | 0.0157 | 0.0019 | 0.0158 | 0.0020 | 0.0150 | 0.0009 | 0.0160 | 0.0022 | |||
| 2000 | 0.0034 | 0.0000 | 0.0045 | 0.0010 | 0.0037 | 0.0002 | 0.0038 | 0.0000 | 0.0042 | 0.0007 | 0.0029 | −0.0004 | 0.0038 | 0.0004 | |||
| 0.4 | 0.15 | 100 | 0.0258 | 0.0026 | 0.0269 | 0.0043 | 0.0281 | 0.0053 | 0.0260 | 0.0025 | 0.0266 | 0.0032 | 0.0280 | 0.0050 | 0.0268 | 0.0042 | |
| 200 | 0.0193 | 0.0033 | 0.0173 | 0.0021 | 0.0162 | 0.0004 | 0.0176 | 0.0018 | 0.0182 | 0.0022 | 0.0176 | 0.0014 | 0.0176 | 0.0022 | |||
| 2000 | 0.0039 | 0.0000 | 0.0048 | 0.0008 | 0.0039 | 0.0000 | 0.0034 | −0.0004 | 0.0048 | 0.0008 | 0.0035 | −0.0004 | 0.0046 | 0.0006 | |||
| 0.8 | 0.2 | 0.1 | 100 | 0.0167 | 0.0004 | 0.0175 | 0.0018 | 0.0179 | 0.0022 | 0.0168 | 0.0009 | 0.0169 | 0.0010 | 0.0174 | 0.0022 | 0.0173 | 0.0036 |
| 200 | 0.0119 | 0.0012 | 0.0119 | 0.0006 | 0.0100 | −0.0010 | 0.0113 | 0.0005 | 0.0118 | 0.0009 | 0.0108 | 0.0001 | 0.0110 | 0.0016 | |||
| 2000 | 0.0025 | −0.0001 | 0.0030 | 0.0003 | 0.0027 | −0.0000 | 0.0028 | 0.0000 | 0.0030 | 0.0004 | 0.0022 | −0.0004 | 0.0027 | 0.0006 | |||
| 0.4 | 0.15 | 100 | 0.0124 | −0.0002 | 0.0126 | 0.0003 | 0.0138 | 0.0010 | 0.0122 | −0.0002 | 0.0124 | 0.0006 | 0.0130 | 0.0013 | 0.0127 | 0.0006 | |
| 200 | 0.0093 | 0.0009 | 0.0089 | 0.0000 | 0.0072 | −0.0010 | 0.0082 | 0.0000 | 0.0087 | 0.0003 | 0.0079 | −0.000 | 0.0083 | 0.0001 | |||
| 2000 | 0.0022 | 0.0000 | 0.0026 | 0.0005 | 0.0021 | −0.0000 | 0.0024 | 0.0002 | 0.0027 | 0.0006 | 0.0017 | −0.0004 | 0.0021 | 0.0001 | |||
Table II.
Simulated RMSE for the Youden Index estimator.
|
λ = −2 |
λ = −1 |
λ = −0.5 |
λ = 0 |
λ = 0.5 |
λ =1 |
λ = 2 |
|||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| J | πW | πZ | M = N | EMP | TN | EMP | TN | EMP | TN | EMP | TN | EMP | TN | EMP | TN | EMP | TN |
| 0.4 | 0.2 | 0.1 | 100 | 0.0665 | 0.0521 | 0.0675 | 0.0524 | 0.0670 | 0.0519 | 0.0695 | 0.0552 | 0.0678 | 0.0532 | 0.0671 | 0.0517 | 0.0659 | 0.0513 |
| 200 | 0.0475 | 0.0369 | 0.0463 | 0.0365 | 0.0450 | 0.0360 | 0.0472 | 0.0365 | 0.0467 | 0.0364 | 0.0468 | 0.0368 | 0.0469 | 0.0367 | |||
| 2000 | 0.0146 | 0.0118 | 0.0146 | 0.0116 | 0.0140 | 0.0112 | 0.0146 | 0.0118 | 0.0147 | 0.0116 | 0.0141 | 0.0113 | 0.0150 | 0.0119 | |||
| 0.3 | 0.2 | 100 | 0.0638 | 0.0514 | 0.0644 | 0.0511 | 0.0650 | 0.0523 | 0.0635 | 0.0514 | 0.0666 | 0.0540 | 0.0649 | 0.0519 | 0.0629 | 0.0511 | |
| 200 | 0.0457 | 0.0365 | 0.0450 | 0.0364 | 0.0433 | 0.0357 | 0.0438 | 0.0360 | 0.0450 | 0.0365 | 0.0448 | 0.0369 | 0.0457 | 0.0367 | |||
| 2000 | 0.0140 | 0.0116 | 0.0143 | 0.0116 | 0.0137 | 0.0115 | 0.0140 | 0.0116 | 0.0141 | 0.0113 | 0.0136 | 0.0112 | 0.0144 | 0.0119 | |||
| 0.4 | 0.15 | 100 | 0.0663 | 0.0522 | 0.0670 | 0.0520 | 0.0671 | 0.0524 | 0.0685 | 0.0538 | 0.0678 | 0.0538 | 0.0682 | 0.0532 | 0.0665 | 0.0520 | |
| 200 | 0.0482 | 0.0374 | 0.0471 | 0.0375 | 0.0445 | 0.0364 | 0.0478 | 0.0372 | 0.0471 | 0.0372 | 0.0471 | 0.0374 | 0.0478 | 0.0379 | |||
| 2000 | 0.0146 | 0.0118 | 0.0150 | 0.0119 | 0.0141 | 0.0115 | 0.0145 | 0.0117 | 0.0148 | 0.0116 | 0.0141 | 0.0114 | 0.0150 | 0.0120 | |||
| 0.6 | 0.2 | 0.1 | 100 | 0.0579 | 0.0471 | 0.0585 | 0.0472 | 0.0584 | 0.0470 | 0.0575 | 0.0458 | 0.0580 | 0.0475 | 0.0575 | 0.0468 | 0.0578 | 0.0465 |
| 200 | 0.0412 | 0.0331 | 0.0403 | 0.0330 | 0.0405 | 0.0326 | 0.0400 | 0.0327 | 0.0406 | 0.0328 | 0.0405 | 0.0329 | 0.0409 | 0.0335 | |||
| 2000 | 0.0129 | 0.0107 | 0.0130 | 0.0105 | 0.0122 | 0.0101 | 0.0126 | 0.0105 | 0.0126 | 0.0104 | 0.0123 | 0.0102 | 0.0130 | 0.0107 | |||
| 0.3 | 0.2 | 100 | 0.0565 | 0.0474 | 0.0549 | 0.0464 | 0.0563 | 0.0475 | 0.0550 | 0.0466 | 0.0561 | 0.0488 | 0.0563 | 0.0479 | 0.0552 | 0.0468 | |
| 200 | 0.0389 | 0.0333 | 0.0386 | 0.0330 | 0.0393 | 0.0330 | 0.0388 | 0.0333 | 0.0391 | 0.0336 | 0.0387 | 0.0335 | 0.0394 | 0.0334 | |||
| 2000 | 0.0122 | 0.0106 | 0.0127 | 0.0106 | 0.0124 | 0.0107 | 0.0120 | 0.0103 | 0.0120 | 0.0103 | 0.0120 | 0.0104 | 0.0125 | 0.0108 | |||
| 0.4 | 0.15 | 100 | 0.0576 | 0.0476 | 0.0567 | 0.0469 | 0.0576 | 0.0474 | 0.0570 | 0.0489 | 0.0577 | 0.0480 | 0.0578 | 0.0479 | 0.0571 | 0.0474 | |
| 200 | 0.0409 | 0.0339 | 0.0402 | 0.0340 | 0.0400 | 0.0332 | 0.0412 | 0.0343 | 0.0405 | 0.0339 | 0.0404 | 0.0334 | 0.0410 | 0.0343 | |||
| 2000 | 0.0127 | 0.0107 | 0.0130 | 0.0107 | 0.0124 | 0.0105 | 0.0125 | 0.0109 | 0.0126 | 0.0104 | 0.0123 | 0.0104 | 0.0129 | 0.0108 | |||
| 0.8 | 0.2 | 0.1 | 100 | 0.0432 | 0.0363 | 0.0428 | 0.0361 | 0.0425 | 0.0357 | 0.0417 | 0.0348 | 0.0416 | 0.0352 | 0.0432 | 0.0362 | 0.0424 | 0.0465 |
| 200 | 0.0299 | 0.0253 | 0.0305 | 0.0255 | 0.0302 | 0.0256 | 0.0295 | 0.0249 | 0.0299 | 0.0251 | 0.0296 | 0.0250 | 0.0301 | 0.0335 | |||
| 2000 | 0.0094 | 0.0082 | 0.0096 | 0.0081 | 0.0093 | 0.0079 | 0.0093 | 0.0080 | 0.0095 | 0.0080 | 0.0093 | 0.0079 | 0.0095 | 0.0107 | |||
| 0.4 | 0.15 | 100 | 0.0415 | 0.0382 | 0.0406 | 0.0369 | 0.0413 | 0.0376 | 0.0410 | 0.0378 | 0.0409 | 0.0370 | 0.0422 | 0.0381 | 0.0414 | 0.0377 | |
| 200 | 0.0297 | 0.0269 | 0.0292 | 0.0267 | 0.0293 | 0.0269 | 0.0289 | 0.0261 | 0.0297 | 0.0270 | 0.0289 | 0.0264 | 0.0292 | 0.0267 | |||
| 2000 | 0.0093 | 0.0085 | 0.0093 | 0.0085 | 0.0093 | 0.0085 | 0.0092 | 0.0083 | 0.0094 | 0.0083 | 0.0091 | 0.0084 | 0.0091 | 0.0085 | |||
Table III.
Simulated bias for the optimal threshold estimator.
|
λ = −2 |
λ = −1 |
λ = −0.5 |
λ = 0 |
λ = 0.5 |
λ = 1 |
λ = 2 |
|||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| J | πW | πZ | M = N | EMP | TN | EMP | TN | EMP | TN | EMP | TN | EMP | TN | EMP | TN | EMP | TN |
| 0.4 | 0.2 | 0.1 | 100 | −0.0005 | −0.0001 | −0.0005 | −0.0001 | −0.0003 | 0.0000 | −0.3105 | 0.1132 | −0.0616 | −0.0085 | −0.0283 | −0.0071 | −0.0107 | −0.0020 |
| 200 | −0.0003 | −0.0001 | −0.0003 | 0.0000 | −0.0002 | 0.0000 | −0.2061 | 0.0527 | −0.0357 | −0.0048 | −0.0185 | −0.0025 | −0.0052 | −0.0009 | |||
| 2000 | −0.0001 | 0.0000 | −0.0001 | 0.0000 | 0.0000 | 0.0000 | −0.0463 | 0.0016 | −0.0061 | −0.0007 | −0.0033 | 0.0003 | −0.0015 | −0.0001 | |||
| 0.3 | 0.2 | 100 | −0.0004 | −0.0001 | −0.0004 | −0.0001 | −0.0003 | 0.0000 | −0.2847 | 0.1170 | −0.0560 | −0.0078 | −0.0221 | −0.0073 | −0.0101 | −0.0023 | |
| 200 | −0.0002 | 0.0000 | −0.0002 | 0.0000 | −0.0001 | 0.0000 | −0.0998 | 0.0488 | −0.0159 | −0.0062 | −0.0099 | −0.0028 | −0.0030 | −0.0013 | |||
| 2000 | −0.0001 | 0.0000 | −0.0001 | 0.0000 | 0.0000 | 0.0000 | −0.0543 | 0.0030 | −0.0065 | −0.0008 | −0.0030 | 0.0002 | −0.0020 | −0.0001 | |||
| 0.4 | 0.15 | 100 | −0.0006 | −0.0008 | −0.0008 | −0.0008 | −0.0004 | −0.0002 | −0.3971 | 0.1095 | −0.0775 | −0.0242 | −0.0356 | −0.0227 | −0.0181 | −0.0159 | |
| 200 | −0.0003 | −0.0001 | −0.0003 | 0.0000 | −0.0002 | 0.0000 | −0.1562 | 0.0343 | −0.0312 | −0.0098 | −0.0191 | −0.0061 | −0.0065 | −0.0029 | |||
| 2000 | −0.0001 | 0.0000 | −0.0001 | 0.0000 | −0.0001 | 0.0000 | −0.0716 | 0.0084 | −0.0093 | −0.0019 | −0.0029 | 0.0000 | −0.0022 | −0.0002 | |||
| 0.6 | 0.2 | 0.1 | 100 | −0.0004 | 0.0000 | −0.0004 | 0.0000 | −0.0003 | 0.0000 | −0.2481 | 0.1160 | −0.0460 | −0.0044 | −0.0232 | −0.0049 | −0.0088 | −0.0012 |
| 200 | −0.0003 | 0.0000 | −0.0003 | 0.0000 | −0.0002 | 0.0000 | −0.2297 | 0.0509 | −0.0342 | −0.0025 | −0.0153 | −0.0021 | −0.0057 | −0.0004 | |||
| 2000 | −0.0001 | 0.0000 | −0.0001 | 0.0000 | 0.0000 | 0.0000 | −0.0305 | 0.0038 | −0.0088 | 0.0001 | −0.0019 | 0.0002 | −0.0012 | 0.0000 | |||
| 0.3 | 0.2 | 100 | −0.0004 | 0.0000 | −0.0004 | 0.0000 | −0.0003 | 0.0000 | −0.2374 | 0.1075 | −0.0500 | −0.0023 | −0.0189 | −0.0040 | −0.0094 | −0.0011 | |
| 200 | −0.0004 | 0.0000 | −0.0003 | 0.0000 | −0.0002 | 0.0000 | −0.1830 | 0.0706 | −0.0385 | −0.0030 | −0.0143 | −0.0020 | −0.0065 | −0.0006 | |||
| 2000 | −0.0001 | 0.0000 | −0.0001 | 0.0000 | 0.0000 | 0.0000 | −0.0684 | 0.0025 | −0.0066 | 0.0003 | −0.0025 | 0.0002 | −0.0015 | −0.0001 | |||
| 0.4 | 0.15 | 100 | −0.0005 | 0.0000 | −0.0004 | 0.0000 | −0.0003 | 0.0000 | −0.3128 | 0.1172 | −0.0538 | −0.0037 | −0.0222 | −0.0048 | −0.0098 | −0.0014 | |
| 200 | −0.0003 | 0.0000 | −0.0003 | 0.0000 | −0.0002 | 0.0000 | −0.2035 | 0.0567 | −0.0360 | −0.0024 | −0.0150 | −0.0026 | −0.0065 | −0.0006 | |||
| 2000 | −0.0001 | 0.0000 | −0.0001 | 0.0000 | 0.0000 | 0.0000 | −0.0513 | 0.0005 | −0.0098 | −0.0004 | −0.0038 | 0.0001 | −0.0018 | −0.0001 | |||
| 0.8 | 0.2 | 0.1 | 100 | −0.0004 | 0.0000 | −0.0004 | 0.0000 | −0.0003 | 0.0000 | −0.3558 | 0.0993 | −0.0376 | 0.0017 | −0.0211 | −0.0018 | −0.0075 | −0.0002 |
| 200 | −0.0003 | 0.0000 | −0.0003 | 0.0000 | −0.0003 | 0.0000 | −0.2469 | 0.0455 | −0.0350 | −0.0005 | −0.0144 | −0.0013 | −0.0064 | 0.0001 | |||
| 2000 | −0.0001 | 0.0000 | −0.0001 | 0.0000 | 0.0000 | 0.0000 | −0.0662 | 0.0002 | −0.0094 | 0.0011 | −0.0038 | 0.0002 | −0.0020 | 0.0000 | |||
| 0.4 | 0.15 | 100 | −0.0006 | 0.0000 | −0.0006 | 0.0000 | −0.0004 | 0.0000 | −0.4483 | 0.1102 | −0.0576 | 0.0062 | −0.0274 | −0.0004 | −0.0087 | 0.0001 | |
| 200 | −0.0003 | 0.0000 | −0.0003 | 0.0000 | −0.0002 | 0.0000 | −0.2639 | 0.0688 | −0.0362 | 0.0004 | −0.0193 | −0.0012 | −0.0066 | 0.0002 | |||
| 2000 | −0.0001 | 0.0000 | −0.0001 | 0.0000 | −0.0001 | 0.0000 | −0.1253 | 0.0074 | −0.0173 | 0.0015 | −0.0057 | 0.0000 | −0.0017 | −0.0001 | |||
Table IV.
Simulated RMSE for the optimal threshold estimator.
|
λ = −2 |
λ = −1 |
λ = −0.5 |
λ = 0 |
λ = 0.5 |
λ = 1 |
λ = 2 |
|||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| J | πW | πZ | M = N | EMP | TN | EMP | TN | EMP | TN | EMP | TN | EMP | TN | EMP | TN | EMP | TN |
| 0.4 | 0.2 | 0.1 | 100 | 0.0021 | 0.0009 | 0.0020 | 0.0009 | 0.0014 | 0.0006 | 1.5855 | 0.6834 | 0.2417 | 0.1070 | 0.1040 | 0.0459 | 0.0411 | 0.0173 |
| 200 | 0.0017 | 0.0007 | 0.0016 | 0.0006 | 0.0011 | 0.0004 | 1.2958 | 0.4576 | 0.1926 | 0.0750 | 0.0844 | 0.0316 | 0.0317 | 0.0120 | |||
| 2000 | 0.0008 | 0.0002 | 0.0008 | 0.0002 | 0.0006 | 0.0001 | 0.5992 | 0.1366 | 0.0912 | 0.0238 | 0.0388 | 0.0096 | 0.0147 | 0.0038 | |||
| 0.3 | 0.2 | 100 | 0.0021 | 0.0010 | 0.0020 | 0.0009 | 0.0015 | 0.0007 | 1.6744 | 0.7421 | 0.2491 | 0.1123 | 0.1036 | 0.0486 | 0.0410 | 0.0186 | |
| 200 | 0.0017 | 0.0007 | 0.0016 | 0.0006 | 0.0012 | 0.0005 | 1.3018 | 0.4708 | 0.1966 | 0.0822 | 0.0838 | 0.0343 | 0.0322 | 0.0131 | |||
| 2000 | 0.0008 | 0.0002 | 0.0007 | 0.0002 | 0.0006 | 0.0002 | 0.6234 | 0.1500 | 0.0929 | 0.0256 | 0.0380 | 0.0103 | 0.0148 | 0.0040 | |||
| 0.4 | 0.15 | 100 | 0.0026 | 0.0136 | 0.0042 | 0.0098 | 0.0020 | 0.0033 | 1.8280 | 0.7217 | 0.3029 | 0.2854 | 0.1307 | 0.2280 | 0.0809 | 0.1807 | |
| 200 | 0.0020 | 0.0009 | 0.0018 | 0.0008 | 0.0014 | 0.0006 | 1.4163 | 0.4512 | 0.2318 | 0.1592 | 0.1011 | 0.0936 | 0.0400 | 0.0590 | |||
| 2000 | 0.0009 | 0.0003 | 0.0008 | 0.0003 | 0.0006 | 0.0002 | 0.6640 | 0.1366 | 0.1078 | 0.0312 | 0.0436 | 0.0128 | 0.0179 | 0.0051 | |||
| 0.6 | 0.2 | 0.1 | 100 | 0.0019 | 0.0008 | 0.0017 | 0.0007 | 0.0013 | 0.0005 | 1.4508 | 0.7340 | 0.2113 | 0.0904 | 0.0863 | 0.0383 | 0.0346 | 0.0142 |
| 200 | 0.0015 | 0.0006 | 0.0013 | 0.0005 | 0.0010 | 0.0004 | 1.1808 | 0.4908 | 0.1650 | 0.0649 | 0.0703 | 0.0270 | 0.0270 | 0.0100 | |||
| 2000 | 0.0007 | 0.0002 | 0.0006 | 0.0002 | 0.0005 | 0.0001 | 0.5429 | 0.1458 | 0.0789 | 0.0209 | 0.0324 | 0.0083 | 0.0125 | 0.0032 | |||
| 0.3 | 0.2 | 100 | 0.0018 | 0.0008 | 0.0017 | 0.0008 | 0.0013 | 0.0006 | 1.5546 | 0.7771 | 0.2178 | 0.0937 | 0.0872 | 0.0393 | 0.0347 | 0.0150 | |
| 200 | 0.0015 | 0.0006 | 0.0013 | 0.0005 | 0.0010 | 0.0004 | 1.2705 | 0.5229 | 0.1712 | 0.0695 | 0.0700 | 0.0284 | 0.0270 | 0.0106 | |||
| 2000 | 0.0007 | 0.0002 | 0.0006 | 0.0002 | 0.0005 | 0.0001 | 0.5834 | 0.1505 | 0.0775 | 0.0220 | 0.0317 | 0.0087 | 0.0126 | 0.0033 | |||
| 0.4 | 0.15 | 100 | 0.0019 | 0.0009 | 0.0018 | 0.0008 | 0.0013 | 0.0006 | 1.5057 | 0.7608 | 0.2199 | 0.1030 | 0.0920 | 0.0441 | 0.0375 | 0.0168 | |
| 200 | 0.0016 | 0.0006 | 0.0015 | 0.0006 | 0.0010 | 0.0004 | 1.2393 | 0.4976 | 0.1810 | 0.0757 | 0.0744 | 0.0318 | 0.0292 | 0.0121 | |||
| 2000 | 0.0007 | 0.0002 | 0.0007 | 0.0002 | 0.0005 | 0.0001 | 0.5749 | 0.1489 | 0.0845 | 0.0236 | 0.0347 | 0.0095 | 0.0135 | 0.0037 | |||
| 0.8 | 0.2 | 0.1 | 100 | 0.0018 | 0.0008 | 0.0018 | 0.0007 | 0.0013 | 0.0006 | 1.6429 | 0.7715 | 0.2082 | 0.0899 | 0.0870 | 0.0365 | 0.0324 | 0.0136 |
| 200 | 0.0015 | 0.0006 | 0.0014 | 0.0005 | 0.0011 | 0.0004 | 1.3347 | 0.5104 | 0.1683 | 0.0654 | 0.0683 | 0.0257 | 0.0253 | 0.0094 | |||
| 2000 | 0.0006 | 0.0002 | 0.0007 | 0.0002 | 0.0005 | 0.0001 | 0.6427 | 0.1557 | 0.0780 | 0.0206 | 0.0313 | 0.0082 | 0.0120 | 0.0031 | |||
| 0.4 | 0.15 | 100 | 0.0021 | 0.0010 | 0.0021 | 0.0009 | 0.0015 | 0.0007 | 1.9928 | 0.8118 | 0.2458 | 0.1133 | 0.0972 | 0.0451 | 0.0357 | 0.0168 | |
| 200 | 0.0017 | 0.0007 | 0.0015 | 0.0006 | 0.0012 | 0.0005 | 1.6514 | 0.5513 | 0.1955 | 0.0809 | 0.0779 | 0.0321 | 0.0291 | 0.0116 | |||
| 2000 | 0.0007 | 0.0002 | 0.0007 | 0.0002 | 0.0005 | 0.0002 | 0.7475 | 0.1643 | 0.0887 | 0.0247 | 0.0352 | 0.0099 | 0.0130 | 0.0037 | |||
4. ADJUSTING FOR COVARIATES
For the CCS data, information on the age for each subject is available. Such explanatory factors (covariates) may influence the ROC curve, the Youden Index, and the optimal threshold value of the marker of interest. Faraggi [15] and Smith and Thompson [25] considered adjustments for continuous covariates, while Tosteson and Begg [26] considered ordinal test results. Schisterman et al. [16] discussed how the TN approach for estimating the ROC curve and its AUC for spiked data could be adjusted for covariates using standard linear and logistic regression methods.
We briefly review their methodology and apply it to adjusting Ĵ and t̂* for covariates. Generally, they assume that the the (possibly transformed) non-zero marker values X and Y depend linearly on p1 − 1 and p2 − 1 explanatory variables, respectively. Set
| (14) |
where X̃ = (x1, x2,..., xm)′, Ỹ =( y1, y2,..., yn)′, and βD and βH are column vectors of unknown parameters of sizes p1 and p2, respectively. Let Z̃D be an m × p1 matrix where the elements of the first column are all 1's and the other elements are the values of the explanatory variables for the diseased sample. Z̃H is similarly defined for the healthy sample. εD and εH are column vectors of size m and n, respectively, which are assumed to be composed of independently distributed normal variables with expectation 0 and variances and , respectively. The covariates for the diseased sample are not necessarily identical to those of the healthy sample. Standard regression modeling techniques need to be used in order to decide on which covariates to include. The adequacy of the model should be examined using residual analysis.
These linear regression models apply only to the non-zero part of the mixture distribution of the marker. The probability that the marker is zero (for the diseased or healthy subjects) can also be affected by covariates. A logistic model can be used to model these probabilities. For the diseased and healthy groups, respectively, we set
| (15) |
where γD and γH are p3 and p4 dimensional column vectors of unknown parameters, whereas VD and VH are column vectors of sizes p3 and p4, respectively, having 1 as the first element. VD and VH represent the covariates on which the probability of a zero marker value is dependent. These are not necessarily the same as the covariates used in (14).
The formulae in Section 2.3 for sensitivity, specificity, J, and t* remain the same, but now πZ, πW, μD, and μH are to be interpreted as functions of given covariate values. Confidence intervals for J and t* can be readily obtained using the bootstrap [27].
5. AGE ADJUSTMENT FOR THE CCS DATA
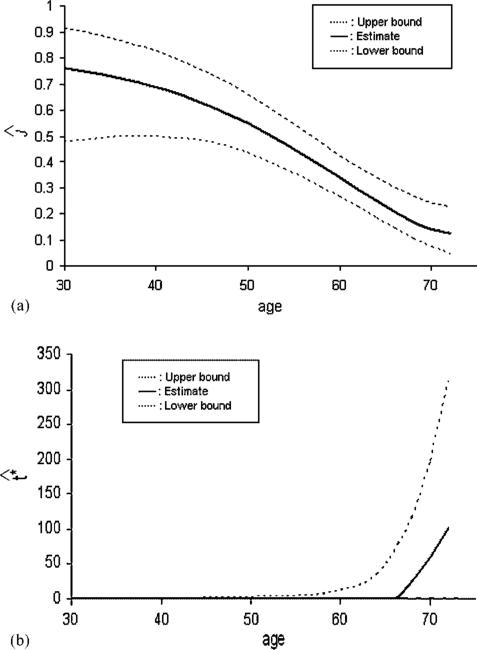
For the CCS marker data, information on each subject's age is available. The linear regression models (14) after a log transformation, using age as a possible explanatory variable, were examined. For both the healthy and diseased groups, age was found to be statistically significant (p = 0.0001, 0.001 for the healthy and diseased, respectively). Residual analysis showed no reason to reject the normal assumption for the log-transformed marker data. We examined the addition of a quadratic term in age to the linear models and it was found not to be significant. The logistic models (15) were also applied and age was found to be necessary for the healthy group and not significant (p = 0.131) for the diseased group. These models were then used to estimate J and t* as a function of age. The results are presented in Figure 6. The point-wise confidence intervals are computed using the percentile bootstrap method. The estimated Youden Index falls with increasing age. At age 30, Ĵ = 0.76 (specificity = 0.94, sensitivity = 0.82), at age 56, Ĵ = 0.43 (specificity = 0.61, sensitivity = 0.82), while at age 70, Ĵ = 0.14 (specificity = 0.58, sensitivity = 0.57). The Ĵ = 0.431 obtained when ignoring age (see Section 2) corresponds to an age of 56 and gives a wrong impression of the effectiveness of the marker.
Figure 6.
(a) Youden Index and (b) optimal threshold with 95 per cent confidence intervals for the CCS marker.
Figure 6(a) demonstrates how ignoring age gives an incorrect picture of the marker effectiveness. Clearly, the marker is better for younger men and is less effective with increasing age. Figure 6(b) indicates that the estimated optimal threshold remains at zero for most of the age range and is greater than zero for higher ages for which the marker is not very useful. This seems to suggest that the detection of the presence or absence of calcium captures most of the information in this marker.
6. DISCUSSION
This paper deals with the estimation of the Youden Index and its associate threshold or cutoff value for marker data that has a mass at zero but can be considered continuous on the positive real line. We combine a parametric mixture approach along with the use of a Box–Cox transformation. The estimates of the Youden Index and its associated threshold value obtained through this TN approach were shown by simulation to perform better than the commonly used non-parametric empirical procedure. In addition, the TN approach is shown to be readily generalizable to permit adjustment of the estimates for explanatory variables. A referee has pointed out that a mass at another point (with the remaining values greater than that point) could be handled similarly simply by a translation of the marker values. A mass at some other point in the midst of the data would require more complicated procedures since formulae (3) and (4) for sensitivity and specificity would no longer hold.
ACKNOWLEDGEMENTS
The authors would like to thank the referees, Associate Editor and Editor for their helpful comments. This work was supported by the Intramural Research Program of the National Institutes of Health, National Institute of Child Health and Human Development.
Contract/grant sponsor: National Institutes of Health
Contract/grant sponsor: National Institute of Child Health and Human Development
Footnotes
This article is a U.S. Government work and is in the public domain in the U.S.A.
REFERENCES
- 1.Zhou XH, Obuchowski NA, McClish DK. Statistical Methods in Diagnostic Medicine. Wiley; New York: 2002. [Google Scholar]
- 2.Shapiro DE. The interpretation of diagnostic tests. Statistical Methods in Medical Research. 1999;8:113–134. doi: 10.1177/096228029900800203. [DOI] [PubMed] [Google Scholar]
- 3.Youden WJ. Index for rating diagnostic tests. Cancer. 1950;3:32–35. doi: 10.1002/1097-0142(1950)3:1<32::aid-cncr2820030106>3.0.co;2-3. [DOI] [PubMed] [Google Scholar]
- 4.Kramar A, Faraggi D, Fortune A, Reiser B. mROC: a computer program for combining tumour markers in predicting disease states. Computer Methods and Programs in Biomedicine. 2001;166:199–207. doi: 10.1016/s0169-2607(00)00129-2. [DOI] [PubMed] [Google Scholar]
- 5.Schisterman EF, Perkins N, Liu A, Bondell H. Optimal cut-point and its corresponding Youden Index to discriminate individuals using pooled blood samples. Epidemiology. 2005;16:73–81. doi: 10.1097/01.ede.0000147512.81966.ba. [DOI] [PubMed] [Google Scholar]
- 6.Fluss R, Faraggi D, Reiser B. Estimation of the Youden Index and its associated cutoff point. Biometrical Journal. 2005;47:458–472. doi: 10.1002/bimj.200410135. [DOI] [PubMed] [Google Scholar]
- 7.Perkins NJ, Schisterman EF. The Youden Index and the optimal cut-point corrected for measurement error. Biometrical Journal. 2005;47:428–441. doi: 10.1002/bimj.200410133. [DOI] [PubMed] [Google Scholar]
- 8.Greiner M, Pfeiffer D, Smith RM. Principles and practical application of the receiver-operating characteristic analysis for diagnostic tests. Preventive Veterinary Medicine. 2000;45:23–41. doi: 10.1016/s0167-5877(00)00115-x. [DOI] [PubMed] [Google Scholar]
- 9.Otto M, Wiltfang J, Schütz E, Zerr I, Otto A, Pfahlberg A, Gefeller O, Uhr M, Giese A, Weber T, Kretzschmar HA, Poser S. Diagnosis of Creutzfeldt–Jakob disease by measurement of S100 protein in serum: prospective case–control study. British Medical Journal. 1998;316:577–586. doi: 10.1136/bmj.316.7131.577. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Lamy P-J, Grenier J, Kramar A, Pujol J-P. Pro-gastrin-releasing peptide, neuron specific enolase and chromogranin A as serum markers for small cell lung cancer. Lung Cancer. 2000;29:197–203. doi: 10.1016/s0169-5002(00)00113-6. [DOI] [PubMed] [Google Scholar]
- 11.Grmec S, Gasparovic V. Comparison of APACHE II, MEES and Glasgow Coma Scale in patients with nontraumatic coma for prediction of mortality. Critical Care. 2001;5:19–23. doi: 10.1186/cc973. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Wehler M, Kokoska J, Reulbach U, Hahn EG, Strauss R. Short-term prognosis in critically ill patients with cirrhosis assessed by prognostic scoring systems. Hepatology. 2001;34:255–261. doi: 10.1053/jhep.2001.26522. [DOI] [PubMed] [Google Scholar]
- 13.Geisser S. Comparing two tests used for diagnostic or screening proceses. Statistics and Probability Letters. 1998;40:113–119. [Google Scholar]
- 14.Shaw LJ, Raggi P, Schisterman EF, Berman DS, Callister TQ. Prognostic value of cardiac risk factors and coronary artery calcium screening for all-cause mortality. Radiology. 2003;228:826–833. doi: 10.1148/radiol.2283021006. [DOI] [PubMed] [Google Scholar]
- 15.Faraggi D. Adjusting ROC curves and related indices for covariates. Journal of the Royal Statistical Society—Series D—The Statistician. 2003;52:179–192. [Google Scholar]
- 16.Schisterman EF, Reiser B, Faraggi D. ROC analysis for markers with mass at zero. Statistics in Medicine. 2006;25:623–638. doi: 10.1002/sim.2301. [DOI] [PubMed] [Google Scholar]
- 17.Zou KH, Hall WJ. Two transformation models for estimating an ROC curve derived from continuous data. Journal of Applied Statistics. 2000;27:621–631. [Google Scholar]
- 18.Zou KH, Hall WJ. Semiparametric and parametric transformation models for comparing diagnostic markers with paired design. Journal of Applied Statistics. 2002;29:803–816. [Google Scholar]
- 19.Faraggi D, Reiser B. Estimation of the area under the ROC curve. Statistics in Medicine. 2002;21:3093–3106. doi: 10.1002/sim.1228. [DOI] [PubMed] [Google Scholar]
- 20.O'Malley A, Zou KH. Bayesian multivariate hierarchical transformation models for ROC analysis. Statistics in Medicine. 2006;25:459–479. doi: 10.1002/sim.2187. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Zou KH, Tempany CM, Fielding JR, Silverman SG. Original smooth receiver operating characteristic curves estimation from continuous data: statistical methods for analyzing the predictive value of spiral CT of ureteral stones. Academic Radiology. 1998;5:680–687. doi: 10.1016/s1076-6332(98)80562-x. [DOI] [PubMed] [Google Scholar]
- 22.Molodianovitch K, Faraggi D, Reiser B. Comparing the areas under two correlated ROC curves: parametric and non-parametric approaches. Biometrical Journal. 2006;48:745–757. doi: 10.1002/bimj.200610223. [DOI] [PubMed] [Google Scholar]
- 23.Hanley JA. The robustness of the ‘Binormal’ assumptions used in fitting ROC curves. Medical Decision Making. 1988;8:197–203. doi: 10.1177/0272989X8800800308. [DOI] [PubMed] [Google Scholar]
- 24.Hanley JA. The use of the ‘binormal’ model for parametric ROC analysis of quantitative diagnostic tests. Statistics in Medicine. 1996;15:1575–1585. doi: 10.1002/(SICI)1097-0258(19960730)15:14<1575::AID-SIM283>3.0.CO;2-2. [DOI] [PubMed] [Google Scholar]
- 25.Smith PJ, Thompson TJ. Correcting for confounding in analyzing receiver operating characteristic curves. Biometrical Journal. 1996;38:857–863. [Google Scholar]
- 26.Tosteson ANA, Begg CB. A general regression methodology for ROC curve estimation. Medical Decision Making. 1988;8:204–215. doi: 10.1177/0272989X8800800309. [DOI] [PubMed] [Google Scholar]
- 27.Efron B, Tibshirani RJ. An Introduction to the Bootstrap. Chapman & Hall; London: 1993. [Google Scholar]