Applying the Lorenz curve to disease risk to optimize health benefits under cost constraints

Abstract

This paper shows how the Lorenz curve can be used, together with models of disease risk, to allocate scarce resources so as to optimize a health benefit. Consider the example of breast cancer mortality. If there were sufficient resources to provide all women with mammograms, a certain maximal number of lives could be saved. Suppose, however, that only a fraction of that amount of money is available for prevention activities. Suppose that a questionnaire could be given to assess a woman’s risk of dying of breast cancer. Depending on the amount of money available, on the ratio of the cost of a questionnaire to the cost of a mammogram, and on the Lorenz curve of the distribution of risks of breast cancer mortality, I calculate the proportion of women who should be given questionnaires, the proportion of women given the questionnaires who should be given mammograms because they have high risks, and the proportion of women not given questionnaires who should be assigned to receive mammograms at random so as to maximize the number of lives saved.

1. INTRODUCTION

Professor Joseph L. Gastwirth is one of the world’s authorities on measurement of income inequality(Gastwirth, 1972; Gastwirth and Glauberman, 1976). In 1975–1978, he guided my doctoral research in statistics at George Washington University and has remained a collaborator and friend since then. One of Joe’s many strengths is his ability to connect ideas from different disciplines. When I was searching for a thesis topic, he suggested that I investigate the Lorenz curve and related quantities, such as the Gini index, as statistics for testing goodness-of-fit to an assumed underlying distribution. It turned out that the resulting procedures had desirable properties for testing whether the underlying distribution was a classical survival distribution, such as the exponential or Weibull distribution(Gail and Gastwirth, 1978a, b). Thus this work, which grew out of Joe’s expertise and interest in measuring income inequality, had applications to survival analysis and to other biostatistical problems, such as testing whether lesions were distributed randomly along a length of artery.

In honor of Joe, I extend the application of the Lorenz curve to the question of how to allocate resources to maximize a public health benefit. Consider a population of N women at risk of developing and dying of breast cancer in a specified time interval, such as ten years. Suppose woman i has risk r_i of dying of breast cancer in the interval, for i=1,…, N. The risks in the population have a distribution F with mean μ = ∫rdF(r). Suppose administering mammography to a woman can reduce her risk of dying by a fraction ρ = 0.25, corresponding to a relative risk of 0.75 for women who have mammography versus those who do not. Some estimates of the effectiveness of screening are even higher(Freedman, Petitti and Robins, 2004). If all women in the population could be given mammography, the expected risk would be reduced to (1 − ρ)μ, and N μρ lives would be saved in expectation. Ideally, sufficient resources would be available to screen the entire population with mammography. If, however, resources are limited and a simple inexpensive questionnaire and corresponding risk prediction model are available to estimate each woman’s risk, it might save more lives to administer the questionnaire to some or all of the women, rank them according to risk, and provide the mammograms to as many women as possible who had the highest risks. We seek to maximize the number of lives saved with a fixed public health prevention budget, C.

The solution to this problem involves the Lorenz curve, $L(q)={\mu }^{-1}{\displaystyle \underset{0}{\overset{{\xi }_q}{\int }}}\mathit{rdF}(r)$, where the quantiles of F, ξ_q, are defined by F (ξ_q) = q. The Lorenz curve has another interesting interpretation. If the density of risk in the population is f, then the density of risk in women who die of breast cancer (cases) is proportional(Gail and Pfeiffer, 2005) to rf(r), which reflects length biased sampling of risk in cases. It follows that the distribution of risk in cases, F_D(q) = P(r ≤ q| case) = L(q). Thus the area under the curve 1 − L(q) as the abscissa q varies from 0 to 1 is the probability that a randomly selected case will have a risk greater than that of a randomly selected member of the general population. For a rare disease, a non-case nearly has distribution F. Hence the area under 1 − L(q) is very nearly equal to the area under the receiver operating curve(AUC)(Gail and Pfeiffer, 2005), a widely used measure of the discriminatory accuracy of the risk measuring instrument. Moreover, the Gini index, which is twice the area between the Lorenz curve and the equiangular line, is approximately equal to 2(AUC) −1. We will call the area under the curve 1 − Lq(q) versus q the AUC, even though it is only an approximation to the AUC. We use the term questionnaire to refer not only to the questionnaire, but also to an associated risk prediction model that uses questionnaire-based data to project the risk of mortality from breast cancer. In this paper, we assume that f is the density of a beta distribution with parameters a₁ and a₂, namely f (r) = {Γ(a₁ + a₂)/Γ(a₁)Γ(a₂)}r^{a₁ −1} (1 − r)^a₂−1. It follows that the distribution of risk in cases is beta with parameters a₁₊₁ and a₂.

2. FURTHER NOTATION AND PROBLEM FORMULATION

Let C_M be the cost of a mammogram and C_S be the cost of administering a questionnaire to determine risk, such as the National Cancer Institute’s Breast Cancer Risk Assessment Tool (BCRAT) (http://www.cancer.gov/bcrisktool/) (Costantino et al., 1999; Gail et al., 1989). That tool is designed to estimate the risk of breast cancer incidence, but we suppose that similar tools could be developed to estimate the risk of dying from breast cancer. If NC_M ≤ C, all women can be screened and the number of lives saved will be N ρμ.

Suppose instead that a proportion g(0 ≤ g ≤ 1) of the women are given the questionnaire and their risks are ranked in increasing order. Of those so ranked, a proportion p (0 ≤ p ≤ 1) with the highest risks are given mammograms, while a proportion m(0 ≤ m ≤ 1) of those women not given the questionnaire are selected at random for mammography. Under this strategy, the expected reduction in deaths, compared to no mammography is

$$\begin{array}{l}N\mu -Ng\underset{0}{\overset{{\xi }_{1-p}}{\int }}\mathit{rdF}(r)-Ng(1-\rho )\underset{{\xi }_{1-p}}{\overset{1}{\int }}\mathit{rdF}(r)\\ -N(1-g)\mu m(1-\rho )-N(1-g)(1-m)\mu \\ =N\mu \rho [g\{1-L(1-p)\}+(1-g)m].\end{array}$$

The fraction, B, of the maximum possible reduction, N μρ, is

$$B=g\{1-L(1-p)\}+(1-g)m.$$ (1)

The cost of this strategy is NgC_S + NgpC_M + N (1 − g)mC_M ≤ C. If we take as the unit of cost the total amount needed to give mammograms to all women, NC_M, then the total cost can be re-expressed as

$$gk+gp+(1-g)m\le h\equiv C/N{C}_M,$$ (2)

where k = C_S/C_M. The objective is to maximize B in equation (1) over g, p, and m subject to (2).

If h ≥ 1, we can afford to give mammograms to all women, and the values g = 0 and m = 1 yield the maximal B = 1. Thus we need to consider the constrained problem h < 1. To find these constrained solutions, we used the function “fmincon” in MATLAB Version 7.0.1 to minimize −B subject to the constraint (2) and the constraints that g, p and m each be confined to the interval [0,1]. A useful criterion is B/h, the ratio of the number deaths prevented by procedure that minimizes B to the number of deaths prevented by giving mammograms to a random sample of hN women.

3. RESULTS

Optimal constrained solutions for B are shown in Table 1 for k=0.02 and 0.1, for h=0.9, 0.5, and 0.1, and for beta distributions with parameters (a₁, a₂) equal to (6.55, 321), (4.23, 207) and (1, 49), which correspond respectively to AUC values of 0.607, 0.632 and 0.748. The first distribution is has the same AUC value as the BCRAT model for breast cancer incidence, and the second distribution has the same AUC value as a model with the BCRAT risk factors (age at menarche, age at first live birth, number of breast biopsies, and number of first degree relatives with breast cancer) and with seven single nucleotide polymorphisms that are associated with breast cancer risk(Gail, 2008). The third model has a higher discriminatory accuracy with AUC=0.748.

Table 1.

Optimal Strategies and Fraction(B) of Maximum Attainable Lives Saved for Several Risk Distributions, Amounts of Resources (h) and Questionnaire-to-Mammogram Cost Ratios (k). The Parameters g, p, and m Define the Optimal Strategy

a1	a2	AUC	k	h	g	p	m	B	B/h
6.55	321	0.607	0.02	0.9	1.000	0.880	0	0.945	1.05
				0.5	1.000	0.480	0	0.632	1.26
				0.1	0.757	0.112	0	0.148	1.48
4.23	207	0.632	0.02	0.9	1.000	0.880	0	0.965	1.07
				0.5	1.000	0.480	0	0.667	1.33
				0.1	0.863	0.096	0	0.166	1.66
1	49	0.748	0.02	0.9	1.000	0.880	0	0.992	1.10
				0.5	1.000	0.480	0	0.830	1.66
				0.1	1.000	0,080	0	0.277	2.77
6.55	321	0.607	0.10	0.9	0.331	0.598	1.000	0.914	1.02
				0.5	1.000	0.400	0	0.551	1.10
				0.1	0.228	0.349	0	0.111	1.11

Note: The quantity AUC is the probability that a randomly selected woman with breast cancer has a risk higher than that of a randomly selected woman from the general population. For a rare disease, this is very nearly equal to the area under the receiver operating curve. Other parameters include: the parameters of the beta distribution of risk, a₁ and a₂, the ratio k of the cost of a questionnaire risk assessment to the cost of a mammogram, the money available, h, expressed in as a fraction of the amount of money needed to give all women mammograms, the optimal proportion who get questionnaires, g, the optimal proportion p of women with questionnaires with the highest risk who get mammograms, the proportion, m, of woman who did not get questionnaires who were randomly selected for mammograms, and the ratio B of deaths saved by the optimal choices of g, p and m divided by the deaths saved by giving all women mammograms.

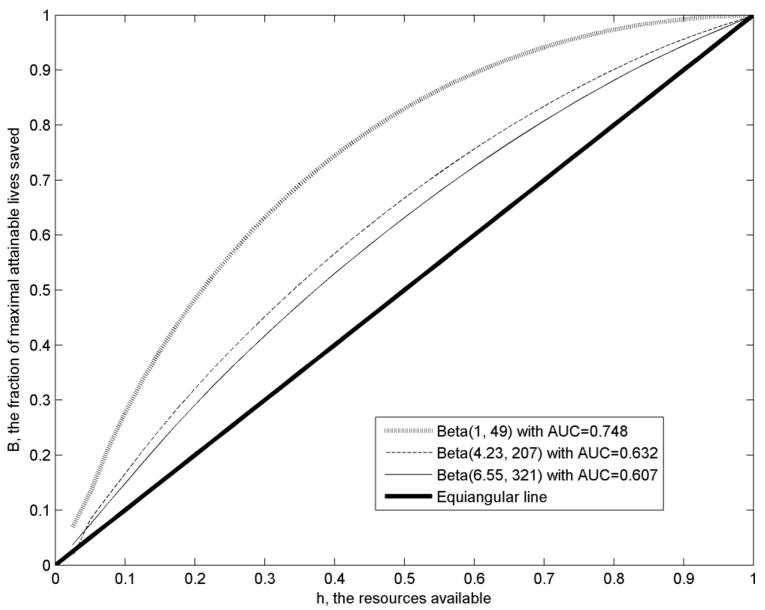
If the cost of a screening questionnaire is much smaller than that of a mammogram (k=0.02), m is always zero for the parameter values in Table 1. This reflects the fact that it is most efficient to prescreen with the questionnaire and to give mammograms only to women ranked as having the highest risk; the proportion of women given the questionnaire who get mammograms, p, is determined by the amount of money available. For each risk distribution, the optimal B increases with h. The ratio B/h indicates how much the questionnaire screening has increased lives saved compared to simply taking a random sample of the population. The greatest relative savings B/h occurred for h=0.1. Notice that B and B/h increase with the AUC of the risk model. For example, for h=0.5, B=0.632 for the model with AUC=0.607, compared to B=0.667 for the model with AUC=0.632, a 5.5% improvement. If h=0.1, the improvement is 100(0.166−0.148)/0.148=12.2%. The model with AUC=0.748 has improvements over the model with AUC=0.607 of 31.3 % and 87.2% for h=0.5 and h=0.1 respectively. Figure 1 shows the fraction of lives, B, that can be saved using the optimal strategy, as h varies from 0.025 to 1. The values of B are highest for the risk distribution with AUC=0.748 and lowest for the risk distribution with AUC=0.607. For a given value of h, the vertical distance from one of these loci to the equiangular line, B–h, is a measure of how much the optimal screening strategy increases the fraction of lives saved over simple random sampling of the population. Thus for k=0.02, the questionnaire screening strategy can increase the number of lives saved appreciably, compared to random sampling of the population to allocate mammograms, especially if the questionnaire and associated risk prediction model have good discriminatory accuracy.

Figure 1.

Plot of B, the Fraction of Maximal Attainable Lives Saved Against the Resources Available, h, Expressed as a Fraction of the Resources Needed to Give Mammograms to All Women. The Three Curves Correspond to Risk Distributions with Various AUC Values. The Equiangular Line Is Also Shown. The Cost Ratio Is k = 0.02.

If k=0.1, so that the questionnaire costs one tenth as much as a mammogram, the optimal solution may include some random sampling of the population (Table 1). For the model with AUC=0.607, and for h=0.9, the optimal solution occurs at g=0.331, p=0.598 and m=1, yielding B=0.914, which is only a slight improvement over simple random sampling (B/h=1.02). The optimal strategy is to give the questionnaire to only 33.1% of the women, and give mammograms to the 59.8% of those women with the highest risk. Then one should give mammograms to all the remaining women (66.9%) who did not get a questionnaire. Thus, relatively high questionnaire costs limit the usefulness of questionnaire screening. For h=0.5 and h=0.1, there is no random sampling of women because all the money is spent on screening and on giving mammograms only to the women with high questionnaire risk (Table 1). In these cases, the relative efficiencies compared to random sampling are also small (B/h=1.10 for h=0.5 and B/h=1.11 for h=0.1) because the questionnaire costs so much.

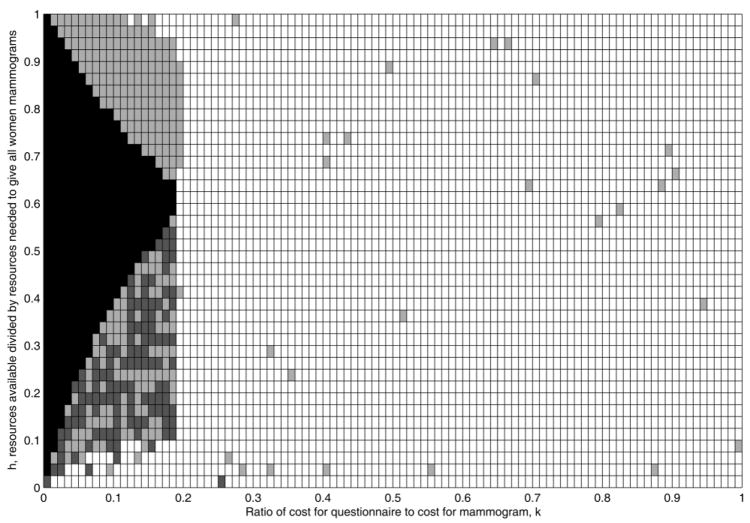
There are four basic strategies defined by: (1) g=1, which is in black in Figure 2; (2) 0<g<1 with m=0, which is in dark grey in Figure 2; (3) 0<g<1 with m>0, which is in light grey in Figure 2; and (4) g=0, which is in white in Figure 2. These four conditions require progressively less reliance on the questionnaire ranking and more reliance on random sampling. In strategy (1), all the women are given questionnaires, and the remaining money is spent on giving mammograms to a proportion p of those women at highest risk. In strategy (2), a fraction 0<g<1 of the population is given a questionnaire, and the remaining money is spent on giving mammograms to a proportion p of those women at highest risk. In strategy (3), a fraction 0<g<1 of the population is given a questionnaire, some of the remaining money is spent on giving mammograms to a proportion p of those women at highest risk, and the remainder is spent on giving mammograms at random to a fraction m of the women who did not get the questionnaire. In strategy (4), none of the women get questionnaires, and all the money is spent giving mammograms to a proportion m=h of randomly selected women. To examine circumstances under which these various strategies were optimal, I considered the risk distribution with AUC=0.607 (Figure2). For this risk distribution, strategy (1) is never optimal for k>0.175. Note that whether strategy (1) is optimal depends on both h and k. For values of h>0.65, strategy (3) that employs some random sampling is optimal for certain values of k. For values of h<0.575, strategy (2), which employs no random sampling women without questionnaires, can be optimal, provided k is not too large. As the questionnaire costs increase to k>0.2, strategy (4) is usually optimal, namely to select women at random for mammograms until the money runs out.

Figure 2.

Plot of Optimal Strategy for Various Pairs (k,h). For Each Pair, the Optimal Strategy is: (1) g=1 (Black); (2) 0<g<1, m=0 (Dark Grey); (3) 0<g<1, m>0 (Light Grey); or (4) g=0 (White).

4. DISCUSSION

Risk models are often evaluated using standard criteria, such as calibration, positive and negative predictive value, and AUC. Yet other criteria directly related to a given application may give more insight into the usefulness of a risk model, particularly one with modest discriminatory accuracy (Gail and Pfeiffer, 2005). The present paper evaluates the usefulness of inexpensive questionnaire-based risk models to increase the number of lives saved by mammography when the resources are insufficient to provide mammograms to the entire female population. One can imagine other settings where an inexpensive method of assessing risk might be useful in allocating scarce resources for a more expensive diagnostic procedure. Similar considerations might apply to allocating a scarce preventive vaccine to groups at highest risk of fatal infection or to allocating a scarce or expensive treatment to patients at greatest risk of dying without it.

The approach outlined in this paper assumed that risk models for breast cancer mortality are available, whereas widely used models predict the risk of breast cancer incidence, not death. In order to conform to the paradigm in this paper, new models of the risk of death from breast cancer would need to be devised. Such models might in fact build on models of breast cancer incidence. It as assumed that mammography reduces the risk of death by a factor ρ for all members of the population. There is some suggestion that this factor is smaller in young women(Freedman et al., 2004). Thus a more realistic development of these ideas needs to take the heterogeneity of effectiveness of mammography by age into account. Although there is debate on the value of ρ (Freedman et al., 2004), the criteria in this paper, such as B and B/h, do not depend on ρ nor on the average breast cancer mortality rate, μ, nor on the size of the population, N.

This work suggests further lines of research. It would be useful to define the precise conditions under which each of the four strategies is optimal. The optimal strategy depends in a complicated way on the Lorenz curve and on k and h, as shown in Figure 2. It would also be useful to examine how the results would change if the questionnaire-based risk model failed to rank risks correctly.