Costs of height gain in rainforest saplings: main-stem scaling, functional traits and strategy variation across 75 species

Abstract

Background and Aims

Height gain plays an important role in plant life-history strategies and species coexistence. Here main-stem costs of height gain of saplings across species within a rainforest community are compared.

Methods

Scaling relationships of height to diameter at the sapling stage were compared among 75 woody rainforest plant species in subtropical eastern Australia using standardized major axis regression. Main-stem costs of height gain were then related to other functional traits that reflect aspects of species ecological strategies.

Key Results

Slopes (β) for the height–diameter (H–D) scaling relationship were close to 1·3, in line with previous reports and with theory. Main-stem volume to achieve 5 m in height varied substantially between species, including between species within groups based on adult height and successional status. The variation was largely independent of other species traits, being uncorrelated with mature plant height (H_max) and with leaf size, and weakly negatively correlated with wood density and seed size. The relationship between volume to reach 5 m and wood density was too weak to be regarded as a trade-off. Estimated main-stem dry mass to achieve 5 m height varied almost three-fold across species, with wood density and stem volume contributing roughly equally to the variation.

Conclusion

The wide range in economy of sapling height gain reported here is presumed to be associated with a trade-off between faster growth and higher mortality rates. It is suggested that wide diameters would have a stronger effect in preventing main-stem breakage in the short term, while high wood density would have a stronger effect in sustaining stem strength over time.

INTRODUCTION

Plant size (measured as mass, height or diameter) can span ten orders of magnitude over the ontogenetic lifetime of an individual tree. Size exerts a powerful influence on plant form, function and life history (Niklas, 1995; Westoby et al., 2002). Coexisting trees can vary considerably in height at similar diameters (diameter at breast height, dbh; Thomas, 1996; King, 1996; Sterck et al., 2001; Kohyama et al., 2003; Poorter et al., 2003, 2006), and diameter–height relationships influence the ‘safety factor’ of species against buckling (Putz et al., 1983; van Gelder et al., 2006).

Two alternative interpretations can be suggested for the smaller diameter at a given height (e.g. dbh) of some species compared with others. One is that narrow-dbh species reflect a fast-growth strategy with a concomitant high risk of stem breakage. The other possibility is that narrow-dbh species compensate for limited basal thickening by having strong, high-density wood. Dense wood has a higher modulus of rupture (Niklas, 1994) and makes trees less vulnerable to breakage. If narrow-dbh species invested more in wood density, then the biomass cost of height gain and the risk of breakage might be similar across different stem-widening strategies.

Thomas (1996) examined the hypothesis that understorey trees have thicker stems (at a common height) than canopy trees in the same assemblage because diameter increment continues even after trees attain their maximum height (King, 1990). Interestingly, he found no correlation between diameter at a common height and maximum height at maturity (H_max). However, a number of studies have subsequently reported that adult shade-tolerant sub-canopy trees have thicker stems than canopy trees at the same height (King, 1996; Sterck et al., 2001; Kohyama et al., 2003; Poorter et al., 2003, 2006; King et al., 2006a), suggesting that the height–diameter (H–D) relationship does vary in relation to H_max (Thomas, 1996; King et al., 2006b; Poorter et al., 2006; Osunkoya et al., 2007). Because the diameter–height ratio increases progressively with growth, and species ranking can switch with reference to height, a more general approach to addressing this question is to assess the slope and intercept of log diameter versus log height graphs (Kerkhoff et al., 2006; Poorter and Bongers, 2006; Warton et al., 2006).

The functional basis for the expectation that some traits are influenced by growth form (plant size) is well established (see, for example, Moles et al., 2005). In addition, trait-based approaches to community ecology can potentially link ecological strategy variation and functional diversity (via scaling relationships and performance currencies) to community assembly and species coexistence (Westoby and Wright, 2006; Grime, 2006; McGill et al., 2006). Strong correlations across species have been reported for leaf size, specific leaf area (SLA) and maximum height (e.g. Fonseca et al., 2000); between leaf size, wood density, seed size and maximum height (Ackerly et al., 2002; Cornwell et al., 2006; Cornwell and Ackerly, 2009); and between shade tolerance (reflecting successional status), wood density and maximum height (Falster and Westoby, 2005; discussed in Poorter, 2008; and see Reich et al., 2003; Wright et al., 2007).

This paper compares investment in main stem at the sapling stage across 75 species in Australian subtropical rain forest. The following questions are addressed: (1) how did species vary in the main-stem investment used to attain a given height, and what were the contributions to this variation from allometry (H–D relationships) and from wood density; and (2) were those architectural traits associated with other species traits for which data were available and that are thought to be ecologically significant, namely adult stature (potential maximum height as H_max), shade tolerance, leaf size and seed size?

MATERIALS AND METHODS

Site and selection of species

Diameter at breast height over bark (dbh) and height for plants >1·0 and <10 cm dbh were collected in 2000–2001 for 18 134 individual understorey trees, small trees and shrubs from 20 previously established permanent plots in sub-tropical rain forest in eastern Australia (Kariuki and Kooyman, 2005; Kariuki et al., 2006). The aim at the time was to supplement data for larger trees (3000 individuals >10 cm dbh, representing 117 species) that had been permanently tagged and monitored for growth over decades. Individual trees were removed from the dataset if they belonged to species represented by low numbers of individuals (predominantly shade-tolerant canopy tree species), if their stems were recorded as broken or had measurements that clearly indicated they were damaged, or if they had dbh <1 cm. The resulting data covered a total of 11 111 individual plants representing 75 species from the total of 138 recorded (Supplementary Data Table S1, available online). The species came from 32 families and 62 genera, and varied substantially in adult stature and successional status.

Of the 75 species included in the study 70 were classed as shade-tolerant and five as shade-intolerant, based on local knowledge at seedling and sapling stages (Kooyman, 1996; Kariuki and Kooyman, 2005; Kariuki et al., 2006). Shade-intolerant species included both pioneers and canopy trees, and shade-tolerant species included shrubs, understorey trees and canopy trees. Rather than using these as categories, the continuous trait of maximum height at maturity as a potential predictor was used, along with shade-tolerance.

Diameter was measured at 1·3 m above ground level using a steel diameter tape or calliper. Height was measured to the topmost foliage using an extendable height pole. Species-level data for leaf size, wood traits (including density) and seed size were taken from published floras and other sources, including Bootle (1983), Stanley and Ross (1983–1989, volumes 1–3), Floyd (1989, pp. 268–270), Harden (1990–1993, volumes 1–4 with revisions), Ilic et al. (2000) and Cornelissen et al. (2003). Minimum and maximum leaf sizes reported in the floras generally reflected the range of variation in leaf size on mature plants, and juvenile leaf sizes were excluded from consideration. Leaf size reported here is for whole simple leaves and for lateral leaflets of compound leaves. Leaf size was estimated using maximum leaf length and width, where area = length × width × 0·70 (cm²), which has been shown to correlate well with photographic area estimates of rainforest tree leaves (e.g. Kraft et al., 2008). Seed size was estimated using maximum dimensions of embryo plus endocarp (length + width/2, in millimetres; reflecting average diameter). Wood density estimates for adults [dry kg m⁻³; van Gelder et al. (2006) found that adult and juvenile wood density were well correlated across species, r = 0·91, P < 0·001] were extracted from published sources. Estimated maximum height at maturity (H_max) was based on field information previously collected by R.M.K. that reflects maximum canopy height (m) for species in this location (at largest known diameters, at reproductive maturity). This provides a single value for maximum potential height for each species.

Data analysis

Relationships between height and diameter were described by fitting standardized major axis (SMA) lines, given that the questions were about co-ordination between these two growth measures, rather than about predicting one from the other (Warton et al., 2006). Tests equivalent to analysis of covariance (common slope, different elevations given a common slope, confidence intervals for slopes and elevations) were implemented through SMATR software (Falster et al., 2003, 2006; Warton et al., 2006).

RESULTS

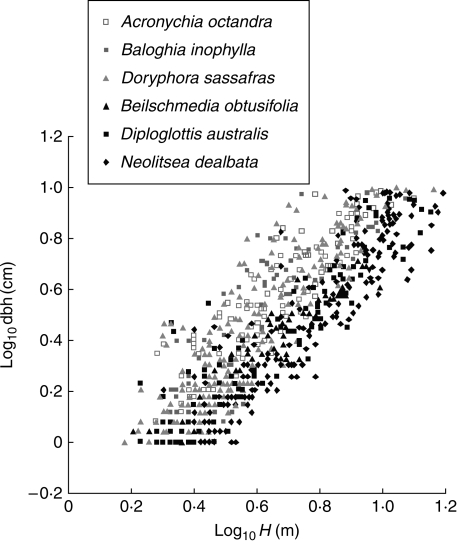
The increase in logD appeared to be linear with logH within this range of size (data shown for six species in Fig. 1; slopes and intercepts included to illustrate the main features). There was substantial scatter in the data, individual saplings within a species having quite a wide range of diameters at a given height. The scatter probably reflected the considerable variation in light and factors associated with forest structure, disturbance, stem density, and interaction effects and competition (Niklas, 1995; King, 1996; Henry and Aarssen, 1999; Niklas et al., 2003; Kariuki et al., 2006; Poorter et al., 2006). Despite the scatter around the height–diameter relationships, some species clearly tended to have greater diameter than others, at a given height (Fig. 1).

Fig. 1.

Scatterplot illustrating the relationships between log₁₀ dbh and log₁₀ height for six species. Each data point is an individual stem in the range 1–9·9 cm dbh for the six species shown in the legend that represent three each with high and low stem volume at a (low) common height. Taxonomic information for all species referred to in this study is provided in the Supplementary Data. SMA slope (β) and intercept (α) values are: Acronychia octandra – β = 1·27, α = –0·29, r² = 0·81; Baloghia inophyla – β = 1·33, α = –0·35, r² = 0·75; Doryphora sassafras – β = 1·468, α = –0·44, r² = 0·8; Beischmeidia obtusifolia – β = 1·10, α = –0·34, r² = 0·87; Diploglottis australis – β = 1·17, α = –0·37, r² = 87; Neolitsea delabata – β = 1·31, α = –0·51, r² = 0·84.

There were no consistent or interpretable differences in slopes between species (Fig. 2A, B, and Supplementary Data Table S1). The common scaling slope of the D–H relationship across the 75 species was β = 1·321, and most slopes fell between the 3/2 expected under elastic similarity and the 1/1 expected under geometric self-similarity models for stem strength and safety (McMahon, 1973; McMahon and Kronauer, 1976; Niklas, 1994, 1995). After Bonferroni correction there were only three species with slopes significantly shallower than β = 1·32, and five species with slopes significantly steeper. Neither group of species had features that stood out from those of other species (see Supplementary Data Table 3a–b). The extreme low slope shown in Fig. 2 was not among those that were significantly different.

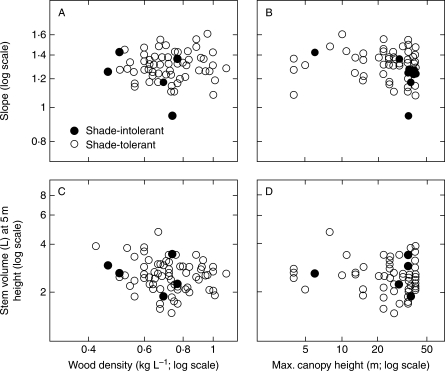
Fig. 2.

Scatterplots relating SMA slopes and volume for saplings at a common height (5 metres) to wood density and estimated maximum height at maturity. Two species groups are shown: shade-intolerant and shade-tolerant, as indicated. The species with the shallowest estimated slope is Alphitonia excelsa, a shade-intolerant tree with medium wood density. SMA slopes represent log₁₀ dbh-diameter (cm) to log₁₀ height (m) for saplings from 75 species in the range 1–10 cm dbh.

SMA fits to the relationships between diameter and height growth differed between species mainly in elevation (intercept of logH–logD graphs) rather than in slope. Diameter (dbh) at a reference height of 5 m was calculated using the SMA line fitted for each species, and varied approx. 1·8-fold (2·5–4·4 cm) across the 75 species.

The range of dbh at 5 m height translated into an approx. three-fold range of stem volume (Fig. 2C, D). Stem volumes were approximated as cones at the common height of 5 m, where V = πr²h)/3, h = 5 m (500 cm) and r was radius at the base of the cone, calculated as r/dbh = 5/(5–1·3). This approximation is not likely to be exact, but we believe it provides a reasonable relative ranking among species. The approx. three-fold range of main-stem volume used to achieve a common height (in this case 5 m) was consistent with the findings of King et al. (2006a).

We considered whether either the logD–logH slope or the estimated main-stem volume to reach 5 m height might be correlated with potential canopy height or with wood density (Fig. 2). Falster and Westoby (2005) and Poorter (2008) had previously noted that species with low potential heights were markedly different depending on whether they were shade-tolerant (understorey species) or shade-intolerant (pioneer species). Accordingly, we tested for interaction, i.e. for response to maximum height or to wood density having different slope depending on shade tolerance. These interaction terms were not significant (Table 1), and nor were any of the main effects except for a weak (r² = 0·025) tendency towards shallower slope in species with greater maximum heights (Table 1).

Table 1.

Summary data for analyses of covariance corresponding to Fig. 2

Dependent variable	Source	Type III sum of squares	d.f.	Mean square	F	P-value
Slope	Shade-tolerance	0·003	1	0·003	1·94	0·17
	Wood density	0·003	1	0·003	1·62	0·21
	Shade-tolerance × wood density	0·005	1	0·005	3·00	0·09
	Error	0·114	71	0·002
Slope	Shade-tolerance	0·003	1	0·003	1·77	0·19
	Maximum height	0·008	1	0·008	4·92	0·03
	Shade-tolerance × maximum height	0·005	1	0·005	3·01	0·09
	Error	0·112	71	0·002
Main-stem volume at 5 m	Shade-tolerance	0·000	1	0·000	0·03	0·87
	Wood density	0·005	1	0·005	0·56	0·46
	Shade-tolerance × wood density	0·000	1	0·000	0·03	0·85
	Error	0·666	71	0·009
Main-stem volume at 5 m	Shade-tolerance	0·000024	1	0·000024	0·003	0·96
	Maximum height	0·001	1	0·001	0·07	0·79
	Shade-tolerance × maximum height	0·000067	1	0·000067	0·007	0·93
	Error	0·679	71	0·010

The predicted variable is either slope of the logD–logH relationship (log scaled) or estimated main-stem volume at 5 m height (log scaled). Predictor variables are shade-tolerance (categorical) and either wood density or maximum canopy height (log scaled).

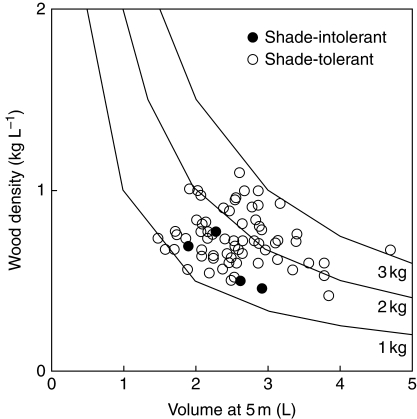
Dry mass investment in the main stem to achieve 5 m sapling height is the product of stem volume and wood density. Consideration was given to whether thicker stemmed species might tend to comprise lighter wood. Larger dbh and hence stem volume at 5 m height was not significantly correlated with lower wood density (r = 0·17, P = 0·14; Fig. 3).

Fig. 3.

Scatterplot of stem volume at a common height and wood density for 75 species. The lines represent the contours of main-stem mass (volume × density) for values of 1, 2 and 3 kg, and provide the link between points of equal cost of height growth in relation to the two measures. Shade-intolerant species (n = 5) and shade-tolerant species (n = 70) are indicated. van Gelder et al. (2006) found that adult and juvenile wood density was well correlated across species (r = 0·91, P < 0·001). Estimates of species sapling strength and safety in the understorey using measures of MR (modulus of rupture) and ME (modulus of elasticity) for adult stems showed strong correlation with (adult) wood density (see Supplementary Data, Appendix S6).

Contours in Fig. 3 indicate main-stem dry mass at 5 m sapling height calculated as estimated volume × wood density. The numbers should be interpreted comparatively between species more than absolutely because the stem volume is approximate, the wood density has been taken from adult stems elsewhere and some of the volume will be bark rather than wood. The more economical main stems were both narrow in dbh and also fairly low in wood density; more expensive main stems were either wide in dbh or had high wood density. Wood density and main-stem volume were almost equally important as sources of variation across species in estimated dry mass of main stem (54 vs. 46 %, multiple regression). Most species lay within about a two-fold range in each dimension (wood density approx. 0·5–1·0, main-stem volume approx. 2·0–4·0 L).

Sapling main-stem volume at 5 m height was only weakly positively correlated with the size of leaves (P < 0·1), and negatively (but not significantly) correlated with seed size (Table 2).

Table 2.

Cross-species correlation coefficients (r) between trait values (including stem volume at 5 m height) using species means; n = 75 except for wood density (n = 72).

	log10 max. height	log10 wood density	log10 leaf area	log10 seed size
log10 max. height	1
log10 wood density	−0·14	1
log10 leaf area	0·25**	0·30***	1
log10 seed size	0·30***	0·22**	0·18	1
log10 stem volume	−0·07	−0·17	0·20*	−0·18

Significant relationships are in bold: * P < 0·1, ** P < 0·05, *** P < 0·01.

DISCUSSION

In the saplings examined here, diameter generally increased relatively faster than height (SMA common slope across species β = 1·32, a two-fold increase in height being associated with an approx. 2·5-fold increase in dbh). This happened in a similar way across species, and in shade-intolerant compared with shade-tolerant species. The slope was in line with previously reported results for tropical rain forest species (Kohyama, 1987, 1991; Kohyama and Hotta, 1990; King, 1990; Niklas, 1995) and was consistent with theory (see, for example, Niklas, 1995; Thomas, 1996; Sterck and Bongers, 1998; Sposito and Santos, 2001). Shifting D–H ratios through ontogeny (Sterck and Bongers, 2001; Poorter et al., 2005) are thought to reflect taller stems requiring greater mechanical support, having different respiratory loads and fluid requirements, and eventually in the exposed canopy experiencing different conditions (Givnish, 1988; Niklas, 1994). In addition, as plants approach their maximum height, and with the onset of reproduction and a resultant shift in the allocation of energy, height growth must slow further compared with diameter (Charnov, 1993; Enquist et al., 1999; Koch et al., 2004). Studies including larger size classes have described non-linear diameter–height allometric relationships during ontogeny (Niklas, 1995; Thomas, 1996), and significant differences based on successional status (King, 1981; Alvarez-Buylla and Martinez-Ramos, 1992; but see Sterck and Bongers, 1998).

The increase in the logD–logH relationship (unlike its slope) did differ substantially across species among these saplings, corresponding to an estimated three-fold range in main-stem mass required to achieve a common height. King et al. (2006a) found a similar level of variation in biomass allocation across the 21 rainforest tree species they sampled from Pasoh Forest Reserve in Peninsular Malaysia, although they compared main-stem biomass at 17 m height.

In the present study, among species that required greater mass, some had higher wood density and others had wider stems. However, the trade-off between stem width and wood density was weak at best (negative correlation, r = 0·17, P = 0·14). This is somewhat contrary to the expectation of a trade-off between wood density and stem thickness in relation to safety factors (Enquist et al., 1999; Wright et al., 2003; King et al., 2006a; van Gelder et al., 2006).

Whether this range from high to low main-stem costs of height gain was associated with other aspects of plant ecological strategy was assessed. Indicators available were seed size, maximum height, leaf size, wood density and shade-tolerance. These traits were correlated among each other (Table 2) in patterns similar to those previously reported elsewhere. For example, seed and leaf size were positively correlated with H_max (Leishman et al., 2000; Moles et al., 2004), and wood density was negatively correlated with leaf size and positively correlated with seed size.

Interestingly, within the species sampled, the range from high to low main-stem costs proved to be unrelated to seed size, to leaf size and to shade-tolerance. The absence of a relationship to shade-tolerance was especially interesting, as it might be expected that shade-intolerant species typically were growing in higher light, and in general, open-grown stems are expected to be shorter and thicker, whereas stems in high-density stands are taller and thinner (Niklas, 1995; Niklas et al., 2003).

In summary, across the species sampled, main-stem expense to reach 5 m did not show any trend in association with H_max or with wood density. Main-stem expense to achieve 5 m height also varied largely independently of the other ecological traits available to us. Higher main-stem expense implies lower allocation to leaves and roots and hence slower growth than might otherwise have been the case. It seems likely that the benefit of higher main-stem expense lies in improved survival. Although continued height gain in the understorey helps trees to avoid overtopping and suppression, this must be balanced against risks of damage from limb and tree falls in order to maximize survival to reproduction (King, 1990; Kohyama and Hotta, 1990; Niklas, 1995; Thomas, 1996; Poorter et al., 2003; Falster, 2006; Osunkoya et al., 2007; Poorter, 2008). Previous studies have found positive correlations across tree species between lower wood density, higher growth rate and increased mortality rate (Enquist et al., 1999; Wright et al., 2003; King et al., 2006a; van Gelder et al., 2006). Our results show that stem width contributes as much as wood density to variation in main-stem cost, so growth and mortality rates might be more tightly related to overall main-stem cost than to wood density alone.

In theory, a combination of wider diameters with lighter wood should have a stronger effect on mechanical strength and hence on preventing main-stem breakage in the short term. The flexural stiffness of sapling stems (force required to produce a given deflection) is proportional to EI, where E is Young's modulus of elasticity, and I is the second moment of cross-sectional area, which for circular stems is πr⁴/4. At a given mass per length of stem, flexural stiffness would be substantially greater in sapling species with large diameters, because the fourth-power effect of increasing diameter is expected to outweigh the corresponding decrease in wood density (a strong correlate of modulus of elasticity). On the other hand, stems with high wood density would be expected to suffer less from attack by borers and fungi (e.g. Augspurger, 1984) and to sustain stem strength better over time. Possibly these factors could influence the wide range of alternative ways that a given main-stem cost is incurred.

SUPPLEMENTARY DATA

Supplementary data are available online at www.Aob.oxfordjournals.org and consist of the following information. Table S1: Summary results for species (75) from standardized major axis. Table S2: Trait values, and growth data for 75 species. Table S3: Summary results and trait values for eight species still significant after Bonferroni correction (from standardized major axis results) in relation to tests of the null hypothesis for slope values. Appendix S4: Synthesis of inter-specific comparisons for species-level results for species with 95 % confidence interval that bracketed (H–D = 1 : 1; geometric self-similarity model); and taxa with low R² values. Appendix S5: Binary logistic model for mortality likelihood coefficients, model outputs and mortality statistics (basic by group). Appendix S6: Results of (oridinary least-squares, OLS) regression analysis of relationship between stem safety measures (modulus of rupture and modulus of elasticity) and wood density (for adult wood only). Table S7: Species taxonomic checklist.