Population dynamics of epiphytic orchids in a metapopulation context

Abstract

Background and Aims

Populations of many epiphytes show a patchy distribution where clusters of plants growing on individual trees are spatially separated and may thus function as metapopulations. Seed dispersal is necessary to (re)colonize unoccupied habitats, and to transfer seeds from high- to low-competition patches. Increasing dispersal distances, however, reduces local fecundity and the probability that seeds will find a safe site outside the original patch. Thus, there is a conflict between seed survival and colonization.

Methods

Populations of three epiphytic orchids were monitored over three years in a Mexican humid montane forest and analysed with spatially averaged and with spatially explicit matrix metapopulation models. In the latter, population dynamics at the scale of the subpopulations (epiphytes on individual host trees) are based on detailed stage-structured observations of transition probabilities and trees are connected by a dispersal function.

Key Results

Population growth rates differed among trees and years. While ignoring these differences, and averaging the population matrices over trees, yields negative population growth, metapopulation models predict stable or growing populations because the trees that support growing subpopulations determine the growth of the metapopulation. Stochastic models which account for the differences among years differed only marginally from deterministic models. Population growth rates were significantly lower, and extinctions of local patches more frequent in models where higher dispersal results in reduced local fecundity compared with hypothetical models where this is not the case. The difference between the two models increased with increasing mean dispersal distance. Though recolonization events increased with dispersal distance, this could not compensate the losses due to reduced local fecundity.

Conclusions

For epiphytes, metapopulation models are useful to capture processes beyond the level of the single host tree, but local processes are equally important to understand epiphyte population dynamics.

INTRODUCTION

The spatial distribution of individuals in a plant population is mainly determined by seed dispersal patterns and subsequent establishment success. Most wind-dispersed seeds land near their source and very few travel over large distances (Bullock and Clarke, 2000; Nathan and Muller-Landau, 2000; Tackenberg, 2003). Seedling establishment in orchids can be facilitated by conspecific plants because the chance of forming associations with beneficial mycorrhizal fungi is higher close to established plants (Diez, 2007). However, with increasing plant density, fecundity and survival in a population decrease as a result of increasing competition (e.g. Watkinson and Harper, 1978; Mithen et al., 1984), or as a result of increased attraction of herbivores and seed predators (Feeny, 1976). Dispersal, in turn, is not only influenced by species-specific seed characteristics, but also by the distribution of adult plants and local demographic processes, primarily fecundity (Clark and Ji, 1995; Levin et al., 2003).

In a metapopulation, seed dispersal is necessary to colonize unoccupied habitats, to re-colonize extinct patches, and to transfer seeds from high to low competition patches (Husband and Barrett, 1996). However, high dispersal distances reduce local fecundity and the probability that seeds will reach a suitable habitat. Thus, there is a conflict between seed survival and colonization (Levin et al., 2003), the existence of which was demonstrated for a hypothetical metapopulation (Johst et al., 2002) and for Pinus halepensis (Bohrer et al., 2005). Whether long-distance dispersal is beneficial depends on local population dynamics. For instance, long-range dispersal has a positive effect on metapopulation persistence unless the number of potential dispersers is low due to small population growth rates (Johst et al., 2002). The interactions between fecundity and mean dispersal distance, and the consequences for population maintenance, are little studied.

The effect of spatial distribution in populations is now an essential component of metapopulation models, and has become firmly established in population biology (Hanski and Simberloff, 1997). Classical metapopulation theory focuses on the extinction and re-colonization of local patches regarding neither size and spatial arrangement of the patches nor local population dynamics (Levins, 1969). More recently, metapopulation theory has been considerably extended to include spatially explicit and realistic approaches including declining non-equilibrium, habitat-tracking, and mainland-island metapopulations (Thomas, 1994; Hanski, 1997; Harrison and Taylor, 1997). Most metapopulation models, however, concentrate on regional dynamics and ignore details on the scale of local populations (but see Bohrer et al., 2005; Volis et al., 2005; Mildén et al., 2006).

Previous studies on the population dynamics of vascular epiphytes found survival to be the most important parameter determining population growth rates (Hernández-Apolinar, 1992; Zotz et al., 2005; Zotz and Schmidt, 2006; Winkler et al., 2007), but none of these studies accounted for the spatial structure of epiphyte populations. In the present study, it is demonstrated how the incorporation of spatial structure alters model predictions of population size and the importance of demographic processes for population growth rates of three epiphytic orchids. Spatially realistic matrix metapopulation models are used, where population dynamics at the scale of the local population (individuals growing on one host tree) are based on detailed stage-structured observations of transition probabilities and epiphyte populations on different trees are connected by a dispersal function. The question is asked whether demographic processes differ significantly between trees, and if so, what the consequences for metapopulation structure and persistence are. Furthermore, metapopulations where increased dispersal results in reduced local fecundity are compared with hypothetical models where local fecundity is not related to dispersal.

METHODS AND RESULTS

Study area and species

This study was conducted in the forest reserve ‘Santuario Bosque de Niebla’ adjacent to the Instituto de Ecología, 2·5 km south of Xalapa, in central Veracruz, Mexico (19°31′N, 96°57′W; 1350 m a.s.l.). Average temperature is 19 °C, and annual precipitation is approx. 1500 mm, most of which falls in the rainy season (June to October). The forest is commonly classified as ‘bosque mesófilo de montaña’ (mesophilous montane forest) following Rzedowski (1986). A description of the epiphyte community is given by Hietz and Hietz-Seifert (1995).

The epiphytic orchids Jacquiniella leucomelana (Reichenbach f.) Schlechter, J. teretifolia (Sw.) Britton & P. Wilson, and Lycaste aromatica (Graham ex Hook.) Lindley were censused. Reproductive plants of J. leucomelana and J. teretifolia were found on trees with a diameter at breast height (dbh) >14 cm, and L. aromatica only on trees >50 cm dbh (Hietz et al., 2006). None of the species is restricted to a single host tree species although there are preferences for Quercus spp., which are dominating the forest (Hietz et al., 2006).

Population census

In an area of approx. 3 ha within the Santuario Bosque de Niebla all accessible individuals on ten trees were tagged in August 2001. Individuals on a tree were treated as a subpopulation, resulting in five subpopulations of J. leucomelana, and six of J. teretifolia and L. aromatica (Fig. 1). According to epiphyte density estimates in this part of the forest, approx. 25 % of J. leucomelana, 60 % of J. teretifolia, and 75 % of L. aromatica individuals were sampled (Hietz et al., 2006; M. Winkler, unpubl. res.). In February of the years 2002–2005, survival, vegetative growth and reproduction of the tagged individuals, and new seedlings were recorded. In the Jacquiniella species, the ramets, open flowers, dehisced flowers and fruits were counted, and the length of the longest ramet was measured to the nearest 0·5 cm. In L. aromatica, the number of peduncles and fruits was recorded. The height, breadth and width of each living pseudobulb of L. aromatica were measured in the first census, and only height of the new pseudobulb in the subsequent censuses because width and length are highly correlated with height (Winkler, 2001). Pseudobulb volume was calculated as an ellipsoid

1

where H, B and W are pseudobulb height, breadth and width, respectively. The sum of the volume of all living pseudobulbs was the size of an individual.

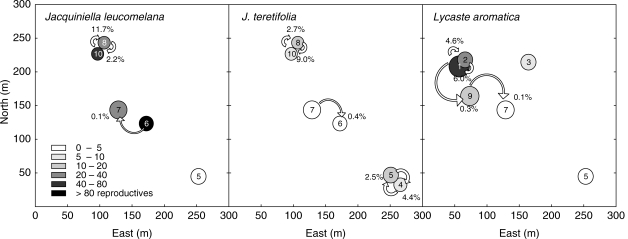
Fig. 1.

Characteristics of epiphyte subpopulations on ten trees: position of occupied trees, seed flow as estimated with a dispersal model for orchid seeds (Murren and Ellison, 1998), and number of reproductive individuals. Arrows indicate the direction and magnitude of seed flow between trees with numbers indicating the mean probability (%) over three years (February in years 2002–2005) that a seedling on a target tree originates from a given source tree. The difference between the indicated probability and 100 % equates to seeds originating from the same tree (population). Trees not connected by arrows contribute <0·1 % of seeds. The size of the tree symbol is proportional to the tree diameter.

Spatially averaged matrix population models

To characterize population dynamics, the stage-classified transition matrices of Lefkovitch (1965) were used. Four stage classes were distinguished with a combination of reproductive and size criteria (Table 1). The size threshold of seedlings (s) was defined as the 95th percentile size of 1-year-old or younger seedlings. Non-reproductive adults (a) were considered to be at least the size of the 5th percentile of reproductive plants, i.e. plants that had reached the size of reproducing individuals (f), but had not yet produced flowers or currently had none. Other individuals were grouped as juveniles (j).

Table 1.

Definition of stage classes according to the presence of flowers or fruits (F), length of the longest ramet (L), number of pseudobulbs (N_p) and cumulative pseudobulb volume (V_p)

		Stage
Species	Criterion	Seedlings (s)	Juveniles (j)	Non-reproductive adults (a)	Reproductive adults (f)
Jacquiniella leucomelana	F	No	No	No	Yes
	L (cm)	≤1·5	>1·5–3	>3	Any
J. teretifolia	F	No	No	No	Yes
	L (cm)	≤1·5	>1·5–10·5	>10·5	Any
Lycaste aromatica	F	No	No	No	Yes
	Np	1	Any	Any	Any
	Vp (cm3)	≤0·4	>0·4–31·5	>31·5	Any

Transition matrices (A), where the individuals of all host trees were pooled, were built for each of the three projection intervals (February 2002 to February 2003, 2003–2004, and 2004–2005), and a mean matrix was calculated using the function ‘mean.list’ of the R-library popbio (R 2·7·0; R Development Core Team, 2008; Stubben and Milligan, 2007). These matrices contain the probabilities of transition from stage x at the beginning of a projection interval (a year, time t − 1) to stage y at the end of the interval (time t). Fecundity (F, i.e. the ‘transition’ from f-stages to the s-stage) is the number of newborn seedlings (n_s) at time t divided by the number of reproductive individuals (n_f) at time t − 1. Deterministic population growth rates λ_det (the dominant eigenvalue of the transition matrix) were calculated following Caswell (2001) for single-year matrices (see Table S1 in Supplementary Data, available online) and for mean matrices (Table 2).

Table 2.

Comparison of deterministic (λ_det) and stochastic (λ_s) growth rates of populations of epiphytic orchids

	SUM	MMemp	MMadj
Jacquiniella leucomelana
λdet	0·895	1·025	0·986
λs (95 % CI)	0·893 (0·892–0·894)	1·025 (1·024–1·025)	0·963 (0·960–0·965)
J. teretifolia
λdet	0·980	1·127	1·106
λs (95 % CI)	0·960 (0·959–0·962)	1·110 (1·109–1·111)	1·089 (1·086–1·091)
Lycaste aromatica
λdet	0·949	1·007	1·007
λs (95 % CI)	0·949 (0·948–0·949)	1·007 (1·006–1·007)	1·007 (1·006–1·007)

Given are λ_det of mean matrices over three years and λ_s (with 95 % confidence interval from simulations over 50 000 time steps) for spatially averaged matrix models (SUM) and metapopulation models [MM_emp = metapopulation models where the transitions within each host tree and dispersal between host trees are calculated separately (empirical metapopulation model); MM_adj = metapopulation models based on MM_emp where transition probabilities for stages with an initial frequency of less than five individuals were replaced by probabilities of the corresponding spatially averaged matrix model (adjusted metapopulation model)].

For each mean matrix, an elasticity matrix was constructed:

2

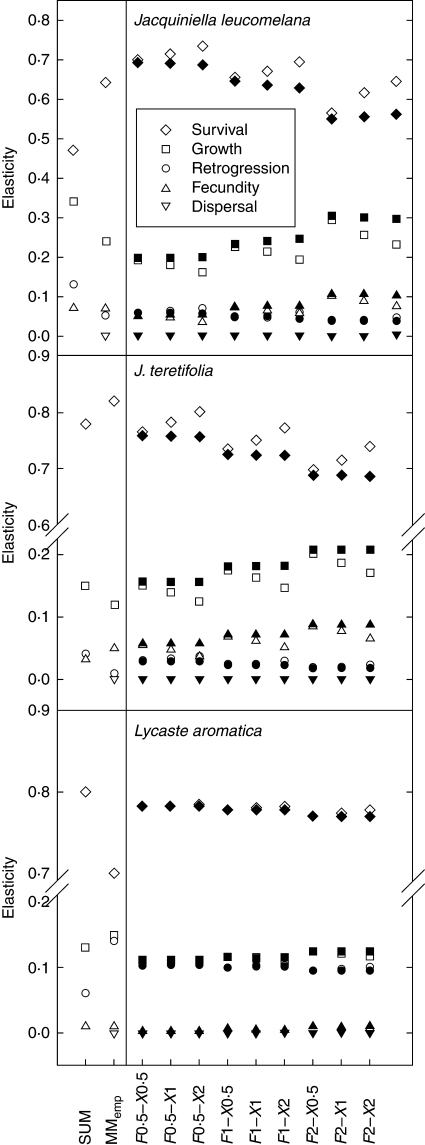
where a_ij is an entry in the transition matrix. The elasticity value for a particular matrix element (e_ij) measures the effect of changes in a_ij on λ (Caswell, 2001). Elasticity values were summed up across demographic processes (survival, growth, retrogression, fecundity and dispersal) to represent their proportional impact on population growth rates (Silvertown et al., 1993; Fig. 3A).

Fig. 3.

Elasticity of the (meta)population growth rate to demographic processes (survival, growth, retrogression, fecundity, dispersal) of epiphytic orchids. The elasticity values from mean matrices are given over three years (February in 2002–2005): a spatially averaged matrix model (SUM); a metapopulation model where the transitions within each host tree and dispersal between host trees are calculated separately (empirical metapopulation model, MM_emp); and metapopulation models where fecundity (F) and mean dispersal distance (X) were each multiplied by 0·5, 1 and 2 to create nine scenarios each for models including a conflict between seed survival and colonization (open symbols), and for models lacking this conflict (i.e. within-tree fecundity constant regardless of dispersal; closed symbols).

Unless stated otherwise, all analyses were computed using S-Plus 2000 (MathSoft Inc., 1988–1999).

Metapopulation matrix models

To account for the spatial structure of the populations, metapopulation matrices (A_m) were constructed (in the following ‘empirical metapopulation models’). These matrices consist of tree-specific transition submatrices (A_{tree1 … n}) on the main diagonal and migration submatrices (M) describing dispersal between trees (Caswell, 2001):

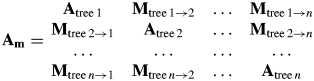3

M-submatrices contain only zeros except for fecundity. In metapopulation models the fecundity (F_m) value in each submatrix represents the number of newborn seedlings on a target tree (tree_TA) divided by the number of reproductive plants of a source tree (tree_SO):

4

The seedlings on each tree_TA were assigned to a source tree proportional to the number of seeds that tree contributed to the seed rain reaching a target tree assuming equal germination and survival of seeds from all source trees.

5

As seed rain is difficult to measure in the field, the number of reproductive plants on tree_SO (n_f-SO) was used, and the total number of reproductive plants (n_f-TOTAL) as a proxy for their seed yield assuming equal seed output per reproductive plant.

6

7

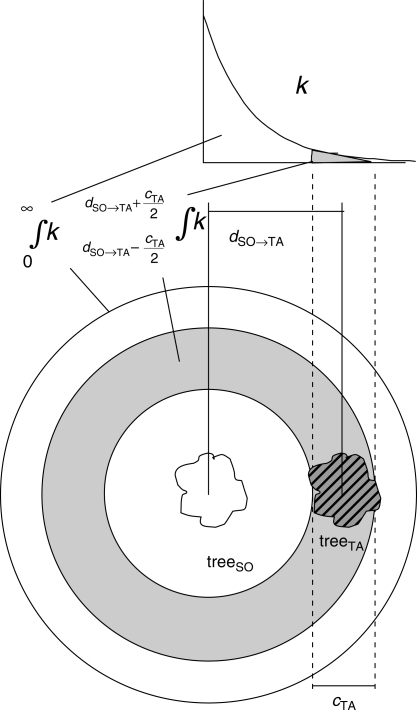
where p_SO→TA is the probability that a seed produced on tree_SO was dispersed to tree_TA, assuming equal dispersal in all directions. This probability is reflected by the area under the dispersal kernel k at the distance d_SO→TA ± c_TA/2 (crown diameter of tree_TA) between tree_SO and tree_TA in relation to total curve area (Fig. 2):

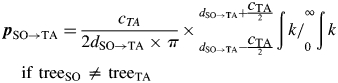8

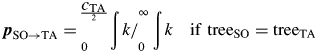9

where k is the distance-probability function describing the dispersal kernel (following Clark et al., 1998), a function of the distance between trees (d_SO→TA) and the mean dispersal distance of seeds (X):

10

Mean dispersal distance of seeds depends on seed and canopy characteristics, and on release height, and was calculated following Murren and Ellison (1998):

11

where U_f (wind velocity above canopy, 4·9 m s⁻¹), α (degree of canopy openness, 2·14), λ (factor describing the spread of settling particles around their estimated mean location, 1·53), and U_t (terminal seed velocity, 0·157 m s⁻¹) were adopted from Murren and Ellison's model for the epiphytic orchid Brassavola nodosa (Murren and Ellison, 1998). The mean canopy height in the forest (z) is 24 m (Williams-Linera and Tolome, 1996), and h, the seed release height, was set to the mean height of reproductive plants in a given source tree at the time of a given census. Empirical metapopulation models for each of the three years are shown in Table S2 in Supplementary Data, available online.

Fig. 2.

Calculation of the probability p_SO→TA that a seed produced by epiphytic orchids on a source tree (tree_SO) was dispersed to a target tree (tree_TA). This probability corresponds to the area under the dispersal kernel k covered by the target tree (hatched area) in relation to the total area covered by the seed shadow of the source tree (area enclosed by the outermost ring). The shaded area is the area at the distance d_SO→TA ± c_TA/2 (crown diameter of tree_TA) between tree_SO and tree_TA (compare eqns 8 and 9 in the text).

Because transition probabilities become inaccurate with low population sizes, an ‘adjusted metapopulation model’ was also calculated where transition probabilities for stages with an initial frequency of less than five individuals were replaced by probabilities of the spatially averaged matrix model, i.e. the mean of the entire population. Deterministic growth rates of mean empirical and adjusted metapopulation matrices are given in Table 2 and elasticity values in Fig. 3A.

Spatially averaged matrix model vs. metapopulation model

Deterministic population growth rates of mean spatially averaged matrices were below one, and of empirical metapopulations above one in all species. Population growth rates of adjusted metapopulation models, where transition probabilities of a small subpopulation are replaced by the population mean, were also consistently higher than those of spatially averaged matrices (Table 2).

In both spatially averaged and metapopulation models, survival was the most important demographic process as indicated by elasticity analysis (Fig. 3). In the Jacquiniella species, the elasticity of population growth rate to survival increased when incorporating spatial structure, whereas the elasticity to growth, retrogression and fecundity decreased. In Lycaste aromatica, this pattern was reversed. Elasticity analysis of the empirical metapopulation model showed that dispersal had no effect on metapopulation growth rate in any of the species studied.

Effect of temporal and spatial variation

To evaluate the effect of temporal (observation years) and spatial (host trees representing subpopulations) variation in transition probabilities on the fate of a plant, loglinear analyses were carried out following Horvitz and Schemske (1995) and Caswell (2001). The dependence of individual fate (F) on the explanatory variables state (S), year (Y) and tree (T) based on four-way contingency tables derived from transition probabilities of the empirical metapopulation model was examined. It was assumed that F is affected by S. Thus, all models included the SF interaction and the three-way interaction of explanatory variables, entailing the null model STY,SF. Additional models included the interactions of F with Y, T or both, leading to the models STY,SFY, STY,SFT and STY,SFY,SFT. These models were compared to the saturated model (SFYT), which considered all possible interactions. The model with the lowest Akaike information criterion (AIC) was regarded as the best model. The AIC-value of the best model was subtracted from that of the other models; rescaled values are given as ΔAIC (Burnham and Anderson 1998; Caswell, 2001). STY,SFY,SFT (i.e. interactions of F with both Y and T) was the best model for both Jacquiniella species. Jacquiniella. leucomelana was more variable among years (i.e. compared with STY,SF the model STY,SFY improved the model fit more than STY,SFT), while J. teretifolia showed stronger variability across host trees. For L. aromatica neither temporal nor spatial variation was found (Table 3).

Table 3.

Log-linear analyses of the effect of the host tree (T) and year (Y) on fates (F) of epiphytic orchids conditional on their initial state (S) based on four-way contingency tables (T,Y,S,F) following Caswell (2001)

Model	Log-likelihood ratio	d.f.	P	AIC	ΔAIC
Jacquiniella leucomelana
STY,SF	581·1	176	<0·001	229·1	276·5
STY,SFY	251·8	144	<0·001	–36·2	11·2
STY,SFT	473·4	128	<0·001	217·4	264·8
STY,SFY,SFT	144·6	96	0·001	–47·4	0
SFYT	0	0		0	47·4
Jacquiniella teretifolia
STY,SF	682·9	272	<0·001	138·9	397·9
STY,SFY	441·4	240	<0·001	–38·6	220·4
STY,SFT	245·7	192	0·005	–138·3	120·8
STY,SFY,SFT	60·9	160	1·000	–259·1	0
SFYT	0	0		0	259·1
Lycaste aromatica
STY,SF	336·1	236	<0·001	–135·9	0
STY,SFY	281·0	204	<0·001	–127·1	8·8
STY,SFT	189·5	156	0·035	–122·5	13·4
STY,SFY,SFT	138·8	124	0·172	–109·2	26·7
SFYT	0	0		72*	207·9

P-values indicate the significance of the deviation of a model from the saturated model SFYT. The model with the lowest Akaike information criterion (AIC) was regarded as the best model (given in bold). Log-likelihood ratio statistic was used to calculate AIC.

* AIC of the saturated model deviates from zero, because one degree of freedom will be deducted for each structural zero by function loglm (Venables and Ripley, 2002).

To account for environmental stochasticity, the environment was modelled using independent and identically distributed sequences (Caswell 2001). This sequence of independent and identically distributed random variables was used to select one of the three yearly matrices. Resulting stochastic population growth rates (λ_s, calculated using the function ‘stoch.growth.rate’ of the R-library popbio with 50 000 time intervals) were similar to deterministic growth rates both for spatially averaged, and empirical and adjusted metapopulation models (Table 2). The empirical metapopulation model showed that two subpopulations of J. teretifolia, and one of J. leucomelana and L. aromatica, respectively, were growing or stable (data not shown). The number of extinctions (a tree was scored as ‘occupied’ if it harboured at least one orchid individual in >50 % of 1000 repetitions) and subsequent recolonizations in the course of 50 years was recorded. The number of occupied trees decreased to two in J. leucomelana, and three in J. teretifolia and L. aromatica after 50 years. The empirical metapopulation model predicted no recolonization of extinct subpopulations in any of the species (data not shown).

Fecundity, dispersal distance and the conflict between seed survival and colonization

In an epiphyte metapopulation, a seed can either stay within its natal host tree or be dispersed beyond it (conservation-of-individuals law), in which case seed survival is less probable and local fecundity is reduced. In other words, a larger mean dispersal distance (X) in eqn (11) results in a ‘fatter’ tail of the dispersal kernel, but simultaneously fewer seeds are left within the crown of the source tree. Thus local fecundity and population growth rate will decrease with increasing X. To demonstrate the effects of this conflict on metapopulation growth rates, and extinction/recolonization dynamics, a series of metapopulation scenarios was constructed with varying fecundities (F) and mean dispersal distances (X) based on transition probabilities of the adjusted metapopulation models. Fecundity in the transition (A_{tree1 … n}) and migration (M) submatrices was calculated as:

12

where F is the fecundity of the corresponding spatially averaged matrix (A), and m is a multiplication vector (containing 0·5, 1 and 2), p_SO→TA was calculated applying eqns (8)–(11), where X was increased or decreased relative to the original value (i.e. multiplied with m). A combination of the variations in X and F results in nine scenarios (F0·5–X0·5, F0·5–X1, F0·5–X2, F1–X0·5, F1–X1, F1–X2, F2–X0·5, F2–X1 and F2–X2). These scenarios were compared with hypothetical metapopulation models where the conservation-of-individuals law was invalidated, i.e. assuming no reduction of local fecundity with increasing X by keeping the number of seeds dispersed within tree_SO constant and independent of X (i.e. p_SO→TA = 1 for A_{tree1 … n} submatrices in eqn 12).

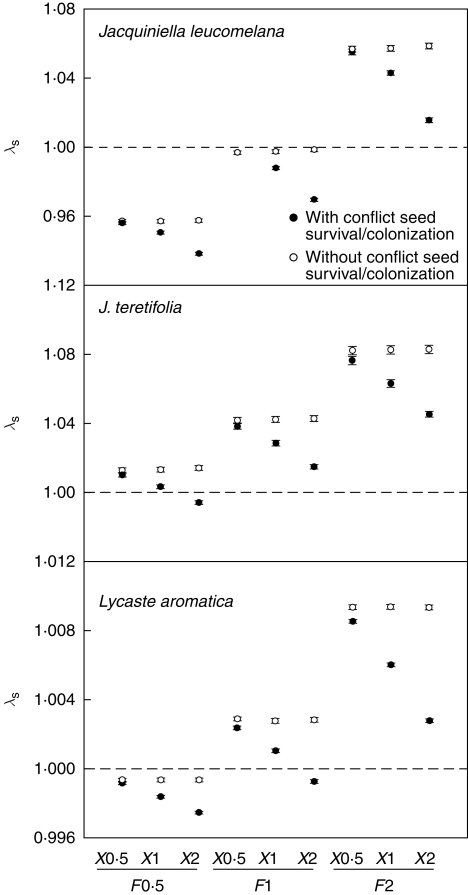
The difference in metapopulation growth rates between models with and without the conflict between seed dispersal and colonization increased with both increasing F and X (Fig. 4). Deterministic and stochastic metapopulation growth rates (calculated as described above) hardly differed, thus only λ_s values are shown. Elasticity analysis of mean matrices (carried out as described above) of both Jacquiniella species indicated that, in metapopulations, models including the conflict between seed survival and colonization, survival and retrogression were more important for metapopulation growth rates compared with the models with the conservation-of-individuals law invalidated, while growth and fecundity were less important (Fig. 3B). The differences increased with increasing X but were not significant (pairwise t-test, all P > 0·05). In L. aromatica, there were no differences between the two models.

Fig. 4.

Conflict between seed survival and colonization of epiphytic orchids demonstrated as the difference in stochastic population growth rates (λ_s) between metapopulation matrix models with or without this conflict, as indicated. Given are simulated λ_s over 50 000 time steps (±95 % CI). Three annual metapopulation transition matrices (February in years 2002–2005) where the transitions within each host tree and dispersal between host trees are calculated separately. Within-tree fecundity values (F) and mean dispersal distance (X) were multiplied by 0·5, 1 and 2 to create nine scenarios (F0·5–X0·5, F0·5–X1, F0·5–X2, F1–X0·5, F1–X1, F1–X2, F2–X0·5, F2–X1 and F2–X2).

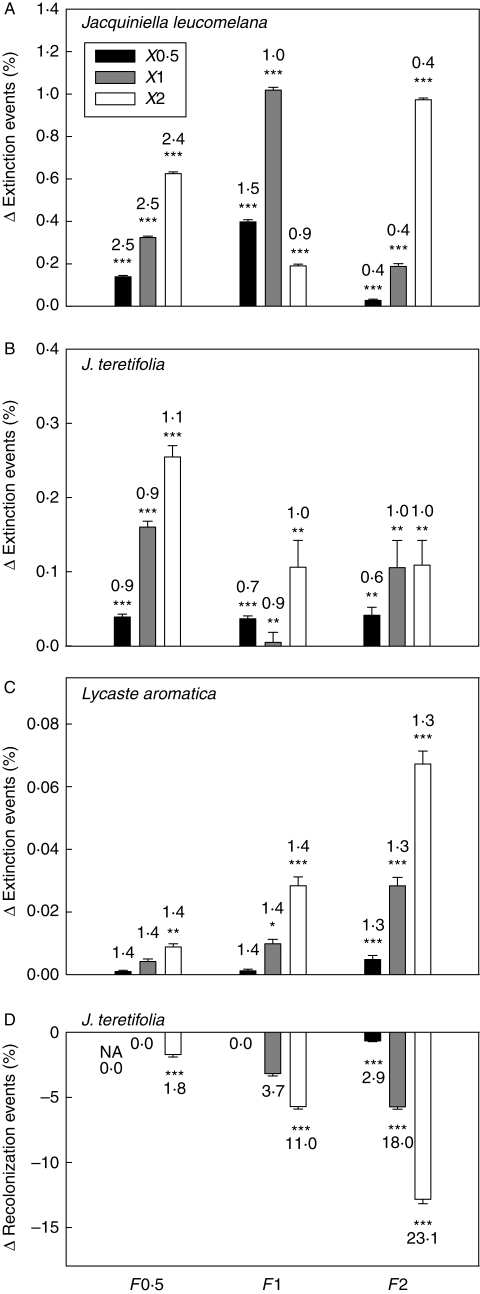
Stochastic models were calculated for each of the scenarios as described above. At each time step, one of the three yearly matrices was randomly drawn with equal probability and multiplied with the population vector of the previous year. This process was repeated 1000 times. For each tree, extinction (i.e. no individuals left on a tree) and recolonization events in the course of 50 years in percentage of possible extinctions (tree is occupied at time t − 1) and recolonizations events in percentage of possible extinctions (tree is empty at time t − 1), respectively, were recorded. Metapopulation models including the conflict between seed survival and colonization predicted more extinctions (Fig. 5A–C) and fewer recolonizations (Fig. 5D) than models with no such conflict. The larger X was within a given F, the stronger was the conflict. The difference in extinctions of L. aromatica and of recolonizations of J. teretifolia also increased with increasing F. Both F and X had a significant effect in all species (significant F : X interaction in two-factor ANOVAs, all P < 0·001).

Fig. 5.

Conflict between seed survival and colonization of epiphytic orchids demonstrated as the difference in extinction and recolonization events between metapopulation matrix models with or without this conflict. Differences (mean ± s.e.) are shown for (A–C) extinction events in percentage of possible extinctions (tree is occupied at time t − 1) and (D) recolonization events in percentage of possible recolonizations (tree is empty at time t − 1). Models were run over 50 years with 1000 repetitions of permutations of three annual transition matrices (February in years 2002–2005) where the transitions within each host tree and dispersal between host trees are calculated separately. Within-tree fecundity (F) and mean dispersal distance (X) were multiplied by 0·5, 1 and 2 to create nine scenarios. There were no recolonizations in Lycaste aromatica and <10 in Jacquiniella leucomelana. Numbers indicate extinction and recolonization events (%) in the models without the conflict. * P < 0·05, ** P < 0·01, *** P < 0·001 (t-tests between models including and lacking the conflict).

DISCUSSION

Spatial arrangement and model predictions

The populations of most epiphytic orchids studied with spatially averaged matrix models seem to be declining (Calvo, 1993; Tremblay and Ackerman, 2001; Zotz and Schmidt, 2006). Also, repeated photographs of epiphytes on eight trees revealed a negative balance between birth and mortality for Encyclia ochracea, Jacquiniella teretifolia and Lycaste aromatica, with only the creeping orchid Dichaea neglecta increasing (Hietz, 1997). Ignoring the differences among host trees and averaging matrices over trees, population growth rates below one suggest that the populations of the three epiphytic orchids studied were also declining (Table 2).

In contrast, Tremblay et al. (2006) applied Levin's metapopulation model (Levin, 1969) to analyse population dynamics of an epiphytic/lithophytic orchid alongside a riverbed and found that the metapopulation of Lepanthes rupestris is stable. However, their study did not account for local population dynamics and assumed all subpopulations to be equidistant and of equal size. Metapopulation models which relax unrealistic assumptions (Lopez and Pfister, 2001; Higgins and Cain, 2002; Baguette and Schtickzelle, 2003) suggest that neither spatial heterogeneity nor local population dynamics should be disregarded. Therefore, our present spatially realistic simulation approach (Hanski, 1997) combines classical population models not accounting for spatial structure at all and metapopulation models that entirely disregard within-tree (i.e. local patch) dynamics, enabling a direct comparison between models including and those ignoring spatial structure. In contrast to spatially averaged matrix models, metapopulation models predicted stable or even growing populations of the three orchids; also when transition probabilities were adjusted to account for low individual numbers on individual trees (Table 2).

The role of trees in metapopulation dynamics

In both spatially averaged and metapopulation model survival is by far the most important demographic process determining population growth, followed by growth (Fig. 3A). Dispersal had next to no influence in the metapopulation model, thus local processes dominate over regional ones (compare, for example, Volis et al., 2005). Why then do the population growth rates of the models diverge?

The fate of individuals of both Jacquiniella species was significantly affected by the host tree to which they were attached (Table 3; compare Horvitz and Schemske, 1995; Zotz and Schmidt, 2006). This may be related to the size or species of the host tree. For instance, trees with larger branches and a more corrugated bark or thick bryophyte mats may offer better conditions to epiphytes in terms of water supply (Hietz et al., 2002). Some of the Jacquiniella host trees are deciduous and the increased light availability compared with evergreen trees might be beneficial.

In the metapopulation models, only some trees had an influence on population growth rates. Whether a subpopulation contributed to the growth of the metapopulation was determined by its growth rate (Table S2 in Supplementary Data, available online). A subpopulation with a growth rate >1 is predicted to grow and to persist, regardless of its initial size. In contrast, in a spatially averaged matrix where individuals from growing and shrinking subpopulations are lumped together, large subpopulations have more weight because they harbour more individuals. If these large subpopulations happen to be in decline, so is the whole population. Thus, spatially averaged models of epiphytic orchids might underestimate population growth, which could explain the negative growth rates found in most models of epiphytes populations (Calvo, 1993; Tremblay and Ackerman, 2001; Zotz and Schmidt, 2006).

Dispersal, fecundity and the conflict between seed survival and colonization

Dispersal is a key process that shapes the spatial dynamics of plant populations and influences the probabilities of colonizing new sites as well as the extinction of existing populations (Nathan and Muller-Landau, 2000). According to the present elasticity analysis, dispersal had only a very small effect on population growth rates (Fig. 3B). Although there was some seedling ‘exchange’ between trees, dispersal beyond adjacent trees was a very rare event in our models (Fig. 1). The leptokurtic dispersal kernel for wind-dispersed seeds based on wind-channel experiments (Murren and Ellison, 1998) used in the present study could have underestimated the ‘fatness’ of the tail of the curve (Bullock and Clarke, 2000). However, independent population genetic studies of orchids (Trapnell and Hamrick, 2004; Jacquemyn et al., 2007; but see Trapnell et al., 2004) also show that most recruitments occur within a few metres from the mother plant. Seed numbers in orchids are very high (Arditti and Ghani, 2000), reflecting the small chance of finding a safe site including a fungal partner for germination. The number of seedlings relative to seed production (number of seeds/capsule × number of fruits; M. Winkler and P. Hietz, unpubl.res.) was 0·4 ‰ in J. leucomelana, 0·1 ‰ in J. teretifolia, and only 0·006 ‰ in L. aromatica. Seed dispersal to other trees was therefore orders of magnitudes higher than effective seedling exchange. One caveat of the present metapopulation model is that it ignores colonization of new trees (Snäll et al., 2003). Lepanthes rupestris initially colonizes unoccupied trees with a mean probability of 1·1 % per year (Tremblay et al. 2006), but distances between trees are much smaller than in the forest studied here. Thus, colonization events are probably very rare in the present system, given the low seedling exchange rates among local populations (Fig. 1).

As the chance of finding a safe site beyond the patch of origin is low, increasing dispersal distance results in reduced seed survival at the (meta)population level (Levin et al., 2003; Bohrer et al., 2005; Cousens et al., 2008). The more seeds are dispersed beyond their natal tree and the farther they travel on average, the more get lost in the unsuitable matrix between host trees (e.g. Bohrer et al., 2005) and, as they become unavailable for local fecundity, they reduce local population growth. This conflict was evident in the populations of the epiphytic orchids studied where population growth rates (Fig. 4), as well as extinctions and recolonizations of local patches (Fig. 5) differed significantly between models where local fecundity was affected by dispersal distance and those where local fecundity was kept constant.

Bohrer et al. (2005) suggest that selection should favour long-distance dispersal under intermediate local extinction frequencies. Populations with low extinction probabilities do not profit from long-distance dispersal because patch turnover is slow and most available patches are eventually occupied. In populations with high local extinction pressure, a high proportion of seeds lost through long-distance dispersal, most of which will not found a new population, would increase the probability of local extinction. Therefore traits enhancing local survival, including lower dispersal distance, should be selected for (Bohrer et al., 2005). Apart from extinctions as a consequence of demographic stochasticity (overall low population size in combination with spatial isolation), epiphyte populations are particularly prone to environmental stochasticity such as branchfall (Hietz, 1997; Zotz et al., 2005; Zotz and Schmidt, 2006), suggesting rather high local extinction rates. Particularly in species growing in large clusters, such as the orchids studied here, the fall of individual branches may wipe out the entire population on a tree, but the effect of high rates of extinctions caused by the host tree's death (Overton, 1994; Snäll et al., 2005; Tremblay et al., 2006) in this context remains unknown. With increasing mean dispersal distance extinction probabilities increased (Fig. 5A–C) and population growth rates decreased (Fig. 4) in the epiphytic orchids because more seeds travelled beyond the original – suitable – patch and were mostly lost. Though increasing mean dispersal distance also increased the number of recolonization events (Fig. 5D), these could not compensate for the reduced local fecundity (Fig. 4).

The conflict between seed survival and colonization was more pronounced in the two Jacquiniella species, which prefer thinner branches and where survival had less and fecundity had more influence on population growth rates than in Lycaste (Figs 4 and 5). In the latter species, where population growth rates are almost independent of fecundity, how many seeds get lost in the unsuitable matrix between host trees has little effect as long as the trees do not die.

Conclusions

When analysing the population dynamics of three epiphytic orchid species in a metapopulation context, both regional (between-tree) and local (within-tree) processes were important in the populations of Jacquiniella spp., though the latter dominated. Since most trees in the forest appear to be suitable habitats for Jacquiniella spp. (in the sense that at least some individuals can germinate and establish there) they may be characterized as ‘spatially extended populations’ (Freckleton and Watkinson, 2002). However, if a host tree effect (e.g. availability of mycorrhizal fungi) considerably shortens the number of suitable trees, the populations may be categorized as ‘regional ensembles’ where the amount of unsuitable habitat exceeds that of suitable sites (Freckleton and Watkinson, 2002). In contrast to Jacquiniella spp., the persistence of the non-equilibrium metapopulation (sensu Harrison and Taylor, 1997) in L. aromatica depended on a single subpopulation with measurable exchange only between two neighbouring trees (Table S2 in Supplementary Data available online). We found the metapopulation concept useful to capture processes beyond the level of a single host tree. It may produce more realistic and accurate analyses of epiphyte populations and uncover potential bias in spatially averaged matrix models. However, the analysis of the conflict between seed survival and colonization showed that processes ensuring local survival should be selected for, whereas long-distance dispersal played a minor role in population maintenance. Thus, also in metapopulation models, local demographic processes are important and need to be included.

SUPPLEMENTARY DATA

Supplementary data are available online at www.aob.oxfordjournals.org and consist of the following files. Table S1: Spatially averaged transition matrices of populations of epiphytic orchids. Table S2: Metapopulation matrices (empirical metapopulation models) of populations of epiphytic orchids.