Identifying ontogenetic, environmental and individual components of forest tree growth

Abstract

Background and Aims

This study aimed to identify and characterize the ontogenetic, environmental and individual components of forest tree growth. In the proposed approach, the tree growth data typically correspond to the retrospective measurement of annual shoot characteristics (e.g. length) along the trunk.

Methods

Dedicated statistical models (semi-Markov switching linear mixed models) were applied to data sets of Corsican pine and sessile oak. In the semi-Markov switching linear mixed models estimated from these data sets, the underlying semi-Markov chain represents both the succession of growth phases and their lengths, while the linear mixed models represent both the influence of climatic factors and the inter-individual heterogeneity within each growth phase.

Key Results

On the basis of these integrative statistical models, it is shown that growth phases are not only defined by average growth level but also by growth fluctuation amplitudes in response to climatic factors and inter-individual heterogeneity and that the individual tree status within the population may change between phases. Species plasticity affected the response to climatic factors while tree origin, sampling strategy and silvicultural interventions impacted inter-individual heterogeneity.

Conclusions

The transposition of the proposed integrative statistical modelling approach to cambial growth in relation to climatic factors and the study of the relationship between apical growth and cambial growth constitute the next steps in this research.

INTRODUCTION

The study of forest tree growth components has long suffered from the difficulty associated with obtaining biologically meaningful growth data on the basis of retrospective measurements. In classical forest tree growth study, the retrospective growth data are either not explicitly related to the years of growth or the years of growth are unevenly sampled within the growth data. This is a definitive drawback if one wants to relate inter-annual growth fluctuations to climatic factors. For some pine species, the systematic location of a tier of branches at the top of the shoot greatly facilitates the retrospective measurement of the length of successive annual shoots along the trunk (see Cannell et al., 1976). However, for many conifers and broadleaved trees, this type of retrospective measurement is far more difficult. The development of expertise in plant morphology and architecture – see Barthélémy and Caraglio (2007) for a survey – has enabled the retrospective measurement of annual shoot characteristics along the trunk of various tree species including cedar (Sabatier et al., 2003), beech (Nicolini et al., 2001), oak (Heuret et al., 2003) and walnut (Sabatier and Barthélémy, 2001). This has opened new perspectives for the study of forest tree growth components.

Tree structure development can be reconstructed at a given observation date from external morphological markers (such as cataphyll or branching scars) corresponding to past events. Observed apical growth, as given for instance by the length of successive annual shoots along a tree trunk, is assumed to be mainly the result of three components: an ontogenetic component, an environmental component and an individual component. The ontogenetic component is assumed to be structured as a succession of roughly stationary phases that are asynchronous between individuals (Guédon et al., 2007), while the environmental component is assumed to take the form of local fluctuations that are synchronous between individuals. This environmental component is thus assumed to be a ‘population’ component as opposed to the individual component. The individual component represents the growth level deviation in each phase of a tree with reference to the average tree. The key question tackled in Guédon et al. (2007) was whether the ontogenetic growth component along an axis at the growth unit or annual shoot scale takes the form of a trend (i.e. a gradual change in the mean level) or of a succession of phases. Their results support the assumption of abrupt changes between roughly stationary phases rather than gradual changes. These phase changes corresponding to new morphological events (e.g. root development, branching, flowering; see Barthélémy and Caraglio, 2007) are probably expressions of endogenous equilibriums. Their starting assumption was a decomposition model in which observed growth is the result of two components, one ontogenetic and one environmental (mainly of climatic origin); see Hanson et al. (2001) for the tree response to rainfall. In their approach, only plant response variables were considered. In order to characterize the environmental component better, we here propose to incorporate both plant response variables and climatic explanatory variables in dedicated statistical models. An interesting consequence of the assumption of succession of phases is the fact that the phases identified can be used as an instrumental device to differentiate the influence of climatic factors (environmental component) and the inter-individual heterogeneity (individual component) between phases. The individual component may cover effects of diverse origins but always includes a genetic effect; see Bradshaw and Settler (1995) and Danusevicius (2001) for the effect of genetic factors on annual shoot length and Segura et al. (2008) for the effect of genetic factors on tree architecture. Other effects correspond to the local environment of each individual; see Waring et al. (1987) and Lefèvre et al. (1994) for the impact of pathogen infestation on leaf photosynthesis and Robinson et al. (2001), Pinno et al. (2001) and Dolezal et al. (2004) for the competition between plants for light resources. These factors are rarely measurable retrospectively for each individual (Heuret et al., 2003) and when accessible, the measurements are time consuming (Jalkanen et al., 1994).

Véra et al. (2004) introduced Markov switching linear mixed models to jointly model growth phases, the effect of time-varying climatic factors and inter-individual heterogeneity (see also Chaubert et al., 2007). Unlike the approach based on hidden semi-Markov chains proposed by Guédon et al. (2007), the length of each growth phase was not explicitly modelled in Markov switching linear mixed models. Here we propose to use semi-Markov switching linear mixed models that generalize both hidden semi-Markov chains and Markov switching linear mixed models. In a semi-Markov switching linear mixed model, the underlying semi-Markov chain represents both the succession of growth phases and their lengths, while the linear mixed models attached to each state of the semi-Markov chain represent both the effect of time-varying climatic explanatory variables and inter-individual heterogeneity. The effect of climatic explanatory variables is modelled as a fixed effect and inter-individual heterogeneity as a random effect. Thus, the introduction of random effects makes it possible to decompose the total variability into two parts: variability due to inter-individual heterogeneity and residual variability.

Semi-Markov switching linear mixed models were applied to the analysis of successive annual shoots along Corsican pine and sessile oak trunks previously analysed in Guédon et al. (2007). We were interested in both population properties and individual behaviour with regard to tree growth components and we therefore investigated how the effect of climatic factors and inter-individual heterogeneity change with ontogeny, considered here as successive growth phases.

MATERIALS AND METHODS

Growth component analysis is illustrated by examples corresponding to species with contrasted plasticity (monocyclic versus polycyclic species), to different forest stand management practices (trees born in the nursery and later transplanted versus natural regeneration) and sampling protocols (all the trees versus only the dominant and co-dominant trees). The characteristics of the two data samples are summarized in Table 1.

Table 1.

Characteristics of the data samples

	Corsican pines	Sessile oaks
No. of sequences (length range)	103	65
	6 years old: 31 (6)	15 years old: 45 (10–15)
	12 years old: 29 (9–11)	29 years old: 19 (15–24)
	18 years old: 30 (15–17)
	23 years old: 13 (20–21)
Annual shoot length (cm) range, mean, s.d.	0–85, 31·82, 20·73	1–148, 38·04, 26·42
Silvicultural intervention	none	thinning
Origin	nursery	natural regeneration

Corsican pines (Pinus nigra subsp. laricio var. corsicana)

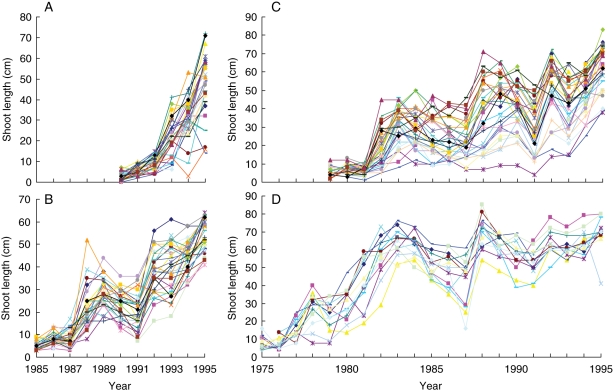
The data set comprised four sub-samples of Corsican pines planted in a forest stand in the ‘Centre’ region (France): 31 6-year-old trees (first year not measured), 29 12-year-old trees (first year not measured), 30 18-year-old trees (first year not measured) and 13 23-year-old trees (two first years not measured). Trees in the first two sub-samples (6 and 12 years old) were selected on the basis of the distribution of tree height (i.e. dominant, co-dominant and dominated classes) within the stand while trees in the two other sub-samples (18 and 23 years old) were selected on the basis of the distribution of diameter at breast height within the stand. Trees in the first sub-sample (6 years old) remained in the nursery in an open location for 2 years before transplantation while trees in the three other sub-samples remained in the nursery for 3 years before transplantation. Plantation density was 1800 stems ha⁻¹ for the first sub-sample (6 years old) and 2200 stems ha⁻¹ for the three other sub-samples. Tree trunks were described by annual shoot where two quantitative variables were recorded for each annual shoot, namely length (in cm) and number of branches per tier; see Fig. 1 for the ‘length of the annual shoot’ variable. The first non-measured annual shoots (immediately after germination) were always very short. The trees were not subject to any silvicultural interventions. Data for daily rainfall (in mm) were supplied by Météo France (Chambon-la-Forêt, a close meteorological forest station) for the period from 1975 to 1995 (year of the last elongated shoot for the four sub-samples).

Fig. 1.

Four sub-samples of Corsican pines: length of successive annual shoots along trunks of (A) 6-, (B) 12-, (C) 18- and (D) 23-year-old trees.

Sessile oaks (Quercus petraea)

The data set comprised two sub-samples of sessile oaks: 46 15-year-old trees and 19 29-year-old trees (last 24 years measured). These trees, originating from natural regenerations, were observed in a private forest near Louppy-le-château (north-east France). It should be noted that the silvicultural practices employed favoured synchronous germination in the years following mass fruiting; see Heuret et al. (2000) for more details. Stand density was 2000 stems ha⁻¹. Tree trunks were described by annual shoot where the length (in cm) was recorded for each annual shoot. Sessile oak is characterized by polycyclic growth, i.e. an annual shoot may be composed of several successive growth units (i.e. portion of the axis built up between two resting phases), while Corsican pine is mainly characterized by monocyclic growth with very little polycyclism in early plant life. Data for daily rainfall (in mm) were supplied by Météo France (Saint-Dizier meteorological station) for the period from 1973 to 1997 (year of the last elongated shoot for the two sub-samples).

Methods

This section first introduces Gaussian hidden semi-Markov chains (GHSMCs) where the observation models are simple Gaussian distributions. In the present context, the succession of growth phases and the length of each phase (in number of years) are both represented by a non-observable semi-Markov chain while the length of the successive annual shoots (in cm) in each growth phase is represented by Gaussian observation distributions attached to each state of the semi-Markov chain. Hence, each state of the semi-Markov chain represents a growth phase. A J-state Gaussian hidden semi-Markov chain is defined by four subsets of parameters:

1. Initial probabilities (π_j; j = 1, … , J) to model which is the first phase occurring in the sequence measured for a tree.

2. Transition probabilities (p_ij; i, j = 1, … , J) to model the succession of growth phases along a tree trunk.

3. Occupancy distributions attached to non-absorbing states (a state is said to be absorbing if, after entering this state, it is impossible to leave it) to model the growth phase length in number of years (i.e. the time spent in each growth phase). As possible parametric state occupancy distributions, binomial distributions B(d, n, p), Poisson distributions P(d, λ) and negative binomial distributions NB(d, r, p) with an additional shift parameter d ≥ 1 were used.

4. Gaussian observation distributions to model annual shoot length in each growth phase (a Gaussian distribution can be viewed as a degenerate linear model with just an intercept, and without explanatory variables).

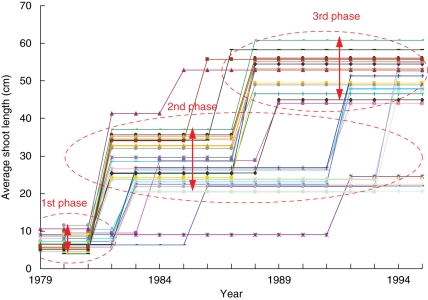
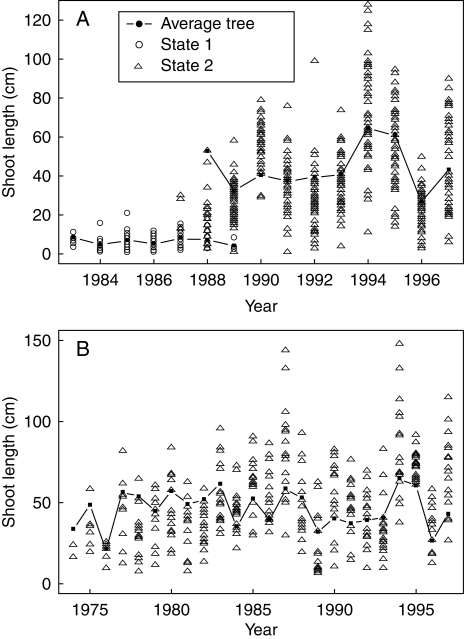
GHSMCs are formally defined in the Appendix. A ‘left–right’ three-state GHSMC composed of two successive transient states followed by a final absorbing state was estimated on the basis of the four sub-samples of Corsican pines (from 6 to 23 years old). A state is said to be transient if after leaving this state, it is impossible to return to it. In a ‘left–right’ model, the states are thus ordered and each state can be visited at most once. As the last year of measurement is arbitrary with regard to tree development, the length of the last growth phase is assumed to be systematically truncated (or ‘right-censored’) and cannot be modelled. The estimated model was used to compute the most probable state sequence for each observed sequence using the so-called Viterbi algorithm (Guédon, 2003). The restored state sequence can be viewed as the optimal segmentation of the corresponding observed sequence into sub-sequences, each corresponding to a given growth phase. The optimal segmentations of the 18-year-old Corsican pines are represented as step functions (there are at most three steps corresponding to the three identified growth phases) in Fig. 2, with the level of each step corresponding to the empirical mean estimated on the basis of the segment extracted from the original sequence. These step functions show the degree of synchronism between individuals for the successive phases but also, more interestingly, highlight inter-individual heterogeneity in each phase.

Fig. 2.

Eighteen-year-old Corsican pines: optimal segmentations computed using the estimated GHSMC viewed as step functions.

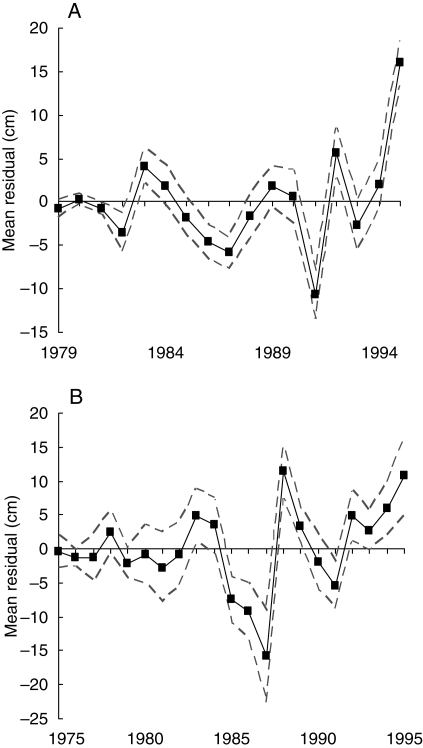
A residual sequence was computed for each individual by subtracting from the original sequence the step function deduced from the estimated model. The pointwise means computed from the 18-year-old tree residual sequences were significantly >0 for the years 1983, 1992 and 1995 and <0 for the years 1982, 1986, 1987 and 1991 (Fig. 3A). The pointwise means computed from the 23-year-old tree residual sequences were significantly >0 for the years 1983, 1988, 1989, 1992, 1994 and 1995 and <0 for the years 1985, 1986, 1987 and 1991 (Fig. 3B). It was assumed that these average residuals correspond roughly to the synchronous fluctuations between individuals in response to climatic factors.

Fig. 3.

Pointwise means and associated confidence intervals computed from the residual sequences of (A) 18- and (B) 23-year-old trees.

In cases where climatic explanatory variables are available, a statistical model for analysing this type of tree growth data should be able to model jointly:

1. the succession of roughly stationary growth phases that are asynchronous between individuals;

2. the effect of time-varying climatic explanatory variables; and

3. inter-individual heterogeneity.

We therefore chose to build semi-Markov switching linear mixed models (SMS-LMMs). This family of statistical models broadens the family of Markov switching models; see Frühwirth-Schnatter (2006) for an overview of Markov switching models. A semi-Markov switching linear mixed model combines:

1. a non-observable J-state semi-Markov chain which represents both the succession of growth phases and their lengths, and

2. J linear mixed models, each one attached to a state of the underlying semi-Markov chain. Each linear mixed model represents, in the corresponding growth phase, both the effect of time-varying climatic explanatory variables as fixed effects and inter-individual heterogeneity as a random effect; see Verbeke and Molenberghs (2000) for an overview of linear mixed models applied to longitudinal data.

SMS-LMMs are formally defined in the Appendix.

The observed annual shoot length Y_a,t for tree a being in state (or growth phase) j at time t is modelled by the following linear mixed model:

where β_j1 + β_j2X_t is the contribution of the fixed effects for state j, β_j1 the intercept which represents the growth level, β_j2 the regression parameter and X_t the climatic explanatory variable common to all the trees at time t. ξ_a,j ∼ N(0, 1) is the random effect attached to tree a being in state j and τ_j the standard deviation induced by the inter-individual heterogeneity in state j. The random effects are assumed to follow the standard Gaussian distribution N(0, 1). ε_a,t|S_a,t = j ∼ N(0, σ_j²) is the error term corresponding to tree a being in state j at time t and σ_j² the residual variance.

In this statistical model, individual tree status is assumed to be different in each growth phase. For a given individual, the average shoot length within a phase can be higher than that of the ‘average tree’ then lower in the following phase, as illustrated by the Corsican pine example (Fig. 2). The introduction of random effects makes it possible to decompose the total variability Γ_j² in state j into two parts:

where τ_j² is the variability due to inter-individual heterogeneity and σ_j² is the residual variability.

SMS-LMMs were estimated using a Monte Carlo expectation maximization (MCEM)-like algorithm (McLachlan and Krishnan, 2008) whose elementary iteration decomposes into three steps: sampling of state sequences given random effects, random effect predictions given state sequences and maximization (Chaubert-Pereira et al., 2008). At convergence of the iterative estimation algorithm, the median predicted random effects were computed for each individual based on the random effects predicted for each state in each sampled state sequence. The most probable state sequence given the median predicted random effects was computed for each observed sequence using a Viterbi-like algorithm (Guédon, 2003). Statistical methods for SMS-LMMs are implemented in a module that will be integrated in the OpenAlea software platform for plant modelling (Pradal et al., 2008).

Standard errors computed for the regression parameters of SMS-LMMs are only valid if the underlying semi-Markov chain is ergodic (i.e. such that each state is visited many times). In the present case of non-ergodic models, we chose to compute β_j2 × mad_j(X) for each state j where mad_j(X) is the mean absolute deviation of the climatic explanatory variable in state j. This indicator gives empirical evidence of the significant or non-significant character of the climatic effect.

A 95 % prediction interval can be computed to check whether the influence of the predicted random effect for each growth phase is significant. This 95 % prediction interval (Hulting and Harville, 1991) is given by:

where n is the number of trees, sd(ξ_j) the empirical standard deviation of the predicted random effect for growth phase j and t_0·975(n − 1) the 0·975th quantile of the Student t distribution with n − 1 degrees of freedom. If a predicted random effect does not belong to the 95 % prediction interval, the influence of this random effect is significant, i.e. there is a marked difference between this individual and the ‘average tree’ in the corresponding growth phase.

RESULTS

Corsican pines: length of annual shoots

It was assumed that the ontogenetic component was common to the four sub-samples. We thus chose to estimate a single ‘left–right’ three-state SMS-LMM, composed of two successive transient states followed by a final absorbing state, on the basis of the four sub-samples of Corsican pines (from 6 to 23 years old). Hence, a given ontogenetic phase corresponds to different ranges of years for the different sub-samples and the regression parameters β_j2 for cumulative rainfall are estimated more accurately for each growth phase j (Fig. 1). The practical approach discussed in Guédon et al. (2007) was applied to determine the number of phases, i.e. the number of states of the underlying semi-Markov chain.

Corsican pine is a monocyclic species (with very little polycyclism in early plant life) where the organogenesis period ranges approximately from early July to late October and the elongation period from early May to late July (see Lanner, 1976; Fig. 4). In temperate regions, rainfall can have a one-year-delayed effect (on the number of phytomers) or an immediate effect (on shoot elongation) depending on whether it occurs during organogenesis or elongation; see Cannell et al. (1976). We thus chose to use cumulative rainfall over a period covering organogenesis and elongation of an annual shoot and to centre this climatic explanatory variable; see Fitzmaurice et al. (2004) for discussion of the centring issue. Because of the centring, the intercept β_j1 is directly interpretable as the average length of successive annual shoots within growth phase j.

Fig. 4.

Corsican pine: organogenesis and elongation periods (based on assumptions from Lanner, 1976). Semi-Markov switching linear models (i.e. without random effects for modelling inter-individual heterogeneity) were estimated for different periods covering organogenesis and elongation periods. The best period (in bold) was chosen on the basis of the best observed data log-likelihood (log L).

In order to define the most significant period, a ‘left–right’ three-state semi-Markov switching linear model (i.e. without random effects for modelling inter-individual heterogeneity) was estimated for different periods on the basis of the four sub-samples of Corsican pines. In this sensitivity analysis, the period was selected on the basis of observed data log-likelihood (Fig. 4). Longer periods giving rise to less relevant results were also tested (results not shown). Centred cumulative rainfall (in mm) from June the previous year to June of the current year, which covers one organogenesis period and one elongation period, was finally selected. A ‘left–right’ three-state SMS-LMM was thus estimated with this centred cumulative rainfall as explanatory variable.

Population properties.

The iterative estimation algorithm was initialized with a ‘left–right’ model such that π_j > 0 for each state j, p_ij = 0 for j ≤ i and p_ij > 0 for j > i for each transient state i, 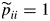and 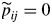for j ≠ i for the final absorbing state. The fact that states 1 and 2 are the only possible initial states (with π₁ = 0·95 and π₂ = 0·05 at convergence) and that state 2 cannot be skipped (i.e. p₁₃ = 0 at convergence) is the result of the iterative estimation procedure (see Fig. 5). The estimated transition probability matrix is thus degenerate, i.e. for each transient state i, p_{i i+1} = 1 and p_ij = 0 for j ≠ i + 1. This deterministic succession of states supports the assumption of a succession of growth phases. It should be noted that the estimated state occupancy distributions for states 1 and 2 (Fig. 5) are far from geometric distributions in terms of shape and relative dispersion; see the Appendix for the definition of the geometric state occupancy distributions of Markov chains. These estimated state occupancy distributions have a low dispersion (Table 2), which expresses a strong structuring in the succession of growth phases along the tree trunks. This is an a posteriori justification of the semi-Markovian modelling of growth phases.

Fig. 5.

Corsican pine: estimated underlying semi-Markov chain. Each state is represented by a vertex which is numbered. Vertices representing transient states are edged by a single line while the vertex representing the final absorbing state is edged by a double line. Possible transitions between states are represented by arcs (attached probabilities always equal to 1 are not shown). Arcs entering in states indicate initial states. The attached initial probabilities are noted. The occupancy distributions of the non-absorbing states are shown above the corresponding vertices. The red lines correspond to occupancy distributions estimated for a simple GHSMC and the black lines correspond to occupancy distributions estimated for a SMS-LMM.

Table 2.

Corsican pine: comparison of estimated Gaussian hidden semi-Markov chain (GHSMC) parameters with estimated semi-Markov switching linear mixed model (SMS-LMM) parameters (state occupancy distributions and marginal observation distributions)

	State
	1	2	3
Occupancy distribution (year), mean, s.d.
GHSMC	P(1, 1·88)	NB(1, 4·36, 0·5)
	2·88, 1·37	5·31, 2·93
SMS-LMM	B(2, 4, 0·37)	NB(1, 73·29, 0·94)
	2·73, 0·68	5·56, 2·20
Regression parameters
Intercept (βj1) (cm)	7·09	25·79	50·25
Cumulative rainfall
Parameter βj2 (cm mm−1)	2·7 × 10−3	16·5 × 10−3	30·9 × 10−3
Average cumulative rainfall effect
βj2 × madj(X) (cm)	0·23	1·71	3·76
βj2 × madj(X)/βj1	3·2 × 10−2	6·6 × 10−2	7·5 × 10−2
Variability decomposition
Random variance τj2	5·79	49·89	69·39
Residual variance σj2	4·74	39·95	76·86
Total variance Γj2	10·53	89·84	146·25
Proportion of inter-individual
heterogeneity (%)	54·99	55·53	47·45
Marginal observation distribution (μj, Γj) (cm)
GHSMC	6·97, 3·26	26·30, 9·12	54·35, 11·39
SMS-LMM	6·99, 3·24	25·88, 9·48	50·32, 12·09

For each observation linear mixed model, the intercept, the regression parameter for cumulative rainfall, the average cumulative rainfall effect and the variability decomposition are given.

The state occupancy distributions estimated for a GHSMC (i.e. without taking into account the effect of climatic explanatory variables and inter-individual heterogeneity) and for a SMS-LMM were compared. When the effects of climatic explanatory variables and inter-individual heterogeneity were taken into account, this rendered the growth phases more synchronous between individuals; see the estimated state occupancy distributions, in particular their standard deviations, for the two models in Table 2 and Fig. 5.

The optimal segmentation into growth phases was computed for each observed sequence using a Viterbi-like algorithm. The optimal segmentations of the observed sequences were used, in particular, to compute the characteristics of the first year in each growth phase, the mean centred cumulative rainfall and the average cumulative rainfall effect in each growth phase (see below).

The characteristics (median and dispersion) of the first year in each growth phase were extracted for the four sub-samples of Corsican pines using either the estimated GHSMC or the estimated SMS-LMM. The median first year in the second growth phase for the four sub-samples was similar for the two models (Table 3). The median first year in the third growth phase for the 6-year-old Corsican pines was similar for the two models. A shift of 1 year was noted for the median first year in the third growth phase between the two models for 12-, 18- and 23-year-old Corsican pines. The dispersion of the first year in the second and third growth phases was greatly reduced in the SMS-LMM case compared with the GHSMC case for 18-year-old Corsican pines (Table 3).

Table 3.

Corsican pine: median first year in state 2 and state 3 for each sub-sample deduced from the estimated Gaussian hidden semi-Markov chain (GHSMC) and semi-Markov switching linear mixed model (SMS-LMM) (corresponding standard deviations are given in parentheses)

	6 years old	12 years old	18 years old	23 years old
State 2
GHSMC	1993 (0·56)	1988 (0·42)	1982 (1·93)	1978 (1·04)
SMS-LMM	1993 (0·56)	1988 (0·50)	1982 (0·56)	1978 (1·17)
State 3
GHSMC	1995 (0·35)	1993 (1·00)	1988 (2·56)	1981 (0·78)
SMS-LMM	1995 (0·38)	1992 (0·87)	1989 (1·27)	1982 (0·77)

The marginal observation distribution of the linear mixed model attached to growth phase j is the Gaussian distribution N(μ_j, Γ_j²) with μ_j = β_j1 + β_j2E_j(X) and Γ_j² = τ_j² + σ_j² where E_j(X) is the mean centred cumulative rainfall in growth phase j. The marginal observation distribution represents the length of the annual shoots in growth phase j. The marginal observation distributions for the different growth phases are well separated (little overlap between marginal observation distributions corresponding to two successive states); compare the mean difference μ_j+1 − μ_j between consecutive states with the standard deviations Γ_j and Γ_j+1 in Table 2. The fixed part of the three observation linear mixed models (i.e. β_j1 + β_j2 × centred cumulative rainfall for each growth phase j) for 18- and 23-year-old trees is shown in Fig. 6. This confirms that the growth phases are well separated with little overlap and correspond to a growth increase. This constitutes another validation of the assumption of a succession of growth phases; see Guédon et al. (2007) for a more in-depth analysis of the marginal observation distributions.

Fig. 6.

Corsican pine: fixed part of the three observation linear mixed models (i.e. β_j1 + β_j2 × centred cumulative rainfall for each state j) represented by lines, and observed annual shoot lengths for state 1, state 2, and state 3, as indicated; (A) 18- and (B) 23-year-old trees.

The average cumulative rainfall effect (i.e. the average amplitude of the climatic fluctuations) was computed as β_j2 × mad_j(X) for each growth phase j where mad_j(X) is the mean absolute deviation of the centred cumulative rainfall in growth phase j. The effect of cumulative rainfall was weak in the first growth phase (of slowest growth) whereas it was stronger in the last two growth phases (less in the second than in the third phase; see Table 2).

The proportion of inter-individual heterogeneity, defined by the ratio between the random effect variance τ_j² and the total variance Γ_j², was greater in early plant life (first two growth phases, approx. 55 %) and decreased slightly in the last growth phase (approx. 47 %). This large proportion of heterogeneity can be explained by the transplantation effect, the lack of thinning and the sampling strategy (trees chosen to cover the entire range of behaviours).

Individual behaviour.

The correlation coefficient between the predicted random effect in state 1 and the predicted random effect in state 2 was 0·28 while the correlation coefficient between the predicted random effect in state 2 and the predicted random effect in state 3 was 0·61. Hence, the behaviour of an individual is more strongly related between the last two growth phases than between the first two growth phases.

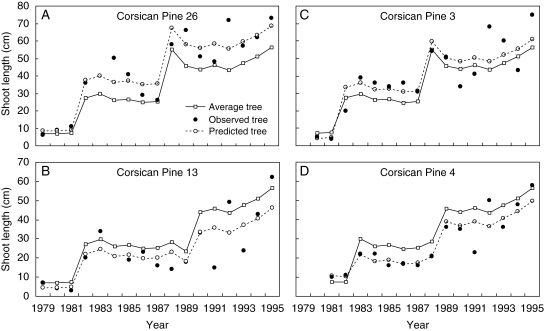
The 95 % prediction interval was computed using the random effect predicted for each tree in each growth phase. Of the 103 Corsican pines, 50 had a significant random effect in each growth phase (G1 + G2 + G3 + G4 in Table 4) and of these 50 individuals, 29 showed a common behaviour over all growth phases (i.e. growing either more rapidly or more slowly than the ‘average tree’ in all growth phases) but 21 showed different behaviours between growth phases. This is an a posteriori justification of the assumption of a random effect attached to each growth phase. The average tree profile (i.e. β_sa,t1 + β_sa,t2 × centred cumulative rainfall for each year t) and the predicted tree profile (i.e. average tree profile value + τ_sa,tξ_a,sa,t for each year t) can be computed for each Corsican pine a on the basis of the optimal segmentation of the observed sequence and the predicted random effects computed using the estimated SMS-LMM. The regression parameters β_j1 and β_j2 describe patterns of change in the mean response over year (and their relation to explanatory variables) in the Corsican pine population, while τ_jξ_a,j describes the deviation in growth phase j of the ath tree profile with reference to the average tree profile; see Fig. 7 for the predicted tree profiles of four Corsican pines. The tree status with reference to the average tree can be common to all growth phases but modulated in terms of deviation between growth phases; see Corsican pine 26 and Corsican pine 13 in Fig. 7. The tree status can also be different in each growth phase; see Corsican pine 3 and Corsican pine 4 in Fig. 7. However, most of the Corsican pines had a common behaviour over the two last growth phases (Table 4). The more general assumption of a random effect attached to each growth phase is thus more representative of Corsican pine behaviour than the assumption of a random effect common to all the growth phases.

Table 4.

Classification of Corsican pine behaviour between growth phases

	Behaviour
Group	State 1	State 2	State 3	No. of Corsican pines
G1	* =	* =	*	29
G2	* =	*≠	*	6
G3	*≠	* =	*	13
G4	*≠	*≠	*	2
	n.s.	* =	*	11
	n.s.	*≠	*	4
	* =	n.s. =	*	1
	*≠	n.s.≠	*	5
	* =	*	n.s.	9
	*≠	*	n.s.	10
	n.s.	n.s.	*	4
	n.s.	*	n.s.	2
	*	n.s.	n.s.	7

A 95 % prediction interval was computed for each state. If the random effects do not belong to this 95 % prediction interval, they were assumed to be significant (*). If the random effects belong to this 95 % prediction interval, they were assumed to be non-significant (n.s.). The behaviour between two growth phases can be identical (=) or different (≠). This classification was established on the basis of the predicted random effects.

Fig. 7.

Four selected 18-year-old Corsican pines: average tree profile (i.e. β_sa,t1 + β_sa,t2 × centred cumulative rainfall for each year t) represented by squares and solid line, predicted tree profile (i.e. average tree profile value +τ_sa,tξ_a,sa,t for each year t) represented by circles and dotted lines, and observed annual shoot lengths (i.e. y_a,t for each year t) represented by closed circles. The average and predicted tree profiles were computed for each selected Corsican pine on the basis of the optimal segmentation of the observed sequence computed using the estimated SMS-LMM.

Corsican pines: number of branches per tier

In Guédon et al. (2007), a hidden semi-Markov chain was built on the basis of bivariate sequences, the two observed variables being the length of the annual shoot and the number of branches per tier. Instead of considering these two observed variables on an equal footing, we chose here to investigate an alternative assumption in which the length of the annual shoot influences the number of branches located at its top. The number of branches per tier is strongly correlated with annual shoot length (r = 0·66). Hence, when introducing annual shoot length as an explanatory variable, it is no longer necessary to model explicitly the phases for the ‘number of branches per tier’ response variable. A simple linear mixed model was thus estimated where both annual shoot length and centred cumulative rainfall were taken into account as explanatory variables (and their influences modelled as fixed effects). As climatic explanatory variable, the centred cumulative rainfall (in mm) from August to December of the current year was selected, this covering the organogenesis period of offspring shoots (following Lanner, 1976). This climatic explanatory variable was found to be not correlated with the annual shoot length explanatory variable (r = 0·07). The influence of cumulative rainfall was not significant (P ≈ 0·79) while, as expected, annual shoot length had a marked effect. As most of the inter-individual heterogeneity was already taken into account in the annual shoot length explanatory variable, the proportion of inter-individual heterogeneity was less than 14 %.

Sessile oaks

Sessile oak is a polycyclic species for which the organogenesis periods for all cycles, except the first, and the elongation periods range approximately from March to September and the organogenesis period for the next-year first cycle ranges approximately from August to October (Lavarenne et al., 1971; Champagnat et al., 1986; Fontaine et al., 1999). Centred cumulative rainfall (in mm) from August the previous year to August of the current year was selected as climatic explanatory variable on the basis of a sensitivity analysis comparing various periods covering annual shoot organogenesis and elongation.

A ‘left–right’ two-state SMS-LMM composed of a transient state followed by a final absorbing state was estimated on the basis of the two sub-samples of sessile oaks. The optimal segmentation into growth phases was computed for each observed sequence using a Viterbi-like algorithm. As in the Corsican pine case, the growth phases were more synchronous between trees than with a GHSMC (Table 5). Nevertheless, the gain in synchronism was less marked than in the Corsican pine case; see the characteristics of the state occupancy distributions in Tables 2 and 5.

Table 5.

Sessile oak: comparison of estimated Gaussian hidden semi-Markov chain (GHSMC) parameters with estimated semi-Markov switching linear mixed model (SMS-LMM) parameters (state occupancy distributions and marginal observation distributions)

	State
	1	2
Occupancy distribution (year) mean, s.d.
GHSMC	B(1, 8, 0·52)
	4·64, 1·32
SMS-LMM	B(1, 7, 0·63)
	4·77, 1·18
Regression parameters
Intercept βj1 (mm)	6·07	45·98
Cumulative rainfall
Parameter βj2 (cm mm−1)	11·5 × 10−3	73·9 × 10−3
Average cumulative rainfall effect
βj2 × madj(X) (cm)	1·57	9·7
βj2 × madj(X)/βj1	25·9 × 10−2	21 × 10−2
Variability decomposition
Random variance τj2	2·02	33·45
Residual variance σj2	10·64	416·33
Total variance Γj2	12·66	449·78
Proportion of inter-individual heterogeneity (%)	15·96	7·4
Marginal observation distribution (μj, Γj) (cm)
GHSMC	6·35, 3·79	45·18, 24·18
SMS-LMM	6·32, 3·56	45·98, 21·21

For each observation linear mixed model, the intercept, the regression parameter for cumulative rainfall, the average cumulative rainfall effect and the variability decomposition are given.

The marginal observation distributions for the two growth phases were well separated (little overlap between the two marginal observation distributions); compare the mean difference μ₂ − μ₁ with the standard deviations Γ₁ and Γ₂ in Table 5. The fixed part of the two observation linear mixed models (i.e. β_j1 + β_j2 × centred cumulative rainfall for each growth phase j) for 15- and 29-year-old trees is shown in Fig. 8. It should be noted that only the second phase of fastest growth is represented in the 29-year-old sessile oaks. This confirms that the two growth phases are well separated with little overlap. This constitutes a validation of the assumption of a succession of growth phases.

Fig. 8.

Sessile oak: fixed part of the two observation linear mixed models (i.e. β_j1 + β_j2 × centred cumulative rainfall for each state j) represented by lines, and observed annual shoot lengths for state 1 and state 2, as indicated; (A) 15- and (B) 29-year-old trees: all trees are in the second growth phase.

The effect of cumulative rainfall was weak in the first growth phase but far stronger in the second (Table 5). As in the Corsican pine case, the effect of the climatic explanatory variable was roughly proportional to the growth level; see the joint variations of the intercept β_j1 and the cumulative rainfall parameter β_j2 with growth phase j in Tables 2 and 5. The relative effect of cumulative rainfall was far stronger for the sessile oaks than for the Corsican pines; see the β_j2 × mad_j(X)/β_j1 ratios in Table 5, which are more than 3·1 times the corresponding ratios in Table 2.

Unlike for the Corsican pines, total variability was roughly proportional to growth level (see μ_j and Γ_j in Tables 2 and 5). Inter-individual heterogeneity was greater in early plant life (first growth phase). However, the proportion of the variability due to inter-individual heterogeneity was around 16 % in the first growth phase (of slowest growth) and less than 8 % in the second growth phase (of fastest growth). The small proportion of variability due to inter-individual heterogeneity can be explained by the fact that the individuals were selected from among dominant or co-dominant trees (not from among all the possible tree statuses as in the Corsican pine case), by thinning and by synchronous natural regeneration for each sub-sample.

The behaviour of the 15-year-old trees between the two growth phases was compared. In the same manner as for the Corsican pines, a 95 % prediction interval was computed for each individual and each growth phase. Of the 20 sessile oaks that had a significant random effect for each growth phase, 12 showed a common behaviour over the two growth phases. Again, in the same manner as in the Corsican pine case, the assumption of a random effect attached to each growth phase was thus more realistic than the assumption of a random effect common to all the growth phases.

DISCUSSION

Our starting assumption was a decomposition model in which observed apical growth is the result of three components: an ontogenetic component, an environmental ‘population’ component and an individual component. For both Corsican pine and sessile oak, the ontogenetic component takes the form of a succession of growth phases. Each phase corresponds to a set of potentialities related to annual shoot organization (see Sabatier and Barthélémy, 1999; Barthélémy and Caraglio, 2007). The local growth conditions (competition between trees, light availability) modulate the shoot length and consequently the branching process (Nicolini et al., 2000). Therefore, individual tree status can change with growth phase, as highlighted by the estimated SMS-LMMs. For instance, a tree can grow more slowly in the first phase than the average tree, then more rapidly in the second phase. In forestry, it is often assumed that a ‘dominant’ tree (i.e. chosen among the largest diameter trees at the mature stage) is dominant throughout its development. This sometimes entails difficulties in result interpretations (Fantin and Morin, 2002). The statistical models introduced here enabled us to highlight changes of social status between phases. This type of behaviour should be integrated in future forest stand production models in order to predict more accurately tree production. More generally, the proper characterization of population properties and individual properties should be helpful in building future forest stand models integrating individual characterizations (Goreaud et al., 2002).

When the effect of climatic explanatory variables and inter-individual heterogeneity were taken into account, this rendered the growth phases more synchronous between individuals than with a simple GHSMC. The growth phases identified by the estimated SMS-LMMs were not defined only by the average length of annual shoots but also by the amplitude of synchronous fluctuations between individuals due to climatic factors and by the proportion of inter-individual heterogeneity; see β_j1, β_j2 × mad_j(X) and τ_j²/Γ_j² respectively in Tables 2 and 5. This is an a posteriori justification of the building of an integrative statistical model representing both the ontogenetic, environmental and individual components.

The environmental and individual components had very different weights for Corsican pine and sessile oak:

1. The influence of cumulative rainfall was far weaker in Corsican pine than in sessile oak. The greater sensitivity of sessile oak to this climatic factor may be explained by its plasticity due to its capacity to produce more than one growth unit in a growing season (Barthélémy and Caraglio, 2007), the production of supplementary growth units being partly monitored by environmental conditions; see Sabatier et al. (2003) for an illustration in Atlas cedar.

2. The proportion of inter-individual heterogeneity was far greater for Corsican pine than for sessile oak.

Despite these greatly contrasted weights of environmental and individual components, the changes with growth phase were similar. The influence of the climatic explanatory variable (i.e. cumulative rainfall over a period covering organogenesis and elongation) was weak in the first growth phase (corresponding to early plant life), then increased markedly with growth phase while the proportion of inter-individual heterogeneity decreased more slightly. This contrasted sensitivity to climatic factors in different growth phases can be explained by (1) root establishment, which strongly competes with shoot elongation and herbaceous competition in the first growth phase (Rose and Rosner, 2005; Balandier et al., 2006), and (2) larger leaf area in the subsequent phases, which broadens response possibilities (Sterck et al., 1999).

The far smaller proportion of inter-individual heterogeneity in sessile oak compared with Corsican pine may be explained by the tree origin (natural regeneration for sessile oak versus nursery for Corsican pine with the effects of transplantation and variable root volume; Jacobs et al., 2005), silvicultural interventions (thinning for sessile oak) and sampling strategy (sessile oaks selected from among the dominant or co-dominant trees and Corsican pines chosen to cover the entire range of behaviours). It would be very useful in future studies to evaluate the proportion of inter-individual heterogeneity for various species under similar conditions or for a given species under various conditions such as different plantation densities.

Information is available concerning the organogenesis period of many northern temperate conifers (Sucoff, 1971; Cannell et al., 1976) and other forest trees (see MacDonald et al., 1984; Puntieri et al., 2002). In the present study, assumptions were made based on the sketchy information related to the ‘Resinosa pattern’ (Lanner, 1976) for the Pinus nigra group. Studies on the scheduling of organogenesis and elongation of annual shoots could be helpful in establishing more accurately the climatic period to be considered in statistical models. It would be also interesting to study the effect of other climatic variables such as temperature (Owens et al., 1977; Pensa et al., 2005; Salminen and Jalkanen, 2005; Gordon et al., 2006).

In the present particular context, all data were collected retrospectively, i.e. plant development was reconstituted at a given observation date from morphological markers corresponding to past events. As cambial growth and bark changes obliterate morphological markers, direct observation is restricted to the most recent entities. Hence, sub-samples of trees corresponding to different age classes and growing under similar conditions should be observed with particular care regarding the overlapping of ontogenetic phases between the different sub-samples in order to reconstitute tree ontogenesis. The environmental component can be estimated accurately only if the sample of years corresponding to a given growth phase is of sufficient size. This requirement can be met by observing sub-samples of trees corresponding to different age classes, and growing under similar conditions. In this way, a given growth phase corresponds to different ranges of years for the different sub-samples and the regression parameters β_j2 are estimated more accurately. Finally, sample size should be sufficiently large to estimate the proportion of inter-individual heterogeneity accurately.

The linear mixed model associated with the third growth phase underestimated the observed mean length of successive annual shoots in this phase for the 23-year-old Corsican pines (Fig. 6B). This behaviour highlights a sub-sample or group effect. A possible extension of the observation linear mixed model would be to incorporate a group-wise random effect in addition to the individual-wise random effect and the fixed effect. The difference between individual groups (i.e. inter-group heterogeneity) may have various origins, for instance genetic (Segura et al., 2008), local environment (e.g. density; Uzoh and Oliver, 2006) or soil properties (Meng et al., 2007).

Segura et al. (2008) applied linear mixed models to longitudinal apple tree data. Their models combine an age fixed effect (ontogenetic component), a year fixed effect (environmental component), a genotype random effect with several random interactions. As the number of measurements per apple tree was small (2–4), no structure was imposed on the component of the mean response over time corresponding to the age effect (non-parametric approach corresponding to a saturated model component). This approach is much less appealing when the number of measurements per tree increases (Fitzmaurice et al., 2004). In the present case, it was assumed that the mean response over time of the trees can be considered as the result of an underlying ontogenetic process for which a parsimonious parametric model can be proposed (‘left–right’ semi-Markov chain). In our case the climatic fixed effect plays the role of the year fixed effect of the Segura et al. (2008) approach.

The proposed statistical modelling approach relies on the availability of climatic data. In the case where climatic data are not available, a possibility would be to introduce a year random effect common to all the trees to model the synchronous part of the growth fluctuations; see Picard et al. (2007) for the introduction of this type of random effect in multiple change-point models and David et al. (2007) for the introduction of this type of random effect in linear mixed models.

With SMS-LMMs, the response variable is constrained to be approximately normally distributed. It would be very useful to develop the statistical methodology for semi-Markov switching generalized linear mixed models to take into account categorical or count response variables (e.g. apex death/life, non-flowering/flowering character, number of growth units); see McCulloch et al. (2008) for an introduction to generalized linear mixed models.

The focus of the present study was apical growth. It would be interesting to transpose the proposed integrative statistical modelling approach to cambial growth and thus to study tree rings in relation to climatic factors taking into account inter-individual heterogeneity. It should be noted that this type of approach requires an accurate retrospective dating of tree rings. An avenue for future work would also be to revisit on this new basis the relationship between apical and cambial growth.

APPENDIX

Let {S_t} be a discrete-time Markovian model with finite state space {1, … , J}; see Kulkarni (1995) for a general reference regarding Markov and semi-Markov models.

Markov chains

A J-state Markov chain {S_t} is defined by the following parameters:

1. initial probabilities π_j = P(S₁ = j) with Σ_jπ_j = 1;

2. transition probabilities 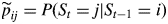with .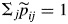

One drawback with Markov chains is the inflexibility in describing the time spent in a given state as the implicit occupancy (or sojourn time) distribution of a non-absorbing state j is the ‘1-shifted’ geometric distribution with parameter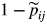

This geometric distribution assumption (the shorter the sojourn time, the higher its probability) is rarely realistic for the modelling of the length of growth phases.

Semi-Markov chains

A useful generalization of Markov chains lies in the class of semi-Markov chains, in which the process moves out of a given state according to an embedded Markov chain with self-transition probability in non-absorbing states p_jj = 0 and where the time spent in a given non-absorbing state is modelled by an explicit occupancy distribution.

A J-state semi-Markov chain {S_t} is defined by the following parameters:

1. initial probabilities π_j = P(S₁ = j) with Σ_jπ_j = 1;

2. transition probabilities:

   1. non-absorbing state i: for each j ≠ i, p_ij = P(S_t = j|S_t ≠ i, S_t−1 = i) with Σ_j≠i p_ij = 1 and p_ii = 0,
   2. absorbing state i: 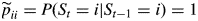and for each .

An explicit occupancy distribution is attached to each non-absorbing state:

As t = 1 is assumed to correspond to a state entering, the following relation is verified:

In the following, we define as possible parametric state occupancy distributions binomial distributions, Poisson distributions and negative binomial distributions with an additional shift parameter d (d ≥ 1) which defines the minimum sojourn time in a given state.

The binomial distribution with parameters d, n and p (q = 1 − p), B(d, n, p) where 0 ≤ p ≤ 1, is defined by

The Poisson distribution with parameters d and λ, P(d, λ), where λ is a real number (λ > 0), is defined by

The negative binomial distribution with parameters d, r and p, NB(d, r, p), where r is a real number (r > 0) and 0 < p ≤ 1, is defined by

Hidden semi-Markov chains

A hidden semi-Markov chain can be viewed as a pair of stochastic processes {S_t, Y_t} where the ‘output’ process {Y_t} is related to the ‘state’ process {S_t}, which is a finite-state semi-Markov chain, by a probabilistic function or mapping denoted by f [hence Y_t = f(S_t)]. As the mapping f is such that f(j) = f(k) may be satisfied for some different j, k, i.e. a given output may be observed in different states, the state process {S_t} is not observable directly but only indirectly through the output process {Y_t}. This output process {Y_t} is related to the semi-Markov chain {S_t} by the observation (or emission) probabilities

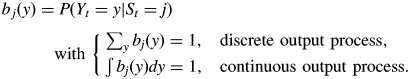The definition of observation probabilities expresses the assumption that the output process at time t depends only on the underlying semi-Markov chain at time t.

Gaussian hidden semi-Markov chains

Let Y_a,t be the observed variable and let S_a,t be the non-observable state for individual a (a = 1, … , n), at time t (t = 1, … , T_a). In the particular case of GHSMCs, the observation distribution attached to state j is assumed to be the Gaussian distribution N(μ_j, Γ_j²). The observation probabilities are defined as follows:

Semi-Markov switching linear mixed models

In the same manner as for a GHSMC, the output process {Y_a,t} of the SMS-LMM for individual a is related to the state process {S_a,t}, which is a finite-state semi-Markov chain, by a linear mixed model (a linear mixed model can be viewed as an extension of a classical linear model where random effects are added to fixed effects; see Verbeke and Molenberghs, 2000). It assumes that the vector of repeated measurements on each individual follows, in each state, a linear regression model where some of the regression parameters are population-specific (i.e. the same for all individuals), whereas other parameters are individual-specific. In our case, the individual status (compared with the average individual) is assumed to be different in each state:

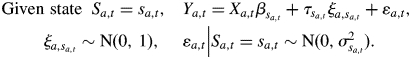The observed probabilities are defined as follows:

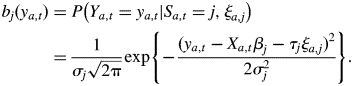In this definition, X_a,t is the Q-dimensional row vector of explanatory variables for individual a at time t. Given the state S_a,t = s_a,t, β_sa,t is the Q-dimensional fixed effect parameter vector, ξ_a,sa,t is the individual a random effect, τ_sa,t is the standard deviation for the random effect and σ_sa,t² is the residual variance. The individuals are assumed to be independent. For convenience, random effects are assumed to follow the standard Gaussian distribution. The random effects for an individual a are assumed to be mutually independent (cov(ξ_a,i, ξ_a,j) = 0; i ≠ j). Observations in different states for an individual a are assumed to be conditionally independent given states (for 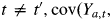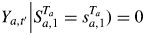if s_a,t ≠ s_a,t′ and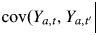 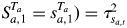if s_a,t = s_a,t′ where 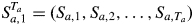denotes the T_a-dimensional vector of non-observable states for individual a).