Parametric and non-parametric modeling of short-term synaptic plasticity. Part II: Experimental study

Abstract

This paper presents a synergistic parametric and non-parametric modeling study of short-term plasticity (STP) in the Schaffer collateral to hippocampal CA1 pyramidal neuron (SC) synapse. Parametric models in the form of sets of differential and algebraic equations have been proposed on the basis of the current understanding of biological mechanisms active within the system. Non-parametric Poisson–Volterra models are obtained herein from broadband experimental input–output data. The non-parametric model is shown to provide better prediction of the experimental output than a parametric model with a single set of facilitation/depression (FD) process. The parametric model is then validated in terms of its input–output transformational properties using the non-parametric model since the latter constitutes a canonical and more complete representation of the synaptic nonlinear dynamics. Furthermore, discrepancies between the experimentally-derived non-parametric model and the equivalent non-parametric model of the parametric model suggest the presence of multiple FD processes in the SC synapses. Inclusion of an additional set of FD process in the parametric model makes it replicate better the characteristics of the experimentally-derived non-parametric model. This improved parametric model in turn provides the requisite biological interpretability that the non-parametric model lacks.

1 Introduction

Synaptic transmission is a nonlinear dynamic process that plays a critical role in signal transmission and information processing in the nervous system (Zucker and Regehr 2002). The term “dynamic” implies that the causal effects of a presynaptic event spread into the future values of the postsynaptic events and are not limited to the present time. The term “nonlinear” means that the combined effect of two or more presynaptic events is different from the simple concatenation of the postsynaptic events that would have been caused by each of the presynaptic events separately. Thus, the process of synaptic transmission can also be viewed as a nonlinear dynamic input–output transformation of a sequence of presynaptic events into postsynaptic events in a manner that is use-dependent (i.e., depends on the specific temporal pattern of presynaptic events) and is also termed short-term plasticity (STP).

STP can be modeled parametrically or non-parametrically for different aims (see Introduction of the companion paper). Parametric models are often developed to explain the underlying biological mechanisms and thus have a predictive power in terms of how the biological processes determine the systems behavior, e.g., input–output transformational property of the system (Dittman et al. 2000). By contrast, non-parametric models are built to quantitatively describe such input–output transformational property in a model-free manner (Krausz and Friesen 1977; Marmarelis and Marmarelis 1978; Berger et al. 1988a,b; Sclabassi et al. 1988; Berger et al. 1994; Bishop 1995; Marmarelis 2004). The advantages of a non-parametric model for such aim are the following: in terms of model configuration, a non-parametric model takes a general model form that is applicable to almost all causal systems, thus avoids potential errors in the postulation of the model structure. In terms of parameter estimation, a non-parametric model is estimated from input–output data collected under broadband condition and inherently valid for such condition.

The main aim of this study is to combine both parametric and non-parametric modeling methods in a synergistic manner to study STP in CNS synapses. In the first half of this study (see companion paper), non-parametric models of synaptic STP are estimated from input–output data simulated with several parametric STP models. Results show that non-parametric model (in the form of Poisson–Volterra kernels) can accurately and efficiently capture the nonlinear dynamics defined by those parametric models. Volterra kernels provide a general and quantitative representation of the synaptic STP. Furthermore, by relating the kernel shapes of the non-parametric model to the key parameters of the parametric model, many insights are gained on how the biological processes (represented by the parameters) shape the input–output functional properties (described by the kernels) of the synapse.

The non-parametric model constitutes a canonical and complete representation of the system (nonlinear) dynamics that is derived directly from the broadband data. Thus, the obtained model is not restricted by any prior assumptions and can be used as the “ground truth” to evaluate the parametric models of the system in terms of its input–output transformational property. In this paper, we estimate the non-parametric Poisson–Volterra kernel (PV) models of the Schaffer collateral to hippocampal CA1 pyramidal neuron (SC) synapse under two extracellular calcium conditions. Results show that the PV models more accurately capture the synaptic nonlinear dynamics than a parametric facilitation/depression (FD) model under both conditions. On the other hand, since these non-parametric models are descriptive representations of synaptic nonlinear dynamics, they can accurately predict the synaptic output under each condition but lack the ability to explain the obtained synaptic nonlinear dynamics in a physiologically-interpretable manner. To get better understanding to the underlying mechanism, we combine the parametric and non-parametric models again—we validate and modify the parametric FD model using the non-parametric PV model. Several significant discrepancies between the experimentally-derived non-parametric model and the equivalent non-parametric model of the parametric model are found in the PV kernels. These discrepancies suggest the presence of multiple FD processes in the SC synapses. Inclusion of an additional FD process in the parametric model makes it replicate better the characteristics of the experimentally-derived non-parametric model. The modified parametric model provides in turn the requisite biological interpretability of the model components—whereby the advocated synergistic use of the two modeling approaches.

2 Materials and methods

2.1 Experimental procedures

2.1.1 Slice preparation

Hippocampal slices were prepared from young adult male Sprague–Dawley rats (80–200 g). Animals first were anesthetized with 5% halothane, and then were decapitated and the hippocampi were rapidly dissected. Both hippocampi were sectioned into blocks while being washed with cold, oxygenated medium and slices of tissue (350 μm thick) then were cut perpendicular to the longitudinal axis using a vibratome (VT-100S; Leica). Slices were incubated with medium consisted of (in mM): 128 NaCl; 2.5 KCl; 1.25 NaH₂PO₄; 26 NaHCO₃; 10 glucose; 2 CaCl₂; 3.0 MgSO₄, aerated with 95% O₂/5% CO₂. Hippocampal slices were maintained at 32°C for 30 min and then at room temperature throughout the entire experiments. During the recording session, slices were transferred to the recording chamber and perfused at flow rates of 2–3 ml/min; the perfusion medium was changed according to the experimental purposes.

2.1.2 Stimulation procedures

A bipolar stimulating electrode (a pair of twisted, insulated nichrome wires) were placed in the Schaffer collateral to orthodromically activate CA1 pyramidal cells. A cut was made between the CA3 and CA1 regions to prevent epileptiform activity in the CA3 region from affecting the recording in CA1. Biphasic current impulses (200 μs in duration) controlled by a stimulator (Master-8; AMPI) were delivered to the tissue via stimulation isolation units (ISO-Flex; AMPI). The stimulation intensity varied from 100 to 700 μA. Since the cells were under voltage-clamp and the synapses could be taken to be independent current sources, the strict control of stimulation intensity was relaxed. Instead of using stimulation/response function (I/O curve), stimulation intensities were chosen to elicit roughly constant EPSC amplitudes reflecting approximately the same number of activated synapses. Under 2 mM [Ca²⁺]_o condition, the baseline EPSC amplitudes were in the range of 150–600 pA; under 1 mM [Ca²⁺]_o condition, the baseline EPSC amplitudes were in the range of 80–300 pA. Too small responses tended to have large variations and too big responses might cause imperfect voltage clamp and spurious EPSCs.

Poisson random impulse trains were generated with an STG 1002 stimulator (MultiChannel Systems) and then sent to Master-8. The inter-impulse intervals were determined offline by a Poisson distribution with a mean interval of 500 ms and a range of 6–5,000 ms. The minimal inter-impulse interval (6 ms) is longer than the reported refractory period of the Schaffer collaterals (Stevens and Wang 1995; Dobrunz et al. 1997). Fixed-interval impulse trains with four frequencies (10, 20, 30 and 40 Hz) were generated with Master-8. Each train was comprised of ten impulses.

2.1.3 Electrophysiological recording procedures

Whole-cell recordings of EPSC were performed with an HEKA EPC-9 patch-clamp amplifier from CA1 pyramidal cells visually identified with an infrared microscope (Olympus BX50WI). The glass micropipette was filled with internal solutions containing (in mM): 95 caesium gluconate, 20 TEACl, 10 NaCl, 5 QX-314, 4 Mg-ATP, 0.4 Na-GTP, 0.1 EGTA and 10 HEPES (pH 7.0, titrated with gluconic acid). Some of the experiments were performed with a reduced formula containing (in mM): 130 caesium gluconate, 5 CsCl, 0.1 CaCl₂, 1 BAPTA and 10 HEPES (pH 7.0, titrated with gluconic acid). Most of the cells were voltage-clamped at a holding potential of −70 mV. Some cells were held at −90 or −120 mV. Glass pipettes were pulled using a horizontal puller (Model P-80 PC; Sutter Instrument Co.). They had a resistance of 2–4 MΩ and were not polished or coated. The serial resistance varied between 5 and 30 MΩ. The input resistance of the cells was higher than 1.0G Ω (on-cell mode). Responses were sampled at 10 or 20 kHz with pulse data acquisition software (HEKA). Recorded data were exported in ASCII format and then imported to pClamp 9.0 (Axon Instruments) and Matlab (The MathWorks, Inc.) for further analysis.

Both fixed-interval and random-interval impulse trains were applied to each cell. In fixed-interval train experiments, each train was repeated 16 times and then averaged. Totally 640 input–output pairs were recorded. In random-interval train experiments, 1,200–3,600 input/output pairs were collected.

2.1.4 Pharmacological manipulations

In addition to cutting the CA3-CA1 connection, high concentration of Mg²⁺ (3 mM) was used in the incubating and recording mediums to minimize multi-synaptic activity (Mody et al. 1987). The Ca²⁺ concentration was altered to manipulate the release probability of the synapses (1 or 2 mM). To simplify postsynaptic mechanisms and get more reliable measurements to the presynaptic release, NMDA receptors and GABA_A receptors were blocked with DAP-V (25 μM) and picrotoxin (100 μM), respectively. In some experiments, GABA_B receptors were blocked by CGP55845a (2 μM). AMPA receptor desensitization blocker cyclothiazide (CTZ) was made daily as a 10 mM stock in dimethyl sulfoxide (DMSO) and diluted to 100 μM final concentration in the perfusion medium immediately prior to application.

Note that, although synaptic transmission involves both presynaptic and postsynaptic mechanisms, most STP studies to date focus on the presynaptic mechanism (Zucker and Regehr 2002). However, since the neurotransmitter release (which is the real output of the presynaptic region) is difficult to measure, researchers typically use the postsynaptically recorded signal (e.g., EPSC) to infer the strengths of synaptic release. In order to do this, it is necessary to simplify the postsynaptic mechanisms by voltage-clamping in the postsynaptic region and by removing postsynaptic voltage-dependent channels (e.g. NMDA). These pharmacological manipulations were used to isolate the presynaptic mechanisms and, therefore, the study of the STP process refers to the presynaptic transformation of a sequence of action potentials arriving at the bouton (input) to the EPSCs (output) recorded from the soma.

2.2 Modeling procedures

2.2.1 Estimation of presynaptic release

As indicated above, STP is primarily caused by presynaptic mechanisms. All-or-none action potentials elicit transmitter releases with varying strengths in the presynaptic terminal which open ionic channels on the postsynaptic membrane. The transmitter release has been shown to have a short duration (Clements et al. 1992) and thus the output signal of the presynaptic terminal can be adequately modeled as a variable-amplitude point-process. Because of the extremely narrow synapse cleft and technical difficulties in direct measurement of transmitter release, the postsynaptic signal (i.e. the sequence of EPSCs) is used to estimate the release strength through deconvolution with a single typical EPSC waveform (Fig. 1). The resulting discrete values, instead of the EPSC peak amplitudes, are used as estimates of the amounts of transmitter release. This method excludes the effect of EPSC temporal summation in the event of overlap and allows almost perfect reconstruction of the continuous EPSC waveforms. In this paper, without further specification, EPSC amplitude refers to the deconvolved amplitude, not the peak amplitude of EPSC. These two amplitudes are the same when there is no temporal summation of overlapping EPSCs.

Fig. 1.

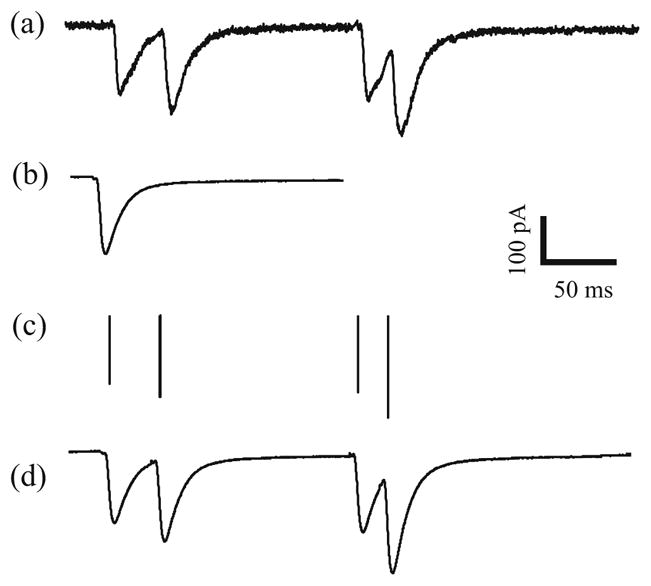
Deconvolution of EPSC train. (a) EPSC train with temporal summations. (b) Typical EPSC profile obtained as an average of isolated EPSCs. (c) the deconvolved discrete signal that represents the sequence of presynaptic releases. (d) EPSC train reconstructed with (b) and (c)

2.2.2 Estimation of the non-parametric model

The employed form of non-parametric model is the reduced form of the discrete-time Poisson–Volterra (PV) model (Marmarelis and Berger 2005) where the PV kernels are estimated using Laguerre expansions (Marmarelis 1993). The mathematical form of the PV model is:

$$\begin{array}{l}y(t_i)=k_1+\sum _{t_i-M<t_j<t_i}{k}_2(t_i-t_j)\\ +\sum _{t_i-M<t_{j_1}<t_i}\sum _{t_i-M<t_{j_2}<t_i}{k}_3(t_i-t_{j_1},t_i-t_{j_2})\\ +\dots \end{array}$$ (1)

where k₁, k₂, and k₃ are the 1^st, 2^nd, and 3^rd order PV kernels of the system. The summations in Eq. (1) take place over all input event times within a past epoch M (termed the “system memory”) prior to t_i. The 1st-order PV kernel, k₁, represents the amplitude of the EPSC attributed to each stimulus impulse alone (i.e., baseline EPSC amplitude). The 2nd-order PV kernel, k₂(τ), represents the change in the present EPSC amplitude contributed by the 2nd-order interaction between the present impulse and a preceding impulse, as a function of their time interval τ. The 3rd-order PV kernel, k₃(τ₁, τ₂), represents the change in the present EPSC amplitude contributed by the 3rd-order interaction between the present impulse and two preceding impulses, as a function of their time intervals τ₁ and τ₂. The 2^nd term in Eq. (1) represents the total 2nd-order contribution from all preceding impulses within the system memory M. The 3^rd term represents the total 3rd -order contribution from all preceding impulses within M.

The model order is determined by means of the predictive accuracy of PV models of ascending order (1^st, 2^nd, 3^rd and 4^th), which is quantified by the normalized root-mean-square error (NRMSE) of the output prediction for Poisson RIT inputs. The 3rd-order model is found consistently to be adequate for capturing the dynamic nonlinearities of the system as reflected on the broadband input–output data (i.e., the obtained 4th-order model decreased NRMSE only marginally (<1%) that does not justify the inclusion in the model of the 4th-order kernel). This is in agreement with the results of the companion computational study (Part I).

All PV kernels for this synapse are estimated with a system memory of 2,000ms and a sampling interval of 1ms. The number of Laguerre basis functions is chosen to be 4, which is the value allowing the most accurate prediction without overfitting, as determined by the model-order selection criterion for Volterra-type models (Marmarelis 2004). The expansion coefficients of the kernels are estimated through ordinary least-squares using singular value decomposition. The optimal value of the Laguerre parameter α was searched in the range from 0 to 0.999 and the average value was found to be 0.920 over the available input–output datasets.

To facilitate interpretation, the “response descriptors” (RD) that are based on the PV kernels are used to describe the system characteristics (see companion paper). The set of RDs for a given system is mathematically equivalent with the PV kernels, as indicated by the defining relations for the 3rd-order model:

$$r_1=k_1$$ (2)

$$r_2(\tau )=k_2(\tau )+k_3(\tau ,\tau )$$ (3)

$$r_3({\tau }_1,{\tau }_2)=2k_3({\tau }_1,{\tau }_2)$$ (4)

These defining relations indicate that the 1st-order RD, r₁, is equal to the baseline EPSC amplitude; the 2nd-order RD, r₂(τ), represents the total change (including both 2^nd and 3rd-order) in the present EPSC amplitude caused by a single preceding impulse, as a function of their time interval τ; the 3rd-order RD, r₃(τ₁, τ₂), represents the joint effect (exclusive of their individual effects described by r₂(τ₁) and r₂(τ₂)) of two preceding impulses on the present EPSC amplitude, as a function of their time intervals τ₁ and τ₂. Without loss of generality, both r₂ and r₃ are normalized with r₁.

2.2.3 Estimation of the parametric model

As a parametric model of the SC synapse, we consider the widely accepted residual calcium-based facilitation/depression (FD) model (Dittman et al. 2000). In this model, the EPSC is calculated as the product of facilitation and depression factors (F and D). The residual calcium is assumed to be a linear dynamic process. The facilitation and depression factors are calculated on the basis of the residual calcium concentration, using first-order linear differential equations and nonlinear algebraic functions (see Method of the companion paper for more details). The key parameters of this FD model are: the initial release probability (F₁), the maximum paired-pulse facilitation ratio (ρ), the minimum and maximum recovery rates (k₀ and k_max) and the time constants of residual calcium (τ_F and τ_D). These key parameters are estimated using the constrained Quasi-Newton optimization technique (Matlab 6.5; MathWorks, Inc.). Optimal values for τ_F and τ_D were searched in the range of 10–200 ms with a 10 ms step length. Mean values and standard errors of the estimated parameter values calculated over all experiments are reported in Tables 1 and 2. Sensitivity analysis shows that the systems input–output transformation is insensitive to the other model parameters.

Table 1.

Parameter estimates of the FD model obtained from fixed-interval and random-interval datasets under 2 mM [Ca²⁺]_o condition, and the resulting prediction NMRSE of the two parametric models

	FIT-FD estimates	RIT-FD estimates
F1	0.19±0.03	0.26±0.03
ρ	1.42±0.14	1.27±0.08
K0 (s−1)	2.5±0.9	1.2±0.2
kmax (s−1)	13.2±1.4	20.4±2.5
τF (ms)	90	90
τD (ms)	50	50
NRMSE (%)	33±2	28±1

Table 2.

Parameter estimates of the FD model obtained from fixed-interval and random-interval datasets under 1 mM [Ca²⁺]_o condition, and the resulting prediction NMRSE of the two parametric models

	FIT-FD estimates	RIT-FD estimates
F1	0.0048±0.0023	0.0027±0.0011
ρ	1.52±0.18	1.91±0.10
K0 (s−1)	385±177	668±34
kmax (s−1)	436±147	309±19
τF (ms)	120	120
τD (ms)	50	50
NRMSE (%)	39±4	29±3

Most importantly, it is found through comparison with the non-parametric model that this parametric model must be augmented to include a second FD process (with different dynamic characteristics) in order to explain adequately the broadband experimental data. The equation for the total transmitter release of this double-process FD model takes the form:

$$R=N_{\text{f}}\times F_{\text{f}}\times D_{\text{f}}+N_{\text{s}}\times F_{\text{s}}\times D_{\text{s}}$$ (5)

where R is the total release and N denotes the weights for each synaptic process (distinguished by the subscripts f for “fast” and s for “slow”). Without loss of generality, the sum of the two weights is set to unity. Each process is described by a similar FD model with its own set of parameters (Table 3). Since the double-process FD model involves more free parameters, it is more difficult to optimize for each individual cell than the single-process FD model. For this reason, all parameters are optimized with respect to the averaged nonlinearities (i.e. the parameter values are determined through a search that seeks the most accurate replicas of average experimentally constrained kernels), and there is no standard error reported in Table 3.

Table 3.

Parameter estimates of the double-process FD model

	1 mM [Ca2+]o		2 mM [Ca2+]o
	Fast	Slow	Fast	Slow
N	0.4	0.6	0.4	0.6
F1	0.18	0.15	0.51	0.32
ρ	2.5	1.5	0.90	1.2
K0 (s−1)	20	120	1	20
kmax (s−1)	60	130	40	90
τF (ms)	20	200	30	100
τD (ms)	20	50	20	50

3 Results

3.1 Experimental exploration of STP in the SC synapse

The experimental data were collected under two different [Ca²⁺]_o conditions (2 and 1 mM). Under each condition, both fixed-interval trains (FIT) and random-interval trains (RIT) of stimuli were applied. EPSC amplitudes were extracted using the deconvolution technique described in Section 2. Third-order Poisson–Volterra (PV) models of STP in SC synapses were estimated from the RIT datasets that contain PV kernels from which the RDs were computed in order to study the input–output transformatrion characteristics of the SC synapse.

3.1.1 High [Ca²⁺]_o condition (2mM)

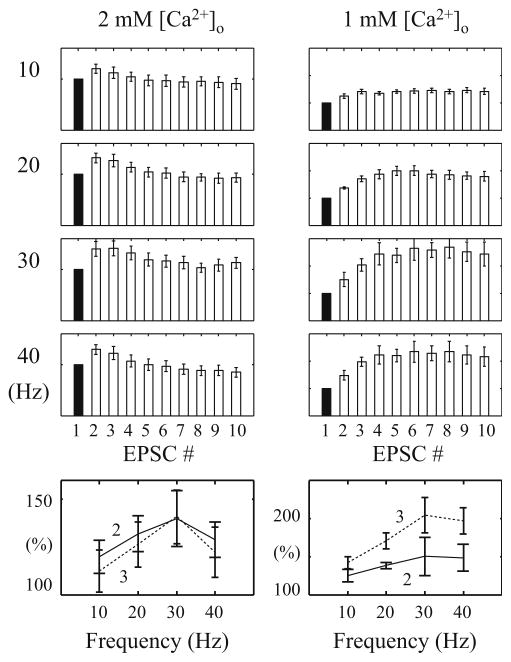
First, we examine experimentally the STP characteristics of SC synapses with the conventional FIT stimulation protocol. Four input frequencies are used (10, 20, 30 and 40 Hz) and each FIT comprises ten impulses. Under the 2 mM [Ca²⁺]_o condition, the EPSCs peak at the second response and then decline in the rest of the responses (Figs. 2 and 3). The ratios of the second responses to the corresponding first responses are 120 ± 9%, 132 ± 10%, 140 ± 15% and 129 ± 10% (mean ± SE; n = 7) and the ratios of the third responses to the first responses are 112 ± 11%, 126 ± 12%, 141 ± 14% and 122 ± 13%, in the 10, 20, 30, and 40 Hz FIT, respectively. This pattern is consistent with the previous reports (Dittman et al. 2000) despite the relatively smaller magnitudes.

Fig. 2.

Fixed-interval EPSC trains elicited with four different frequencies (10, 20, 30, 40 Hz) and under two different [Ca²⁺]_o conditions. Under 2 mM [Ca²⁺]_o condition, the EPSC peaks at the 2^nd response and then declines; while under 1 mM [Ca²⁺]_o condition, the EPSC peaks later and attains almost a steady-state value. Note that the second to the tenth EPSCs (white bars) were normalized with the first EPSC (black bar). Bottom row: the 2^nd (solid lines) and 3^rd (dashed lines) responses as a percentage of the 1^st response

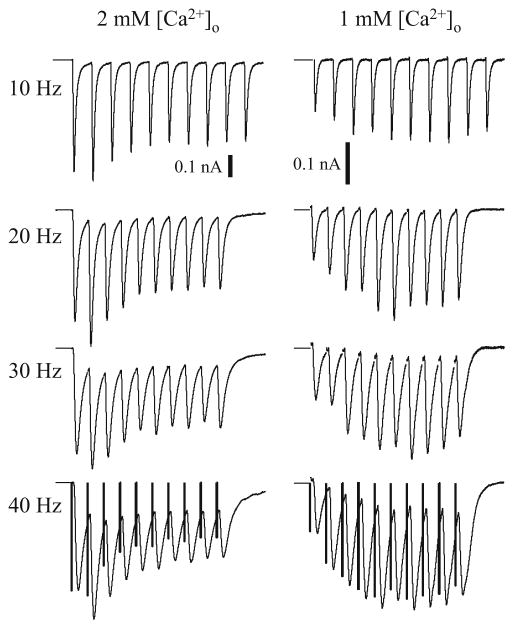
Fig. 3.

Representative fixed-interval EPSC trains with four different frequencies and under two [Ca²⁺]_o conditions. Each EPSC train is the average of 16 sweeps. Bars in bottom row are the deconvolved EPSC amplitudes representing the estimated transmitter release. Note the difference between the deconvolved EPSC amplitudes and the peak EPSC amplitudes due to the temporal summations in the EPSC train

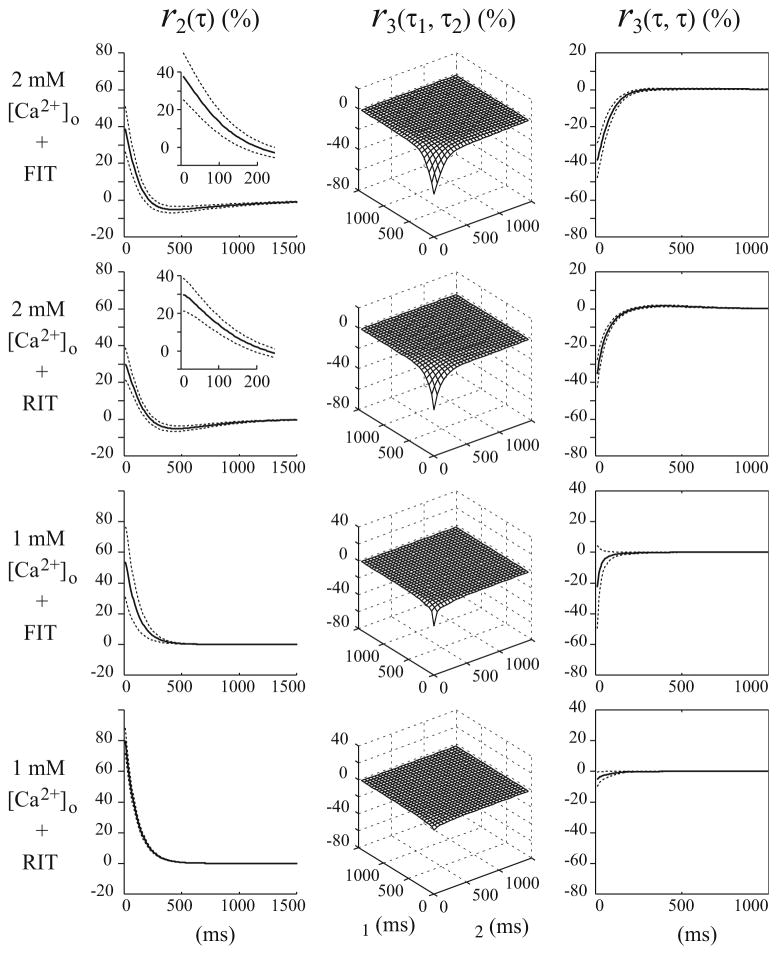
EPSC trains elicited by RIT stimuli with Poisson distribution were then recorded, and 3rd-order PV models were estimated from these input–output datasets that fully characterize the synaptic dynamics with respect to arbitrary inter-impulse intervals (IPIs). The 2nd-order and 3rd-order RDs, r₂ and r₃, are computed from the estimated PV kernels using the expressions in Eqs. (2)–(4) and are shown in the top row of Fig. 4. The 1st-order RD, r₁, is equal to the baseline EPSC recorded from each cell and it is controlled experimentally to be in the range of 150–600pA by adjusting the stimulation intensity. The RDs, r₂ and r₃, are normalized with the corresponding r₁ and then averaged across all nine cells used in this study.

Fig. 4.

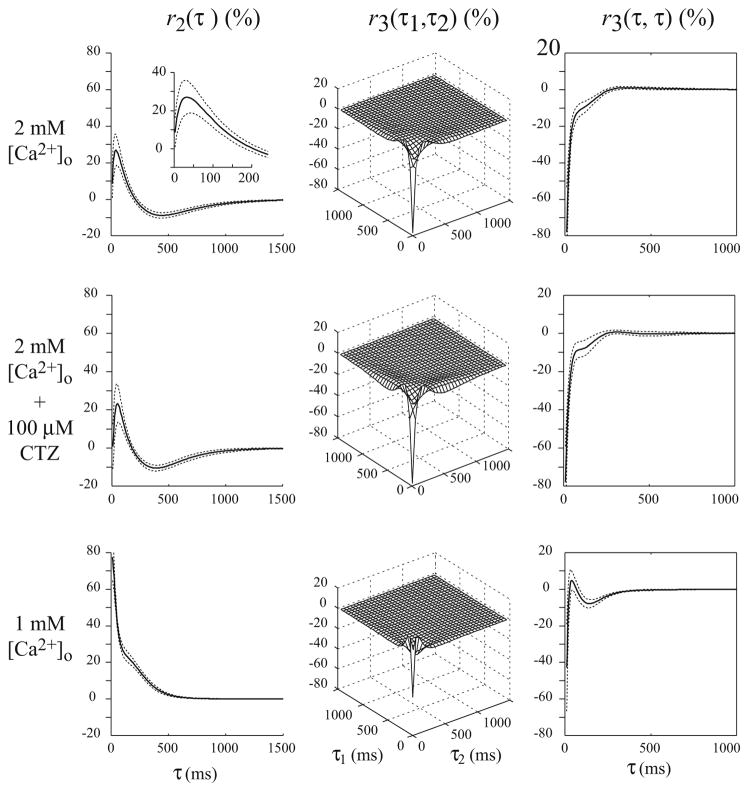
The 2^nd and 3^rd order response descriptors (RDs), r₂ and r₃, of the 3rd-order Poisson–Volterra models of the SC synaptic dynamics obtained from broadband experimental data for different [Ca²⁺]_o and CTZ conditions. Top row inset: the r₂ values for short inter-impulse intervals

In the high-calcium condition (shown in the first row of Fig. 4), the computed r₂ rapidly increases to the peak value of 27 ± 9% in the short IPI range of 6–40 ms; while in the intermediate IPI range of 40–440 ms, r₂ decreases from the peak to a minimum value of −9 ± 2%, crossing into negative values for an IPI around 200 ms. In the long IPI range beyond 440 ms, r₂ returns asymptotically to zero, practically vanishing after an IPI of approximately 1,600 ms. The computed r₃ is primarily negative, reflecting the dominant 3rd-order suppressing effects of pairs of preceding impulses, especially for IPIs shorter than 200 ms, as it is evident in the diagonal slice of r₃ which exhibits a fast initial exponential phase with approximate time constant of 11 ms and a slower phase that can be approximated by the difference of two exponentials with the time constant being approximately 87 ms. These results suggest that the STP dynamics in the SC synapse involve at least two processes with different time constants.

3.1.2 Low [Ca²⁺]_o condition (1mM)

The biphasic form of the computed r₂ and the negative monophasic form of the computed r₃ under the high-calcium condition indicate that the SC synapses have both facilitative and depressive processes. To explore further the transmission characteristics and the underlying mechanisms of SC synapses, the experiments were repeated with lower [Ca²⁺]_o (1 mM). Under low-calcium conditions, the initial release probability of the synapse is suppressed and the synaptic depression caused by vesicle depletion is consequently decreased (Rahamimoff 1968; Creager et al. 1980). The response dynamics are expected to be dominated by the facilitation processes.

Indeed, this dominant facilitation is evident in the FIT responses. As shown in Fig. 3, the EPSC amplitudes increase more in the first four responses (relative to the first response) and then form a broad summit (resembling almost a plateau) over the subsequent responses. The observed ratios of the second responses to the corresponding first responses are 125 ± 8%, 138 ± 4%, 150 ± 25% and 148 ± 18%; and the ratios of the third responses to the corresponding first responses are 142 ± 8%, 171 ± 10%, 204 ± 23% and 197 ± 17%, for the 10, 20, 30, and 40Hz trains, respectively (n = 5).

In the case of RIT stimulation, the computed RDs (Fig. 4, bottom row) indicate that r₂ remains positive for all IPI values and practically vanishes beyond an IPI value of 500 ms (n = 8). A fast rate of decline is observed in the IPI range up to 100ms, where r₂ decays from 178 ± 13% to 126 ± 3% (corresponding to an approximate exponential time-constant of 21 ms), while the rate of decline in the subsequent IPI range of 100–500 ms is much slower (corresponding to an approximate exponential time constant of 197 ms). This result suggests the presence of (at least) two processes of facilitation in the STP dynamics of SC synapses. We also observe in the bottom row of Fig. 4 that r₃ is triphasic and remains negative for most IPI values (i.e., it is slightly positive only for IPI values between 30 and 100 ms). Comparing the absolute values of r₂ and r₃, we observe that the latter is much smaller and has shorter duration. The results show that under the low-calcium condition, the synaptic nonlinearity is primarily a 2nd-order facilitation (Fig. 4, bottom row)—unlike the high-calcium condition where the synaptic nonlinearity appears to be primarily a 3rd-order depression (Fig. 4, top row).

3.1.3 AMPA desensitization does not change the pattern of STP

In this study, several strategies were used to isolate the presynaptic mechanisms of STP: postsynaptic active membrane conductances were voltage-clamped; nonlinear NMDA receptors were blocked by D-APV and high Mg²⁺ in addition to voltage-clamp; GABA_A receptors were blocked by picrotoxin; temporal summations of EPSCs were eliminated by the deconvolution procedure, etc. The purpose is to leave only the AMPA receptors and use them to infer the amounts of presynaptic transmitter releases. However, it is known that the AMPA receptors are subject to desensitization that could potentially influence the estimation of presynaptic release, especially in the short IPIs (Trussell and Fischbach 1989). To eliminate the contribution of AMPA receptor desensitization, a potent AMPA receptor desensitization inhibitor, cyclothiazide (CTZ, 100 μM), was used (Yamada and Tang 1993). After the aforementioned FIT and RIT experiments, CTZ was applied to the perfusion medium and the experiments were repeated after 20 min.

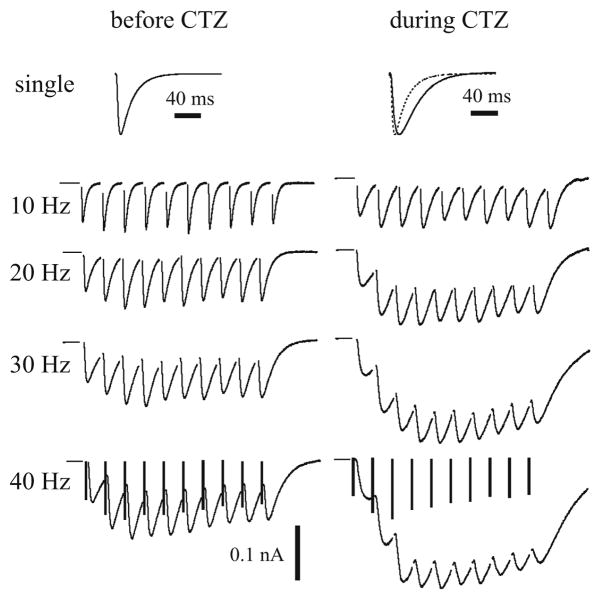
Under CTZ condition, the single EPSC profile is dramatically changed. In a representative cell shown in Fig. 5, the time-to-peak of the EPSC becomes 14.6 ms during CTZ application, compared to 8.7 ms in the previous experiments (control condition). The extent of EPSC is also broadened, e.g., the area of the EPSC is increased by 77% during CTZ application after normalizing the peak amplitudes. Due to the slower kinetics of desensitized AMPA receptors, the effect of temporal summations of EPSCs in a train is greater than the control condition due to the larger overlap. For example, in the 40 Hz train (Fig. 5, bottom row), the ratios of the second to the first EPSC peak amplitudes are 2.2 with CTZ and 1.6 in control; the ratios of the third to the first EPSC peak amplitudes are 3.1 with CTZ and 1.9 in control. However, the values of the deconvolved EPSC amplitudes are not significantly changed. In the same 40 Hz train, the ratios of the second to the first deconvolved amplitudes are 1.5 with CTZ and 1.4 in control; the ratios of the third to the first deconvolved amplitudes are 1.7 with CTZ and 1.6 in control. These results demonstrate that AMPA desensitization has strong effects on the EPSC waveforms but not on the deconvolved amplitudes of estimated transmitter release.

Fig. 5.

Representative fixed-interval EPSC trains before and during CTZ application. The bars in bottom row denote the deconvolved EPSC amplitudes, which are not significantly affected by CTZ despite the dramatic changes in the corresponding EPSC waveforms

Consistent with the FIT results, the RDs (r₂ and r₃) are not significantly changed by CTZ application, as illustrated in the middle row of Fig. 4 (n = 4). This result of negligible CTZ effect on the STP dynamics of SC synapses under 2 mM [Ca²⁺]_o condition indicates that the observed STP dynamics are almost exclusively due to presynaptic mechanisms.

3.1.4 Prediction of random EPSC trains with 3rd-order non-parametric models

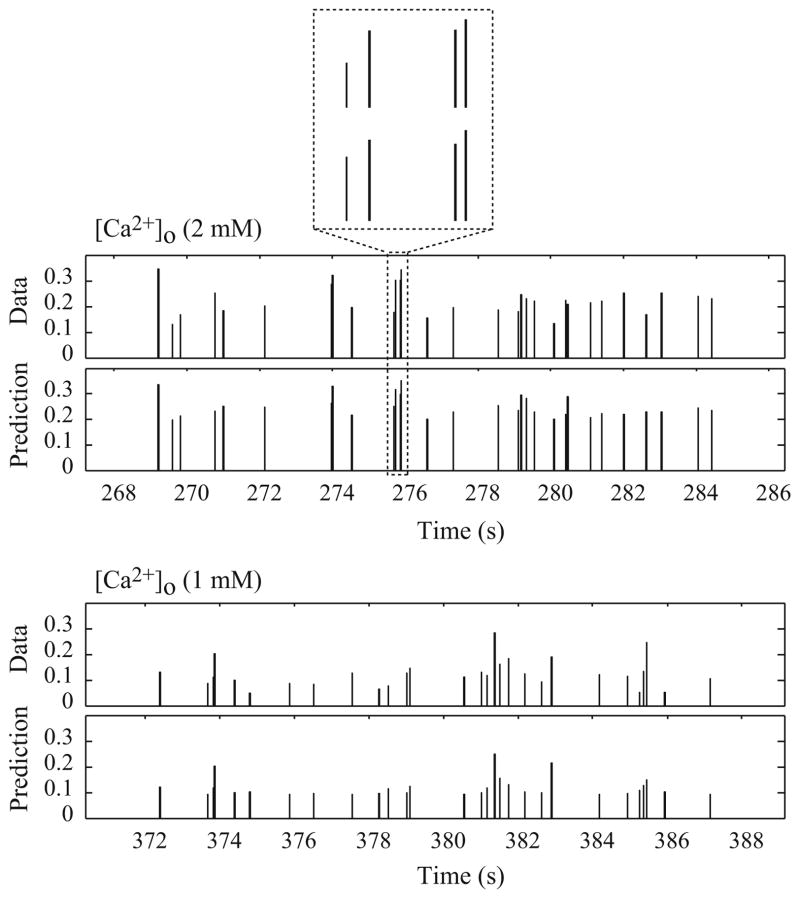
One of the major strengths of the non-parametric model is that it is estimated directly from broadband experimental data (representing a broad repertoire of possible inputs) and retains predictive capability to a broad range of input patterns. The obtained kernels can be used not only to characterize the input–output properties of the system, but also to accurately predict the system output for a given input. For each cell/experiment, the 3rd-order PV model is estimated with random input–output data of 800–3,200 event pairs, and then used to predict the output for a different random input dataset of 400–1,600 events. To evaluate the predictive capability of the estimated model, the NRMSE of the model prediction is calculated based on the predicted outputs and the respective recorded outputs. Our results show that under both high and low [Ca²⁺]_o conditions, the 3rd-order PV models are able to predict accurately the EPSC amplitudes (see Fig. 6). For high [Ca²⁺]_o condition, the NRMSE was 23 ± 2% (n = 9), and for low [Ca²⁺]_o condition, the NRMSE was 24 ± 3% (n = 8).

Fig. 6.

Prediction of the deconvolved EPSC trains elicited by Poisson random-interval stimulation using the 3rd-order Poisson–Volterra models for the two calcium conditions

3.2 Parametric vs. non-parametric modeling of STP dynamics in the SC synapse

3.2.1 Inadequacy of the current parametric FD model

In order to test the adequacy of the parametric FD model (Dittman et al. 2000) for Poisson RIT inputs (i.e., a broad repertoire of operating conditions—and not simply periodic inputs), we estimate the 3rd-order PV models of the SC synapse using two types of broadband input–output data: (1) the data resulting from the simulation of the parametric FD model for a Poisson RIT input, and (2) the experimental data collected from the actual synapse for the same input. Comparison of the obtained PV kernels for the two cases allows rigorous and quantitative assessment of the adequacy of the parametric FD model, since the kernels constitute a canonical (i.e., general and complete) representation of the system dynamics that can be considered “ground truth”.

Based on the respective RDs computed from the estimated kernels (Figs. 4 and 7), the two non-parametric models (i.e., their respective kernels) are qualitatively consistent under high-calcium conditions (i.e., the r₂ is primarily positive and the r₃ is primarily negative). However, when one compares these results with higher quantitative standards, then it is evident that the experimentally derived results (i.e. the “true” non-parametric model of the STP dynamics in the SC synapse shown in Fig. 4) exhibit more complex patterns in both r₂ and r₃, with subtle features that are not evident in the RDs obtained from the simulations of the parametric model. In other words, the parametric model does not capture all aspects of the STP dynamics and nonlinearities associated with the transmission characteristics of the SC synapse—both in terms of the functional outcome (i.e. the prediction of the synaptic output as shown in the NRMSE result) and the underlying biological mechanisms (which appear to comprise more processes in reality than included in the parametric model). This observation suggests that the parametric FD model oversimplifies the form of the STP dynamics in the SC synapse and a more complex parametric model is needed to account for the experimentally observed data.

Fig. 7.

RDs of the 3rd-order Poisson–Volterra models obtained by use of the simulated input–output data of the parametric FD models with parameters estimated from the fixed-interval and random-interval datasets under the two calcium conditions

A note should be made about the intrinsic variations of the biological processes that subserve synaptic transmission. Several studies have shown that central synapses are heterogeneous in release probability, facilitation and depression (Dobrunz and Stevens 1997; Hanse and Gustafsson 2001a). In this study, both the parametric FD model and the non-parametric PV model are estimated with EPSCs derived from populations of SC synapses in which cross-synapse variations are largely averaged. More importantly, to eliminate the effect of the remaining variations on the comparison of performance between parametric models and non-parametric models, both types of models are estimated using the same input–output datasets that are recorded from the same cell.

It is also interesting to examine the effect of the utilized input on the parameter estimates. To explore this, the parameters of the parametric FD model are estimated with both types of input–output data: FIT and RIT datasets, for each cell under each [Ca²⁺]_o condition. This results in two sets of parameter estimates (denoted as FIT-FD and RIT-FD estimates) that are reported in Tables 1 and 2. Considerable differences exist in most of the key parameter estimates. It is also evident that the NMRSE of the parametric model prediction for a Poisson RIT input is lower when the RIT-FD parameter estimates are used, since the RIT input contains a broader repertoire of stimulation patterns and thus yields more accurate parameter estimates (Tables 1 and 2).

In order to illustrate further the effect of the utilized input on the obtained models, we show in Fig. 7 the RDs of the 3rd-order PV models obtained by use of the synthetic input–output data of the parametric FD models with parameters estimated from both the FIT and RIT datasets. These two non-parametric models quantitatively and intuitively represent the functional input–output properties of the two parametric FD models (FIT-FD and RIT-FD). Significant differences are evident for both RDs (r₂ and r₃) under the low-calcium condition, but the differences are subtle for the high-calcium condition.

Most importantly, we wish to compare the RDs of the non-parametric models estimated from the FD model (shown in Fig. 7) and from the experimental data (shown in Fig. 4) for the same RIT input under the two calcium conditions. The results indicate that both FIT-FD and RIT-FD RDs have significant differences from the RDs of the experimentally-derived non-parametric model.

Specifically, under 2 mM [Ca²⁺]_o condition, the r₂ values of the experimentally-derived non-parametric model (i.e., the true r₂) shows peak paired-pulse facilitation at about 40ms IPI (Fig. 4, top row), but this peak is not captured by the r₂ values of either the FIT-FD or the RIT-FD model, which are both monotonically decaying in the IPI range up to 400 ms (Fig. 7). The FIT-FD results also overestimate the paired-pulse facilitation for short IPIs more than the RIT-FD results, relative to the results of the experimentally-derived non-parametric model. The latter peak value is 27 ± 9%, while the peak values for the FIT-FD and RIT-FD models are 39 ± 12% and 30 ± 9% respectively. The more severe overestimation of the FIT-FD model is probably due to the fact that the FIT inputs lack IPIs shorter than 25 ms, where the synapses exhibit weak paired-pulse facilitation (as shown in Fig. 4). Another difference is evident in the values of the negative (depressive) phase of r₂ for IPIs around 400 ms, where the parametric models exhibit less depressive characteristics. Significant differences are also observed in the 3rd-order RDs, where the diagonal slice of the true r₃ shows a more complex shape that can be fit in the early part (short IPIs) by an exponential with time constant of 11ms and in the late part (IPIs from 300 to 500 ms) by an exponential with a time constant of 87 ms, while the diagonal slice of r₃ of the FD models can be fit by a single exponential function with time constant of 69 ms for the FIT-FD model and 56 ms for the RIT-FD model. Notably, the magnitude of 3rd-order depression is much larger in the results of the experimentally-derived non-parametric model. Differences are also evident at the off-diagonal values of r₃. These results suggest that more than one FD processes may be active in the actual SC synapse.

Under 1mM [Ca²⁺]_o condition, the r₂ values of the experimentally-derived non-parametric model exhibit a complex shape that contains at least two exponentials (Fig. 4, bottom row), while the r₂ values for the FIT-FD and RIT-FD models exhibit single exponential shapes (with comparable time constants of 107 and 103 ms, respectively). This result again suggests that the parametric FD model oversimplifies the facilitation process. In terms of the 3rd-order RD, the r₃ values of the experimentally-derived non-parametric model are much stronger and exhibit a more complex shape than its FD-model counterparts. The diagonal slice of r₃ exhibits a triphasic form with strong depression for short IPIs and weak depression for long IPIs, while both FD-model counterparts have a single exponential shape with negligible depression at short IPIs (notably the RIT-FD model exhibits very small values for all IPIs).

In order to compare quantitatively the predictive capability of the various models, we compute the NRMSE of the output prediction for Poisson RIT inputs. Results show that, under both [Ca²⁺]_o conditions, the predictions of the experimentally-derived non-parametric models are significantly more accurate than the corresponding FD models (paired t-test, P < 0.01), and the RIT-FD models are more accurate than the corresponding FIT-FD models (paired t-test, P<0.01). Since the RIT-FD models and the experimentally-derived non-parametric models are estimated from the same input–output datasets, their difference in NRMSE is solely due to their different model configurations. The FIT-FD models have the same model configuration with the RIT-FD models but different parameter values that were estimated from the FIT input–output datasets, thus the fact that the RIT-FD model performs better than the FIT-FD model is a result of the greater “richness” of the RIT datasets that contain a vastly broader variety of input (and consequently output) patterns.

It is evident from these results that the current parametric FD model cannot account for all the nonlinear dynamics captured by the 3rd-order non-parametric model for RIT inputs.

3.2.2 Modification of the parametric FD model

Based on the above experimental and simulation results, it appears necessary to augment the parametric FD model by including a second FD process with different residual calcium time constants (τ_F and τ_D). The resulting “double-process FD model” of the STP dynamics in SC synapses incorporates two sets of facilitation/depression mechanisms that are driven by two different residual calcium dynamics (fast-decaying calcium and slow-decaying calcium). The FD process with fast calcium dynamics is denoted as “fast FD process”, while the other is named “slow FD process”. Note fast/slow residual calcium dynamics do not necessary result in fast/slow FD dynamics, since the latter are mainly determined by the other key model parameters. These key parameters (e.g., the initial release probabilities and recovery rates) are estimated and shown in Table 3. As shown in Eq. (5), the total release probability can be represented as the weighted linear summation of the release probabilities of the two processes.

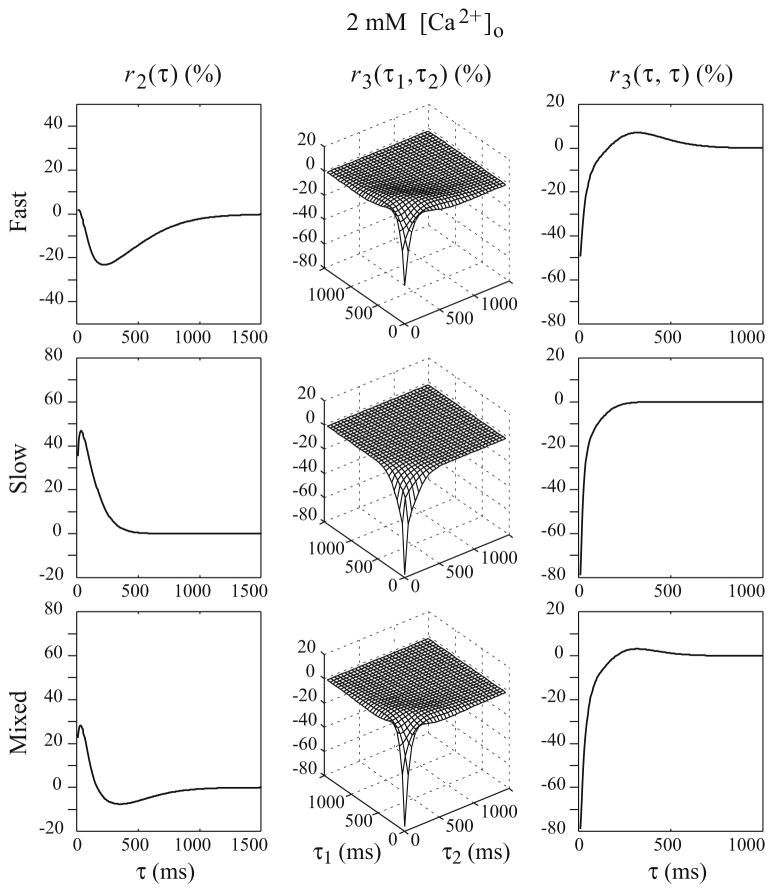
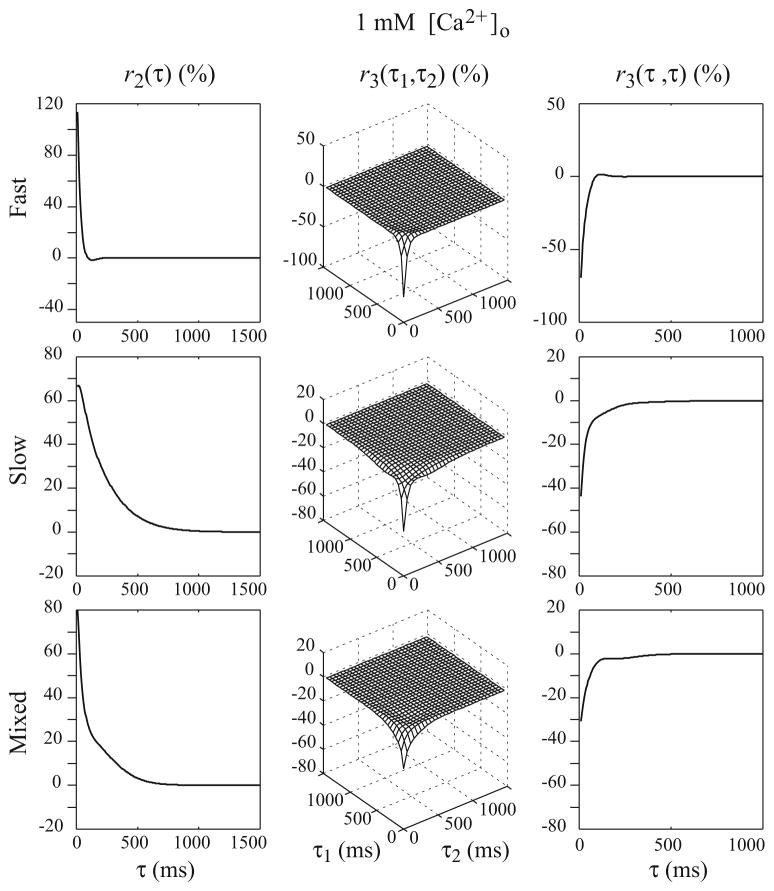
Results show that the 2^nd and 3rd-order RDs of the double-process FD model of SC synapse are closer to their counterparts of the experimentally-derived non-parametric model (which are considered to represent the “ground truth”) under both high and low [Ca²⁺]_o conditions (see Figs. 8 and 9).

Fig. 8.

The computed 2^nd and 3^rd order RDs of the parametric double-process FD model of the SC synapse with parameters estimated from the random-interval input–output experimental data under 2 mM [Ca²⁺]_o condition

Fig. 9.

The computed 2^nd and 3^rd order RDs of the parametric double-process FD model of the SC synapse with parameters estimated from the random-interval input–output experimental data under 1 mM [Ca²⁺]_o condition

The computed 2^nd and 3rd-order RDs of the slow and fast FD processes of the double-process FD model under 2mM [Ca²⁺]_o condition are shown in Fig. 8. It is evident that the negative phase of r₂ is mostly due to the fast process, which has a fairly high release probability (0.51). In this process, the first impulse causes the release of more than half of the available vesicles; the maximum paired-pulse ratio cannot exceed one by definition and r₂ is primarily negative. For very short IPIs, the release is enhanced by residual Ca²⁺ accumulation and the paired-pulse ratio (0.90) is close to its maximum possible value. The r₂ values for this process are close to zero in this IPI range. For longer IPIs, the release is less facilitated and the recovery of depression is less accelerated due to the decay of residual Ca²⁺. The r₂ values show strong paired-pulse depression. When the IPI is further increased, all parameters recover to their original values and the values of r₂ return back to zero. Due to these reasons, the form of r₂ for the fast process becomes U-shaped and causes the negative phase in the r₂ of the overall model. The fast FD process also shows strong depression in r₃. This is not surprising since its release probability is so high that there are only very few vesicles available after two consecutive releases, even with the facilitatory effect of the residual Ca²⁺.

The slow process has a relatively lower release probability (0.32), which allows paired-pulse facilitation. This process is the main contributor of facilitation in the r₂ of the overall model (Fig. 8). Also, the form of r₂ for the slow process is bell-shaped for short IPIs and the peak of facilitation is properly lagged by 40 ms (as in the experimentally-derived non-parametric model) instead of happening at the shortest IPI which is the case for the single-process FD model. This can be explained by its high recovery rate and the fact that the number of releasable vesicles is increasing over time, although the facilitation effect is declining. This tradeoff between facilitatory and depressive mechanisms makes the r₂ bell-shaped instead of monotonically decreasing. The results shown in the third row of Fig. 8 (that include both the fast and the slow process) are nearly identical to the experimentally-derived non-parametric model (Fig. 4, top row).

The results under 1 mM [Ca²⁺]_o condition are shown in Fig. 9. The initial release probabilities of the two processes are relatively low, while the paired-pulse facilitation ratios are high. For both processes, depletion plays a smaller role than under 2 mM [Ca²⁺]_o condition. The values of r₂ are big and the values of r₃ are relatively small. The difference in the shape of r₂ for the fast FD process between the high and low [Ca²⁺]_o condition is caused by at least two reasons: (1) the initial release probability is decreased from 0.51 to 0.18, leading to smaller depletion of the releasable vesicle pool and weaker depression, and (2) the recovery rate is higher in low rather than in high [Ca²⁺]_o condition. The second reason is seemingly contradictory to the residual calcium-dependent recovery hypothesis, which suggests that the recovery from depletion is positively correlated to the residual calcium concentration–lower [Ca²⁺]_o then should cause slower, instead of faster, recovery rate. However, it must be noted that these two recovery rates are estimated with different initial release probabilities that may have different levels of the “energy barrier” between the depleted and resting states (i.e., it is likely that the low initial release probability state is easier to recover from the depleted state than the high initial release probabilities state). The slow FD process has a positive slow-decaying r₂ and a negative but relatively small r₃ due to the enhanced recovery rate. The high recovery rate prevents the values of r₃ from having a slow and negative component, which is indeed not observed in the experimental data. The overall r₂ caused by these two FD processes (Fig. 9, third row) shows a shape similar to its non-parametric counterpart (Fig. 4, bottom row), while the overall r₃ values still retain some differences between the non-parametric model and the parametric double-process FD model.

4 Discussion

In this study, the nonlinear dynamics of STP in hippocampal SC synapses are characterized using a non-parametric Poisson–Volterra (PV) model obtained directly from experimental input–output data collected during Poisson random-interval train (RIT) stimulation. The model provides better prediction of the output data than a parametric facilitation/depression (FD) model. The implication of this finding is that the experimentally-derived non-parametric model captures better the nonlinear dynamic characteristics of synaptic transmission and constitutes a more complete functional description of the biological processes involved. Consequently, we used this non-parametric model as the “ground truth” for assessing quantitatively the adequacy of the aforementioned parametric model and to explore ways of improving the parametric model by including additional terms/parameters that represent additional biological processes involved in synaptic transmission. This task was achieved by estimating and evaluating the non-parametric surrogates of the parametric model. Evaluation of the surrogates using the experimentally-derived non-parametric model suggested a double-process mechanism of STP in SC synapse comprising a fast-calcium FD process and a slow-calcium FD process.

Both the low (1 mM) and high (2 mM) [Ca²⁺]_o condition results suggest such double-process mechanism. As we know, STP is determined by facilitation and depression: facilitation is the synaptic enhancement caused by the action of calcium remaining in the presynaptic terminal after preceding action potential(s); depression is simply caused by the depletion of the pool of release-ready transmitter vesicles. With low [Ca²⁺]_o and the subsequent small initial release probability, only a small portion of the transmitter vesicles are released after a stimulus. The size of the release-ready vesicle pool remains relatively constant and the effect of the depletion-dependent depression was weak. STP under this condition thus primarily reflects the dynamics of facilitation. This is verified by the prominent positive r₂ and small negative r₃ in the PV model under low [Ca²⁺]_o condition. The double-exponential shape r₂ suggests that there are two distinct processes of facilitation.

When the [Ca²⁺]_o is elevated, the initial release probability of synapses is increased; depletion mechanism is more involved and the PV model reflects the interplay of both facilitation and depression. Both r₂ and r₃ under high [Ca²⁺]_o condition show patterns distinct from those under low [Ca²⁺]_o condition. Interestingly, the two processes show different levels of sensitivity to the [Ca²⁺]_o elevation: in the short inter-impulse intervals where the fast process is involved, r₂ is almost reversed and shows very weak facilitation in the high [Ca²⁺]_o condition; r₃ become significant and shows strong depression. By contrast, in the longer inter-impulse intervals where the slow process is more involved, r₂ and r₃ are not dramatically changed. These results suggest that the fast FD process is more sensitive to the [Ca²⁺]_o elevation than the slow FD process.

Double-process facilitation in STP has been reported in a variety of synapses from different species (Eccles et al. 1941; Zengel et al. 1980; Gage and Murphy 1981; Zengel and Magleby 1982). To our knowledge, this study is the first to suggest its existence in hippocampal synapses of the rat. There are several reasons why this mechanism may have been overlooked by previous studies with traditional paired-pulse or fixed-interval stimulation protocols, but not by this one. First, instead of directly measuring the paired-pulse facilitation as a function of inter-impulse interval, in this study, the 2nd-order RD, r₂, (which is equivalent to the paired-pulse modification function) is computed from the estimated PV kernels of the non-parametric model that is obtained from broadband RIT data where the intervals between impulses are randomly varying, while the traditional paired-pulse or fixed-interval train protocols only include a small subset of possible input patterns. RIT allows to capture the fine details of the STP pattern. Secondly, the STP dynamics of SC synapses are investigated under two calcium conditions in this study, making the differences between the two processes more visible by comparing the results under these two conditions. Lastly, when the STP dynamics are studied using paired-pulse or fixed-interval train protocols, some transient mechanisms may have been mixed with facilitation and depression due to the non-stationary nature of these protocols. By contrast, in the non-parametric approach the model was estimated with RIT data that do not alter the stationarity of the system.

There could be multiple ways of modifying the parametric FD model to better fit the experimentally-identified nonlinear dynamics. We propose the double-process FD model for the following two reasons: First, the double-process FD model introduces minimal extension of the FD model in terms of the modeled mechanisms and dynamic processes (but not minimal number of extra open parameters). Additional model parameters can be readily explained using the existing residual calcium-facilitation/depression framework, which is supported by many other independent studies. Second, there are experimental evidences suggesting the existence of two types of synapses. Using minimal stimulation protocol, Hanse and Gustafsson recorded single CA1 synapses and showed their heterogeneity in initial release probability (Hanse and Gustafsson 2001b). Furthermore, the distribution of initial release probability had two peaks, which is consistent with our double-process FD model. Despite these reasons, however, it should be pointed out that, although the double-process FD model accurately replicates the experimentally-identified STP nonlinear dynamics under two calcium conditions, it still should not be considered as a conclusive representation of the CA1 synapse. For example, this study does not rule out the possibility of having a more complex residual calcium dynamics and/or different types of active zones in a single synapse (as opposed to different types of synapses), since it is carried out at the synaptic population EPSC level. Instead, as a parametric model, our double-process FD model provides new mechanistic predictions/hypotheses, e.g., the relations between initial release probability, paired-pulse facilitation ratio, and recovery rate (Table 3), that can be tested with further studies, e.g., recording and modeling of single synapses.

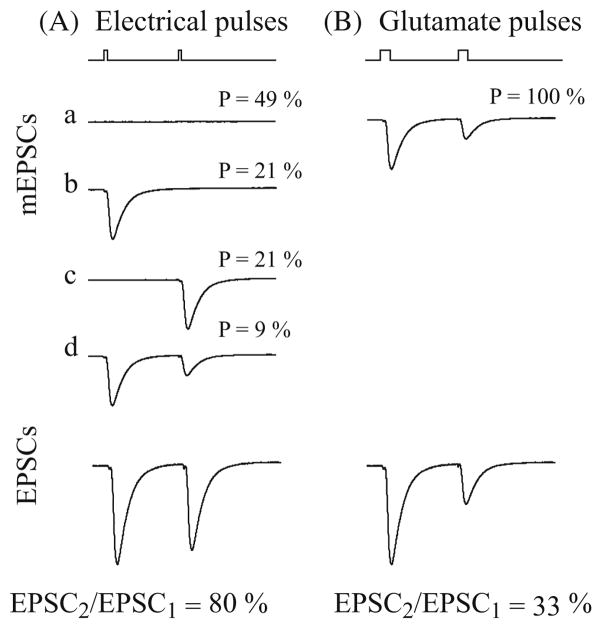
Besides transmitter vesicle depletion, another mechanism that can cause use-dependent depression of synaptic strength is the desensitization of postsynaptic receptors (Jones and Westbrook 1996; Wadiche and Jahr 2001). Consecutive exposure of ligand-gated channels to their agonist can lead some of the channels to the non-responsive desensitized state. However, consistent with other reports (Hjelmstad et al. 1997; Hashimoto and Kano 1998; Silver et al. 1998), this study showed that AMPA receptor desensitization does not play significant role in STP. The negative-going component in r₂ under high [Ca²⁺]_o condition was not blocked by the AMPA receptor desensitization blocker CTZ. This component was more likely due to the nonlinear dynamics in the presynaptic regions. Previous experiments have shown that profound desensitization of AMPA receptor occurred on miniature excitatory postsynaptic currents (mEPSC) elicited by brief pulses of glutamate (Trussell and Fischbach 1989). Paired-pulse responses in these studies revealed that desensitization can reduce the amplitude of the second mEPSC to less than 30% of the amplitude of the first mEPSC with a 6 s inter-impulse interval. The time course of recovery of the second mEPSC in a pair could be fitted by a simple exponential curve with a time constant of 9.2 ms. However, such strong depression was not reflected in the estimated PV kernels or RDs of our non-parametric model. This apparent discrepancy could be reconciled by taking into account the stochastic nature of transmitter release. Hippocampal SC synapses, as well as other central synapses, tend to have extraordinarily low release probabilities. The average initial release probability was estimated to be around 0.3. This means that the probability of postsynaptic AMPA receptors being exposed to consecutive transmitter releases is very small (the probability of release over two consecutive pulses is 0.09). This situation is distinct from the paired glutamate pulse experiment in which desensitization always occurs (Fig. 10).

Fig. 10.

Simulated experiment showing that the paired-pulse depression caused by AMPA receptor desensitization is attenuated by the probabilistic releases. (A) mEPSCs and EPSCs elicited by pairs of electrical pulses. a, b, c and d are the four possible patterns of mEPSCs. Desensitization only occurs in d. (B) mEPSCs and EPSCs elicited by pairs of glutamate pulses. Desensitization always occurs. In both (A) and (B), the second EPSCs were normalized by the amplitude of the first EPSC. Note the different levels of depression caused by desensitization

Previous studies also showed the existence of depletion-independent mechanisms of depression in the synaptic STP (Hsu et al. 1996; Dobrunz et al. 1997; Kraushaar and Jonas 2000; Waldeck et al. 2000; Gover et al. 2002; Kirischuk et al. 2002; Pedroarena and Schwarz 2003; Fuhrmann et al. 2004). These forms of depression mechanisms are not included in the present parametric modeling, but potentially can be added to better explain the obtained STP dynamics. For example, the double-process FD model still underestimates the paired-pulse depression in short IPIs under high [Ca²⁺]_o condition (Fig. 8, bottom-left), compared to the experimental data (Fig. 4, top-left). This discrepancy is likely to be caused by the lack of such mechanisms (e.g., inactivation of presynaptic N-type Ca²⁺ channels shown by Dobrunz et al.) in the parametric model. Indeed, the proposed combined parametric/non-parametric modeling strategy should be used iteratively for the discoveries and characterizations of new underlying mechanisms.

In summary, the main result of this study is the corroborated proposition that an experimentally-derived non-parametric model constitutes a rigorous quantitative tool for assessing the input–output property of any proposed model and provides the quantitative means to guide the manner in which possible improvements of a parametric model can be achieved by inclusion of additional terms/parameters (representing additional biological processes). This issue was examined here in the context of synaptic transmission in the hippocampus but has broad applicability to all neuronal systems. Therefore, this study may serve as an experimental/modeling paradigm for other applications in the context of systems neuroscience.