Modeling the Nonlinear Properties of the in vitro Hippocampal Perforant Path-Dentate System Using Multielectrode Array Technology

Abstract

A modeling approach to characterize the nonlinear dynamic transformations of the dentate gyrus of the hippocampus is presented and experimentally validated. The dentate gyrus is the first region of the hippocampus which receives and integrates sensory information via the perforant path. The perforant path is composed of two distinct pathways: 1) the lateral path and 2) the medial perforant path. The proposed approach examines and captures the short-term dynamic characteristics of these two pathways using a nonparametric, third-order Poisson–Volterra model. The nonlinear characteristics of the two pathways are represented by Poisson–Volterra kernels, which are quantitative descriptors of the nonlinear dynamic transformations. The kernels were computed with experimental data from in vitro hippocampal slices. The electrophysiological activity was measured with custom-made multielectrode arrays, which allowed selective stimulation with random impulse trains and simultaneous recordings of extracellular field potential activity. The results demonstrate that this mathematically rigorous approach is suitable for the multipathway complexity of the hippocampus and yields interpretable models that have excellent predictive capabilities. The resulting models not only accurately predict previously reported electrophysiological descriptors, such as paired pulses, but more important, can be used to predict the electrophysiological activity of dentate granule cells to arbitrary stimulation patterns at the perforant path.

I. Introduction

THE hippocampus is one of the most extensively studied neuronal systems in the brain because it provides a model system to advance our understanding of the mechanisms that underlie higher cognitive functions, such as learning and memory [1]–[4]. The hippocampus receives neuronal inputs from multiple brain regions that are involved in processing different modalities of sensory information, and its primary function is the formation of mnemonic labels that identify a unified collection of features (e.g., those comprising a person's face) and the creation of both semantic and temporal relations between multiple collections of features (e.g., associating a person's face with a given context) [5]–[7].

The hippocampus is comprised of several subsystems that form a closed loop. The dentate gyrus is the first hippocampal subsystem receiving the primary input of the hippocampus via the perforant path that arises from the entorhinal cortex. It plays a pivotal role in understanding the synaptic integration of the hippocampus because the perforant pathway is the recipient of most of the sensory input to the hippocampal formation. Moreover, the two pathways of the perforant pathway (the lateral and medial perforant paths) receive converging sensory information (e.g., visual, auditory, and olfactory) from other brain regions [8], [9]. The lateral perforant path (LPP) and the medial perforant path (MPP) can be readily isolated as they are anatomically and functionally distinct [10]–[12], exhibiting a number of different physiological [13]–[15] and pharmacological [16]–[19] characteristics. Both pathways converge to a common population of neurons in the dentate gyrus, the granule cells.

Biologically interpretable models of the hippocampus are essential for understanding how sensory modalities are functionally processed and integrated. Parametric models, often used to describe functional properties of cortical areas [20]–[22], are not easy to scale when complex functions in a multineuron network level are involved, since a very large number of parameters are required to represent large numbers of complex interconnected elements. Nonparametric models based on the input–output relationships address the scalability issue successfully because they are concerned with an accurate representation of the input–output mapping without explicit regard to the internal complexity of the system. This relieves us from the burden of specifying the multitude of complex interconnected elements, but also limits our scope to the aggregate effect of these multiple elements and their complex interconnectivity on the observed output of the system (in this case, the population spike in the dentate gyrus). For this reason, nonparametric models can be employed to provide more compact and comprehensive functional representations of hippocampal circuitry [23]–[28].

In this paper, a nonparametric methodological approach (called the Poisson–Volterra modeling approach [29]) is presented that yields models capable of characterizing the nonlinear dynamic characteristics of the manner in which sensory information arriving at the LPP and the MPP is integrated by the granule cells of the dentate gyrus. The obtained model represents a compact quantitative representation of the dentate gyrus based on experimentally available datasets [30], [31], and it is mathematically rigorous and scalable with predictive capabilities [32], [33]. The predictive accuracy of this model is quantitatively evaluated using the normalized mean-square prediction error. This model has the ability to represent the effect of the combined activity of all (known and unknown) neuronal actions and interactions, without explicit knowledge of the underlying neuronal mechanisms. This ability is due to the Poisson–Volterra kernels of the model that are the quantitative descriptors of the full nonlinear neuronal transformations and are unique representations of the associated functional properties.

The Poisson–Volterra model presented in this paper was obtained from data recorded from in vitro hippocampal slices. The electrophysiological activity of the dentate gyrus was measured experimentally using multielectrode arrays [34]–[37]. Each of the two pathways was stimulated with a random point process (a Poisson sequence of impulses), called hereafter a random impulse train (RIT), while the response of a population of granule cells was recorded simultaneously.

The motivation for this work is provided by the need to establish the appropriate Poisson–Volterra model for this system through the analysis of actual experimental data obtained under conditions of random point process stimulation. To validate the obtained results, we performed a comparison with the widely used method of paired-pulse stimulation and its associated measurements of paired impulse functions (PIFs). Since the latter is defined only for a single input, we collected data with an RIT stimulation of each pathway to estimate the requisite Poisson–Volterra models. The extension to simultaneous stimulation of the two pathways with an independent RIT will be presented in the near future.

Several researchers have used the PIF as a tool to describe the dynamic characteristics of the LPP and the MPP [14], [19], [38]. In this paper, we show that the PIF represents only a partial view of the full functional characteristics of the system—the one defined by pairs of stimulating impulses but not triplets or more. We confirmed this fact by comparing the experimentally measured PIF with the PIF computed on the basis of the third-order Poisson–Volterra model estimated with the data collected under RIT stimulation. The latter model accounts for the dynamic interactions of up to three stimulating impulses, which have an effect on the granule cell response (as indicated by the analysis of the data). As more than two impulses appear at either of the two pathways (LPP or MPP), the PIF fails to predict the granule cell output with the same accuracy as the third-order Poisson–Volterra model, since the PIF does not account (by definition) for the interaction among more than two stimulating impulses.

A preliminary version of this work has appeared as a conference poster [39]. The results presented in this paper show that a third-order Poisson–Volterra model is capable of predicting accurately the granule cell output at the dentate gyrus in response to arbitrary patterns of stimulating sequences at the LPP and MPP of the rat hippocampus.

II. Materials and Methods

A. Preparation of Slice and Multielectrode Stimulation

Adult Sprague–Dawley male rats, 7–9 months of age, were used in all experiments. The brain slices were acquired using the following standard electrophysiological procedures [30]. Hippocampi from both hemispheres were dissected under cold (2 °C) artificial cerebro-spinal fluid (aCSF) (NaCl, 128 mM; KCl, 5 mM; NaH₂PO₄, 1.25 mM; NaHCO₃, 26 mM; Glucose, 10 mM; MgSO₄, 2 mM; ascorbic acid, 2 mM; CaCl₂, 2 mM) and aerated with a mixture of 95% O₂ and 5% CO₂. A standard vibratome (VT1000S, Leika, Germany) was used to cut the hippocampus transverse to the longitudinal axis in 400-μm-thick slices. Slices then were left to equilibrate while bathed in cold aCSF for at least 2 h. Subsequently, each slice used for electrophysiological analysis was carefully positioned on top of a multielectrode array, and was held down with a nylon mesh. The slice was positioned so that stimulating electrodes covered the inner blade of the dentate gyrus (see Fig. 1). The positioning of the slice relative to the array was documented with the aid of an inverted microscope (DML, DMIRB, Leika, Germany) and a digital camera (Hitachi VK-C370, Spot Model 2.0.0). Throughout all experiments, slices were perfused with 1 mM MgSO₄ aCSF at a flow rate of 15 ml/min and constantly heated at 33 °C.

Fig. 1.

(a) Experimental setup. (b) Slice of the rat hippocampus and the multielectrode array. Abbreviations: PP: perforant path, DG: dentate gyrus, ML: molecular layer, GCL: granule cell layer. Electrodes positioned at the outer one-third of the molecular layer were chosen as candidates to stimulate the LPP and at the middle one-third of the molecular layer to stimulate the MPP.

A multielectrode array system was used to simultaneously stimulate and record from multiple sites in each hippocampal slice. The system consisted of two components: 1) a custom-designed multisite electrode array to cover the appropriate subregions of the dentate gyrus with 60 microelectrodes in a 3 × 20 configuration [17], [40] and 2) a commercially available multi-channel stimulation-recording system (MEA60 Multi Channel Systems, Germany) (Fig. 1). The microelectrodes were appropriately arranged to allow individual stimulation of each pathway. They were embedded in a planar glass plate, with 28-μm diameter and center-to-center spacing of 50 μm. The array was positioned over the molecular layer (ML), spanning from the fissure to the granule cell body layer.

The stimulation electrodes were chosen in the outer-ML to stimulate the LPP and in the mid-ML to stimulate the MPP. The selection of the stimulating electrodes for the perforant path was confirmed by the following electrophysiological criteria: 1) field excitatory post-synaptic potentials (fEPSPs) showed pair pulse facilitation when the LPP was stimulated, and paired pulse depression when the MPP was stimulated [14], [17], [41]; 2) fEPSPs exhibited a dendritic current sink at the outer ML and a dendritic current source at the middle ML when LPP was stimulated; accordingly, when the MPP was stimulated, fEPSPs exhibited a dendritic current sink at the middle ML and a dendritic current source at the outer ML [42]–[44]; 3) stimulation at the MPP exhibited shorter latencies of the population spike recorded in the granule cell layer [14], [28]. The electrode positioned right below the granule cell layer was used to record the electrophysiological response in the form of population spikes which reflect the synchronous activation of dentate granule cells [45], [46].

B. Experimental Protocol and Data Acquisition

At the beginning of each experiment, input–output (I/O) curves were measured for the LPP and the MPP separately with a series of biphasic pulses (100 μs duration) having intensities that varied between 10 μA and 140 μA (in 10-μA increments, without inducing long-term potentiation). The I/O curve for each pathway was used to determine the stimulation intensity for the experiment as the value that evoked 50% of the maximum population spike response in the granule cell layer. Subsequently, five series of paired pulses (PP) with seven different interpulse intervals (IPI) (50, 100, 200, 300, 500, 750, and 1000 ms) were applied to each pathway. The resulting PPs were used to compute a paired impulse function (PIF), which is the ratio of the population spike amplitude evoked by the second pulse over the one evoked by the first pulse at each IPI (averaged over five PP stimulation series).

Following the PP testing, each pathway was stimulated with an RIT stimuli. Each RIT contained 400 Poisson-distributed impulses (mean interimpulse interval of 500 ms, covering the approximate range of 10–4000 ms). The use of Poisson-distributed RITs was motivated by the desire to employ a class of stimuli capable of testing the system with a wide variety of interimpulse intervals over a relatively short period. This class of stimuli has been shown to be suitable for testing the hippocampus and, furthermore, supports efficient modeling of the nonlinear dynamics of this neuronal system [23], [28]. The parameter of the Poisson distribution that determines the average firing rate of the RIT is consistent with the known firing rates of the respective hippocampal neurons [47], [48]. The stimulation intensity used was the same as for the PP series. The system was tested for stationarity by measuring the I/O curves before and after RIT stimulation, and only data sets that exhibited changes within ±15% of the baseline were included in the analysis.

Experimental data were sampled at 25 kHz per channel and the amplitude of each population spike was extracted for data analysis using a custom interface written in MATLAB (v6.5). This amplitude was defined as the segment of the vertical line between the negative peak of the spike and the tangential straight line connecting the spike onset and offset [49].

C. Volterra Modeling of a Single-Input Single-Output Point-Process System

The data were analyzed using a variant of the general Volterra modeling approach, adapted for a point-process (i.e., impulse sequence) stimulus and the corresponding output sequence of population spikes with variable amplitude [39], [50]). This approach considers the input and the output events/spikes to be contemporaneous (i.e., occurring in the same time bin which is set to 10 ms so that it exceeds the maximum output latency of 7.4 ms observed in our experiments). This modeling approach, called the Poisson–Volterra approach, is applicable to all systems with contemporaneous point-process inputs and outputs. It employs a general model of the system response y(n) to a point-process stimulus [29], [51]

$$\begin{array}{cc}\hfill y\left(n_i\right)& =k_1+\sum _{n_i-\mu <n_j<n_i}{k}_2(n_i-n_j)\hfill \\ \hfill & +\sum _{\begin{array}{c}\hfill n_i-\mu <n_j<n_i\hfill \\ \hfill n_i-\mu <n_{j^{\prime }}<n_i\hfill \end{array}}\sum k_3(n_i-n_j,n_i-n_{j^{\prime }})\hfill \end{array}$$ (1)

where n_i denotes the time of a stimulus event (impulse), y(n_i) is the amplitude of the population spike at the same discrete time, and n_j is the time of occurrence of any jth stimulus event within the time window of μ (system memory) prior to n_i. The functions k₁, k₂, and k₃ are the first-, second-, and third-order Poisson–Volterra kernels and represent the key descriptors of the nonlinear dynamics of this third-order system. Note that the output at all other times is zero. The first-order kernel represents the amplitude of the population spike attributed to each stimulating impulse alone (i.e., in the absence of any other input impulses within the memory extent μ, which was found to be about 1 s for this system). The second-order kernel represents the change(s) in the population spike amplitude caused by interactions between the present stimulus impulse and each of the past stimulus impulses within the memory extent μ. Finally, the third-order kernel represents the change(s) in the population spike amplitude caused by interactions between the present stimulus impulse and any two preceding stimulus impulses within the memory extent μ, not accounted for by the second-order model.

In order to reduce the number of free parameters required for kernel representation and estimation, the kernels were expanded on a Laguerre basis (i.e., they were approximated with linear combinations of exponentially decaying Laguerre functions [32]). The unknown Laguerre expansion coefficients were estimated from the data using least-squares fitting methods, as detailed in [32]. The kernels can be reconstructed using the respective estimated expansion coefficients.

The predictive accuracy of the obtained Poisson–Volterra model (that contains the estimated kernels) was evaluated using the normalized mean square error (NMSE) of the model prediction versus the system actual output, defined as

$$\mathrm{NMSE}=\frac{\sum _i{(Y_{{\mathrm{pr}}_i}-Y_{{\text{data}}_i})}^2}{\sum _i{Y}_{{\text{data}}_i}^2}$$ (2)

where Y_pr is the predicted amplitude of the population spikes and Y_data is the recorded amplitude of the population spikes. The value of the NMSE cannot become zero, even for a perfect model, due to the inevitable presence of measurement errors and noise in the data. Therefore, interpretation of the numerical values of the computed NMSE must be made in the context of the noise conditions and possible measurement errors in each case. Typically, NMSE values of less than 0.1 are deemed to indicate satisfactory predictive capability of the model that validates its specific form.

The kernel estimation procedure and the nonlinear modeling/analysis of the LPP and MPP systems were performed with the use of a specialized software package (LYSIS) that has been developed by the Biomedical Simulations Resource at the University of Southern California and is distributed to the biomedical community free of charge [52]. The statistical significance of the obtained estimates of the Laguerre expansion coefficients (from which the kernels and the Poisson–Volterra model predictions are constructed) was evaluated by applying the Student's t-test at the significance level of p < 0.01.

D. Comparison Between PP and RIT Analysis

The descriptor widely used for PP characterization/evaluation has been the paired impulse function (PIF) [14], [19], [42]. The measured PIF is defined as the ratio of the amplitude Y₂ of the second pulse (test response) over the amplitude Y₁ of the first pulse (conditioning) resulting from stimulation with paired pulses with a given interpulse interval (IPI) Δn = n₂ – n₁, where n₁ is the time of occurrence of the first pulse and n₂ is the time of occurrence of the second pulse

$$\mathrm{PIF}\left(\Delta n\right)=\frac{Y_2}{Y_1}.$$ (3)

Note that the PIF values are non-negative and depend on the IPI. For a given IPI, PIF values of greater than 1 indicate PP facilitation, while PIF values of less than 1 indicate PP depression. In the context of the proposed approach, the estimated kernels can be used to compute the first and second responses due to a PP stimulus with any IPI, equivalent to the one measured in the PP experiments. For instance, the test response Y₂ can be computed by use of the Poisson–Volterra model of (1) as follows:

$$Y_2=k_1+k_2\left(\Delta n\right)+k_3({\Delta }_n,\Delta n)$$ (4)

where Δn is the IPI between the two stimulus impulses. Since the first-order kernel represents the amplitude of the population spike attributed to an isolated impulse stimulus, it defines the conditioning response and we can obtain an estimate PÎF of the PIF from a series of PP experiments as

$$\mathrm{P}\widehat{\mathrm{I}}\mathrm{F}\left(\Delta n\right)=1+\frac{k_2\left(\Delta n\right)+k_3(\Delta n,\Delta n)}{k_1}.$$ (5)

The estimated PÎF will be a close approximation of the measured PIF if, and only if, the employed third-order Poisson–Volterra model is an adequate model for the subject system. To examine the adequacy of the employed model, we compared the measured PIFs with the estimated PÎFs for all experimental preparations, and quantified the degree of agreement by computing their correlation.

III. Results

In this study, five experiments with RIT stimulation were performed in vitro for each of the two pathways—LPP and MPP—selected according to standard electrophysiological criteria [14], [17], [25], [41], [42], [44]. A third-order Poisson–Volterra model was used to analyze the RIT data [29], [30], [39], [50], [51]. Three Laguerre basis functions were found to be appropriate as a tradeoff between model complexity and prediction accuracy. The optimal values of the Laguerre parameter α were found to vary slightly among experiments: α = 0.994±0.003 for the LPP, and α = 0.992±0.002 for the MPP. Note that there are ten free parameters in each estimated third-order Poisson–Volterra model.

Over the five experiments analyzed for both inputs, the mean and standard deviation of the first-order kernel (k₁) were 127.79 μV ±20.3 μV for the LPP and 244.27 μV ±56.2 μV for the MPP. The mean values of the estimated second (k₂)- and third (k₃)-order kernels over the five experiments are shown in Fig. 2 for the LPP and in Fig. 3 for the MPP, after normalization (division) by k₁.

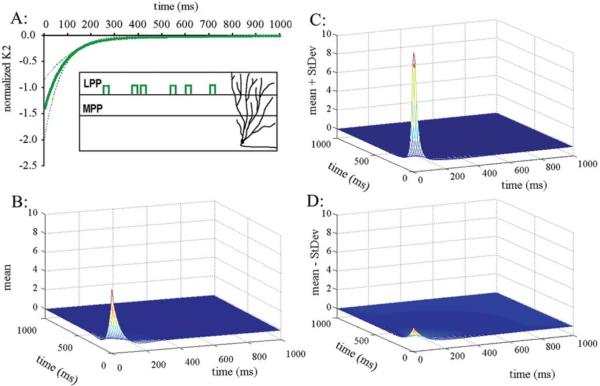
Fig. 2.

(A) Mean values of the normalized second-order kernels (k₂) over five different experiments in the LPP case. The dotted lines mark ± one standard deviation. This kernel exhibits a gradually declining inhibitory characteristic up to about 500 ms. (B) The mean values of the normalized third-order kernels (k₃) over the five experiments. This third-order kernel exhibits an early facilitatory phase that rapidly declines and crosses into a shallow inhibitory phase shortly after 50 ms, relaxing back to zero values around 400 ms. (C) The mean values of k₃ plus one standard deviation. (D) The mean values of k₃ minus one standard deviation.

Fig. 3.

(A) The mean values of the normalized second-order kernels (k₂) over five different experiments in the MPP case. The dotted lines mark ± one standard deviation. This kernel exhibits an early facilitatory phase, rapidly declining and crossing into an inhibitory phase around 100 ms that relaxes back to zero values around 1000 ms. (B) The mean values of the normalized third-order kernels (k₃) over the five MPP experiments. This third-order kernel exhibits an early inhibitory phase that rapidly declines into a slower inhibitory phase around 100 ms and relaxes back to zero values around 500 ms. (C) The mean values of k₃ plus one standard deviation. (D) The mean values of k₃ minus one standard deviation.

In Fig. 2(A), the mean values of the estimated k₂ exhibit a gradually declining inhibitory characteristic up to 500 ms. Fig. 2(B) shows the mean values of the estimated k₃ that exhibit an early facilitatory phase, rapidly declining and crossing into a shallow inhibitory phase shortly after 50 ms. The latter relaxes to zero values around 400 ms. Fig. 2(C) shows the mean values of k₃ plus one standard deviation, and Fig. 2(D) shows the mean values of k₃ minus one standard deviation. The results in the MPP case are shown in Fig. 3 in the same sequence. Fig. 3(A) shows the mean k₂ to exhibit an early facilitatory phase, rapidly declining and crossing into an inhibitory phase around 100 ms that relaxes back to zero values around 1000 ms. Fig. 3(B) shows the mean k₃ to exhibit an early inhibitory phase, rapidly declining to a slower inhibitory phase around 100 ms. The latter relaxes back to zero around 500 ms. Fig. 3(C) and (D) show the mean values of k₃ plus and minus one standard deviation, respectively.

A. Comparison Between the Paired Pulse (PP) and RIT Analysis

In order to compare the two main approaches of stimulation and analysis for the study of neuronal nonlinearities (facilitation and depression), we use the measured and the estimated PIF for the two pathways, following the methodology described in the previous section. These measurements can be used to assess the ability of the advocated Poisson–Volterra model to reproduce the functional characteristics (i.e., the PIF) studied through the PP approach. Note that a PIF value of greater than 1 indicates that the population spike amplitude due to the second pulse is greater than the one due to the first pulse (facilitation), while the reverse is true for PIF less than 1 (depression). The results are compared in Fig. 4 (averages over five experiments with PP and RIT stimulation applied the same preparation).

Fig. 4.

The measured PIF (obtained through PP stimulation) and the estimated PÎF (obtained through RIT stimulation and Poisson–Volterra analysis) for LPP (A) and MPP (B) using a third-order Poisson-Volterra model, and for LPP (C) and MPP (D) using a second-order Poisson–Volterra model. The dotted lines show ± one standard deviation for the RIT case and the bars show the standard deviation range for the PP case.

We see that the estimated PÎF from the RIT data closely tracks the measured PIF from the PP data. The only slight deviation is observed in the MPP case for IPI > 200 ms. We surmise that this is due to the third-order dynamics of the system in this case (see Discussion). These findings indicate that the proposed third-order Poisson-Volterra model is adequate for representing the PP results and, in fact, reveals additional information about the system dynamics of order higher than second (when they exist, as in the MPP case for IPI > 200 ms) that is not obtainable with PP stimulation. To examine this point further, we compared the estimated PÎF using a second-order Poisson–Volterra model with the measured PIF. As shown in Fig. 4(C) and (D), the estimated PIF using the second-order model fails to closely track the measured PIF using PP stimulation, demonstrating the inadequacy of the second-order model or, in other words, demonstrating the fact that there are significant third-order interactions in the system.

B. Predictive Capabilities Using the PP and RIT Analysis

In addition to providing a quantitative description of the nonlinear characteristics in the form of kernels or PIF, the proposed Poisson–Volterra model has predictive capabilities for arbitrary stimulus patterns, as illustrated in Fig. 5 for the LPP case and in Fig. 6 for the MPP case. A comparison between the predicted responses using the third-order Poisson–Volterra model and using the measured PIF suggests that the Poisson–Volterra model can predict the population spike amplitudes evoked by RITs better than the measured PIF. The NMSE value for the model prediction was 4.87%±0.47% in the LPP case, and 4.13%±0.38% in the MPP case. Using the measured PIF, the associated prediction NMSE value was 7.86%±0.62% in the LPP case and 6.93%±0.59% in the MPP case. The NMSE values for both the LPP and the MPP cases were significantly lower (p < .01) for the Poisson–Volterra model than the respective measured PIF model. This is probably due to the fact that our model takes into consideration the entire history of the stimulus impulses and third-order interactions, whereas the PIF model uses the current and only one previous stimulus impulse.

Fig. 5.

Actual response (A) and model predictions using the measured PIF model. (B) Third-order Poisson-Volterra model (C) in the LPP case.

Fig. 6.

Actual response (A) and model predictions using the measured PIF model (B) and the third order Poisson-Volterra model (C) in the MPP case.

The predictive power of the Poisson–Volterra model can be further validated using out-of-sample predictions, where the system output is predicted for an arbitrary stimulus using kernels obtained from a different input–output dataset (segment shown in Fig. 7). Visual assessment and the computed NMSE values demonstrate the out-of-sample predictive power of the Poisson–Volterra model. For the example of Fig. 7, the insample NMSE is 5.22% and the out-of-sample NMSE is 6.37% for the LPP case, while the respective NMSE values for the MPP case are 3.54% and 4.34%.

Fig. 7.

Actual system responses [panels (a)] and the Poisson–Volterra model predictions [panels (b)] for an out-of-sample dataset in the LPP case (A), and the MPP case (B).

IV. Discussion

We have presented and experimentally validated a nonparametric, third-order Poisson–Volterra model that describes the dynamic characteristics of the LPP and the MPP of the dentate gyrus of the rat hippocampus. Experimental data were obtained by stimulating the afferents of each pathway with RITs and simultaneously recording the activity of the granule cells at the dentate gyrus (population spikes). In the advocated approach, the functional properties of the two pathways are fully represented by Poisson–Volterra kernels. The performance of this modeling approach was compared with the widely used method of paired pulses (PP) in terms of predictive capability to arbitrary stimulus patterns and the corresponding paired impulse functions (PIFs) obtained with the two approaches.

The results of this study show that the proposed Poisson–Volterra model has superior predictive capabilities and its kernels exhibit consistent waveforms across all experiments that are distinctive for each pathway and describe uniquely the LPP and the MPP neuronal transformations. This model exhibits better predictive capabilities than the predictions provided by the measured PIF of the widely used PP approach, as illustrated in Figs. 5 and 6. The superior predictive capability of the Poisson–Volterra model is probably due to the fact that this model takes the interactions among multiple stimulus impulses into consideration (i.e., triplets in this case, including the current/reference impulse) possibly found within the memory epoch of the system (about 1 s) in the course of the random stimulation of the system with an RIT. This is, of course, in addition to the effects of single stimulus impulses found within the memory epoch of the system (i.e., pairs of stimulus impulses when the current/reference impulse is included). These two types of nonlinear dynamic interaction of the current impulse with a single preceding impulse (second-order interactions) and with a pair of preceding impulses (third-order interactions) are quantified separately by the second-order and third-order Poisson-Volterra kernels, respectively. On the other hand, the PIF measurement of the PP approach is based only on the effects of a single preceding stimulus impulse (i.e., only second-order interactions). The predictive power of the proposed model was demonstrated using insample predictions (Figs. 5 and 6) and out-of-sample predictions (Fig. 7).

Although second-order Poisson–Volterra models have been used previously to model the dentate gyrus [25], [39] and the CA1 area of the hippocampus [30], a third-order model was found to be necessary in this study in order to fully characterize the nonlinear dynamics of the LPP and the MPP neuronal transformations. Specifically, the NMSE value dropped to 4.88±0.47% for the third-order model relative to the NMSE value of 6.71±0.75% when the second-order model was used, a drop that was found to be statistically significant (p < 0.01). The fact that the inclusion of the third-order term enhances the capability of the model to closely track the recorded response (i.e., the population spike amplitudes) is further illustrated in Fig. 8 for an arbitrary dataset in the LPP case. Another piece of evidence that corroborates the validity of the third-order model is the fact that the computed PÎF using the second-order model fails to closely track the measured PIF using PP stimulation, while the PÎF computed from the third-order model follows the measured PIF closely (see Fig. 4).

Fig. 8.

Actual system response (A) and the predicted responses using the second-order (B) and the third-order (C) Poisson–Volterra model in the LPP case. It is evident that the population spike amplitudes are predicted better by the third-order model than by the second-order model.

One issue not addressed by the presented model is in reference to the possible dynamic interactions between the LPP and MPP in influencing the neuronal activity at the dentate gyrus during simultaneous stimulation of both pathways. Future research will extend the model to include a quantitative representation of these dynamic (and nonlinear) interactions and will evaluate their combined effect in improving model prediction accuracy.

The use of RIT experimental stimuli in the context of the Poisson–Volterra modeling approach is premised on the requirement of employing the correct model order (third, in this case). Therefore, if any comparison of performance is attempted with other approaches (e.g., PP stimulation), it has to be with the correct model order. Any comparisons with a truncated Poisson–Volterra model (e.g., of second order) are not appropriate or meaningful. The comparison with the PP approach (which is confined by the definition of second-order interactions) is made in this paper only because the latter has been widely used, and not because it is necessarily appropriate for this system that has been shown to exhibit third-order interactions as well. Thus, the main point conveyed by this comparison is that this system exhibits third-order interactions and, consequently, the proper tool to study its full dynamics is a third-order Poisson–Volterra model (not the PP approach which is confined by definition to second-order interactions).

The application of the RIT stimulation in the context of Poisson–Volterra modeling requires greater computational effort. However, this incremental difference in computational effort is gradually diminishing as the computational means improve. In our opinion, the level of computational effort (within reason) should not be a critical determinant when the validity of the obtained results is at stake.

We now turn to the important (and perennial) question of the physiological significance of these findings and the interpretation of the shapes of the obtained Poisson–Volterra kernels in a manner that advances our scientific understanding of the system. Let us begin by making the semantic distinction between the terms “inhibition” and “depression.” The former denotes an action that results in a negative electrophysiological effect (e.g., hyperpolarization) and the latter denotes a modulatory action that results in the reduction of a variable of interest. In this sense, when the effect of a preceding pulse is to reduce the response to the current pulse (relative to what it would have been in the absence of the preceding pulse) then we consider this to be depressive. The opposite of a depressive action is called “facilitatory,” while the opposite of inhibitory is termed excitatory. With regard to the granule cells, three regions of lags (i.e., the time difference between the preceding pulse and the present) with distinctive response characteristics have been reported in the literature: an early depressive region (less than 40 ms), a middle facilitatory region (from 40 ms to about 200 ms), and a late depressive region (from about 200 ms to about 2 000 ms). These depressive regions are often called inhibitory in the early literature.

Specifically, the early depressive characteristics of the granule cells (for lags less than 40 ms) have been attributed to GABA-mediated IPSPs [53] and a GABA-mediated increase in chlorium conductance that reduces the excitability of granule cells [54]. Also, early negative values indicating depressive characteristics (up to lags of 100 ms) have been attributed to the recurrent (feedback) activation of the GABAergic basket cells [28], [46], [55]–[57]. Other studies have reported that this early depressive phase may be regulated by presynaptic metabotropic receptors [58], [59].

Such early negative values (representing depressive effects) are seen in the LPP second-order kernel and in the MPP third-order kernel (see Figs. 2 and 3). The ability to estimate reliable kernels that quantify these characteristics offers the attractive prospect of measuring the precise quantitative effects of chemical blocking in order to delineate the individual protagonists in this regard. Note that the third-order LPP kernel and the second-order MPP kernel exhibit positive values in these early lags (up to 100 ms), indicative of facilitation that may be attributed to NMDA-mediated synaptic events. Similar facilitation characteristics are observed at intermediate lags of the third-order LPP kernel and may be attributed to augmentation of excitatory transmitter release [60], [61] or presynaptic inhibition of GABA release [62]–[64]. This is consistent with the reported facilitation in the region of intermediate lags. This is also evident in the PIF values measured through PP stimulation or computed from the third-order Poisson–Volterra model of the LPP, but it is not seen in the PIF values of the MPP (see Fig. 4).

At longer lags (200–1000 ms), the obtained kernels have negative values in agreement with the depressive characteristics of granule cells reported previously [28], [38], [65], which may be due to a voltage-dependent and/or calcium-activated potassium conductance [66]–[68]. These effects are quantitatively reflected on the estimated kernel values and the measured PIF values for both pathways. However, we note that the PIF does not provide satisfactory predictions for triple-pulse stimulation (i.e., it does not capture the third-order interactions that have been shown to exist in this system) and does not separate the second-order from the third-order effects that are clearly delineated by the opposite polarity (facilitation versus depression) of the second- and third-order kernels for both pathways. This initial interpretation of the obtained kernels is only a small first step and a far greater effort will be required before a complete physiological interpretation can be achieved and the full scientific benefit of this analysis can be realized. We plan to exert this effort in our future work and hope that others will join us to accelerate this process.

We finally note that the neuronal dynamics in the brain are generally nonstationary. The specific form of nonstationarity varies widely depending on the context and timing of each type of electrophysiological activity. In many cases of interest, one may find intervals of time within which the nonstationarity is small and approximate stationarity can be assumed in order to facilitate the analysis of the data. Although our group has pioneered several methods of nonstationary analysis, the stationary analysis still offers significant practical advantages and remains as more accessible to the peer community. This is the rationale for selecting the “stationary data records” in this study and employing stationary analysis as an initial step. The next step may be to extend our study to the nonstationary analysis of this system. For similar practical reasons of facilitating the analysis of the data for the nonlinear modeling of this system, we have “synchronized” the input/ouput point processes (by suppressing the short-response latency and introducing the “reduced form” of the Poisson–Volterra kernels). Obviously, both of these conditions limit the general applicability of this approach in the aforementioned cases.

To summarize, the modeling approach presented in this paper defines a general framework that can be used to advance our understanding of how distinct sensory modalities are being processed and integrated within different regions of the hippocampus. In this sense, its potential extends beyond the specific results and the effect of LPP and MPP stimulation on the granule cell output is presented herein and can be readily applied to modeling other parts of the nervous system.

Biography

Angelika Dimoka (S'01–M'06) was born in Larissa, Greece. She received the B.S. degree in physics from the University of Crete, Heraklion, Greece, in 1998 and the M.S. and Ph.D. degrees in electrical engineering and biomedical engineering from the University of Southern California (USC), Los Angeles, in 2001 and 2006, respectively.

Currently, she is on the Faculty of the Department of Bioengineering, University of California, Riverside. Her research interests include the nonlinear systems analysis of nervous systems, electrophysiology of hippocampus, and experimentally identifying and modeling nonlinear dynamic interactions among different information pathways of the nervous system. More specifically, she is investigating how multiinput/output nonlinear mathematical models can capture the functional properties of the hippocampus due to asynchronous activation of its afferent information pathways.

Dr. Dimoka is a member of the Biomedical Engineering Society and the Society for Neuroscience.

Spiros H. Courellis was born on June 3, 1962 in Nemea, Greece. He received the Electrical and Computer Engineering Diploma from the Aristotle University of Thessaloniki, Thessaloniki, Greece in 1985; the M.S. degree in electrical engineering from the California Institute of Technology, Pasadena, in 1986; and the Ph.D. degree in electrical engineering from the University of Southern California, Los Angeles, in 1992.

From 1993 to 2004, he was a Research Associate with the Biomedical Engineering Department at the University of Southern California. He was also involved in industrial R&D, education, and leadership. Currently, he is a Research Assistant Professor of Biomedical Engineering at the University of Southern California, Los Angeles, and an Assistant Professor of Computer Science at California State University, Fullerton. His main research interests are in the areas of computational modeling of neural systems, biologically inspired information fusion systems, biosensors, neural computation and memory, embedded computing, sensor networks, and distributed implantable secure medical devices.

Dr. Courellis is a member of the ACM and the Society for Neuroscience.

Ghassan I. Gholmieh was born in Beirut, Lebanon, in 1973. He received the B.Sc. degree in chemistry and the M.D. degree from the American University of Beirut, Beirut, Lebanon, in 1994 and 1998, respectively, and the Ph.D. degree in biomedical engineering with an emphasis on Neural Engineering from the University of Southern California, Los Angeles, in 2002.

He concurrently pursued an internal medicine residency at the University of Southern California and went on to become Board in Internal Medicine certified in 2005. His Ph.D. work focused on the development of the hippocampal-based biosensor for the detection and classification of neurotoxins. His main research interests are in the areas of nonlinear dynamic modeling, biosensors, neural computation, antiepileptic drugs (AED) effects on short-term plasticity, and novel AED discovery.

Dr. Gholmieh is a member of EMBS and the Society for Neuroscience.

Vasilis Z. Marmarelis (M'79–SM'94–F'97) was born in Mytiline, Greece, on November 16, 1949. He received the diploma in electrical engineering and mechanical engineering from the National Technical University of Athens, Athens, Greece, in 1972 and the M.S. and Ph.D. degrees in engineering science (information science and bioinformation systems) from the California Institute of Technology, Pasadena, in 1973 and 1976, respectively.

After two years of postdoctoral work at the California Institute of Technology, he joined the faculty of Biomedical and Electrical Engineering at the University of Southern California, Los Angeles, where he is currently Professor and Director of the Biomedical Simulations Resource, a research center funded by the National Institute of Health since 1985 and is dedicated to modeling/simulation studies of biomedical systems. He was Chairman of the Biomedical Engineering Department from 1990 to 1996. His main research interests are in the areas of nonlinear and nonstationary system identification and modeling, with applications to biology and medicine. Other interests include spatiotemporal and multiinput/multioutput modeling of nonlinear systems with applications to neural information processing, and closed-loop nonlinear system modeling and control. He has invented a system for high-resolution 3-D ultrasonic imaging and tissue classification that is currently tested/evaluated for clinical applications to early detection of breast cancer and osteoporosis. He is coauthor of the book Analysis of Physiological System: The White Noise Approach (Plenum, 1978; Russian translation: Mir Press, 1981; Chinese translation: Academy o f Sciences Press, 1990), editor of three research volumes on Advanced Methods of Physiological System Modeling (Plenum, 1987, 1989, and 1994) and author of a recent monograph on Nonlinear Dynamic Modeling of Physiological Systems (IEEE Press, 2004). He has published many papers and book chapters in the areas of system modeling and signal analysis.

Dr. Marmarelis is a Fellow of the American Institute for Medical and Biological Engineering.

Theodore W. Berger (M'03–SM'04) received the Ph.D. degree from Harvard University, Cambridge, MA, in 1976.

He is the David Packard Professor of Engineering, Professor of Biomedical Engineering and Neuroscience, and Director of the Center for Neural Engineering at the University of Southern California (USC), Los Angeles. He conducted postdoctoral research at the University of California, Irvine, from 1977 to 1978, and was an Alfred P. Sloan Foundation Fellow at The Salk Institute, La Jolla, CA, from 1978 to 1979. He joined the Departments of Neuroscience and Psychiatry at the University of Pittsburgh, Pittsburgh, PA, in 1979, being promoted to Full Professor in 1987. Since 1992, he has been Professor of Biomedical Engineering and Neurobiology at USC, and was appointed the David Packard Chair of Engineering in 2003. In 1997, he became Director of the Center for Neural Engineering, Los Angeles, in 1997, an organization which helps to unite USC faculty with cross-disciplinary interests in neuroscience, engineering, and medicine. He has published many journal articles and book chapters, and is the coeditor of a book recently published by the MIT Press on Toward Replacement Parts for the Brain: Implantable Biomimetic Electronics as Neural Prostheses.

Dr. Berger's thesis work received the James McKeen Cattell Award from the New York Academy of Sciences. During that time, he received a McKnight Foundation Scholar Award, twice received an NIMH Research Scientist Development Award, and was elected a Fellow of the American Association for the Advancement of Science. While at USC, Dr. Berger has received an NIMH Senior Scientist Award, was awarded the Lockheed Senior Research Award in 1997, was elected a Fellow of the American Institute for Medical and Biological Engineering in 1998, received a Person of the Year “Impact Award” from the AARP in 2004 for his work on neural prostheses, was a National Academy of Sciences International Scientist Lecturer in 2003, and an IEEE Distinguished Lecturer in 2004–2005. In 2005, he received a “Great Minds, Great Ideas” Award from the EE Times in the same year, and in 2006, was awarded USC's Associates Award for Creativity in Research and Scholarship.