Interrelationship of Steric Stabilization and Self-Crowding of a Glycosylated Protein

Abstract

In the eukaryotic cell, protein glycosylation takes place in the crowded environment of the endoplasmatic reticulum. With the purpose of elucidating the impact of high concentration on the interactions of glycoproteins, we have conducted a series of small-angle x-ray scattering experiments on the heavily glycosylated enzyme Peniophora lycii phytase (Phy) and its deglycosylated counterpart (dgPhy). The small-angle x-ray scattering data were analyzed using an individual numerical form factor for each of the two glycoforms combined with two structure factors, a hard sphere and a screened coulomb potential structure factor, respectively, as determined by ab initio analysis. Based on this data analysis, three main conclusions could be drawn. First, at comparable protein concentrations (mg/ml), the relative excluded volume of Phy was ∼75% higher than that of dgPhy, showing that the glycans significantly increase excluded-volume interactions. Second, the relative excluded volume of dgPhy increased with concentration, as expected; however, the opposite effect was observed for Phy, where the relative excluded volume decreased in response to increasing protein concentration. Third, a clear difference in the effect of salinity on the excluded-volume interactions was observed between the two glycol forms. Although the relative excluded volume of dgPhy decreased with increasing ionic strength, the relative excluded volume of Phy was basically insensitive to increased salinity. We suggest that protrusion forces from the glycans contribute to steric stabilization of the protein, and that glycosylation helps to sustain repulsive electrostatic interactions under crowded conditions. In combination, this aids in stabilizing high concentrations of glycosylated proteins.

Introduction

It is becoming widely recognized that high-volume occupancy, also known as molecular crowding, can have dramatic effects on the biological function of macromolecules (1). Not only can molecular crowding affect the activity of proteins (2–5); it may also have staggering consequences for their tendency to self-associate and their susceptibility to aggregation (6–8). However, protein glycosylation, i.e., the covalent attachment of oligosaccharides, counteracts many of the undesired effects of molecular crowding. In general, glycosylaton of proteins improves their solubility (9–12) and renders them more resistant to aggregation (13–15).

In vivo, glycosylation appears to be especially important to proteins in the secretory pathway, i.e., secretory proteins that are synthesized from ribosomes situated on the cytosolic side of the endoplasmic reticulum (ER) into the crowded lumen of the ER (16,17). If such proteins are deprived of their natural glycosylation, they often become highly susceptible to irreversible aggregation, and their expression is hampered or completely prevented (18–22). Strong modifications of the physical properties of proteins are also seen in vitro. Hence, glycoproteins often precipitate severely as a response to enzymatic deglycosylation, and the removal of the glycans generally results in much lower kinetic stability (23,24).

Molecular crowding is also relevant for engineered biopharmaceuticals (25) and industrial enzymes (26,27). These applied proteins are in many cases subjected to crowded conditions during production, transport, storage, or use. In particular, crowding is relevant for subcutaneous administration, as extremely high protein concentrations and absolute absence of aggregates are required for this route of delivery (28). In regard to glycosylation, it is interesting to note that PEGylation (the process of covalent attachment of poly(ethylene glycol) (PEG) polymer chains to another molecule) has become an increasingly popular tool for prolonging the bioactivity of pharmaceutical proteins and, furthermore, that glycosylation and PEGylation have similar qualitative effects on the physical stability of proteins (29,30).

Traditionally, the higher solubility of glycoproteins has been explained by the hydrophilicity of the attached glycans (9,23,31–33,35). However, whereas their hydrophilic nature undoubtedly is a prerequisite for their solubilizing properties, this may not offer a complete mechanistic explanation. This has become particularly clear in light of recent findings that in some cases, the peptide surface of glycoproteins is in fact more hydrophilic than the sugar moieties of the attached glycans (37–39). Therefore, in addition to the strong hydration of the glycans, other mechanisms are likely to underlie the modification of physical properties after glycosylation. Elucidation of these phenomena appears to be limited by the scarcity of quantitative experimental information, and to address this, we used small-angle x-ray scattering (SAXS). Biological applications of solution SAXS are primarily aimed at obtaining precise structural information, and this is particularly true in the case of proteins. Samples are routinely diluted to remove the effects of interaction and facilitate accurate structure elucidation. However, SAXS is equally useful for obtaining information on particle-particle interactions at high concentrations, since detailed quantitative information about the type and magnitude of the interactions can be extracted from the SAXS data.

We chose, as a model system, the heavily glycosyalated enzyme Peniophora lycii phytase (Phy, Enzyme Commission (EC) No. 3.1.3.26) and its deglycosylated counterpart (dgPhy). In addition to being highly soluble, this protein shows only small, if any, changes in the peptide structure upon deglycosylation (40), and it therefore appears to be an adequate model for studies of the relationship between glycosylation and crowding.

Materials and Methods

Sample preparation

The enzymatic deglycosylation reaction was carried out with Endo F₁ (EC 2.2.1.96) according to procedures previously described (38). This enzyme detaches the glycans by hydrolyzing the glycosidic bond between the two N-acetylglucosamine groups that connect the glycan and the protein, so that the deglycosylated protein ideally has one N-acetylglucosamine group attached (41) to each of the 10 glycosylation sites. Since the removed glycans do not contain any ionizable groups (e.g., they do not contain sialic acid) and the basicity of the amide groups of the N-acetylglucosamine units is comparable to that of the amide groups of the peptide backbone, the isoelectric point of the protein is expected to be unchanged upon deglycosylation, as indeed was observed in a previous study (38).

Both glycoforms were examined by matrix-assisted laser desorption/ionization time-of-flight mass spectrometry. The mass spectra showed that, as expected, Phy had a fairly broad and roughly symmetric mass distribution (∼55–65 kDa) with a peak located at ∼59,323 Da, hence reflecting the heterogeneity of the glycosylation. On the other hand, dgPhy had a more narrow molecular mass distribution (∼48–49.5 kDa) with a peak at ∼48,466 Da. The extent of deglycosylation found here is very similar to that reported previously (37,38). Judging from the peak positions, and assuming that all sites are glycosylated, this corresponds to an average glycan size of 1474 Da (59,323 − 44,583 Da/10) for the whole glycan and 1253 Da ((59,323 − 44,583 − (10 × 221)) Da/10) for the part of the glycan that is removed by Endo F₁. Therefore, on average, 8.7 glycans have been detached from dgPhy (59,323 – 48,466 Da/1253 Da, where 1253 Da is the average mass of the removed glycans).

Phy and dgPhy were subsequently dialyzed extensively in Spectra/Pore dialyzing membranes (12–14 kDa cutoff) against Milli-Q water (Millipore, Billerica, MA), freeze-dried, and stored at −25°C. The protein powder was redissolved in 50 mM Na-acetate, pH 5.5, stirred gently, and left to equilibrate for at least 15 min. Immediately before use, each sample was individually centrifuged for 5 min at 10,000 rpm and the molar concentrations, which were calculated based on the primary sequence and the algorithm of Kyte and Doolittle (42), were measured on a NanoDrop spectrophotometer (Wilmington, DE) using an extinction coefficient of 50,130 cm⁻¹ M⁻¹ (corresponding to 1.0 mL·mg⁻¹·cm⁻¹ for dgPhy).

SAXS measurements

The SAXS measurements were performed on the European Molecular Biology Laboratory X33 beamline at the DORIS storage ring (Deutsches Elektronen-Synchrotron, Hamburg, Germany). The scattering profiles were recorded on a MAR345 image plate detector covering a range of 0.007 < q < 0.507 Å⁻¹ (q = 4π sinθ/λ, where 2θ is the scattering angle and λ is the wavelength of the beam). Buffer backgrounds were measured before and after analysis of each sample, and an average of the two buffer backgrounds was subtracted from the scattering intensity of the samples. Absolute calibration was based on water measurements (43). As a double check, the forward scattering signal of the samples was compared to that of freshly prepared samples of bovine serum albumin with known protein concentrations (∼4 mg/ml). These reference samples were prepared in cold phosphate buffer, pH 7.4, and centrifuged immediately before use.

Determination of particle form factors

Low-resolution structures of Phy and dgPhy were determined using the ab initio bead modeling program GASBOR (44). To avoid the form factor being affected by interparticle interference effects, which are primarily manifested in the low-q part of the data at high concentration, low- (∼5 mg/ml) and high-concentration (∼25 mg/ml) data sets were merged at 0.18 Å⁻¹. For both glycoforms, the number of dummy residues representing the peptide portion was chosen not as the actual number of amino acid residues in the protein (439), but as the equivalent number of average-weight residues (44,583/135 = 330). For the glycan portion of the proteins, the mass equivalent number of dummy amino acids was corrected for the higher excess scattering-length density per unit mass (Δρ_m) of carbohydrates (2.93 × 10¹⁰ cm/g) (39) compared to that of polypeptides (1.97 × 10¹⁰ cm/g) (39), which corresponds to a correction factor of 1.49. Accordingly, the glycan portions of Phy and dgPhy were represented by 163 (14,740/135 × 1.49) and 43 (3883/135 × 1.49) dummy amino acids, respectively. Thus, Phy and dgPhy were represented by, respectively, 493 and 373 dummy amino acids in total. For dgPhy, the ab initio calculations were performed using the default program values, but in the case of Phy, the so-called histogram penalty terms had to be lowered from 1 × 10⁻³ to 5 × 10⁻⁴ to let the nonpeptide portion of the protein arrange more freely. Using these program settings, χ² values of 5.11 and 8.35 for dgPhy and Phy, respectively, against the experimental data were obtained. For the purpose of exhibiting the bead models, the program DAMAVER was used to align the models (45).

Applied analytical structure factors

Two structure factor models were used: 1), the hard-sphere structure factor calculated in the Percus-Yevick approximation (46), and 2), the structure factor for charged hard spheres interacting via a screened Coulomb potential calculated in the mean spherical approximation (47). In this model, an analytical structure factor for homogenous monodisperse hard sphere is calculated as a function of the hard-sphere radius of interaction and the hard-sphere volume fraction. It is somewhat surprising that the hard-sphere structure factor has been found to give correct quantitative results for block copolymer micelles, which have some degree of soft interaction potential due to the random-coil nature of the polymers (48,49). Consequently, this structure factor is expected also to provide a reasonable description of the particle interference effects of glycosylated proteins. The structure factor for charged hard spheres interacting via a screened Coulomb potential is calculated for monodisperse hard spheres as a function of the hard-sphere radius of interaction, the hard-sphere volume fraction, the effective charge of the spheres, and the Debye length of the surrounding medium. The Debye length used was calculated based on the buffer salt concentration, i.e., 50 mM Na-acetat.

Combining the form factors and the structure factors

Both of these structure factors are only valid for monodisperse, homogeneous, spherical particles. To precisely account for the structure factor effects of phytase at high concentrations, the obtained numerical ab initio form factors were combined with the analytical expressions for the applied structure factors by means of the decoupling approximation (50). For anisotropic particles, the decoupling approximation assumes that the interactions between the particles are independent of their orientation, and an expression based on the form-factor intensity, the form-factor amplitude, and the chosen structure factor, S(q), is obtained:

$$I\left(q\right)=c\mathrm{\times }P\left(q\right)\left[1+\beta \left(q\right)(S\left(q\right)-1)\right],$$ (1)

where

$$\beta \left(q\right)={\langle F\left(q\right)\rangle }_{\text{O}}^2/{\langle F^2\left(q\right)\rangle }_{\text{O}}\text{.}$$ (2)

${\langle \dots \rangle }_{\text{O}}$ and c denote the orientational average and the model scaling parameter, respectively. β(q) is the relation between the square of the orientationally averaged form-factor amplitude (nominator) and the orientationally averaged form-factor intensity (denominator). Both of these form-factor values are output from CRYSOL (51). The form-factor intensity can be found in the ^∗.int file, where the first two columns show the q-value and the I(q) value, respectively. The form-factor amplitude is expanded into spherical harmonics and all the obtained A_lm(q) values are output into the ^∗.alm file, which is in a binary file format (51). For the purposes of this study, only the orientational average of the form-factor amplitude was needed, i.e., the A₀₀(q) term, where only the real part is nonzero. The numerical form-factor amplitudes and intensities were linearly interpolated from the output q values in the ^∗.int and ^∗.alm files to the experimental q values.

Implementation

The binary ^∗.alm file containing the form-factor amplitude information was converted into ASCII format by using the program “conv_alm.exe”, which is available for download from the Svergun Group homepage (52). A home-written Fortran program employing a least-sqaures fitting routine was adapted to this project and used for data analysis. This program is a heavily modified version of a fitting routine originally developed by Jan Skov Pedersen at Risø National Laboratory (Roskilde, Denmark). The program inputs experimental SAXS data and numerical expressions for the form-factor amplitude and intensity. The program furthermore calculates the chosen structure factor as a function of the relevant fit parameters and performs a least-squares fit of the entire model to the experimental data. The original Fortran routine written by J. B. Hayter was included in this program and used for calculating the structure factor effects for charged hard spheres. However, we used our own implementation of the much more simple expression for the hard spheres structure factor.

Model parameters

Using the ab initio approach for the form factor, the only free fit parameters were the structure-factor parameters, the hard-sphere radius of interaction, R_HS, and the hard-sphere volume fraction, ν_HS. In the case of the charged hard-sphere model, though, the effective charge, z_eff, was also taken as a fitting parameter. For the purpose of comparing the excluded-volume fractions of samples with different concentrations, a quantity referred to as the relative excluded volume was calculated:

$${\varepsilon }_{\text{relative}}=\varepsilon /(c/\rho ),$$ (3)

where ɛ is the excluded volume fraction, c is the sample mass concentration, and ρ is the mass density of the protein. The ρ-values of Phy and dgPhy were calculated as 1.396 g/cm³ and 1.365 g/cm³for Phy and dgPhy, respectively (39). These values were calculated by assuming ρ values of the peptide and carbohydrate parts to be, respectively, 1.35 g/cm³ and 1.60 g/cm³ (53,54).

Results

In this work, we recorded the solution scattering of Phy and dgPhy for two salt series with different protein concentrations with the specific aim of exploring the protein-protein interactions (Figs. 1 and 2). A model was fitted to the data in which the form factor (intraparticle scattering) was described using the numerically calculated scattering intensity and amplitude from an ab initio bead model of each of the glycovariants (see Materials and Methods for details). These bead models provide an accurate description of the form factors of the two glycoforms; however, because of the flexible nature of the glycans, the model should be regarded as a static snapshot rather than a unique low-resolution structure, especially in the case of Phy (see the bead models Fig. 3). Two different structure factors were applied which depended on the experimental conditions. For the data sets recorded at 0.3 M and 1.0 M NaCl, a hard-sphere structure factor was used, whereas for the samples without added salt, a hard-sphere structure factor with a screened Coulomb potential was chosen. As a first attempt, the 0.3-M and 1.0-M NaCl data sets were modeled using both the interaction radius and the excluded-volume fraction as fitting parameters (Table 1). For dgPhy, the interaction radius remained practically unchanged; in all cases, the interaction radii were between 26.8 and 27.9 Å. This invariant interaction radius strongly suggests that the protein did not form clusters or oligomers despite the high protein concentrations and ionic strength. The calculated interaction radii for dgPhy seem very reasonable when compared to the radius of the volume-equivalent sphere (5.96 × 10⁴ ų), which equals 24.2 Å if the mass density of the protein is assumed to be 1.35 g/cm³. Furthermore, due to the ellipsoidal shape of the protein particle, the actual interaction radius of dgPhy is expected to be somewhat larger than that of the volume-equivalent sphere.

Figure 1.

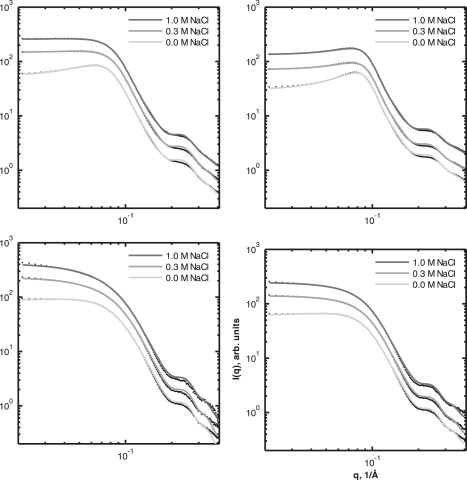
Experimental data (black dots) for Phy (upper) and dgPhy (lower) plotted against model fits (gray lines), where light gray, gray, and dark gray lines represent solutions of 0.0 M, 0.3 M, and 1.0 M NaCl. The Phy protein concentrations were ∼86 mg/ml (left) and ∼153 mg/ml (right) and the dgPhy concentrations were ∼52 mg/ml (left) and ∼80 mg/ml (right). For the purpose of improving the visibility, the 0.3-M and 1.0-M data sets were multiplied by factors of 2 and 4, respectively.

Figure 2.

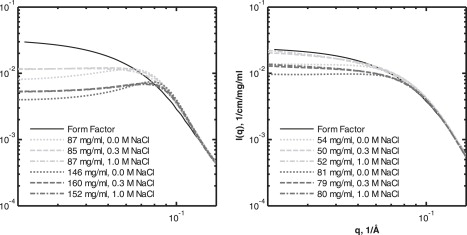
Experimental data of Phy (left) and dgPhy (right) plotted together with the calculated form factor (black solid line). The lower-concentration series (light gray) are ∼86 mg/ml and ∼52 mg/ml for Phy and dgPhy, respectively, and the higher-concentration series (dark gray) are ∼153 mg/ml and ∼80 mg/ml for Phy and dgPhy, respectively. The dotted, dashed, and dash-dotted lines represent concentrations of 0 M, 0.3 M, and 1.0 M NaCl, respectively.

Figure 3.

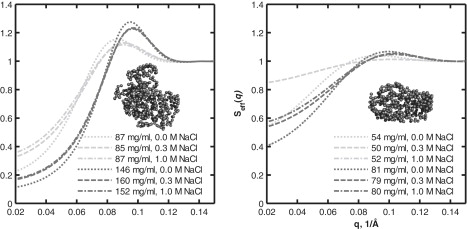
Calculated structure factors and ab initio bead models of Phy (left) and dgPhy (right). The lower-concentration series (light gray) are ∼86 mg/ml and ∼52 mg/ml for Phy and dgPhy, respectively, and the higher-concentration series (dark gray) are ∼153 mg/ml and ∼80 mg/ml for Phy and dgPhy, respectively. The dotted, dashed, and dash-dotted lines represent concentrations of 0 M, 0.3 M, and 1.0 M NaCl, respectively.

Table 1.

Output parameters from modeling with hard-sphere structure factors

	Concentration (mg/ml)	NaCl (M)	Volume fraction	Interaction radius (Å)	χ2
Phy	85	0.3	0.157 ± 4 × 10−4	32.40 + 0.06	56
	87	1.0	0.145 ± 3 × 10−4	32.00 + 0.05	17
	160	0.3	0.243 ± 5 × 10−4	31.20 + 0.05	99
	152	1.0	0.239 ± 5 × 10−4	31.10 + 0.05	65
dgPhy	50	0.3	0.0383 ± 6 × 10−4	27.50 + 0.15	43
	52	1.0	0.0330 ± 7 × 10−4	27.20 + 0.12	38
	79	0.3	0.0863 ± 5 × 10−4	27.90 + 0.11	31
	80	1.0	0.0773 ± 6 × 10−4	26.80 + 0.16	53

The excluded volume fraction and the interaction radius were used as fitting parameters. Some of the listed χ² values are a bit high, but as can be seen from Fig. 1, the deviations of the experimental data from the model fits are primarily found above 0.15 Å⁻¹, and for that reason, this major part of the deviation does not influence the precision of the calculated parameters.

On the other hand, for Phy, a seemingly systematic variation between the interaction radii and the protein concentration was observed; however, due to the choice of sample concentration, the interaction radii practically fell into two groups. The radii for the high-concentration data turned out to be slightly lower than those for the low concentration data, suggesting that the interaction radius actually decreases when the concentration of the sample is increased.

As a second strategy, the data were modeled using a fixed interaction radius, thus leaving the excluded-volume fraction as the only fitting parameter. Furthermore, due to the small differences among the computed interaction radii, average values were used. For dgPhy, the average (27.4 Å) was taken over all data sets, whereas for Phy, two averaged values were used, one for the low-concentration (32.2) and one for the high-concentration (31.15) series (Table 2). As can be seen by comparing the χ² values of Tables 1 and 2, fixing the interaction radius did not significantly reduce the quality of the fitted model for any of the measured data sets.

Table 2.

Output parameters from modeling with screened Coulomb and hard-sphere structure factors

	Concentration (mg/ml)	NaCl (M)	Volume fraction	Interaction radius (Å)	Effective charge	χ2
Phy	87	0.0	0.165 ± 2 × 10−4	32.20	10.70 ± 0.07	73
	85	0.3	0.157 ± 3 × 10−4	32.20	—	57
	87	1.0	0.145 ± 2 × 10−4	32.20	—	18
	146	0.0	0.255 ± 3 × 10−4	31.15	10.10 ± 0.10	79
	160	0.3	0.243 ± 3 × 10−4	31.15	—	98
	152	1.0	0.239 ± 3 × 10−4	31.15	—	64
dgPhy	54	0.0	0.0574 ± 3 × 10−4	27.40	8.37 ± 0.09	41
	50	0.3	0.0383 ± 3 × 10−4	27.40	—	43
	52	1.0	0.0331 ± 3 × 10−4	27.40	—	42
	81	0.0	0.1000 ± 3 × 10−4	27.40	6.44 ± 0.08	47
	79	0.3	0.0858 ± 3 × 10−4	27.40	—	33
	80	1.0	0.0774 ± 3 × 10−4	27.40	—	55

The screened Coulomb structure factor was used to model 0.0-M NaCl data sets, whereas the hard-sphere structure factor was applied for 0.3-M and 1.0-M NaCl data sets. The interaction radius was fixed, thus leaving the excluded-volume fraction and a scaling parameter as the only fitting parameters. The interaction radius was found by averaging the interaction radii listed in Table 1. Two interaction radii were used for Phy, one each for the high- and low-concentration data sets, whereas only one was used for dgPhy.

It is informative to compare the volume of spheres calculated based on the interaction radii of Phy at low (1.40 × 10⁵ Å³) and high (1.27 × 10⁵ ų) concentrations and to compare these values when subtracted relative to the interaction volume of dgPhy (8.61 × 10⁴ ų). When this is done, it becomes evident that the interaction volume available to the glycans is decreased by 24% when going from low to high concentration ((1.27 × 10⁵ − 8.61 × 10⁴ ų)/(1.40 × 10⁵ − 8.61 × 10⁴ ų)).

The low-ionic-strength data (no added NaCl) was modeled using the same fixed interaction radius values as for the high-ionic-strength data (0.3 and 1.0 M NaCl). The screened Coulomb potential structure factor that was applied for the low-ionic-strength data returned basically the same interaction radius values as did the hard-sphere structure factor for the high-ionic-strength data. However, fixing the interaction radius enabled a more accurate estimation of the effective charge of the protein. By using this combination of two structure factors and individual form factors for each of the two glycoforms, we obtained reasonable fits for all the data sets (Fig. 1). The qualities of fit were especially satisfying for the low-q part of the scattering curve, where the structure factor is dominant (<0.15 Å⁻¹). The lower quality of the model fits for the high-q part of the curve (>0.15 Å⁻¹) is in part a consequence of the limited ability of the form factors to account for the finer details in the scattering curve. This is especially pronounced from 0.18 to 0.25 Å⁻¹, where a systematic deviation between the experimental data and the model can be seen for all data sets. In the case of Phy, a clear and apparently systematic deviation between model and data can be noticed in the higher q region. Since these minor deviations are located in the high-q part of the scattering curve only, they do not affect the ability of the model to account for the structure factor, which exclusively influences the low-q part of the curve. This becomes evident when comparing the experimental data with the calculated form factor displayed in Fig. 2. The form factor and the experimental data clearly coincide when q > 0.15, showing that the structure factors have approached unity and therefore no longer contribute to the shape of the scattering curve. In addition, the plots in Fig. 2 reveal several interesting aspects of the nature of the protein-protein interactions. First, the effect of ionic strength is clearly seen: increasing salt concentration diminishes the suppression of the forward scattering, but the relative impact of this effect is decreased when the protein concentration is increased. Second, the marked impact of excluded-volume interactions on the suppression of forward scattering is obvious. However, owing to the linear scale, these observations can more easily be gauged in the calculated structure factors exhibited in Fig. 3. Another feature that can be reproduced in the calculated structure factors is the peaks (0.08–0.10 Å⁻¹) that originate from the incipient ordering of the dissolved particles, i.e., their locations are no longer uncorrelated and certain interparticle distances start to be overrepresented. These peaks can be seen for both glycoforms, but they are clearly much more pronounced for Phy. This becomes especially evident when the structure factors for Phy and dgPhy are plotted together (Fig. 4). The fact that the data series of Phy and dgPhy displayed in Fig. 4 have roughly the same protein weight concentration (∼86 and ∼80 mg/ml for Phy and dgPhy, respectively) makes a comparison reasonable. It can be seen that in addition to the difference in the structure-factor peaks, the structure factor of Phy decreases more precipitously at low q, corresponding to stronger interparticle interactions of Phy.

Figure 4.

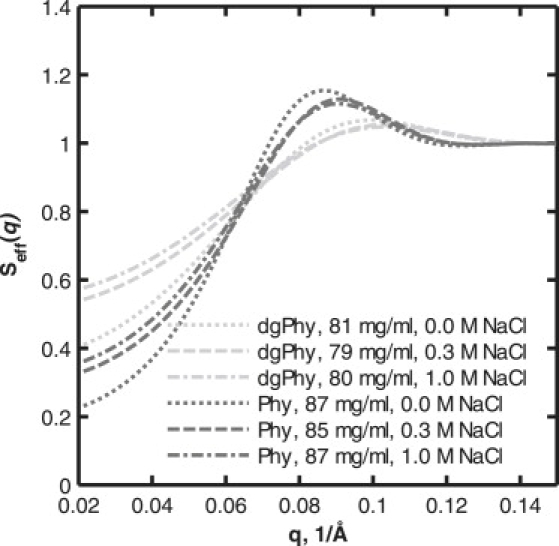
Comparison of structure factors for Phy (dark gray) and dgPhy (light gray). The concentrations of the Phy and dgPhy series were ∼86 mg/ml and ∼80 mg/ml, respectively. The dotted, dashed, and dash-dotted lines represent salt concentrations of 0 M, 0.3 M, and 1.0 M NaCl, respectively. Note the difference in magnitude between the structure factors for Phy and dgPhy despite the fact that the protein concentrations are comparable.

To compare the excluded volume fraction of samples with different protein concentrations, a quantity expressing the relative excluded volume was calculated according to Eq. 3. This quantity was calculated as the ratio between the excluded volume and the actual volume filled out by the protein particles (Fig. 5). Thus, the relative excluded volume expresses the excluded volume relative to unity by relating the volume excluded to the particles and the volume filled out by the particles (see Materials and Methods for details). It is clear from Fig. 5 that glycosylation has a marked impact on the relative excluded volume, and this appears to be especially so when the ionic strength is high. However, the decrease in relative excluded volume with increasing ionic strength is clearly less expressed when the protein is glycosylated despite the fact that the two glycoforms have identical isoelectric points (see Materials and Methods). Another noticeable aspect of Fig. 5 is the differences in the impact of increasing protein concentration; whereas for dgPhy the relative volume increases when the protein concentration is raised, the opposite is true for Phy. Thus, the glycosylation clearly affects not only the degree of excluded volume, but also the response of the excluded volume to increased protein concentration.

Figure 5.

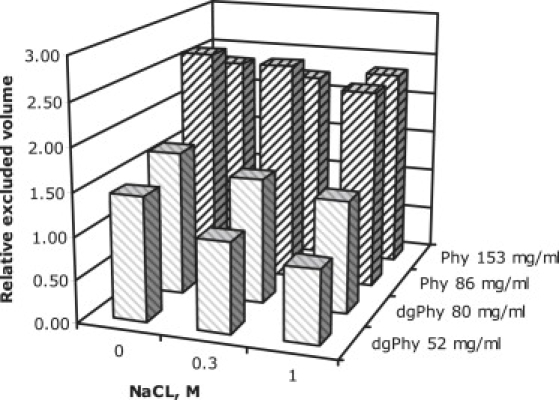
Relative excluded volume, calculated according to Eq. 1, of Phy (dark gray) and dgPhy (light gray). Note the clear difference between the relative excluded volumes of dgPhy and Phy (∼75% larger for Phy) at comparable concentrations of 80 and 86 mg/ml, respectively. Also note that the relative excluded volume of dgPhy increases when the concentration is raised, whereas it is decreased in the case of Phy.

Discussion

Biochemical reactions often occur in environments in which a substantial fraction of the total volume is occupied by various macromolecules, a condition often referred to as molecular crowding (55). As a consequence, the configurational space, and hence the configurational entropy, of each of the macrosolutes can be dramatically decreased. This causes an increase in the chemical potential of macromolecular species and a concomitant increase in the free energy of the solution (56). Other effects, in particular electrostatic interactions between closely spaced polyelectrolytes, also give rise to pronounced nonideality of biological solutions (57–59). The excluded-volume effect favors association processes, i.e., all processes that lower the free energy of the solution by decreasing the fraction of excluded volume (6). These processes include association processes such as oligomerization, aggregation, flocculation, and precipitation. In regard to proteins, it is worthwhile to note that these association phenomena are highly disfavored by glycosylation. To rationalize this, the key questions are how glycans affect interparticle interactions and how this governs the important effects of glycosylation.

The results presented here quantify the enhanced excluded-volume interactions generated by the glycans on phytase. This is manifested in two ways. First, the hard-sphere interaction radius is increased from 27.4 Å for dgPhy to 32.2 Å for Phy for a solution of approximately the same weight concentration. Thus, the glycan mantle of Phy considerably increases the effective hard-sphere radius that each protein sterically excludes to other protein molecules. The impact of glycosylation is also evident from the total excluded-volume fraction for each of the two glycovariants. This is particularly obvious from the relative excluded-volume fraction displayed in Fig. 5, where it is evident that glycosylation, in accordance with the higher interaction radius of Phy, significantly increases the relative excluded-volume fraction. This observation is in line with the prevailing notion that glycans are adsorbed not to the protein surface, but to solvent-exposed and protruding structures (60–64). In accordance with this finding, an increasing number of NMR studies and molecular dynamics simulations depict the glycans as flexible and dynamic (61,65).

In principle, the kinetic stability of the protein might be affected in a number of ways, e.g., by a changed diffusion rate (7); however, the changes in excluded-volume interactions are likely to be by far the most important. Even for such moderately concentrated samples as the ∼80 mg/ml series measured here, the relative excluded volume for Phy is almost twice that of dgPhy. Taken alone, this would lower the apparent solubility constant and, consequently, force the protein toward precipitation (56). However, the solubility of glycosylated proteins is generally much higher than that of their deglycosylated counterparts, and this is also the case for Phy and dgPhy. Thus, the higher excluded volume of Phy relative to dgPhy must be counterbalanced by an opposing effect that improves its solution stability despite the excluded-volume effects.

Several aspects of the SAXS data presented here indicate that this counterbalancing effect is likely to be a protrusion force originating from the attached glycans, i.e., a force similar to steric stabilization of colloids by grafted polymers. These forces arise as a consequence of the increasing spatial confinement of the attached polymers when two interfaces approach each other. Even in the absence of any other type of interaction, the spatial confinement of the polymers gives rise to a repulsive force due to the decrease in entropy upon confinement. Therefore, this type of repulsive force by attached polymers is essentially entropy-driven (66). The finding that the interaction radius of Phy decreases slightly as a response to increased protein concentration, and hence increased volume occupancy, clearly suggests that the protein might be sterically stabilized by protrusion forces. Furthermore, the observation of a reduction in the relative excluded volume for Phy, but not for dgPhy, upon a twofold increase in the protein concentration is also compatible with the notion of a glycan-dependent protrusion force. Thus, if no spatial confinement of the attached glycans takes place, one would expect the relative excluded volume to increase exponentially with increasing protein concentration, and this is clearly not the case.

This observation is similar to the reported brushlike behavior of the polysaccharides on the heavily glycosylated mucin protein lubricin (67). The lubrication capabilities of this protein have been explained by a long-ranging soft potential origination from the polymer brushes and the reluctance of the brushes to interpenetrate due to the charges from the sialic acid capping the glycans. Although Phy is not sialated, the brushlike stabilizing mechanism is likely to be similar.

The notion of brushlike protrusion forces is also in line with two recent studies (one experimental and one computational) that independently provided evidence for strong interparticle glycan-protein interactions (39,68). In both of these studies, an expanding effect of the glycan on the conformational ensemble of the denatured protein was seen, and in both cases this effect was attributed to steric glycan-polypeptide interactions. In accord with these observations, we suggest that entropy-driven steric stabilization by glycosylation plays an important role in maintaining colloidal stability of glycoproteins in crowded environments.

The effective charge of two glycovariants, as it turned out, was not the same despite identical isoelectrical points (38). However, this observation is in accordance with previous investigations of the impact of ionic strength on the aggregation kinetics of Phy and dgPhy (38). In this study, it was shown that the increase in salinity to a higher degree slowed the aggregation rate of dgPhy, thus suggesting that attractive electrostatic interactions had a more significant role in the aggregation process of denatured dgPhy. The existence of attractive electrostatic potentials despite a net positive charge have been observed for several other proteins, including ribonuclease A (69), α-chymotrypsinogen (70,71), and β-lactoglobulin A (72), and it has been suggested that these potentials are a result of the anisotropic charge distribution (73). Furthermore, for all three proteins, computational investigations have suggested that pairwise electrostatic interactions are attractive in individual configurations (74–76). Moreover, such electrostatic interactions are likely to increase in strength with increasing concentration and decreasing interparticle distance. Therefore, one might speculate that the less concentration-sensitive effective charge of Phy could be due in part to bulky glycans obstructing some of the favorable electrostatic interactions, e.g., by keeping oppositely charged surface residues apart. In any case, the results presented here indicate that the presence of the surface-attached glycans helps the protein to sustain its repulsive electrostatic interactions in crowed conditions.

Conclusion

Biological processes frequently occur in heavily crowded environments. This increases the chemical potential of the macromolecules due to their mutual impenetrability. In general, macromolecular crowding generates a driving force toward more compact structures, thus favoring adducts over monomeric species. However, protein glycosylation appears to be one of nature's strategies to cope with high-volume occupancy stress. The results presented here suggest that the underlying mechanism is steric stabilization, i.e., entropy-driven protrusion forces originating from confinement of the surface-attached glycans. This type of stabilization is especially important in crowded environments as the stabilizing effect increases progressively and the available volume decreases due to the decreasing conformational entropy of the glycans upon confinement. In addition, our data analysis suggests that glycosylation affects the electrostatic interactions in crowded conditions. Despite the fact that deglycosylation leaves the isoelectric point of the protein unaltered, the noncharged surface-attached glycans increase the effective charge interactions of the protein in concentrated solution. Hence, glycosylation may also play a role in sustaining the repulsive Coulomb interactions under crowded conditions.