In Vivo Impedance of the Gerbil Cochlear Partition at Auditory Frequencies

Abstract

The specific acoustic impedance of the cochlear partition was measured from 4 to 20 kHz in the basal turn of the gerbil cochlea, where the best frequency is ∼40 kHz. The acoustic impedance was found as the ratio of driving pressure to velocity response. It is the physical attribute that governs cochlear mechanics and has never before been directly measured, to our knowledge. The basilar membrane velocity was measured through the transparent round window membrane. Simultaneously, the intracochlear pressure was measured close to the stapes and quite close to the cochlear partition. The impedance phase was close to −90° and the magnitude decreased with frequency, consistent with stiffness-dominated impedance. The resistive component of the impedance was relatively small. Usually the resistance was negative at frequencies below 8 kHz; this unexpected finding might be due to other vibration modes within the cochlear partition.

Introduction

The fundamental attributes of an acoustic signal are amplitude and frequency, and their encoding by the auditory system is initiated in the frequency-tuned motion of the inner ear's sensory tissue. This study aims to quantify the physical properties of the cochlea's sensory tissue that give rise to the tuning, and are represented in the tissue's mechanical impedance. This quantification will provide constraints and/or support for cochlear models. To very briefly summarize auditory mechanics: The snail-shaped mammalian cochlea (the auditory part of the inner ear) is a fluid-filled bone with the geometry of a hose spiraling around a central cylinder (Fig. 1 A). If uncoiled, the cochlear length would be ∼3.5 cm in human and ∼1.1 cm in gerbil, the mammalian cochlea under study here. The hose is split lengthwise by the flexible cochlear partition (CP), which includes the sensory tissue of the organ of Corti and is bounded on one side by the fibrous basilar membrane (BM). Sound stimulation results in vibration of the eardrum and ossicles; the vibration of the stapes drives the cochlear fluid. This launches a traveling wave of CP motion down the cochlear spiral (1). The wave has its maximum displacement at frequency-dependent locations, high frequencies closer to the base (close to the stapes), and low frequencies further along the spiral in the cochlear apex. This is known as tonotopic tuning. Simple cochlear models readily demonstrate the cochlear traveling wave, which is principally based on the stiffness of the CP coupled to fluid mass. Longitudinally decreasing stiffness gives rise to tonotopic tuning. In a passive (dead) cochlea, the tuning is quite broad. The great beauty of cochlear mechanics is that in a live, healthy cochlea at low and moderate acoustic stimulus levels, the response peak is up to hundreds of times higher and substantially sharper than it would be in a passive cochlea. Forces exerted by the organ of Corti's outer hair cells (OHCs) are responsible for this response amplification (reviewed in (2)). Hair cells are the transducer elements within the intricately ordered cellular structure of the organ of Corti; sound-induced vibrations of their hairlike stereocilia produce modulations in intracellular current and voltage. In inner hair cells (IHCs), these responses are conveyed via chemical synapses to auditory neurons, while in OHCs the electrical responses are transduced to mechanical forces (3–6). The localized boosting provided by OHC forces poses a challenge for remediation in the hearing-impaired, since it cannot be reproduced by the one-stop amplification of a hearing aid. Therefore, both clinically and scientifically, understanding the cochlea's mechanics is a central goal of auditory neuroscience.

Figure 1.

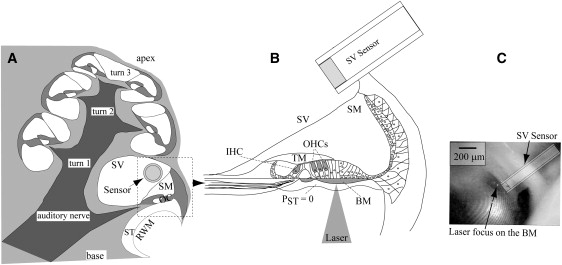
Experimental approach. (A) Cross section of a gerbil cochlea. The scala vestibuli (SV) sensor is inserted adjacent to the stapes, which is not in view, and a cross section of the sensor is shown to indicate its position. (B) Enlarged and rotated view of the basal turn showing the pressure sensor in SV. V_BM was measured by a LDV whose laser beam was directed through the round window membrane (RWM) and focused on the basilar membrane (BM). Due to the flimsiness of the RWM, the cochlear pressure there is approximately atmospheric (time-varying component zero) and the RW fluid level was low so that the cochlear pressure at the basal BM was approximately zero. (C) Image from an in vivo measurement with the laser focused on the BM. Scale bar = 200 μm. The plane of the BM is not exactly perpendicular to the line of sight, so its width is foreshortened in the image. The sensor was not in focus in the image, so a transparent sketch was drawn to clarify its location. IHC, inner hair cell; OHC, outer hair cell; OC, organ of Corti; SM, scala media; ST, scala tympani; and TM, tectorial membrane.

Condensing the CP's mechanical properties to an impedance is very useful for the exploration of such physical concepts as traveling waves and energy flow (7), the impact of impedance roughness (8), and local injection of energy (9,10). As a brief review of mechanical impedance, for a linear spring-mass-dashpot mechanical system, constructed in series and excited with a harmonic force of radian frequency ω, the mechanical impedance, Z_M, is written as

$$Z_{\text{M}}=F/V=-i[S/\omega -M\omega ]+R\text{.}$$ (1)

In Eq. 1, F is the driving force, V is the velocity, S is the spring constant, M is the mass, and R is the resistance. In general, the impedance of viscoelastic biomaterials is not that of a simple spring-mass-dashpot system; in particular, the real part of the impedance is typically frequency-dependent, not a constant resistance. Nevertheless, the simple case provides a useful guide: the imaginary part of the impedance represents reactive (energy-storing) forces due to inertia or the restoring force of stiffness; the real part represents resistive (energy dissipating, absorbing, or creating) forces. For studies of cochlear mechanics, the specific acoustic impedance of the CP (Z) is particularly relevant, where F is replaced by ΔP, the pressure difference across the CP, as

$$Z=\Delta P/V\text{.}$$ (2)

Cochlear models show that the imaginary component of Z (Z_imaginary) is essential to the cochlear traveling wave and tonotopic tuning, while the real part of Z (Z_real) is responsible for the rapid attenuation of the response beyond its peak and, when negative, for the boosting of the response within the peak that occurs in healthy, active cochleae (9,11).

In past work, Z has been estimated in a variety of ways: static or quasistatic stiffness has been measured in intact and semi-intact cochleae, typically as a point stiffness (1,12–17) from which acoustic stiffness can be derived. The point impedance of the isolated organ of Corti (OC) was recently measured over a wide frequency range (18). Z has also been estimated via inverse methods, by coupling BM motion measurements to cochlear models (9,10,19).

To directly measure the acoustic impedance that is most relevant for cochlear mechanics, the CP would be in its natural state, with stimulation to the cochlea via the normal acoustic route; the local pressures on both sides of the CP would be measured simultaneously with the local CP velocity. Such a measurement was recently made using intracochlear pressure and pressure gradients (20,21). The present measurements are along the same lines, but used a Laser-Doppler vibrometer (LDV) to measure CP velocity at the BM (V_BM) directly. (For this macro-mechanical study—as opposed to a micromechanical study that examined motions within the OC—we assumed the CP moved as a unit, and V_BM was used to represent the velocity of the CP.) With pure tone stimulation to the eardrum, ΔP and V_BM were simultaneously measured at the base of gerbil cochlea in vivo where the peak (best) frequency (BF) was ∼40 kHz. Z was found as the ratio of ΔP and V_BM. Two particular objectives of this study were to determine whether the stiffness was frequency-independent and to characterize the size- and frequency-dependence of the resistance, Z_real. Experimental limitations (see ΔP Measurement, below) restricted the analysis of impedance to frequencies to approximately an octave below the BF (i.e., well-sub-BF) at the place of measurement. In a healthy cochlea, nonlinear boosting of the cochlear response occurs at frequencies close to the BF; thus, this is not a study of nonlinear mechanics. Instead, it is a study of the well-sub-BF frequency region where the BM velocity and pressure responses are linear and robust. In a healthy cochlea, well-sub-BF responses do not change upon death, local damage, or acoustic overstimulation (21–23). It is notable that the responses in the study cochleae scaled linearly close to the ∼40 kHz BF. This was not unexpected due to the known vulnerability of the very basal region (24). Nevertheless, we expect the well-sub-BF impedance we measure to be as it would be in a healthy cochlea (Supporting Material, section S2.2.)

We found that the magnitude of Z decreased with frequency in the well-sub-BF region, with a phase close to −90°, which indicates that Z was stiffness-dominated. The specific acoustic stiffness was approximately frequency-independent. Z_real was much smaller than Z_imaginary. Unexpectedly, at low frequencies (particularly below 8 kHz), Z_real was usually negative and this persisted postmortem. To understand the underlying basis for the mechanical impedance will require looking inside the CP, at the micromechanics of its cellular, acellular, and fluid components. In vitro micromechanical studies have shown evidence for tectorial membrane resonances and waves (25,26) and intrapartition fluid flow (27), with OHCs providing rhythmic forcing (28). An analysis of our findings in these terms would be a useful follow-up to this study.

Methods

Animal preparation

Animal procedures were approved by the Institutional Animal Care and Use Committee of Columbia University. Experiments were performed in anesthetized young adult gerbils, 50–70 g in mass. Ketamine (40 mg/kg) was administered first to sedate the animal. Sodium pentobarbital (60 mg/kg with 10 mg/kg supplements) was used throughout the experiment for maintenance of anesthesia and the analgesic buprenorphine (20 mg/kg) was administered every 6 h. At the end of the experiment, the animal was sacrificed with sodium pentobarbital. A tracheotomy was performed to maintain a patent airway. The animal core temperature was maintained at ∼37°C with a heating blanket. The left bulla was exposed and widely opened with great care to access the cochlea. The dorsal surface of the skull was fixed to a head-holder with dental cement and firmly attached to a small goniometer, which was used to orient the head for simultaneously positioning a pressure sensor in scala vestibuli (SV) and focusing the interferometer laser on the BM. A small hole (diameter ∼200 μm) was hand-drilled through the bony wall of SV close to the stapes for sensor insertion. The round window membrane (RWM) was left intact.

ΔP measurement

The fiber-optic micro-pressure sensor was ∼125 μm in diameter. Sensor construction and calibration have been reported previously ((21,29) and Supporting Material, section S1.1). ΔP was approximated by SV pressure, P_SV (reported in dB relative to 20 μPa peak), which was measured in the basal turn SV close to the stapes (SV sensor in Fig. 1). This approximation required that the round window (RW) fluid was low, so that the pressure on the BM side of the CP in scala tympani (ST) could be considered atmospheric, with time-varying component equal to zero. Low RW fluid is normal and during the measurements, a piece of tissue was sometimes used to maintain the low level. By distancing the pressure measurement from the OC slightly (Fig. 1 B), we lost the ability to measure ΔP at frequencies close to the BF. This is because close to the BF, fluid pressure varies significantly close to the OC. In contrast, at frequencies somewhat below the BF, spatial variations are small (e.g., (30,31)). In addition, the SV pressure near the stapes does not vary much across frequencies over distances of at least 0.5–1.5 mm (20,32,33). More quantitatively, P_SV measured distant from the OC can be used fairly well to find ΔP for frequencies <1/2 the local BF (Supporting Material, section S1.2). This limits the measurements of Z here to frequencies <20 kHz. With the frequency limitation of this technique, there is no need for the pressure sensor and velocity measurement to be precisely longitudinally aligned.

V_BM measurement

V_BM was measured with a LDV (OFV-534 and VD-06 decoder; Polytec, Waldbronn, Germany). The LDV's Helium-Neon laser was focused on the preparation with a 10× Mitutoyo lens (Aurora, IL) with 33.5-mm operating distance. The focused spot size (1/e²) is 3 μm. V_BM was measured through the transparent RWM at a location with BF ∼40 kHz without reflecting beads or foils. We also made measurements on the RWM, in part to determine whether reflection from this surface influenced the BM results (34). Because of the desired zero-pressure condition in ST, we could not use a coverslip to stabilize the fluid level. Thus, the fluid surface could move in response to the sound stimulation, which might introduce an error into the V_BM measurement ((35) and Supporting Material, sections S1.3–S1.5).

Z calculation

From the above, we find the specific acoustic impedance of the CP, magnitude and phase, as

$$\left|Z\right|=\frac{\left|P_{\text{SV}}\right|}{\left|V_{\text{BM}}\right|}\text{and}\text{angle}\left(Z\right)=\text{angle}\left(P_{\text{SV}}\right)-\text{angle}\left(V_{\text{BM}}\right)\text{.}$$

Sound stimulation and data acquisition

Pure tones were generated by a Tucker-Davis Technologies (TDT) system III (Gainesville, FL) and delivered to the ear canal via a closed system by a Radio Shack tweeter (Fort Worth, TX). The sampling rate of the TDT system was 5.12 μs. Stimulus and acquisition programs were written in MatLab (The MathWorks, Natick, MA) and the TDT visual design studio. Responses were measured for ∼1 s and time-locked averaging was performed; the averaged data were stored in segments of 4096 points. This data was later analyzed by Fourier transform with MatLab. Sound pressure levels (SPLs) are reported as dB SPL (decibels relative to 20 μPa peak). The sound level was calibrated within 3 mm of the eardrum using a 1/2 inch probe tube microphone (Brüel & Kjær, Nærum, Denmark). The frequency-dependent transfer function of the probe tube microphone was accounted for when setting the SPL and analyzing the data. For this study of linear mechanics, stimulus levels of 80–90 dB were typically used. To couple P_SV and V_BM, we needed to account for the relative delay between the opto-electronic processing of the pressure sensor and LDV. The delay was determined by simultaneously measuring the motion of a pressure-sensor membrane (driven with sound in air) with the LDV and the sensor fiber optic, as illustrated and described in Fig. 3 of de la Rochefoucauld et al. (32). With the present LDV demodulator, the LDV output was delayed 8 μs relative to the pressure sensor output.

Figure 3.

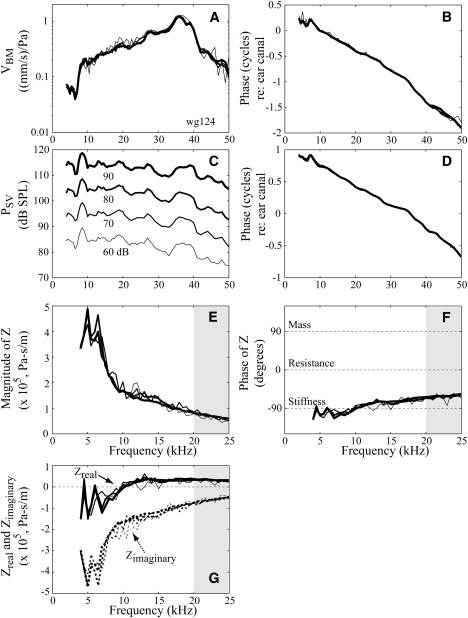
Level independence of sub-BF-Z. Same format as in Fig. 2. Different line types signify SPLs of 60, 70, 80, and 90 dB (wg124).

Results

Results from six animals are reported here. Several experiments preceded these and were used to determine the anatomical approach. The initial cochlear condition was checked by compound action potential (CAP) threshold responses (threshold criterion ∼5 μV p-p) to tone pips, measured with an electrode on the bone surrounding the RW opening. Initial CAP thresholds were typical, generally low at frequencies <20 kHz (29,36), but variable and often high at frequencies >20 kHz (Fig. S5 A). This is consistent with the notoriously fragile base of the gerbil cochlea (24). Placement of the SV sensor could cause CAP threshold loss (29), with the rather extreme case in Fig. S5 showing >20 dB loss at 20 kHz. The Z-value was derived from the simultaneous measurements of P_SV and V_BM. The stability of P_SV and V_BM are documented in Supporting Material, section S2. As explained above, the methodology limited the upper frequency to ∼20 kHz, an octave below the local BF. Below 4 kHz, V_BM was often in the noise. Therefore, we present Z results in the well-sub-BF range from 4 to 20 kHz.

Basic observations of well-sub-BF Z: In vivo, postmortem, and SPL variations

Fig. 2 shows typical Z results, found with V_BM measured at three close-by locations and plotted as mm/s normalized to stimulus pressure. Positions 1 and 3 were very close to each other, with position 2 ∼50-μm apical (Fig. 2 H). V_BM amplitude and phase (Fig. 2, A and B) varied a little at the different locations. The phase of V_BM was delayed several cycles relative to the ear canal pressure (Fig. 2 B). The amplitude and phase of P_SV (Fig. 2, C and D) were consistent with previous reports (e.g., (20,29)). In brief, P_SV at the stapes is typically quite flat with frequency through 40 kHz, with a gain relative to the ear canal pressure of ∼25 dB (responses of ∼ 115 dB with 90 dB stimuli). The phase is delaylike, with a delay of ∼30 μs. There is often a notch in the amplitude and corresponding phase irregularity at ∼7 kHz. This has been noted in both P_SV and stapes motion and discussed previously (20,29,37).

Figure 2.

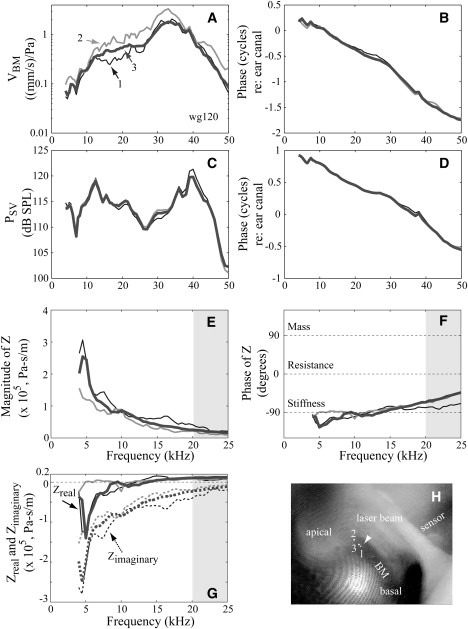
Basic characteristics of sub-BF-Z. (A) V_BM amplitude normalized to ear canal pressure. (B) V_BM phase. (C) P_SV amplitude. (D) P_SV phase. Phase of P_SV and V_BM were referenced to ear canal pressure. (E) Magnitude of Z. (F) Phase of Z; impedance phases corresponding to pure stiffness, pure mass, and pure resistance are indicated in the figure as a guide. (G) Real and imaginary part of Z. Dotted lines are used for the imaginary component. (H) Experimental approach photograph from the experiment, with the three locations of V_BM measurement noted. In panels A–G, locations 1–3 are coded by line style: thin black lines, thick gray lines, and thick black lines, respectively. In panels E–G, the gray area above 20 kHz demarks the upper limit of validity. Because our ΔP approximation is not accurate in this region, Z could not be measured there. (wg120, SPL = 90 dB.)

The lower three panels show Z as magnitude, phase (Fig. 2, E and F), and real and imaginary parts (Fig. 2 G). From 4 to 20 kHz, the magnitude (Fig. 2 E) decreased with increasing frequency, except for a wiggle at the lowest frequency. The phase (Fig. 2 F) was close to −90°, indicating that Z was stiffness-dominated. The phase calculated from location 2 was more stiffnesslike at frequencies <10 kHz than the others, in which there was up to 40° offset from −90°. At ∼10 kHz, the impedances at all three locations were almost purely stiffness. The position-dependent variation in Z was due to variation in V_BM responses. The major variation was due to a small change in the velocity phase of position 2 below 10 kHz; from 10 to 20 kHz, the phases at the different locations overlay. When plotted as real and imaginary parts (Fig. 2 G), Z_imaginary was negative, and decreased in absolute value from ∼2 × 10⁵ Pa-s/m at 4 kHz to 2 × 10⁴ Pa-s/m at 20 kHz. Both the negative sign and the decrease in absolute value with frequency are as expected for a stiffness. Z_real measured at location 2 started with a negative value of −4 × 10⁴ Pa-s/m at 4 kHz, then above 5 kHz became positive with a value of ∼0.7 × 10⁴ Pa-s/m that persisted with little change up to 20 kHz. Z_real measured at locations 1 and 3 was negative at a value of −1 × 10⁵ at 5 kHz, and increased steadily up to 10 kHz, then became positive or approximately zero and flattened to ∼1 × 10⁴ Pa-s/m at 20 kHz. We expected positive resistance in the well-sub-BF region under study and the appearance of negative resistance was an unexpected but common finding. At frequencies above 20 kHz, the limitation of this technique is apparent in the upward sweep of Z phase, which is caused by a relatively rapid accumulation of V_BM phase compared to P_SV phase. (It should be noted that in studies in which pressure was measured <100 μm from the BM, the pressure does show traveling wave phase accumulation (21,30,38).)

Fig. 3 shows that cochlear responses and thus Z were independent of level. Negative resistance was observed at frequencies below 10 kHz, and varied positive due to fine structure at ∼5 kHz. These aspects of Z were also independent of level. Close to the BF in a healthy preparation, we would expect nonlinear responses. This was not apparent in these preparations, but its absence does not diminish the results from the robust well-sub-BF region of this study (Supporting Material, section S2.2). Fig. 4 shows how the postmortem condition affected the well-sub-BF Z. These data are from the same animal as Fig. 2: in vivo (dotted, data from position 3 in Fig. 2) and postmortem 30 min (solid, V_BM measured from the same spot). At frequencies from 4 to 20 kHz V_BM (Fig. 4, A and B) and P_SV (Fig. 4, C and D) were very similar in vivo and postmortem, leading to similar Z (Fig. 4, E–G). Z_real was negative at frequencies below 8 kHz in vivo, and this remained so postmortem.

Figure 4.

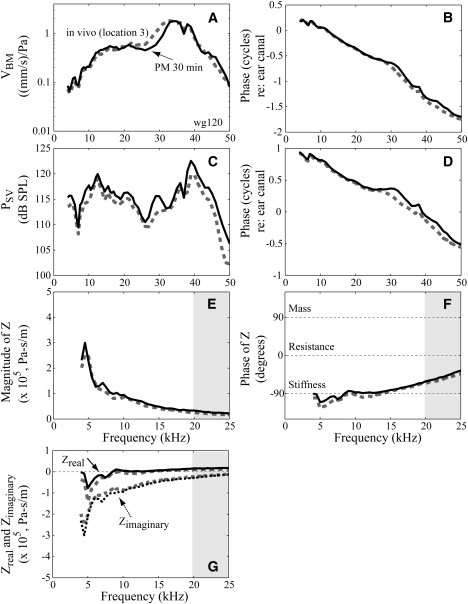
Sub-BF-Z in vivo and postmortem. Same format as in Fig. 2. The solid line represents measurements made at the same locations ∼30 min postmortem. (wg120, SPL = 90 dB.)

Because Z phase was close to −90°, small phase variations were responsible for qualitative changes in Z_real. Because of this sensitivity, possible systematic phase errors are discussed at length in Supporting Material, section S1. On the same note, small seemingly random variations in V_BM phase occurred with small changes in measurement location. For example in the 5–8 kHz region of Fig. 2, the resistance appeared negative at locations 1 and 3 and positive at location 2. The observed phase variations are consistent with the literature where, at well-sub-BF frequencies, it is common to see a range in BM motion phase of 40–50° at slightly different locations in a single experiment (35,39–41). Some of this variation is likely due to the factors discussed in the Supporting Material. However, it seems likely that the micromechanics of the CP also contribute to the variability in V_BM phase.

Z and acoustic stiffness across animals

Fig. 5 shows grouped Z results from the six animals that contributed to this study. The magnitude of Z decreased with increasing frequency from 2–7 × 10⁵ (at 4 kHz) to 0.2–1 × 10⁵ Pa-s/m (at 20 kHz). The phase of Z was usually within ±30° of −90°, indicating that Z was stiffness-dominated. Z_real was generally negative at frequencies below ∼5–8 kHz. In the negative region, Z_real grew rapidly in absolute value as frequency decreased. From ∼8 to 20 kHz, Z_real was almost frequency-independent with a value <0.5 × 10⁵ Pa-s/m. Z_imaginary was negative (stiffnesslike) with an absolute value that decreased with frequency from 2–7 × 10⁵ (at 4 kHz) to 0.2–1 × 10⁵ Pa-s/m (at 20 kHz). Multiplying the absolute value of Z_imaginary by radian frequency gives specific acoustic stiffness, plotted in Fig. 5 E. The acoustic stiffness was almost constant with frequency in each individual animal, with erratic frequency variations that do not seem significant. The range of stiffness values across animals was 0.2–1.3 × 10¹⁰ Pa/m. (Supporting Material, section S4, discusses the phase of Z in other species.)

Figure 5.

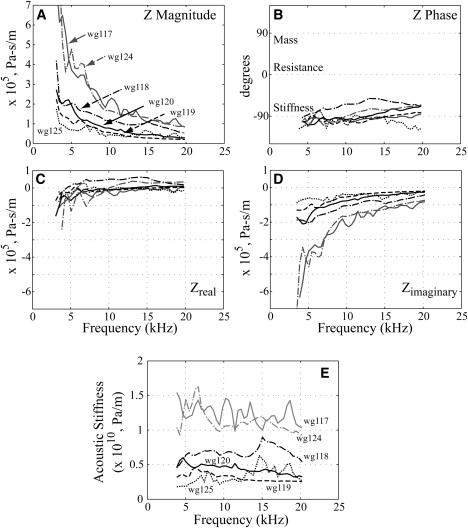
Values of Z from six animals. (A) Magnitude of Z. (B) Phase of Z. (C) Real part of Z. (D) Imaginary part of Z. (E) Acoustic stiffness. Each line represents an average composed of several runs from an individual animal.

Discussion

Equation 1 in the Introduction, giving the impedance of a single-mode spring-mass-dashpot system driven by a force F, provides a framework for the discussion. In our analysis, the CP is driven locally by the fluid pressure as in Eq. 2, so the mass, stiffness, and resistance of Eq. 1 are normalized to area. The simple equation is likely too simple but is nevertheless a useful reference point. The real part of the impedance, Z_real, for which driving pressure and velocity are in phase, represents damping or energy absorption. However, if the observed Z_real is negative, energy is being injected into the system, not absorbed. When driving pressure and displacement are in phase, Z is imaginary; Z_imaginary represents the restoring forces due to CP stiffness. CP mass also contributes to Z_imaginary, acting to diminish the effective stiffness (Eq. 1). CP mass is not expected to become significant until the frequency is close to or perhaps higher than the BF, so in our study stiffness is expected to dominate Z_imaginary (as was assumed in the stiffness calculation just above).

Cochlear partition impedance is at the center of cochlear mechanics. The coupling of partition stiffness and the inertia of the cochlear fluid provides the physical substrate for the cochlear traveling wave. The longitudinal variation in partition stiffness is the physical feature that governs tonotopic tuning and the details of this variation are still being explored (16,17,42). In some cochlear models, CP resistance determines the place at which the response drops precipitously after peaking (43), while in others CP mass plays the decisive role (7). A recent study aimed at this question found that the OC mass was influential to tuning in the very base, but less so just slightly apical (19). This study measured Z in vivo under natural conditions through a wide frequency range and tested several of our assumptions about its characteristics. In our observed well-sub-BF frequency range, up to an octave below the BF, Z was expected to possess stiffness and resistance, and thus have a negative imaginary part and a positive real part. The reality was a bit more complicated—while Z_imaginary was negative as expected, Z_real was usually negative at frequencies <∼8 kHz. Below, we discuss our observations of Z_real and Z_imaginary in turn.

Imaginary part of Z and stiffness

Stiffness has been probed with very direct experiments and with combined theoretical/experimental approaches. The most common direct experimental method for finding stiffness is a point stiffness measurement at the BM. The result, in units of N/m, is then typically combined with a radial beam model to find the specific acoustic stiffness in Pa/m (12–17). These point stiffness measurements were either static or quasistatic, and were performed in vivo; in vitro in full cochlear turns; and in vitro in the hemicochlea. As an important advance, the frequency-dependent impedance to OC compression was measured through a very wide frequency range with the OC excised and laid flat on the BM (18). In that study, Z_imaginary was negative and decreased in absolute value with increasing frequency, as expected for stiffness-dominated impedance. To explain the theoretical/experimental approaches, in a cochlear traveling-wave model Z_imaginary and fluid inertia largely determine the cochlear traveling wave's wavelength, and measurements of two of these three quantities can be used to find the third. Z_imaginary can thus be found by coupling phase observations (to find wavelength) to a cochlear model (which prescribes the fluid inertia) (7,9,10,19). A different theoretical/experimental approach is to use the Young's modulus of the protein filaments that form the primary structural component of the BM, and a beam model of the BM radial fibers to predict the BM stiffness (12,42,44). For our study of Z, we measured the intracochlear driving pressure and BM motion response with normal acoustic stimulation. One previous set of measurements also measured the driving pressure and BM motion responses upon acoustic stimulation, but used pressure gradients to derive BM motion (20,21). This study's laser-based BM motion measurement is thought to be more exact.

Fig. 6 compares our present values of CP acoustic stiffness in the base of the gerbil cochlea with those that have been found previously. The point stiffness measurements (15–17) have been recast as specific acoustic stiffness using a beam model (13,19). These are straight lines since the stiffness was measured at one low frequency. The width of these thick lines gives the stiffness range from each study. The dot-dashed lines are from a combined model/experimental study (19) and are single-valued because the stiffness was assumed to be independent of frequency. The modeling results in Yoon et al. (44) were almost frequency-independent and the small amount of frequency dependence was not included in the plot. The results from this study are the average of the six curves in Fig. 5. The range of stiffness values in all these studies is certainly due in part to true longitudinal variations within the cochlear base. However, the nearly two-orders-of-magnitude variation is larger than expected based on the range found in individual point stiffness studies and likely some of the range is erroneous. Including more information from the studies can help to establish the most reliable range. A clustering of values at ∼5 × 10⁹ Pa/m includes results from two point stiffness studies (intact cochlea, in vivo and in vitro), the current study, and the lower stiffness value from de la Rochefoucauld and Olson (19). The higher stiffness value from de la Rochefoucauld and Olson (19) was from a region of the cochlea that was not well described by the box model employed in the study and the slightly more apical measurement that is within the clustering of Fig. 6 is more reliable. The stiffness values from Olson (21) are on the low side, but the quantitative aspects of those results are relatively less reliable due to the study's approximate method for finding V_BM. The stiffness in Yoon et al. (44) is also lower than the clustered values. However, the overly large traveling wave phase variations of that (modeling) study argue that the stiffness value used was too low. The data from Emadi et al. (17) are also on the low side, perhaps due to the effect of the open edge of the hemicochlea preparation. For all these reasons, 3–8 × 10⁹ Pa/m seems like the most robust range for the specific acoustic stiffness in the base of the gerbil cochlea.

Figure 6.

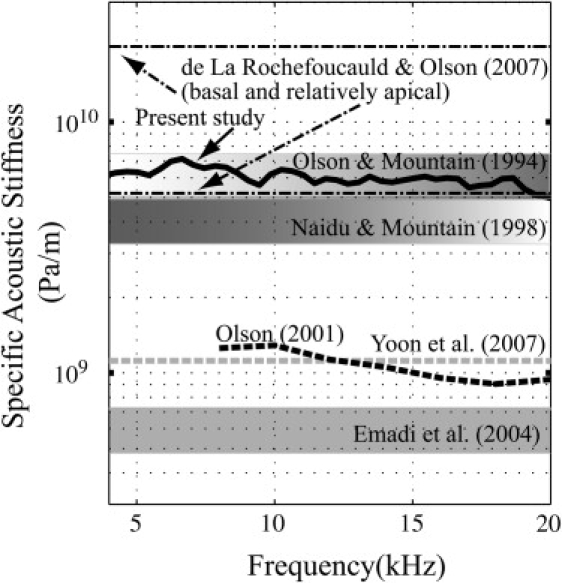
Specific acoustic stiffness of the CP at the base of the gerbil cochlea from several studies.

Real part of Z and resistance

Referring to our grouped results in Fig. 5, Z_real was usually significantly smaller than Z_imaginary in absolute value. Fig. 5 C showed that in five of our six animals, Z_real was negative or very close to zero from 4 to 10 kHz. In the region from 10 to 20 kHz, Z_real remained negative or close to zero in three animals, and became slightly positive in two. Through most of this frequency range, the sixth animal (wg118) had Z_real close to one-quarter the size of Z_imaginary, and positive. The sizes of Z_real varied from ∼−1 × 10⁵ Pa-s/m at 5 kHz to +0.2 to +0.5 × 10⁵ Pa-s/m at frequencies >10 kHz. We proceed by discussing how these results compare to previous studies of CP resistance. We then ask whether the acoustic resistance we measure could conceivably be counteracted (when the resistance is positive) or produced (when the resistance is negative) by known OHC forces.

The cochlear partition resistance has been estimated with direct measurements and with modeling or hybrid modeling/experimental studies. In passive computational cochlear models, tissue stiffness and resistance have been based on a viscoelastic modulus (e.g., (31)). The elastic modulus produces the stiffness and the loss modulus, typically chosen with size 5% of the real part, produces tissue resistance. This type of viscoelastic mechanical impedance is known in polymeric material including biomaterials (45) although the size of the loss modulus can be >5% (46). In models of active cochlear mechanics, significant progress was made when it was shown that the dramatic difference between passive and active BM responses was due to OHC forces that acted as a locally negative resistance (9,11,47,48). To discuss one of these studies in more detail: By applying an inverse method to observations of BM motion, de Boer and Nuttall (9) found the real and imaginary parts of Z. The results demonstrated longitudinal-location and stimulus-level dependent variations in Z_real in a healthy, active cochlea. Just basal to the response peak, Z_real was negative at low stimulus levels and positive at high levels. Further basal, Z_real was positive and less level-dependent. In this region Z_real was generally ∼1/4 the size of Z_imaginary. Results from this region can be compared with our results, which probed regions well basal to the BF peak.

Compression impedance was directly measured in Scherer and Gummer (18). The measured Z_real was positive, and like Z_imaginary, it decreased with increasing frequency. The study compared the impedances at different longitudinal and radial locations, and generally the absolute value of Z_real was just slightly smaller than Z_imaginary. The decreasing size of Z_real with frequency is like that of polymeric biomaterials and indicated that the tissue cannot be modeled with a Kelvin-Voigt model in which resistance is a frequency-independent dashpot. The authors pointed out that diminishing tissue resistance with frequency was likely important for maintaining high frequency responses in the cochlea.

Experimental probes of acoustic impedance that were based on intracochlear pressure measurements (20,21) sometimes detected regions of negative resistance in active, nonlinear cochleae (21). The negative resistance sometimes appeared in sub-BF frequency regions where the responses at the BM scaled linearly, which is consistent with these findings. However, negative resistance was not robust in those studies; the robust finding of those studies was that in active cochleae with strongly nonlinear V_BM, Z was only mildly nonlinear.

To compare these results, we begin with the value of Z_real when it was positive. In this study, its size was usually a small fraction of Z_imaginary, as in Taber and Steele (31). However, the positive resistance did not decrease in absolute value systematically with frequency; instead, it was relatively flat. Both the real/imaginary ratio and frequency dependence differ from what was found in Scherer and Gummer (18), and this could be due to the methodological difference as those measurements compressed the OC locally, whereas in ours it was displaced with pressure.

Regarding our detection of negative Z_real, while this is predicted in active cochlear models, the specifics of our observations are not in line with the predictions. We observed level-independent negative resistance in the well-sub-BF region, whereas inverse method results (9) found level-dependent negative resistance at locations basal but close to the peak (corresponding to frequencies slightly below the local BF, when measuring at one location). The discrepancy with these results requires further scrutiny. To probe it, we examined the effect of assigning a negative resistance to the very base of a two-dimensional short wave cochlear model (43), and found the BM amplitude to be not much changed compared to the response with positive resistance. In contrast, the same fraction of negative resistance relative to stiffness, assigned close to the peak, caused a large change in V_BM amplitude (Fig. S6). Zweig (10) also studied partition impedance with an inverse method. He found negative resistance that extended through the entire region basal to the peak, but noted that the negative resistance had little effect on the response except close to the peak—a conclusion our Fig. S6 supports. Thus, the inverse method is effective for probing the nonlinear response near the peak, but is not very sensitive to the resistance substantially basal to the response peak, and low frequency negative resistance could conceivably be missed when applying the method. At the same time, the robustness of the negative resistance we find sets it apart from labile and level-dependent negative resistance.

OHC forces have been measured in vitro, and we can ask if they are big enough to counteract the observed positive resistance and conversely to produce the observed negative resistance. We will consider these in turn, and start by determining the size of effective OHC pressure from the OHC forces reported in the literature. Low frequency somatic forces of 10 nN (49) and high frequency forces of 0.26 nN (50) have been observed. These forces were responses to applied membrane voltages of ∼100 mV and 20 mV, respectively, which are higher than the ∼10 mV saturation level of OHC voltage in vivo (51). Therefore, 0.1–1 nN is a reasonable upper limit for the physiologically relevant OHC electro-mechanical somatic force. OHC bundles can exert active forces up to 0.4 nN (6). We recast these forces as pressures to compare to our results; this requires dividing by an area. Dividing by the cross-sectional area of an OHC (∼1 × 10⁻¹⁰ m²) gives the pressure exerted by the OHC. It is necessary to multiply this pressure by the fraction of the OC area OHCs occupy, ∼0.1. This results in an upper limit of OHC-induced pressure of 0.1 × (0.1 – 1 nN)/ (1 × 10⁻¹⁰ m²) = 0.1–1 Pa.

Could this OHC pressure counteract the positive resistance we observe? Consider the positive resistance in Fig. 3, which was almost constant from 13 to 20 kHz, with a value of ∼3 × 10⁴ Pa-s/m. This positive resistance value was the second largest of the six animals. The cochlear nonlinearity that is tied to OHC forces is apparent at frequencies close to the BF, and the flatness of the resistance through 20 kHz makes it reasonable to extend this value through the BF for this discussion. To find the resistive pressure, we must multiply the resistance by V_BM. It makes sense to consider a V_BM that occurs at a stimulus level at which cochlear amplification is operational in a healthy cochlea, but beginning to saturate, say 70 dB SPL. From Fig. 3, at 70 dB SPL and at the BF, V_BM would be 6 × 10⁻⁵ m/s, thus the resistive pressure would be 1.8 Pa. In a nonlinear cochlea, the velocity at 70 dB would be somewhat bigger than in the linear preparation here, so we might expect positive resistance pressures of up to 18 Pa. Thus, at 70 dB the resistive pressure would be partly compensated by ∼1 Pa OHC forces but the resistance would still be net positive. This is roughly consistent with the predictions of cochlear models (9).

Could the OHC pressure produce the negative resistance we observe? Consider Fig. 2. Here, at frequencies below 10 kHz, the resistance at two of the three locations was negative (Fig. 2 G), with a value (at 6–8 kHz) of ∼5 × 10⁴ Pa-s/m. V_BM in this region at the 90 dB stimulus level used is ∼6 × 10⁻⁵ m/s. Thus, with the 90 dB stimulus, the negative resistive pressure exerted by the CP, Z_real × V_BM, was 3 Pa. This is somewhat larger than the ∼1 Pa maximum calculated above. In addition, the very subtle postmortem change we observed in Fig. 4 means electro-mechanical motility is not likely the basis for the negative resistance, since, postmortem, the driving voltage of endocochlear potential is greatly reduced (22). From another angle, the lack of level dependence means that whatever gives rise to the negative resistance operates linearly up to SPLs of at least 90 dB SPL. At 90 dB SPL, V_BM at frequencies below 10 kHz is ∼0.1 mm/s, and decreasing with frequency. This corresponds to a displacement of only ∼2 nm, even at 90 dB SPL. Thus, where negative resistance was observed, the displacements are small enough to support the plausibility of micromechanical cellular forces as the source of the negative resistance.

In the conceptual framework of impedance in a single-mode vibration system, negative resistance means local energy input. For our observed negative resistance to be due to energy input there must be stored energy in the OC that runs down slowly, postmortem. Alternatively, something that belies the applicability of the local impedance framework might be responsible for the negative resistance—for example, longitudinal forces exerted via fluid flow (27,52) or tectorial membrane dynamics (53). Theoretical modeling that explores the impact of micromechanics on macromechanics would throw some light on the findings here. On the experimental side, measurements in a cochlea in which the OC has been removed are planned for the future.

Conclusion

In this study we quantified the mechanical properties of one of nature's most fascinating mechanical instruments, the cochlea. With pure tone stimulation to the eardrum, driving pressure, P_SV, and velocity, V_BM, were measured in vivo at the base of gerbil cochlea and the cochlear partition impedance, Z, was found as their ratio. With the limitations of this technique, Z could be measured at a frequency approximately one octave below the 40 kHz BF at the place of measurement. This frequency region is linear and our objective was to quantify the region's linear impedance. In our results the magnitude of Z decreased with frequency, with a phase close to −90°, indicating that Z was stiffness-dominated. The specific acoustic stiffness was approximately frequency-independent with a value of ∼5 × 10⁹ Pa/m, which is in line with previous quasistatic stiffness measurements. The absolute value of Z_real was much smaller than Z_imaginary. At frequencies up to ∼8 kHz, Z_real was usually negative and this persisted at high stimulus levels and postmortem. The size- and frequency-dependence of the stiffness and resistance provide quantitative information for cochlear models. The unexpected negative resistance might be a view to micromechanics and is an interesting puzzle for the future.

Supporting Material

Seven figures are available at http://www.biophysj.org/biophysj/supplemental/S0006-3495(09)01149-7.