How Does a Simplified-Sequence Protein Fold?

Abstract

To investigate a putatively primordial protein we have simplified the sequence of a 56-residue α/β fold (the immunoglobulin-binding domain of protein G) by replacing it with polyalanine, polythreonine, and diglycine segments at regions of the sequence that in the folded structure are α-helical, β-strand, and turns, respectively. Remarkably, multiple folding and unfolding events are observed in a 15-μs molecular dynamics simulation at 330 K. The most stable state (populated at ∼20%) of the simplified-sequence variant of protein G has the same α/β topology as the wild-type but shows the characteristics of a molten globule, i.e., loose contacts among side chains and lack of a specific hydrophobic core. The unfolded state is heterogeneous and includes a variety of α/β topologies but also fully α-helical and fully β-sheet structures. Transitions within the denatured state are very fast, and the molten-globule state is reached in <1 μs by a framework mechanism of folding with multiple pathways. The native structure of the wild-type is more rigid than the molten-globule conformation of the simplified-sequence variant. The difference in structural stability and the very fast folding of the simplified protein suggest that evolution has enriched the primordial alphabet of amino acids mainly to optimize protein function by stabilization of a unique structure with specific tertiary interactions.

Introduction

Proteins fold by a complex transition from a very broad ensemble of unfolded conformations to the well-defined native state, which is the functional structure. The complexity originates from the many degrees of freedom and the delicate balance of enthalpic and entropic contributions to the free energy from the polypeptide chain and solvent molecules (1–3). Thus, despite protein folding involves one single chain (in aqueous solvent), it is described more appropriately as a phase transition than as a simple chemical reaction (3,4).

Evolution has selected sequences for specific biological functions, which, except for the natively unfolded proteins, require a thermodynamically stable folded structure (5). Although folding efficiency is not under direct evolutionary pressure, fast folding (i.e., in the microsecond to second timescale) is necessary for many biological functions that have to be fine-tuned in time, such as signal transduction and rapid adaptation to changes in the environment. Concerning a stable functional state, it has been suggested that a sufficiently high diversity of interactions is required for folding to a unique state with an energy much more favorable than decoy structures (6,7). Diversity of interactions requires a heterogeneous amino-acid alphabet. Theoretical analysis and computer simulations have suggested that selection of sequences that yield a native conformation with a pronounced energy minimum, i.e., an energy gap with respect to other structures, solves the problem of kinetic accessibility of the native conformation (8–11). Furthermore, by a comprehensive computational analysis of the folding cooperativity in several widely used lattice models, it was observed that the model based on a 20-letter alphabet is the most cooperative, whereas two- and three-letter models are much less cooperative (12).

On the experimental side, random libraries of sequences with only three types of amino acids (leucine, glutamine, and arginine) have been expressed in Escherichia coli (13–15). By means of circular dichroism measurements, only 1% of the sequences were shown to fold. These results led the authors to conclude that the key elements of protein design are in the proper placement of hydrophobic residues along the polypeptide chain to ensure the formation of a well-packed hydrophobic core. In another experimental study the sequence of the SH3 domain was simplified by using only five types of amino acids (glycine, alanine, isoleucine, lysine, and glutamate) (16). The study was conducted using the phage-display technique to select for native function. Despite the dramatic change in sequence, the folding rates of the simplified versions of the SH3 protein were very close to the folding rate of the wild-type. Moreover, nuclear magnetic resonance analysis provided evidence of a well-packed core consistent with the thermodynamic stability of the folded state.

Because of the timescales involved and systematic error of the atomistic model, the simulation of reversible folding of polypeptides by transferable potentials is still very far from the routine. Here, we attack the complexity of the folding process by designing and simulating a putatively primordial protein, a variant of the immunoglobulin-binding domain of protein G with a simplified sequence (termed protein ssG hereafter). The simplified (i.e., low complexity) sequence of protein ssG consists of only three types of residues, glycine, alanine, and threonine, which are distributed to preserve the secondary structure propensity of the wild-type sequence. This study was inspired by the following questions:

• What is the folding mechanism of a protein with simplified sequence?

• Is its folded state topologically equivalent to that of the wild-type, and is it uniquely defined?

• Is its denatured state heterogeneous, i.e., does it contain native and/or nonnative secondary structure elements and topologies?

• Are there misfolded states that might promote aggregation?

The simulation results indicate that the protein ssG folds rapidly and reversibly to the native topology of the wild-type but has a fluidlike folded state devoid of specific hydrophobic contacts. Furthermore, the strong propensity for regular secondary structure formation results in a framework model of folding with parallel pathways. Notably, the heterogeneous unfolded state ensemble of protein ssG includes kinetic traps with high β-sheet content, which are likely to be aggregation-prone.

Methods

Reduced amino-acid alphabet and simplified sequence of protein G

A necessary condition for proteinlike sequences, namely sequences resulting in an energy gap between folded state and decoys, is that the effective number of amino-acid types m_eff is larger than the number of conformations per residue γ (6). Assuming that a single residue can be found in three states of secondary structure—helix, β, and turn/loop—we hypothesized that the condition m_eff > γ might hold for native topologies mainly defined by secondary contacts, adopting an extremely simplified alphabet of only three amino acids. In other words, our Ansatz is that it is sufficient to choose three amino acids specifically prone to form the aforementioned secondary structure to reproduce the starting fold. Thus, to enforce secondary structure propensity and remove frustration, the sequence of protein G was simplified into only alanines, threonines, and glycines at segments that in the folded structure are α-helical (residues 23–37), β-strand (residues 1–9, 12–20, 40–47, and 50–56), and turns, respectively. Threonine was chosen not only because it is a moderately β-prone residue but also to counterbalance the hydrophobicity of alanine and glycine. Moreover, threonine is the most abundant residue in the wild-type sequence and it is present in 24% of β-strand segments. Table 1 shows the sequences of wild-type protein G and the variant protein ssG. The sequence identity is only 23%, and the 13 identical residues are almost uniformly distributed along the 56-residue sequence except for Thr¹⁶-Thr¹⁷-Thr¹⁸ in the second strand of the N-terminal β-hairpin.

Table 1.

Sequences of proteins G and ssG

Sequences
Protein G	MTYKLILNGKTLKGETTTEAVDAATAEKVFKQYANDNGVDGEWTYDDATKTFTVTE
Protein ssG	TTTTTTTTTGGTTTTTTTTTGGAAAAAAAAAAAAAAAGGTTTTTTTTGGTTTTTTT
Secondary structure string	-EEEEEEEESSEEEEEEEE-SSHHHHHHHHHHHHHHH----EEEEETTT-EEEEE-

The secondary structure string was determined using the x-ray structure (19). In the DSSP string, the letters E, H, S, T, and the hyphen symbol (-) correspond to extended, α-helical, bend, hydrogen-bonded turn, and unstructured, respectively (47).

Molecular dynamics simulations and coarse-graining

The implicit solvent model and the protocols used for the molecular dynamics simulations (17), as well as the method utilized for coarse-graining of the conformational space, are presented in the Supporting Material.

Markov chain approach, causal grouping, and mean first-passage times (MFPT)

From the time series of C_α-RMSD clusters, a one-step transition matrix T(τ) of conditional probabilities can be estimated by using the relation

$$T_{\text{ij}}\left(\tau \right)=P_{\text{ij}}^{\text{eq}}\left(\tau \right)/P_{\text{i}}^{\text{eq}}\simeq n_{\text{ij}}\left(\tau \right)/n_{\text{i}},$$ (1)

where the indexes i, j are state labels, P^eq_i = n_i/M is the equilibrium probability of the state i (n_i snapshots over a total number of M), and $P_{\text{ij}}^{\text{eq}}$(τ) = n_ij(τ)/(M – 1) is the probability flux for the transition i → j at the lag time τ, where n_ij(τ) is the total number of transitions i → j. All the quantities are estimated within the lag time τ of 20 ps, which is the saving time of the trajectories. To test the Markov property of the time series at the lag time τ, a non-Markovian flux was estimated by comparing the one-step transition matrix T_jk(τ) with the two-step transition matrix T_ijk(τ) for the transition i → j → k. The two-step transition matrix is

$$T_{\text{ijk}}\left(\tau \right)=P_{\text{ijk}}^{\text{eq}}\left(\tau \right)/P_{\text{ij}}^{\text{eq}}\simeq n_{\text{ijk}}\left(\tau \right)/n_{\text{ij}}\left(\tau \right),$$ (2)

where $P_{\text{ijk}}^{\text{eq}}$(τ) and n_ijk(τ) are, respectively, the probability flux and the total number of transitions i → j → k. The Markov property is valid if the identity T_ijk(τ) = T_jk(τ) is satisfied for any i. Using the relation in Eq. 2 and summing up over all the two-step transitions, one obtains the total non-Markovian flux

$$F\left(\tau \right)=1-\sum _{\text{i}\to \text{j}\to \text{k}}{P}_{\text{i}}^{\text{eq}}{T}_{\text{ij}}\left(\tau \right)T_{\text{jk}}\left(\tau \right)\text{.}$$ (3)

The non-Markovian flux is a probability flux, which reflects the overall error made by assuming the Markov approximation on a time series at a certain lag time τ. The statistical significance of the clusters plays an important role if one is interested to describe a time series adopting a Markov approximation.

A procedure based on the reassignment of the clusters memberships is employed here to achieve the “Markovianity” of the time series: the snapshots of the low-populated clusters are reassigned to the statistically significant clusters according to their causal connectivity along the time series. In other words, the procedure lumps together conformers that are close in time but not necessarily in space. Such lumping is attained by reprocessing the time series of clusters to obtain a time series of causally grouped mesostates: when a snapshot of an insignificant cluster (size < cutoff) is encountered, it is causally reassigned to the next significant cluster (size ≥ cutoff). The cutoff is chosen such that the resulting time series are Markovian, or more precisely, have a non-Markovian flux <1%. For the present simulation of protein ssG, 200 causally grouped mesostates resulted from a cluster size cutoff of 250 snapshots (see Fig. S2 in the Supporting Material). The simplicity of the procedure is rooted in the hypothesis that the dynamics of the polypeptide takes place only between stable states where the system can partially diffuse, losing memory of previously explored states. Remarkably, at the lag time of 20 ps, the overall error of the Markov approximation is <1% for the 200 causally grouped mesostates, whereas it is 7.5% if one considers, for the transition matrix, the 3124 clusters with two or more snapshots (see Fig. S2). The difference justifies the adoption of the causally grouped mesostates for the Markov approximation. Thus, once a time series of causally grouped mesostates is provided, the transition matrix T_ij(τ) can be estimated, where now the indexes i, j run from 1 to 200.

To provide evidence that the validity of the Markov approximation at lag time τ = 20 ps is good enough for longer timescale extrapolations, transition matrices for lag times up to 20 ns were determined from the causal grouped time-series. The relaxation times corresponding to the eigenvalues show robustness in the values of the slower relaxation times (see Fig. S3) within these time ranges. Moreover, the distributions of the first passage times to the folded states calculated from molecular dynamics and using the Markov approximation compare very well in both their shape and timescales (see Fig. S4), indicating a substantial equivalence in the kinetics of the original and the modeled processes. These two results suggest that the Markov approximation adopted for the causal grouped mesostates at 20 ps of lag time is robust enough to infer the long time kinetics of the folding process.

The equilibrium counterpart of the transition matrix T(τ) is the matrix of mean first-passage times (MFPT) M whose entries M_ij give the mean hitting time for the transitions between the mesostates i → j, averaged over all the possible connecting pathways. By assuming the ergodicity of the underlying finite Markov chain, the M_ij matrix is given by a system of linear equations such as

$$\begin{array}{c}{M}_{\text{ij}}=\tau +\sum _{\text{k}\ne \text{j}}{T}_{\text{ik}}\left(\tau \right)M_{\text{kj}}\\ M_{\text{ii}}=\sum _{\text{k}}{T}_{\text{ik}}\left(\tau \right)\left(M_{\text{ki}}+\tau \right)\end{array},$$ (4)

that are exactly solvable when the number of states is small. Assigning the index 1 to the folded mesostate, then the first column of the MFPT matrix (M_i1) gives the mean folding times from individual mesostates to the folded one. To facilitate the reading of the M matrix, the indexes were sorted in such a way that the low numbers (from 1) are the mesostates with small folding times, whereas large numbers (up to 200) have longer folding times. Thus, the first row of the M matrix satisfies the inequalities M_{1 1} ≤ M_{2 1} ≤ ⋯ ≤ M_{200 1}. The indexes of the sorted MFPT matrix are adopted for the labeling of the mesostates throughout this work.

Static and dynamic correlations of secondary structure

The time series of strings of secondary structure (termed SSS[8], see Supporting Material) allows the adoption of information theory methods to investigate the underlying structural mechanisms of folding. For each residue, a probability π_i(s) can be defined where i is the residue number and s is one of the eight secondary structure symbols. Similarly, a pairwise probability π_ij(ss′) is defined between two residues i and j, and secondary structure s and s′. Both probabilities are estimated from the time series of SSS[8]. The static correlation between pairs of residues can be evaluated from the ensemble of visited strings by calculating the pairwise mutual information. In information theory, the mutual information between two random variables measures their mutual dependence (18). With the probabilities previously defined the mutual information between two residues is defined as

$$I_{\text{ij}}=\frac{1}{\ln 8}\sum _{{ss}^{\prime }}{\pi }_{\text{ij}}\left({ss}^{\prime }\right)\ln \frac{{\pi }_{\text{ij}}\left({ss}^{\prime }\right)}{{\pi }_{\text{i}}\left(s\right){\pi }_{\text{j}}\left(s^{\prime }\right)},$$ (5)

which is a normalized quantity that is zero when the residues i and j are totally uncorrelated, and one when they are totally correlated.

The static mutual information can be generalized to obtain a correlation function with the aim to evaluate the dynamics of formation of secondary structure. We define a time-dependent pairwise probability π_ij(ss′, t) that two residues i, j assume secondary structure ss′ at the time t. The time-dependent mutual information is defined as

$$I_{\text{ij}}\left(t\right)=\frac{1}{\ln 8}\sum _{{ss}^{\prime }}{\pi }_{\text{ij}}\left(s{s}^{\prime },t\right)\ln \frac{{\pi }_{\text{ij}}\left({ss}^{\prime },t\right)}{{\pi }_{\text{i}}\left(s\right){\pi }_{\text{j}}\left(s^{\prime }\right)},$$ (6)

from which the pairwise normalized correlation function between two residues reads

$$C_{\text{ij}}\left(t\right)=\frac{I_{\text{ij}}\left(t\right)-I_{\text{ij}}\left(\mathrm{\infty }\right)}{I_{\text{ij}}\left(0\right)-I_{\text{ij}}\left(\mathrm{\infty }\right)},$$ (7)

where I_ij(∞) and I_ij(0) are the equilibrium and the static values of the mutual information, respectively.

Results and Discussion

All analyses are based on a 15-μs molecular dynamics simulation of protein ssG at 330 K started from a fully extended conformation with the backbone dihedral angles equal to 180°. First the 750,000 snapshots (saved every 20 ps) were clustered by C_α RMSD (see the Supporting Material). From the resulting 132,006 clusters, the causal grouping procedure generated 200 mesostates (see Methods). The most populated mesostate contains 3.5% of the snapshots (Table 2) and corresponds to the native topology of protein G.

Table 2.

Properties of the 50 most populated causally grouped mesostates sorted according to statistical weight P_i

Rank∗	Pi [%]	ΔGi [kcal/mol]	ΔEi [kcal/mol]	−TΔSi [kcal/mol]	Mi1 [ns]	α-Helix [%]	β-Sheet [%]
1	3.5	−1.0	−12.4	11.4	1	25	44
49	2.7	−0.9	−4.8	3.9	11	24	41
127	2.5	−0.8	−2.5	1.7	90	64	4
147	2.1	−0.7	3.0	−3.7	95	57	5
133	1.8	−0.6	3.7	−4.3	92	51	9
128	1.8	−0.6	3.9	−4.5	90	53	8
35	1.6	−0.5	−8.8	8.3	9	26	44
186	1.6	−0.5	0.9	−1.4	101	64	3
183	1.6	−0.5	2.9	−3.4	98	53	10
16	1.6	−0.5	−4.8	4.3	4	29	38
119	1.6	−0.5	−7.9	7.4	87	55	13
182	1.5	−0.5	1.6	−2.1	98	67	3
134	1.4	−0.4	4.3	−4.7	92	52	8
153	1.3	−0.4	−0.2	−0.2	96	63	4
125	1.3	−0.4	1.6	−2.0	89	53	10
164	1.2	−0.3	−6.2	5.9	96	42	29
139	1.1	−0.3	6.6	−6.9	94	38	16
123	1.1	−0.3	1.9	−2.2	89	53	10
24	1.0	−0.2	2.2	−2.4	6	35	27
179	1.0	−0.2	0.5	−0.7	97	43	21
174	1.0	−0.2	6.1	−6.3	97	40	15
171	1.0	−0.2	7.3	−7.5	96	39	19
152	1.0	−0.2	6.7	−6.9	96	43	13
138	1.0	−0.2	6.0	−6.2	94	32	24
105	1.0	−0.2	3.3	−3.5	83	47	14
48	0.9	−0.1	−5.9	5.8	11	22	44
4	0.9	−0.1	−10.4	10.3	2	25	37
200	0.9	−0.2	−1.4	1.2	314	0	74
198	0.9	−0.1	−2.7	2.6	201	2	60
172	0.9	−0.1	7.7	−7.8	97	31	22
132	0.9	−0.1	1.2	−1.3	92	31	31
129	0.9	−0.1	2.0	−2.1	90	46	15
121	0.9	−0.1	0.0	−0.1	88	32	32
116	0.9	−0.1	2.9	−3.0	87	51	9
10	0.9	−0.1	−5.9	5.8	3	28	39
91	0.8	−0.1	4.8	−4.9	73	12	45
87	0.8	−0.0	1.8	−1.8	68	31	30
75	0.8	−0.1	8.4	−8.5	38	34	20
21	0.8	−0.1	1.9	−2.0	5	28	31
184	0.8	−0.0	0.6	−0.6	99	41	23
161	0.8	−0.1	−1.0	0.9	96	27	37
76	0.7	−0.0	4.7	−4.7	43	32	21
47	0.7	0.0	−0.5	0.5	11	25	38
29	0.7	0.0	−0.6	0.6	7	32	28
162	0.7	0.1	−6.5	6.6	96	43	26
151	0.7	0.0	3.7	−3.7	96	39	20
137	0.7	0.0	0.6	−0.6	93	26	34
124	0.7	0.1	−1.6	1.7	89	59	7
118	0.7	0.1	0.4	−0.3	87	47	16
113	0.7	0.0	7.9	−7.9	87	39	13

Average effective energy (sum of force field and SAS solvation energy) relative to the whole simulation ΔE_i = 〈E_i〉 – 〈E〉, where the 〈E_i〉 and 〈E〉 values are calculated over the snapshots in the causally grouped mesostate i and the whole trajectory, respectively. Note that, in any force field, the absolute value of the effective energy is arbitrary and only ΔE values relative to a reference state are meaningful. The free energy differences are calculated by the relation $\Delta G_{\text{i}}=-k_{\text{B}}T{\sum }_{\text{j}}{P}_{\text{j}}\ln \left(P_{\text{i}}/P_{\text{j}}\right)$. Consequently, the entropy contribution to the free energy difference, TΔS_i, is calculated using the relation −TΔS_i = ΔG_i – ΔE_i.

^∗The rank reflects the folding time M_i1 calculated by the equilibrium evolutions of the Markov chain. Structures in mesostates with rank in boldface are shown in Figs. 3 and 4.

Fast folding to a molten globule

Multiple folding and unfolding events are sampled along the 15-μs trajectory as illustrated by the time series of C_α root mean-square deviation (RMSD) from the x-ray structure (PDB code 1pgb) and the fraction of native contacts (Fig. 1). Note that the term “folding” is used here in a relaxed sense to indicate that the molten-globule state with native topology has been reached. In fact, in simulation segments where the conformation has the native topology, the C_α RMSD oscillates between 2.5 Å and 5 Å from the x-ray structure, the radius of gyration varies between 9 Å and 11 Å, and the fraction of native contacts between 0.6 and 0.9. These range of values reflect a fluidlike behavior typical of a molten globule. Such behavior emerges also from the structural overlap of the conformations in the most populated mesostate (Fig. 2 A). More quantitatively, the average value of the pairwise C_α RMSD within this mesostate is 3.5 Å. Interestingly, within the most populated mesostate the largest structural variability is observed at loops L1, L3, and L4 (Fig. 2 A), in agreement with the largest deviations between x-ray structure (19) and nuclear magnetic resonance conformers (20,21).

Figure 1.

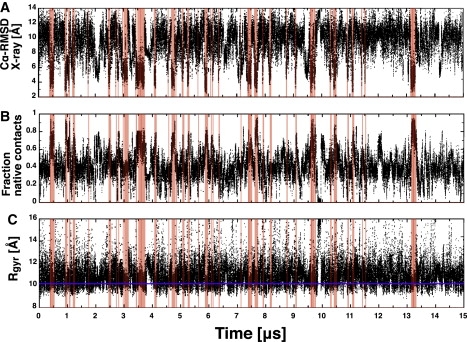
Rapid and reversible folding of protein ssG. Folding events along the time series are emphasized by pink vertical stripes. (A) Time series of the C_α RMSD from the x-ray structure (PDB code 1pgb). The two N-terminal and two C-terminal residues were excluded from the RMSD calculation. (B) Time series of the fraction of native contacts in the backbone. The native contacts were defined using the x-ray structure and considering the heavy atoms in the backbone for residues that are ≥3 distant along the sequence. A contact exists when the distance is smaller than 7 Å, which yields 422 native contacts in the x-ray structure. (C) Time series of the radius of gyration with the blue line corresponding to the native radius of gyration of protein G (R_gyr = 10.2 Å). The mean first-passage time to reach the folded mesostates, calculated on the time series, is 163 ± 157 ns (see Fig. S4).

Figure 2.

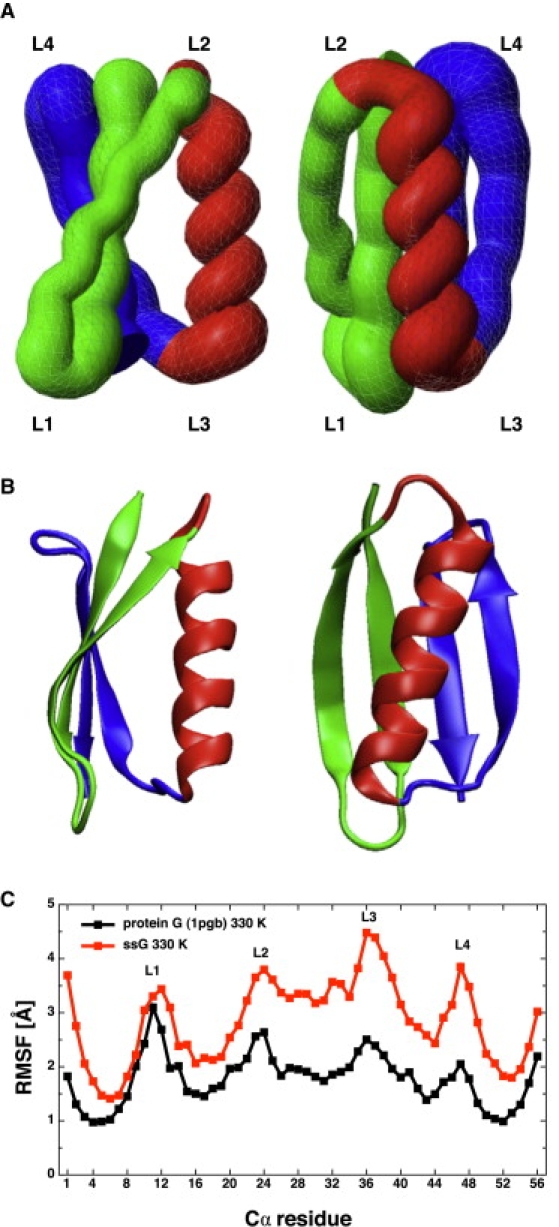
Comparison of the molten-globule state extracted from the simulations of protein ssG (A) and the x-ray structure of protein G (B). The N-terminal β-hairpin, central α-helix, and C-terminal β-hairpin are in green, red, and blue, respectively. The tubelike rendering in panel A was generated using MOLMOL (48) and 100 snapshots from the most populated mesostate. Note that the topology of protein ssG is the same as the one of the wild-type protein but the lack of long side chains and specific contacts in the former results in a flatter β-sheet and a slightly different orientation of the α-helix with respect to the β-sheet. (C) Comparison of C_α root mean-square fluctuations (RMSF). For both proteins, the RMSF values are calculated at the same temperature (330 K) and by averaging over the same number of 1-ns intervals extracted from trajectory segments during which the proteins are in the folded state (i.e., RMSD <5.0 Å from the x-ray structure and the center of the most populated mesostate for the wild-type and protein ssG, respectively).

As a basis of comparison, using the same temperature, three 1-μs simulations of the wild-type sequence started from a fully extended structure got trapped into compact nonnative conformations with a C_α RMSD from the x-ray structure ranging from 7 to 14 Å. Note also that in control simulations started from the folded state the wild-type protein is structurally stable on a 1-μs timescale. Importantly, the native structure of the wild-type protein is more rigid than the folded conformation of protein ssG, as shown by the root mean-square fluctuations (RMSF) calculated using portions of the trajectories where the system is in the folded state (Fig. 2 C). The RMSF plots show significantly larger fluctuations for the simplified-sequence variant than the wild-type except for the loop L1. That the two proteins have qualitatively similar RMSF profiles along the sequence is a consequence of the essentially identical topology of the folded state.

Heterogeneity of the unfolded state

The network representation of the 200 causal mesostates (nodes) and their transition matrix (links) illustrates the configuration space of protein ssG (Fig. 3). A semiquantitative description of the free energy basins emerges from the thickness of the links and size of the nodes, which reflect the probabilities of internode transition and node population, respectively. Moreover, the quality-threshold algorithm is used to partition the network into basins, which are emphasized by different colors in Fig. 3. Note that the network of causal mesostates is more informative than the original conformational space network (22), which depicted the dynamic connectivity but did not show quantitative information on kinetics. The basin of the folded mesostate includes also other mesostates with the secondary structure of protein G, and has a population of 21.7% (red basin in Fig. 3). Although its most populated mesostate has the correct protein G topology, it contains other mesostates with one hairpin flipped (mesostate 35 in Fig. 3). These mesostates with slightly different topology interconvert very rapidly within the most populated basin. The mesostates in the folded basin are stabilized mainly by enthalpy (see red basin in Fig. 3 and details in Table 2). In particular, the most populated mesostate has an average effective energy 12.4 kcal/mol more favorable than the effective energy averaged over the entire trajectory. The most populated basin is in fast exchange with a basin (of statistical weight of 6.3%) that contains mesostates having both hairpins flipped with respect to the native topology of protein G (mesostate 49 and green basin in Fig. 3; see also Table 2).

Figure 3.

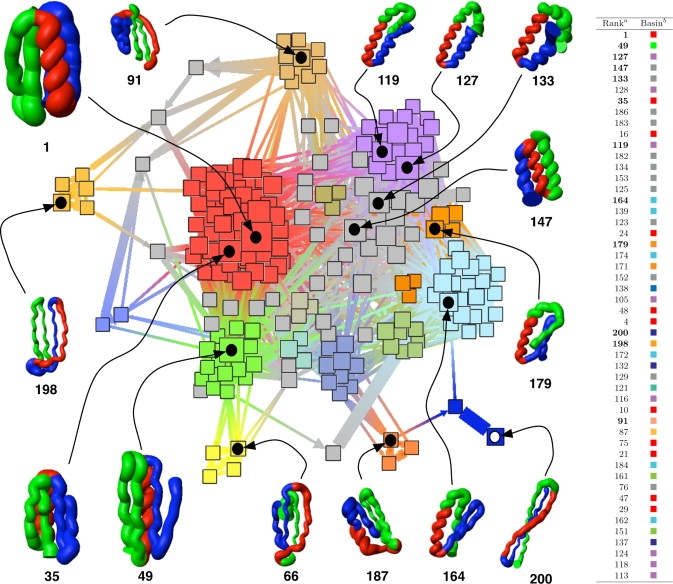
The network representation of the transition matrix. The tubelike rendering of representative conformations was generated as in Fig. 2A. The nodes are the 200 mesostates determined by causal grouping whereas the links are the transition probabilities T_ij extracted from the trajectory. The size of the nodes is proportional to their population, although the size of the links reflects the probability value in the transition matrix with a lag time of 20 ps. The position of the nodes in the network was determined by the spring-embedder visualization algorithm of the program TULIP (49), which takes into account the values of the transition matrix to optimize the node positioning in the plane. The color of the nodes is assigned according to basin's membership, which is determined by clustering the transition matrix of the 200 mesostates using the quality-threshold algorithm with a cutoff of T_ij > 0.0001. Color assignment begins from the node that has the largest number of neighbors with link value, i.e., transition probability, above the cutoff. With this procedure, 52 basins were identified and the most populated includes the folded mesostate. Of these 52 basins, 28 and 9 consist of only one and two mesostates, respectively (gray nodes). Yet, the total weight in one-mesostate and two-mesostate basins is only 18% and 9%, respectively. ^(a) The rank reflects the folding time M_i1 calculated by the equilibrium extrapolation of the Markov chain, and is the same as in Table 2. ^(b) The color of the nodes specifies the basin's membership.

The unfolded state is heterogeneous and is made up of mesostates with different relative amount of α-helical and β-sheet content (see Table 2). The three-helix bundle mesostates 133 and 147 (gray-shaded nodes in Fig. 3; see also Table 2) connect two unfolded basins with a mixture of α-helical and β-sheet content. One of these two basins has statistical weight of 10.3% (blue in Fig. 3) and includes conformations with a three-stranded β-sheet packed against a long helix (mesostate 164), whereas the other has a weight of 13.1% (purple in Fig. 3) and includes mesostates with two long helices and a short β-hairpin (mesostate 119). Notably, at the border of the network there are several mesostates with a very high β-sheet content (e.g., mesostates 66, 198, and 200 with a β-sheet content of 55%, 60%, and 74%, respectively). They can be considered off-pathway traps because the main folding transitions connect the unfolded basins consisting of conformations with mixed secondary structure content to the folded basin (see next subsection).

Folding mechanisms: kinetic accessibility of mesostates

The distribution of the first-passage times to reach the folded mesostate, calculated on the time series of 200 causally grouped mesostates, is a single exponential curve with a mean folding time of 163 ns (see Fig. S4). This apparent simplicity is in striking contrast with the complexity of the transition-matrix network (Fig. 3). As explained in Methods, the equilibrium extrapolation of the Markov chain is the matrix of MFPT values, which gives the equilibrium transition time between pairs of states. The graphical rendering of the MFPT matrix shows in a compact way the kinetic distance between all pairs of causal mesostates (Fig. 4). The band structure of the MFPT matrix provides useful information on the folding mechanism of the ssG protein. The horizontal bands are due to the fact that the MFPT matrix is a directed matrix, so that the mean time to go from a mesostate i to j is different than for the inverse transition, because the corresponding pathways are different in general. The bands give the overall kinetic accessibility of individual mesostates. There are four rather distinct kinetic regions of the conformation space. Mesostates 1–60 rapidly exchange with the folded mesostate and can be accessed from all other mesostates within 100–300 ns. Mesostates 61–104 are transient and most of them separate the folded region from the unfolded basins. In the region 105–175 are located most of the unfolded basins (α/β and only α-structures), while the fourth region, mesostates 176–200, includes the kinetic traps with high β-sheet content.

Figure 4.

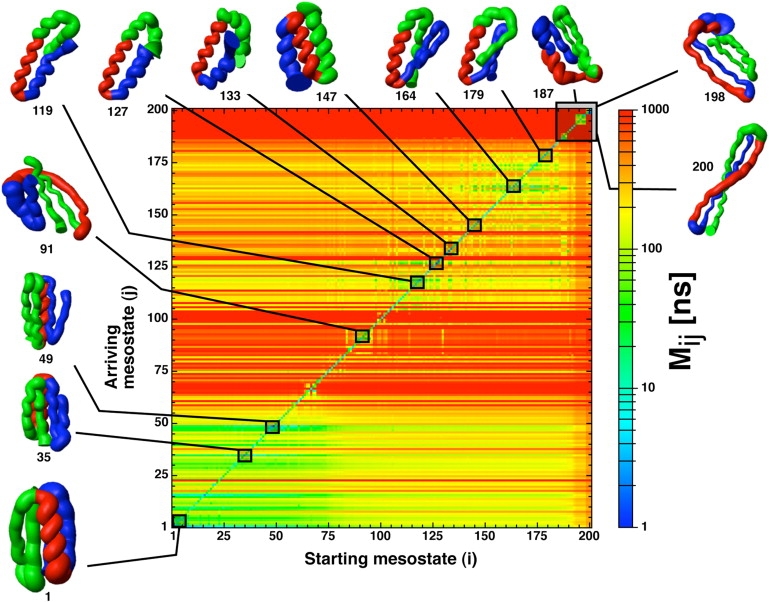
Folding kinetics illustrated by the sorted MFPT matrix M_ij of the 200 causally grouped mesostates. An element of the matrix is the MFPT for the i → j transition at equilibrium. Note that the matrix is not symmetric because each entry is an MFPT value and not a flux. The flux is the reciprocal of the MFPT value multiplied by the equilibrium probability, which yields a symmetric matrix (shown in Fig. S5). Horizontal rows are equilibrium transitions from all the mesostates i (x axis) to a specific j (y axis). The indices (i,j) are ordered from 1 (fastest relaxation to the most populated mesostate, which belongs to the molten-globule state with native topology) to 200 (slowest relaxation). The green-yellow band in the bottom indicates that the nativelike molten-globule state can be reached rapidly from all other mesostates. The conformations with high β-sheet content are kinetically most distant from the most populated mesostate. The mesostates with helical bundles and/or mixed α- and β-content interconvert rapidly.

Folding mechanisms: secondary and tertiary structure formation

The secondary structure formation is analyzed by means of pairwise correlations whose calculation is based on the mutual information between pairs of residues (see Methods). Both static and dynamic correlations are calculated for all residue pairs. The static correlation is evaluated by calculating the normalized mutual information between pairs of residues on the ensemble of strings of secondary structure observed in the simulation of ssG protein (Fig. 5). The modular pattern of the matrix suggests that the interactions responsible for the secondary structure formation are mainly taking place between the homopolymer segments of the protein. The highest correlations are observed for the local secondary structure, in particular the residues involved in the α-helix and the two native β-hairpins (correlation ≳ 20%). Long-range correlations define all possible tertiary topologies corresponding to a four-stranded β-sheet packed on a helix. These correlations are weaker than the local ones. Their averaged values are ∼4% for S1S4, ∼3% for both S1S3/S2S4, and ∼1% for S2S3. Notice that the S1S4 correlation corresponds to the β-strand arrangement as in the correct protein G topology. The long-range correlations S2-H and H-S3 are weaker than those mentioned above, and give rise to a long helix involving residues Thr¹²-Ala³⁷ or Ala²³-Thr⁴⁷, respectively. Overall, the static correlations indicate that there is a propensity of protein ssG to assume the very same secondary structure of protein G.

Figure 5.

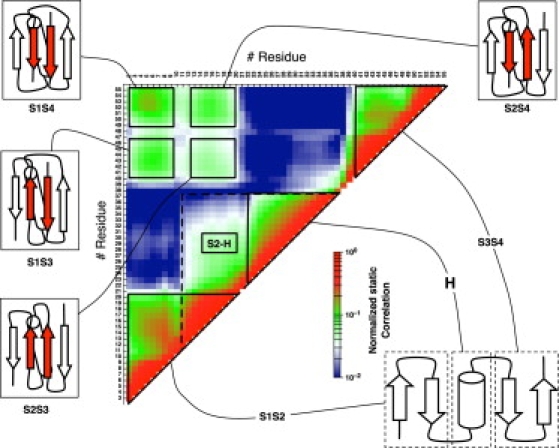
Matrix of the static correlation of secondary structure I_ij (Eq. 5). The modular pattern suggests that the interactions responsible for secondary structure formation are present between the homopolymer segments of the protein ssG. The cartoons are shown to illustrate the secondary structure elements having the highest correlations. Abbreviations: H = Ala²³–Ala³⁷ for the poly-Ala and S1 = Thr¹–Thr⁹, S2 = Thr¹²–Thr²⁰, S3 = Thr⁴⁰–Thr⁴⁷, and S4 = Thr⁵⁰–Thr⁵⁶ for the poly-Thr.

Dynamic correlations provide a mechanistic view of the sequence of events in secondary structure formation. The correlations are evaluated by calculating the mutual information between pairs of residues as a function of time and then averaging within the defined fragments (see Methods). The times at which the dynamic correlation reaches a value of 0.5 for the α-helix and the C-terminal β-hairpin S3S4 are similar (∼5 ns), whereas those for the N-terminal β-hairpin S1S2 and the parallel arrangement of S1S4 are ∼10 ns and 15 ns, respectively (Fig. 6). All other combinations of β-strands, which yield nonnative topologies, have slower correlation times, suggesting a sequence of events for folding which is compatible with a diffusion-collision mechanism (23,24). According to such a mechanism, and with the zipper model of folding (25,26), individual elements of secondary structure (the α-helix, S1S2, or S3S4) can form independently from each other. Interactions among segments that are distant along the sequence, (e.g., native S1S4, and nonnative S1S3 or S2S4) promote the formation of a complex tertiary structure by coalescence.

Figure 6.

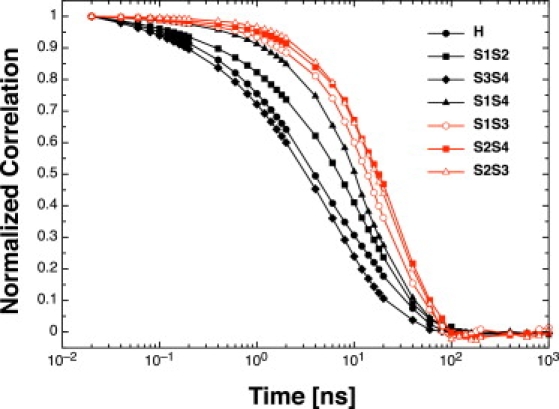
Dynamic correlation between secondary structure elements C_ij (Eq. 7). Native and nonnative elements of secondary structure are in black and red, respectively. Different timescales for secondary structure formation suggest a folding mechanism compatible with the framework model. The curve H represents the autocorrelation within the poly-Ala α-helix, while S1S2 (N-terminal β-hairpin), S3S4 (C-terminal β-hairpin), S1S4 (N/C-terminal two-stranded parallel β-sheet), as well as the nonnative arrangements S1S3, S2S4, and S2S3, reflect the association of poly-Thr β-strands.

Conclusions

We have studied the folding mechanisms of a simplified protein whose sequence consists of only three types of residues: glycine, alanine, and threonine. Molecular dynamics simulations of the simplified-sequence variant of protein G (termed ssG) provide strong evidence that a heteropolymer with a limited assortment of monomer types is able to adopt a complex topology. In fact, reversible folding to the wild-type native topology has been achieved in this work by using a force-field-based (i.e., transferable) potential. Note that structured peptides (α-helices and β-sheets) fold to the correct conformation with the very same force-field and implicit solvent model as documented in previous simulation studies (27–31). Moreover, the folding kinetics of helical peptides, and in particular deviations from single-exponential, are reproduced correctly (31).

The Markov-chain analysis of the atomistic simulations of protein ssG was used to investigate the unfolded state and folding mechanism, which is not possible by conventional experimental techniques. Three main results emerge from this analysis.

First, rapid folding is observed for a simplified-sequence variant of a protein with α/β topology. It should be emphasized that this topology is more heterogeneous than the all-β topology of wild-type and simplified variants of protein SH3 (16). The Markov-chain analysis indicates that the lack of diversity of interactions results in a free-energy landscape devoid of frustration so that conformations with significantly different content of secondary structure interconvert very rapidly. The correlation analysis for secondary structure formation suggests that the molten-globule state is reached through multiple pathways (32) and by a diffusion-collision mechanism (framework) (23–26), which is due to the strong secondary structure propensity of the helical segment and the two β-hairpins. In fact, the initial folding events are the independent formations of the local elements of secondary structure. The assembly of regular elements of secondary structure takes place by coalescence and is mainly driven by backbone-backbone hydrogen bonding. The extremely low heterogeneity of side-chain types allows the system to explore a large variety of topologies that are compatible with the secondary structure of protein G. Moreover, the molten globular character of the folded state of protein ssG and its fast folding time are likely to be a consequence of the lack of correlation between contact energies and loop closure entropies as energy landscape theory has suggested (33). When such a correlation is strong, one observes cooperative folding. The effects of the absence of such a correlation, which in protein ssG is a consequence of the lack of energy heterogeneity due to the reduced amino-acid alphabet, has been experimentally reported on protein S6 through circular sequence permutations (33,34). There, the sequence permutation resulted in faster folding and less rigid native structure, which is also observed here for protein ssG.

Second, the folded state of the protein ssG is much more flexible than that of the wild-type protein G. Therefore, reduced alphabets of amino acids seem to be suitable to define globular folds with abundant secondary structure elements, but they do not encode for the specificity of tertiary contacts required for a native, i.e., functional, structure. However, low complexity alphabets of amino acids have been shown by recent experimental works to be suitable for molten globular active enzymes (35,36). Furthermore, simplified sequences of a three-helix bundle fold (protein G_A88) and an α/β fold (protein G_B88, which is the very same domain of protein G used in our simulations) with 88% sequence identity were shown to possess different structure and function (37). Therefore, the information determining the fold seems to be “highly concentrated in a few amino acids” (37), i.e., only 7 of 56, and very recent results by the same authors indicate only 3 of 56 (38). Our simulation results, in particular the variety of topologies observed for protein ssG (which include the folds of both protein G_A88 and G_B88), provide the following explanation of the experimental findings: It is likely that both folds are populated by both G_A88 and G_B88, but only one fold, the statistically predominant one, is observed in the ensemble experiments. Moreover, the relative statistical weight can be easily shifted toward a particular fold by changing only a small subset of the residues.

Third, despite the reduced diversity in the interactions, the denatured state is heterogeneous, as it consists of structures with a secondary structure content ranging from fully α-helical to fully β-sheet. The latter are kinetic traps and might promote aggregation. Interestingly, Langevin dynamics simulations with a coarse-grained model of an amphipathic polypeptide indicate that a minor increase (≤1 kcal/mol) in relative stability of a β-aggregation prone state can result in a dramatic acceleration of fibril formation rates (39,40). On the experimental side, protein G (more precisely the same domain of protein G as in this study) was shown to form amyloid fibrils under mild denaturation conditions (41). Furthermore, several double mutants with reduced thermodynamic stability were observed to aggregate with high reproducibility in the same study. In other words, by controlling the stability of the protein, through mutations or variation of the experimental conditions, it was possible to modulate the ability to form fibrils. Notably, the key requirement for fibril formation was to choose conditions in which the population of intermediate states present during the unfolding transition was maximized. Furthermore, by comparing mutations at different strands of protein G, the same authors have provided evidence that the overall stability of protein G is the key determinant for amyloid formation and not the specific location of destabilizing mutations (42).

On the basis of the experimental data on protein G amyloid-fibril formation and our simulation results, we suggest that the enrichment of a primordial (i.e., reduced) alphabet of residues has been directed by evolution toward a double purpose: the optimization of protein function (which in most cases requires a stable folded structure) and at the same time the elimination of nonnative conformations that are aggregation-prone by means of frustration and competing interactions. Dramatically reduced alphabets of amino acids seem to be suitable to define elementary folds but they do not encode the sufficient complexity such that both these optimization prescriptions can be achieved by evolution. It is important to underline that our simulation study, per se, does not shed light on the effects of evolution, as only one simplified sequence was investigated. Moreover, it is not (yet) possible to simulate the reversible folding of the wild-type sequence of protein G with an atomistic and transferable force field. To try to emulate evolution, we plan to run implicit solvent (43) simulations of the reversible folding of simplified-sequence variants of protein G consisting of amino-acid alphabets of increasing complexity, i.e., from low to an intermediate number of side-chain types. Remarkably, in a recent experimental study, a simplified sequence was shown to fold into a molten-globule conformation (four-α-helical bundle), and later mutated to an O₂ transport protein with well-defined native structure by gradually increasing the diversity of amino-acid types from 3 (Glu, Lys, and Leu) to 14 (44).

We conclude by quoting from an article by F. Crick of 41 years ago (45):

“It certainly seems unlikely that all the present amino acids were easily available at the time the code started. Certainly tryptophan and methionine look like later additions. Exactly which amino acids were then common is not yet clear, though most lists would include glycine, alanine, serine, and aspartic acid.”

The simplified three-letter alphabet used in this simulation study included two of these four residues, plus threonine (which is similar to serine). Furthermore, glycine and alanine were first observed (together with aspartic acid) in the remarkable experiment of Miller (46) on the amino-acid synthesis under primitive conditions.