Abstract
We propose a mechanism for the formation of membrane oscillations and traveling waves, which arise due to the coupling between the actin cytoskeleton and the calcium flux through the membrane. In our model, the fluid cell membrane has a mobile but constant population of proteins with a convex spontaneous curvature, which act as nucleators of actin polymerization and adhesion. Such a continuum model couples the forces of cell-substrate adhesion, actin polymerization, membrane curvature, and the flux of calcium through the membrane. Linear stability analysis shows that sufficiently strong coupling among the calcium, membrane, and protein dynamics may induce robust traveling waves on the membrane. This result was checked for a reduced feedback scheme and is compared to the results without the effects of calcium, where permanent phase separation without waves or oscillations is obtained. The model results are compared to the published observations of calcium waves in cell membranes, and a number of testable predictions are proposed.
Introduction
Cell membranes support a variety of wavelike and oscillatory phenomena that involve shape deformations, cytoskeleton activity, ion currents, and adhesion. In this article, we wish to concentrate on membranal waves and shape oscillations that are associated with fluctuations in the cellular concentration of calcium ions Ca2+. Such calcium waves are observed in different cell types, for example in migrating cells (1–3), fertilized egg cells (4), and cells undergoing phagocytosis (1,5). Some of these waves are observed to propagate along the cell membrane at velocities of 10–100 μm/s, which is much faster than the membrane waves observed recently in the lamellipodia of motile cells (6–10) with typical velocity of 0.1–0.3 μm/s. The fast type of calcium waves are most likely due to voltage-gated channels, do not involve the slow dynamics of the membrane shape and cytoskeleton rearrangement, and are not the subject of this article. The slower type of membrane waves do involve membrane shape oscillations and the cytoskeleton, and were recently shown to involve calcium influx into the cell (3,11,12) (they are furthermore independent of the activity of voltage-gated calcium channels). Calcium and shape oscillations appear also in dendritic spines, where large calcium influxes inhibit the observed motion (13–16). The typical shape oscillation period of the dendritic spines is ∼1–100 s, and they have been shown to depend on the activity of actin polymerization.
There are several models that couple calcium ion channels, pumps, local ion concentration (transmembrane potential), and chemical reactions, which give rise to a wide spectrum of dynamical behaviors including propagating waves and oscillations of calcium in cellular membranes (for example, (17,18)). These models apply to the fast type of calcium-membrane waves, and do not include the dynamics of the cytoskeleton or membrane shape. The slower type of calcium-membrane waves involve the dynamics of the shape fluctuations of the membrane and the forces induced by the cytoskeleton. Recent models that couple these degrees of freedom with the calcium influx (12,19) demonstrated the role played by the contractile forces of the actin-myosin cytoskeleton. Here we investigate the dynamics of the coupled membrane-cytoskeleton-calcium system where the protrusive forces of actin polymerization are dominant, rather than contractile forces due to myosin motors. Systems where the protrusive force of actin polymerization is dominant in determining the local membrane shape are actin-driven cellular protrusions such as lamellipodia and filopodia. We will base our treatment on our previous models that coupled the cytoskeleton to the membrane (20,21); in these models, membranal clusters that induce actin polymerization exert a protrusive force on the membrane, serve as adhesion anchors for the protrusions, and are affected themselves by the membrane shape through their own spontaneous curvature. Such a model was shown to give rise to instabilities, phase separation, or damped waves, depending on the sign of the spontaneous curvature and the parameters of the model. It therefore describes spontaneous shape and phase transitions in the cell membrane-cortical cytoskeleton, such as membrane protrusions (microvilli, filopodia, etc.), and the associated segregation of membrane components. Without coupling to the calcium, these models describe permanent phase separation (Turing instability), which does not show any wave-instability (i.e., robust waves). Recent works provide further experimental support for this model, by demonstrating the role played by curved membrane proteins in the recruitment of cortical actin filaments during the formation of membrane protrusions (22–25).
The effects of the concentration of calcium ions Ca2+ on the actin cytoskeleton and adhesion are numerous, and mostly inhibitory:
-
1.
Increased calcium promotes the binding of actin-severing and capping proteins such as Villin (26) and Gelsolin (16,27), thereby reducing the level of actin polymerization and the resulting protrusive force acting on the membrane (15,28).
-
2.
Calcium ions induce conformational relaxation of integrins (11,29,30), reducing the cell adhesion to the external substrate.
On the other hand, the cytoskeletal and adhesion forces applied to the membrane, as well as the aggregation of membrane proteins, can induce an increase in the calcium concentration in the cell, by
-
1.
Deforming the membrane and activating stretch-activated channels (SACs) (30), thereby increasing the calcium influx into the cell, and
-
2.
By inhibiting the activity of plasma membrane calcium pumps (31) or directly inducing the opening of calcium channels (32), thereby decreasing the outflux and increasing the influx.
There are recent experimental works (33) that demonstrate the ability of forces applied to the membrane to induce an influx of calcium ions, which result in a remodeling of the cortical actin network. Note that the influx of calcium and its release from internal stores in response to mechanical stimulation (33) is also regulated by the release of adenosine triphosphate (ATP) from the cell and the resulting activation of purinergic receptors. This ATP-calcium pathway is also responsible for the well-documented calcium waves that propagate in cultures of glia and astrocyte cells (34,35), where the roles of the actin cytoskeleton, myosin, and adhesion were also established. We also mention that calcium ions have an impact on many cellular components, and may also induce an increase in the actin cytoskeleton activity under certain conditions (36). Furthermore, the actin filaments have a variety of direct and indirect interactions with many ion channels and pumps (37).
The complete set of interactions among the cytoskeleton, ion channels, and calcium is far too complex to capture in a single model, and our simple model only demonstrates the principles that allow this system to support oscillatory behavior. We conclude that there are several existing pathways that give rise to a negative feedback loop among the local protrusive forces of actin, the concentration of membrane proteins, and the influx of calcium ions. A negative feedback loop represents a basic ingredient for driving the wave and oscillatory phenomena, which we calculate below (Fig. 1).
Figure 1.
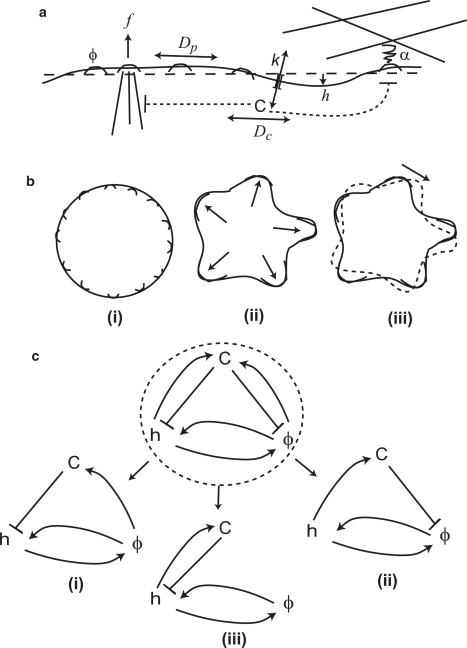
(a) Scheme of our model; one-dimensional flat membrane with local height deviation h and a concentration of membrane proteins (MP) ϕ that diffuse with coefficient Dp and activate actin polymerization of protrusive force , and adhesion to external substrate α. The local calcium concentration C depends on the influx through channels and outflux through pumps, diffuses with coefficient Dc and inhibits the actin-driven force and adhesion (dashed lines). (b) The stable system (i) is uniform and mixed, whereas the Turing instability (ii) leads to stationary phase separation, and the wave-instability (iii) leads to oscillatory or propagating domains. (c) The overall feedbacks and coupling of our model (Eqs. 2–4) and the simpler subcases (i–iii) that give rise to wave instability.
The detailed study of the model without the calcium was given in the literature (20,21). For completeness, we mention here the key results:
-
1.
Increasing actin force can induce phase separation at a higher transition temperature compared to thermodynamic equilibrium (38). Adhesion of the cell to the external substrate acts in the same manner.
-
2.
Increasing the adhesion strength can drive the phase separation transition at lower actin force, and vice-versa.
-
3.
Increasing membrane tension acts to lower the transition temperature, and raise the values of actin force and adhesion needed to induce phase separation.
These results are in qualitative agreement with observation on actin-driven cellular protrusions. In this article, we build on the understanding of these simpler models to tackle the added complexity of the calcium.
In Model and Linear-Stability Analysis, we give the equations of our model, where we expand our previous models of the coupled membrane-cytoskeleton (20,21) by introducing a third component that represents the local cellular calcium concentration close to the membrane. We then perform a linear-stability analysis of the model, which allows us to map the conditions that give rise to wave-instability. Although the models without the calcium produced instabilities that correspond to phase-separated domains that do not propagate, the addition of calcium can cause these domains to oscillate and propagate as waves. Readers not interested in the mathematical derivations can skip Model and Linear-Stability Analysis. The resulting phase diagrams, which capture the behavior as a function of the various physical parameters of the model, are described in Phase-Diagrams for the Coupled Membrane-Actin-Calcium System. In Discussion and Conclusion, we compare the results of our model to observations of calcium-driven oscillations observed in cells, and conclude with future directions.
Model and Linear-Stability Analysis
Coupled membrane-actin with calcium
For simplicity, we shall develop our model within the assumptions of a flat, infinite fluid membrane, which contains a conserved amount of membrane protein clusters (MP) (21). We denote the local normalized concentration of MP by and the local normal displacement of the membrane by . The MP in our model represent protein clusters that promote both the polymerization of actin filaments at the membrane, and the formation of adhesion to the external substrate (Fig. 1 a). The normalized concentration, or area-coverage, is defined as , where is the local concentration and nsat is the saturation value of the concentration of MP (21).
Furthermore, we assume that the temperature T affects only the entropy. This assumption holds only near the homeostatic balance of the cell, which is the regime we are considering. We incorporate into our model the active forces exerted due to the MP on the membrane by extra terms in the free energy (adhesion) and the equation of motion (actin polymerization force) (21). We will include the effects of calcium that we listed above into our model as reaction terms in the equations of motion for , , and (the local cellular calcium concentration close to the membrane at position ).
The free energy expression (at temperature T) of the membrane in our model is (21)
| (1) |
where the first term in Eq. 1 stands for the surface tension (σ) and the cell-substrate adhesion expressed as a negative surface tension (α); the second term accounts for the curvature bending energy with modulus κ, where the MP have a spontaneous curvature radius of R, which is assumed to be close to the characteristic correlation length of the membrane, (39); the third term gives the entropy of the MP (within the Ginzburg-Landau approximation); the fourth term stands for the aggregation potential of the MP (J) (40); and the last term is the line tension of the MP aggregate (40). The typical size of the MP is given by its length scale ɛ. The ratio ɛ/R appears to be the natural small parameter of the model, as will be explained below.
The dynamical equations for h and ϕ are derived from the free energy (through its variational derivatives), and include the protrusive actin force (proportional to the MP concentration, ϕ) and the effects of Ca2+ expressed by standard reaction terms, coupling between h, ϕ, and C. The dynamical equations are therefore (similar to (21))
| (2) |
| (3) |
| (4) |
where ϕ0 and C0 are the equilibrium concentrations and Dp and Dc the diffusion coefficients of MP and Ca2+, respectively. The effective viscosity of the cell and surrounding fluid is given by η. In the following, we shall assume ϕ0 = 1/2. This value is arbitrary, and the system can be expanded around any protein density. We choose a protein area coverage that is far from the extreme cases of 0 or 1. The reference temperature, T0, was chosen to be the point where the entropy of MP is equal to their aggregation energy, i.e., T0 = J/4 (21). In fact, our model implies that T0 lies in the physiologically relevant range, since the temperature variation considered is ∼10% at ∼T0. T0 turns out to be the critical temperature for phase separation in a passive system, i.e., without actin and calcium. In our model, however, we expect to find various kinds of phase separations both below and above T0.
The actin protrusive force term in Eq. 2 is postulated to be proportional to the local concentration of MP, with coefficient f (20,21), which is inhibited by the effect of calcium (15,16,26) (with coefficient β); the last term in this equation accounts for the osmotic pressure at the equilibrium concentration. The inhibition of adhesion by calcium (29) is described by the second term of Eq. 3 (with coefficient ζ).
The first term of the calcium dynamics in Eq. 4 describes the balance between the inward current through channels and the outward pumping (41) (with coefficient k); the second term is the diffusion term of calcium ions, with coefficient Dc; the third term stands for the effect of reduction outward pumping of the Ca2+ due to the local concentration of MP (31), or increasing influx due to opening of calcium channels (32) (with coefficient γ); and the last term describes the increased influx due to the opening of SACs by the local membrane curvature (30) (with coefficient ξ). Note that in our previous model (21) we demonstrated that the actin polymerization drives the aggregation of MP, so the inhibition of calcium pumps (31) or activation of calcium channels (33) due to high concentration of MP, introduces in our scheme a direct negative feedback mechanism (Fig. 1 c (i)). It is assumed here that protrusions that stretch the membrane outwards induce an influx, proportional to the external calcium concentration Cext (which is usually much larger than C0, see Appendix A in the Supporting Material). To simplify our model we assume here that the calcium channels and pumps are uniformly distributed over the cell membrane. The derivation of Eq. 4 and calculation of the dependence of the equilibrium intracellular calcium concentration, C0, on the variable extracellular value, Cext, are given in detail in Appendix A in the Supporting Material.
Linear-stability analysis
For the sake of simplicity, the following analysis will be one-dimensional, and the variables will therefore become functions of x and t only. We now transform the equations into dimensionless units; we set the radius of spontaneous curvature, R, to be the unit length; the typical time of diffusion of MP over the area of R2, τ, to be the unit time; and the reference temperature, T0, to be the unit energy kBT (hereafter, we omit the Boltzmann constant kB). The numerical values of all of the constant parameters of our model appear in Table 1. Thus, all the numerical parameters of the model can be expressed in a dimensionless form by means of R, τ, and T0. We perform the standard linear stability analysis on the system of equations given in Eqs. 2–4, by assuming an expansion of the variables around their initial (equilibrium) values to first order: h(x, t) = h0 + δh(x, t), ϕ(x, t) = ϕ0 + δϕ(x, t), and C(x, t) = C0 + δC(x, t). We next perform a spatial Fourier transform, and get the linearized system
| (5) |
where , (see Appendix A in the Supporting Material), and two new parameters are defined (21) as
| (6) |
The parameter Σ shows the competition between the positive surface tension, σ, and the average adhesion of the membrane, α, and can be regarded to as the effective surface tension; whereas μ shows the competition between the entropy (proportional to T), and the aggregation interactions of the MP, with J = 4 T0, and can be regarded to as the generalized temperature.
Table 1.
The numerical values of the model parameters
| Parameter | Value in SI units | In model units | Reference |
|---|---|---|---|
| R | 50 nm | 1 | |
| ɛ | 2 nm | 0.04 R | Estimation |
| τ | 2.5 ms | 1 | From Dp |
| T0 | ≈300 K | 1 | By definition |
| k | 0.01 s−1 | 2.5 × 10−5τ−1 | (12) |
| fmax | 2 nN/μm2 | 62.5 T0/R3 | (55) |
| C0T | 0.1 μM | 6 × 10−5R−3 | (12) |
| Cext T | 2 mM | 1.2 R−3 | (12) |
| κ | 8 × 10−20 J | 20 T0 | (56) |
| σ | 30 pN/μm | 18.75 T0/R2 | (57) |
| Dp | 1 μm2/s | 1 R2/τ | (20) |
| Dc | 0.2 μm2/s | 0.2 R2/τ | (12) |
| η | 100 g/m s | 1.25 Tτ/R3 | (20) |
Starting from the equilibrium state of ϕ = ϕ0 = 1/2, C = C0, we look for instabilities that indicate a phase transition of the calcium-membrane-cytoskeleton system, either to an oscillatory pattern or a stationary phase separation (42,43) (Fig. 1 b). For the system to become unstable, at least one of the eigenvalues, ω, of L in Eq. 5 should possess a positive real part (Turing instability), whereas a nonzero imaginary part yields a wave instability. As shown in Fig. 1 c, our general model contains three subcases that give rise to a wave instability:
-
Subcase 1.
Through the direct calcium-induced inhibition of actin polymerization (β) and reduction of outward calcium pumping due to membrane protein concentration (γ), or
-
Subcase 2.
The calcium-induced inhibition of the activity of the MP (ζ), and the bending activation of SACs (ξ), or
-
Subcase 3.
The direct calcium-induced inhibition of actin polymerization (β) and the bending activation of SACs (ξ).
In the following, we will describe in detail only the first subcase 1, and consequently neglect the two other coupling effects, taking ζ = ξ = 0. Note that subcase 1 is similar in its feedback couplings to the myosin-driven wave instability described in Shlomovitz and Gov (10). Subcase 2 is expected to yield results similar to those of subcase 1, due to the similarity of their schemes; this subcase turned out to be more complicated to handle, therefore it was left out of this work. On the contrary, subcase 3 yields indeed a different behavior, and below, it is briefly described.
It should be noted that using the above formulation, the three parameters related to Ca2+: β, γ, and C0, usually appear when they are multiplied together. We therefore introduce a control parameter B ≡ βγC0, which can be regarded to as the generalized control parameter of calcium activation.
The system described by Eq. 5 is of rank 3. The stability analysis of such a system is described in detail in Appendix B in the Supporting Material, and for our particular system the results are summarized in Appendix C in the Supporting Material.
Different stability behaviors
In general, we get four possible types of dynamic behaviors: two types of Turing instabilities and two types of the wave instability. They are described in Fig. 2:
-
1.
The first one (Fig. 2 a) is the type-I Turing instability. This is a typical long-wavenumber instability: it starts at zero wavevector and ends at some q = qp. In the long time limit, the zero mode can become dominant, and in a living cell this should cause cellular polarization (21).
-
2.
The traveling-wave instability (Fig. 2 b) may be seen as the complex extension of the type-I Turing: the real parts of the growth rates ω1, 2 exhibit type-I instability (while ω1 is the dominant), but at small wavevectors, the imaginary parts (Fig. 2 d) of ω1, 2 are nonzero (and conjugate), while their real parts (Fig. 2 c) are positive, hence yielding the traveling wave behavior.
-
3.
For q > qw, the system is expected to exhibit the behavior of type-II Turing instability (Fig. 2 e). This is a short-wavenumber instability, which exists for some range of modes, qn < q < qp, while the zero mode remains stable. In some cases, the most unstable mode q∗ can remain dominant for a long time, and cause a star-shaped cell (21) (Fig. 1 b (ii)). However, the results of linear stability analysis, both for the long-wavenumber and short-wavenumber patterns, cannot uniquely define the long-time dynamics. It can be deduced only from a solution of the full, nonlinear model.
-
4.
The fourth type is the damped wave (Fig. 2 f): the real part of the growth rate ω1 exhibits type-II instability (while ω2 is always negative, hence stable); at small modes, the imaginary parts (Fig. 2 h) of ω1, 2 are nonzero while their real parts (Fig. 2 g) are both negative, hence yielding the damped wave behavior; for q > qn, the system is expected to behave like type-II instability.
Figure 2.
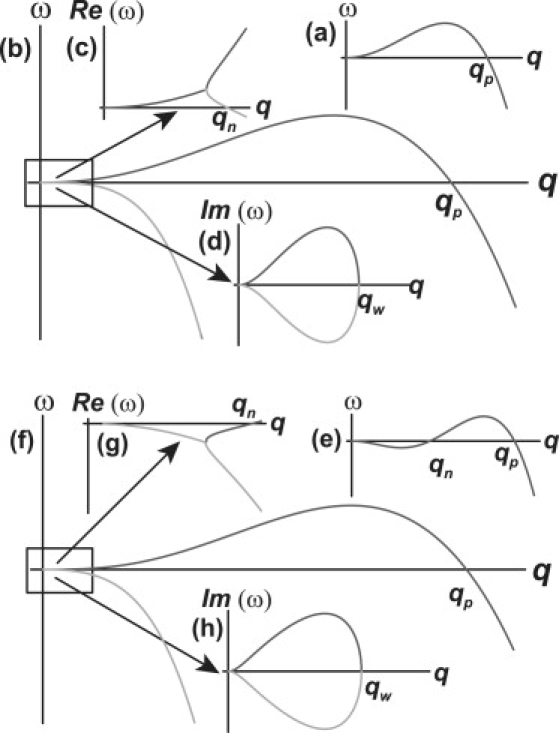
Illustrations of the instability patterns in our model: (a) the type-I Turing: the instability starts at zero mode and ends at some q = qp; for a long time, the zero mode is expected to be dominant; in a living cell, this should cause polarization. (b) Traveling wave: the real parts of the growth rates ω1, 2 exhibit type-I instability (while ω1 is the dominant), but at small modes, the imaginary parts (d) of ω1, 2 are nonzero (and conjugate), while their real parts (c) are positive, hence yielding the traveling wave behavior; for q > qw, the system is expected to exhibit the behavior of type-II instability (d). (e) The type-II Turing: the instability exists for some range of modes, qn < q < qp; as the zero mode remains stable, the most unstable mode q∗ should become dominant for a long time, and bring to a starlike shape of a cell. (f) Damped wave: the real part of the growth rate ω1 exhibits type-II instability (while ω2 is always negative, hence stable); at small modes, the imaginary parts (h) of ω1, 2 are nonzero while their real parts (g) are both negative, hence yielding the damped wave behavior; for q > qn, the system is expected to behave like type-II instability.
We now briefly describe the behavior of subcase 3 (Fig. 1 c). In this case, we could not find wave instability behavior for any values of the control parameters. The real parts of the two eigenvalues which represent oscillatory behavior (i.e., have imaginary parts) are always negative, thus they are stable (damped waves). An instability and phase separation is still possible through the third eigenvalue, which can have a positive real part in some range of wavevectors. However, it does not have an imaginary part in this range, and therefore, subcase 3 can give rise only to Type-I or Type-II phase separation, but not to oscillatory (or traveling wave) behavior.
Phase-Diagrams for the Coupled Membrane-Actin-Calcium System
In this section, we explain the different regimes (i.e., phases) of phase separation obtained from our model (scheme i of Fig. 1 c), and also describe the measurable predictions of the maximum oscillation frequency (standing-waves solution) and the group wave velocity (an estimation is given in Eq. S14 in the Supporting Material). The phase separations are indicated through the use of the linear stability analysis, whereby instability of a certain type (see Different Stability Behaviors) yields an appropriate type of phase separation. Namely, the Turing instability, which occurs when all the eigenvalues, ω, are real, and at least one of them becomes positive, leads to the permanent phase separation of the MP, together with the Ca2+ concentration and the formation of membrane protrusions; whereas the wave instability, which occurs when the imaginary parts of the two complex-conjugated eigenvalues become nonzero, leads to the appearance of either oscillatory or propagating (not necessarily cyclic) patterns of the phase separation. The critical conditions for these different types of instabilities to occur are calculated in Linear Stability Analysis.
It must be emphasized that the linear stability analysis can only give indications on the tendency of the system to spontaneously initiate the formation of nonuniform patterns (static or oscillatory). The later time evolution of these structures involves the nonlinear terms in Eqs. 2–4, and is therefore beyond the linear analysis presented here.
To make later comparisons with experiments, we turn back to the physical parameters T, σ, and α, rather than the model parameters μ and Σ, by substituting from Eq. 6. In all the following graphs, we take ɛ, κ, k, σ, Dp, Dc, and η to be as in Table 1. The rate of pumping the calcium out of the cell kout is typically 100 times slower than the rate of calcium influx (kin), as measured in Matthews et al. (44), and given by the value of k in Table 1. The control parameters of our model are: the temperature T, the cell-substrate adhesion strength α, the effective actin protrusive force , and the effective calcium activity coefficient B. Note that since , changing the overall level of intracellular calcium βC0 changes both B and , whereas changing either f or γ (the inhibition of outward calcium pumping) induces independent changes in and B, respectively.
The transitions lines that we plot in Figs. 3 and 4 are the following:
-
1.
Black line: The boundary between the regions of traveling waves and damped waves is given by Eq. S11 in the Supporting Material, giving the critical temperature Tw and adhesion αw along this transition line.
-
2.
Dashed line: Oscillatory behavior appears at the critical line determined by the roots of Eq. S10 in the Supporting Material.
-
3.
Dotted line: The critical temperature Tcr, actin force , or adhesion strength αcr above (or below) which the system remains stable (with a very weak dependence on the calcium activation parameter B), is given by the roots of Eq. S7 in the Supporting Material.
-
4.
Gray line: The transition between Type-I and Type-II instability (Fig. 2) occurs along the line given by the roots of Eq. S9 in the Supporting Material.
Figure 3.
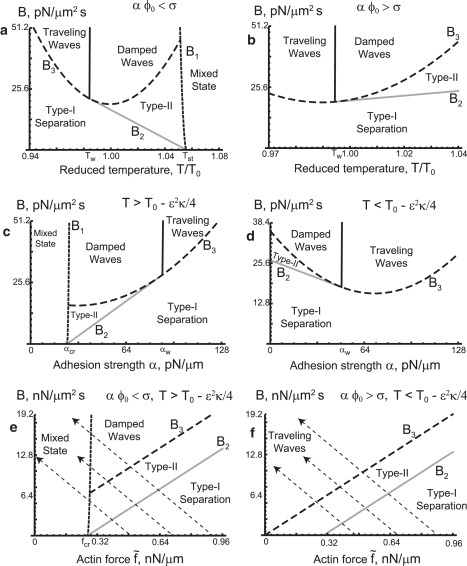
The phase diagram of our model, on the planes of B, versus the other control parameters, as follows. (a) The diagram on the plane of B versus T, with and α = 48 pN/μm < σ/ϕ0, i.e., adhesion weaker (on average) than the surface tension; Tcr can be considered a good approximation to the critical value of the phase separation even for nonzero B. (b) The same diagram, but this time for α = 64 pN/μm > σ/ϕ0, i.e., adhesion stronger (on average) than the surface tension, so the phase separation occurs for each temperature. (c) Phase diagram on the plane of B versus α, with and T = 1.01 T0 > T0 − ɛ2κ/4, i.e., μ > 0; here, again, there is a region of the mixed state, approximately for α < αcr. (d) Phase diagram on the plane of B versus α, for T = 0.985 T0 < T0 − ɛ2κ/4, i.e., μ < 0; for this temperature, there is always a phase separation. (e) Phase diagram on the plane of B versus , with α = 48 nN/μm and T = 1.01 T0; only damped waves can exist for these values, and there is also a mixed state for . (f) Phase diagram on the plane of B versus , with α = 80 nN/μm and T = 0.98 T0; only traveling waves can exist for these values, and there is phase separation for all . In both panels e and f, the dashed arrows indicate trajectories of the system when βC0 is increased, affecting both B and .
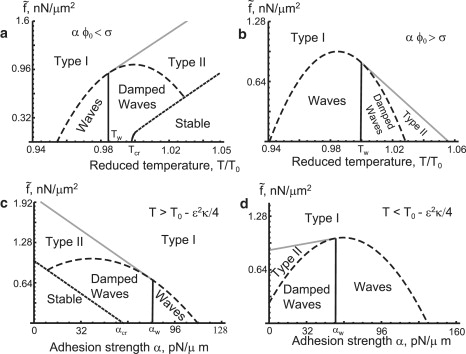
Figure 4.
(a) The phase diagram of our model, on the plane of versus T, with B = 20.48 pN/μm2 s and α = 48 pN/μm < σ/ϕ0, i.e., adhesion weaker (on average) than the surface tension, so a mixed state exists. (b) The same diagram, but with α = 72 pN/μm > σ/ϕ0 and B = 19.2 pN/μm2 s, i.e., adhesion stronger (on average) than the surface tension, hence there is a phase separation for all T. (c) Phase diagram on the plane of versus the adhesion strength α, with B = 20.48 pN/μm2 s and T = 1.005 > T0 − ɛ2κ/4, a mixed state exists. (d) The same diagram, but with B = 20.48 pN/μm2 s and T = 0.99 < T0 − ɛ2κ/4, the phases separate for each α. In panels a–d, the term “Waves” indicate waves-instability (propagating waves).
In Figs. 3 and 4 we plot the phase diagrams of our model. Fig. 3 shows the phase diagram of our model, on the planes of B, versus the other control parameters (temperature, actin force, and adhesion), as follows.
Fig. 3 a: Phase diagram on the plane of B versus T, with and α = 48 pN/μm < σ/ϕ0, i.e., adhesion weaker (on average) than the surface tension; the line B1(T), which shows the largest temperature of phase separation for different B, is very steep in the relevant range of B, and therefore Tcr can be considered a good approximation to the critical value of the phase separation even for nonzero B.
Fig. 3 b: Same as Fig. 3 a, but for α = 64 pN/μm > σ/ϕ0, i.e., adhesion stronger (on average) than the surface tension, so the phase separation occurs for each temperature.
Fig. 3 c: Phase diagram on the plane of B versus α, with and T = 1.01 T0 > T0 − ɛ2κ/4, i.e., μ > 0; here, again, there is a region of the mixed state, approximately for α < αcr.
Fig. 3 d: Phase diagram on the plane of B versus α, for T = 0.985 T0 < T0 − ɛ2κ/4, i.e., μ < 0; for this temperature, there is always a phase separation.
Fig. 3 e: Phase diagram on the plane of B versus , with α = 48 pN/μm and T = 1.01 T0. We find that only damped waves can exist for these values, and there is also a mixed state for .
Fig. 3 f: Phase diagram on the plane of B versus , with α = 80 pN/μm and T = 0.98 T0. Here we find that only traveling waves can exist for these values, and there is phase separation for all . Note that when one increases the parameter βC0, both B and change, and the system moves along the trajectories indicated by the diagonal dashed arrows.
In Fig. 4, we plot the phase diagram in the versus T (panels a and b) and versus α (panels c and d). These phase diagrams should be compared to those we obtained in the absence of the calcium-induced negative feedback (21), where the regions of oscillations and waves were absent. Both the actin force and the adhesion are parameters that the cell can control internally, and in response to the external conditions (type of substrate, etc.).
For Fig. 4 a and b, increasing actin force raises the phase-separation temperature (38), whereas waves exist only for low values of actin force, and near the thermodynamic critical temperature T0.
For Fig. 4, c and d, we find that: 1), large actin force leads to vanishing oscillations and full cell polarization; and 2), the oscillations have a reentrant dependence on the adhesion, whereby strong adhesion leads to the vanishing of the oscillations and full cell polarization, but too weak adhesion leads to damped oscillations and a uniform cell. Intermediate values of the adhesion can allow the formation of robust waves.
Fig. 5 describes the oscillatory and wave behavior of our model, for different adhesion strength α, actin force , and effective calcium activity constant B. We plot the wavevector qmax of the mode with the maximum frequency of oscillations ωmax = Im(ω(qmax)) (Eqs. S12 and S13 in the Supporting Material). We also plot the mean group velocity of the wave, 〈Vg〉, using Eq. S14 in the Supporting Material. Physically, at the wavevector qmax there is a maximum in Im(ω(qmax)), which corresponds to an oscillating standing wave mode.
Figure 5.
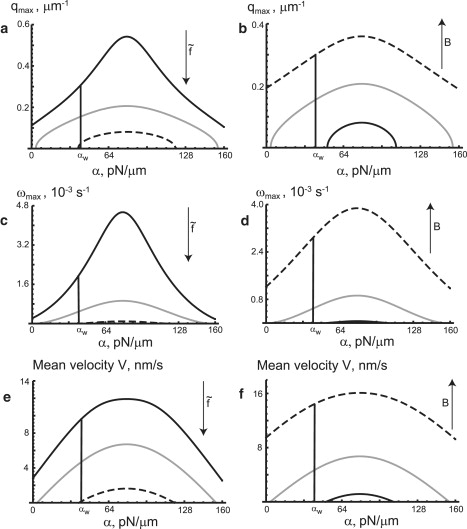
The oscillatory and wave behavior of our model, for different adhesion strength α, actin force , and effective calcium activity constant B. The regions of α > αw and α < αw correspond to wave-instability and damped waves, respectively. (a) The graph of the mode of the maximum wave frequency, qmax, versus α for different values of , as follows. (b) The graph of qmax versus α, but this time for different values of B. (c) The graph of the maximum frequency itself, Im(ω(qmax)), versus α, for different values of . (d) The graph of Im(ω(qmax)) versus α, for different values of B. Physically, qmax and Im(ω(qmax)) yield the oscillating (standing wave) mode and frequency of the system. The graphs of mean group velocity of the wave, 〈Vg〉, versus α, is shown in panel e (for different values of ) and in panel f (for different values of B). T = 0.98 T0 for all the graphs. In panels a, c, and e, B = 38.4 pN/μm2 s and the values of are: 0.16 nN/μm2 (black lines), 0.8 nN/μm2 (gray lines), and 1.6 nN/μm2 (dashed lines). In panels b, d, and f, and the values of B are: 19.2 pN/μm2 s (black lines), 38.4 pN/μm2 s (gray lines), and 89.6 pN/μm2 s (dashed lines). One can see that the magnitude of all the values shown in this graph increases with increasing B and decreases with increasing .
In Fig. 5, a and b, we plot qmax versus α, for different values of and B, respectively. In Fig. 5, c and d, we plot the maximum frequency itself, ωmax, versus α (see Eqs. S12 and S13 in the Supporting Material), for different values of and B, respectively. The mean group velocity of the wave, 〈Vg〉, versus α, is shown in Fig. 5 e (for different values of ) and in Fig. 5 f (for different values of B). T = 0.98 T0 for all the graphs. In panels a, c, and e, B = 38.4 pN/μm2 s and the values of are: 0.16 nN/μm2 (black lines), 0.8 nN/m2 (gray lines), and 1.6 nN/μm2 (dashed lines). In panels b, d, and f, and the values of B are: 19.2 pN/μm2 s (black lines), 38.4 pN/μm2 s (gray lines), and 89.6 pN/μm2 s (dashed lines).
We find from these figures that the magnitudes of qmax, ωmax, and 〈Vg〉 increase with increasing calcium coupling B, and decrease with increasing actin force (see ωmax in Fig. S1 in the Supporting Material). We did not show graphs of these values versus the temperature T, since they are very similar to those versus α, but the adhesion α is a more relevant cellular control parameter.
Discussion and Conclusion
Let us compare our model results to a number of cellular systems which exhibit oscillations and coupling among calcium, actin, and the cell membrane (shape). It should be noted that the observed phenomena is likely to be in the nonlinear regime, so that comparing to our linear-stability analysis should be considered as qualitative, not necessarily giving the exact quantitative values of the parameters at the transition from one type of behavior to the other. Still, the linear analysis should give the correct overall form of the phase-diagram, provided that our model is applicable.
The first examples come from the observations of the shape fluctuations (i.e., twitching) of dendritic spines and filopodia (14,16). In these systems, the increase in the calcium influx corresponds to a lowering of the actin polymerization, as we describe in the model schemes of Fig. 1 c (i and iii). The observed frequency of fluctuations is ∼ωexp ∼10−2 Hz, which is of the order of our estimates given in Fig. 5 and Fig. S1. These fluctuations are observed to cease when the overall calcium level in the cell is increased, for example in response to stimulation of AMPA or NMDA receptors (16). This corresponds in our model to an overall lowering of the effective actin force in the cell due to the increase in C0 and B. In Fig. 3 e, we find that such a change can lead in our model to a transition from damped waves to a stable state. Note that in this regime there are no spontaneous oscillations, which in our model correspond to wave-instability (traveling-waves, Fig. 3 f). Indeed in this cellular system the calcium and shape fluctuations seem to be initiated by an external trigger in the form of a neurotransmitter. Note that in the regime of Fig. 3 f, increasing the calcium levels (increasing C0 and B) strengthens the oscillations.
When the activity of actin polymerization is decreased in this system through the addition of cytochalasin-D, the observed frequency of spontaneous fluctuations increases (45), which is in qualitative agreement with our result shown in Fig. 5 c and Fig. S1 b. Increasing the size of the synaptic contact of the spines, which increases the amplitude of the calcium influx (the parameter B in our model), is observed to increase the frequency of spontaneous fluctuations (46,47), as our model predicts (Fig. 5 d and Fig. S1 a). Note that in this system increasing the actin activity () results in the formation of a larger synapse, thereby leading to an increased B. Since these two factors have opposite effects on the frequency (Fig. 5 and Fig. S1), the observations suggest that the increase in B dominates.
We next turn to oscillations observed in motile, adhering, or spreading cells. In migrating cells (3), calcium oscillations are found to be triggered at the leading edge, where the actin activity is localized, and these oscillations are dependent on the functioning of calcium channels. Furthermore, the frequency of oscillations is observed to decrease with a decrease in the calcium concentration, as our model predicts (decrease in B in Fig. 5 d and Fig. S1 a). Another example of a motile cell with calcium oscillations is given in Fache et al. (48), where the observed frequency is ∼10−1–10−2 Hz (somewhat larger than the values that we calculate, Fig. 5 and Fig. S1), and is observed to be independent of the calcium concentration C0. Although we predict that the frequency increases with the calcium influx B, we note that the effective actin force is also reduced when C0 increases, and leads to a reduction in the frequency. These two opposing effects, if they balance each other, can give rise to a constant frequency as a function of C0.
Adhering cells exhibit calcium oscillations that are much slower (ω ∼10−3 Hz) and involve the negative feedback between the calcium and the adhesion (11). This observed oscillation frequency is similar in magnitude to the values we calculate from our model (Fig. 5 and Fig. S1). The negative feedback between the calcium and the adhesion is similar to the subcase shown in Fig. 1 c (ii), where the calcium inhibits the activity of MP (decrease in ϕ). As expected from our model, the increase in calcium is observed to induce a local retraction of the membrane, i.e., the calcium influx lowers the local actin polymerization (protrusive) force, and therefore decreases locally the membrane height parameter h (Fig. 1 c).
A variety of cell types exhibit spontaneous calcium waves and oscillations (49), but there is no clear data relating these oscillations to the dynamics of the actin cytoskeleton. The frequency of oscillations is ∼10−1–10−2 Hz, which is again not too different from our calculated values. These oscillations are observed to either cease or decrease in frequency when calcium is reduced (buffered), as we predict (decrease in B in Fig. 5 d and Fig. S1 a). In some egg-cells, relatively slow calcium waves are observed to be associated with a retraction of the membrane (50), which arises in our model due to the local decrease in actin polymerization.
Finally, there are recent experiments on nonadhering cells that show marked calcium-driven oscillations (12,51), where the myosin-induced contractility seem to play the major role. The myosin contractility is not included in our current model, but nevertheless, we can make some qualitative comparisons to our model:
-
1.
The experiments find that decreasing myosin contractility decreases the oscillation frequency. Since lower myosin contractility corresponds to larger effective actin protrusive force (52), this corresponds to an increase in which indeed is predicted to lead to lower frequency (Fig. 5 c and Fig. S1 b).
-
2.
When the calcium concentration drops below some threshold the oscillations cease, as we also predict (Fig. 3, a–d, and Fig. S1 a).
To conclude, our model introduces a simple coupling of the membrane shape-actin-calcium system, which is clearly dominant in various cellular regions that are rich in cortical actin, such as cellular protrusions. The qualitative agreement between the model and the observations in various cells lends support to the notion that this model captures some of the main interactions in this system. Furthermore, our model allows us to make several predictions that are yet to be tested:
-
1.
When the actin polymerization force is increased, while maintaining a constant overall level of calcium (C0, B), the frequency of oscillations should decrease (Fig. 5 c and Fig. S1 b),
-
2.
We expect that adhering cells will exhibit oscillations when the adhesion is intermediate, while losing this behavior for both large and very low adhesion (Fig. 4, c and d),
-
3.
Large membrane tension will push the oscillations to appear at a higher calcium activity threshold (Fig. 3, c and e).
Future elaborations of our model may be pursued by adding additional players, such as the calcium-triggered myosin contractility (10,12,19,53), the possible aggregation of the ion channels and pumps in response to the shape changes (28), and the process of calcium-triggered vesicle release (exocytosis) (35,54), which depends on the availability of actin filaments and myosin motors (carrying the vesicles as cargo). The released molecules, such as ATP, feed-back into the dynamics by triggering the influx of calcium. Such models may allow us to reveal the role of each player in this complex system, and provide testable predictions.
Acknowledgments
We thank Edward Bormashenko and Arik Yochelis for fruitful discussions and consultations, and the Robert Rees Fund for Applied Research and the Alvin and Gertrude Levine Career Development Chair for their support.
This research was supported by the Israel Science Foundation (grant No. 337/05).
Footnotes
Alex Veksler's present address is Department of Physics, Lehigh University, Bethlehem, PA 18015.
Supporting Material
References
- 1.Kindzelskii A.L., Petty H.R. Intracellular calcium waves accompany neutrophil polarization, formylmethionyl leucylphenylalanine stimulation, and phagocytosis: a high speed microscopy study. J. Immunol. 2003;170:64–72. doi: 10.4049/jimmunol.170.1.64. [DOI] [PubMed] [Google Scholar]
- 2.Huang J.-B., Kindzelskii A.L., Clark A.J., Petty H.R. Identification of channels promoting calcium spikes and waves in HT1080 tumor cells: their apparent roles in cell motility and invasion. Cancer Res. 2004;64:2482–2489. doi: 10.1158/0008-5472.can-03-3501. [DOI] [PubMed] [Google Scholar]
- 3.Rondé P., Giannone G., Gerasymova I., Stoeckel H., Takeda K. Mechanism of calcium oscillations in migrating human astrocytoma cells. Biochim. Biophys. Acta. 2000;1498:273–280. doi: 10.1016/s0167-4889(00)00102-6. [DOI] [PubMed] [Google Scholar]
- 4.Suzuki K., Tanaka Y., Nakajima Y., Hirano K., Itoh H. Spatiotemporal relationships among early events of fertilization in sea urchin eggs revealed by multiview microscopy. Biophys. J. 1995;68:739–748. doi: 10.1016/S0006-3495(95)80289-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Worth R.G., Kim M.-K., Kindzelskii A.L., Petty H.R., Schreiber A.D. Signal sequence within FcγRIIA controls calcium wave propagation patterns: apparent role in phagolysosome fusion. Proc. Natl. Acad. Sci. USA. 2003;100:4533–4538. doi: 10.1073/pnas.0836650100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Hinz B., Alt W., Johnen C., Herzog V., Kaiser H.-W. Quantifying lamella dynamics of cultured cells by SACED, a new computer-assisted motion analysis. Exp. Cell Res. 1999;251:234–243. doi: 10.1006/excr.1999.4541. [DOI] [PubMed] [Google Scholar]
- 7.Machacek M., Danuser G. Morphodynamic profiling of protrusion phenotypes. Biophys. J. 2006;90:1439–1452. doi: 10.1529/biophysj.105.070383. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Döbereiner H.-G., Dubin-Thaler B.J., Hofman J.M., Xenias H.S., Sims T.N. Lateral membrane waves constitute a universal dynamic pattern of motile cells. Phys. Rev. Lett. 2006;97:038102. doi: 10.1103/PhysRevLett.97.038102. [DOI] [PubMed] [Google Scholar]
- 9.Giannone G., Dubin-Thaler B.J., Rossier O., Cai Y., Chaga O. Lamellipodial actin mechanically links myosin activity with adhesion-site formation. Cell. 2007;128:561–575. doi: 10.1016/j.cell.2006.12.039. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Shlomovitz R., Gov N.S. Membrane waves driven by actin and myosin. Phys. Rev. Lett. 2007;98:168103. doi: 10.1103/PhysRevLett.98.168103. [DOI] [PubMed] [Google Scholar]
- 11.Giannone G., Rondé P., Gaire M., Haiech J., Takeda K. Calcium oscillations trigger focal adhesion disassembly in human U87 astrocytoma cells. J. Biol. Chem. 2002;277:26364–26371. doi: 10.1074/jbc.M203952200. [DOI] [PubMed] [Google Scholar]
- 12.Salbreux G., Joanny J.F., Prost J., Pullarkat P. Shape oscillations of non-adhering fibroblast cells. Phys. Biol. 2007;4:268–284. doi: 10.1088/1478-3975/4/4/004. [DOI] [PubMed] [Google Scholar]
- 13.Segal M. Dendritic spines and long-term plasticity. Nat. Rev. Neurosci. 2005;6:277–284. doi: 10.1038/nrn1649. [DOI] [PubMed] [Google Scholar]
- 14.Korkotian E., Segal M. Spike-associated fast contraction of dendritic spines in cultured hippocampal neurons. Neuron. 2001;30:751–758. doi: 10.1016/s0896-6273(01)00314-2. [DOI] [PubMed] [Google Scholar]
- 15.Brünig I., Kaech S., Brinkhaus H., Oertner T.G., Matus A. Influx of extracellular calcium regulates actin-dependent morphological plasticity in dendritic spines. Neuropharmacology. 2004;47 doi: 10.1016/j.neuropharm.2004.07.038. 669–476. [DOI] [PubMed] [Google Scholar]
- 16.Oertner T.G., Matus A. Calcium regulation of actin dynamics in dendritic spines. Cell Calcium. 2005;37:477–482. doi: 10.1016/j.ceca.2005.01.016. [DOI] [PubMed] [Google Scholar]
- 17.Lechleiter J., Girard S., Peralta E., Clapham D. Spiral calcium wave propagation and annihilation in Xenopus laevis oocytes. Science. 1991;252:123–126. doi: 10.1126/science.2011747. [DOI] [PubMed] [Google Scholar]
- 18.Falcke M. Reading the patterns in living cells—the physics of Ca2+ signaling. Adv. Phys. 2004;53:255–440. [Google Scholar]
- 19.Kapustina M., Weinreb G.E., Costigliola N., Rajfur Z., Jacobson K. Mechanical and biochemical modeling of cortical oscillations in spreading cells. Biophys. J. 2008;94:4605–4620. doi: 10.1529/biophysj.107.121335. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Gov N.S., Gopinathan A. Dynamics of membranes driven by actin polymerization. Biophys. J. 2006;90:454–469. doi: 10.1529/biophysj.105.062224. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Veksler A., Gov N.S. Phase transitions of the coupled membrane-cytoskeleton modify cellular shape. Biophys. J. 2007;93:3798–3810. doi: 10.1529/biophysj.107.113282. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Mattila P.K., Pykalainen A., Saarikangas J., Paavilainen V.O., Vihinen H. Missing-in-metastasis and IRSp53 deform PI4,5P2-rich membranes by an inverse BAR domain-like mechanism. J. Cell Biol. 2007;176:953–964. doi: 10.1083/jcb.200609176. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Saarikangas J., Hakanen J., Mattila P.K., Grumet M., Salminen M. ABBA regulates plasma-membrane and actin dynamics to promote radial glia extension. J. Cell Sci. 2008;121:1444–1454. doi: 10.1242/jcs.027466. [DOI] [PubMed] [Google Scholar]
- 24.Mattila P.K., Lappalainen P. Filopodia: molecular architecture and cellular functions. Nat. Rev. Mol. Cell Biol. 2008;9:446–454. doi: 10.1038/nrm2406. [DOI] [PubMed] [Google Scholar]
- 25.Saarikangas J., Zhao H., Pykäläinen A., Laurinmäki P., Mattila P.K. Molecular mechanisms of membrane deformation by I-BAR domain proteins. Curr. Biol. 2009;19:95–107. doi: 10.1016/j.cub.2008.12.029. [DOI] [PubMed] [Google Scholar]
- 26.Revenu C., Courtois M., Michelot A., Sykes C., Louvard D. Villin severing activity enhances actin-based motility in vivo. Mol. Biol. Cell. 2007;18:827–838. doi: 10.1091/mbc.E06-05-0423. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Nicholson-Dykstra S., Higgs H.N., Harris E.S. Actin dynamics: growth from dendritic branches. Curr. Biol. 2005;15:R346. doi: 10.1016/j.cub.2005.04.029. [DOI] [PubMed] [Google Scholar]
- 28.Lange K. Microvillar Ca++ signaling: a new view of an old problem. J. Cell. Physiol. 1999;180:19–34. doi: 10.1002/(SICI)1097-4652(199907)180:1<19::AID-JCP3>3.0.CO;2-K. [DOI] [PubMed] [Google Scholar]
- 29.Mould A.P., Garratt A.N., Puzon-McLaughlin W., Takada Y., Humphries M.J. Regulation of integrin function: evidence that bivalent-cation-induced conformational changes lead to the unmasking of ligand-binding sites within integrin α5 β1. Biochem. J. 1998;331:821–828. doi: 10.1042/bj3310821. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Jacques-Fricke B.T., Seow Y., Gottlieb P.A., Sachs F., Gomez T.M. Ca+2 influx through mechanosensitive channels inhibits neurite outgrowth in opposition to other influx pathways and release from intracellular stores. J. Neurosci. 2006;26:5656–5664. doi: 10.1523/JNEUROSCI.0675-06.2006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Vanagas L., Rossi R.C., Caride A.J., Filoteo A.G., Strehler E.E. Plasma membrane calcium pump activity is affected by the membrane protein concentration: evidence for the involvement of the actin cytoskeleton. Biochim. Biophys. Acta. 2007;1768:1641–1649. doi: 10.1016/j.bbamem.2007.03.012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Nolz J.C., Gomez T.S., Zhu P., Li S., Medeiros R.B. The WAVE2 complex regulates actin cytoskeletal reorganization and CRAC-mediated calcium entry during T cell activation. Curr. Biol. 2006;16:24–34. doi: 10.1016/j.cub.2005.11.036. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Pingguan-Murphy B., El-Azzeh M., Bader D.L., Knight M.M. Cyclic compression of chondrocytes modulates a purinergic calcium signaling pathway in a strain rate- and frequency-dependent manner. J. Cell. Physiol. 2006;209:389–397. doi: 10.1002/jcp.20747. [DOI] [PubMed] [Google Scholar]
- 34.Cotrina M.L., Lin J.H.C., López-García J.C., Naus C.C.G., Nedergaard M. ATP-mediated glia signaling. J. Neurosci. 2000;20:2835–2844. doi: 10.1523/JNEUROSCI.20-08-02835.2000. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Cotrina M.L., Lin J.H.C., Nedergaard M. Cytoskeletal assembly and ATP release regulate astrocytic calcium signaling. J. Neurosci. 1998;18:8794–8804. doi: 10.1523/JNEUROSCI.18-21-08794.1998. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Gerke V., Creutz C.E., Moss S.E. Annexins: linking Ca2+ signaling to membrane dynamics. Nat. Rev. Mol. Cell Biol. 2005;6:449–461. doi: 10.1038/nrm1661. [DOI] [PubMed] [Google Scholar]
- 37.Mazzochi C., Benos D.J., Smith P.R. Interaction of epithelial ion channels with the actin-based cytoskeleton. Am. J. Physiol. Renal Physiol. 2006;291:F1113–F1122. doi: 10.1152/ajprenal.00195.2006. [DOI] [PubMed] [Google Scholar]
- 38.Liu A.P., Fletcher D.A. Actin polymerization serves as a membrane domain switch in model lipid bilayers. Biophys. J. 2006;91:4064–4070. doi: 10.1529/biophysj.106.090852. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Evans A.R., Turner M.S., Sens P. Interactions between proteins bound to biomembranes. Phys. Rev. E Stat. Nonlin. Soft Matter Phys. 2003;67:041907. doi: 10.1103/PhysRevE.67.041907. [DOI] [PubMed] [Google Scholar]
- 40.Safran S.A. Westview Press; Boulder, CO: 2003. Statistical Thermodynamics of Surfaces, Interfaces, and Membranes. [Google Scholar]
- 41.Li Y.-X., Rinzel J., Keizer J., Stojilković S.S. Calcium oscillations in pituitary gonadotrophs: comparison of experiment and theory. Proc. Natl. Acad. Sci. USA. 1994;91:58–62. doi: 10.1073/pnas.91.1.58. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Reigada R., Buceta J., Lindenberg K. Nonequilibrium patterns and shape fluctuations in reactive membranes. Phys. Rev. E Stat. Nonlin. Soft Matter Phys. 2005;71:051906. doi: 10.1103/PhysRevE.71.051906. [DOI] [PubMed] [Google Scholar]
- 43.Reigada R., Buceta J., Lindenberg K. Generation of dynamic structures in nonequilibrium reactive bilayers. Phys. Rev. E Stat. Nonlin. Soft Matter Phys. 2005;72:051921. doi: 10.1103/PhysRevE.72.051921. [DOI] [PubMed] [Google Scholar]
- 44.Matthews B.D., Overby D.R., Mannix R., Ingber D.E. Cellular adaptation to mechanical stress: role of integrins, Rho, cytoskeletal tension and mechanosensitive ion channels. J. Cell Sci. 2006;119:508–518. doi: 10.1242/jcs.02760. [DOI] [PubMed] [Google Scholar]
- 45.Meng Y., Zhang Y., Tregoubov V., Janus C., Cruz L. Abnormal spine morphology and enhanced LTP in LIMK-1 knockout mice. Neuron. 2002;35:121–133. doi: 10.1016/s0896-6273(02)00758-4. [DOI] [PubMed] [Google Scholar]
- 46.El-Husseini A.E.D., Schnell E., Chetkovich D.M., Nicoll R.A., Bredt D.S. PSD-95 involvement in maturation of excitatory synapses. Science. 2000;290:1364–1368. [PubMed] [Google Scholar]
- 47.Vazquez L.E., Chen H.J., Sokolova I., Knuesel I., Kennedy M.B. SynGAP regulates spine formation. J. Neurosci. 2004;24:8862–8872. doi: 10.1523/JNEUROSCI.3213-04.2004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Fache S., Dalous J., Engelund M., Hansen C., Chamaraux F. Calcium mobilization stimulates Dictyostelium discoideum shear-flow-induced cell motility. J. Cell Sci. 2005;118:3445–3458. doi: 10.1242/jcs.02461. [DOI] [PubMed] [Google Scholar]
- 49.Skupin A., Kettenmann H., Winkler U., Wartenberg M., Sauer H. How does intracellular Ca2+ oscillate: by chance or by the clock? Biophys. J. 2008;94:2404–2411. doi: 10.1529/biophysj.107.119495. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Parry H., McDougall A., Whitaker M. Microdomains bounded by endoplasmic reticulum segregate cell cycle calcium transients in syncytial Drosophila embryos. J. Cell Biol. 2005;171:47–59. doi: 10.1083/jcb.200503139. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Paluch E., Piel M., Prost J., Bornens M., Sykes C. Cortical actomyosin breakage triggers shape oscillations in cells and cell fragments. Biophys. J. 2005;89:724–733. doi: 10.1529/biophysj.105.060590. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Medeiros N.A., Burnette D.T., Forscher P. Myosin II functions in actin-bundle turnover in neuronal growth cones. Nat. Cell Biol. 2006;8:216–226. doi: 10.1038/ncb1367. [DOI] [PubMed] [Google Scholar]
- 53.Shlomovitz R., Gov N.S. Physical model of contractile ring initiation in dividing cells. Biophys. J. 2008;94:1155–1168. doi: 10.1529/biophysj.107.111351. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Haydon P.G. GLIA: listening and talking to the synapse. Nat. Rev. Neurosci. 2001;2:185–193. doi: 10.1038/35058528. [DOI] [PubMed] [Google Scholar]
- 55.Prass M., Jacobson K., Mogilner A., Radmacher M. Direct measurement of the lamellipodial protrusive force in a migrating cell. J. Cell Biol. 2006;174:767–772. doi: 10.1083/jcb.200601159. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.Evans E., Needham D. Physical properties of surfactant bilayer membranes: thermal transitions, elasticity, rigidity, cohesion, and colloidal interactions. J. Phys. Chem. 1987;91:4219–4228. [Google Scholar]
- 57.Raucher D., Sheetz M.P. Cell spreading and lamellipodial extension rate is regulated by membrane tension. J. Cell Biol. 2000;148:127–136. doi: 10.1083/jcb.148.1.127. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


