Anomalous Dynamics of Melanosomes Driven by Myosin-V in Xenopus laevis Melanophores

Abstract

The organization of the cytoplasm is regulated by molecular motors, which transport organelles and other cargoes along cytoskeleton tracks. In this work, we use single particle tracking to study the in vivo regulation of the transport driven by myosin-V along actin filaments in Xenopus laevis melanophores. Melanophores have pigment organelles or melanosomes, which, in response to hormones, disperse in the cytoplasm or aggregate in the perinuclear region. We followed the motion of melanosomes in cells treated to depolymerize microtubules during aggregation and dispersion, focusing the analysis on the dynamics of these organelles in a time window not explored before to our knowledge. These data could not be explained by previous models that only consider active transport. We proposed a transport-diffusion model in which melanosomes may detach from actin tracks and reattach to nearby filaments to resume the active motion after a given time of diffusion. This model predicts that organelles spend ∼70% and 10% of the total time in active transport during dispersion and aggregation, respectively. Our results suggest that the transport along actin filaments and the switching from actin to microtubule networks are regulated by changes in the diffusion time between periods of active motion driven by myosin-V.

Introduction

The organization of the cytoplasm is regulated by molecular motors that distribute organelles and other cargoes along cytoskeleton tracks to their correct destination in the cytoplasm. Three different classes of molecular motors are involved in this task: dynein and kinesin motors, which transport cargoes toward the minus- and plus-ends of microtubules, respectively, and myosin motors, responsible for the transport along actin filaments toward the barbed-end (reviewed in (1,2)). Although microtubule motors are considered responsible for long-distance transport, actin-dependent motors are believed to support local, short-distance movement of cargoes (3,4).

Our knowledge of molecular motors has grown rapidly over the past decades thanks to the development of single molecule techniques that provided unique information regarding the biophysical properties of these nanomachines (e.g., (5,6)). However, intracellular transport of cargoes cannot be completely elucidated by only considering the properties of the isolated motors. The function of motors in living cells is regulated by complex mechanisms that determine properties that are different from those observed in the in vitro experiments.

In recent years, single-particle tracking (SPT) techniques have been applied to follow the motion of organelles and other intracellular cargoes. These experiments allowed extracting information of the transport properties from the analysis of the cargoes trajectories (e.g., (7,8)).

One of the most widely used cellular systems for the study of intracellular transport is that of the melanophore cells (9). These cells have pigment organelles called melanosomes, which contain the black pigment melanin and thus, they can be easily imaged using bright-field transmission light microscopy and tracked with millisecond temporal resolution and nanometer precision (10). Pigment organelles can be distributed in the cells in two configurations: either aggregated in the perinuclear region or homogeneously dispersed in the cytoplasm. The transport of pigment organelles during aggregation and dispersion is regulated by signaling mechanisms initiated by the binding of specific hormones to cell surface receptors, which results in the modulation of cAMP concentrations (11,12). Pigment dispersion requires the plus-end directed microtubule motor kinesin-2 (13) and the actin motor myosin-V (14), whereas aggregation is powered by the minus-end directed motor cytoplasmic dynein (15).

To enable us to understand, fully, how transport is developed in living cells, it is necessary to have a complete understanding of the in vivo properties of each family of motors and of the coordination among them. Although properties of microtubule-dependent transport have been extensively studied by SPT (8,10,16,17), we still do not know important aspects of the properties and regulation of actin-dependent transport in living cells.

Rogers and co-workers (14,18) have demonstrated that melanosomes move along actin filaments driven by the molecular motor myosin-V. They showed that the expression of a dominant negative form of this motor induces aggregation of melanosomes in the cell periphery as it is observed when actin-dependent transport is eliminated by chemical depolymerization of actin (14).

An important contribution to the comprehension of myosin-dependent transport in living cells was done by Snider et al. (19), who studied the actin-dependent transport of melanosomes. They explained the motion properties of myosin-V driven melanosomes by considering that organelles are transported through a randomly organized actin network. According to their model, an organelle moves along a linear filament and once it reaches an intersection between actin filaments it may switch tracks. This motion mechanism defines trajectories that, in a long timescale, resemble a random walk. Although this model could satisfactorily explain the diffusivelike behavior of organelles for time lags longer than ∼5 s, it presents significant divergences in a shorter time window, as also pointed by these authors. This discrepancy suggests that a different process underlies the dynamics of melanosomes in this short timescale.

In this work, we explored the transport driven by myosin-V in living cells by using a tracking method that allowed us to determine melanosome trajectories with higher temporal resolution than previous studies revealing new, surprising properties of myosin-V driven-transport. We show that actin-mediated transport can be explained on the basis of a transport-diffusion model, which considers that melanosomes may detach from actin tracks and reattach to a nearby filament after a given time of diffusion to resume the active motion. Our results suggest that transport driven by myosin-V along actin filaments is regulated by switches between periods of active transport and of diffusion. The model predicts that organelles spend significantly longer times in active transport during dispersion and therefore, explains the experimental observation that melanosomes travel longer distances in this condition of stimulation of the cells. This process may also regulate the transference of organelles initially transported along actin filaments to the microtubule network in living cells.

Materials and Methods

Melanophore cell culture and transfection

Immortalized Xenopus laevis melanophores were cultured as described in Rogers et al. (20). To track the movement of individual organelles, the number of melanosomes in cells was reduced by treatment with phenylthiourea (16).

To study transport along actin filaments, the cells were incubated at 0°C for 30 min with 10-μM nocodazole to depolymerize microtubules (7). Transport along microtubules were studied in cells incubated with 10 μM latrunculin B (Biomol International, Plymouth Meeting, PA) for at least 30 min to depolymerize actin filaments (10). Melanophores were stimulated for aggregation or dispersion with 10 nM melatonin or 100 nM MSH, respectively. The samples were observed between 5 and 15 min after stimulation. All the measurements were performed at 21°C.

Cells were transfected using the FuGENE 6 transfection reagent (Boehringer Mannheim, Fremont, CA), following the vendor's protocols with a plasmid encoding an enhanced green fluorescent protein-tagged myosin-V tail. Expression of this plasmid results in a dominant-negative inhibition of myosin-V driven melanosome transport (14). The plasmid was a kind gift of Dr. Vladimir Gelfand (Northwestern University, Chicago, IL).

Samples preparation for imaging

For microscopy measurements, cells were grown for two days on 25-mm round coverslips. Before observation, the coverslips were washed in serum-free 70% L-15 medium and mounted in a custom-made chamber specially designed for the microscope.

Tracking experiments

Single particle tracking experiments of melanosomes moving along actin filaments in wild-type cells were carried out in a model No. IM 35 microscope (Carl Zeiss, Oberkochen, Germany) adapted for SPT using a 63× oil-immersion objective (numerical aperture = 1.25) under illumination with a tungsten-halogen lamp. A charge-coupled device camera (PixelVision, Tigard, OR) was attached to the video port of the microscope for imaging the cells. Movies were registered at a speed of 14 frames/s.

Tracking experiments of melanosomes in transfected cells were carried out in an Olympus IX70 microscope using a 60× water-immersion objective (numerical aperture = 1.2). A cMOS camera (Pixelink, Ottawa, Ontario, Canada) was attached to the video port of the microscope for imaging the cells at a speed of 50 frames/s.

Trajectories of melanosomes were recovered from the movies registered as described above using the pattern-recognition algorithm described in Levi et al. (10). This algorithm is included in the program Globals for Images developed at the Laboratory for Fluorescence Dynamics (University of California at Irvine, Irvine, CA). The program, which also contains some of the tools used for trajectory analysis, can be downloaded from the Laboratory for Fluorescence Dynamics website (www.lfd.uci.edu).

Results and Discussion

Melanosomes transport along actin filaments

Melanophores were treated with nocodazole as described in Materials and Methods to depolymerize microtubules. After this treatment, aggregation and dispersion of melanosomes were induced by addition of melatonin and MSH, respectively. Movies of regions of the cells were recorded from which a total of 134 trajectories of melanosomes moving along actin filaments were obtained in aggregation and dispersion by using the pattern-recognition algorithm.

To illustrate the different transport systems of melanosomes in living cells, Fig. 1 A shows representative trajectories of melanosomes moving along actin filaments and microtubules during dispersion. These trajectories present qualitatively different characteristics: whereas motion along microtubules generally follows long curvilinear paths, transport along actin filaments is usually more tortuous and the distances traveled by the organelles are shorter. These different properties reflect the organization of microtubules and actin filament in the cell cytoskeleton and are related to the persistence lengths of these polymers (17.7 μm and 110–5035 μm for actin filaments and microtubules of growing sizes in the in vitro conditions (21,22), and 30 μm for microtubules in living cells (23)). In addition, the characteristics of the trajectories of organelles in living cells are related to other factors such as the mechanochemical properties of the motors responsible for the transport, the rheological characteristics of the cell cytoplasm, and the concentration and entanglement of the filaments that constitute the tracks.

Figure 1.

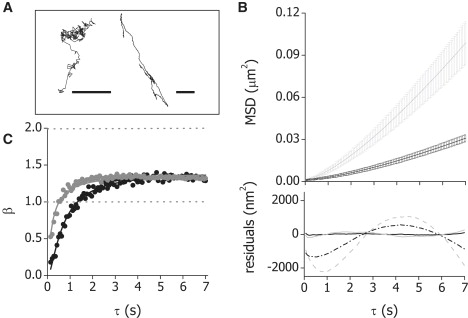
Actin-dependent dynamics of melanosomes in living Xenopus laevis melanophores. (A) Representative trajectories obtained for melanosomes moving along actin filaments (left panel) or microtubules (right panel). Both trajectories lasted for 20 s. Bars, 1 μm. (B) Average mean-square displacement determined from the analysis of 86 and 47 trajectories, during aggregation (black line) and dispersion (gray line), respectively. The error bars represent the standard error. The bottom panel show the residuals obtained by fitting the experimental data measured during aggregation (black line) and dispersion (gray line) to either Eq. 3 (continuous line) or the equation corresponding to the model proposed by Snider et al. (19): $MSD=D_{\text{app}}\left[t-{\tau }_{\text{c}}(1-e^{-t/{\tau }_{\text{c}}})\right]$, where D_app is the apparent diffusion coefficient of melanosomes along the actin network and τ_c is the characteristic time of crossover between the short- to long-time behavior (dashed lines). (C) Average β-value as a function of the lag time τ during aggregation (black line) and dispersion (gray line).

To explore the factors that determine the characteristics of the trajectories of melanosomes moving along actin filaments, we calculated the mean-square displacement (MSD) for every trajectory as

$$MSD\left(\tau \right)=\langle {\left(x(t+\tau )-x\left(t\right)\right)}^2+{\left(y(t+\tau )-y\left(t\right)\right)}^2\rangle ,$$ (1)

where x and y are the coordinates of the particle, τ is a lag time and the brackets represents the time average.

Fig. 1 B shows that the average distance traveled by the organelles during dispersion is significantly longer than during aggregation, as was previously observed (19,24). To further explore the behavior observed in this figure, we calculated the logarithmic derivative of the MSD (β) defined as (25)

$$\beta =\frac{\mathit{d}\ln MSD}{\mathit{d}\ln \tau }\text{.}$$ (2)

Fig. 1 C shows that β increases with τ, approaching a constant value of ∼1.4 during aggregation and dispersion. This value is >1 (value expected for random diffusion (26)) and <2 (corresponding to a model of directional transport along a straight path (26)) indicating that the behavior at this short timescale can be described as superdiffusive (see, for example, (27–29)).

The time-dependent increase of β indicates that there is a second process responsible for melanosomes motion at short time lags. This behavior can be simply due to the presence of an uncorrelated noise inherent to SPT experiments (30). Thus, the simplest empirical equation with the minimum set of parameters that can explain the experimental data showed in Fig. 1 is

$$MSD\left(\tau \right)=MS{D}_{\text{o}}+A_1{\left(\frac{\tau }{{\tau }_{\text{o}}}\right)}^{\alpha },$$ (3)

where τ_o is a reference value arbitrarily set to 1 s, A₁ is a constant depending on the motion properties of the particle, and MSD_o is the residual MSD.

This equation was fitted to the trajectories obtained during aggregation and dispersion of melanosomes (see for example, Fig. 2 D). Fig. 2, A–C, shows the distribution of the parameters obtained by fitting Eq. 3 to every trajectory measured during dispersion and aggregation. In both cases, the distributions of MSD_o and α followed exponential-decay and Gaussian functions, respectively. In contrast, A₁ values during aggregation followed an exponential-decay function whereas during dispersion the distribution is shifted to higher values and could be fitted with a log-normal function. We fitted the mentioned functions to the experimental data of MSD_o, A₁, and α and obtained the characteristic values for these parameters shown in Table 1. The characteristic A₁ value during dispersion is approximately threefold higher than the value measured during aggregation. The rest of the parameters do not change significantly with the stimulation condition of the cells.

Figure 2.

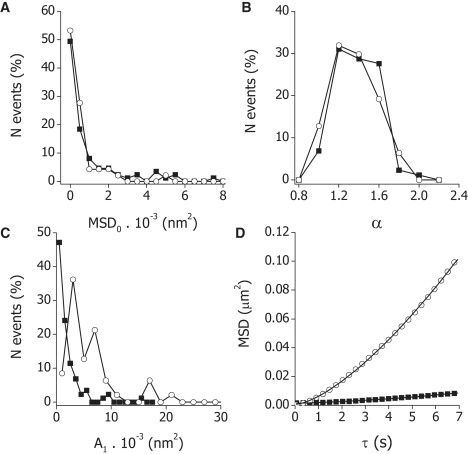
Quantification of actin-dependent motion of melanosomes. Trajectories of melanosomes in Xenopus laevis melanophores previously treated to depolymerize microtubules were determined as described in the text. MSD was calculated for every trajectory and Eq. 3 was fitted obtaining distributions of MSD_o (A), A₁ (B), and α (C) in cells stimulated for aggregation (▪) or dispersion (○).The bin size of each histogram was set by following the method proposed previously (42), adapted to data after either exponential-decay (A_o and A₁ during aggregation), Gaussian (α), or log-normal (A₁ during dispersion) distributions. Representative MSD data obtained from individual trajectories of melanosomes during aggregation (▪) or dispersion (○). Continuous lines correspond to the fitting of Eq. 3 to these experimental data (D). For clarity, one in every four data points is represented in the plot.

Table 1.

Characteristic parameters of melanosomes transport along actin filaments

Condition	A0c [nm2]	A1c [nm2]	σA1	αc	σα
Aggregation	560 ± 30	1500 ± 50	—	1.37 ± 0.03	0.27 ± 0.03
Dispersion	600 ± 30	4100 ± 1000	0.6 ± 0.2	1.33 ± 0.02	0.24 ± 0.02

The parameters were obtained by fitting the data showed in Fig. 2 with the distribution functions indicated in the legend to the figure. In the case of A₁ during dispersion, the following log-normal distribution was fitted to the data: $N=\frac{N_{\text{o}}}{A_1{\sigma }_{A_1}\sqrt{2\pi }}{e}^{-\frac{{\left(\ln (A_1/A_{1c})\right)}^2}{2{\sigma }_{A_1^2}}}$, where N is the number of events, N_o is a parameter related to the amplitude of the distribution, and, A_1c and σ_A1 are the characteristic value of A₁ and standard deviation of the lognormal distribution, respectively.

The parameters A₁ and α are directly related to melanosome transport; therefore, in the following sections, we explore the behavior expected for these parameters according to different transport models. On the other hand, MSD_o is related to an uncoupled process faster than the temporal resolution. In the last section, we discuss the process that might underlie this parameter.

Analysis of the dynamics of melanosomes with models considering active transport

Snider et al. (19) proposed that the motion of myosin-V driven melanosomes could be explained by considering that organelles are actively transported through a randomly organized actin network. According to this model, the organelles move along linear filaments and once they reach an intersection between actin filaments, they may switch tracks. This motion mechanism defines trajectories that, in a long timescale, resemble a random walk. In that work, the behavior was described as the solution of a Langevin equation that considers active transport (MSD ∝ τ²) and diffusion (MSD ∝ τ) in short and long temporal windows, respectively. To explain the properties of the actin-dependent transport observed with different stimulation conditions, they proposed that the probabilities of switching tracks when the organelles reach to an intersection is ∼50% during aggregation and 0% during dispersion.

Although this model could satisfactorily explain the behavior of MSD for time lags longer than ∼5 s, the bottom panel of Fig. 1 A shows that it presents significant divergences in the studied time window.

To fully understand the behavior expected for myosin-driven melanosomes according to the model described by Snider et al., we simulated trajectories of the organelles transported at a constant speed of 75 nm/s through an actin network with properties determined before (19) and fitted the simulated trajectories with Eq. 3 (see Supporting Material for further details in the simulations).

Fig. S1 show the distributions of the parameters obtained from these simulations. Whereas the mean experimental value of α was ∼1.3–1.4 (Table 1), the model proposed by Snider gives mean α-values of 1.725 ± 0.009 and 1.98 ± 0.06 for aggregation and dispersion, respectively. On the other hand, the distributions of A₁ obtained from the simulations were narrower than those experimentally determined (Fig. 2) and centered in ∼6400 and 5500 nm², respectively. Moreover, the model proposed by Snider et al. predicts that during dispersion, the average A₁ value decreases with a parallel increase of the average α-value. This prediction does not agree with our experimental observations, which show that A₁ is higher during dispersion while the value of α remains the same (Table 1). This suggests that the behavior of myosin-driven melanosomes in the time window studied in this work cannot be explained by a model that only considers continuous motion along the actin network.

In a recent work, Ali et al. (31) explored the in vitro behavior of myosin-V when reaching intersections between actin filaments. These authors found that 15% of myosin molecules stepped over the intersecting filament, 48% turned left or right with equal probability, and 37% terminated their run. Based on these observations, we simulated trajectories of melanosomes as described above, but considering that myosin-driven organelles can either turn left or right, or step over when reaching intersections between actin filaments, according to the relative probabilities determined by Ali et al. (31). In a first approximation, we did not consider that organelles may terminate the run upon reaching intersections. We analyzed the simulated trajectories as described before and observed that the model predicts a mean α-value of 1.67 ± 0.02 and a narrow distribution of A₁ values centered at ∼6300 nm² (Fig. S1). These values are higher than those experimentally determined (Table 1) showing that this model cannot explain the properties of melanosome trajectories. Moreover, the model does not provide an explanation for the differences observed in the distribution of A₁ for aggregating and dispersing cells.

Since Ali et al. (31) observed that motors may detach from the track when reaching an intersection between actin filaments, it is reasonable to postulate that this would also happen in vivo. Therefore, we decided to study the behavior of melanosomes when they are freely moving in the cell cytoplasm or actively transported by myosin-V.

Dynamics of melanosomes diffusing in the cytoplasm of living melanophore cells

To characterize the dynamics of melanosomes when they are not being actively transported by myosin-V, we transfected Xenopus melanophores cells with a plasmid encoding an enhanced green fluorescent protein-tagged myosin-V short tail. Since this form of myosin-V cannot attach to actin filaments, expression of this plasmid results in a dominant-negative inhibition of myosin-V driven melanosome transport (14). Before the tracking experiment, cells were treated with nocodazole as described before. Melanosomes were tracked as described in Materials and Methods and MSD(τ) was calculated for every trajectory (Fig. 3).

Figure 3.

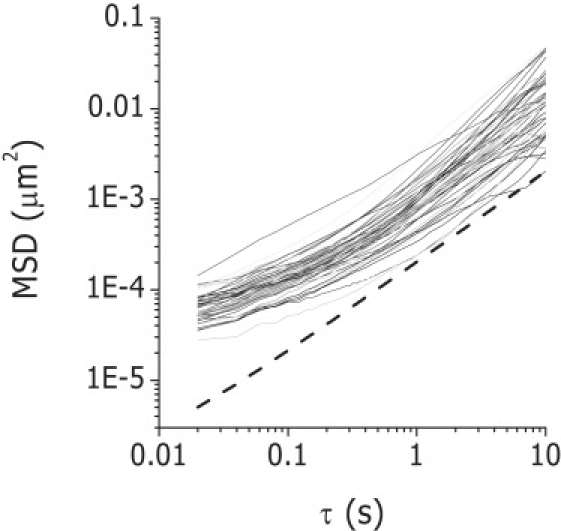
MSD analysis of melanosome trajectories in cells expressing a dominant-negative myosin-V construct. Trajectories of melanosomes in cells expressing a myosin-V short-tail construct were registered as described in Materials and Methods (N trajectories = 56). The dashed line shows the behavior expected for a random diffusion model.

The average value of MSD after a lag time of 7 s was 9 ×10⁻³ μm², i.e., three times smaller than the values measured in wild-type cells (Fig. 1). According to this value, melanosomes in the dominant negative cells move a maximum distance of ∼50 nm in the studied time range, i.e., <10% of the melanosome average diameter (20).

We also analyzed the value of MSD obtained by extrapolation at τ = 0 s and verified that this value was 54 ± 4 nm², which is approximately the value expected according to the error of the tracking method (see above) and significantly lower than the characteristic values determined for MSD_o during aggregation and dispersion (Table 1).

Fig. 3 shows that at a short timescale, MSD increases with τ slower than expected for a pure diffusive process, behavior that may be consequence of elastic trapping (32). At a longer timescale, MSD grows linearly with the lag time as was also reported by Tseng et al. for microspheres passively moving in the cytoplasm of fibroblasts (32).

Even though this result suggests that, in a first approximation, the cytoplasm of Xenopus laevis melanophores behaves as a viscoelastic medium being mostly elastic at short timescales and viscous at long timescales (32), motion of inert particles in the cytoplasm of other cells had been reported to be influenced by other factors such as the remodeling and reorganization of the cytoskeleton (29). Therefore, the observed behavior cannot be interpreted in basis of a simple model of diffusion since other unknown forces probably contribute to melanosome motion. Moreover, subdiffusion in a short-time range is intrinsic to SPT (30), and thus we cannot rule out the contribution of noise to the observed behavior.

Dynamics of melanosomes during active transport along actin filaments

By visual examination of the trajectories (see, for example, the inset to Fig. 4), periods can be detected in which melanosomes seems to be following curvilinear paths and regions in which the organelles present a diffusionlike motion, similar to that observed in cells expressing the mutant form of myosin-V. We analyzed the speed of the organelles during periods of linear motion lasting >50 nm and verified that it followed a wide distribution which could be fitted with a log-normal function with a characteristic value v_m = 70 ± 20 nm/s and standard deviation σ_v = 0.6 ± 0.2 (Fig. 4). The characteristic value determined from this distribution is not significantly different from the average velocity values reported previously in the literature for myosin-driven melanosomes in aggregating and dispersing cells (19) suggesting that during these periods of curvilinear motion the organelles are transported by myosin-V along actin tracks.

Figure 4.

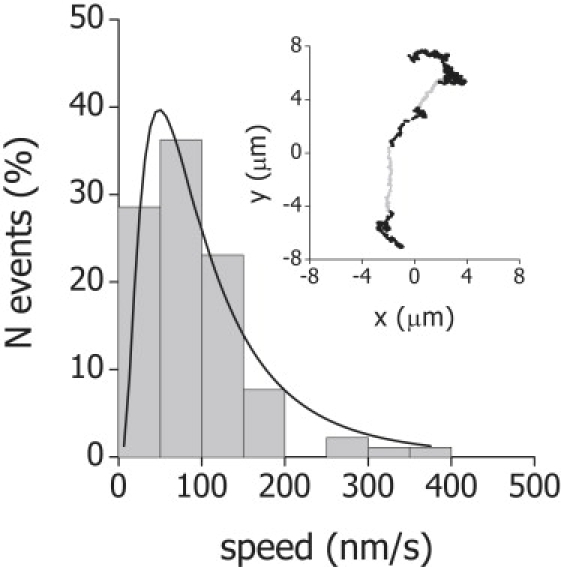
Speed distribution of melanosomes transported by myosin V. Trajectories of melanosomes were registered as described previously and the speed of the organelles in 91 regions of linear motion (shaded lines in the inset to the figure) were analyzed. The experimental histogram was fitted with a lognormal distribution function (continuous line) with the best-fitting parameters indicated in the text. The bin size of each histogram was set by following the method proposed previously (42).

A model for the dynamics of melanosomes transported by myosin-V

According to the results showed above, we proposed a model for the transport of melanosomes in which the organelles moving along an actin filament may detach from the track, diffuse passively in the cytoplasm, and reattach to a nearby actin filament after a given time of diffusion resuming the active motion.

In a previous work, Gross et al. (16) showed that the number of molecules of myosin-V attached to each melanosome decreases during aggregation and estimated that the average number of myosins per melanosome is 65 and 88 for aggregation and dispersion, respectively. Taking this data into account, we proposed that melanosomes diffusing in the cytoplasm in cells stimulated for dispersion have a higher probability of reattaching to a filament and thus the diffusion time is shorter in this condition.

To test the proposed model, we run numerical, hybrid simulations schematically represented in Fig. S2. In these simulations, a myosin-V driven melanosome is considered as a particle initially moving along a linear track at a constant speed v_i randomly chosen from the velocity distribution determined before (Fig. 4). The particle moves along this track for a given distance λ_i given by the properties of the actin network and the processivity of the motor.

As we mentioned before, Snider et al. (19) measured the distributions of actin filament lengths (L) and number of intersections among them (Nt) in melanophores. We randomly sampled two values, L_i and Nt_i, from these distributions and calculated a free path between intersections l_i = L_i/Nt_i. We also sorted a second distance d_i from the run-length distribution of myosin-V determined from the in vitro assays (33) and compare l_i and d_i (see Supporting Material for further details):

• 1.If l_i > d_i, λ_i is given by the processivity of the motor and therefore λ_i = d_i: In this case, the particle detaches from the track after traveling the distance λ_i, and diffuse for a given time t_diffusion afterwards.
• 2.If l_i < d_i, the distance traveled by the particle is λ_i = l_i and the particle moves until it reaches the intersection: In this situation, the particle may switch to the intersecting filament, step over it or detach from the track, and diffuse during t_diffusion. The probabilities of these events were those determined by Ali et al. (31) from in vitro assays.

As we mentioned before, the motion of free melanosomes during diffusion is complex and therefore cannot be modeled in an easy way. Thus, the trajectories of simulated particles during diffusion periods were segments randomly taken from trajectories of melanosomes in cells expressing the dominant-negative myosin-V construct for lasting t_diffusion.

Once a cycle of simulation is finished, new values of v_i and λ_i are sorted as described before and a new cycle is performed. This process is repeated for the chosen total time and the simulated trajectories are resampled afterwards with a time resolution of 70 ms.

To study the dependence of MSD with t_diffusion, we performed hybrid simulations after systematically changing this parameter in the range 0.5–120 s. The simulations were run for 70 s to make them comparable to the experimental trajectories. MSD was calculated for every simulated trajectory and fitted with Eq. 3.

Fig. 5 A shows that the mean value of A₁ decreases with the diffusion time. Qualitatively, it can also be observed that the distribution of this parameter also depended on t_diffusion, showing a transition from an exponential-decay-like behavior at high values of t_diffusion to a Gaussian-like behavior at low t_diffusion values. On the other hand, Fig. 5 B shows that the mean value of α slowly decreases with t_diffusion. This parameter followed a normal distribution in the analyzed range (Fig. 5, inset).

Figure 5.

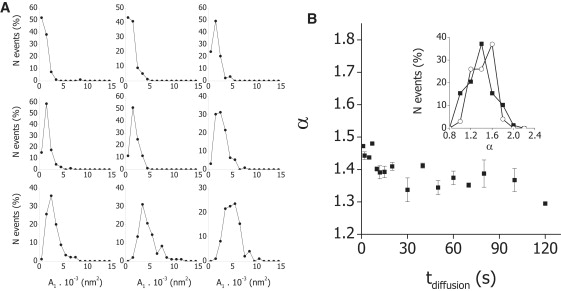
Predictions of the transport-diffusion model. One-hundred trajectories of melanosomes were simulated for each studied condition considering the transport-diffusion model proposed in this work and increasing diffusion times. MSD was calculated for every trajectory and fitted with Eq. 3. (A) Dependence of A₁ on the diffusion time. The distribution of A₁ obtained by analyzing 100 trajectories for each condition is represented at diffusion times of seconds: 120, 100, 80, 60, 40, 20, 10, 3, and 1 (top-left to bottom-right). (B) Dependence of α on the diffusion time. The distribution of α obtained at each diffusion time was fitted with a Gaussian function and the mean value was plotted as a function of the diffusion time. The error bars correspond to the errors obtained from the fitting. (Inset) Distribution of α obtained by considering t_diffusion of 3 s (○) and 100 s (▪).

By comparing Figs. 2 and 5 and the characteristic values of α and A₁ presented in Tables 1 and 2, it can be observed that the distribution and characteristic values of A₁ and α during dispersion and aggregation are not significantly different from those obtained by simulation of the transport-diffusion model with 3 and 100 s of diffusion time, respectively. This result strongly suggests that the differences observed in the behavior of myosin-V transported melanosomes during aggregation and dispersion are due to a lower probability of reattachment of melanosomes to actin tracks during aggregation with respect to dispersion.

Table 2.

Characteristic parameters of melanosomes transport obtained by hybrid-simulations of the transport-diffusion model

Diffusion time (s)	A1c [nm2]	σA1	αc	σα
100	1700 ± 300	—	1.37 ± 0.04	0.25 ± 0.04
3	4000 ± 600	0.3 ± 0.1	1.44 ± 0.05	0.24 ± 0.05

We also analyzed the behavior of melanosomes in the long time-window explored by Snider et al. (19), by performing hybrid-simulations of the transport-diffusion model in this timescale (Fig. S3). We verified that MSD depends linearly on τ up to 100 s and 50 s when considering t_diffusion of 3 and 100 s, respectively. This figure shows that the predictions of the transport-diffusion model agree with the behavior of melanosomes during dispersion and aggregation in a long-time window. In the case of t_diffusion=100 s, MSD presented a negative deviation from the linearity for τ-values higher than 50 s, i.e., beyond the time range analyzed by Snider et al. (19), suggesting that behavior of melanosomes presents a transition to a subdiffusive regime in this time window.

On the other hand, the slope of the MSD versus τ plot is equal to the apparent diffusion coefficient (D_app) for melanosomes transported along the randomly organized actin network (19). We verified that the transport-diffusion model predicts D_app values of 0.017 and 0.004 μm²/s for t_diffusion of 3 and 100 s, respectively. These values are approximately those of the data reported by Snider et al. (19) and those that can be calculated from MSD data of melanosomes in dispersing and aggregating cells showed by Gross et al. (16).

Thermal jittering of melanosomes attached to actin filaments

As we mentioned before, MSD_o could be associated with the noise inherent to SPT experiments. If this were the case, the value of MSD_o would be 2σ² (30), where σ is defined as the standard deviation in the position of a particle due to noise of the tracking system. According to this value, we would expect an MSD_o value of ∼20 nm², which is significantly lower than the values of MSD_o determined during aggregation and dispersion. This result indicates that a different process, with a faster kinetics than the temporal resolution of the tracking method, underlies this parameter. As it is also indicated before, this value is higher than the residual MSD measured for melanosomes in cells expressing a dominant negative form of myosin-V, suggesting that the higher MSD_o values observed in wild-type cells are related to a process occurring when the organelles are attached to the actin track.

The simplest explanation for this result is to consider that MSD_o is related to thermal jittering of the melanosomes when attached to the track through the myosin motor. For example, in the case of kinesin, it has been observed in vitro that the stalk of the motor acts as a linker between the microtubule and bead, pivoting around its anchor point, and that the linker develops some restoring forces against thermal forces (34). Similarly, we hypothesize that the fluctuations resulting in the observed MSD_o values result from the elastic restoration of melanosomes tethered to an actin filament by myosin during the active transport periods. According to the value of MSD_o observed in wild-type cells, the amplitude of these fluctuations should be ∼20 nm, which is comparable with the fluctuations observed for a bead tethered to an actin filament by myosin-V (35,36). However, additional experimental tests should be carried out to verify this hypothesis.

Final Remarks

In this work, we have studied the properties and regulation of the transport of pigment organelles along actin filaments in living Xenopus laevis melanophores using single particle tracking.

The analysis of organelle trajectories obtained after stimulating the cells for aggregation and dispersion showed that the motion of melanosomes cannot be described by considering the active transport driven by myosin-V alone. We proposed a transport-diffusion model, which considers that melanosomes may detach from actin tracks and reattach to nearby filaments after a given time of diffusion to resume the active motion.

The transport-diffusion model can also explain the longer distances traveled by melanosomes during dispersion observed by us and others (16,19). This result could be interpreted considering that the diffusion time between periods of active transport is shorter in this condition. According to the simulations performed in this work, the estimated average diffusion time is ∼3 and 100 s for dispersing and aggregating cells, implying that the percentage of time spent by melanosomes in active transport is ∼70% and 10%, respectively. Importantly, these average diffusion times are estimations since some of the parameters of the model were taken from in vitro experiments in conditions far from those observed in living cells. On the other hand, the experiments done in this work required the depolymerization of the microtubule network, which may also affect parameters of the model such as the distribution of melanosome velocities along actin tracks. Moreover, we would not expect the same diffusion time for all melanosomes in each stimulation condition, but instead a distribution of diffusion times which will be related to the probability of attachment to nearby actin filaments, and therefore to the properties of the local environment and the distribution, activity, and number of motors attached to the melanosomes.

One of the cellular components that may have an effect on the parameters obtained from the transport-diffusion model is that of the intermediate filaments (IFs), since it has been shown that these filaments influence the cytoplasmic organization of organelles (reviewed in (37)). In a recent work, Kural et al. (38) showed that IFs play a key role on the transport of melanosomes along microtubules; specifically, they found that the run length of these organelles moving along microtubules in living cells increases ∼50% in cells, overexpressing a dominant negative vimentin mutant, showing that these filaments hinder the organelles. Moreover, they observed that IFs have an impact in the in vivo dynamics of myosin-V, since its steps occur five times faster in the absence of IFs, probably due to a lower, local viscosity. However, it seems that encounters with other actin filaments determine the run length of melanosomes driven by myosin-V since the mean free path (i.e., the average distance a cargo travels on a single filament) of melanosomes moving along actin filaments is not significantly different from the average value expected if the organelles start randomly on a filament and travel to the end of it (19). This result indicates that in the absence of microtubules, myosin-V principally detaches from the tracks when encountering an actin filament and not before. Agreeing with these results, the transport-diffusion model proposed in our article shows that the experimental trajectories of melanosomes can be explained if >80% of the detachments results from encounters with actin filaments.

The proposed model agrees with previous data showing that although the velocity of myosin-V seems not to depend on cAMP (19), the association of the motor to pigment organelles changes with the levels of this second messenger (16). In that previous work, Gross et al. (16) showed that the average number of myosin motors attached to each melanosome is ∼65 and 88 for aggregating and dispersing cells. In the framework of the transport-diffusion model, the higher number of copies of myosin motors may contribute to the higher probability of reattachment to actin tracks during dispersion and therefore to a lower t_diffusion.

Importantly, the difference in the number of myosin motors attached to the organelles in the different stimulation conditions of the cells seems not to be high enough to determine the ∼30-fold increase in the diffusion time of melanosomes during aggregation. However, there are other factors that may also help to explain this result.

First, it has been demonstrated that the activity of myosin-V is regulated by different cellular components (see, for example, (39)). Thus, some of the myosin motors attached to the organelles may be activated or inhibited upon stimulating the cells for dispersion and aggregation.

Second, there may be changes in the organization of myosin-V molecules on the membrane of melanosomes in the different stimulation conditions. Motors may be clustered or homogeneously distributed in the organelle membrane, affecting the probability of attachment to the filament tracks.

Third, the method used by Gross et al. (16) involves the isolation of the organelles and thus the numbers of myosin-V motors per melanosome in aggregation and dispersion might not be the same as in the in vivo conditions, since motor molecules may detach from the organelles during the purification. As far as we know, there are not experimental data to rule out any of these hypotheses.

One of the key questions in the field is how organelles initially moving along actin filaments switch to microtubules and vice versa. In the particular case of melanosome transport, it is believed that aggregation of pigment organelles occurs predominantly along microtubules, whereas dispersion requires the contribution of both the actin and microtubule transport systems.

Our model also agrees with this observation: melanosomes spend longer times in diffusion during aggregation, and therefore, microtubule-motors bound to them—in particular, dynein, whose activity increases in this condition (40)—have a higher probability of attaching to microtubule tracks and resume the motion along these cytoskeleton filaments. On the other hand, melanosomes in dispersing cells spend more time in active transport along actin filaments and therefore the probability of switching to the microtubule network by this mechanism is lower. This hypothesis also agrees with a previous model proposed by Slepchenko et al. (41), who suggested that the transfer rate of melanosomes from actin filaments to microtubules is higher in aggregating than in dispersing cells.

In conclusion, we showed that the dynamics of melanosomes driven by myosin-V in living melanophores could be explained by a transport-diffusion model, which takes into account that melanosomes may detach from actin tracks and reattach after a given time of diffusion to resume the active motion. Our results suggest that this mechanism could contribute to regulate the transport properties along actin filaments and the switching from the actin to the microtubule networks in living cells.