Tryptophan Conformations Associated with Partial Unfolding in Ribonuclease T1

Abstract

The origin of the biexponential fluorescence decay of Trp in ribonuclease T1 under mildly destabilizing conditions, such as increased pH or temperature, or the presence of detergent, is still not understood. We have performed two extended replica-exchange molecular dynamics simulations to obtain a detailed representation of the native state at two protonation states corresponding to a high and low pH. At high pH, the appearance of partially unfolded states is evident. We found that this pH-induced destabilization originates from increased global repulsion as well as reduced local favorable electrostatic interactions and reduced H-bonding strength of His²⁷, His⁴⁰, and His⁹². At high pH, alternative tryptophan rotamers appear and are linked to a distorted environment of the tryptophan, which also acts as a separate source of ground-state heterogeneity. The total population of these alternative conformations agrees well with the amplitude of the experimentally observed secondary fluorescence lifetime.

Introduction

The interpretation of the time-resolved fluorescence decay of tryptophan in proteins continues to challenge both experimentalists and theoreticians. The most often cited model, known as the rotamer model, provides a simple explanation for the ubiquitous multiplicity of fluorescence lifetimes (1–3). According to this model, each lifetime component is associated with a single rotamer state or a narrow distribution of rotamer states, which, upon excitation, decays at a characteristic exponential rate. Since the environment of each rotamer state can be very different, and since the Trp fluorescence quenching rate is very sensitive to the electrostatic field, different rotamers are expected to have different lifetimes. Spectral relaxation, another often-cited model, also relies on the sensitivity of Trp fluorescence to the electrostatic field (4). A redistribution of the electron charge upon electronic excitation causes a dielectric response of the protein environment (or the Trp side chain itself by a rotamer shift). A change of the dielectric field on the timescale of the excited-state lifetime (on the order of nanoseconds) in turn causes a change in the fluorescence quenching rate. The dielectric relaxation model and the rotamer model may jointly contribute to the nonexponential decay, as relaxation might occur within single rotamer states. Both models have gained their share of supporters over the past decades.

This work focuses mainly on a primary condition for the rotamer model, namely the existence of Trp rotamers in the electronic ground state. Recently, we reported an efficient equilibrium molecular dynamics (MD) simulation on the Bacillus caldolyticus cold shock protein using an adapted version of the replica-exchange method (REM) (5). To improve sampling efficiency, exchanges between replicas were performed at increased temperature and volume while the protein was restrained within the native state. The generated ensemble of protein structures was distributed between two long-lived Trp rotamers, the populations of which correlated well with fluorescence-lifetime amplitudes. The single Trp side chain of B. caldolyticus cold shock protein is relatively solvent-exposed (43% (5)), allowing for side-chain flexibility. The next logical step was to examine whether the Trp side chain may also adopt alternative conformations when buried inside the protein matrix, and how those alternative conformations are related to protein structure and dynamics.

Ribonuclease T1 (RNase T1) from the mold fungus Aspergillus oryzae contains a single tryptophan side chain, Trp⁵⁹, which resides in a hydrophobic protein environment and is almost completely shielded from solvent. Only one Trp⁵⁹ rotamer could be identified in all x-ray crystal and NMR structures. Earlier molecular mechanics and MD studies suggested that Trp⁵⁹ resides in a conformationally restricted region (6). Its side chain conformational freedom is restrained within one rotamer state by the protein matrix, and rotamer interconversions are very unlikely (7,8).

The RNase T1 crystal structure (Fig. 1) contains one α-helix and two antiparallel β-sheets, A and B. Sheet A consists of two β-strands (βA and βB). Sheet B, composed of five β-strands (β1–β5), is strongly twisted to form an open barrel and harbors the RNase T1 active site. When the single-stranded RNA substrate is bound to the enzyme, it acts as the missing sixth strand to complete the β-barrel. The α-helix is tightly bound to sheet B to increase stability. Extra stability is provided by two disulfide bonds, Cys²-Cys¹⁰ and Cys⁶-Cys¹⁰³. Trp⁵⁹ is part of strand β2, which, it has been suggested, is part of the folding core (9). The indole ring of Trp⁵⁹ is located between the helix at one side and the loops between helix-β1 and β2-β3 at the other side of the plane.

Figure 1.

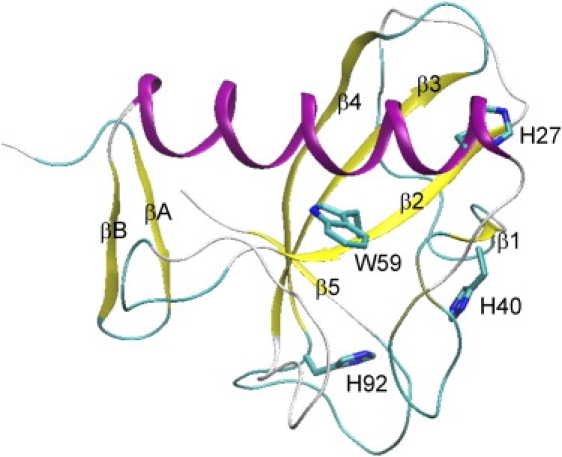
Ribbon diagram of the RNase T1 crystal structure (PDB code 9RNT).

RNase T1 cleaves the phosphodiester bond of single-stranded RNA at the 3′ position of guanosine nucleotides with high specificity. The two-step cleavage mechanism involves a transesterification to produce a 2′,3′-cyclic phosphate followed by hydrolysis to the 3′-phosphate. The affinity for the substrate is highest at the guanine binding site (residues 42–62 and 98), whereas the cleavage occurs at the catalytic site. Residues involved in catalytic activity are Tyr³⁸, His⁴⁰, Glu⁵⁸, Arg⁷⁷, and His⁹² (10).

The fluorescence intensity decay of RNase T1 is well described as a single-exponential process at pH ≤6, whereas at higher pH, two exponential terms are required (11–15). A biexponential decay has also been observed at pH 5.5 at increased temperature or in the presence of guanidine hydrochloride detergent (16).

In this work, we present the results of two extended simulations of RNase T1 using the same REM scheme as in our earlier work (5), with different protonation states, corresponding to high and low pH, aiming to elucidate the conformational states that might be responsible for the biexponential fluorescence decay. At the same time, the wealth of information acquired from the simulations provided us with a detailed description of the RNase T1 native-state dynamics and stability.

Methods

Replica-exchange molecular dynamics

The details of the MD simulations and analysis are provided in the Supporting Material. The initial structure was obtained from the x-ray structure of RNase T1 (Protein Data Bank (PDB) code 9RNT). REM simulations were carried out based on the method of Paschek and García (17). Trial swaps were performed between replicas with different temperatures and volumes. The acceptance probability for replica exchange between two states i and j with corresponding temperatures T_i and T_j and box volumes V_i and V_j is given by (17)

$$P_{\text{acc}}=\min \{1,\exp [{\beta }_i\left(U{\left(x_i\right)}^{V_i}-U{\left(x_j\right)}^{V_i}\right)-{\beta }_j\left(U{\left(x_i\right)}^{V_j}-U{\left(x_j\right)}^{V_j}\right)]\},$$ (1)

where β = 1/kT and U(x)^V is the potential energy of the state with coordinates x and volume V. The energy U(x_i)^Vj is approximated as

$$U{\left(x_i\right)}^{V_j}\approx U{\left(x_i\right)}^{V_i}-\left(P_i\prime -\frac{M}{{\beta }_i\prime V_i}\right)\left(V_j-V_i\right),$$ (2)

where M represents the number of molecules in the simulation box, and P_i′ and β_i′ denote the instantaneous pressure and temperature. An analogous expression is used for U(x_j)^Vi. The justification (17) for Eq. 2 is based on the idea that only small volume changes occur between two neighboring replicas (0.00925 g cm⁻³ density change). Due to this energy approximation, however, the detailed balance condition is only approximately satisfied.

It was observed that, for efficient sampling of the Trp⁵⁹ side chain, reduced densities and high temperatures were necessary. When the system was heated without reducing the density, χ² transitions became very unlikely due to the high system pressure. Therefore, 40 replicas were distributed exponentially over a 300–645 K temperature range and evenly over a 1.02–0.65 g cm⁻³ density range. Temperature and volume exchange moves occurred simultaneously. Volume changes were performed such that only intermolecular distances were altered. To mitigate the small nonequilibrium effects that stem from Eq. 2, after the exchange was accepted, densities were allowed to change gradually over a time period of 0.15 ps, followed by a 0.15 ps equilibration time before data collection. In this time frame, the nonequilibrium effects caused by sudden volume changes disappeared exponentially.

For the generation of starting conformations, each replica was heated to its target temperature, changed gradually to the desired density and subsequently simulated for 1 ns without replica exchange moves. Replicas were simulated in the NVT ensemble. The time constant for temperature coupling was 0.5 ps. Exchanges were attempted every 0.5 ps. Acceptance probabilities varied between 0.13 and 0.26. Both REM simulations were carried out for 66 ns per replica, the last 17.5 ns of which were used to calculate the reported thermodynamic properties.

Dead-end elimination method

To investigate whether backbone flexibility is necessary to accommodate alternative Trp rotamers, the REM simulations were compared with a dead-end elimination (DEE) (18) analysis on the possible Trp conformations. The identification of the rotamer clusters occurred as previously described by Hellings et al. (19). A full-hydrogen model and energy-minimized x-ray structure (PDB code 9RNT) was used as the starting structure. Four internal crystallographic water molecules (WAT¹⁰⁷, WAT¹⁰⁸, WAT¹¹⁰, and WAT¹²⁴) were included in the calculation and were allowed to rotate. The used rotamer library was an enhanced version of the library of De Maeyer et al. (20). The DEE algorithm has been implemented in the BRUGEL package (21) using an adapted version of the CHARMM22 force field (22).

Results

We have conducted extended REM simulations of RNase T1 in two different protonation states. In the first protonation state, all histidine residues (His²⁷, His⁴⁰, and His⁹²) are doubly protonated, corresponding to pH 6. In the second protonation state, all His residues are singly protonated, corresponding to pH 8. His²⁷ is deprotonated at N^δ1, and His⁴⁰ and His⁹² are deprotonated at N^ɛ2 (23).

The RNase T1 native state

Backbone deviations and fluctuations

The backbone root mean-square deviation (bRMSD) histograms at pH 6 (Fig. 2) reveal a flexible native state with most bRMSD values ranging between 1 and 3.3 Å, well below the restraint value of 4.5 Å. Three substates are evident: a major peak at 2.0 Å and two minor peaks at 1.4 and 2.5 Å. At pH 8, the protein deviates much more from the x-ray structure (Fig. 2). Here, we find large peaks at 2.2 Å and 3.1 Å and a shoulder at 3.3 Å. The small peaks at 4.0 Å and 4.3 Å contain alternative Trp⁵⁹ conformations (vide infra). From the size of the error bars, it is clear that both simulations have not yet fully equilibrated.

Figure 2.

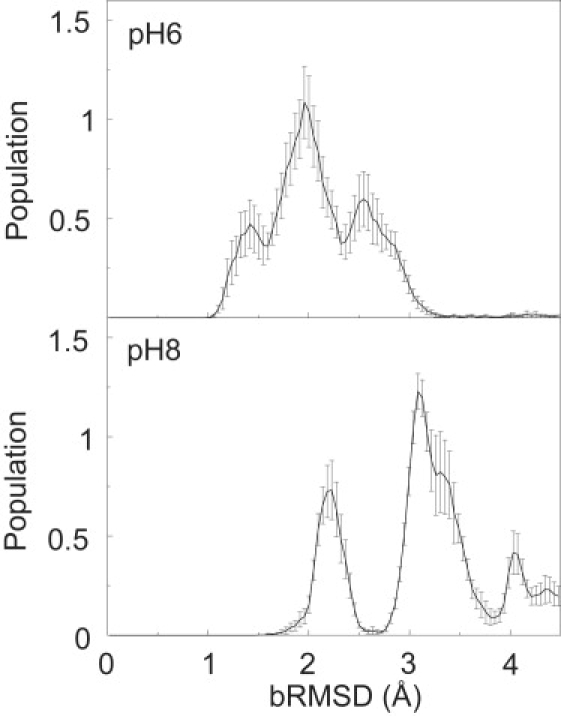
Normalized populations of the backbone RMSD from the x-ray structure for the simulations at pH 6 and pH 8.

Looking at the average bRMSD per residue (Fig. 3), deviations from the x-ray structure are found mainly in the loops. The highest divergence is located in the loops between strands β1 and β2 and between strands β4 and β5, which are both part of the guanine binding site. In both basic and acidic pH simulations, the catalytic residues remain close to the x-ray structure, with the exception of His⁹², located in the loop between β4 and β5. The configuration around Trp⁵⁹ is highly preserved in solution, in agreement with deuterium exchange experiments (9). At pH 8, additional divergence from the x-ray structure is found at the N-terminus, in β-sheet A, at the N- and C-terminal ends of the helix, in the loop between the helix and strand β1, in strand β5, and at the C-terminus.

Figure 3.

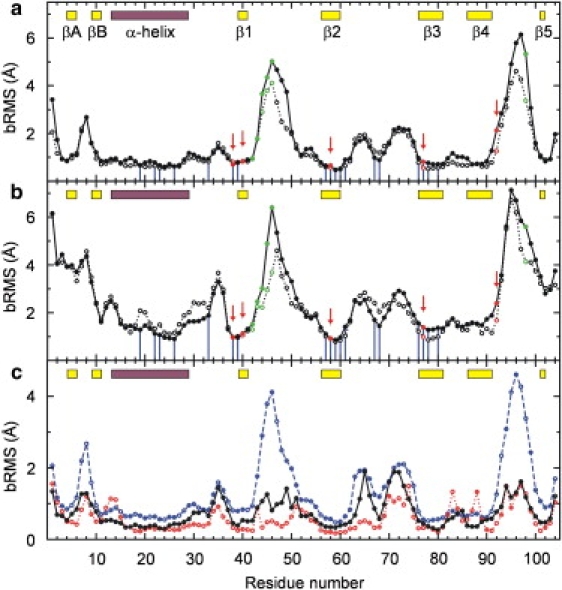
Average bRMS fluctuation (open circles) and bRMSD (solid circles) from the x-ray structure per residue at (a) pH 6 and (b) pH 8. Arrows (red) indicate residues involved in catalytic activity; light circles (green) indicate residues located in the guanine binding site; vertical droplines (blue) indicate residues located within a 4.5-Å sphere around Trp⁵⁹. Color bars at top indicate the β-strands (yellow) and α-helix (purple) of the x-ray structure. (c) bRMS fluctuations for the pH 6 simulation (dashed line) and the NMR structures 1IYY (25) (solid line) and 1YGW (26) (dotted line).

The bRMS fluctuations are very similar to the average bRMSD values (Fig. 3, a and b) at both pH values. Thus, the protein fluctuates around its x-ray conformation, supporting a funnel-like shape of the RNase T1 energy surface (24).

The shape of the bRMS fluctuation curve at pH 6 is strikingly similar to the NMR-derived data of the Gln²⁵ isozyme of RNase T1 at pH 5.5 (PDB code 1IYY) (Fig. 3 c) (25). The higher flexibility for the pH 6 simulation in the loops βA-βB, β1-β2, and β4-β5 can be expected, considering that NMR structures are generated using distance restraints and dihedral angles. Whereas the NMR signal is ensemble-averaged, this signal is usually imposed onto single structures during NMR refinement, thereby possibly biasing the resulting structural ensemble. The flexibility in such an “NMR ensemble” may therefore not be representative of fluctuations that take place in solution.

The overall fold was also very similar to the NMR structure of Lys²⁵-RNase T1 at pH 5.5 (PDB code 1YGW) (26), but some marked differences are apparent (Fig. 3 c). Compared to our simulation data and 1IYY, increased disorder of residues 12–14, 83, and 88, and decreased disorder of residues 44–50 and 64–66 was observed in 1YGW. Lys²⁵ is H-bonded with either Glu²⁸ or Asp²⁹, and all three residues are located on the α-helix and are not involved in any other local interaction. Therefore, we don't expect the Lys²⁵Gln mutation to have a large effect on the global protein conformation, despite a 0.9 kcal mol⁻¹ decrease of stability (27).

Different protocols were used for the structure determinations of 1IYY and 1YGW. 1IYY was determined by the hybrid distance geometry/simulated annealing protocol based on distance and dihedral angle constraints from nuclear Overhauser effect intensities and ³J coupling constants. The final set of structures was selected on the basis of minimum total energy and restraint violations. The 1YGW structures were generated using target function calculations based on nuclear Overhauser effect intensities, ³J coupling constants, and amide proton exchange rates. The final structure ensemble was selected comparing the global precision of structures with order parameters derived from ¹⁵N relaxation time measurements. Note that ¹⁵N spin relaxation techniques monitor the reorientation of ¹⁵N-H bond vectors on the picosecond to nanosecond timescale (28), serving as a lower limit of the actual degree of disorder.

Secondary structure

The average bRMSD and bRMS fluctuations are related to loss of secondary structure (Fig. S1). Most structural elements of the x-ray structure are preserved in the pH 6 simulation, apart from the H-bonded turns between the loops βA-βB, β1-β2, and β4-β5. In contrast, at pH 8 the secondary structure content is strongly reduced for strands βA, βB, and β5, the β-bridge formed by residues 33 and 38, and at the C- and N-terminal sides of the α-helix.

Protein substates

In Fig. 4, the free energy as a function of bRMSD and the fraction of native contacts (Q) is shown. At pH 6, most conformations retain >74% of the native contacts and are located within one of three free-energy basins separated by low barriers. The pH 8 simulation spans a much broader free-energy surface. Many substates are visible and Q values range between 0.46 and 0.85.

Figure 4.

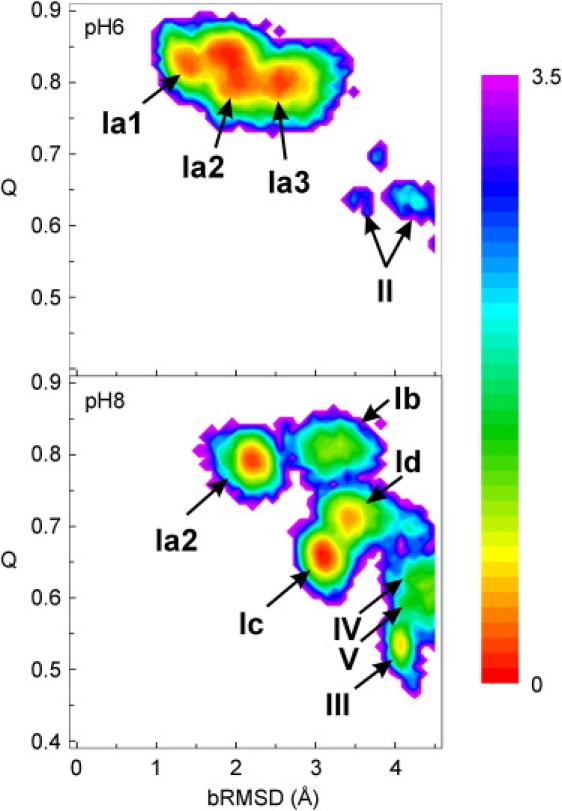
Free energy (kcal mol⁻¹) as a function of bRMSD and Q for the REM simulations at pH 6 and pH 8. Trp⁵⁹ rotamers are indicated with roman numerals I–V, as defined in Figs. 6 and 7.

Some representative RNase T1 conformations for the most stable substates shown in Fig. 4 are depicted in Fig. 5. Substates Ia1, Ia2, Ia3, and Ib largely preserve the x-ray fold and differ only in the loops. In state Ic, sheet A, the N-terminal end of the helix and strand β5 are broken. In state Id, strand β5 is broken and large displacements are observed in sheet A and loop β1-β2 and at the N- and C-termini.

Figure 5.

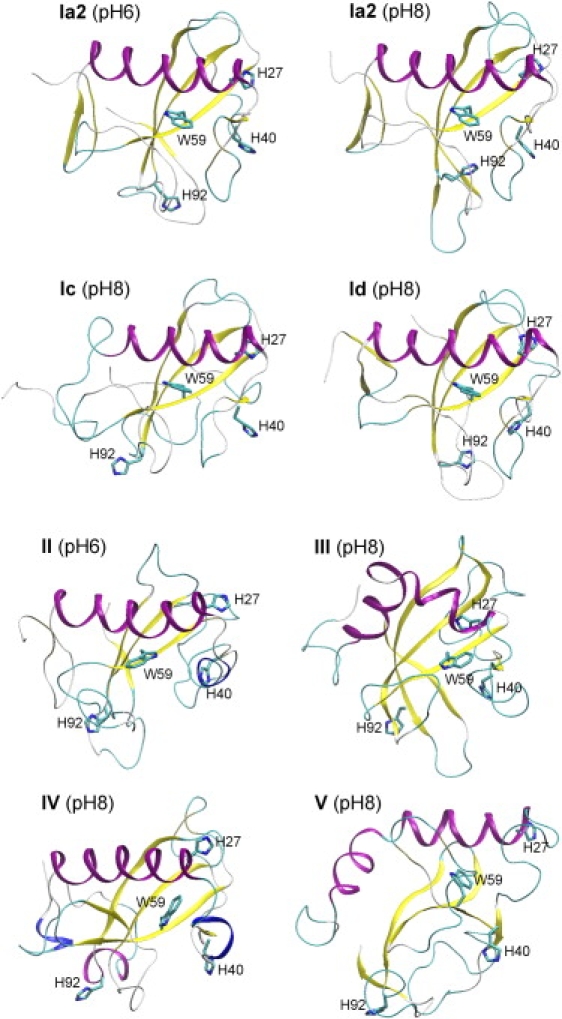
Representative RNase T1 conformations of the most stable substates and alternative Trp⁵⁹ rotamers at pH 6 and pH 8, with numbering according to Figs. 4, 6, and 7. Stereo figures are available in Fig. S2.

States II–V (Figs. 4 and 5) contain more severely distorted secondary structural features and correspond to alternative Trp⁵⁹ conformations, as verified by bRMSD-Q plots for each of the Trp⁵⁹ states. These will be discussed in more detail (vide infra).

Trp⁵⁹ H-bonds

In the RNase T1 x-ray crystal structure, the Trp⁵⁹ indole is H-bonded via the indole nitrogen N^ɛ1-H^ɛ1 with a structural water molecule (WAT¹⁰⁷) that is buried inside the protein. This H-bond is conserved in both pH 6 and pH 8 simulations (−1.21 and −1.23 kcal mol⁻¹, respectively), and is present only when Trp⁵⁹ is in its x-ray rotamer state (vide infra). The H-bonded water stabilizes loop β2-β3 through additional H-bonds with Tyr⁶⁸ N-H and Pro⁶⁰ O, and forms a chain of four H-bonded internal water molecules (WAT¹⁰⁷-WAT¹⁰⁸-WAT¹¹⁰-WAT¹²⁴) located between loop β2-β3 and the helix, connecting the bulk water with the protein interior.

Histidine H-bonds

To uncover the origin of the reduced stability in the pH 8 simulation, we examined in detail the H-bonds that are formed by the histidines. A list of the H-bonds involving the histidines is summarized in Table S7. His²⁷, located at the C-terminal end of the helix, forms an H-bond via the H^ɛ2 of the imidazole nitrogen N^ɛ2 with the Glu⁸² carboxylate oxygen (O^ɛ1 or O^ɛ2), strengthening the interaction between the helix and the turn between β3 and β4. This H-bond is conserved at pH 6, but largely lost at pH 8. At high pH, Glu⁸² mostly orients away from His²⁷ toward the solvent. When His²⁷ is H-bonded to Glu⁸², its rotamer state is fixed at (χ1 = 173°, χ2 = 63°); otherwise, the imidazole ring rotates freely around χ2. H-bonds of His⁴⁰ with Asn³⁶ and Ser³⁷ stabilize the loop between the helix and β1. His⁴⁰ occupies four rotamer states that are favorable for H-bonding. 1), In the x-ray rotamer state (χ1 = 52°, χ2 = −120°), His⁴⁰ N^δ1-H^δ1 is H-bonded with Asn³⁶ main-chain O and/or Ser³⁷ main-chain O. The doubly protonated form is extra stabilized by an H-bond between N^ɛ2-H^ɛ2 and Glu⁵⁸ O^ɛ1/ɛ2. 2), Rotamer (χ1 = 176°, χ2 = −110°) forms an H-bond with Glu⁵⁸ O^ɛ1/ɛ2 via N^δ1-H^δ1. 3), Rotamer (χ1 = −53°, χ2 = 134°) H-bonds with Glu⁵⁸ O^ɛ1/ɛ2 via N^δ1-H^δ1 and is strengthened at pH 6 by H-bonds with Asn³⁶ main-chain O and/or Asn³⁶ O^δ1 via N^ɛ2-H^ɛ2. 4), Rotamer (χ1 = 62°, χ2 = 76°) facilitates H-bonding between N^δ1-H^δ1 and Lys⁴¹ main-chain O. Here, the REM results do not agree well with the NMR data. In 1IYY, rotamers (χ1 = 20°, χ2 = 41°) and (χ1 = −3°, χ2 = −70°) are present for His⁴⁰. In 1YGW, only rotamer (χ1 = 69°, χ2 = 80°) is observed. His⁹² is located at the start of the very flexible loop β4-β5, allowing the formation of many rotamers and H-bonds. The difference in total His⁹² H-bonding interaction energy between the two pH simulations is relatively small.

Thermal unfolding

At pH 7, RNase T1 is most stable at 267 K (29). The experimentally determined midpoint of thermal unfolding, T_m, ranges between 321.1–323.8 K at pH 7 and 327 K at pH 5.5 (29–31). RNase T1 unfolding is well described by a two-state process between a native (N) and unfolded (U) state (31,32).

Fig. S3 shows the bRMSD populations at various temperatures between 300 K and 331 K. At pH 6, substates Ia1 and Ia2 gradually decrease with concomitant population increase of substate Ia3, and the region with bRMSD > 3.5 Å. Between 312 K and 331 K, the population of substate Ia3 stays constant. At 3.5 Å bRMSD, the population is very low for all plotted temperatures, indicating that the unfolding transition state is located at this bRMSD value. Note that for the majority of protein structures (82%), the bRMSD is <3.5 Å at 331 K. In contrast, at pH 8, the protein appears much more sensitive to a temperature increase. The peaks below 3.8 Å decrease at a much faster rate, whereas above this bRMSD value, the population increases markedly. At 331 K, most structures (73%) have bRMSD values >3.8 Å. Unfortunately, we were unable to compare absolute values with experimentally determined T_m values, because bRMSD values >4.5 Å were not allowed in our simulations.

Tryptophan rotamers

Dead-end elimination

The result of the DEE calculation, based on 9RNT is shown in Fig. 6. The major rotamer cluster I (χ1 = 170°, χ2 = −120°) corresponds to the x-ray conformation of Trp⁵⁹. The minor cluster II (χ1 = −180°, χ2 = 90°) is much less stable. The nonbonded energy difference of Trp⁵⁹ with the protein environment, E_Trpnb(II) − E_Trpnb(I), equals 11.1 kcal mol⁻¹. Rotamer I is stabilized by H-bonding of indole N^ɛ1-H^ɛ1 with WAT¹⁰⁷. Simultaneously, rotamer II is destabilized by interactions between Trp⁵⁹ C^ζ3-H^ζ3 and the water oxygen. This result is consistent with the single fluorescence lifetime data at low pH 6. The DEE plot of 8RNT, crystallized at pH 5.2, was very similar (although minor energy differences were noted), confirming its high structural similarity with 9RNT, which crystallized at pH 7.

Figure 6.

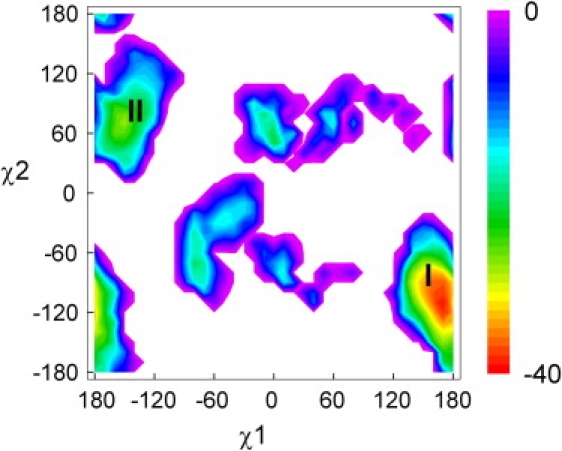
DEE result of the nonbonded interaction energy (kcal mol⁻¹) of Trp⁵⁹ with the surrounding protein in the function of χ1 and χ2.

Rotamer populations from replica exchange

The REM free energy plots of the Trp⁵⁹ χ1 × χ2 map at pH 6 (Fig. 7) strongly resembles the DEE plot (Fig. 6). With 0.994 ± 0.005 of the population within rotamer state I, rotamer II is negligible at 300 K. As the pH increases and/or the temperature increases, the population of rotamer I decreases and several additional rotamers emerge (Fig. 7 and Fig. S4).

Figure 7.

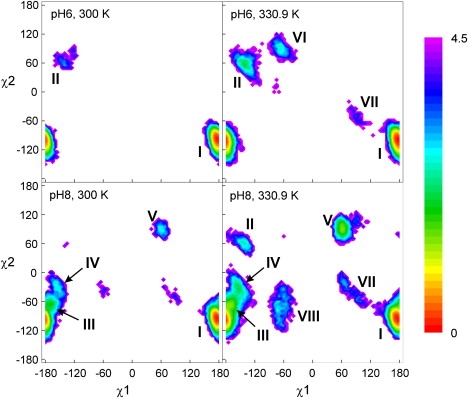
Free energy plotted as a function of Trp⁵⁹χ1 and χ2 from the REM simulations at 300 K and 330.9 K for pH 6 and pH 8.

In Fig. 8, the equilibration of the four highest Trp⁵⁹ rotamer populations over time is shown for the pH 8 simulation. Accurate ratios of the alternative rotamers (III, IV, and V) could not be obtained, but the population of the dominant rotamer (I) seems well equilibrated. At pH 8, we found a rotamer I population of 0.91 ± 0.02. The second highest rotamer (III) has a population of ∼0.05. Note that in the χ1 − χ2 plot, it would be difficult to distinguish rotamers I, III, and IV. The distinction becomes apparent when the free energy is plotted against Q and the bRMSD and χ2 (Fig. 4) for each rotamer.

Figure 8.

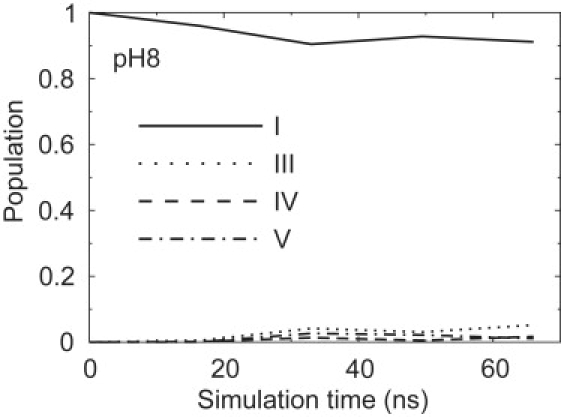
Evolution of the main Trp⁵⁹ rotamer populations at 300 K as a function of simulation time (numbering according to Fig. 7).

As is evident in Figs. 4 and 5, and Fig. S6, a and c, all protein conformations with an alternative Trp⁵⁹ rotameric conformation strongly deviate from the native state. Severe disruption of the secondary structure is evident, most notably sheet A and parts of the helix and sheet B, whereas many contacts between the helix and sheet B have disappeared. In conjunction with the global backbone deviations, the immediate surroundings of the alternative rotamers diverge strongly (Fig. S6, b and d). In contrast, most rotamer I structures keep their Trp⁵⁹ environment very close to the x-ray structure. For the alternative rotamers, deviations are located mainly in the loop helix-β1 and β2-β3. Relative to rotamer I, the strained, nonrotameric conformational states, III and IV, are partially rotated about χ2 (Fig. 7) by steric interaction with the loop helix-β1. Rotamer III is in close contact with the Tyr³⁸ carbonyl and C^α atoms; rotamer IV makes close contact with the Pro³⁹ ring. Both rotamers III and IV kept their respective rotamer state during a 2-ns MD simulation.

Solvent accessibility

The solvent accessibility of Trp⁵⁹ is related to the backbone deviations. Compared to rotamer I, higher average solvent-accessible surface area (SASA) values and standard deviations are observed for all the alternative rotamers (Table 1). However, the limited number of data points does not allow a statistical error estimation for the alternative rotamers.

Table 1.

Trp⁵⁹ solvent accessibilities and indole-carbonyl distances

Rotamer		SASA (SD) (Å2)		Indole-carbonyl distance∗ (Å)
I	(9RNT)	3.3		4.9
I	(pH 6)	4.0 ± 0.2	(3.2)	4.7
I	(pH 8)	5.7 ± 0.3	(4.9)	4.6
II	(pH 8)	23.3	(12.3)	4.6
III	(pH 8)	5.9	(7.7)	4.3
IV	(pH 8)	10.8	(10.0)	4.8
V	(pH 8)	15.2	(7.3)	4.9

^∗Average distance between the center of the indole phenyl ring and the nearest carbonyl carbon atom.

Indole-carbonyl distances

For comparison with the experimental fluorescence lifetime components, we calculated the distance between the center of the indole phenyl ring and the nearest carbonyl carbon (Table 1). For rotamer I, the nearest carbonyl was most often Ala²² (78%). Markedly shorter indole-carbonyl distances were found for rotamer III, due to the carbonyl groups of Tyr³⁸ (65%) and Leu²⁶ (30%). The same trend was observed when the distance between the nearest phenyl carbon and the nearest carbonyl carbon was considered.

Discussion

Sources of protein (de)stabilization

We have performed two extended REM simulations on RNase T1, each with different histidine protonation states, corresponding to pH 6 and pH 8. Our data indicate a strongly reduced stability and increased flexibility at higher pH. This result is consistent with experiment. RNase T1 is most stable at pH 4.5 (33). The conformational stability increases more than 4 kcal mol⁻¹ from pH 9 to pH 5 (34). The increased stability at low pH can be explained by reduced global electrostatic repulsion. In the pH 8 simulation, the protein has a total charge of −9 e. These repulsions are, however, partly screened by the counterions. Another stabilizing effect is caused by local charge—charge interactions and H-bonds between cationic histidines and carboxylate anions. Deprotonation of His²⁷ at N^δ1 causes a weakening of the H-bond interaction with Glu⁸², and a consequent weakening of the tight interaction between turn β4-β5 and the C-terminal end of the helix. The importance of the turn β4-β5 for folding and stability has been demonstrated by Garrett et al. from circularly permuted variants of RNase T1 (35), and by Mullins et al., who observed high protection against deuterium exchange of the backbone amide hydrogens in this region (9). H-bond interactions of His⁴⁰ with Asn³⁶ and Ser³⁷, which stabilize the secondary structure of the loop between the helix and β1, are reinforced in the doubly protonated form of His⁴⁰ by the formation of additional H-bonds, especially with Glu⁵⁸. The effect of this stabilization is clearly seen in Fig. 3 and Fig. S1. Both stabilizing factors also account for the increased pKa values for the three histidines (7.08–7.3, 7.75–7.9, and 7.31–7.8 for His²⁷, His⁴⁰, and His⁹², respectively (23,34)). As a reference, for a histidine in the unfolded state, a pKa value of 6.6 would be expected.

Tryptophan fluorescence and ground-state heterogeneity

Studies of the RNase T1 fluorescence properties have been thoroughly discussed in the literature. The high-fluorescence quantum yield of 0.31 (36) is similar to that of 3-methylindole in various solvents (37). The blue-shifted fluorescence maximum at 320 nm and the fine structure of the fluorescence spectrum are characteristic for the hydrophobic environment (38,39). RNase T1 undergoes a time-dependent spectral shift to longer emission wavelengths characterized by a single dipolar relaxation time of 0.56–0.696 ns, but the spectral shift is very small (∼44 cm⁻¹, ∼0.5 nm) (13,39). The relatively high activation energy for acrylamide quenching (8 kcal mol⁻¹, compared to 3.7 kcal mol⁻¹ for indole derivatives in water (40)) suggested that the protein undergoes fluctuations on the nanosecond timescale, allowing acrylamide molecule diffusion into the protein core (15). No fast-rotational correlation time is associated with anisotropy measurements, suggesting that Trp⁵⁹ is practically immobilized inside the protein matrix (16).

In conjunction with the DEE results, the simulation data suggest that Trp⁵⁹ side-chain flexibility is strongly related to protein stability. Alternative Trp⁵⁹ rotamers are found by our simulation under mildly destabilizing conditions, such as pH or temperature increase. This observation correlates remarkably well with fluorescence decay properties. A single decay with fluorescence lifetime (τ = 4.0 ns) is observed at low pH and temperature, whereas a double-exponential decay (τ1 = 3.9 ns; τ2 = 0.8–1.2 ns) with corresponding amplitudes (α1 = 0.84–0.9; α2 = 0.16–0.1) is observed at high pH or high temperature (8,11). Above pH 7, the amplitude fraction of the major (long) lifetime component coincides well with the population of the dominant rotamer I. Given the high similarity of the Trp⁵⁹ environments for the majority of rotamer I conformations, we assign a single lifetime to this rotamer state. Although the dihedral angle diagram of the fluorophore (Fig. 7) discloses the presence of alternative structures, a full deconvolution of these structures can only be realized by adding extra dimensions of bRMSD and Q. Although the limited sampling of these alternative structures does not provide conclusive evidence, we suspect that their combined heterogeneity is responsible for the minor (short) lifetime component. The short distance between the indole ring of rotamer III and the Tyr³⁸ carbonyl might allow for fast electron transfer quenching, which could explain the short lifetime of the minor decay component. Note also that the rotamers observed at pH 8 and 300 K differ strongly from the ones at pH 6 and 331 K (Fig. 7), suggesting different unfolding pathways in both destabilizing conditions (high temperature or high pH), as is also seen in Fig. S3.

At pH 7.4, acrylamide quenches the minor lifetime component ∼5 times faster than it does the major component, whereas the amplitudes of the two components are approximately independent of quencher concentration, suggesting two Trp conformations (11). Our simulations confirm the rotamer interpretation of the quenching experiments. All the alternative structures have higher SASA values and SASA deviations than rotamer I (Table 1).

Besides multiple Trp conformations (11), several other sources of heterogeneous fluorescence decay of RNase T1 have been suggested in the literature, including multiple protein states (16), multiple excited-state energy transfer acceptors (41), multiple histidine protonation states, and multiple neighboring side-chain isomers (42). According to our simulation data, multiple rotamer states, each associated with a different protein state, are responsible for the lifetime heterogeneity. In the case of rotamers I and III, which are very close in the χ1 × χ2 space (Fig. 7), the protein environment plays a dominant role.

Based on folding studies of an RNase T1 mutant with a single cis peptide bond at Pro³⁹, Kiefhaber et al. (38) suggested that the second lifetime component is related to a residual trans-Pro³⁹ folding intermediate. Since Pro³⁹ is in close contact with Trp⁵⁹ in the native state, a trans ω Tyr³⁸-Pro³⁹ dihedral angle might influence the fluorescence lifetime. With the exception of the highest temperature replicas, we did not observe any trans-Pro³⁹ conformation. However, we cannot exclude the possibility of a trans-Pro³⁹ substate beyond a bRMSD value of 4.5 Å.

The findings presented here may be validated experimentally using point mutations that alter rotamer distributions and fluorescence properties. For instance, further destabilization of the folded state, e.g., by introducing residues that decrease the net protein charge, might raise the alternative rotamers' populations.

In conclusion, we have reached a detailed understanding of the ground-state heterogeneity of a buried Trp in a protein matrix. Deprotonation of the three His groups allows for partial unfolding and appearance of several Trp conformations by destabilizing the native state through reduction of global and local electrostatic interactions. The instability gives rise to multiple ground-state conformations, which can only partly be characterized as different rotamer states, but also show distinctions between degrees of distortion of the protein environment for states that otherwise belong to the same rotamer basin. A temperature increase also destabilizes the native state, but the nature of the partially unfolded states and rotamer states differs from those observed at increased pH.