Extracting the Causality of Correlated Motions from Molecular Dynamics Simulations

Abstract

The information theory measure of transfer entropy is used to extract the causality of correlated motions from molecular dynamics simulations. For each pair of correlated residues, the method quantifies which residue drives the correlated motions, and which residue responds. The measure reveals how correlated motions are used to transmit information through the system, and helps to clarify the link between correlated motions and biological function in biomolecular systems. The method is illustrated by its application to the Ets-1 transcription factor, which partially unfolds upon binding DNA. The calculations show dramatic changes in the direction of information flow upon DNA binding, and elucidate how the presence of DNA is communicated from the DNA binding H1 and H3 helices to inhibitory helix HI-1. Helix H4 is shown to act as a relay, which is attenuated in the apo state.

Introduction

Protein function is intimately related to protein motion. Of particular interest are correlated, or collective motions, which couple the dynamics of different parts of the protein. Such correlated motions are essential for the coupling of binding sites in allosteric regulation (1–3) and the generation of mechanical work in motor proteins (4,5). They also play a role in catalysis, ligand binding, and protein folding (2,6–10). Correlated motions decrease the configurational entropy, which affects the thermodynamics of these processes (9,10). They alter the kinetics by bringing catalytic residues together, by providing the concerted motions necessary to overcome activation barriers, or by modulating tunneling distances in electron or proton transfer reactions (6–10).

Insights into protein-correlated motions are largely obtained from two techniques. The first is nuclear magnetic resonance (NMR). NMR relaxation experiments have been used to measure the order parameter and the internal correlation time for the motion of individual bond vectors (11). These measures give insights into motions on the pico- to nanosecond timescale, and can, in principle, be used to calculate configurational entropies (10). Other NMR experiments probe correlated motions through residual dipolar couplings (12,13) or multiple-quantum spin relaxation (14), or by measuring the change in order parameters for a series of mutants (15), although simulations suggest that the latter merely probes structural changes due to the mutations (16). The second technique, also used in our study, is based on molecular dynamics (MD) simulations. A popular approach is the calculation of the normalized variance-covariance matrix, or Pearson coefficient, from the simulated trajectory (17,18). The Pearson coefficient quantifies the correlation between pairs of atoms, and can also be used to compute the configurational entropy (19). Although the Pearson coefficient can be calculated in a straightforward manner, the method has several disadvantages. It only captures linear correlations, and ignores nonlinear correlations; moreover, only correlations between co-linear vectors are included, while neglecting all correlations between perpendicular motions (20). To solve for these deficiencies, the information theory measure of mutual information has been employed (20). Mutual information is sensitive to all statistical dependencies and includes all linear and nonlinear pairwise correlations, regardless of the relative spatial orientations of the vectors.

In this article, we will address the causality of correlated motions. If the motion of residues i and j is correlated, does residue i drive the motion of residue j, or does residue i respond to the motion of j? This question is particularly pertinent in biology, where correlated motions often have a direction or causal relationship. For example, in hemoglobin, the correlated motions among heme, helix F, and the rest of the protein are driven by oxygen binding to the heme, which induces the motions to which helix F, and the rest of the protein, respond (21,22). Another example is the GroEL chaperone, in which the correlated motions of the equatorial, intermediate, and apical domains, that lead to the opening of the cis cavity, are driven by ATP binding to the equatorial domain (23–25).

We propose to identify the causality of correlated motions from MD simulations, using the information theory measure of transfer entropy (26). Like mutual information, this measure contains all pairwise linear and nonlinear statistical dependencies, and is insensitive to the relative spatial orientation of the motions. Unlike the Pearson coefficient and mutual information, however, transfer entropy is not a symmetric property: the transfer entropy between residues i and j does not equal the transfer entropy between residues j and i. This explicit asymmetry means that the transfer entropy can be used to distinguish between the residues that drive the correlated motion and the residues that respond, between the cause and the effect of correlated motions. The calculation of this information merely requires a standard MD simulation; the transfer entropies are obtained by postprocessing the trajectory. Transfer entropies have been successfully used for signal analysis in other fields, for example for clinical electroencephalography (26–28) and financial data (29), but to our knowledge, no applications to molecular simulation data have been reported. Like other information theory measures, the method is data-intensive and sensitive to noise (27,28). Therefore, we have combined several signal-processing techniques to yield robust and accurate estimates of the transfer entropy, and introduced statistical analyses to optimize the various parameters needed for the calculation. We will summarize our implementation in the methodology section below, and present the technical details in the Appendices.

To illustrate the method, we present its application to Ets-1, a human transcription factor that partially unfolds upon binding its DNA target sequence (30–33). Previous studies revealed that correlated motions are crucial for this highly unusual binding mechanism. Mutation experiments (32) and MD simulations (34) showed that hydrogen bonds between Leu³³⁷ and Gln³³⁶ of helix H1 and the DNA act as a conformational switch, which senses the presence of the DNA and transmits this information to inhibitory helix 1 (HI-1). MD simulations of the folded apo protein, and the metastable, folded Ets-1-DNA complex demonstrated that the conformational switch induces a dramatic change in correlated motions between helix H4 and HI-1 (34). In apo-Ets-1, the motion between H4 and HI-1 is in-phase-correlated, leading to a continuous stabilization of HI-1 through hydrogen bonding and macrodipolar interactions with H4 (Fig. 1 A). In the metastable, folded DNA-bound state, the motion is anti-correlated (out-of-phase), which disrupts the hydrogen bonds and macrodipolar interactions (Fig. 1 B). At the onset of unfolding, the disruptions of these stabilizing interactions lead to the outward motion of HI-1, away from the rest of the protein (Fig. 1 C). It is thought that ultimately, these motions lead to the experimentally observed unfolding of HI-1.

Figure 1.

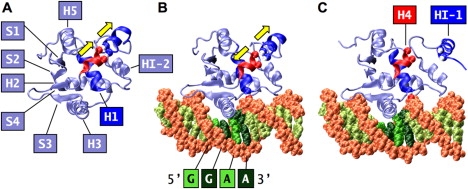
Structure of Ets-1 Δ301. The figure was prepared with VMD (55) and povray (www.povray.org). (A) In apo-Ets-1, the motion between helices H4 and HI-1 is correlated (in-phase), as shown by the parallel arrows. HI-1 is stabilized by the Leu⁴²¹-Phe³⁰⁴ and Leu⁴²²-Lys³⁰⁵ hydrogen bonds with H4 (shown as van der Waals spheres) and macrodipolar interactions with H4. (B) In the metastable, folded Ets-1-DNA complex, the motion between HI-1 and H4 is anticorrelated (out-of-phase), as shown by the arrows. The hydrogen bond between Leu³³⁷ of helix H1 and the T6 phosphate of the complementary DNA strand (shown as van der Waals spheres) acts as a conformational switch. (C) At the onset of unfolding, the anti-correlated motion between H4 and HI-1 lead to the breaking of the Leu⁴²¹-Phe³⁰⁴ and Leu⁴²²-Lys³⁰⁵ hydrogen bonds between H4 and HI-1, respectively, a disruption of the stabilizing macrodipolar interactions between H4 and HI-1, and the outwards motion of HI-1 away from the rest of the protein.

Here we will apply transfer entropies to investigate the cause of the changes in correlated motions in folded Ets-1 upon DNA binding. Our calculations show how the presence of DNA is transmitted through the protein, providing new mechanistic insights into how DNA destabilizes HI-1 at the onset of unfolding. Given the importance of correlated motions for protein function, we expect that the method will be of general use for a wide range of systems.

Methods

The information theory measure of transfer entropy quantifies the statistical coherence between two processes that evolve in time. Since we are interested in the statistical coherence between atomic motions, we take these processes as the positional fluctuations of atoms i and j, although in principle, other scalar or vector quantities could be used as well. The positional fluctuations are given by r_i(t_n) ≡ |x_i(t_n) − 〈x_i〉|, where x is the atomic position and 〈.〉 denotes a time average. Time t_n = nΔt is discrete, with Δt = Mδt a multiple of the MD integration time step δt and M the frequency of saving coordinates. By describing the discrete time processes as stationary Markov processes of order m, the dynamics of the system can be characterized by m-dimensional state vectors, which we will denote by I. Using the method of time delayed embedding (35,36), the state vectors are given by

$$\begin{array}{l}{\mathrm{I}}_k^{{\mathit{\mu }}_{\text{i}}}\equiv {\left(r_{\text{i}}\left(t_k\right),r_{\text{i}}\left(t_{k+{\tau }_{\text{i}}}\right),\cdots ,r_{\text{i}}\left(t_{k+\left(m_{\text{i}}-1\right){\tau }_{\text{i}}}\right)\right)}^{\text{T}},\\ {\mathrm{J}}_k^{{\mathit{\mu }}_{\text{j}}}\equiv {\left(r_{\text{j}}\left(t_k\right),r_{\text{j}}\left(t_{k+{\tau }_{\text{j}}}\right),\cdots ,r_{\text{j}}\left(t_{k+\left(m_{\text{j}}-1\right){\tau }_{\text{j}}}\right)\right)}^{\text{T}},\end{array}$$ (1)

where the time shift τ is a multiple of Δt, and the superscript T indicates the transpose operation. The m and τ embedding parameters can be different for atoms i and j; their specific values are indicated by the superscript μ ≡ (m, τ). Taking time $t_{k+(m_{\text{i}}-1){\tau }_{\text{i}}}$ as the present, ${\mathrm{I}}_k^{{\mathit{\mu }}_{\text{i}}}$ and ${\mathrm{J}}_k^{{\mathit{\mu }}_{\text{j}}}$ describe the histories of the processes, which consist of the present and past m − 1 fluctuations. Similarly, the future fluctuations of atoms i and j are given by

$$\begin{array}{c}{\mathrm{I}}_{k+1}\equiv r_{\text{i}}\left(t_{k+m_{\text{i}}{\tau }_{\text{i}}}\right),\\ {\mathrm{J}}_{k+1}\equiv r_{\text{j}}\left(t_{k+m_{\text{j}}{\tau }_{\text{j}}}\right)\text{.}\end{array}$$ (2)

To reconstruct the dynamical structure of the time series, the proper choice of m and τ is crucial. We discuss our method to optimally select τ and m from the MD trajectory in the Appendices.

If the fluctuations of atoms i and j are independent processes, the conditional probability to observe the future fluctuation of atom i, given its history, is independent of the history of atom j,

$$p\left({\mathrm{I}}_{k+1}|{\mathrm{I}}_k^{{\mathit{\mu }}_{\text{i}}}\right)=p\left({\mathrm{I}}_{k+1}|{\mathrm{I}}_k^{{\mathit{\mu }}_{\text{i}}},{\mathrm{J}}_k^{{\mathit{\mu }}_{\text{j}}}\right)\text{for independent processes,}$$ (3)

where $p\left({\mathrm{I}}_{k+1}\right|{\mathrm{I}}_k^{{\mu }_{\text{i}}})$ is the conditional probability to observe the future fluctuation of atom i, given its history, and $p\left({\mathrm{I}}_{k+1}\right|{\mathrm{I}}_k^{{\mu }_{\text{i}}},{\mathrm{J}}_k^{{\mu }_{\text{j}}})$ is the conditional probability to observe the future fluctuation of atom i, given the histories of atoms i and j. The transfer entropy quantifies the deviation from independence, and is given by the Kullback-Leibler distance (37–39) between these probability distributions (26):

$$T_{\text{j}\to \text{i}}=\sum _{k=0}^{N_m}p\left({\mathrm{I}}_{k+1},{\mathrm{I}}_k^{{\mu }_{\text{i}}},{\mathrm{J}}_k^{{\mu }_{\text{j}}}\right)\log \frac{p\left({\mathrm{I}}_{k+1}|{\mathrm{I}}_k^{{\mu }_{\text{i}}},{\mathrm{J}}_k^{{\mu }_{\text{j}}}\right)}{p\left({\mathrm{I}}_{k+1}|{\mathrm{I}}_k^{{\mu }_{\text{i}}}\right)},$$ (4)

where $p({\mathrm{I}}_{k+1},{\mathrm{I}}_k^{{\mathit{\mu }}_{\text{i}}},{\mathrm{J}}_k^{{\mathit{\mu }}_{\text{j}}})$ is the joint probability distribution of observing the future atomic fluctuation of atom i, and the histories of atoms i and j. The sum is over all possible state vectors: N_m = N − (m − 1)τ, with N the total number of snapshots. By construction, the transfer entropy is a positive quantity, with a minimum value of zero when the fluctuations of atoms i and j are independent, and a maximum of the entropy rate

$$h\left({\mathrm{I}}_{k+1}|{\mathrm{I}}_k^{{\mathit{\mu }}_{\text{i}}}\right)=-\sum _{k=0}^{N_m}p\left({\mathrm{I}}_{k+1},{\mathrm{I}}_k^{{\mathit{\mu }}_{\text{i}}}\right)\log p\left({\mathrm{I}}_{k+1}|{\mathrm{I}}_k^{{\mathit{\mu }}_{\text{i}}}\right)$$

when the fluctuations of atoms i and j are completely coupled; this maximum is reached when i = j, for example. The entropy rate equals the information gained in observing an additional state vector of atom i when all its previous states are known.

A straightforward derivation shows that the transfer entropy can be reformulated as conditional mutual information (I) (27):

$$T_{\text{j}\to \text{i}}=I\left({\mathrm{I}}_{k+1};{\mathrm{J}}_k^{{\mathit{\mu }}_{\text{j}}}|{\mathrm{I}}_k^{{\mathit{\mu }}_{\text{i}}}\right)\text{.}$$ (5)

This conditional mutual information equals the amount of information that knowing the history of the fluctuations of atom j provides about the future fluctuations of atom i, given the history of fluctuations of atom i. Moreover, since the transfer entropy is based on conditional probabilities, T_j→i ≠ T_i→j in general. This means that the measure can be used to identify causal relationships (26). High values of T_j→i indicate that the fluctuations of atom j are strongly driving the fluctuations of atom i, whereas low values indicate a smaller dependence. To quantify whether, on average, the motion of atom j drives the motion of atom i, or whether the motion of atom i drives the motion of atom j, we use the normalized directional index D_j→i (27,28),

$$D_{\text{j}\to \text{i}}=\frac{T_{\text{j}\to \text{i}}}{h\left({\mathrm{I}}_{k+1}|{\mathrm{I}}_k^{{\mathit{\mu }}_{\text{i}}}\right)}-\frac{T_{\text{i}\to \text{j}}}{h\left({\mathrm{J}}_{k+1}|{\mathrm{J}}_k^{{\mathit{\mu }}_{\text{j}}}\right)},$$ (6)

where D_i→j = −D_j→i, with values between −1 and +1. If D_j→i > 0, the fluctuations of atom j drive the fluctuations of atom i, or j is the source of correlations. If D_j→i < 0, the motion of atom i drives the motion of atom j, while atom j responds to the motion of atom i, or j is the sink of correlations. Although the directional index is a measure of causality, it is not a measure of the independence of the two processes: if D_i→j = D_j→i = 0, there is no overall driving motion between atoms i and j, but only if T_j→i = T_i→j = 0 the fluctuations of atoms i and j are independent. Since D_i→j is based on mutual information, the index includes all linear and nonlinear correlations between the two time series.

To limit the effects of statistical noise and to speed up the calculations, we used several specialized techniques. The details of our implementation are described in the Appendices. Although this implementation quantifies the statistical coherence between positional fluctuations, the method could be readily adapted to quantify the statistical coherence between other time-dependent simulation properties, such as displacement vectors, dipole moments, and/or energetic quantities.

Simulation setup

We analyzed the transfer entropy between the C^α atoms of apo and DNA-bound Ets-1 and between the P atoms of DNA and the C^α atoms of Ets-1 using the MD trajectories described in Kamberaj and van der Vaart (34). Since no high-resolution structures are available for the full-length protein, these 15-ns trajectories were generated for Ets-1 Δ301, a construct consisting of residues 301–440 with an intact autoinhibitory module and approximately twofold autoinhibition (33). To probe the interactions that lead to the unfolding of HI-1, the simulations were performed on the folded states of Ets-1. The all-atom simulations were performed with the CHARMM force field (40) in the NPT ensemble, coordinates were saved every 500 steps (every ps), and the simulations included explicit water molecules and ions. The simulated DNA sequence in the Ets-1–DNA complex was 5′-AGTGCCGGAAATGTGC-3′ with the high affinity 5′-GGAA-3′ target sequence. The reader is referred to Kamberaj and van der Vaart (34) for the technical details of the simulations; we used the last 10 ns of the trajectories for the analyses. Given the possibly long timescales of unfolding (33), we did not expect to observe the complete unfolding of HI-1 in the DNA-bound complex in the timescales of the simulation. Instead, we observed the onset of unfolding, consisting of the breaking of the Phe³⁰⁴-Leu⁴²¹ and Lys³⁰⁵-Leu⁴²² hydrogen bonds between HI-1 and H4, the breaking of the Lys³⁰⁵-Glu⁴²⁸ salt bridge between HI-1 and H5, and the outward motion of HI-1, away from H4 and HI-2 (see Fig. 1). Our objective was to identify the interactions and correlated motions that led to the onset of the unfolding; therefore, the simulation of the complete unfolding process was not necessary and the present simulations met our goals.

Results

To probe the change in correlated motions that lead to the destabilization of HI-1 upon DNA binding, we analyzed the transfer entropy between the C^α atoms of Ets-1 in MD trajectories of the folded apo protein in solution, and the metastable, folded Ets-1 in complex with high affinity DNA. Fig. 2 shows the directional index D_j→i between the C^α atoms for apo-Ets-1 (Fig. 2 A) and the Ets-1–DNA complex (Fig. 2 B). In the figure, atom j is on the vertical, and atom i on the horizontal axis. Positive values of D_j→i (in yellow and red) indicate that the information flow is from j to i; that on average, the fluctuations of atom j drive the fluctuations of atom i, and that atom j is the source of the correlations between atoms j and i. Likewise, negative values of D_j→i (in blue) signify that atom j is the sink of the correlations between atoms j and i, and that atom j responds to the motion of atom i. On the diagonal, D_i→i = 0, since $T_{\text{i}\to \text{i}}=h\left({\mathrm{I}}_{\text{k}+1}\right|{\mathrm{I}}_{\text{k}}^{{\mathit{\mu }}_{\text{i}}})$ (Eqs. 4 and 6). Fig. 2 C shows which C^α atoms switched from driver to responder upon DNA binding, and vice versa. Changes from a negative to a positive D_j→i upon DNA binding are shown in red; red horizontals indicate C^α atoms that changed from responder to driver upon DNA binding. The opposite change is shown in blue; atom pairs that did not switch sign of D_j→i are shown in white. For clarity, only one shade of red and blue is used in Fig. 2 C. Fig. 2, D and E, show D_j→i between the P atoms of each DNA strand and the C^α atoms of Ets-1.

Figure 2.

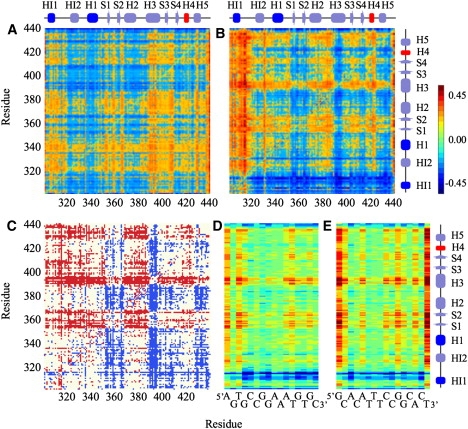
The normalized directional index. Atom j is on the vertical, and atom i on the horizontal axis. (A) D_j→i for the Ets-1 C^α atoms in apo-Ets-1 and (B) the Ets-1–DNA complex. (C) Sign switching of D_j→i upon DNA binding. Changes from negative to positive values are shown in red, changes from positive to negative values in blue, and changes that did not involve a switch of sign (including changes from |D_j→i| ≤ 0.05) are shown in white. (D) D_j→i between the P atoms of the DNA main (strand 1) and (E) complementary strand (strand 2) and the C^α atoms of Ets-1.

Fig. 2 shows dramatic changes in the directional index upon DNA binding. For many atom pairs, ∼36% of the total, the driver and responder switched roles upon DNA binding (Fig. 2 C). Especially S1, S2, H3, S3, S4, and H5 showed many switches from responding to driving residues upon binding. For residue pairs that did not switch, DNA binding increased the absolute magnitude of the directional index for 41% of all atom pairs, while decreasing the absolute magnitude for the remaining 25%. Fig. 2, D and E show that Ets-1 drives most of the correlated motions between the protein and DNA; especially large drivers are H3, S1, and S2.

Of particular interest are the transfer entropies of the H1, H3, H4, and HI-1 helices, which are crucial for the binding mechanism (31–34). H3 is the recognition helix, which binds the major groove of DNA (Fig. 1). In the complex, H3 drives the motion of the DNA P atoms in the binding site (the horizontal for H3 is mostly red and yellow in Fig. 2, D and E). For example, Tyr³⁹⁵ drives the motion of G8 and A9 in strand 1 (the main strand), Arg³⁹¹ drives the motion of the T8 and C9 of strand 2 (the complementary strand), and Arg³⁹⁴ drives the motion of G7, G8, A9, and A10 of strand 1 and T6, T7, C8, and C9 of strand 2. In apo-Ets-1, H3 acts as a sink for the correlated motions (the horizontal for H3 is mostly blue, the vertical is mostly yellow in Fig. 2 A). This means that in the apo-protein, helix H3 responds to the motion of most other protein residues. H3 behaves very differently in the DNA-bound state (Fig. 2 B): in the DNA-complex, H3 is mostly a source of the correlated motions with the other protein residues. This change upon DNA binding makes biological sense: the recognition helix senses the presence of the DNA and transmits this information to the rest of the protein through correlated motions.

Helix H1 contains the conformational switch, consisting of Leu³³⁷ and Gln³³⁶, which hydrogen-bond with the T6 phosphate of DNA strand 2 (32–34). Fig. 2, D and E show that the correlated motions between Leu³³⁷, Gln³³⁶, and this phosphate are driven by the P atom of T6. In apo-Ets-1, H1 is a source for the correlated motions with all other secondary structure elements. In the DNA-bound state, the causality of these correlations is reversed for half the elements. In the complex, H1 is a sink for the correlated motions with S1, S2, H3, S4, and H5, and a source of the correlations with HI-1, HI-2, H2, S3, and H4. H1 becomes a much stronger source for the correlations with HI-1 upon DNA binding, and a slightly stronger source for the correlations with H4.

In the apo-protein, the motion between H4 and HI-1 is in-phase correlated, and H4 stabilizes HI-1 through macrodipolar and hydrogen-bonding interactions. Upon DNA binding, the motion between H4 and HI-1 becomes anti-correlated, and the stabilizing interactions are disrupted (34). H4 is a very weak source for the correlated motions with HI-1, H3, S3, and H5 in the apo protein, and a sink for the correlated motions with the other secondary structure elements. In the DNA-bound complex, H4 is a strong sink for the correlated motions with most residues, and a strong source for the correlations with HI-1. HI-1 is the helix that unfolds upon binding DNA (30–33). In apo-Ets-1, HI-1 is a weak source of the correlations with H3, S3, and H5, and a sink for the correlations with HI-2, H1, S1, S2, H2, S4, and H4. Upon DNA-binding, HI-1 becomes a very strong sink of the correlations with all other protein residues. In addition, parts of HI-1 and the loop between HI-1 and HI-2 are sinks for the correlations with the DNA.

Other regions of interest are the loop region between S3 and S4, which contact the DNA. Correlations between this loop region and the DNA are partially driven by the DNA and partially by the protein. Lys⁴⁰⁴ drives the motion of T3, G4, and C6 and is a sink for the correlation with C5 of strand 1. Thr⁴⁰⁵, Ala⁴⁰⁶, Gly⁴⁰⁷, Lys⁴⁰⁸, and Arg⁴⁰⁹ act as a sink for the correlated motions with T3, G4, C5, and C6 of strand 1. We also observed that the correlated motions between Ets-1 and the highly flexible bases at the end of DNA strands are driven by Ets-1.

From these analyses, a clear picture of the information flow within the protein emerges. The presence of DNA is transferred by a network of correlated motions, and the direction of the information flow is from the driving to the responding residues. The network starts with the DNA sensing H1 and H3 helices. DNA binding changes the H3 recognition helix from a sink to a source of correlated motions, transmitting the information that DNA is present to the rest of the protein by driving correlated motions. The T6 phosphate of DNA strand 2 activates the conformational switch, by hydrogen bonding with Leu³³⁷ and Gln³³⁶ of helix H1, and driving the correlated motions with these residues. In addition, H1 becomes a stronger driver of correlated motions with H4 and HI-1 upon DNA binding. H4, the helix that stabilizes HI-1 in the apo state, and destabilizes HI-1 in the DNA-bound state, plays a central role in the correlated network. Whereas in the apo state, H4 is a very weak source for the correlated motions with HI-1, and either a weak source or weak sink for the correlated motions with the rest of the protein, in the DNA-bound state, H4 is a strong source of correlated motions with HI-1 and a strong sink for the correlated motions with the other protein residues. H4 responds to the motion of all non-HI-1 protein residues in the DNA-bound state, and transmits this information to HI-1 by strongly driving the correlations with this helix. Thus, H4 acts as a relay between HI-1 and the other residues, transmitting the information that DNA is present from all other protein residues onto HI-1; moreover, in the apo state, this relay is attenuated. Finally, HI-1 is on the receiving end of all correlated motions in the DNA-bound state, and strongly responds to the motions of all other residues when DNA is bound.

Discussion

We have used the information theory measure of transfer entropy to extract the causality of correlated motions from MD trajectories. The method dissects each pair of correlated residues into a residue that drives the motion and a residue that responds, and establishes which residues dictate the observed correlations in the system. Combined with existing techniques to calculate the correlations (for example, the Pearson coefficient (17,18) or mutual information (20)), the methods quantifies the flow of information in biomolecules, and gives new insights into how correlated motions relate to biological function.

We illustrated the method by its application to Ets-1, a protein which unfolds its HI-1 helix upon binding the target DNA sequence (30–33). The transfer entropy analysis revealed that the flow of information drastically changed upon DNA binding, showing how the presence of DNA is transmitted by correlated motions. The T6 phosphate which hydrogen-bonds Leu³³⁷ and Gln³³⁶ drives the correlations with these protein residues, activating the conformational switch. The H3 recognition helix drives the correlated motions with the DNA and with the rest of the protein in the complex. In the apo-protein, H4 is either a weak driver or weak sink for the correlated motions with the other residues, while in the complex H4 strongly drives the correlations with HI-1, and strongly responds to the motions of the rest of the protein (including the DNA-binding H1 and H3 helices). HI-1 is a strong sink for the correlations with all other residues (including the DNA) in the complex; its motion is dictated by the rest of the system. Thus, the analysis showed how the information of the presence of DNA is transmitted through the protein, from the DNA-binding H3 and H1 helices, to helix H4 and HI-1. The calculations identified a central role for helix H4 as a relay of information flow between the DNA-binding helices and HI-1 in the DNA-bound state, and showed that this relay is attenuated in the apo state.

In the Appendices, we describe the technical aspects of the calculation of transfer entropies from MD trajectories. We used several techniques to reduce the effects of noise and to speed up the calculation, and statistical analyses to estimate the optimal values of the m and τ embedding parameters. To verify the accuracy and robustness of our implementation, we have performed extensive tests on a large variety of (noisy) dynamical systems (data not shown). Our implementation provides robust estimates of the transfer entropy, and merely requires a trajectory from a standard MD simulation. Given the importance of correlated motions for biological function, we expect that transfer entropies will be useful for the study of a wide range of biomolecular systems.

Appendix A: Transfer Entropy

In practice, we calculate the transfer entropy from the Shannon information entropy H. Using μ ≡ (m, τ), μ + 1 ≡ (m + 1, τ), and the formulation of the transfer entropy as conditional mutual information (Eq. 5),

$$\begin{array}{c}{T}_{\text{j}\to \text{i}}=I\left({\mathrm{I}}_{k+1};{\mathrm{J}}_k^{{\mathit{\mu }}_{\text{j}}}|{\mathrm{I}}_k^{{\mathit{\mu }}_{\text{i}}}\right)\\ =H\left({\mathrm{I}}_k^{{\mathit{\mu }}_{\text{i}+1}}\right)-H\left({\mathrm{I}}_k^{{\mathit{\mu }}_{\text{i}}}\right)-H\left({\mathrm{I}}_k^{{\mathit{\mu }}_{\text{i}}+1},{\mathrm{J}}_k^{{\mathit{\mu }}_{\text{j}}}\right)+H\left({\mathrm{I}}_k^{{\mathit{\mu }}_{\text{i}}},{\mathrm{J}}_k^{{\mathit{\mu }}_{\text{j}}}\right)\text{.}\end{array}$$ (7)

The Shannon entropy (41) is given by

$$H\left({\mathrm{I}}_k^{{\mathit{\mu }}_{\text{i}}}\right)=-\sum _{k}p\left({\mathrm{I}}_k^{{\mathit{\mu }}_{\text{i}}}\right)\log p\left({\mathrm{I}}_k^{{\mathit{\mu }}_{\text{i}}}\right),$$ (8)

where the sum is over all states.

In general, the length of the discrete time processes and the number of states are limited by the sampling. To correct for the finite sampling, we use (42)

$$H\left({\mathrm{I}}_k^{{\mathit{\mu }}_{\text{i}}}\right)=\ln N-\frac{1}{N}\sum _k{n}_k\mathit{\psi }\left(n_k\right),$$ (9)

where sum is over all states, n_k is the frequency of observing state k, and ψ(x) is the derivative of the γ-function (42). Similar expressions can be obtained for the other Shannon entropy terms in Eq. 7. To reduce the effect of noise and to speed up the calculations, we do not use the states ${\mathrm{I}}_k^{{\mathit{\mu }}_{\text{i}}}$ and ${\mathrm{I}}_k^{{\mathit{\mu }}_{\text{i}+1}}$ directly. Instead, we use the technique of symbolization (28,43–46) as described in Appendix D.

Appendix B: Shuffling of Data and Normalization of Transfer Entropies

Since the probability distributions of the time series are not known a priori, the computation of the transfer entropy is complicated and subject to noise (27). Moreover, for large time shifts τ_i and τ_j, a broad joint distribution will be obtained. For such a broad distribution, the transfer entropy can be different from zero even when there is no causal link between the two time series (27). The use of an effective transfer entropy ${\overline{T}}_{\text{j}\to \text{i}}^{\text{E}}$ based on the shuffling of data removes this effect (27,29). We have adopted this measure in our implementation.

The shuffling of a time series I or J completely removes any link between I and J without changing their distributions (27,29). This means that the transfer entropy calculated from a shuffled time series can serve as a significance threshold, to distinguish information flow from artifacts due to insufficient sampling. The new measure is the effective transfer entropy (29)

$${\overline{T}}_{\text{j}\to \text{i}}^{\text{E}}=T_{\text{j}\to \text{i}}-\frac{1}{N_{\text{trials}}}\sum _{n=1}^{N_{\text{trials}}}{T}_{{\text{j}}_{\text{shuffled}}\to \text{i}},$$ (10)

where the second terms represent the averages over all the N_trials random shufflings of the time series. In this study, we used N_trials = 100. The effective transfer entropy is normalized by (27)

$$T_{\text{j}\to \text{i}}^{\text{E}}=\frac{{\overline{T}}_{\text{j}\to \text{i}}^{\text{E}}}{h\left({\mathrm{I}}_{k+1}|{\mathrm{I}}_k^{{\mathit{\mu }}_{\text{i}}}\right)},$$ (11)

where

$$h\left({\mathrm{I}}_{k+1}|{\mathrm{I}}_k^{{\mathit{\mu }}_{\text{i}}}\right)=-\sum _{k=0}^{N_{\text{m}}}p\left({\mathrm{I}}_{k+1},{\mathrm{I}}_k^{{\mathit{\mu }}_{\text{i}}}\right)\log p\left({\mathrm{I}}_{k+1}|{\mathrm{I}}_k^{{\mathit{\mu }}_{\text{i}}}\right)$$

is the entropy rate. In Eq. 11, $T_{\text{j}\to \text{i}}^{\text{E}}$ is distributed in the interval [0, 1]. The preferred direction of flow is given by the normalized directional index $D_{\text{j}\to \text{i}}^{\text{E}}$ (27,28)

$$D_{\text{j}\to \text{i}}^{\text{E}}=T_{\text{j}\to \text{i}}^{\text{E}}-T_{\text{i}\to \text{j}}^{\text{E}},$$ (12)

where $D_{\text{i}\to \text{j}}^{\text{E}}$ is in the interval [−1, 1]. All our reported results are based on the effective transfer entropies, and the normalized directional index (Eq. 12).

Appendix C: Optimization of the M and τ Embedding Parameters

The correct choice of the m and τ embedding parameters is crucial for the proper characterization of the structure of the time series (Eq. 1) (47–49). The objective is to properly describe the dynamics of a lower dimensional space (here, the fluctuations r_i of a subset of atoms) from the full dynamics of the system, where, as an additional complication, the full dynamics are given as discrete solutions of the continuous equation of motions. For example, very small values of τ will result in strongly correlated state vector elements, whereas large values will result in elements that are randomly distributed in the m-dimensional space; the projected trajectories will cross for small values of m, whereas for large values of m, noise will start to dominate and the computation becomes more expensive. This problem has been extensively studied in dynamical systems theory (47–51), and the reader is referred to the original literature for an in-depth treatment of the subject. For example, the mathematical concepts for selecting the state vector dimension m have been reviewed in Noakes (50) and Sauer et al. (51). Several methods have been proposed for estimating the optimal values of m and τ simultaneously (47,48), as well as a method in which they are individually optimized (49). Since a comparison showed its superiority (49), we largely followed the latter approach.

In this approach, the time lag parameter τ is chosen as the time at which the mutual information I(I_k;I_k+τ) has its first minimum (49,52,53). For this purpose, the mutual information is written as a function of τ,

$$\begin{array}{c}I\left({\mathrm{I}}_k;{\mathrm{I}}_{k+\tau },\tau \right)=\sum _{k}p\left({\mathrm{I}}_k,{\mathrm{I}}_{k+\tau }\right)\log \frac{p\left({\mathrm{I}}_k,{\mathrm{I}}_{k+\tau }\right)}{p\left({\mathrm{I}}_k\right)p\left({\mathrm{I}}_{k+\tau }\right)}\\ =H\left({\mathrm{I}}_k\right)+H\left({\mathrm{I}}_{k+\tau }\right)-H\left({\mathrm{I}}_k,{\mathrm{I}}_{k+\tau }\right),\end{array}$$ (13)

where I_k is the value of the time series I at time k, and I_k+τ at time k + τ. Since the calculation of the probability depends on the number of bins used, a dependence of the Shannon entropy on the number of bins is expected (49). In our implementation, we optimize the number of bins, by using the number of bins that maximizes the Shannon information entropy (H(I_k)). As convergence criterion for the number of bins, we use |H(N_bins + 1) − H(N_bins)| < 0.0001; using this method, we optimized τ_i for each atom i.

The optimized number of bins and the optimized time-lag parameters for the C^α atoms of apo-Ets-1 and the Ets-1-DNA complex are shown in Fig. 3. For both systems, τ varied between 1 and 17, and the number of bins between 300 and 450. The value τ is closely correlated to the flexibility of the atoms: the larger the flexibility, the larger the value of τ.

Figure 3.

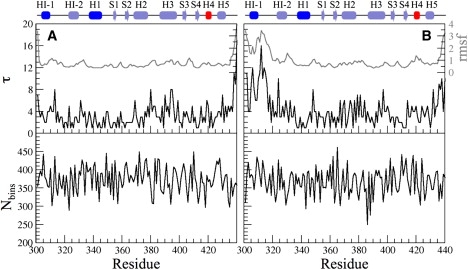
Optimized number of bins (N_bins) and time lag parameters (τ) for the C^α atoms of Ets-1. The root mean-square fluctuation (in Å) of the C^α atoms of Ets-1 is shown in shaded representation. (A) Apo-Ets-1. (B) Ets-1-DNA complex.

After optimizing the time shifts, we used the false nearest-neighbors method (47–49) to obtain the optimal estimate for m. In this method, the Euclidean distance between two state vectors I_k^μ and I_l^μ in the m-dimensional space is given by

$$R_{\text{i}}^m={\left(\sum _{n=0}^{m-1}{\left(r_{\text{i}}\left(t_{k+n\tau }\right)-r_{\text{i}}\left(t_{\text{l}+n\tau }\right)\right)}^2\right)}^{1/2}\text{.}$$ (14)

For notational clarity, we have dropped all subscripts i in μ_i, τ_i, and m_i. The state I_l^μ with the smallest distance is the nearest neighbor of I_k^μ; we will denote the index l of the nearest neighbor by NN. Extending I_k^μ and I_NN^μ by one element into (m+1)-dimensional space, the distance between the extended states is given by

$$R_{\text{i}}^{m+1}={\left({\left(R_{\text{i}}^m\right)}^2+{\left(r_{\text{i}}\left(t_{k+m\tau }\right)-r_{\text{i}}\left(t_{NN+m\tau }\right)\right)}^2\right)}^{1/2}\text{.}$$ (15)

This distance is normalized against the distance in m-dimensional space (52):

$${\gamma }_{\text{i}}^m={\left(\frac{{\left(R_{\text{i}}^{m+1}\right)}^2-{\left(R_{\text{i}}^m\right)}^2}{{\left(R_{\text{i}}^m\right)}^2}\right)}^{1/2}=\frac{|r_{\text{i}}\left(t_{k+m\tau }\right)-r_{\text{i}}\left(t_{NN+m\tau }\right)|}{R_{\text{i}}^m}\text{.}$$ (16)

Here, γ^m_i is compared to a threshold value R_tol, which is determined a priori (49,52) and recommended to be 15 (49,52). If γ^m_i exceeds R_tol, then I_NN^μ is a false nearest neighbor of I_k^μ and f_NN, the frequency of false nearest neighbors, is increased by one. The value of m is increased until f_NN approaches zero. The procedure is repeated to optimize m_i for each atom i.

Fig. 4 shows m and f_NN for apo-Ets-1 and the Ets-1-DNA complex. Similar values were obtained for both systems, with m varying between 6 and 9.

Figure 4.

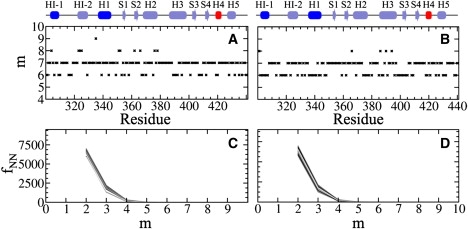
Optimized embedding state dimension m and the frequency of false nearest neighbors f_NN for the C^α atoms of Ets-1. (A) m for apo-Ets-1 and (B) the Ets-1-DNA complex. (C) f_NN for apo-Ets-1 and (D) the Ets-1-DNA complex.

Appendix D: Coarse-Graining of the Time Series

The calculation of the transfer entropy can be greatly sped up, and the effects of noise can be substantially reduced by using the technique of symbolization (28,43–46). In this method, a symbolic sequence {$\hat{\mathrm{I}}$₁, $\hat{\mathrm{I}}$₂, …, $\hat{\mathrm{I}}$_N} is associated with the time-series {I₁, I₂, …, I_N} through coarse-graining (43–45). In the coarse-graining, all information concerning the dynamics of the series is suitably encoded using a partitioning of phase space. The time-series {I₁, I₂, …, I_N} is converted into a symbolic sequence by the rule

$${\hat{\mathrm{I}}}_{\text{j}}\text{=}{\hat{\mathrm{S}}}_{\text{k}}\text{if}{\mathrm{X}}_{\text{k}}\text{<}{\mathrm{I}}_{\text{j}}\text{<}{\mathrm{X}}_{\text{k}+1},$$ (17)

where $\{{\mathrm{X}}_0,{\mathrm{X}}_1,\cdots ,{\mathrm{X}}_{N_{\text{b}}}\}$ is a given set of N_b + 1 critical points, and $\{{\hat{\mathrm{S}}}_0,{\hat{\mathrm{S}}}_1,\cdots ,{\hat{\mathrm{S}}}_{N_{\text{b}}-1}\}$ is a set of N_b symbols, here the numbers 0, 1, 2, etc. Concatenation of the symbols of a subsequence of length m yields the word w_I,

$$w_{\hat{\mathrm{I}}}=\sum _{\text{i}=1}^m{N}_{\text{b}}^{m-\text{i}}{\hat{\mathrm{I}}}_{k+\left(\text{i}-1\right)\tau },$$ (18)

where k indicates the starting position of the subsequence along the sequence {$\hat{\mathrm{I}}$₁, $\hat{\mathrm{I}}$₂, …, $\hat{\mathrm{I}}$_N}. A particular subsequence is uniquely characterized by the word w_I.

The probability of finding a particular value of w_I is calculated from the simulation data, and used to compute the Shannon entropy

$$H\left({\hat{\mathrm{I}}}_k^{\mathit{\mu }}\right)=-\sum _{\left\{w_{\hat{\mathrm{I}}}\right\}}p\left(w_{\hat{\mathrm{I}}}\right)\log p\left(w_{\hat{\mathrm{I}}}\right)\text{.}$$ (19)

Since the time series {I₁, I₂, ···, I} is mapped onto the symbolic sequence {$\hat{\mathrm{I}}$₁, $\hat{\mathrm{I}}$₂, …, $\hat{\mathrm{I}}$_N} uniquely (i.e., the symbolic representation is injective), the entropies H($\hat{\mathrm{I}}$^μ_k) and H(I^μ_k) coincide (54).

We obtain the critical points {X} for a particular series by maximizing the entropy with respect to all possible partitions. Increasing the number of critical points will initially increase the information entropy, but after a sufficient number of critical points, the information entropy plateaus. At this point the optimum number of critical points has been reached: a further increase will not increase the accuracy of the calculation, but does slow down the computation. In our implementation, we optimize both N_b and {X} by maximizing the Shannon entropy through a Monte Carlo approach. We chose N_b = 2, 3, 4, and 5 and randomly selected N_b + 1 critical points X in the range from the minimum to the maximum observed value of the time series. This process is repeated many times (here, 10,000 times) to yield the N_b and X for which the information entropy was a maximum. In a similar way, the joint Shannon information entropy of two discrete symbolic processes {$\hat{\mathrm{I}}$₁, $\hat{\mathrm{I}}$₂, …, $\hat{\mathrm{I}}$_N} and {$\hat{\mathrm{J}}$₁, $\hat{\mathrm{J}}$₂, …, $\hat{\mathrm{J}}$_N} is calculated as

$$H\left({\hat{\mathrm{I}}}_k^{{\mathit{\mu }}_{\text{i}}},{\hat{\mathrm{J}}}_k^{{\mathit{\mu }}_{\text{j}}}\right)=-\sum _{\begin{array}{l}\left\{w_{\hat{\mathrm{I}}}\right\}\\ \left\{w_{\hat{\mathrm{J}}}\right\}\end{array}}p\left(w_{\hat{\mathrm{I}}},w_{\hat{\mathrm{J}}}\right)\log p\left(w_{\hat{\mathrm{I}}},w_{\hat{\mathrm{J}}}\right),$$ (20)

where the sum is over all {w_I} and {w_J} states. Usually the entropy is measured in units of bits; in this case, the logarithmic functions in Eqs. 19 and 20 are computed with base N_b. The Shannon entropies of Eqs. 19 and 20 are used to calculate the transfer entropy of Eqs. 7 and 10.