Education and Cognitive Ability as Direct, Mediating, or Spurious Influences on Female Age at First Birth: Behavior Genetic Models Fit to Danish Twin Data

Abstract

The authors study education and cognitive ability as predictors of female age at first birth (AFB), using monozygotic and dizygotic female twin pairs from the Middle-Aged Danish Twin survey. Using mediated regression, they replicate findings linking education (and not cognitive ability) to AFB. But in a behavior genetic model, both relationships are absorbed within a latent variable measuring the shared family environment. Two interpretations are relevant. First, variance in AFB emerges from differences between families, not differences between sisters within the same family. Second, even in a natural laboratory sensitive to genetic variance in female fertility—during demographic transition—the variance in AFB was non-genetic, located instead within the shared environment.

Biological thinking and genetic models have not often been a part of the sociologist’s toolbox in the past. But this is changing (e.g., Udry 1995; Conley and Bennett 2000; Shanahan, Hofer, and Shanahan 2003).² Wilson (1998) introduced the concept of consilience, in which methods and theories from different disciplines merge into metadisciplines, fringe disciplines, or subdisciplines. Wilson noted an asymmetry between the social and medical sciences, suggesting that the integration of social science methods into the medical sciences has been relatively smooth, whereas medical and biological thinking (and especially genetic reasoning) has not been as easily integrated into many areas of social science, including sociology. The emerging subdiscipline of biodemography (e.g., Vaupel et al. 1998; Rodgers and Kohler 2003; Wachter and Bulatao 2003) illustrates that this asymmetry is beginning to abate, though it bears noting that scholars from outside sociology are providing much of the impetus for this type of consilience.

Social science research is filled with apparently causal relationships that, when subjected to modern scrutiny, turn out to be complete artifacts, or at least tenuous. Mill (1874, bk. 3), in writing on logic and induction, stated his fifth canon of scientific inquiry, the “Method of Concomitant Variation”: “Whatsoever phenomenon varies in any manner whenever another phenomenon varies in some particular manner, is either a cause or an effect of that phenomenon, or is connected with it through some factor of causation.” The last reference in this description is, in modern language, what scientists refer to as a confounding variable. Another type of “factor of causation,” the mediator variable, has been receiving substantial recent attention.

Mediation models are a relatively new methodological innovation used to help account for spurious causal assertions (e.g., Baron and Kenny 1986; Bollen and Stine 1990; MacKinnon, Warsi, and Dwyer 1995; MacKinnon et al. 2002; Preacher, Rucker, and Hayes 2007). Mediation occurs when a third variable intervenes as the probable or putative cause of the apparent causal relationship between two other variables. Within standard linear models, mediation can be represented as the product of certain regression coefficients estimated from simple and multiple regression models (see MacKinnon et al. [1995] for a full specification). These various mediation models are one type of methodological instantiation of Mills’s fifth canon.³

The focus of this article is to dig deeper into a causal relationship identified by a number of authors in the past: the relationship between intelligence, education, and age at first birth (AFB). Scholars of the demographic transition—the rapid drop in fertility that accompanies technological development—point to components of this relationship as among the several interrelated causes of the transition. Potential causes of declining fertility include improved medical care, reduction in infant and maternal mortality, and increased female career and educational opportunity (see Bulatao [2001] for eight different theoretical perspectives on fertility transition).

We demonstrate that standard mediation analysis appears to provide a clear answer to the question of whether education, cognitive ability, or both are causal influences on AFB. However, this conclusion is shown to be misdirected when it is viewed in the context of a richer and more complex modeling approach that embeds the mediation analysis within a behavior genetic model. The first analytic model based on regression methods is a traditional analysis from within sociology and related disciplines. The second is a traditional analytic method used in behavior genetics, though seldom in sociological or demographic research (but see Rodgers, Kohler, et al. [2001], who demonstrated behavior genetic fertility analysis of a different cohort of twins from the Danish Twin Registry; see also Van den Oord and Rowe 2001). Rutter (2003, p. 33) argued that although behavior genetic studies characterized as pure “heritability studies” are limited because they do not account for causal processes, multivariate behavior genetic designs are extremely valuable because “cross-trait analyses can be very informative about causal mechanisms.” This type of cross-trait analysis is the basis for our study of the link between cognitive ability and education as predictors and AFB as the outcome. Those relationships may mediate one another or may be mediated by other relationships. Further, the relationships or their causal mediators may emerge from genetic causation or from environmental causation. Finally, those relationships may be embedded deeply within the family, or they may primarily occur between families, reflecting differences among families but not among the siblings within families.

One approach to our study would be to show how an empirical answer to a standard sociological question transforms into a different answer when genetically informed data and models are used. Part of our presentation does indeed take this approach: a mediation model embedded within a behavior genetic design will result in a shift in our causal understanding. In addition, however, there is a way to frame our results that sociologists may find especially satisfying. We will demonstrate that in a setting that is finely tuned, in unique ways, for genetic answers to emerge, the empirical results speak strongly in favor of social and family-based environmental causes. As Plomin and Rende (1991, p. 162) noted, “The power of behavioral genetics lies in its ability to consider nurture as well as nature—that is, environmental as well as genetic sources of individual differences in behavior.”

To summarize, we organize this article into the following sections. First, we discuss the motivation for our article in relation to demographic transition theory. Second, we review previous literature, focusing on studies that motivate both the methods and the substantive orientation of our study. Third, we describe our data, measures, and models. Next, we present results of a family-level mediated regression analysis of the relationship of cognitive ability and education to AFB, followed by a decomposition of the original correlations, variances, and covariances using a behavior genetic analysis of individual-level data. We conclude with interpretations. Those interpretations explicate and expand our understanding of within- and between-family dynamics; an additional level of richness is added by considering the demographic transition in Denmark.

MOTIVATION: FERTILITY TRANSITION

The demographic transition, characterized first by falling mortality rates, then by falling fertility rates, all in the context of improved health care, has been studied extensively in the demographic sociological literature. The framework involves a complex and highly interrelated network of social, cultural, and biological processes. Untangling the causal relationships has been a complicated enterprise, with only partial success (see, e.g., papers in Bulatao and Casterline 2001). Among the several interrelated dynamics of fertility decline during the demographic transition, education typically plays an important role through several different channels. For example, increases in female education can facilitate increased female labor force participation, income, and bargaining power (e.g., Rosenfeld 1996; Bulatao 2001). Further, education of children can increase as part of a quality-quantity trade-off involving fewer but more highly educated children (e.g., Becker 1991; Watkins 2000; Casterline 2001).

Fertility transition is, almost without exception, directed toward reductions and not increases in overall fertility (Casterline 2001). There must be powerful social or cultural incentives to reduce fertility, because there are powerful evolutionary incentives not to (e.g., Haaga 2001). One of those incentives is, undoubtedly, the attractiveness to women of education and career development. But is this cause or effect? Do women substitute these activities because time is more available in the context of postponed and lower childbearing demands, or do they postpone childbearing as a direct effort to achieve education and career opportunities?

Haaga (2001), in a treatment of fertility decline from an evolutionary perspective, argued for the importance of “cognitive dimensions” as a relatively unexplored feature of the fertility transition framework. He calls these dimensions “factors that might connect aspirations and fertility behaviors” (Haaga 2001, p. 56). For example, intelligent and educated women presumably can manage their childbearing with efficacious contraception. This observation helps motivate the competition we set up between cognitive ability and education as explanations for the timing of the onset of fertility. The question we hope to untangle is whether it is education or cognitive ability (and its positive correlation with education) that drives this process.

We use AFB within this framework because of the role that onset of childbearing plays within fertility transition as countries approach or experience below-replacement fertility. For example, AFB has increased within the United States and other developed societies in recent decades (Morgan 1996; Sullivan 2005), and AFB is an important indicator for the second demographic transition (e.g., Van de Kaa 1987; Lesthaeghe and Neidert 2006). This concept has been used to describe the rise of new living arrangements, such as cohabitation, and delayed and low fertility as a society transforms in part through a shift to postmaterialistic values (also see Knudsen 1993). Second, previous empirical results suggest that within low-fertility countries, the onset of childbearing may be a more relevant biosocial measure of fertility than number of children (e.g., Kohler, Rodgers, and Christensen 1999), because of its substantial variation across individuals, its strong connection to education and human capital accumulation (especially for women), and its strong empirical link to the second demographic transition framework. Finally, AFB is often associated with other features of the family environment, many of which are important aspects of demographic transition theory, including socioeconomic status (SES), parental education, and parental IQ (see, e.g., Wichman, Rodgers, and MacCallum 2006).

In earlier research based on almost 100 years of the Danish twin data, Kohler et al. (1999, 2002) used measures of completed family size and having at least one child to document moderate effects of the shared family environment and low genetic effects, except for cohorts experiencing two periods of demographic transition. The pattern was reversed for cohorts born in the late 19th century, who experienced rapid fertility decline during the first demographic transition, and for cohorts born after around 1950, who experienced the second demographic transition. Based on these findings, Kohler et al. (1999, 2002) further developed a theory that during fertility transition with rapidly changing fertility patterns, latent genetic variance is realized.⁴ This release of variance occurred when fertility behavior was strongly normative, and genetically based individual differences between females in their motivation for childbearing were suppressed by the social norms regarding childbearing. Only in societies with reproductive choice and effective contraception is genetic variance in childbearing motivations likely to be expressed as observed fertility differentials. This theory, and the subsequent empirical support, motivates our linking of onset of fertility behavior (maternal AFB) to fertility transition theory. Kohler and Rodgers (2003) further investigated the education-fertility link using the Danish twin data, although they did not use AFB within their study. Heaton and Forste (1998) suggested that there should be an education-fertility link in countries undergoing demographic transition, but not elsewhere.

These findings can be interpreted in relation to the demographic transition in Denmark. Fertility choice theory leads to the prediction that, during demographic transition, and in other settings with emerging fertility choice, the relative importance of heritabilities should increase. In natural fertility regimes, on the other hand, norms regulating fertility override individual differences in fertility motivation. Udry (1996) suggested that only when the family’s role in defining appropriate fertility behavior abates do underlying and latent genetic differences have the potential to emerge. This theory plays an important role in the interpretation of our results.

The demographic transition is especially interesting in relation to the data used in our study. There have been two demographic transitions identified in Denmark (Van de Kaa 1987). The first occurred in the late 19th century, and the second followed World War II (see Knudsen [1993] for a presentation of these and more recent fertility statistics). The members of the Middle-Aged Danish Twin (MADT) survey—especially older members—began reproductive behavior shortly after the end of World War II, in the late 1940s, the 1950s, and the 1960s, during the second demographic transition. Kohler et al. (1999) estimated a time series of heritability coefficients using data from the Danish twin registry (but not including the MADT sample) and showed that the proportion of variance in completed family size associated with genetic differences rose during both demographic transitions, especially during the second one, a finding consistent with fertility choice theory.

PREVIOUS LITERATURE

Substantial evidence exists linking increases in (especially female) education and AFB (Wilkie 1981; Rindfuss and Hirschman 1984; Jeffery and Basu 1996; Heaton and Forste 1998). Rindfuss and St. John (1983) showed education to be the most powerful determinant of the timing of first birth in the United States, and Kreyenfeld (2006) argued for the causal influence of maternal education on patterns of AFB in Germany. Retherford and Sewell (1989) used Wisconsin data and found a significant correlation between intelligence and AFB, but in a mediation analysis they discovered that education mediated the link from intelligence to AFB and was the more likely causal antecedent. Rowe, Vesterdal, and Rodgers (1999) used National Longitudinal Survey of Youth (NLSY) data to model income and found the same pattern as Retherford and Sewell (1989): education was a more direct (and likely causal) antecedent for differences in income than intelligence.

Neiss, Rowe, and Rodgers (2002) replicated Retherford and Sewell’s (1989) results using the same variables in the NLSY. They defined a model in which IQ and education were used as predictors of AFB. The starting point of their analysis was a correlation between IQ and AFB (r_IQ,AFB) of .31. Following that, in a simple path model with IQ predicting both education and AFB, and education simultaneously predicting AFB (a standard mediation model), r_IQ,ED = .78 and r_ED,AFB = .26, whereas the original IQ-AFB correlation dropped substantially when controlled for education: r_IQ,AFB = .11. Obviously, most (about two-thirds) of the observed correlational link between IQ and AFB passed through education in these data. But in this study, the correlations and variances/covariances linking these variables were also decomposed into their kinship components. This analysis suggested that a direct mediating influence of education on AFB was no longer meaningful, once the underlying factors associated with genetic and shared environmental variance were defined: “The association between IQ, education and age of first birth was carried through the common genetic and environmental influences” (Neiss et al. 2002, p. 272). In other words, the behavior genetic analysis suggested that the patterns in the conventional mediation model were illusory. Rather than directly influencing AFB (as earlier findings suggested), Neiss et al. found that education and IQ are part of a general configuration of both environmental and genetic factors that are shared among these three variables. This finding illustrates how genetically informed designs can lead to fundamental revisions in traditional sociological results. The Neiss et al. methodology is similar to the one we adopt in this article.

It is important for the conceptual orientation of this current study to distinguish causal processes that occur within families from those that occur primarily outside the family environment. For example, the long-standing and often-observed negative relationship between birth order and intelligence that has been demonstrated in many cross-sectional data sets (e.g., Belmont and Marolla 1973) has recently been identified as a between-family effect with little if any within-family status. In other words, birth order (a variable measuring differences between children within families) has been a proxy within cross-sectional data sets for many between-family differences that appear to be the actual causal agents (e.g., SES, education, parental IQ, etc.). When IQ patterns were studied among siblings within families in the NLSY (and other data sets as well), the negative birth order–intelligence relationship substantially weakened or even disappeared (e.g., Rodgers et al. 2000; Rodgers 2001; Wichman et al. 2006). Within the current study, we will also distinguish between these two sources of variability to identify whether the emerging patterns have within-family status or rather reflect differences between families (or possibly both).

METHOD

Data

The Danish twin registry is one of the oldest and most complete twin registries in the world (see Christensen et al. [2006] and Skytthe et al. [2002] for additional information and references). Information on Danish twins is available going back to cohorts born in 1870, including virtually every twin pair born in Denmark since that time (the few exceptions are instances of nonresponse due to emigration, and for the cohorts born from 1870 to 1930, only twin pairs surviving to age 6 were registered). The registry is organized in sections based on birth cohort and interview method. In the current study, we use the MADT sample, a random sample from the population of twins born from 1931 to 1952. The surveyed sample contains 40 twin pairs from each annual birth cohort within each of three genetic categories: monozygotic (MZ) twin pairs, dizygotic same-sex (DZSS) twin pairs, and dizygotic opposite-sex (DZOS) twin pairs. The total MADT sample size is 5,280 individual twins, or 2,520 twin pairs (including 240 twin pairs that were not complete).

In 1998, when twin respondents ranged in age from 46 to 67, a 1.5-hour survey was administered that collected information on (among other variables) education, cognitive ability, and fertility. Eighty-three perecent of the surviving twins in the MADT sample completed this survey. The primary dependent variable in the current study, AFB, was only collected from females, and thus we focus on female twin pairs. The resulting sample sizes used in subsequent analyses include 330 MZ female twin pairs (660 individual twin respondents) and 291 female DZ twin pairs (582 individual respondents), a total of 621 twin pairs with 1,242 individual respondents.

Measurement Scales

Education was measured by combining two separate questions related to basic schooling and vocational schooling. There are six ordinal coding categories, which range from ninth-grade education or less, coded as 1, to more than four years of academic education (e.g., doctor, economist, lawyer, or MSc Engineering), coded as 6. Female MZ and female DZ education means were virtually identical (for MZ twins, mean = 2.80, SD = 1.5; for DZ twins, mean = 2.78, SD = 1.5.) Another study that has used this measure of education is Osler, McGue, and Christensen (2007).

Cognitive ability was measured as a composite of the five cognitive scales administered to Danish twin respondents in 1998. Those scales were developed to reflect cognitive functions that are sensitive to aging, including fluency (the number of animals named in one minute), digit-span forward (a short-term memory task that involves repeating strings of numbers), digit-span backward (a more difficult short-term memory task that involves repeating strings in the opposite of the order in which they were presented), digit symbol substitution (a timed digit substitution task), and delayed recall (a long-term memory task). An older Danish twin sample was used as a norming sample, and Z-scores were computed for each scale, then summed. Across a sample of 4,186 MADT respondents, lower-bound reliability (coefficient α) was .74, with two-year stability of the composite of .71 (N = 3,018). The mean cognitive ability scale score was 4.8 for female Danish twins (SD = 3.5). Female MZ twins had a mean of 5.0 (SD = 3.3), and DZ twins had a mean of 4.6 (SD = 4.6). McGue and Christensen (2001) used this scale in earlier research.

We used retrospective self-report to measure AFB. This measure had a mean of 24.3, a standard deviation of 4.1, and a range of 16–39. The distribution of AFB was approximately bell-shaped, with a slight positive skew. For female MZ twins, the mean AFB was 24.13 (SD = 5.5), and for female DZ twins it was 24.00 (SD = 4.2). There is obviously missing data on the AFB variable as a result of natural censoring; our analysis only treats female twin pairs in which both members of the twin pair had given birth.

To assess potential selection bias due to this censoring, we computed means for our three variables. The first members of female twin pairs in which both sisters had children had means of 4.8 (SD = 3.5) for cognitive ability, 2.7 (SD = 1.5) for education, and 24.0 (SD = 5.6) for AFB. These compare to the first twins whose sisters had not had children, whose means were 5.6 (SD = 3.7) for cognitive ability, 3.1 (SD = 1.5) for education, and 25.1 (SD = 3.8) for AFB. There was an approximate 6:1 ratio of twin pairs in which both sisters had children to those in which at least one had not (slight differences were due to idiosyncratic missing-data patterns).

Analysis Plan

First, we fit simple phenotypic models to predict AFB from cognitive ability, education, and a combination of the two. Next, we fit mediation models to investigate whether education mediated the cognitive ability link to AFB, and vice versa. Figure 1 is a pictorial representation of the phenotypic mediation model. The latent variables for cognitive ability (COG), education (ED), and AFB are each measured with two indicators, the scores of each member of the twin pair (without distinguishing MZ from DZ twins, in this analysis). The suffix numbers in figure 1 refer to twin 1 and twin 2 (and the loadings are constrained to be equal). Because the twin scores are combined in the latent variables, this is actually a model based on family measures; no within-family variance is accounted for by this model. The variances on the latent variables are fixed to 1, which creates standardized latent variables. This structural model was investigated in the phenotypic analysis, and these links are investigated here as well (but in the context of the behavior genetic structure defined in the measurement model).

Fig. 1.

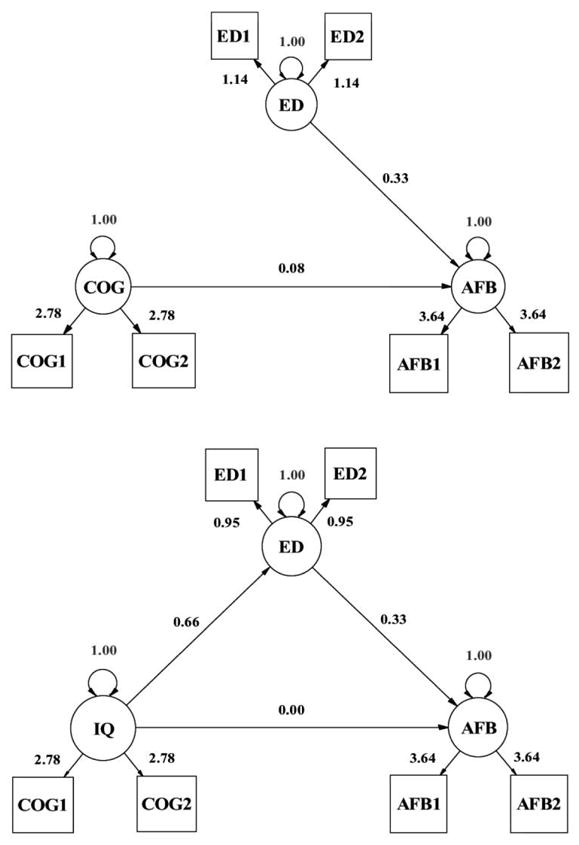
The top portion is the basic phenotypic model, predicting AFB from cognitive ability (COG) and education (ED). The bottom portion is the overall mediation model, predicting AFB from COG and ED.

Next, we use the MZ-DZ twin structure to partition the variances into genetic, shared environmental, and nonshared environmental variance (the last of which is confounded with measurement error within the standard behavior genetic model applied to twin designs). The phenotypic regression analysis uses only between-family variance, whereas the behavior genetic analysis is based on both within- and between-family variance, which will be important in the interpretation of our results. Further, in this analysis, we investigate the same links between the primary variables as we do in the phenotypic analysis (but in the context of the behavior genetic structure defined in the measurement model). In the behavior genetic analysis, we can identify whether there are common factors associated with genetic variance or shared common environmental variance (using multivariate behavior genetic analyses). Common (shared) environmental variance emerges from processes common to siblings within a family, processes that act theoretically to make siblings similar to one another. Nonshared variance, sometimes called “unique variance,” emerges from processes that make siblings different.

The overall multivariate behavior genetic model that we will fit is shown in figure 2. Though the model appears to be complex, there is a great deal of redundancy within the model, and the complexity is only apparent. The presented model is only half of the overall model, for just DZ twin pairs. The MZ model is almost identical. Within the figure, the left half of the model is for the first member of the twin pair, and the right half is for the second member.

Fig. 2.

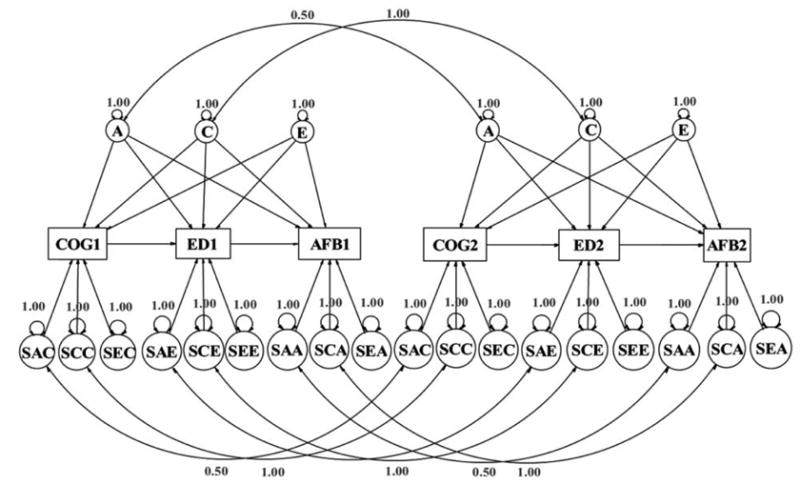
Overall behavior genetic model for DZ twins. In the six latent variables at the top of the figure, A = additive genetic variance, C = shared environmental variance, and E = nonshared environmental variance or measurement error. In the 18 latent variables at the bottom, the first two letters are either SA (specific additive genetic variance), SC (specific shared environmental variance), or SE (specific nonshared environmental variance or measurement error); the third letter is either C (cognitive ability), E (education), or A (age at first birth).

Behavior genetic models that partition the overall variance into a genetic/shared environment/nonshared environment and measurement error structure are often called ACE models in the behavior genetic literature (e.g., Neale and Cardon 1993). Despite the complexity of its appearance, the model contains only three basic processes. The three latent variables (denoted with circles in fig. 2) are labeled A for additive genetic variance, C for common environmental variance (also called shared environmental variance), and E for a combination of error variance and nonshared environmental variance (note that these last two sources of variance, non-shared environmental and error variance, are inherently confounded in twin designs). This type of multivariate model is called a “competing pathways” ACE model in the behavior genetics literature, because each of the latent variables is allowed to potentially define a link to each of the measured (manifest) variables, denoted by rectangles.

Within figure 2, a number of double-headed arrows are included that connect across twin pairs, which represent correlations. In this DZ model, a double-headed arrow links the two As, with fixed coefficients of .50, because DZ twins share (on average) 50% of their segregating genes. Another double-headed arrow links the two Cs, with fixed coefficients of 1.0 (because DZ twins share 100% of their shared family environment). The MZ twin model for the three latent variables on the top of the diagram is the same, except that the correlation link between the As is 1.0, because MZ twins share 100% of their genes. There are equivalent double-headed arrows for the specific sources of variance at the bottom of the figure, linking equivalent As and Cs from the two sides of the diagram. The fixed coefficient of the link between As is 1.0 for MZ twins and .50 for DZ twins. Cs are linked with a coefficient of 1.0 for both twin-pair types.

Obviously, the ACE latent variables at the top of the diagram are shared by the three measured variables; this is the multivariate part of the model. The latent variables at the bottom account for variance specific to each source. The first letter in each of these variable names is S, for “specific.” The second letter is A, C, or E, depending on which of these three components it represents. The A, C, and E components are correlated (as shown by double-headed arrows) across the two members of the kinship pair in the same way that the shared factors at the top are linked. The third letter is either C (for cognitive ability), E (for education), or A (for AFB). It is important conceptually to recognize that every single latent variable within this model accounts for exactly one of these three types of variance: genetic (A), shared environmental (C), or nonshared environmental/measurement error (E).

The two halves of the structural diagram in figure 2, corresponding to twin 1 and twin 2, are identical for each type of twin pair. The coefficients associated with the paths from the latent variables to the measured variables (the squares) are estimated by the model-fitting routine. However, the equivalent coefficients for each member of the twin pair, and across the two types of twin pairs (MZ and DZ), are constrained to be equal within this model. In other words, the genetic influence represented by the latent variable A is assumed to be the same for each member of the twin pair and for both MZ and DZ twins. Thus, there are 20 parameters to be estimated in figure 2 (one for each single-headed arrow on the left-hand side going from a latent variable to a measured variable, as well as the two between the measured variables) from the six variances and 15 covariances associated with COG1, ED1, AFB1, COG2, ED2, and AFB2. With 21 variances and covariances for MZ twins and 21 for DZ twins (a total of 42 original data values), there are 22 degrees of freedom available to test the fit of the model. Or, if correlations instead of covariances are used (which would provide standardized parameter estimates), there are 15 correlations each for the MZ twins and the DZ twins, leaving 10 degrees of freedom to test the fit of the model. When submodels are estimated, these will have more degrees of freedom to test the fit (because all of the original correlations and covariances are used, but fewer parameters are estimated). The links from latent to measured variables are referred to in the structural equation modeling (SEM) literature as the measurement model. Because the latent variables are assumed to be the causal sources of the measured variables, these measurement models imply a factor analysis. The latent variable variances are fixed at 1.0 so that their measurement scale is a standard scale. In addition to the measurement model, causal arrows between the measured variables are also linked within the structural model (e.g., in fig. 2 we define two single-headed arrows linking cognitive ability to education and education to AFB).

The typical model-fitting exercise involves evaluating the importance of the various links within the model. In each case, we evaluate whether the increase in fit that occurs by including the link is enough to justify the loss of parsimony (i.e., the increased complexity) associated with adding the link. We are searching for simpler models than the one shown in figure 2, models that fit nearly as well as the general model but have greater parsimony. These questions are evaluated within the fitting routine by comparing likelihood statistics (usually −2 log likelihood) that have relationships to the theoretical chi-square distribution and can therefore be evaluated statistically using the chi-square test. Alternatively, Akaike information criterion (AIC) or root mean square error of approximation (RMSEA) fit statistics can be used to evaluate the fit of the model (though the loss function used to optimize the solution is based on the likelihood-based statistics). For our purposes, we used the SEM program Mx, which was originally developed as a specialized behavior genetic SEM fitting routine. We also present 90% confidence intervals (CIs), which are the default CIs constructed within Mx using a sophisticated routine (see Neale and Miller 1997) that involves moving each parameter estimate within the likelihood space—and allowing other parameter estimates to shift optimally at the same time—until the limits of the 90% CI are identified. Using a 90% CI instead of a 95% CI tunes the model-fitting routine to err on the side of including variables rather than excluding them. Thus, the variables that are eventually included within the final model are ones that were given substantial opportunity to explain the sample variances and covariances.

The behavior genetic model described above has a number of important assumptions that underlie the legitimacy of the model. The first assumption is that genetic influences combine additively. Many interesting genetic influences are nonadditive (e.g., genetic dominance, or epistasis). Behavioral geneticists call the proportion of variance associated with purely additive effects “narrow-sense heritability,” as opposed to “broad-sense heritability” (which accounts in addition for nonlinear genetic variance). There are diagnostic indicators of violation of the additive model (e.g., large negative estimates associated with the common environmental variance, denoted c²), and methods have been proposed to account for genetic dominance (e.g., Waller 1994). A second important assumption is that there is ignorable assortative mating on the outcome of interest. Positive assortative mating would be a source of genetic similarity in DZ twins that is not accounted for by the model, and by leaving it out, one would allow heritability coefficients estimating additive genetic variance to be biased downward. This assumption has been investigated in a number of studies, which typically suggest small though nonzero assortative-mating indicators. However, these coefficients are not typically of a size that would substantially bias or influence the results (see, e.g., Plomin 1990). A third assumption, the equal environments assumption (EEA), is the most controversial (though it is also well studied, and its robustness properties are well understood by behavior geneticists). This assumption is that “monozygotic (MZ) and dizygotic (DZ) twins are equally correlated in their exposure to environmental events of etiologic importance for the trait under study” (Kendler et al. 1993, p. 21). If, for example, MZ twins are more similar than DZ twins for environmental reasons, this would violate the EEA. For certain outcomes (such as clothing choice), young MZ twins are likely to be treated more similarly by their parents than DZ twins. But most outcomes, including the ones within our study, are less likely to violate the EEA. Both theoretical and empirical support exists suggesting that MZ and DZ twins are not differentially treated by their parents and family environments in ways that would affect the similarity of their intelligence, education, or AFB. For example, Kendler et al. (1993) showed that when parents are incorrect about zygosity, there are no effects of perceived zygosity on a number of investigated traits and behaviors. Further, the effects of violating the EEA are well known and can be used to frame the results against possible nonrobustness (Rutter [2003] offers a less optimistic view).

RESULTS

In table 1, we present twin correlations and covariances showing the basic relationships between cognitive ability, education, and AFB (measured both across the twin pairs and within twin individuals). The COG-AFB correlations are marked with one asterisk, and the ED-AFB correlations are marked with two. Studying these patterns shows that education correlates slightly more than cognitive ability with AFB.

TABLE 1.

Overall Twin Correlations, Variances, and Covariances for Twin 1 and Twin 2 in Female Danish Twin Pairs in MADT Sample

	COG1	ED1	AFB1	COG2	ED2	AFB2
COG1 …	12.20	.39	.13*	.35	.28	.12*
ED1.....	2.00	2.23	.24**	.28	.61	.18**
AFB1 …	2.18	1.74	24.31	.12*	.18**	.28
COG2 …	4.23	1.47	2.01	12.20	.39	.13*
ED2.....	1.47	1.36	1.34	2.00	2.23	.24**
AFB2 …	2.01	1.34	6.79	2.18	1.74	24.31

Note.— Correlations are above the diagonal, variances on the diagonal, and covariances below. COG = cognitive ability; ED = education; AFB = age at first birth. Suffix nos. indicate twin 1 or twin 2.

^*COG-AFB correlation.

^**ED-AFB correlation.

Figure 1, which has already been described, contains the coefficients estimated by fitting the phenotypic regression model. The zero-order estimated coefficient between COG and AFB (without including education in the model) was a regression coefficient of .20. In a simple multiple regression form of this model (the top portion of fig. 1), b_COG→AFB = .08, and b_ED→AFB = .33. But when the mediation model was defined (the bottom portion of fig. 1), the original coefficient of b_COG→AFB = .08 went to 0, b_COG→ED = .66, and b_ED→AFB = .31. We note that these results are very similar to those from the Neiss et al. (2002) study from the United States. MacKinnon, Lockwood, and Williams (2004) provide statistical tests and confidence intervals to test whether b_COG→AFB is still significant after introducing a mediator, although there is no point in testing whether a sample coefficient of zero is different from a population parameter of zero. The links from COG to ED and ED to AFB are both statistically significant.

Next we report the results of reversing cognitive ability and schooling within this framework. The simple zero-order relationship between ED and AFB is b_ED→AFB = .66. When we fit a mediation model, with COG mediating this large relationship between ED and AFB, there was no mediation effect. The b_COG→AFB was estimated to be exactly zero (and this is actually the same model estimated above, shown in the bottom portion of fig. 1). Thus, the two mediation analyses suggest that ED fully mediates the COG→AFB link, but COG does not mediate the ED→AFB link.

If we stopped at this point, we would conclude that education mediates all of the apparent relationship between cognitive ability and AFB in this sample (and is the more likely causal variable). However, this result can be illusory, masking the broader family effects contained in a behavior genetic model. The illusion is the result of performing an analysis based solely on between-family variance. Our next analysis uses kinship information that accounts for variance both within and across families. This analytic approach, which is the basis for behavior genetic analysis, is itself based on the correlational structure shown in table 1, except that it is separated into MZ and DZ categories.

In table 2, we present the table 1 twin correlations and covariances partitioned into the two twin categories, MZ and DZ twins. The univariate COG-ED-AFB relationships are marked with one asterisk, and the multivariate COG-ED-AFB relationships are marked with two. A brief inspection of the univariate patterns across the twin categories shows obvious genetic variance underlying COG and ED and shared environmental variance in AFB.

TABLE 2.

Twin Correlations, Variances, and Covariances for MZ and DZ Twin Pairs

	COG1	ED1	AFB1	COG2	ED2	AFB2
MZ twins:
COG1 …	10.94	.36	.12	.53*	.38**	.08**
ED1.....	1.75	2.11	.21	.38	.71*	.15**
AFB1 …	2.13	1.67	30.13	.08	.15	.19*
COG2 …	5.81	1.81	1.45	10.94	.36	.12
ED2.....	1.81	1.51	1.21	1.75	2.11	.21
AFB2 …	1.45	1.21	5.71	2.13	1.67	30.13
DZ twins:
COG1 …	13.58	.41	.15	.18*	.19**	.17**
ED1.....	2.29	2.37	.28	.19	.51*	.24**
AFB1 …	2.23	1.81	17.71	.17	.24	.45*
COG2 …	2.39	1.09	2.63	13.58	.41	.15
ED2.....	1.09	1.20	1.50	2.29	2.37	.28
AFB2 …	2.62	1.50	8.05	2.23	1.81	17.71

Note.—Correlations are above the diagonal, variances on the diagonal, and covariances below.

^*Important univariate correlation.

^**Important multivariate correlation.

In the multivariate patterns in table 2, the COG-ED link is strongly suggestive of shared genetic variance (compare the MZ correlation of .38 between the cognitive ability of one twin and the education of the other to the corresponding DZ correlation of .19). The ED-AFB link, however, shows obvious shared common environmental variance and no shared genetic variance (note the sizable cross-twin correlations of .15 and .24 for MZ and DZ twins, respectively, both of moderate size but not positively related to genetic relatedness).

When we fit the overall model in figure 2, the direct links between the measured variables (COG, ED, and AFB) were also evaluated, in the context of this overall model. By refitting the overall model in figure 2 and evaluating the various paths for their contribution to the fit of the model, we identified the best-fitting reduced model. This model is shown in figure 3, where one-half of the model (for one type of twin pair, DZ twins) is shown; estimated parameter values in the MZ half of the model are constrained to be identical. Within this model, no link can be dropped without significantly reducing the fit of the model, and no link from the original model in figure 2 can be added that significantly improves the fit. The confidence intervals are presented, and none of these contain zero within the interval. The maximum likelihood chi-square value for the model in figure 3 is 39.4 (df = 21; there are 30 independent correlations—15 for the MZ twins and 15 for the DZ twins—that are used to estimate the nine free parameters shown in fig. 3). This chi-square statistic can be used to reject the fit of this model at the .05 level. However, the AIC = −26.6, and the RMSEA = .020, results both strongly supportive of the quality of the model’s fit (an RMSEA less than .05 is typically viewed as indicating excellent model fit, while an AIC less than 0.0 indicates that the reduced model fits better than the full model when parsimony is also taken into consideration). Within the presentation in figure 3, the parameter values are standardized, for ease of interpretation. One implication of standardizing is that the squared standardized parameter values of the links into each measured variable sum to 1.0, so that we can decompose these into percentage of variances.

Fig. 3.

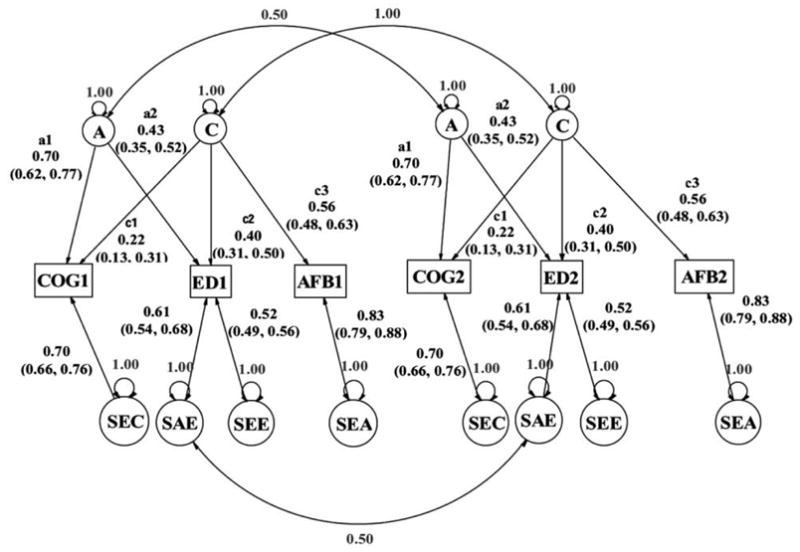
Best-fitting model from evaluation of the links in the model in fig. 2. Note that only the half of the model for DZ twin pairs is shown here; the MZ half of the model is constrained to have identical path coefficients. That model differs from this one only in that the two paths linking the latent A factors have a correlation of 1.0 instead of .5.

The joint additive genetic factor is shared only between our two primary independent variables, cognitive ability and education (not including AFB). The joint shared environmental factor is shared with all three of the measured variables. Figure 3 can be further inspected for the patterns among the specific latent variance sources for each measured variable, which are at the bottom of the diagram.

Of particular note is that, in addition to the model’s depiction of the behavior genetic relationships among these variables, there are no longer any significant links among the three measured variables. These links dropped out empirically; they were not constrained to be zero, but rather were estimated by the model to not contribute to the best-fitting model. Because of its interpretational importance, we note that even the link between education and AFB, which had a high coefficient in the phenotypic model, dropped out once the kinship structure was accounted for.

In addition to the results in figure 3, we also present statistics from this analysis in table 3, which presents the univariate heritabilities (h²) and shared environmental variance (c²) estimated for each of our primary variables (and we add the Neiss et al. [2002] results to show the similarity). AFB had no univariate heritability, so it had no genetic variance to overlap that of cognitive ability or education in figure 4 (and note the absence of patterned correlations or covariances in relation to genetic category in table 2). But there is substantial c² underlying AFB, and a large proportion of this has multivariate overlap with the variance from cognitive ability and education.

TABLE 3.

Univariate Heritabilities (h²) and Shared Environmental Variances (c²) from This Study and Neiss et al. (2002)

	This Study	Neiss et al.
h2:
COG …	.52	.32
ED.....	.48	.50
AFB …	.00	.06
c2:
COG …	.02	.35
ED.....	.25	.23
AFB …	.26	.20

Fig. 4.

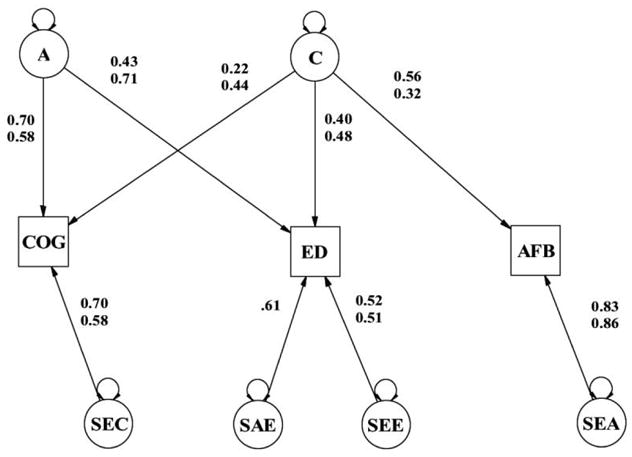
Comparison of standardized parameter estimates from best-fitting models from this study and from Neiss et al. (2002). (Note that only one-quarter of the model is shown here, for only one member of a twin pair, and only one type of twin.) Neiss et al. parameter estimates are in parentheses below the ones from the current study.

Our ultimate outcome variable in this study is AFB among the female Danish twins. According to our best-fitting model in figure 3, the variance in that outcome can be attributed to two sources. Sixty-nine percent (.83²) of its overall variance is unique nonshared or measurement error variance. The remaining 31% (.56²) of it is shared common environmental variance shared with both education and cognitive ability. This is the most interesting source of variance, for scientific and policy-related purposes, because it suggests that education, cognitive ability, and AFB operate as a single factor, rather than being separated as previous research using simpler models implied.

DISCUSSION

Substantive Findings and Interpretations

We first consider the mechanisms that motivate a look at the relation between education or cognitive ability and age at first birth. In relation to the link between cognitive ability and AFB, motivating questions are, Do women who delay childbearing do so because of their intelligence? Are smart women better at using birth control? Are smart women financially better off and thus able to afford medical support (efficacious birth control or medical abortions) for delayed childbearing? Are smart women less motivated to have children?

In relation to the link between education and AFB, the motivating questions overlap the ones just stated, but they differ in important ways. Does education have a causal influence on AFB? The first important subquestion relates to causal direction: Do women delay childbearing to pursue education, or do women who are highly educated know how to delay childbearing, or both? This question of causal direction does not have a parallel in the same link for intelligence, because it is unlikely that delaying childbearing would lead to increased cognitive ability (which is theoretically closer to a trait concept than acquiring education is). This is a strong logical argument, because evidence for the former link (delayed childbearing→education) is not logically confounded with the same link for cognitive ability. Previous research has addressed this question. For example, Wilkie (1981) and Rindfuss and Hirschman (1984) found that an increase in women’s schooling preceded a decrease in fertility. Johnson and Rodgers (2006) obtained explicit indicators from medium and low-income women who had recently given birth that documented considerable perceived loss of educational opportunity because of childbearing. The current study, however, as well as Neiss et al. (2002), focused on the causal direction in which there is “competition” in explaining AFB, the one from either cognitive ability or education to AFB.

However, our empirical findings move these questions concerning specific links into the background and render them virtually irrelevant. What do our analytic patterns suggest about the links between education and cognitive ability and AFB? First, the mediated regression analysis was consistent with a common finding in the research literature (e.g., Retherford and Sewell 1989), that education, not cognitive ability, is causally related to AFB. If we were to stop at this finding, we would develop scientific and policy implications for the role of education in affecting women’s AFB.

However, these direct links are absorbed within the behavior genetic structure of the competing pathways factor model, suggesting that these individual pieces are not where the most important part of the story is told. First, in terms of the genetic components, education and cognitive ability share common genetic variance. This is not surprising, because the genetic components of cognitive ability would themselves act to create educational opportunities in many different ways (also see Tambs et al. 1989; Rowe et al. 1999). But these are our two independent variables, and this finding does not address our central question. The second common factor combines cognitive ability, education, and AFB through a common latent variable accounting for shared (common) environmental variance. This finding suggests that the rearing family environment is implicated in the common variance underlying individual differences between AFB, cognitive ability, and education.

These patterns can best be described in relation to within- and between-family variance (see Rodgers et al. [2000] for further specification of this logic). The finding that education has a strong causal influence on AFB is not technically incorrect in the context of simple models. But it is incorrect when our more complex and better-fitting (genetically informed) models are considered. The regression mediation findings only account for between-family variance. This analysis, in which the families differ on education, cognitive ability, and AFB, compares families to one another; within-family processes were not assessed, because there was no within-family variance in the data. The behavior genetic analysis is more nuanced and helps us locate the source of the causal relationships, because the design accounts for, and the data potentially contain, both within-and between-family variance. Only when between- and within-family variance are separated and explicitly modeled can we logically identify and attribute causal explanation separately to these two sources (see also Rodgers et al. 2000; Wichman et al. 2006).

The behavior genetic analysis suggests that differences in education and cognitive ability among sisters in the same family are not correlationally or causally related to differences in AFB, even though the data and model can be used to identify such relationships. Sisters share the same rearing family environment, and this shared environment is the location of the causal link from education to AFB. In other words, if two sisters have substantial differences in their educational outcomes, these are not expected to translate into differences in their AFB. But differences between families, especially in education, do result in differences in AFB. This finding parallels research locating the family structure–intelligence relationship in between-family variance, rather than the (long-believed) within-family interpretation of this relationship (Wichman et al. 2006).

The finding that education does not have as direct a link to AFB—that the link will not, for example, account for differences between sisters, but is rather absorbed by an overall factor—is not new. For example, McClamroch (1996) suggested that the link between education and AFB is itself mediated by contraceptive efficacy. Kohler et al. (1999) used a different methodology from the current study, as well as a broader subset of the Danish twins (not including the MADT subsample), but found a similar result: “The genetic influences on fertility constitute a distinct effect, rather than being merely a consequence of genetic influences on educational attainment” (Kohler et al. 1999, p. 281).

The results from the current study were similar to those from Neiss et al. (2002), which used approximately the same methodology with U.S. data from the NLSY (note that the NLSY respondents had their first births starting in the 1970s, whereas the MADT survey respondents had their first children starting in the late 1940s). However, there was a small shared genetic factor including AFB in the U.S. study. In that best-fitting model, the variance in AFB was partitioned as 74% unique variance or measurement error (compared to our 69%), 10% shared c² (compared to our 21%), 10% individual c², and 6% shared h².

We note that our dependent variable, AFB, may function somewhat differently as an outcome than many other fertility variables. The simple fact that we (as well as Neiss et al. [2002]) found relatively small heritability in AFB is one example of this. Recent studies have documented important and systematic genetic variance underlying many other fertility variables, including age at first attempt to get pregnant (Rodgers, Kohler, et al. 2001), ever having a child (Kohler et al. 1999), fertility motivation (Rodgers and Doughty 2000), age at first intercourse (Miller et al. 1999; Rodgers, Rowe, and Buster 1999), and marriage (Trumbetta and Gottesman 2000), and there have been a number of studies of direct fertility variables such as completed family size (Kohler et al. 1999; Rodgers, Kohler, et al. 2001; Christensen et al. 2003; Rodgers, Bard, and Miller 2007; see Rodgers, Kohler, et al. 2001 and Kohler et al. 2006 for summaries). One partial explanation for this lower heritability is that AFB may have substantially more random variation contained in its measure than other fertility variables. For example, in addition to a female’s own preferences and goals, AFB is affected by contraceptive failure, partner preferences and goals, infertility, and other factors outside of her control. Age at first intercourse, age at marriage, and even total number of children may be more strongly under an individual’s control than AFB. A larger error variance in AFB than in other fertility variables would place more variance into the E part of the ACE model, taking explained variance away from the A component (as well as from C). However, none of the remaining variance was identified as genetic variance, either.

Though AFB may have more random variation than other fertility variables, we frame this suggestion against an observation that provides a counterbalancing effect. The reproductive culture in Denmark involves open and early use of efficacious contraception, relatively low fertility rates, and relatively early first intercourse. As noted by Rodgers, Kohler, et al. (2001, p. 34), “In this type of culture, there is less contraceptive failure than in the United States and greater control over fertility.” The implication of this observation is that even though AFB may operate somewhat differently than other fertility variables, the Danish culture provides an excellent setting in which to study this variable, because at least some of the random processes that operate in other developed countries are not so relevant there.

We conclude this section by suggesting theoretical sources of influence on AFB that would operate as the model in figure 2 suggests. These sources by definition are shared by sisters in the same family, but would distinguish sisters in different families. The most obvious source would be characteristics of the parents, including rearing style and approaches to sex and reproductive education. Though maternal education was absorbed by the shared common environmental factor, it can also be an important contributor to the overall factor. But parental education is also a part of the overall family culture, which may extend back many generations. The overall family culture is another example of a potential influence.

Relation to Demographic Transition Theory

Denmark during the time period associated with the MADT fertility onset data was an ideal natural laboratory in which to observe genetic influences on age at first birth, for several reasons. First, the timing of the second Danish demographic transition coincided with the timing of childbearing during this cohort, and fertility choice theory (Udry 1996; Rodgers et al. 2007) links declining fertility with the release of latent genetic variance. Second, a number of significant univariate heritabilities have been identified in relation to other fertility variables in the Danish twins and more generally (Kohler et al. 1999, 2002; Rodgers, Hughes, et al. 2001). Third, multivariate relationships have been identified among fertility variables from this period and slightly later (Rodgers, Kohler, et al. 2001; Rodgers et al. 2007). But there was no genetic variance identified, even in a setting in which theory and past empirical results suggested there would likely be such variance. There was no univariate h², and the multivariate model showed that the shared c² was important, but shared h² played no role in the best-fitting model.

This finding suggests that AFB as a fertility variable may function differently from most other fertility variables. AFB does not seem to respond to the fertility choice that emerges during fertility decline (driven, at least in part, by the widespread use of effective contraception). This is not to say that AFB does not change during demographic transition—it certainly does (e.g., Morgan 1996)—but the dynamics of its change appear to have little to do with latent genetic fertility motivation being released. Rather, they are related to shared family environmental influences. These influences appear to operate fairly similarly on all females in the (Danish) family, contributing to between-family but not within-family variance. Both education and cognitive ability are measures that are part of a “family culture” that acts to broadly influence AFB.

This finding is further supported by similarities between the current study and Neiss et al. (2002). In that study, univariate and multivariate heritabilities were existent for AFB, though very low (accounting for 6% of the overall variance in AFB). There are enough differences between the U.S. family culture of childbearing beginning in the 1970s and the Danish culture of childbearing beginning in the late 1940s that we might expect processes sensitive to those cultures to be potentially different. But instead they were quite similar, adding further support for the argument that AFB has a stable and consistent (across time and culture) relation to the shared family environment, the environment in which children are raised and learn the family culture. Parents obviously have a strong role of influence within the family environment, and we posit that fundamental and cross-cultural features of that parental influence are likely to be causal within the relationships defined in our anlaysis. But in addition, there may well be influences from earlier generations that have passed on as causal influences through the parents as well (see Rodgers et al. [in press] for a cross-generational perspective on the transmission of fertility behavior). In summary, we view these results as supporting the broad and abiding power of the parents and overall family environment in affecting the AFB decision similarly across sisters from the same family.

We can speculate that high-ability Danish parents in the period around 1950–70 may have encouraged their daughters to postpone childbearing for education because they thought their daughters would benefit more from further education than from starting a family early in life. Prior to fertility transition, this encouragement probably was missing or would not have worked. But this encouragement reflected not just a focus on education, but a broader family culture that included (among other factors) nurturing cognitive excellence as well. Broadly, AFB was (explicitly or implicitly) influenced by features of this family culture. The common-factor interpretation that is supported by the current research suggests that influence on AFB existed as a part of this family cultural context, not as a separate focus, and also not distinguishable as differences between daughters in the same family.

The most important finding from this study is that features of the family environment, shared by the twins as they grew up, contributed to an underlying factor that combined cognitive ability, education, and AFB. This common factor occurred within a culture of fertility decline, in which fertility choice was both available and effective. However, the genetic variance in AFB that could have emerged, that was predictable in such a culture, and that has been identified in other fertility variables (Kohler et al. 1999; Rodgers, Hughes, et al. 2001) was not present, a finding that further supports the potency of the shared family environment in accounting for differences across families in AFB. On the basis of our findings within this study, combined with those in other studies, whether education has a direct and causal link within the family to AFB is in substantial doubt. But differences between families in their influence on AFB appear to be the dynamic and important source of this influence.