Continuous Flow Driven Inversion for Arterial Spin Labeling Using Pulsed Radiofrequency and Gradient Fields

Abstract

Continuous labeling by flow driven adiabatic inversion is advantageous for arterial spin labeling (ASL) perfusion studies, but details of the implementation, including inefficiency, magnetization transfer, and limited support for continuous-mode operation on clinical scanners has restricted the benefits of this approach. Here a new approach to continuous labeling that employs rapidly repeated gradient and RF pulses to achieve continuous labeling with high efficiency is characterized. The theoretical underpinnings, numerical simulations, and in-vivo implementation of this pulsed continuous ASL (PCASL) are described. In-vivo PCASL labeling efficiency of 96% relative to continuous labeling with comparable labeling parameters far exceeded the 33% duty cycle of the PCASL RF pulses. Imaging at 3 Tesla with body coil transmission was readily achieved. This technique should help to realize the benefits of continuous labeling in clinical imagers.

Introduction

Arterial Spin Labeling (ASL) (1,2) permits the noninvasive measurement of perfusion with MRI. Rather than injecting a flow tracer, ASL employs radio frequency and magnetic field gradient pulses to invert naturally existing water spins in the feeding arteries. The technique shows promise for clinical evaluation of central nervous system disorders (3,4) and is a useful investigational tool (5).

Labeling of arterial blood can be achieved with a number of different strategies. Continuous ASL attempts to continuously invert (2) or saturate (1) blood as it passes a particular plane. Pulsed ASL (6,7) employs a single pulse to define a volume containing arterial blood for labeling. Theoretical (8) and experimental studies (9) have demonstrated that continuous ASL produces greater signal-to-noise ratio than pulsed ASL, but the benefits can be reduced by imperfect practical implementation (10).

Practical implementation of continuous ASL faces a number of challenges. Almost all continuous ASL methods employ a variant of the original flow driven adiabatic inversion with constant RF and constant gradient (11). This basic approach can only be used to image a single slice, parallel to the labeling plane, because off-resonance saturation of the tissue of interest by the applied RF cannot be corrected accurately across multiple slices. The use of a separate, small RF coil for the labeling RF(11-13) can overcome this limitation, but it requires special hardware, a favorable labeling geometry, and usually a longer distance between labeling plane and target organ. Modifications of the continuous labeling strategy to compensate for off-resonance errors across larger volumes by modulating the RF and/or gradient waveforms have been proposed. The most widely used approach, amplitude modulation of the labeling RF for the control (14), has been successfully applied in numerous studies but it suffers from limited efficiency (15), especially as the RF field is reduced to overcome power limits at high field (9,16-18).

The implementation of all these methods is made more difficult by the limited support of continuous mode operation for long RF pulses on commercially available imagers. RF hardware on standard scanners often prevents performance of continuous labeling. RF amplifiers optimized for pulsed operation typically cannot support continuous ASL because of constraints on RF duty cycle, especially for body coil transmit. The increased prevalence of array coil reception for improved signal-to-noise ratio and parallel imaging has made body coil transmit standard even for head imaging.

This study reports the theory and implementation of a new strategy for continuous ASL using pulsed RF and gradient fields, which we refer to as pulsed-continuous arterial spin labeling (PCASL). Because the RF is pulsed, it is highly compatible with RF hardware optimized for pulsed operation. Moreover, it does not require any additional hardware. Despite the reduced RF duty cycle, the duty cycle of labeling is effectively 100%, as in standard continuous ASL. A preliminary account of this method was reported previously (19), and a recent work used a different approach to explore optimization of PCASL (20).

Theory

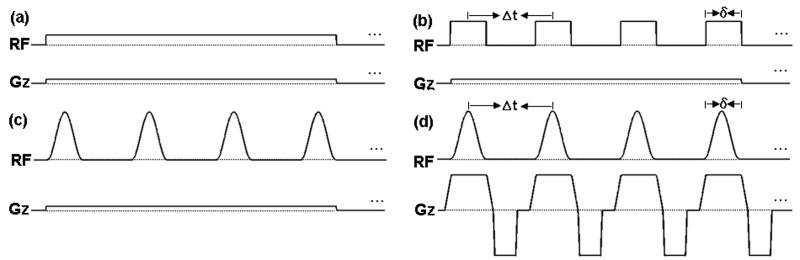
In the original implementation of flow driven adiabatic inversion, constant RF and gradient fields (Figure 1a) were applied and the flowing spins were inverted because they follow the effective field, a vector combination of the RF and gradient fields in the rotating frame, as it rotates from positive to negative (2,11). Due to the constraints on pulsed RF amplifiers in many commercial imagers, RF pulses cannot be applied in such a continuous manner. It is natural to try breaking up a continuous rectangular RF into a train of rectangular RF pulses (Figure 1b) separated by a gap. However, the rectangular RF pulse train will cause a number of aliased labeling planes. To see this, we represent the rectangular RF pulse train with rectangular width δ and spacing Δt as:

Figure 1.

Different potential RF and gradient patterns for continuous labeling. (a) constant RF pulse, constant gradient. (b) Rectangular RF pulse train, constant gradient. (c) Hanning RF pulse train, constant gradient. (d) Hanning RF pulse train, variable gradient with strong gradient during RF pulses.

$${\mathit{\text{RF}}}_b\left(t\right)=\frac{1}{\mathrm{\Delta }t}\mathit{\text{comb}}\left(\frac{t}{\mathrm{\Delta }t}\right)\ast \mathit{\text{rect}}\left(\frac{t}{\delta }\right)$$ [1]

where $\mathit{\text{comb}}(t)=\text{∑}_{n=-\infty }^{\infty }\delta \left(t-n\right),\mathit{\text{rect}}\left(t\right)=\{\begin{array}{cc}1& |t|<½\\ 0& \mathit{\text{otherwise}}\end{array}$, and * is the convolution.

The Fourier transform of RF_b(t) is given by:

$$F\left\{{\mathit{\text{RF}}}_b\left(t\right)\right\}=\mathit{\text{comb}}\left(f\mathrm{\Delta }t\right)\cdot \delta \text{sin}c\left(\pi \delta f\right)$$ [2]

From Eq. [2], one can see we have aliased labeling planes located at f = n/Δt in frequency space, modulated slowly by a broad sinc function. With a constant applied gradient g in the z direction, this corresponds to labeling planes at z= n/(γgΔt), where γ is the gyromagnetic ratio 2.675 × 10⁸ rad/s/T.

To eliminate the undesired aliased planes, a more selective RF pulse train is needed so that its Fourier response drops more rapidly. A Hanning pulse, for example, can be used instead of rectangular pulse. We can represent a Hanning RF pulse train with width δ by:

$${\mathit{\text{RF}}}_c\left(t\right)=\frac{1}{\mathrm{\Delta }t}\mathit{\text{comb}}\left(\frac{t}{\mathrm{\Delta }t}\right)\ast H(\frac{t}{\delta })$$ [3]

where H(t) is the Hanning function $H\left(t\right)=\{\begin{array}{cc}\hfill 0.5+0.5\text{cos}(2\pi t)\hfill & \left|t\right|<½\\ \hfill 0\hfill & \mathit{\text{otherwise}}\end{array}$.

The Fourier transform of RF_c(t) can be given by:

$$F\{{\mathit{\text{RF}}}_c(t)\}=\mathit{\text{comb}}(f\Delta t)\cdot F\{H(\frac{t}{\mathit{\delta }})\}$$ [4]

where

$$F\{H(\frac{t}{\mathit{\delta }})\}=\mathit{\delta }\text{sin}c\left(\pi \delta f\right)\frac{1}{2(1-{\delta }^2{f}^2)}$$ [5]

Comparing Eq. [4] and Eq. [2], we can notice that the Fourier transform of the Hanning pulse train drops quadratically faster with frequency than the rectangular pulse train. However, the response of the Hanning pulse is still too broad to remove all of the labeling planes. The first aliased labeling plane is at f =1/Δt where the Hanning response is still well above zero unless the pulse duration equals the pulse spacing, a condition incompatible with the objective of reduced RF duty cycle.

Fortunately, the RF pulse can be made more spatially selective by increasing the gradient amplitude during each Hanning pulse (denoted by G_max) relative to the average gradient applied between the center of two RF pulses (denoted by G_ave) (Figure 1d). Aliased labeling planes will occur at z= n/(γ G_aveΔt), but the first zero of the Hanning response, a reasonable measure of its effective half width, will be at z= 1/(γ G_max δ). Hence aliased labeling planes will be suppressed as long as the condition

$$\frac{G_{\max }}{G_{\mathit{\text{ave}}}}\gg \frac{\mathrm{\Delta }t}{\delta }$$ [6]

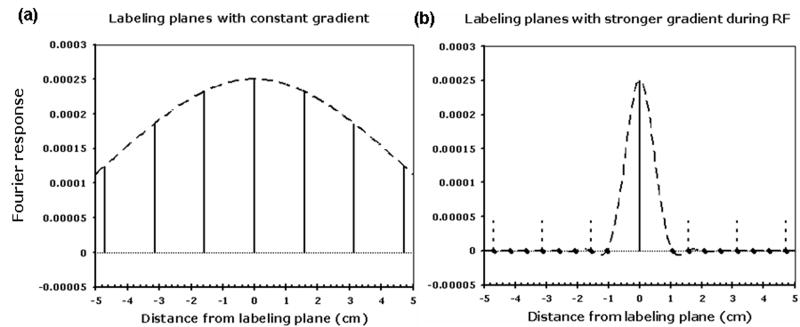
is met. The aliased labeling plane locations both with constant gradient and with strong gradient during RF pulses are shown in Figure 2a and 2b respectively.

Figure 2.

Suppression of aliased labeling planes with a stronger gradient during the RF pulse. When a constant gradient of 1mT/m is used, (a), many aliased labeling plans (solid vertical lines) are within the excitation profile of an individual RF pulse (dashed curve). When the gradient during the RF pulse is increased to 9 mT/m, without changing the average gradient, the primary labeling plane is unaffected (solid vertical line) but the aliased labeling plans, (vertical dashed lines) are suppressed because they fall outside the narrower excitation profile of the RF pulses (dashed curve). A pulse repetition time, Δt, of 1500 μs was used in this simulation.

The logic of the above paragraphs is based on Fourier analysis, which is only valid in the low tip angle regime of the Bloch equations. To justify the success of the pulsed RF approach for adiabatic inversion in the large tip angle regime, we parallel the logic of the original constant RF and gradient flow driven adiabatic inversion. Adiabatic inversion occurs if there is a gradual rotation of a steady state magnetization direction. For traditional constant RF and gradient, the steady-state direction of magnetization is along the effective field. If the effective field is slowly rotated, the magnetization tends to follow the effective field. In the case of repeated pulses of RF, a steady state also exists (21). This steady state is very similar to the corresponding steady state with constant RF and gradient, except that the steady state is a repeated pattern because of aliasing. Other work has demonstrated the strong tendency for the pulsed steady state to follow changes in RF amplitude (22), supporting its adiabatic nature.

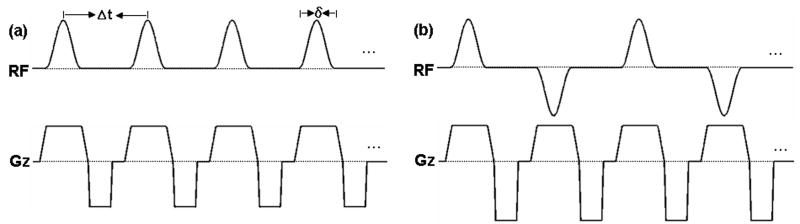
A flow driven adiabatic inversion strategy can be designed using pulsed RF and gradients by the above concepts. In the pulse sequence of Figure 3, selective Hanning shaped RF pulses are applied at equal spacing. For the label, we add some imbalance in the gradients to cause a position dependent phase shift. The average gradient over the time between pulses (denoted by G_ave) should be comparable to the value used for continuous flow driven adiabatic inversion and the average B₁ over the same time interval should be comparable to the continuous case. For the control, we choose to maintain a 180° phase shift for all positions. This is achieved by alternating the sign of the RF from pulse to pulse and assuring there is zero average gradient between each pair of pulses. In this case, the average B₁ of RF pulses (denoted by B1_ave) is zero but the averaged RF power, and hence the magnetization transfer (MT) effects, will be matched between the control and label sequence. The control sequence is essentially a True FISP sequence (23).

Figure 3.

The proposed pulsed-continuous ASL sequence: (a) the labeling pulse sequence with B1_ave ≠ 0, G_ave ≠ 0, (b) the control pulse sequence with B1_ave = 0, G_ave = 0.

In the preceding paragraphs, it was assumed that the labeling plane was located at isocenter. In general, shifting of a gradient modulated RF pulse can be achieved by modulating the frequency of the RF synthesizer with a waveform identical to the gradient waveform (24). Because the RF is pulsed during constant gradient in the PCASL sequence, this frequency modulation can be replaced with a simple frequency shift of the applied RF combined with phase shifting of successive RF pulses. The frequency shift of the RF pulses is given by the standard Δω = γ G_max Δz, where Δz is the offset distance. The phase shift between RF pulses is given by Δφ = γ G_ave Δz Δt. Since G_ave is zero for the control sequence, the phase shift is zero except for the sign alternation.

Methods

Numerical Simulation

We first used numerical simulation to explore the inversion efficiency of a wide range of the PCASL sequence parameters. The Bloch equations were numerically integrated using a previously described approach (25). The approach integrates the equations of motion by making rotations in the rotating frame of the RF around the effective field. This algorithm requires a time step size small compared to 1/γB₁, T2, and the characteristic time of any RF and gradient shape changes.

Simulations were performed for a range of average RF amplitudes (0.1 – 4 μT), average gradient strengths (0.01 - 4 mT/m), and a range of ratios of maximum gradient strength to average gradient strength (3 - 15). Relaxation times T₁ and T₂ of 1.55 s and 0.25 s for arterial blood were selected from a range of literature values (26-29). The sensitivity of efficiency to the precise T1 and T2 value was considered in additional simulations. A Hanning window shaped pulse of 500 μs duration and a spacing between two RF pulses (Δt) of 1500 μs were used. The integration was performed over a time range extending from 10 s before inversion to 10 s after inversion with an integration step size of 0.01 ms. Magnetization transfer (MT) effects were not included in the simulation. The simulation was implemented in MATLAB (MathWorks Inc., Natick, MA). It took 1 s to calculate the efficiency for each velocity on a 2.8 GHz Pentium IV Dell dimension 340, Red Hat Linux OS.

Because simulations of the amplitude modulated control approach (14) are highly sensitive to the relative timing of the RF waveforms and the time the spin crosses the labeling plane, we explored the effect of different delays between the RF waveform and the spin position timing. No detectable effect was observed on the simulations of PCASL so a single delay was used for the results shown.

Efficiency was calculated by correcting the measured efficiency at the end of integration period for the T₁ decay experienced from the time the spin crossed the labeling plane. Laminar flow was assumed to estimate the inversion efficiency over the vessel's cross-section. In laminar flow, the flow can be characterized solely by the velocity at the center of the vessel, which is also the maximum velocity, vmax, in the vessel cross-section. Calculations were performed for a range of maximum velocities (0.001-100cm/s). The efficiency for laminar flow was calculated as the weighted average of the efficiencies at many different individual velocities (25):

$$\mathit{\text{eff}}=\frac{1}{2v_{\text{max}}^2}{\int }_0^{v_{\text{max}}}v\epsilon \left(v\right)\mathit{\text{dv}}$$ [7]

Where ε(v) is the efficiency for spins with velocity v. The integration was evaluated within an error of 0.01 using the recursive adaptive Simpson quadrature algorithm (26).

In vivo Measurements

In vivo studies were performed to show the feasibility of PCASL on human subjects and to verify the consistency between the in vivo efficiency and simulation results. Two ASL strategies were implemented. First, PCASL was implemented to test for the efficiencies of the pulsed continuous labeling. A Hanning window shaped pulse of 500 μs duration, a spacing between two Hanning pulses of 1500 μs, and a labeling duration of 1.5 s were chosen for RF pulses. The RF repetition rate was limited to 1.5 ms by hardware constraints of the RF system. Second, traditional single slice continuous ASL was implemented as a reference to quantify the efficiency for the PCASL method. A square shaped pulse of 200 ms duration, and a 375 ms interval between the start of successive pulses was used to approximate continuous RF pulses. The gradient was broken up in the same manner. The 375 ms spacing was chosen so that the pulse could be repeated an integer number of times (4 times) for a total labeling duration of 1.5 s. In each 375 ms period, a 200 ms pulse was set in the middle to approximate the duration of PCASL despite reduced duty cycle. The reduced duty cycle (53.33%) of the continuous study was required by the RF hardware. A post-labeling delay (27) of 1.5 s was selected to allow enough time for the labeled blood to arrive in the region of interest. Background suppression (28,29) was performed during the labeling delay duration to minimize errors related to motion or other instabilities. This suppression employed repeated saturation of the imaged slab 4.1 s before imaging, a selective inversion pulse 3.04 s before imaging, and four nonselective inversion pulses applied 1.49 s, 0.69 s, 0.26 s, 0.06 s before the image acquisition. Three selective pulses that saturate the water protons inferior to the imaging slab were applied at 1.04 s, 0.40 s, and 0.12 s before image acquisition. Unlabeled blood flowing into the image will not be background suppressed and may contribute to pulsation artifacts on the images. The inferior saturation pulses effectively suppress the inflowing, unlabeled blood. This pulse timing was calculated using an algorithm for minimizing the squared residual background signal across a broad range of T₁. However, background suppression was not performed in one of the experiments to evaluate the systematic subtraction error between control and label because suppression tends to attenuate this error.

For quantitative evaluation, labeling strategies were implemented before a single-shot Fast Spin Echo (FSE) sequence with a partial k-space image acquisition. The sequence was performed with a TR of 6 s and a TE of 25 ms in a 5-mm-thick axial slice through the superior part of the lateral ventricles. FSE images were obtained using 64 × 64 matrix on a 24-cm field of view. Raw data were saved from each channel of the manufacturer's 8 channel head array coil. The specific absorption rate (SAR) of the 3T PCASL sequence, as determined by the manufacturer's power monitor, never exceeded 1.1 W/kg averaged over the whole body for any period of 10 seconds.

Six different subjects (four males and two females, 18-62 years old) were studied on a GE 3.0 Tesla EXCITE scanner using the receive only 8-channel head array coil and the body transmit coil, following a protocol approved by the institutional committee on clinical investigations and after obtaining written informed consent. The 1-hour scan began with a brain localizer. Next a 3-dimensional time of flight MR angiogram (TR: 31 ms; TE: out of phase; Flip Angle: 15°; Matrix: 320 × 160; Slice Thickness: 2.8 mm; FOV: 25 cm; Receiver Bandwidth: 20.83 kHz; Scan Duration: 2.03 minutes) was performed to choose the labeling location. This labeling location was selected through both internal carotid arteries and both vertebral arteries before their confluence to form the basilar artery. Because the labeling might be sensitive to off-resonance, higher-order B₀ shimming (30) was performed to optimize field uniformity in a region placed in the brain stem including the intended labeling plane. The rest of the scan was broken into three conceptually separable ASL studies. The labeling parameters of study 1 and study 2 are listed in Table 1. The third study focused primarily on systematic error sources.

Table 1.

The labeling parameters of PCASL and CASL sequence of study 1 and 2.

Parameters		Study 1	Study 2
			1	2		3
PCASL	B1ave (μT)	1.7	1.7	1.7	1.7	1.7
	Gmax (mT/m)	9	9	9	9	3
	Gave (mT/m)	1	1	0.5	1.5	1
CASL	B1ave (μT)	1.7	3.6	1.7	1.7	1.7
	Gave (mT/m)	1	2.5	1	1	1

In study 1, PCASL was separately tested for the efficiencies of both control and label methods. The efficiencies of the PCASL control and label were evaluated by comparing the images with those when the control and label slabs were symmetrically placed above the slice near the top of the head. Label and control were varied from TR to TR in a repeated pattern of (control, label, label, control), which is more robust to scanner drifts. To test for systematic errors, alternate blocks of 4 TRs were applied first below and then above the brain. These blocks of 8 TRs were then performed with the gradient sign reversed to correct for MT asymmetry (31). The sequence of PCASL was implemented for 52 repetitions. The implementation for 52 repetitions include three ‘16TR blocks’ plus one additional (control, label, label, control) pattern. In the data analysis, we throw the data from the first 4TR block (control, label, label, control) to ensure the steady state of blood flow magnetization. Continuous ASL was implemented immediately after the PCASL sequence to avoid interaction between the two ASL methods. The gradient sign reversal was also implemented in an interleaved timing to compensate for the MT asymmetry. The amplitude of average RF irradiation and average gradient in the continuous ASL were matched to PCASL. The label and control for the continuous ASL were interleaved in the same pattern as PCASL. The sequence of continuous ASL was performed for 48 total repetitions.

In study 2, the combined efficiency of PCASL as a function of labeling parameters was evaluated. We applied the labeling and control only proximal to the imaging plane. As in the first study, the continuous ASL was also included as a reference to calculate the relative efficiency. Fourteen pairs of the label and control images for PCASL and 12 pairs for continuous ASL were acquired in the sequence. Different combinations of G_max, G_ave and B1_ave for the continuous reference were tested for their effects on labeling efficiency, table 1.

In study 3, the PCASL method was tested for systematic errors due to imperfect matching of direct off-resonance irradiation effects on tissue signal for label and control. The same image center was used as the previous axial study. Coronal images were acquired for the PCASL sequence with the control and labeling applied distal to the image section at the top of the brain. For comparison purpose, we also acquired coronal images when the control and labeling were applied proximal to the image section. Twelve pairs of label and control images were acquired for signal averaging. Background suppression sequence was turned off in this systematic error study.

In a final study, PCASL labeling was performed prior to a 3D whole brain acquisition in one of the volunteers. This study served to demonstrate the feasibility of multiple slice acquisition with the PCASL labeling method. Background suppression with the selective region expanded to 192mm axial slab was performed and image acquisition was an interleaved stack of spirals fast spin echo acquisition. One of eight interleaved spiral gradient waveforms was performed for each excitation at each of 40 centrically ordered slice encodes. The eight interleaves were acquired in separate acquisitions with a TR of 6 seconds. 3 averages of label and control pairs required a total of 288 seconds. The resulting images had nominal in plane resolution of 3.4 mm and slice thickness of 4 mm.

Image Analysis

All image data were saved as raw echo intensities and reconstructed offline with custom software. Partial Fourier raw data was acquired at lines –m ≤ u ≤ N/2 (m = 6, N= 64). The low frequency phase map of each coil was estimated from the Fourier transformation of the image generated by Hanning filtering the center portion of the raw data at lines –m ≤ u ≤ m. The final image was combined from each coil image, weighted by the conjugate of the corresponding low resolution phase map. A Region of interest (ROI) for each subject was defined to contain the entire brain.

For the first study, the relative combined inversion efficiency was defined as the ratio of the PCASL average difference signal when control and label are set below the brain to the average CASL difference signal after compensating for the duty cycle difference (dividing the CASL difference signal by dcycle). dcycle is the duty cycle of continuous ASL, which is 53.33% in our study. Previous simulations of adiabatic fast passage demonstrate that the labeling efficiency may not have a linear relationship with the RF duty cycle in the pulsed-form CASL(32). Simulation was performed to calculate the mean labeling efficiency for the laminar flow across the different time when spin passes through the labeling plane. The simulation result shows that the relative efficiency is within 2% difference with the RF duty cycle. This linearity between the RF duty cycle and labeling efficiency is likely valid because of the long pulse period (375 ms) used in the CASL sequence. This improvement with longer labeling blocks (A pulse period of 100 ms was better approximated by a linear relationship than a pulse period of 20 ms) was suggested in previously reported simulations (32). The relative efficiency loss of the control pulse was defined as the ratio of the PCASL average difference signal when the control is set below the brain compared with above the brain to the average CASL difference signal after compensating for the duty cycle difference. Because of the very low SNR in the average difference signal between controls in PCASL, we used the low-resolution phase map from the average difference signal between control and label when applied below the brain to phase correct the images from each coil. The relative systematic error between control and label pulses was defined as the ratio of the average PCASL difference signal between control and label when applied above the brain to the average CASL difference signal after compensating for the duty cycle difference. The relative efficiency of labeling pulse was defined as the ratio of the PCASL average difference signal when the label is set below the brain compared with above the brain to the average CASL difference signal after compensating for the duty cycle difference. We used low-resolution phase maps to correct the phase of the image from each coil as in the relative efficiency calculation of control pulse.

For the second study the relative combined efficiency described for the first study was employed. For the third study, frequency-dependent off-resonance saturation effects were analyzed by averaging the difference images (between the control and label images) across the phase direction.

Results

Simulations

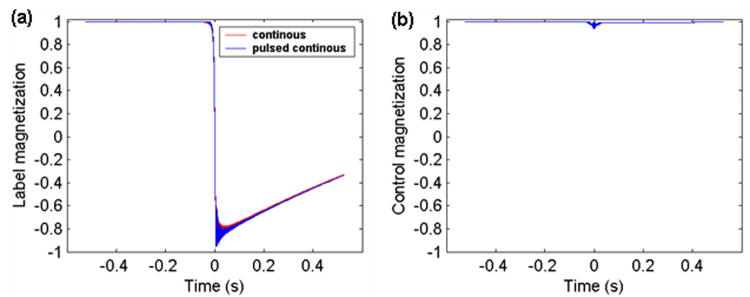
The Bloch equation simulations confirm that the behavior of inflowing spins for the PCASL experiment is very similar to the continuous labeling experiment (Figure 4a). The PCASL control produces only a slight perturbation to inflowing spins and causes less than 1% loss of longitudinal magnetization, Figure 4b.

Figure 4.

Time courses of longitudinal magnetization of spins flowing across the labeling plane at t = 0. (a) during the label for PCASL (overlaid with continuous ASL with same average gradient and average B₁ amplitude); (b) during the control for PCASL from the numerical simulation of the Bloch equations.

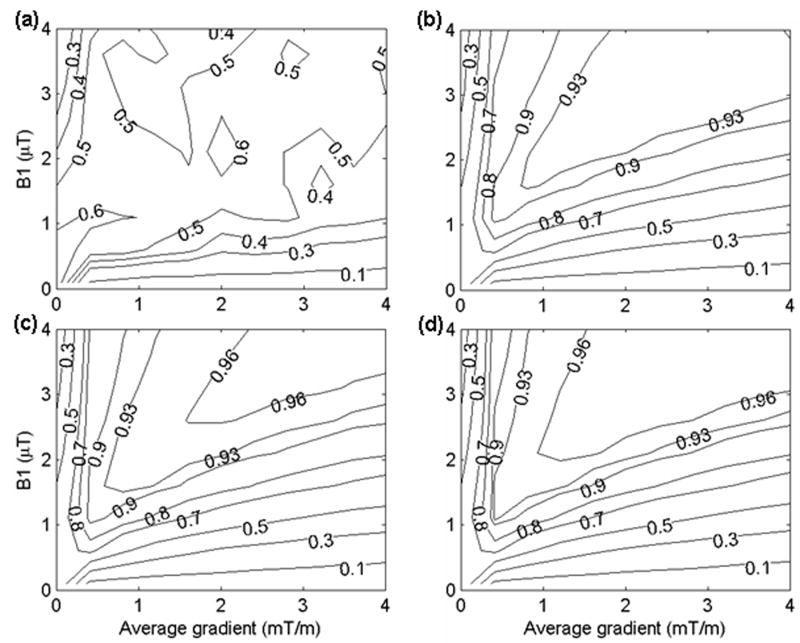
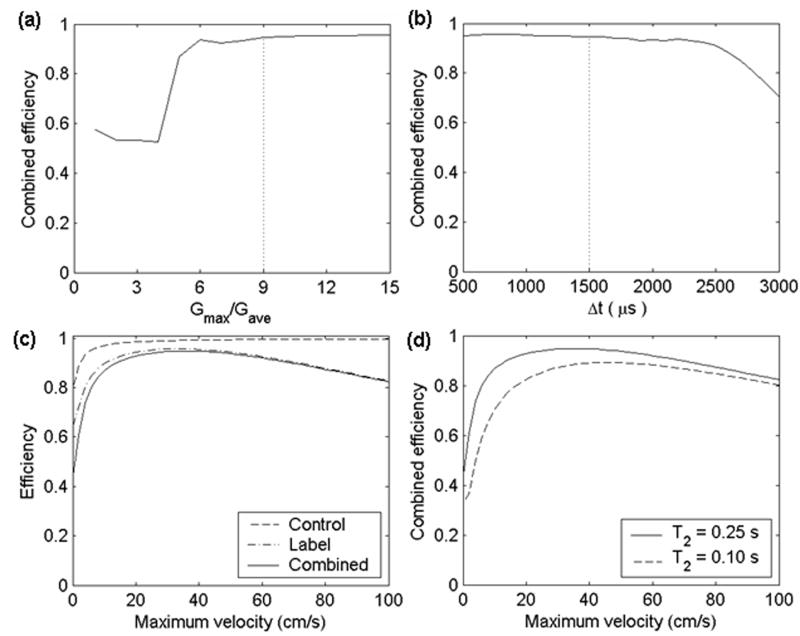
As shown in the theory section, the ratio of G_max/G_ave determines the location of the aliased labeling planes. If G_max/G_ave is too small, some of the aliased labeling planes will fall within the main lobe of the RF pulse response. The inversion efficiency was simulated as a function of RF amplitude and average gradient amplitude at several different G_max/G_ave (Figure 5). It can be seen that the labeling will suffer from inefficiency if the aliased labeling planes appear well above zero in the Fourier response of the Hanning function (Figure 5a). For G_max/G_ave ≥ 9, PCASL is similar to but slightly less efficient than continuous ASL (compare Figure 5c and 5d with Figure 2 in ref [(25)]). The inversion efficiency decreases as the average gradient increases. The inversion efficiency is an increasing function of G_max/G_ave. The bigger the ratio of G_max/G_ave is, the more efficient the labeling is. However, in reality the incremental benefit in efficiency by increasing the gradient must be weighed against the performance, peripheral nerve stimulation, and acoustic noise limits of the imaging system. To further clarify the optimization of G_max/G_ave, the inversion efficiency is plotted as a function of G_max/G_ave for a fixed B1_ave and G_ave (Figure 6a). The inversion efficiency tends to stabilize to its maximum at approximately G_max/G_ave = 9.

Figure 5.

Simulated inversion efficiency for laminar flow in a vessel as a function of RF field amplitude (μT) and average gradient amplitude (mT/m) at different ratio of G_max and G_ave: (a) G_max/G_ave = 2; (b) G_max/G_ave = 6; (c) G_max/G_ave = 9; (d) G_max/G_ave = 15. A constant maximum vessel velocity of 40.3 cm/s was assumed. An average gradient of 1 mT/m was used. This simulation is based on 500 μs Hanning shaped RF pulse and 1500 μs pulse repetition time. Contours are shown at efficiency values (0.1, 0.3, 0.5, 0.7, 0.8, 0.9, 0.93, 0.96) except efficiency values (0.4, 0.6) are added in (a) for clearer visibility of the efficiency distribution. The values shown were calculated using a correction for T₁ decay as well as velocity-weighting.

Figure 6.

Simulated inversion efficiency for laminar flow in a vessel as a function of (a) the ratio G_max/G_ave. A constant maximum vessel velocity of 40.3 cm/s is assumed; (b) time gap between two RF pulses (Δt). A constant maximum vessel velocity of 40.3 cm/s was assumed, and the maximum gradient of 9 mT/m was used; (c) maximum velocity for control and label strategy in contrast with combined efficiency. A maximum gradient of 9 mT/m was used; (d) maximum velocity (cm/s) for different T₂ blood relaxation times: T₂ = 0.25 s; T₂ = 0.10 s while keeping T₁ as a constant 1.55 s; There is no noticeable efficiency difference between T₁ = 1.55 s and T₁ = 1.3 s for fixed T₂ of 0.25s. An average RF amplitude and gradient of 1.7 μT and 1 mT/m were used in the above simulations.

The effect of the time gap between two RF pulses (Δt) on the inversion efficiency is considered in Figure 6b. The inversion efficiency begins to drop substantially at Δt of approximately 2300 μs. The flip angle of each pulse increases as Δt increases since the same average RF amplitude was used for each Δt. At this spacing of RF pulses, the flip angle of each pulse is approximately 59°. Also, the number of pulses experienced by a fast moving spin decreases with greater time gap. This suggests that high inversion efficiency requires spins to experience many small tip angle pulses while crossing the labeling plane.

Simulations indicate that the flow velocity dependence of the PCASL inversion efficiency is similar to the continuous inversion efficiency. The inversion efficiency of the PCASL label and control strategy, and combined efficiency are plotted as a function of velocity (Figure 6c). Inefficiency in the labeling of slower spins is primarily mediated by T₂ decay. The dependence of inversion efficiency on blood relaxation times was also evaluated (Figure 6d). There was no noticeable difference even if the T₁ blood relaxation time in the simulations was reduced to 1.3 s, a value well below most literature values at 3 T, but the inversion efficiency was quite sensitive to the T₂ blood relaxation time.

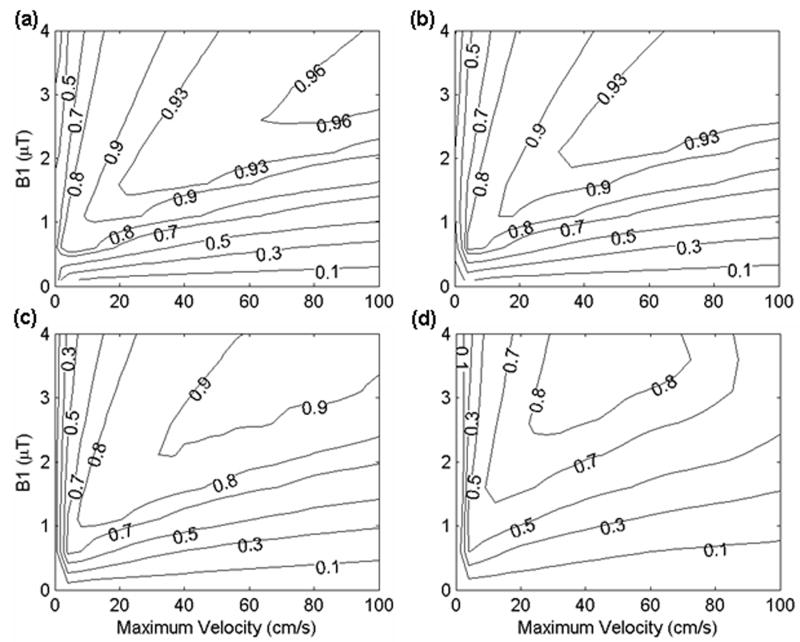
If magnetic field nonuniformity shifts the resonance frequency at the labeling plane, significant effects on the labeling efficiency of PCASL are to be expected. Off-resonance causes a shift of the labeling planes in Figure 2b. If the shift moves the labeling plane outside the slice profile of the excitation pulse, reduced efficiency will occur. It is important to investigate the sensitivity of efficiency to off-resonance. Inversion efficiency was plotted as a function of RF amplitude and velocity for different frequency offsets (Figure 7). For small offsets, the theoretical efficiency for experimental parameters easily achievable can be greater than 90% (Figure 7a and 7b). The efficiency of PCASL can be 80% at frequency offset 1/(4Δt) (equivalent to 167 Hz). As the frequency offset increased to 3 /(8Δt) (equivalent to 250 Hz), the efficiency drops to 60%.

Figure 7.

Simulated inversion efficiency for laminar flow in a vessel as a function of RF field amplitude (μT) and maximum velocity (cm/s) at (a) frequency offset = 0, (b) frequency offset = 1/(8Δt), (c) frequency offset = 1/(4Δt), (d) frequency offset = 3/(8Δt). A maximum gradient and average gradient of 0.9 and 0.1 were used. A constant maximum vessel velocity of 40.3 cm/s was assumed. Contours are shown at efficiency values (0.1, 0.3, 0.5, 0.7, 0.8, 0.9, 0.93, 0.96).

In-vivo Measurements

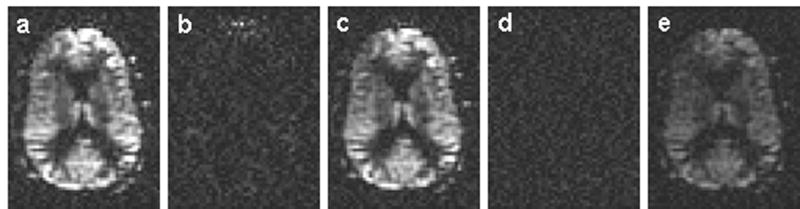
In-vivo studies confirmed the basic conclusions of the simulations. Example images are shown in figure 8. Efficiency measured in the first study was very encouraging, The efficiency (mean ± SD) relative to continuous labeling was 0.96 ± 0.14 for control minus label, 0.91 ± 0.04 for the control (1- the loss of control efficiency), and 1.06 ± 0.16 for the label. Label and control efficiencies were separately measured by subtracting images obtained with the labeling plane above the head from the labeling plane below. When label and control above the head were subtracted, a signal relative to continuous labeling of -0.01 ± 0.02 was measured, indicating little systematic error. Assuming an absolute efficiency for the continuous experiment with 1.7 μT RF and 1 mT/m gradients of 90% (from ref [(25)]) these relative efficiencies correspond to absolute efficiencies of 0.86 ± 0.12, 0.82 ± 0.04, 0.96 ± 0.15, and -0.01 ± 0.02 respectively. The results indicate that the main efficiency loss is from the control experiment.

Figure 8.

Single slice pulsed-continuous image of (a) label below – label above; (b) control below –control above; (c) control below – label below; (d) control above – label above; and 55% duty cycle continuous image of (e) label above – label below. The in-vivo experiment used an average B₁ amplitude of 1.7 μT, maximum gradient of 9 mT/m, and average gradient of 1 mT/m with 500 μs Hanning shaped RF pulse and 1500 μs pulse repetition time.

In our second study, we evaluated the effect of different gradient amplitudes on efficiency. The combined PCASL inversion efficiency relative to a power matched continuous ASL was 0.84 ± 0.10. This lower relative efficiency in this study partially reflects the higher absolute efficiency of the 3.6 μT RF and 2.5 mT/m gradient continuous experiment used (The absolute efficiency of these parameters is estimated to be 96% according to ref (25)). Using this estimate of the continuous inversion efficiency, the absolute inversion efficiency of this second PCASL study is 0.81 ± 0.10. The relative inversion efficiency of PCASL with average gradient amplitude of 0.5 and 1.5 mT/m are 0.94 ± 0.20 and 0.89 ± 0.06 relative to 1.7 μT RF, 1mT/m continuous ASL. Assuming the inversion efficiency of constant RF amplitude of 1.7 μT and constant gradient of 1 mT/m was 90% (25), leads to absolute PCASL inversion efficiencies of 0.85 ± 0.18 and 0.80 ± 0.05 respectively. Despite the fairly high average efficiency of inversion for 0.5 mT/m, the standard deviation was also high, perhaps suggesting sensitivity to velocity (15) or some other subject dependent factor. The inversion efficiency of PCASL is reduced to 0.56 ± 0.10 when the applied maximum gradient is 3 mT/m. This corresponds to 0.50 ± 0.09 absolute inversion efficiency. As supported by the simulations (Figure 5a), this low ratio of G_max and G_ave allows aliased labeling planes within the main lobe of the RF response. These aliased labeling planes can then saturate the magnetization.

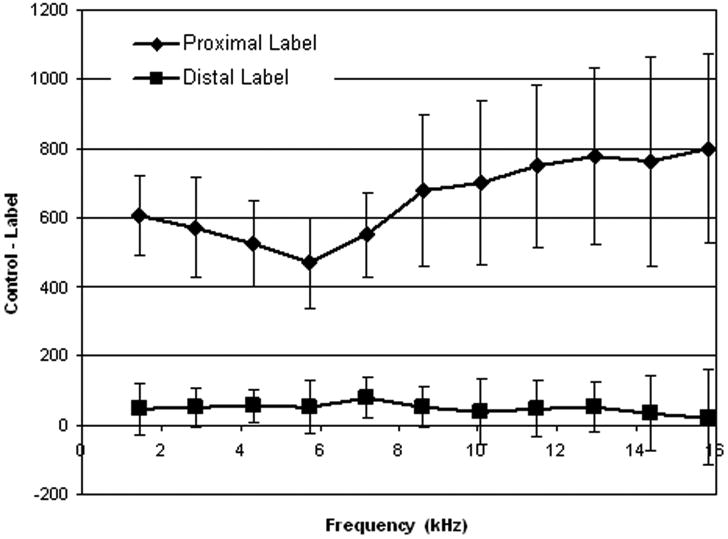
Systematic error is an additional important concern for any labeling strategy. Our measurements of the residual subtraction error when label and control are applied above the head show a very small positive error, Figure 9. This error is small compared to the perfusion signal when the label and control are applied below the brain. Still, this small level of error should be further studied. Interestingly, when background suppression is applied, as in our first in-vivo study of this work, no detectable error was measured. Background suppression can attenuate small residual subtraction error.

Figure 9.

The mean signal difference when control and label are applied distal and proximal to the imaging plane as a function of frequency offset. Distance z from the labeling plane was converted to a frequency offset using γG_maxz. Proximal labeling produces a large signal difference, while distal labeling above the brain produces a very small signal difference.

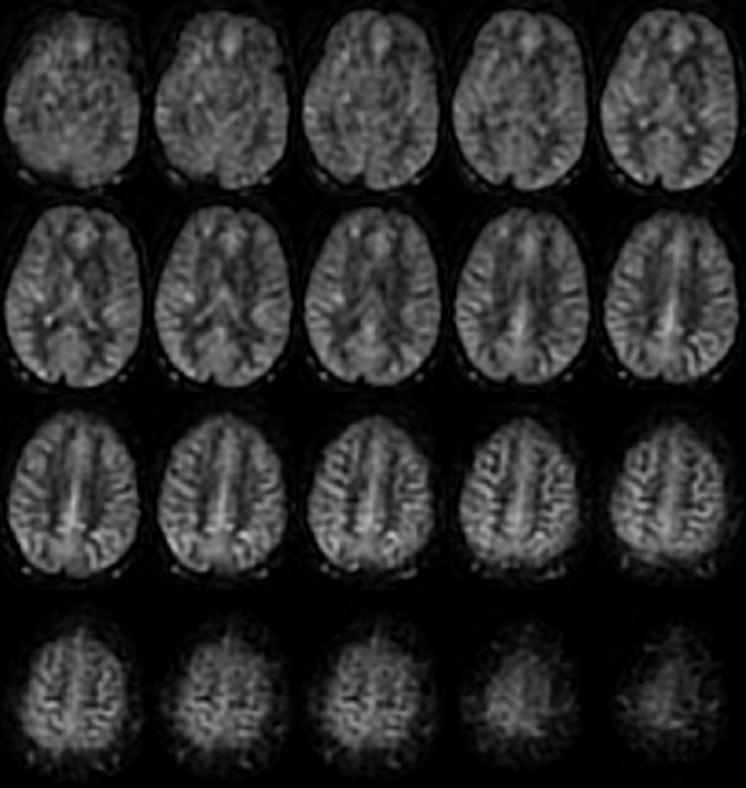
The acquisition of multiple slices using the PCASL technique is readily feasible. Label minus control difference images from a 3D acquisition (Figure 10) showed consistent perfusion contrast without contamination from artifacts or systematic errors.

Figure 10.

Multi-slice perfusion difference images from a 3D whole-brain acquisition using the PCASL label and control strategy.

Discussions

These results support the utility of PCASL as a strategy for multi-slice perfusion imaging. Single-slice imaging was used in the experiment to make the protocol in a reasonable time limit (less than 1 hour scan). PCASL appears to be a practical and efficient solution to continuous labeling on systems with only pulsed RF capability. The strategy has higher inversion efficiency than the amplitude modulated control technique (14) for comparable RF and gradient parameters. Another advantage is that the higher gradient amplitude during the RF causes more rapid drop in magnetization transfer saturation of tissue with distance from the labeling plane. Hence PCASL should be considered the preferred software method for multi-slice continuous ASL even on systems with CW capacity. Comparison of sensitivity and ease of use with hardware systems (33) for continuous labeling is an important future direction.

The similarity between PCASL and the widely used True FISP sequence suggest that PCASL will be compatible with most modern MRI systems. Since True FISP is frequently employed in body imaging with array coil reception, PCASL should also be compatible with such configurations. PCASL does require fast and accurate gradient and RF systems and is generally more technically demanding than the continuous RF and gradient of traditional flow driven adiabatic inversion. Indeed, the extent to which the residual experimental inefficiency of PCASL reported here is a result of hardware imperfections is difficult to separately assess.

Since PCASL uses pulses to achieve the desired B1_ave, it always will deposit more power in the subject than a comparable constant RF used for continuous labeling. For the 500μs Hanning pulse and 1500μs repetition time employed here, the peak RF pulse amplitude is 6× higher than B1_ave. In power limited applications, the average B₁ will have to be lowered relative to constant RF continuous labeling. Still, the advantages of multi-slice imaging and the convenience of operation on pulsed RF amplifiers make PCASL an attractive option. At 3 Tesla, we were still able to achieve high in-vivo efficiency (81% absolute efficiency) with the same power as traditional CASL for 3 T.

The in-vivo efficiency is slightly lower than predicted by the simulation. The difference of efficiency between in-vivo experiments and the simulation could be caused by the relatively high T₂ value employed. However, lower T₂ values would also affect the constant RF labeling studies. Our experiments, however, suggest that inefficiency of the control dominates the signal loss. The high loss of efficiency measured in the control, approximately 18% saturation, cannot be explained by reasonable T₂ values. Possibly magnetization transfer during the control could play a role (34,35). Despite the slight overall reduction in efficiency relative to the simulations, the changes in in-vivo efficiency with labeling parameters show excellent agreement with the simulated theoretical efficiency for all the parameters in the second study. Regression between the simulation and experimental results show a linear relationship with (in-vivo inversion efficiency) = 1.01 × (simulated inversion efficiency) - 0.11.

The effects of cardiac cycle variation of blood velocity on labeling efficiency were ignored in our simulations. Prior work simulating effects of cardiac pulsation on CASL efficiency (15,32,36) suggest that the efficiency is relatively insensitive to velocity such that cardiac cycle effects can be ignored. Cardiac cycle effects on velocity can have greater impact when the labeling and control schemes are more velocity sensitive, as for the amplitude modulated control method (15,27).

The similarities between PCASL and True FISP also suggest that off-resonance errors, which are a major challenge for balanced SSFP, should be evaluated. Our simulations suggest that off-resonance effects are small until the off-resonance produces a phase shift approaching π during one Δt. This condition is identical to the True FISP condition. In our study, we performed shimming at the labeling plane to ensure accurate measurements of efficiency. However, we have not found this to be essential for routine clinical use at 3 Tesla. Moreover, high-order shimming may cause inhomogeneity to the imaging volume, which may appear as image artifacts. Likewise, selection of labeling plane location by 3D MRA, as performed in this study, does not appear to be required. Clinical experience with this approach will be a subject of future reports.

A modification of the PCASL technique to selectively label individual vessels has been introduced by Wong (37). In that implementation, an alternative control sequence, which alternates the RF sign but leaves the gradient as in the label, is employed. This sequence has favorable properties for vessel selective labeling. However, this alternative control introduces an approximate doubling of the off-resonance sensitivity relative to the control employed here.

In summary, we have reported a successful new technique for continuous ASL that permits wider use than many previous methods. Its high efficiency, multi-slice capability, and broad compatibility with existing scanner hardware make it an attractive option for perfusion imaging and potentially angiography with ASL.