Ideal Observer Analysis of Signal Quality in Retinal Circuits

Abstract

The function of the retina is crucial, for it must encode visual signals so the brain can detect objects in the visual world. However, the biological mechanisms of the retina add noise to the visual signal and therefore reduce its quality and capacity to inform about the world. Because an organism’s survival depends on its ability to unambiguously detect visual stimuli in the presence of noise, its retinal circuits must have evolved to maximize signal quality, suggesting that each retinal circuit has a specific functional role. Here we explain how an ideal observer can measure signal quality to determine the functional roles of retinal circuits. In a visual discrimination task the ideal observer can measure from a neural response the increment threshold, the number of distinguishable response levels, and the neural code, which are fundamental measures of signal quality relevant to behavior. It can compare the signal quality in stimulus and response to determine the optimal stimulus, and can measure the specific loss of signal quality by a neuron’s receptive field for non-optimal stimuli. Taking into account noise correlations, the ideal observer can track the signal to noise ratio available from one stage to the next, allowing one to determine each stage’s role in preserving signal quality. A comparison between the ideal performance of the photon flux absorbed from the stimulus and actual performance of a retinal ganglion cell shows that in daylight a ganglion cell and its presynaptic circuit loses a factor of ~10-fold in contrast sensitivity, suggesting specific signal-processing roles for synaptic connections and other neural circuit elements. The ideal observer is a powerful tool for characterizing signal processing in single neurons and arrays along a neural pathway.

1. Introduction

A fundamental problem for all sensory systems is to detect a stimulus in the presence of noise. Detection requires the stimulus to be distinguished from the background which may include other stimuli. The problem is that noise in the evoked response introduces uncertainty about the presence of the stimulus (Shannon, 1948). Neural signals are invariably mixed with noise from a variety of sources, some in the external world, some from synaptic inputs, and some from the neuron’s biochemical and biophysical properties. The noise limits the neural signal quality and therefore its capacity to inform the brain (Geisler, 1989; Laughlin, 1989). This is exemplified in a retinal neuron such as a ganglion cell whose task is to transmit visual signals crucial for an organism’s survival (Barlow, 1981, 1982). The task of inferring the presence of a stimulus from the visual signal is easier when little noise is present, but when the noise obscures the signal, the constraints of evolution are challenged (Figure 1).

Figure 1.

A lizard at the center of image (delineated by white bars at edge) appears camouflaged by its visually noisy environment, making it difficult for a predator to detect. Eye and twig motion, rain, photon fluctuation, and biological sources add to the noise. Although the detection process in mammals is likely cortical, noise from retinal circuitry is a limiting factor for fine contrast discrimination in daylight (Borghuis et al., 2009).

Because vision and ultimately the organism’s survival depends on the ganglion cell’s signal quality, which is limited by noise and dynamic range, circuits presynaptic to a ganglion cell must have evolved, within the bounds of biological constraints, to maximize signal quality of the ganglion cell’s spike train. This suggests that presynaptic components such as retinal layers, local circuits within a layer, neurons within a circuit, and biophysical properties of the neural compartments all have specific roles in determining the ganglion cell’s signal quality. For some extensively-studied circuits of the vertebrate retina, such as the rod-bipolar pathway, much is known about how signal and noise are processed to benefit the ganglion cell’s signal quality (Barlow et al., 1971; Taylor & Smith, 2004; Dunn et al., 2006). However, although the general response properties of retinal cell classes, e.g. horizontal, bipolar, amacrine and ganglion cells are known, the exact functional role for most cell types and their specific circuits is not --and investigation into their specific effects on the ganglion cell’s signal quality has only just begun (Freed, 2005; Levine, 2007; Murphy & Rieke, 2008; Borghuis et al., 2009).

To determine the role of each circuit component, a method is needed to measure and compare signal quality between different neurons and stages of the circuit. To be relevant to survival, the measured signal quality must be a metric that can be related to a behavioral task performed by the organism. A basic measure of the quality of a neural response is its signal-to-noise ratio (SNR), the ratio of the amplitude of a signal to its associated noise (Figure 2) (Fechner, 1851; Hecht et al., 1942; Rose, 1942; Barlow, 1957, 1978, 1982; Green & Swets, 1988; Meister & Berry, 1999; Dhingra et al., 2003, 2005; Cohn, 2004). With accurate measurements of SNR from recordings of the ganglion cell and neurons in its presynaptic circuit, their contribution to signal quality might be determined. This goal seems achievable because a wide variety of methods for testing specific points in the circuit are available, for example, multi-electrode recordings, functional imaging, specific knockouts and pharmacological blockers, and biophysically-based computational models. If signal quality in the ganglion cell and its presynaptic circuit could be objectively compared, one might locate the noise sources that limit the ganglion cell’s capacity to inform the brain, and determine the specific roles for each component of the ganglion cell’s presynaptic circuit. Further, if one could identify the spatio-temporal components of the evoked response that can inform about a behaviorally-relevant stimulus, this would provide a tentative definition for the neural code, and these informative components could be compared along a pathway. What is needed is a behaviorally-relevant method applicable to a wide variety of signals, and a rationale for how to apply it.

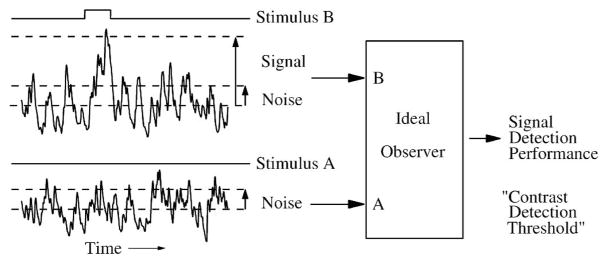
Figure 2.

A fundamental task for a sensory system is to detect a stimulus in the presence of noise. The ideal observer analyzes the responses to a pair of stimuli (A,B) to discriminate between them on the basis of a statistical description of the signal to noise ratio (SNR). As the amplitude of stimulus B is increased, its probability of being detected in the neural response increases, which characterizes the neural system’s performance (right). In this example, stimulus A is null, and the visual task is called “detection”. For the purpose of this example SNR is the amplitude of the signal of interest (the evoked response) divided by the standard deviation of the associated noise.

In this synthesis, we describe a paradigm to objectively measure the SNR of a neural signal. The basic ideal observer method we describe is widely used and well-matched for use on retinal signals. We cannot claim that it is the best one for measuring neural signal quality, because several appropriate methods exist and others are actively being developed (see Appendix). The ideal observer’s advantage is that it accurately measures binary discriminations using a decision rule defined by the sensory task, which provides a metric of signal quality in units of the tested stimulus parameter (e.g. contrast sensitivity), and is therefore appropriate for comparison with behavioral results (Parker & Newsome, 1998). However, to go beyond an understanding of the basic method, i.e. to measure behaviorally-relevant SNR through the retina and identify specific roles for circuit components, one must have an appreciation of the signal processing roles of retinal circuitry, the effect of noise sources and receptive fields on SNR, and a basic understanding of how to track sensitivity along a pathway. These principles and an introduction to ideal observer analysis are included in this article. Although we present some practical details, this article is not intended to be a comprehensive “how-to” manual, but rather a thorough introduction to the application of ideal observer analysis to the retina.

2. Ideal observer

An ideal observer determines the sensitivity of a neural system to an incremental change in a stimulus. In a discrimination task, the ideal observer chooses the stimulus with the highest probability given the neural responses. As a practical example for characterizing retinal signals, we outline a method using a discriminant template. The following sections build on this example to show how the ideal observer can objectively compare neural signals.

2.1. The sensory task

To evaluate the SNR of a specific system, one decides 1) what stimulus parameter to test, 2) what sensory task is to be performed, and 3) how the responses are to be measured (Barlow, 1962; Geisler, 1989; Thibos & Levick, 1990; Parker & Newsome, 1998). For the visual system, (1) stimulus contrast is a commonly tested parameter. (2) Classification of the response based on amplitude is a common task. However, the best stimulus for a task is not always known at the outset (Parker & Newsome, 1998; Johnson, 1980a,b). One can start by searching for a stimulus that evokes the most sensitive response i.e. the one with the largest amplitude or the highest SNR. (3) Next, one can analyze specific components of the response, for example, transient or sustained components, or all components together. The SNR obtained will of course depend on what components of the response are measured. The components of interest and their associated noise must be measured under the same conditions, i.e. the noise is quantified as any variability of the recorded signal that could obscure the evoked response (Field & Rieke, 2002a,b). In addition, because every method for measuring signal quality creates some bias, either from the type of stimulus, the recording method, the signal components measured, or inadequate sample size, a valid comparison between the quality of different signals can only be made when these factors are taken into account. When the quality of different signals is measured with identical stimulus and measurement paradigms, an unbiased comparison can be made between different points in a neural pathway or between a neuron and behavior of the whole organism. We will describe in more detail below how ideal observer analysis meets these requirements.

2.2. Algorithm for measuring performance

The ideal observer is an algorithm that discriminates between neural responses to different stimuli. It is presented with a system’s responses to repeated stimuli that differ in one parameter. Because the responses contain noise, they may be difficult to distinguish (Figure 2). For each response, the observer chooses which stimulus was most likely. The stimulus parameter is varied, and consequently the observer’s performance varies: when the stimuli differ by a small amount, the system’s responses are indistinguishable and therefore the observer chooses at nearly chance level, but when the stimuli differ by a larger amount, the observer chooses the correct stimulus more often. This relatively simple procedure quantifies how well the system’s response discriminates between the stimuli (Figure 2) (Barlow, 1978; Johnson, 1980b; Fechner, 1851; Geisler, 1989; Geisler et al., 1991). By definition, an observer that measures the quality of a response in this manner using all available signal components that can inform about the stimulus is called “ideal” (Rose, 1942; DeVries, 1943; Barlow, 1962; Green & Swets, 1988; Geisler et al., 1991).

If the system under study is a theoretical model, the noise distributions can be precisely defined, so the observer can readily achieve this perfect ideal. However, when the system under study is a real neural circuit or a computational model of one, knowledge of the noise distributions may be limited. In this case the observer can still be ideal in the sense that it uses all the available signal components, but it must learn the properties of the noise distributions from the system’s responses. For most retinal responses, where the noise distributions are approximately Gaussian and change little with a small change in the stimulus, the rules for discrimination are relatively simple. Therefore, we present here a simple near-optimal method and explain for typical retinal measurements how to approach optimality with incremental improvements (Geisler et al., 1991; Dhingra & Smith, 2004; Chichilnisky & Rieke, 2005).

2.3. Definition of paradigm

A paradigm called “two-alternative forced choice” is widely used in psychophysics (Green & Swets, 1988; Geisler, 1989), but it has also been used to assess the performance of neural signals (Geisler et al., 1991; Dhingra et al., 2003; Dhingra & Smith, 2004; Chichilnisky & Rieke, 2005; Dunn et al., 2006). A pair of stimuli, differing in one parameter, say, contrast, are repeatedly presented to a neural system, and the responses are given to the ideal observer. In the general case, to maximize accuracy the ideal observer chooses the stimulus category with the highest probability given the neural responses (see Appendix A.2). In our example, the ideal observer accumulates the probabilities for the binary discrimination by constructing a pair of histograms of response amplitude during a training period (Figure 3). The responses can be any physiological record, e.g. voltage, current, spike rate or spike time. Each stimulus presentation and its associated response is called a “trial”, and for each trial the ideal observer chooses which stimulus was presented on the basis of the probabilities from the histograms. A plot of the fraction of correct responses vs. the contrast increment defines the performance (Figure 3). An advantage of this experimental paradigm is that its measure of neural performance allows a direct comparison with behavioral performance because both are a metric for the same visual task.

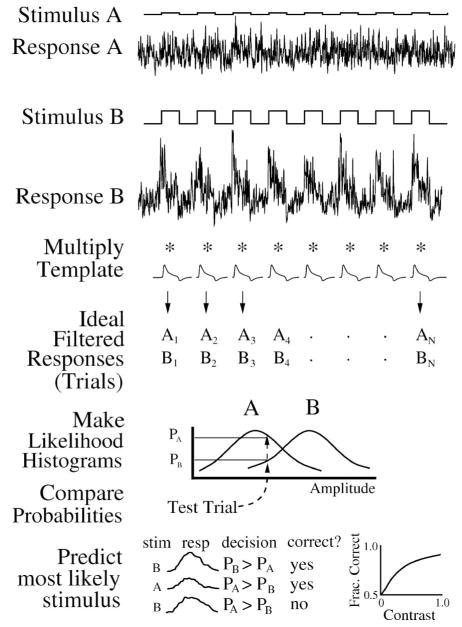
Figure 3.

Ideal observer single-interval two-alternative forced choice method for neural responses. Top, responses to a pair of repeated stimuli (A, B) are multiplied by a template to produce an ensemble of filtered responses (trials = A₁…A_n, B₁…B_n). Stimulus A has low contrast but for a detection experiment would have zero contrast. Middle, for all but one trial, make “likelihood” PDF histograms, then look up probability for that trial to find most likely stimulus. Bottom, repeat over all trials, tally correct responses, and plot as a neurometric function. In this conceptual example, responses A and B are from model data, but the ideal observer similarly analyzes real data.

Consider a specific example, the response of a brisk-transient (alpha/Y) ganglion cell to a flash of light (Enroth-Cugell & Robson, 1966; Peichl & Wässle, 1983; Dhingra et al., 2003). The response is noisy, evident in an intracellular recording of its graded potential and also in a recording of its spike train. The graded potential response has an initial transient that decays to a maintained depolarization, as modeled in Figure 4, and contains static and dynamic nonlinearities. In this example, a non-stationary Poisson distribution generated the noise, which passed through a saturating synapse, so the noise varied in a complex manner with stimulus amplitude and time. Because a typical neural response contains noise that varies with the synaptic release rates and the amount of saturation, the transient and sustained portions of the response may contribute differently to the overall signal quality (Figure 4). Therefore the response can inform the brain not only through changes in its amplitude but also in its temporal pattern (Geisler, 1991). The objective for the ideal observer is to measure this ability to inform about the stimulus.

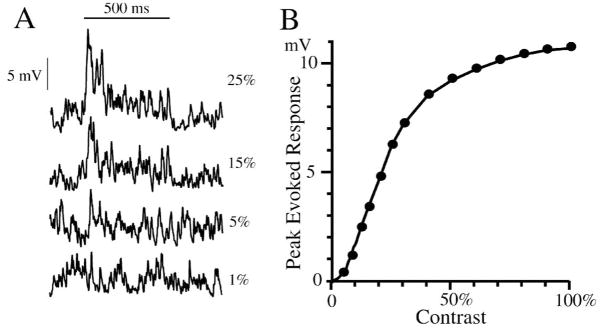
Figure 4.

Model of alpha cell response to light flash (500 ms duration) shown without spikes. (A) Responses to different contrasts (1% – 25%) show a ~100 ms transient at stimulus onset, with a low-amplitude sustained plateau, and a relatively high level of noise. The transient at light off has a reduced amplitude but also reduced noise. The smallest detectable response is ~5%, but without ideal observer measurements, it is difficult to discern. (B) The contrast response curve shows a threshold nonlinearity near zero and saturation above 0.5 contrast. Overall, the response is nonlinear, but within a small contrast increment the response noise distributions change by only a small amount. The model was constructed to provide conceptual data for figures 3–10 in this article.

The basic paradigm assumes that the average responses and their noise distributions do not vary over the repetitions of the stimulus (Green & Swets, 1988). If these properties vary, the performance measured may not approach the ideal maximum that would otherwise be possible. This can be evaluated by comparing, for example, trials taken from the beginning and end of the stimulus sequence (Appendix D in Geisler et al., 1991). Adaptation effects are a common difficulty in use of the ideal observer, and must be carefully controlled by the experimenter.

2.4. Dimensional reduction and the ideal filter

For each trial, the observer makes the decision between the 2 stimuli on the basis of a single comparison between their probabilities. Therefore, when an observation consists of a single dimension, the observer directly compares the probabilities of the 2 responses (see Appendix A.1). However, when an observation consists of multiple dimensions, for example, when multiple time bins are defined to capture a response’s temporal components, each potentially informative, the observer must combine them. One way to accomplish this is dimensional reduction using an ideal template filter (Figure 5; see Appendix, A.2; Duda et al., 2001). The ideal filter is related to the theory of “matched filters” that optimally remove noise from a known signal (Figure 5A; Turin, 1960; Baylor et al., 1980; Laughlin, 1996; Kay, 1998; Bialek & Owen, 1990; Armstrong-Gold & Rieke, 2003). It is a “discriminant template”, or set of bin weights, each multiplied with the corresponding response bin from each trial (Figure 5B,C). The individual weighted bin products are summed across all the bins, and the total represents the response amplitude for the trial (Figure 5C). The discriminant template is constructed to optimally separate the pair of response sets on a one-dimensional scale (Figure 5D; Duda et al., 2001). It removes any patterns of noise that are dissimilar to the responses, i.e. those that cannot inform the brain about the discrimination task. The remaining noise components, which cannot be removed from the signal by a linear filter because they comprise the same patterns as the signal, therefore limit the response’s signal quality and SNR. The result is a set of response amplitudes, one for each trial, transformed to maximize the set’s collective ability to inform about the discrimination task (van Rossum & Smith, 1998; Dhingra & Smith, 2004; Chichilnisky & Rieke, 2005). This procedure of dimensional reduction from many bins to one greatly simplifies the process of discrimination between the pair of stimuli (see Appendix, A.2; Duda et al., 2001; Thakur et al., 2007).

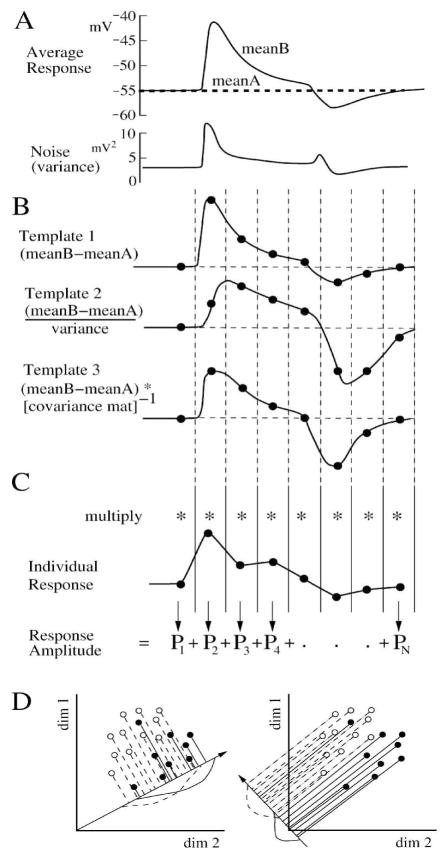
Figure 5.

Discriminant templates for dimensional reduction. (A) Average response and noise from Figure 4A (25% contrast) as a function of time. (B) Three linear templates which take into account progressively more statistical detail from the responses. The templates are constructed from the difference between the average responses. (C) Individual responses are multiplied bin-for-bin by one of the templates, and the products (Pn) are summed to give the ideal filtered response amplitude. (D) Geometrically, the template is a vector that sets a projection angle for each dimension (bin). It optimally projects the multidimensional responses onto one dimension to maximize SNR. The two figures show the same 2 sets of 2D points, showing dimensional reduction and projection onto lines pointing in different directions. The directions of the lines are defined by the templates. The points are correlated in the two dimensions, and most projections do not separate them (left, overlapping curves), but Fisher LDA optimally separates them in the projection at right. After Duda et al., (2001).

The template for the discriminant filter can be constructed in several ways (Baylor et al., 1980; Watson et al., 1983; Dhingra & Smith, 2004; Chichilnisky and Rieke, 2005; Dunn et al., 2006; Thakur et al., 2007). Using the standard linear discriminant, if the noise is uncorrelated and constant over the bins, the optimal template is equal to the average signal, the difference between the mean responses to the pair of stimuli (Figure 5B, Template 1) (Duda et al., 2001). If the noise varies over the bins, the optimal template is equal to the difference between the means divided by the variance (Figure 5B, Template 2) (Duda et al., 2001). These templates set the contribution of each bin according to its SNR. If the noise is correlated between bins, the optimal template is equal to the difference between the means times the inverse covariance matrix, calculated as the Fisher Linear Discriminant (“Fisher LDA”) (Figure 5B, Template 3; see Appendix, A.2; Duda et al., 2001; Dhingra & Smith, 2004; Averbeck & Lee, 2006; Borghuis et al., 2008). With an adequate number of trials, the Fisher LDA template is generally the most accurate of the 3 because it takes into account noise correlations (Figure 5D). Often it is helpful to try all 3 templates on full and partial data sets to compare the incremental improvements in performance (Chichilnisky & Rieke, 2005; Averbeck & Lee, 2006; Borguis et al., 2008). A comparison of the results of templates 1 and 2 will show the significance of changes in variability across dimensions (bins). A comparison of templates 2 and 3 will show the significance of taking correlations into account (Latham & Nirenberg, 2005; Averbeck & Lee, 2006). When sufficient data are available, some highly nonlinear responses may be optimally discriminated by a nonlinear function of bin values (see Appendix, A.2). When only 1 bin is considered, there is no need for dimensional reduction, and the ideal filter template reduces to a single constant of unit value.

2.5. Likelihood and test sets

The histograms that determine the ideal observer’s choice are called the “likelihood histograms” (Figure 3). They are constructed from the likelihood set, the trials that define for each stimulus the response mean and variability, similar to the “probability of the response given the stimulus” from Bayes’ Rule (Green & Swets, 1988; Duda et al., 2001; Geisler, 2004; Ma et al., 2006; Gold & Shadlen, 2007). Each likelihood histogram is normalized to unit area, giving a pair of probability density functions (PDFs), which are look-up tables containing the probability that a given response is evoked by a certain stimulus. Because each stimulus in the paradigm is presented with equal frequency, the likelihood histogram probability for a response is proportional to the probability that a stimulus evoked that response (Green & Swets, 1988; Geisler et al., 1991). To measure discrimination performance one evaluates how well the stimuli can be distinguished on a trial-by-trial basis using another set of trials, called the test set. The likelihood and test sets must be different, and for best accuracy they should be as large as possible (see Appendix A.2).

To generate the test set, the “jack-knife” paradigm is commonly used, in which the likelihood set comprises all trials but one, and that one trial is tested against the likelihood set (Efron, 1981; Duda et al., 2001). Then the entire process is repeated, each time with a different individual test trial removed from the likelihood set, so that all the trials are tested (Figure 3). Because both likelihood and test sets comprise almost the entire set of trials, this paradigm maximizes the sample size which improves accuracy. To find the accuracy of a certain number of trials, one measures performance of a subset, e.g. one quarter of the trials, then compares the performance of the resulting 4 shorter runs (Efron, 1981; Geisler et al., 1991; Dhingra & Smith, 2004).

2.6. Likelihood rule and neurometric curve

As described above, for each response in the test set the ideal observer chooses the stimulus with the highest probability in the likelihood set, i.e. the one that was most likely (Figure 3) (Geisler, 1991; Dhingra & Smith, 2004). The choice, based on the ratio of the probabilities, is called the likelihood ratio decision rule, a simplified Bayes’ Rule that is optimal because no other decision rule reflects more accurately the probability of the stimulus given the response (Green & Swets, 1988; Geisler, 1989; Duda et al., 2001). The choice of the most likely stimulus is equivalent to comparing the likelihood ratio to a criterion, which for equal presentation frequencies is set to 1. This decision rule makes no assumptions about the nature of the pair of stimulus/response distributions except what is known about the stimulus, i.e. its temporal and spatial position, and that the stimuli are presented with equal probability. To summarize the system’s performance, the number of correct choices is plotted against the test parameter, e.g. contrast. This produces a “neurometric” curve showing how much contrast is required to generate a response with any given degree of reliability (fraction correct) (Figure 6) (Geisler et al., 1991; Parker & Newsome, 1998; Dhingra et al., 2003). The threshold for distinguishing the pair of stimuli is the amount of contrast that produces a predetermined criterion level of performance. The criterion is normally set to 1 standard deviation, and the corresponding performance (fraction correct) can be determined by integrating the noise distribution (Geisler, 2004). For Gaussian distributions and the paradigm described here (one stimulus of a pair presented to a neural system), this criterion is equivalent to 68% correct responses (see Appendix A.3; Geisler et al, 1991; Green & Swets, 1988).

Figure 6.

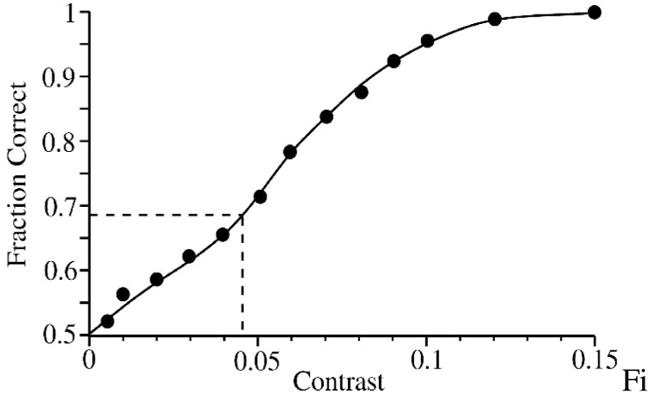
The neurometric data for a contrast detection task (zero vs. above-zero) for the model that produced the responses in Figure 4. For a decision based on a single stimulus presentation (single-interval task), threshold criterion is set at 68%, giving a contrast detection threshold of ~4.5%. The curve was fit by eye.

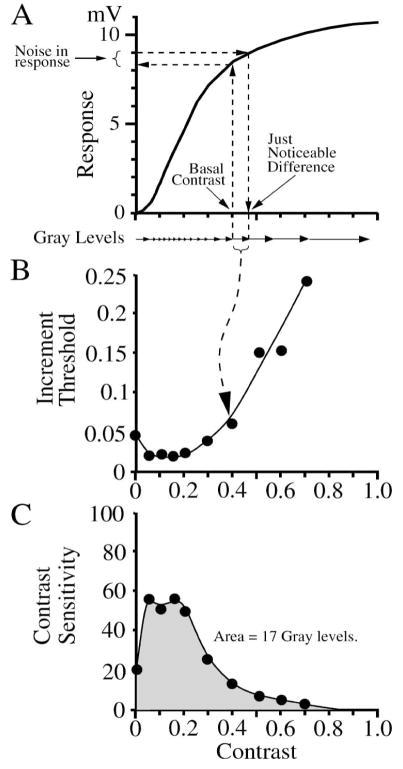
2.7. Contrast sensitivity and gray levels

The difference in amplitude between two stimuli that produces a criterion level of performance is a fundamental definition of the amount of noise in the system, and can be stated as an equivalent “noise contrast” (Barlow, 1957; Pelli, 1990; Cohn, 2004; Dunn & Rieke, 2006). When measured from zero (mean background), this is called the “contrast detection threshold” because it is the smallest contrast signal that can be detected. When measured from an above-zero contrast, this smallest increment is called the “increment threshold” or “just-noticeable-difference” and represents one distinguishable signal level, or “gray level”, which is a fundamental measure of a system’s ability to perform the discrimination task (Barlow, et al., 1987; Geisler et al., 1991; Victor & Nirenberg, 2008). The increment threshold is equivalent to the noise at a certain contrast divided by the slope of the response vs. contrast curve (Figure 7A). More generally, the increment threshold need not be measured as a function of contrast, for it can be a metric of sensitivity for any stimulus parameter, e.g. background intensity, wavelength, or spatial and temporal parameters such as size, position, direction, duration, timing, frequency, and velocity.

Figure 7.

Determining the number of distinguishable stimulus levels or “gray levels”. (A) Response vs. contrast curve from Figure 4B. The increment threshold or just noticeable difference is the minimum contrast increment that produces a discriminable response given the noise present. It is equal to the derivative of the response vs. contrast curve divided by the noise level as measured by the ideal observer. (B) An increment threshold is measured by the ideal observer for each level of contrast from the model data of Figure 4. The dip in threshold at 0.1–0.2 contrast is due to the nonlinearity in the contrast response near zero from (A). (C) The contrast sensitivity is the inverse of the increment threshold. Integrating the area under the contrast sensitivity curve gives the number of gray levels. The gray level compression is the contrast sensitivity divided by the number of gray levels; in this example, the maximum gray level compression (at 0.05 contrast) = ~3. The curves were fit by eye.

If the system were linear and the noise did not vary, the increment threshold would be the same throughout the contrast range. However, neural responses typically have significant nonlinearities, for example saturation in the response to high contrasts (Figure 7A), and their noise can vary with signal amplitude (Dhingra and Smith, 2004). Therefore, to determine sensitivity throughout the neuron’s dynamic range, increment thresholds are measured for each of a series of contrasts (Figure 7B). The contrast sensitivity is defined as the inverse of the increment threshold, e.g. an increment threshold of 1% means a contrast sensitivity of 100 (Figure 7B) (Enroth-Cugell & Robson, 1966), which is equivalent to the derivative of the response vs. contrast curve divided by the noise level. If contrast sensitivity vs. contrast were constant, it would define the total number of increment threshold steps or gray levels. More generally, the total number of gray levels is computed as the integral of sensitivity over the contrast range (Figure 7C) (Barlow et al., 1987; Dhingra & Smith, 2004). This is an overall measure of the ability of the system over its full dynamic range to perform the binary discrimination task (see Appendix A.4; Dhingra & Smith, 2004; Victor & Nirenberg, 2008), and is similar to other aggregate measures of behavioral performance (Abrams et al., 2007).

The number of gray levels represents the system’s total sensitivity in the sense that it compares signal gain and noise over the system’s dynamic range. Gain and noise are influenced by physical properties of the neural circuit that can be further dissected by ideal observer analysis of the neural components and their biophysical properties such as saturation and nonlinear summation. When the noise in a neural response increases with contrast, or the response saturates at high contrasts due to limited dynamic range (Figure 4), more gray levels are generated at low contrasts at a cost of fewer gray levels at high contrasts (Figure 7A,C). We quantify this as the amount of “gray level compression”, defined as the ratio of the contrast sensitivity to the number of gray levels. Typically, the maximum gray level compression factor for a brisk-transient ganglion cell is 3–5 (see Figure 4 of Dhingra & Smith, 2004).

3. The neural code

The signal quality determined by the ideal observer depends on the stimulus and on which components are analyzed from the neural response. The ideal observer can analyze temporal or spatial patterns from a variety of measures of neural activity such as graded potentials or spikes. The ideal discriminant template provides a tentative definition of the “neural code”.

3.1. Measuring response components

A neuron may inform the brain in several ways, reflected in its responses evoked by different stimuli (Johnson, 1980a,b; Rieke et al., 1997; Warland et al., 1997; Parker & Newsome, 1998; Meister & Berry, 1999; Fairhall et al., 2001; Machens et al., 2005; Victor, 2005a,b). For each stimulus pair, the ideal discriminant template defines the pattern of response components that best categorizes the evoked responses. This ideal discriminant template is called the “neural code” for the stimulus (Johnson, 1980a,b), because it reflects the components of the evoked response (the waveshape) that can inform the organism about the sensory task. In the example, the initial transient response to a flash of light has a higher SNR than the later sustained portion (Figure 4), so the template coefficients for the initial transient are larger. These components may be analyzed together by reducing all the bins into a single dimension with the ideal filter template as described above. Or they can be analyzed separately in single bins, to measure the SNR of the response over time (Figure 8) (Dhingra & Smith, 2004). Because the single-bin method uses the optimal likelihood decision rule without dimensional reduction, it provides a useful comparison and check on the optimality of dimensional reduction methods.

Figure 8.

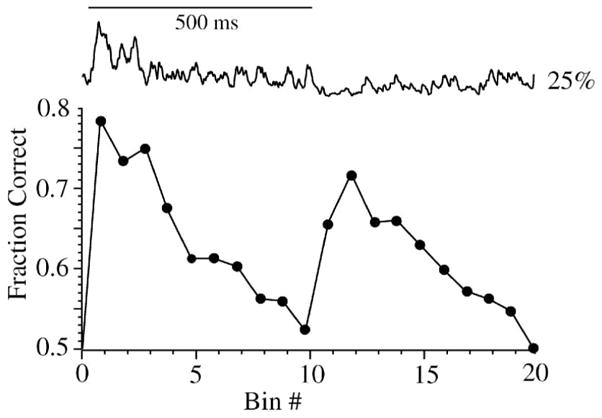
Performance of the response over time determined by single-bin analysis. Top, single response to flash of 25% contrast (500 ms) from Figure 4. Bottom, performance of individual time bins when comparing 0% vs. 25% contrast from Figure 4. Two peaks are evident, showing that both the depolarizing transient at stimulus onset and the hyperpolarizing transient at stimulus offset provide substantial discriminability. The depolarizing transient has much greater noise but also considerable amplitude. The hyperpolarizing transient has a lower amplitude, but also considerably reduced noise. Single-bin analysis uses the optimal likelihood decision rule and thus is a check for other discrimination methods.

Similarly, a spike train can be analyzed by the ideal observer according to the binned spike rate over the entire response interval, in single bins to measure how performance changes with time, or by measuring the statistics of spike timing or inter-spike intervals (Barlow & Levick, 1969; Dhingra et al., 2003; Dhingra & Smith, 2004; Victor, 2005b; Davies et al., 2006; Chase & Young; 2007; Thakur et al., 2007; Zeck & Masland, 2007; Gollisch & Meister, 2008a). Higher-order spike statistics can also be analyzed, combining rate and timing codes (Geisler et al., 1991; Victor, 2005a,b, 2006; Davies et al., 2006; Zeck & Masland, 2007). To check the spike code for optimality, the observer can compare results from different levels of detail, e.g. the spike count as a single sum, the binned spike rate, the spike intervals, and combinations of intervals (Geisler et al., 1991; Dhingra et al., 2003). Therefore, the neural code is the set of discriminant templates generated by the ideal observer to analyze the responses to variation in a dimension of a specific stimulus (Johnson, 1980b). As in Section 2.1 above, where we explained that the SNR varies with 1) the stimulus parameter to test, 2) sensory task, and 3) how the responses are measured, the neural code depends on these as well.

3.2. Temporal bins, characteristic time constant

Another important factor in measurement of SNR by the ideal observer is the length of the time bin. A bin length too long reduces SNR by averaging signal components of high SNR with components of low SNR, or by averaging signal components of opposite sign, so short time bins are required to register the discriminability in a transient or biphasic response (Figure 9). Typically, with sufficient trials, when bin length is shortened beyond a certain duration, performance does not increase further (Figure 9). This duration defines the “characteristic time constant” of a neuron’s response, which is a fundamental component of the neural code related to its temporal precision (Chichilnisky & Kalmar, 2003; Dhingra et al., 2003; Dhingra & Smith, 2004; Chichilnisky & Rieke, 2005; see also Butts et al., 2007). However, with insufficient trials, bin lengths shorter than the characteristic time constant typically underestimate performance because fewer data points are accumulated in each bin, causing inaccurate PDFs. Therefore, to give a lower bound on performance for a given number of trials, one can bracket bin durations around the characteristic time constant (Dhingra et al., 2003). A comparison of the characteristic time constant of two different neural codes, for example for the graded potential and spikes of a neuron, can give intuition about the neuron’s signal processing function. Thus, the measurement mode (voltage, spike rate, timing, pattern), characteristic time constant, and the set of discriminant templates for the specific stimulus along the test dimension are all included in the “neural code”.

Figure 9.

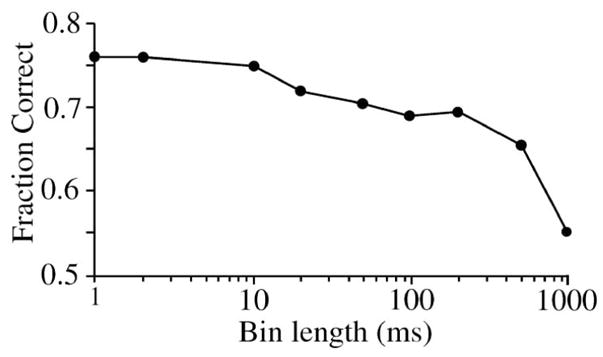
Effect of different bin durations on performance for model shown in Figure 4. For long bins (500–1000 ms), performance is reduced because the excitatory and inhibitory components of the biphasic response are averaged together and therefore subtract. For shorter bins, performance improves down to 10 ms (the characteristic time constant), where the transient response fills one bin, allowing its template coefficient to be given greater weight. A data set generated with insufficient trials (not shown) reduces performance for short bins < characteristic time constant. Response to contrast 0.05. trials=200, template=2.

3.3. Spatial bins

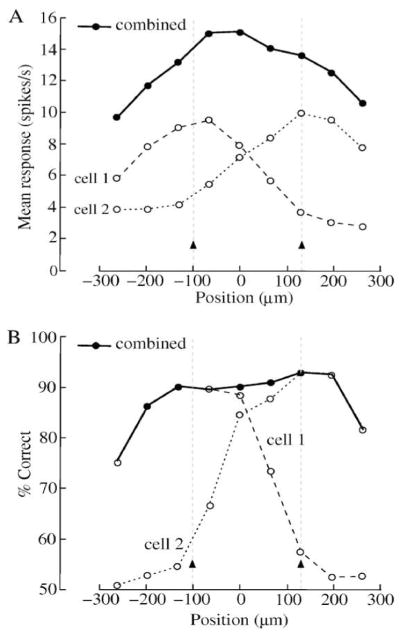
The ideal observer can be generalized to include a set of spatial bins, each representing a different point in space, for example, recordings from neighboring neurons (Borghuis et al., 2008; Gollisch & Meister, 2008a). Each spatial bin may include temporal bins, and these can all be included in the ideal template filter (Figure 10). With this paradigm, the neural code for a specific stimulus is defined more generally as a spatio-temporal template across an array of neurons (Parker & Newsome, 1998; Chen et al., 2006; Nicolelis & Ribeiro, 2006). Spatial and temporal correlations can be taken into account as described above using template (3) made with Fisher LDA (Figure 5B) or with a higher-order method (Appendix A.2). For example, recordings from several cells made with a multi-electrode array can be analyzed with this approach to determine the spatio-temporal code of a neuronal population. It is not necessary to know in advance precisely which neurons receive the strongest signal evoked by the stimulus, because the ideal template filter weights the spatial and temporal bins according to their ability to inform about the discrimination task (Borghuis et al., 2008). Thus the ideal observer can measure and compare the performance of single neurons and the collective performance of arrays of neurons, using a variety of codes (Gollisch & Meister, 2008a).

Figure 10.

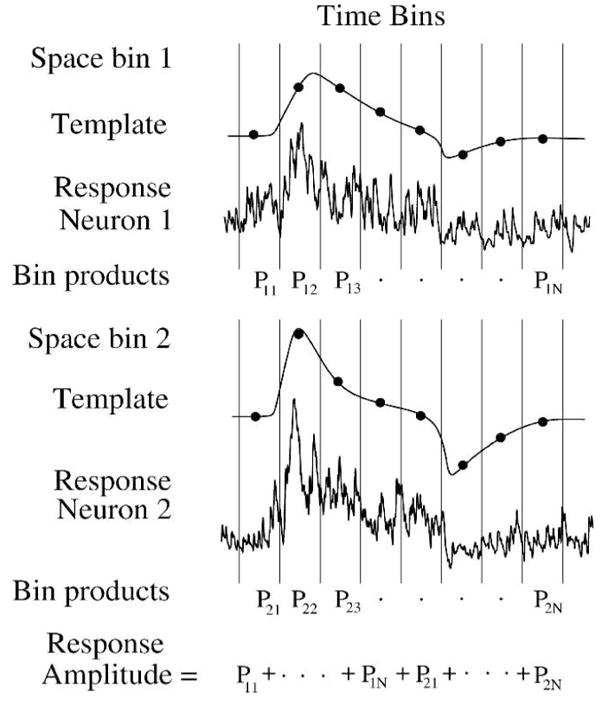
The ideal observer can measure performance in multiple neurons. Each neuron is assigned a space bin which comprises time bins and a corresponding template. Individual responses (shown from Figure 4A) are multiplied bin-for-bin by the templates, and the products are summed as for single neuron responses. Comparing analysis from template 2 (mean/var) and template 3 (mean*covar⁻¹) (Figure 5B) gives crucial insight into importance of noise correlations for sensitivity.

4. Tracking sensitivity

Geisler (1989) proposed to track the processing performed by the visual system by applying the ideal observer sequentially to the visual system’s different stages. If one could measure the level of performance available at each stage, a comparison between different stages would show the effect of each stage’s processing. Measurements from the different stages can be directly compared to behavioral performance because the ideal observer uses a decision rule defined by the same visual task. With a focus on neurons and synaptic relationships in the different retinal layers, this approach can be applied to retinal circuitry (Figure 11). To accurately track discriminability from one neural array to the next, the ideal observer can track the responses resulting from convergence and divergence.

Figure 11.

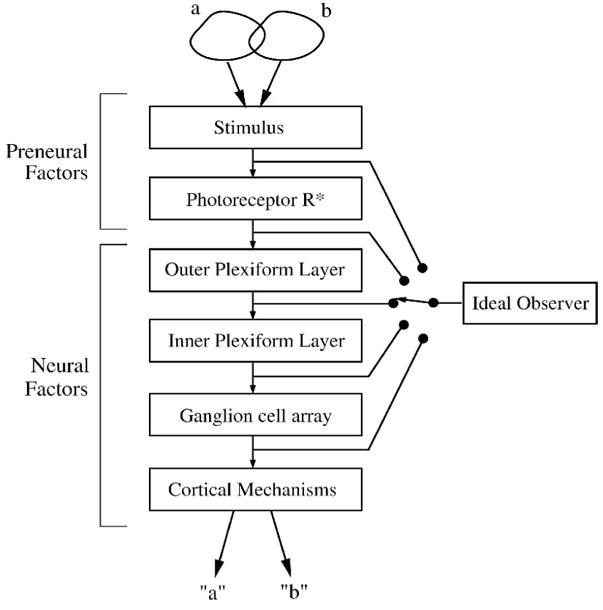
One paradigm for use of ideal observer: identify sources of behaviorally-relevant loss of performance step-by-step. The visual system is a series of stages which process the response evoked by the stimulus. Early stages affect the performance of later stages. The ideal observer is applied sequentially to each stage, either real or modeled, and the resulting performances are compared to discover the stages’ signal-processing roles. The stimulus, optical factors, and activation of rhodopsin (R*) are often included in an ideal model of the preneural factors that defines the maximum performance. Accuracy of this paradigm depends on the capture of all the response components evoked by the stimulus available at each stage. After Geisler (1989).

To compare the signal quality of individual retinal neurons along a pathway, one must account for how noise interacts with a neuron’s receptive field. A neuron’s sensitivity is set by noise sources and signal processing mechanisms such as receptive field center and surround. These receptive field mechanisms attenuate some components of the evoked response and thus decrease the neuron’s ability to inform about the stimulus. Therefore, when comparing sensitivity between neurons a useful concept is the optimal stimulus. This section expands upon these topics, starting with a short overview of noise and receptive field mechanisms. Later, the section gives several examples of ideal observer measurement of retinal performance which show that in daylight the retina loses a factor of ~10-fold from stimulus to ganglion cell spike train.

A variety of noise sources exist in neural circuits (van Rossum et al., 2003; Faisal et al., 2008). Neural signals are carried and transmitted by discrete events such as photon absorptions, ion channel gating, vesicles of neurotransmitter, and action potentials (spikes). The discrete nature of these quantal signals limits their signal quality and ability to inform about a sensory task because any quantization process adds noise and limits the number of possible different messages (Shannon, 1948; Northrop, 2005). Random fluctuations in the rate or number of the discrete events generates Poisson noise, which reduces SNR. Noise from Poisson mechanisms is equal to the square root of the mean, called the “square root rule” (Rose, 1942; DeVries, 1943; Faisal et al., 2008) that applies for many biological noise mechanisms. In a pathway with many independent noise sources, the largest tend to dominate because uncorrelated noise sums as root-mean-square.

4.1 Noise in the stimulus

Absorption of light is described by a Poisson distribution, which generates noise according to the square root rule (Rose, 1942; DeVries, 1943). The light level sets the mean number of photons absorbed and therefore defines the SNR, which places an upper bound on the SNR available for retinal signals. A first step in identifying this stimulus-associated noise is to develop an “ideal model” of the stimulus (Barlow, 1962, 1977), equivalent to a “stimulus defined exactly” (SDE) model (Geisler, 1989). The model precisely specifies the relevant stimulus properties, including the spatio-temporal distribution of photon flux and absorption by photoreceptors, and the associated random photon noise (Barlow, 1962; Barlow et al., 1971; Banks et al., 1987; Geisler 1989; Kiorpes et al., 2003; Xu & Abshire, 2005; Dunn et al, 2006). The photon absorption by photoreceptors is estimated by calculating the known optical factors, which include absorption and dispersion through the eye, retina, and in the outer segment’s photopigment. The stimulus set and ideal model are presented to the ideal observer, which then determines the maximum sensitivity available to the retina by calculating the signal and noise for an individual photoreceptor and for the entire stimulated array using the square root rule (Geisler, 1989; Kiorpes et al., 2003; Dunn et al., 2006).

4.2. Noise in retinal circuitry

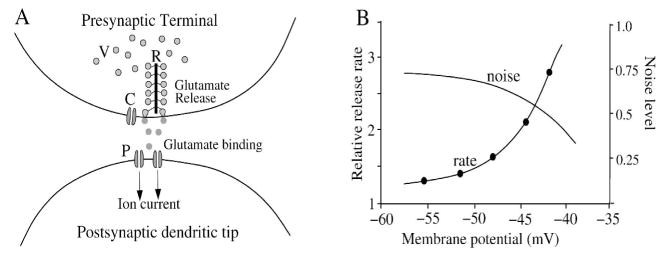
The release of neurotransmitter in synaptic vesicles is a major source of noise for the retina (Ashmore & Copenhagen, 1983; Laughlin et al., 1987; Copenhagen, 1991; Croner et al., 1993; Freed, 2000, 2005; Passaglia & Troy, Berntson & Taylor, 2003; Demb et al., 2004; DeVries et al., 2006; Murphy & Rieke, 2006, 2008; Faisal et al., 2008). Vesicle release, controlled by the local calcium level, carries most visual signals that reach ganglion cells and the brain (Katz & Miledi, 1967; Sudhof, 2004; Heidelberger et al., 2005; Morgans et al., 2005; Midorikawa et al., 2007; LoGiudice & Matthews, 2007). The ribbon structure at the photoreceptor and bipolar cell synapse collects vesicles to form a release-ready pool allowing higher transient release rates (Figure 12A) (Sterling & Matthews, 2005; Heidelberger et al., 2005; Singer & Diamond, 2006; Midorikawa et al., 2007; Matthews & Sterling, 2008; Jackman et al., 2009). The release mechanism is subject to the thermodynamic limitations of equilibrium binding and diffusion, and some evidence points to Poisson release statistics (Barrett & Stevens, 1972; Freed, 2000, 2005). However, there is also some evidence for refractory mechanisms that could regularize release statistics (DeVries, 2001; Palmer et al., 2003; Freed et al., 2003; also see Schein & Ahmad, 2005), and compound fusion on the ribbon may allow multi-vesicle bursts of release (Singer et al., 2004; Matthews & Sterling, 2008). Further, vesicle size at a release site varies, which adds to the quantal variability seen in the postsynaptic cell (Hartveit & Veruki, 2006). The release rate at a typical ribbon synapse is thought to range between 15–100/s for tonic release, but 10-fold higher for phasic release (Ashmore & Copenhagen, 1983; Berntson & Taylor, 2003; Choi et al., 2005; Sterling & Matthews 2005; Freed, 2005; DeVries et al., 2006; Sheng et al., 2007; LoGiudice & Matthews, 2007; Jackman et al., 2009). A Poisson rate in this range at an individual release site will generate robust noise (Figure 12B). However, a synapse’s contribution to ganglion cell signal quality depends on how the synapse’s signal is combined with signals from other neurons (Sterling & Freed, 2007).

Figure 12.

The synaptic release mechanism is noisy, with limited dynamic range. (A) Vesicles (V) diffuse through presynaptic terminal and tether to ribbon (R). Calcium channels (C) sense the membrane voltage and open, allowing calcium entry, which causes vesicles to bind and fuse with cell membrane, releasing quanta of glutamate. The quanta diffuse across the synaptic cleft and bind to postsynaptic receptors (P), opening postsynaptic ion channels. (B) The synaptic release rate follows calcium L-type channel voltage activation, which is approximately exponential within the physiological range (redrawn from Witkovsky et al., 1997). Assuming a Poisson rate of 15–100 ves/s, the noise level calculated by the square root rule at an active release site over a 100 ms integration period (1.5–10 ves) ranges from 30–100% of the mean signal (SNR = ~1–3). A step in light level can evoke a much higher rate of phasic release (100–1000 ves/s) and thus can transmit a light response with higher SNR (Jackman et al., 2009).

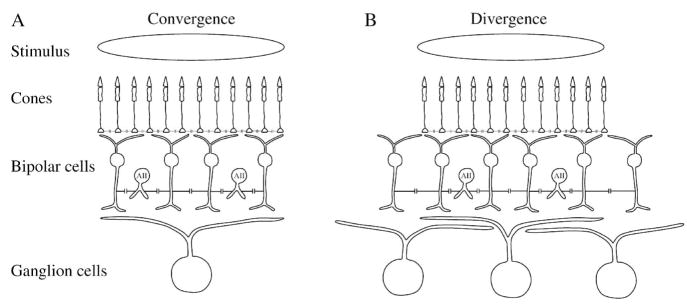
4.3. Convergence, divergence, and correlation

To make comparisons between the performance of different retinal layers, one must take into account all signals received and transmitted by a neuron. These are defined by the convergence and divergence, respectively (Figure 13A) (Sterling et al, 1988; Strettoi et al., 1992; Vardi & Smith, 1996). Many bipolar cell types collect signals from several photoreceptors (Cohen & Sterling, 1990b; MacNeil et al., 2004; Schein et al., 2004; Wassle et al., 2009), and a typical ganglion cell collects signals from many bipolar cells (Sterling et al., 1988). This convergence, along with lateral electrical coupling from gap junctions, averages the signal, improves SNR, prevents aliasing, and removes uncorrelated signals (Lamb & Simon, 1976; Hare & Owen, 1990; Tsukamoto et al., 1990; Levitan & Buchsbaum, 1996; Mills, 1999; DeVries et al., 2002; Trexler et al., 2005). A similar averaging action takes place temporally in bipolar cells, where membrane capacitance along with a synaptic filter (in On-bipolar cells) comprises a low-pass temporal filter (Copenhagen et al., 1983; Shiells & Falk, 1994; Bialek & Owen, 1990; Armstrong-Gold & Rieke, 2003; Burkhardt et al., 2007).

Figure 13.

Consequences of anatomical convergence and divergence from an extended stimulus. (A) Convergence to a neuron defines its receptive field. Signal from a spot of light over ganglion cell receptive field center converges from ~2000 cones through ~500 bipolar cells to one large brisk-transient ganglion cell, such as found in cat. Noise in ganglion cell’s presynaptic circuit is averaged by dendritic summation and electrical coupling. Cones are electrically coupled, as are AII amacrines and cone bipolars. To track performance of the converging circuit for the ganglion cell center response, one must measure performance of signals in cone and bipolar cell arrays in the ganglion cell’s presynaptic circuit and compare with ganglion cell performance. For a full accounting, circuitry conveying surround (not illustrated here) must also be included. (B) Divergence from a stimulus defines the neural code. From same spot of light, signal diverges from ~2000 cones through ~750 bipolar cells to ~7 brisk-transient ganglion cells. Noise in neighboring ganglion cells is correlated to some extent because the divergence causes them to share some presynaptic circuitry and noise sources. To fully track behaviorally-relevant performance from the stimulus, one must measure performance of all bipolar and ganglion cells that receive the signal from the stimulus.

Successive retinal stages are also synaptically connected with divergence (Figure 13B) (Sterling et al., 1988). A cone transmits a signal to more than one bipolar cell of a given type, and several bipolar cells of different types (Cohen and Sterling, 1990b; MacNeil et al., 2004; Schein et al., 2004; Wassle, 2004; DeVries et al., 2006; Wassle et al., 2009). Therefore the noise components of photoreceptor signals are transmitted in common to neighboring bipolar cells, adding correlations to the bipolar cell signals. Further, the AII amacrine makes gap junction contacts with several bipolar cell types (McGuire et al., 1984; Cohen & Sterling, 1990a; Mills & Massey, 1995; Trexler et al., 2005; Massey, 2008), and the AII array is strongly interconnected (Kolb, 1979; Smith & Vardi, 1995; Vardi & Smith, 1996; Bloomfield & Volgyi, 2004). The resulting correlations between bipolar cell signals are likely involved in correlations seen in ganglion cell spike trains (Perkel et al., 1967; Meister et al., 1995; Kenyon et al., 2004; Shlens et al., 2006; Schneidman et al., 2003, 2006; Liu et al., 2007; Nirenberg & Victor, 2007; Trong & Rieke, 2008).

The noise correlations in an array’s collective signal must be taken into account when measuring the performance of the array. This can be accomplished with the Fisher LDA template (Figure 5D) or a higher-order discrimination method. Noise correlations in neurons with similar evoked responses can reduce SNR and the discriminability of a stimulus (Johnson, 1980b; Zohary et al., 1994; Abbott & Dayan, 1999; Parker & Newsome, 1998; Latham & Nirenberg, 2005; Chen et al., 2006; Murphy & Rieke, 2008; Borghuis et al., 2008, Trong & Rieke, 2008), because the correlated noise components cannot be averaged to reduce variability. However, correlated responses transmitted through diverging synaptic pathways provide redundancy which can be useful (Trong & Rieke, 2008). For example, 2 adjacent bipolar cells may receive correlated responses from a cone, but their ribbon synapses generate additional uncorrelated noise that can then be averaged by re-convergence downstream in a ganglion cell (see Figures 13 & 14). Signal correlations between neural responses can inform about spatial components of the stimulus (Johnson, 1980b; Meister et al., 1995; Meister & Berry, 1999; Schneidman et al., 2003; Latham & Nirenberg, 2005; Shlens et al., 2008). The functional role of correlations within presynaptic circuits and between ganglion cells is not fully understood (Trong and Rieke, 2008) and can be studied with the ideal observer.

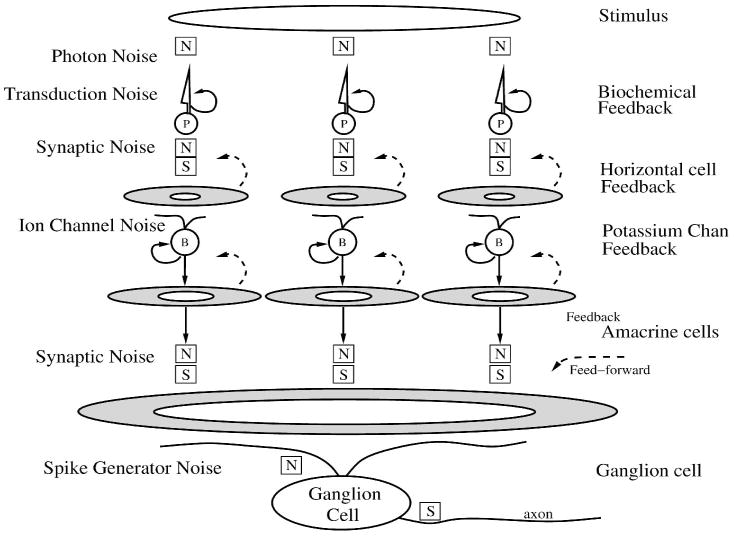
Figure 14.

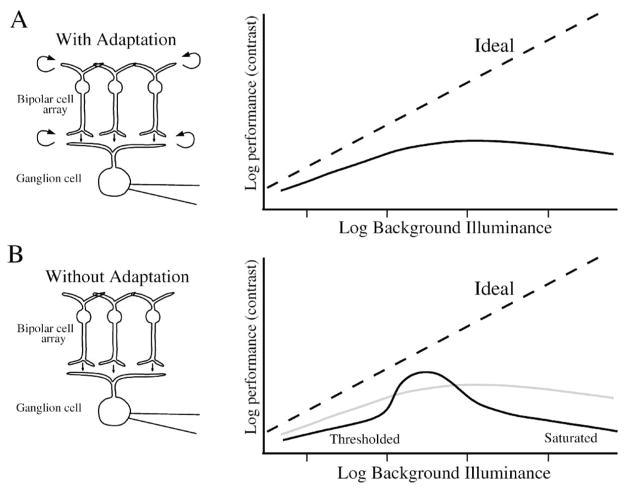
Adaptation in a visual pathway prevents deterioration of SNR. Arrays of rods, cones (P) and bipolar cells (B) transduce a noisy stimulus and transmit their response through noisy synapses (N). The ganglion cell collects signals from many cones to reduce noise (Tsukamoto et al., 1990). The synapses would saturate (S) without adaptation, which originates in biochemical feedback in the outer segments of rods and cones, potassium channels in cones and bipolar cells (looped arrows), and feedback from horizontal cells and amacrine cells (dashed arrows). Center-surround receptive fields for 2 layers of neurons presynaptic to ganglion cell are generated by their local circuits, for the purpose of adaptation to prevent saturation of synapse and and masking by noise. The 2 layers of center-surround processing both contain subtractive and divisive components and therefore interact in a complex manner. The ganglion cell center-surround receptive field is the convolution of the presynaptic receptive fields and their synaptic weighting functions (Smith & Sterling, 1990). Spike generator adds noise when creating spike train that saturates at high spike rates.

4.4. Adaptation from receptive field components

A ganglion cell’s presynaptic circuit can collect signals of a much wider dynamic range than can be transmitted through individual synapses (Figures 12 & 14). A typical ganglion cell responds to a 10 log unit range of light signals (Sakmann & Creutzfeldt, 1969; Troy et al., 1999), which is a challenge for the retina because the dynamic range of neural mechanisms is much less (Figure 12). The dynamic range for gating of synaptic signals is ~20 mV, controlled by calcium channels in the presynaptic terminal (Figure 12B) (Wu, 1994; Witkovsky et al., 1997; Heidelberger et al., 2005). Therefore, synaptic release in a visual pathway without adaptive modulation would saturate at membrane potentials outside the range of synaptic gating. Further, a typical brisk-transient ganglion cell’s spiking is limited to ~300 Hz, and over an integration time of ~100 ms, it saturates to a maximum of ~30 spikes (Dhingra et al., 2003). Noise mixed with such a saturated signal at a later stage of processing would limit its signal quality.

To reduce saturation, extend operating range, and maximize SNR, retinal neurons and circuits dynamically adjust their response amplitude (Sakmann & Creutzfeldt, 1969; Enroth-Cugell & Shapley, 1973; Shapley & Enroth-Cugell, 1984; Tranchina et al., 1984; Victor, 1987; Laughlin, 1989; Kaplan & Benardete, 2001;Manookin & Demb, 2006; Dunn & Rieke, 2006;Dunn et al., 2006, 2007; Zaghloul et al., 2007; Gaudry & Reinagel, 2007; Clifford et al., 2007; Wark et al., 2007). This process is called adaptation, and is usually accomplished through negative feedback, a mechanism in which the output of an amplifier is inverted, then summed with the incoming signal (Figure 14; van Hateren, 2007). Adaptation in the retina is implemented by several types of mechanism, some biochemical, as in calcium feedback of the photoreceptor outer segment (Burns & Arshavsky, 2005), some biophysical, as in auto-feedback of protons released by synaptic vesicles (DeVries, 2001; Palmer et al., 2003), potassium channel activation (Barnes and Hille, 1989; Maricq & Korenbrot, 1990a,b; Demontis et al., 1999; Mao et al., 2002; van Rossum et al., 2003), sodium channel inactivation (Kim & Rieke, 2003), or temporary depletion of the vesicle pool (von Gersdorff & Matthews, 1997; Singer & Diamond, 2003, 2006), and some through synaptic feedback, as in horizontal cell feedback to cones (Wu, 1994; Smith et al., 2001; Fahrenfort et al., 2005; van Hateren, 2007), or amacrine cell feedback at GABAergic or glycinergic synapses on bipolar cell terminals (Freed et al., 2003; O’Brien et al., 2003; Lukasiewicz, 2005; Molnar & Werblin, 2007; Zaghloul et al., 2007; Li et al., 2007).

These types of adaptation are similar in form. In a process called “predictive coding” (Srinivasan et al., 1982), the retina collects signals over a spatially and/or temporally extended “surround” region, and subtracts them from the “center” signal. Retinal synaptic transfer functions are nonlinear, with a threshold and an exponential transfer function (Figure 12), and therefore the center-surround subtraction in some neurons imparts a divisive adaptational component (Merwine et al., 1995). Because the surround overlaps with the center, the two signals are partially correlated, and the subtraction reduces the magnitude of the resulting “center-surround” signal. The feedback signal from the surround opposes any change in the center signal, reducing the signal transmitted about the background illumination and effectively giving the circuit a greater operating range (Eliasmith & Anderson, 2003; Molnar & Werblin, 2007; van Hateren, 2007). Thus, negative feedback from horizontal cells to cones, and from amacrine cells to bipolar cell terminals in the inner plexiform layer (IPL) removes signal excursions before they are transmitted through the feedforward synapse (Figure 14)(van Hateren, 1993; Smith, 1995, 2008; DeVries et al., 2002). This feedback regulates release of glutamate by the cone and bipolar ribbon synapse to prevent saturation and vesicle depletion (Lukasiewicz, 2005; Dunn et al., 2006; Zaghloul et al., 2007; see also Veruki et al., 2006; Singer & Diamond, 2006; Smith, 2008).

Although the correlated center and surround signals subtract, any uncorrelated noise in the surround signal adds to the center with the root-mean-square rule. Therefore the spatio-temporal extent of the optimal predictive surround region, and the location of the underlying feedback circuit, is inversely related to the SNR in the visual signal: the lower the SNR, the wider the surround should extend (Srinivasan et al., 1982; Atick & Redlich, 1990; Dunn et al., 2007; Smith, 2008). As a result of the pathway’s multiple adaptation mechanisms, the output from retinal ganglion cells is exquisitely sensitive without much saturation (Sakmann & Creutzfeldt, 1969; Enroth-Cugell & Shapley, 1973; Shapley & Enroth-Cugell, 1984; Atick & Redlich, 1990; Harris et al., 2000; Fairhall et al., 2001; van Hateren & Snippe, 2001; Jin et al., 2005; Clifford et al., 2007; Durant et al., 2007; Li et al., 2007). The ideal observer can measure and compare the performance of center and surround, before and after adaptation has occurred, to explore hypotheses about how such processing maximizes signal quality.

4.5. Optimal stimulus and efficiency

Although some neural responses may be evoked by more than one stimulus, each stimulus interacts with a neuron’s spatio-temporal receptive field in a different way. Therefore, it is useful to define the concept of a neuron’s optimal stimulus, the one that evokes a neural response with highest efficiency (Barlow, 1962, 1978). As we will explain below, this concept is useful when comparing signals along a pathway (Geisler, 1989; Pelli, 1990; Thibos & Levick, 1990). The classical definition of efficiency is “quantum efficiency” for which the optimal stimulus evokes the largest ratio of the “equivalent photon count” to the actual photon count, where the equivalent photon count is the number of photons that would produce the SNR evident in the neural response, and the actual photon count is the number of photons absorbed from the stimulus (Barlow, 1962, 1978; Barlow & Levick, 1969; Barlow et al., 1971; Watson et al., 1983; Geisler, 1989; Pelli, 1990; Thibos & Levick, 1990; Hemila et al., 1998; van Rossum & Smith, 1998; Field & Rieke, 2002a; Schein & Ahmad, 2006).

The most natural definition of efficiency for exploration by the ideal observer is based on SNR. For this definition, the optimal stimulus evokes the highest ratio of measured SNR to ideal SNR, where the ideal SNR is determined by a model of the stimulus based on Poisson absorption of photons by the photoreceptor outer segments (Barlow, 1962; Watson, 1983; Geisler, 1989, 2004). Because the SNR of a light stimulus with Poisson statistics is equal to the square root of the photon count, the ratio of measured to ideal SNR is equal to the square root of the quantum efficiency (Barlow, 1978; Watson et al., 1983; Geisler, 1989, 2004). For example, for a flashed spot stimulus that evokes a threshold response measured by the ideal observer in a retinal ganglion cell, the SNR is unity, and the ideal SNR (mean/s.d.) is equal to the square root of the absorbed photon flux from the spot stimulus. When the spot’s spatio-temporal dimensions and contrast maximize the ratio of measured to ideal SNR, that combination of stimulus parameters is optimal. Further, a measurement of efficiency need not include a measurement of ideal SNR, nor does it require the optimal stimulus, because the ideal observer can measure and compare sensitivity to any stimulus at any 2 points along a neural pathway.

Although a full description of how to find the optimal stimulus is beyond the scope of this article, a good starting estimate for many retinal neurons is the linear spatio-temporal receptive field derived from a reverse correlogram (Watson et al., 1983; Jones & Palmer, 1987; Sakai et al, 1988; Rowe & Palmer, 1995; Edin et al., 2004; Dhingra & Smith, 2004; Ringach & Shapley, 2004; Victor, 2005a; Werblin & Roska, 2007; Benda et al., 2007). Automatic methods can estimate an optimal stimulus efficiently (Klein, 2001; Alcalá-Quintana et al., 2005; Machens et al., 2005; Lewi et al., 2006; Benda et al., 2007). For nonlinear responses such as those of On-Off ganglion cells, higher order methods can determine the optimal stimulus (Fairhill et al., 2006; Schwartz et al., 2006; Gollisch & Meister, 2008b).

4.6. Loss of sensitivity in receptive field circuit

A neuron’s receptive field can be considered a neural filter that attenuates some components of the signals it receives (Figure 15A; Pelli, 1990; Hemila et al., 1998). However, performance measured by an ideal observer is unaffected when processed by a linear filtering function, because this type of function is invertible. For example, a low-pass filter applied to a neural signal attenuates high frequencies, which one might expect to modify the signal’s performance. But being an invertible function, such a filter reduces the high frequency components of both signal and noise in an identical way, narrowing the 2 PDF peaks and reducing their separation proportionately (Figure 3), so the sensitivity as measured by the ideal observer does not change. The rule applies both in time and space, so linear filtering operations such as temporal low-pass filtering by capacitance and spatial averaging by gap junction coupling per se have no effect on performance measured by the ideal observer (DeVries et al, 2002). One might wonder, therefore, whether a neuron’s performance should be affected by its receptive field. However, performance can decline when nonlinearities or noise are inserted between the linear filter and the ideal observer (Figure 15A) (DeVries et al., 2002; Chichilnisky & Kalmar, 2003; Borghuis et al., 2009). Also, sampling operations such as optical diffraction and binning (Figure 9) are irreversible and therefore can affect SNR (Levitan & Buchsbaum, 1996).

Figure 15.

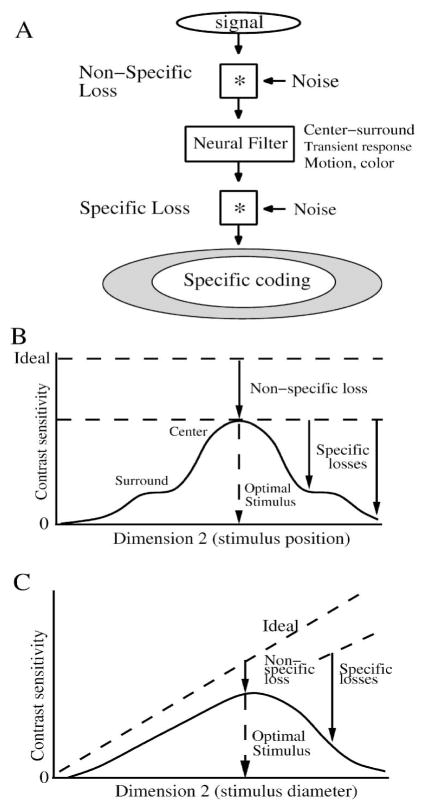
Noise mechanisms in a neural circuit cause different types of loss in performance. (A) Noise mixed with the signal before and after a neural filter induces a “non-specific” loss. After the neural filter attenuates some signal components, downstream noise and nonlinearities generate a “specific” loss. B) Conceptual plot of SNR of a neuron’s response evoked by varying one dimension of the stimulus, in this case the neuron’s contrast sensitivity for a small spot. The contrast sensitivity varies when the stimulus is varied across a second dimension (e.g. spatial position), giving a characteristic shape (solid line). The maximum possible performance (dashed line) is determined from an ideal model of the stimulus. The optimal stimulus has the highest ratio of SNR in the response to SNR in the stimulus, which defines the non-specific loss. In addition, suboptimal stimuli induce specific losses generated by the receptive field. Both center and surround generate sensitivity but their specific losses differ. Compare to Figure 21. (C) Contrast sensitivity of same neuron plotted vs. the diameter of a centered spot. In this case, ideal performance varies with the size of the spot. A small spot evokes little response, and noise present in the circuit reduces SNR. The optimal size spot generates the largest SNR relative to ideal. Larger spots than optimal evoke a reduced response along with robust noise, reducing SNR relative to ideal. Shape of the contrast sensitivity curve relative to ideal defines the pattern of specific performance loss.

The signal and noise components attenuated by a neuron’s linear receptive field may also be attenuated by a static nonlinearity such as a threshold or saturation. When downstream noise is mixed with the attenuated components, it masks them and reduces the performance measured by the ideal observer. The receptive field filter thus becomes a source of “specific” performance loss (Figure 15A). Because noise mechanisms distributed throughout the circuit reduce performance in all signal components, the circuit also contributes a “non-specific” performance loss (Figure 15A). Therefore when measuring loss of performance with the ideal observer, the amount of loss measured from one point to the next in a circuit depends on which stimulus dimensions are probed, which signal components are studied, and to what extent they are specifically attenuated by receptive fields (Pelli, 1990; Hemila et al., 1998).

Typically, a retinal neuron has one optimal stimulus for which its performance is the greatest (Figure 15B,C). Performance for this stimulus is limited by the non-specific loss, i.e. the accumulated losses from all the noise sources in the circuit that mix with the evoked response. As described above, to evaluate the amount of non-specific loss, one constructs an ideal model which determines the noise level intrinsic to the stimulus, using the optical factors of the eye and pigment absorption (Geisler, 1989). When probed with non-optimal stimulus parameter values, performance is reduced because of the receptive field’s specific losses which have a characteristic shape (Figure 15B,C).

At each stage of processing along a sensory pathway, inevitably SNR is reduced from noise, gradually reducing performance in later stages (Figure 16) (Banks et al., 1987; Davila & Geisler, 1991; Abshire & Andreou, 2001; DeVries et al., 2002; van Rossum et al., 2003; Victor, 2006; Sterling & Freed, 2007). Therefore, SNR and stimulus discriminability measured by an ideal observer along a sensory pathway cannot be increased. This is known as the data processing inequality (Cover & Thomas, 1991). Although SNR compared from one stage to the next in a pathway may appear more concentrated when carried by a smaller number of quanta (Sterling & Freed, 2007), the pathway’s performance is always reduced by the synaptic noise. To determine the role of each signal-processing mechanism in generating noise and reducing SNR requires measuring the performance at each stage in the pathway (Geisler, 1989).

Figure 16.

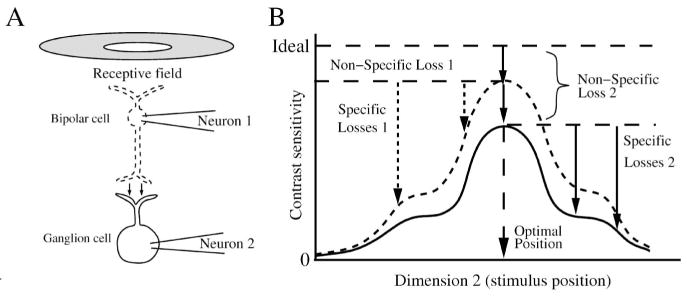
Loss of SNR in a non-converging pathway. (A) A bipolar cell (neuron 1) collects a center-surround receptive field and transmits it with some loss in performance (contrast sensitivity) to a ganglion cell (neuron 2). Figure omits inhibition from amacrine cells to the bipolar and ganglion cells that modifies performance of their centers and surrounds. (B) The optimal stimulus induces a non-specific loss in the bipolar cell and the ganglion cell, and non-optimal stimuli induce specific losses. The optimal stimulus for both neurons is nearly identical because the receptive field center profiles are similar. Synaptic noise at the bipolar cell ribbon synapse causes all contrast sensitivities for the bipolar cell to be greater than the corresponding contrast sensitivities for the ganglion cell. The ganglion cell’s non-specific loss is equal to the bipolar’s non-specific loss plus the pathway (synaptic) loss. For clarity, the neural performances are shown magnified relative to ideal; the actual losses are 2–10-fold.

4.7. Optimal stimuli differ in pathway

Neurons in a pathway differ in their optimal stimuli for SNR because their receptive fields and noise sources differ, causing different specific losses (Figure 17). The specific loss induced by a presynaptic neuron’s receptive field can sum with losses in other neurons in the pathway to generate a non-specific loss for a postsynaptic neuron. For example, small bipolar cell receptive fields presynaptic to a ganglion cell contribute to its larger receptive field by convolution with the spatial weighting function of their synapses onto its dendritic tree (Figure 14) (Freed & Sterling, 1988; Smith & Sterling, 1990). Because the bipolar cell’s receptive field is smaller (Berntson & Taylor, 2000), its optimal stimulus will be too, but this stimulus is not optimal for the ganglion cell (Figures 14, 17). In response to the ganglion cell’s larger optimal stimulus, the bipolar cell’s surround will subtract most of its center signal, and the resulting signal transmitted from the bipolar cell will have a lower SNR than if its optimal stimulus were larger. A similar situation of bias from receptive field size exists when comparing performance of horizontal cell and ganglion cell. Although the apparent mismatch between specific losses in two neuron types in a pathway may seem paradoxical, it is a consequence of the different local circuits responding to a specific stimulus.

Figure 17.

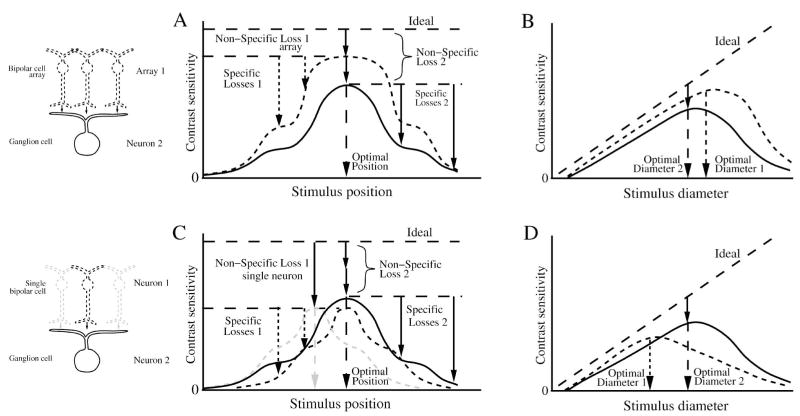
Loss of SNR for neurons in a converging pathway. (A), (B) Contrast sensitivity compared for a ganglion cell (neuron 2) and its converging presynaptic array of bipolar cells (array 1). When probed with a small flashed spot across the receptive field (A), and with different diameter centered spots (B), the converging bipolar cell array has a larger optimal stimulus and greater performance than the ganglion cell. The ganglion cell’s non-specific loss comprises the bipolar array’s non-specific loss plus the loss in synaptic transmission to the ganglion cell. (C), (D) Contrast sensitivity compared for the ganglion cell and a single presynaptic bipolar cell (neuron 1). The bipolar cell (dotted black) has the same optimal stimulus position as the ganglion cell because it is centered in the ganglion cell receptive field. (C) Bipolar cells have greater non-specific loss than the ganglion cell because they collect fewer inputs. Bipolars with offset position (dotted gray) show the same non-specific loss, but differ in their optimal stimulus (gray dashed arrow). Note that for the same stimulus, some of the bipolar cell performances are greater than the ganglion cell performances. (D) the optimal stimulus for a bipolar cell is smaller than for the ganglion cell. For small spots the bipolar cell performance is greater than the ganglion cell’s because the ganglion cell receives noise from bipolars outside the stimulus. Figure omits inhibition from amacrine cells that will modify performance of ganglion cell center and surround. As in the previous figure, the neural performances are shown magnified relative to ideal for clarity.

4.8. Bias in comparing performance

When comparing performance between two neurons at different points in a circuit, in order to establish that the comparison is unbiased, several caveats are necessary. One might attempt to use identical experimental paradigms, for example, to analyze the responses to identical sets of stimuli, with identical time bins. While the ideal performance of the stimulus will be the same, the interaction of the stimulus with the different receptive fields of the two neurons causes a bias in the measurement of their performance (Figure 17). Each neuron’s performance is biased from the extent of its receptive field, which reflects convergence from different numbers of signal and noise sources in its presynaptic circuit.

Similarly, the time bin duration will interact with the potentially differing temporal waveshape of the two neural codes to cause a bias. One might attempt to eliminate the bias by determining the optimal stimulus and the characteristic time constant for each neuron, then measure each neuron’s performance with the appropriate stimulus and time bin duration. However this will induce a bias in the comparison due to the difference in ideal performance associated with each stimulus, and due to a different variability associated with each bin duration (Figure 9). The reason is that a larger stimulus will give a higher ideal performance by the square root law because it has a greater photon flux, and a longer time bin will reduce the measured variability because it averages responses from more time steps. A similar bias exists if spikes are being measured, because the spiking mode analyzed (rate, interval, timing) can be be optimized for each neuron (Geisler et al., 1991; Dhingra & Smith, 2004). One can determine the bias through several comparisons, for example for neurons with small and large receptive fields, a comparison of their performances for a) the optimal stimulus for each neuron, b) the optimal stimulus for the smaller neuron, or c) the optimal stimulus for the larger neuron (Figure 17).

To compare performance between neural stages, one can track either convergence or divergence. To track the performance of the presynaptic circuit for a ganglion cell, one compares the collective performance of the converging neurons (Figures 18, 19). But the converging neurons may differ in receptive field extent from the ganglion cell (Figures 13, 14), so individually their optimal stimulus will differ (Figure 17). For example, the performance of each converging bipolar cell is biased by its smaller receptive field size. However, when the performance of all the bipolar cells presynaptic to a ganglion cell is measured together, their collective performance will be greater than that of the ganglion cell (Figure 17). This comparison is unbiased because it tracks the collective performance of all the signals responsible for the ganglion cell’s performance.

Figure 18.

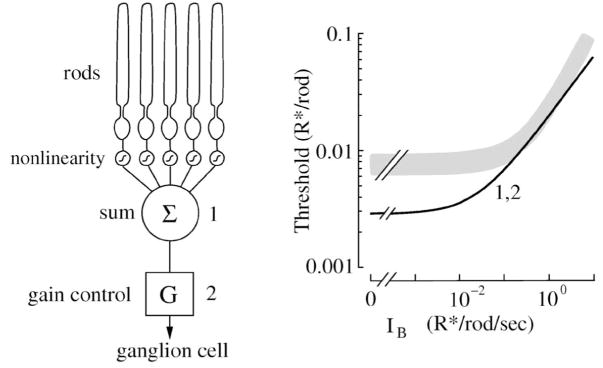
Comparison of performance of mouse ganglion cell and model. The experimental task was to detect a dim flash of light at different backgrounds, measured as the threshold photon flux (R*) that produced a response equal to the standard deviation (Dunn et al., 2006). Left, model of rod convergence to the ganglion cell, including 4096 rods, each converging through a synaptic nonlinearity, summation, and gain control. Right, gray trace shows threshold of ganglion cell (+/−SEM), and black trace shows threshold photon flux of model. At low backgrounds, threshold of the ganglion cell was ~3-fold higher than the model. At higher backgrounds, as gain was reduced, performance of the model approached the performance of the ganglion cell. This suggested that an extra noise source must exist in the pathway, for example, at the rod bipolar to AII amacrine synapse. Threshold curves were identical for a site after summation (1) and for a site after the gain control (2). The reason is that the gain control was noiseless. Performance of the array of rods was greater than the ganglion cell. The ideal observer allows an unbiased comparison between real cell and model at different stages. Compare this model to Figure 17. Redrawn from Dunn et al. (2006).

Figure 19.

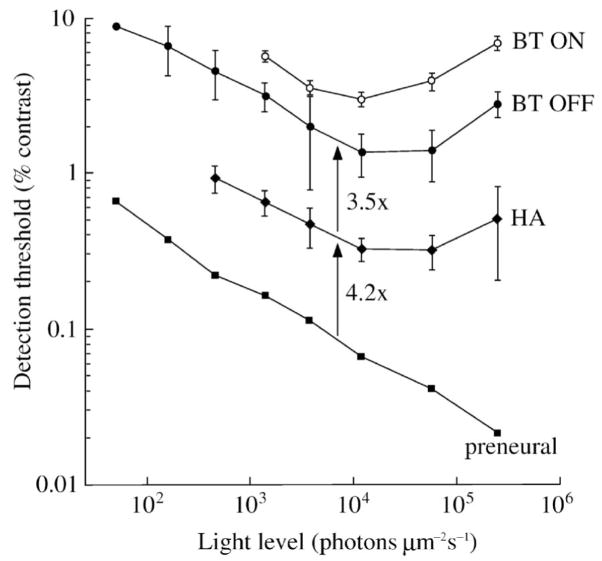
Retinal circuitry progressively loses contrast sensitivity from one layer to the next. Simultaneous recordings from A-type horizontal cells (HA, intracellular) and brisk-transient ganglion cells (BT OFF, BT ON, extracellular spikes) analyzed by the ideal observer compare the contrast threshold between an ideal model of preneural factors, horizontal cells, and ganglion cells. The total loss of sensitivity from the stimulus through the retinal circuit converging to a ganglion cell’s spike train is ~10-fold. Sensitivity varies with background light level, and the optimal background for both horizontal and ganglion cells is in the low photopic range. At the optimal background, the ganglion cell and HA both lose sensitivity from their presynaptic layer by a factor of ~4-fold. Synaptic noise at cone and bipolar cell ribbon synapses is the likely candidate for the measured losses. Stimulus was a flashed spot of light (500 μm dia, 100 ms, 2 Hz). Compare to Figures 15–17. Redrawn from Borghuis et al., 2009.

To track the total available performance between neural stages, one compares the collective performance of the neurons diverging from the stimulus, i.e. all the neurons at each stage that produce an evoked response (Figure 13B). As above, the diverging neurons in different stages may differ in size and also in their optimal stimuli. The ideal observer can measure the performance of an array of neurons by including for each neuron a spatial bin that is analyzed with the appropriate template filter (Figure 10; Borghuis et al, 2008). For this measurement it is not necessary before starting the recording to know the spatial extent of the neural code, i.e. precisely which neurons can inform about the stimulus, because the neural code is automatically computed by the discriminant filter algorithm. Any neurons that do not convey stimulus discriminability are ignored by the template filter (Parker & Newsome, 1998). When the performance of arrays of cells in two or more stages of the diverging network is measured, a comparison of the stages’ performance will determine the overall loss between stages, as originally conceived by Geisler (1989). Because the performance measured by the ideal observer of a diverging array of neurons is greater than the performance of one of them, the network converging from a stimulus to a single neuron typically can show a greater loss than the network diverging from the same stimulus.

When all signal convergence and divergence are taken into account, performance tracked between retinal layers is approximately independent of the size of neurons or arrays. For example, for a large spot of light that stimulates an array of 2000 cones, the performance loss across one synaptic connection from a cone to the 8–10 bipolar cells that receive its signal (Cohen and Sterling, 1990b; MacNeil et al., 2004; Wassle et al., 2009) is the same as the loss from the stimulated array of cones to the array of bipolar cells that receive their collective signal. The reason is that taking the ratio of performances between different layers normalizes by the array size.

4.9. Examples of tracking retinal sensitivity

To understand the importance of making correct comparisons without bias in ideal observer measurements, consider some recent studies that tracked sensitivity of retinal circuits. A study of gain control in the rod circuit converging to mouse alpha ganglion cells used the ideal observer to measure ganglion cell thresholds at backgrounds where mainly rods are active (Figure 18; Dunn et al., 2006). Although there is evidence that in the dark a mammalian ganglion cell maintains nearly ideal performance, signaling single photons (Barlow et al., 1971; Mastronarde, 1983), how the scotopic rod pathway to the ganglion cell preserves the single photon signal and how the pathway regulates its sensitivity with background is not known (Smith and Vardi, 1995; van Rossum et al., 1998; Schein & Ahmad, 2005, 2006).

To evaluate this sensitivity, the ideal observer measured performance of real ganglion cell responses and compared it to performance of a model of the ganglion cell’s scotopic rod circuit. The model consisted of a statistical description of a single rod’s response to a dim flash in the presence of a background, which included previously measured noise sources in the rod (Field & Rieke, 2002b), and a description of how responses were combined in the ganglion cell. The model also contained a threshold nonlinearity which removed the baseline noise in each rod’s signal before it was summed by convergence through the rod bipolar pathway to the ganglion cell (van Rossum & Smith, 1998; Field & Rieke, 2002a). The ideal observer used a two-interval forced-choice task, which consisted of 2 trials, one containing a flash stimulus, and the other containing no flash (see Section A.3). A discrimination template was constructed from the average response, and the threshold was based on which trial gave a response greater than the standard deviation, giving a measurement of threshold flash intensity.

Thresholds measured from the real ganglion cell were ~3-fold higher than for the model for dim backgrounds, but real and model performance converged when backgrounds approached moonlight (~1 R*/rod/s). This result implies that in dim backgrounds, the real circuit for rod convergence has other noise sources beyond those included in the rod response model, such as synaptic noise (see Figures 16,17; Taylor & Smith, 2004; Schein & Ahmad, 2005, 2006), but that at brighter backgrounds the real system’s gain control reduces the effect of the extra noise (Dunn et al., 2006).

A recent study measured the loss in sensitivity from the stimulus through the cones’ synaptic response to the ganglion cell’s spike train (Figure 19; Borghuis et al., 2009). Simultaneous recordings of horizontal cells and ganglion cell responses to a flashed spot of light (500 μm dia, 100 ms), were presented to an ideal observer to determine the contrast threshold of both cells. A preneural model of photon absorption by rods and cones applied to a simple square-root rule ideal observer (see Appendix) set a benchmark for comparison with the measured thresholds. Although the contrast thresholds for horizontal cell and ganglion cell were similar (~1–2%), the receptive fields of the 2 neuron types differed, which induced a bias into the comparison. To estimate the bias, a low-contrast full-field stimulus allowed measuring the loss in sensitivity induced for a spot stimulus by gap junction coupling between horizontal cells. In response to the full-field stimulus no lateral current flowed through the gap junctions, which allowed a greater evoked response in the horizontal cell. This gave an estimate of the extent of coupling, which then allowed estimating the effect of the coupling on reducing synaptic input noise. The result implied that although the coupling between horizontal cells reduced the synaptic input noise, it reduced the response evoked by the spot even more due to the mismatch between the stimulus and the receptive field size (Figures 15C,17B), for an overall reduction in SNR due to coupling of ~2-fold.

To make an unbiased comparison of the performances of horizontal cell and ganglion cell, the contrast threshold of the horizontal cell was scaled appropriately to give the corresponding threshold for the signal from a single cone (see Figure 17; Hemila et al., 1998). This single cone synaptic threshold was then re-scaled for the number of cones converging to the ganglion cell and the reduction in sensitivity due to the ganglion cell’s specific losses (Figure 17). This calculation depended on the knowledge that the horizontal cell array collects from all cones (Borghuis et al., 2009), that the horizontal cells recorded (type A) are closely coupled, and that the array of bipolar cells projecting to the ganglion cell also collects from the same cone synapses as the horizontal cells (Freed & Sterling, 1988; Cohen & Sterling, 1990; Wassle et al., 2009). One also expects additional losses in the bipolar cell associated with synaptic variability, e.g. inhibitory feedback from amacrine cells. The loss in sensitivity at background levels in the range of mesopic (twilight) through mid-photopic (daylight) was similar to psychophysical measurements (Geisler, 1989), and was consistent with a simple model of vesicle release at the cone synapse showing greater discriminability at lower release rates (Choi et al., 2005). Overall, the measurements showed a loss of 4.2-fold from the preneural model to the cone output, and 3.5-fold from the cone output to the Off-brisk-transient ganglion cell spike train (Figure 19). This result implies that in twilight and daylight, retinal circuits limit the contrast sensitivity of the visual system, and further that sensitivity is lost incrementally by each synaptic stage (Borghuis et al., 2009).

To track performance of a retinal circuit from one point to the next, often one must compare performance of a synaptic signal to a spike train (Figure 20; Dhingra & Smith, 2004; Murphy & Rieke, 2006). This is a challenge because of the different signal modes: graded potentials are continuous and spike trains are discrete and often discontinuous. For example, the ganglion cell spike generator is transient so the the spike train may have a different optimal stimulus and a different characteristic time constant than the synaptic potentials driving it (Figures 9, 15; Lankheet et al., 1989; van Rossum et al., 2003; Dhingra & Smith, 2004). Further, its signal code may include spike intervals and patterns not available in an analog code (Victor, 2005).

Figure 20.

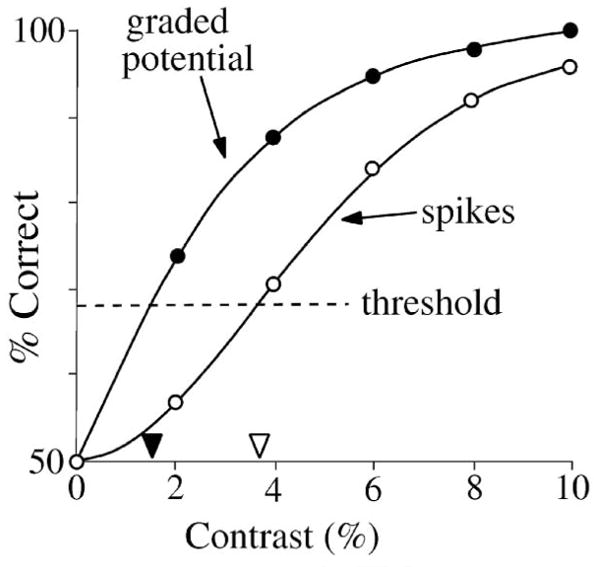
Threshold for spikes in a guinea pig ganglion cell in vitro is 2-fold higher than graded potential (Dhingra & Smith, 2004). The experimental task was to detect a spot of light (100 ms, 500 μm, 2 Hz) from background in a single-interval two-alternative forced-choice task. Threshold was defined the contrast that gave 68% correct. The ideal observer allowed a a relatively unbiased comparison between simultaneously recorded spikes and graded potential (see text). Compare to Figure 6. Redrawn from Dhingra & Smith (2004).

In our study of the brisk-transient ganglion cell (Dhingra & Smith, 2004), the optimal bin length for spikes was ~20 ms, whereas for graded potentials it was ~40 ms (see Figure 9 legend). However, the performance for both graded potential and spikes varied only slightly over bin lengths in the range 20–50 ms, so we chose a bin length of 40 ms. Applying the ideal observer for graded potential and spikes recorded simultaneously from the same cell, we found that the contrast sensitivity of the graded potential was consistently 2-fold higher (Figure 20; Dhingra & Smith, 2004). Similarly, the number of gray levels in the graded potential was ~2-fold higher. We attribute the difference in performance of graded potential and spikes to 2 factors: ion channels in the ganglion cell which add noise (van Rossum et al., 2003; Dhingra & Smith, 2004, Dhingra et al., 2005; Demb et al., 2004; Margolis & Detwiler, 2007), and the limited sampling (spike) rate (Demb et al., 2004; Dhingra & Smith, 2004). In a similar study, the ideal observer measured the effect of blocking Na⁺ channels on the performance of the ganglion cell (Dhingra et al., 2005).

A recent study of simultaneous recordings of spike trains in ganglion cell pairs highlighted the use of the ideal observer to compare the performance of single and multiple neurons (Figure 21; Borghuis et al, 2008). A small spot of light was flashed at different locations across the receptive fields of two adjacent On-brisk-transient ganglion cells in guinea pig retina. The spot evoked different firing rates at different positions, and the summed firing rate of both cells peaked between their receptive field centers (Figure 21A). Contrast detection performance measured by the ideal observer for each cell also varied with position (Figure 21B). However, when the performance of the pair of cells was analyzed together, using a discrimination template that contained both spatial and temporal bins, the detection performance was relatively constant with position (see Figures 10, 17). The study determined that the performance of the On-brisk-transient ganglion cell array diverging from such a small-spot stimulus is equal to the performance of one cell (see Figure 13B). The study went on to explore the effect of spatial separation between Gaussian receptive field centers, showing that a separation of ~2-sigma maximizes the information transmitted by an array of ganglion cells (Borghuis et al., 2008).

Figure 21.

Simultaneous recordings from neighboring ganglion cells show that contrast sensitivity across the array is spatially invariant (Borghuis et al. 2008). A spot was flashed at different locations across the receptive fields of a pair of On-brisk-transient ganglion cells. A, At suprathreshold contrast (3.2%), firing rate of a cell increased when the spot was close to its receptive field center. The sum of the firing rates of the cells varied with spot position and peaked halfway between the 2 cells. B, An ideal observer measured detection performance based on the response of either cell, or both combined. Performance varied across the receptive field when measured for each cell alone, but was constant when measured for both together. Arrowheads show receptive field centers. Compare to Figures 15–17. Redrawn from Borghuis et al. (2008).

4.10. Comparisons with behavioral results

The final step is to compare the performance of different neural stages of the visual system with behavioral performance (Geisler, 1989). Although in starlight the performance of mammalian ganglion cells and behavior is nearly ideal (Barlow et al., 1971; Barlow, 1972), in twilight and daylight the efficiency of the cone pathways drops (Figure 19; Borghuis et al., 2009; Geisler, 1989). To measure the efficiency between retina and behavior, a multi-electrode array can measure signals diverging from a small spot of light covering one ganglion cell receptive field center or from a more extended stimulus (Warland et al., 1997; Segev et al., 2004; Shlens et al., 2006; Borghuis et al., 2008). An observer looking at the responses of an array of ganglion cells is analogous to a cortical cell receiving the same responses. The decision rules of the brain are thought to comprise an evaluation similar to the observer in a Bayesian discrimination task (Geisler, 1989; Johnson, 1980a; Rieke et al., 1997; Chen et al., 2006; Gold & Shadlen, 2007), so with the same set of stimuli, the cortical cell could in principle derive the same performance. Therefore, when the visual discrimination task is identical, ideal observer measurements of performance of single neurons or arrays can be directly compared with behavioral measurements (Barlow et al., 1971; Parker & Newsome, 1998). The optimal stimulus for the behavioral task defines the convergence through the retina to the cortical center responsible, i.e. the behavioral receptive field (Figure 13; Watson et al., 1983).

Using ideal observer measurements with specific stimuli, one can tentatively assign and compare losses for the sequential stages of the retinal to cortical projection. Contrast threshold measured by the ideal observer in a ganglion cell spike train for a small flashed spot is ~0.5–1% (Dhingra et al., 2003; Dhingra & Smith, 2004; Borghuis et al., 2008, 2009), which is similar to psychophysical threshold for a similar stimulus (Watson et al., 1983; see also Kiorpes et al., 2003). If this comparison were unbiased without caveat, it would suggest that little performance for this threshold stimulus is lost in the integration of the ganglion cell spike train by the brain (Barlow et al., 1971; Barlow, 1972). However, retinal and cortical circuitry and therefore signal integration and sensitivity would be expected to vary between species. Assuming similar species, for a measured loss between retina and cortex there could be many possible explanations, including incomplete convergence or synaptic noise in cortex, a difference in the characteristic integration time, or some other loss in efficiency of the cortical mechanism (see Section A.3; Barlow, 1962).

As described above, efficiency of signal coding and integration depends on the specific stimulus. A large stimulus that extends over many ganglion cells can be coded in retina as efficiently as a smaller one because of the parallel structure of retinal circuitry, but cortical integration of a large stimulus, especially one that requires a complex pooling mechanism, seems likely to include some additional loss. One would therefore expect that cortical signal integration for small brief stimuli would be more efficient than for complex stimuli extended in time and space (Watson et al., 1983; Chen et al., 2006). However, irrespective of which stimulus is integrated most efficiently for behavior, the losses associated with transmission of its evoked response through retina, and in its projection to and within cortex, can be measured by the ideal observer and compared with behavioral performance (Chen et al. 2006).

5. Discussion

Ideal observer analysis is a powerful method for determining a neural pathway’s performance. For a binary discrimination task, it finds the smallest distinguishable stimulus increment, and over the response’s full dynamic range it measures the number of distinguishable signal levels. These metrics of performance represent fundamental quantitative measures of neural signal quality that allow comparisons to be made between different loci along a pathway. In this section, we evaluate the ideal observer and its use in exploring the function of retinal circuitry.

5.1. Overview of the observer

Our use of the term “ideal observer” follows Geisler (1989) who described ideal-observer analysis for comparing performance of different stages of the visual system (Figure 11). A stimulus is presented to a system, and the system’s responses are given to the ideal observer, which measures the performance available in a specific binary discrimination task. The responses can be taken from a real neuron, a simulation that includes sources of noise, or a theoretical model of a noise distribution such as the number of photons absorbed from a stimulus (Barlow, 1962; Geisler, 1989). The observer need not know any details about the system that generated the response, because in each of the above cases knowledge about the noise distribution is derived from the data set. In the case of a real neuron, the duration of the recording session limits the number of trials and thus the accuracy with which the neural response can be analyzed. In the case of a simulation, the limitation is from its relevancy, i.e. how accurately it represents the real neural circuit. In the case of a theoretical model of the stimulus (ideal model), the stimulus and optical absorption factors can be specified to some accuracy, so the noise distribution is known to a corresponding accuracy. Whether or not the precise noise distribution is known, the ideal observer’s power rests in its ability to measure and objectively compare the performance of the data sets it is given.

The ideal observer has been used for a variety of purposes, and for each it may require a different algorithm. For a theoretical model that defines a Poisson distribution, the observer can be very simple, consisting of the square root rule. For the responses of a neural circuit or a realistic model, the properties of the noise distributions are learned from the data set so the algorithm must be more complex (see Appendix A.2). To find the appropriate algorithm and level of accuracy, the observer is tested incrementally (Geisler et al., 1991). For constant uncorrelated noise, the ideal discriminant template can be as simple as the average evoked response, but it can be elaborated to take into account variable or correlated noise. These incremental comparisons allow an evaluation of different properties of the noise distributions, e.g. the gain in performance when correlations are taken into account. If the responses are highly nonlinear and the amount of data is sufficient, potentially more accurate higher-order methods for discriminating the stimulus can be incrementally applied. The duration of the time bins can be bracketed to determine the characteristic temporal summation time in the neural code. Different signal modes can be analyzed, for example, graded potential, spike count, rate, timing, intervals, and higher-order patterns (Geisler et al., 1991; Dhingra et al., 2003; Dhingra & Smith, 2004; Chichilnisky & Rieke, 2005). The single-bin mode allows tracking the performance available at different times or different response components. The overall concept is that the observer can be incrementally optimized, depending on the type of measurement for which it is applied (Geisler et al., 1991).

Although other measures of performance will differ from a Bayesian ideal observer decision rule, the paradigm outlined here for tracking performance and discovering the role of neural circuits does not depend critically on the exact measure because any method for measuring SNR of neural signals reflects the neural circuit’s convergence, divergence and noise mechanisms. Many other methods are possible with the same discrimination task (Victor & Nirenberg, 2008). For example, Shannon information could be substituted for the Bayesian measurement of average performance (see Appendix A.4). The advantage of ideal observer analysis is the analogy to a behavioral trial-by-trial decision. The Bayesian method employed by the ideal observer uses a decision rule defined by the visual task which provides a metric of signal quality referenced to the tested stimulus parameter (e.g. contrast threshold), allowing measurements from models and retinal responses to be compared directly to behavioral performance (Barlow et al., 1971; Banks et al., 1987; Geisler, 1989). Although one could argue that Bayesian performance measured from models and real neurons cannot be compared with behavior of different species because the comparison has so many confounding factors, we believe such comparisons are not moot because they have provided useful insight (Barlow et al., 1971; Geisler, 1989, 2004; Parker & Newsome, 1998; Dhingra et al., 2003; Chichilnisky & Rieke, 2005; Dunn et al., 2006; Borghuis et al., 2009).

5.2. The discriminant template and neural code

The ideal observer example presented here uses the likelihood decision rule, based on the probabilities of the responses to 2 stimuli, to decide which one to choose. However, when observations of neural responses are made in several dimensions (bins), a variation of the likelihood decision rule is necessary. When noise in the response dimensions is uncorrelated the likelihood probabilities over all the bins are independent and therefore can be multiplied, which is the basis for one type of ideal observer (Geisler et al., 1991; Geisler, 2004). However when the distributions of noise in response dimensions are correlated, the decision rule must be more complex (see Appendix, A.2). The Fisher LDA discriminant template is one way to solve this problem. The linear discriminant template is a set of coefficients multiplied with an individual multidimensional response that reduces the response into one dimension, to optimally separate responses to a pair of stimuli (Figure 5). However, the discriminant need not be linear, and for some highly nonlinear responses a nonlinear template or other higher-level methods may be more accurate (see Appendix, A.2). Using an appropriate dimensional reduction method, the ideal observer can measure the sensitivity of one neuron or an array of neurons, taking into account their temporal and spatial correlations (Latham & Nirenberg, 2005).

We have chosen to illustrate Fisher LDA as an example because it is a relatively simple first-order method and has been used to analyze retinal responses (Duda et al., 2001; Dhingra & Smith, 2004; Foffani & Moxon, 2004; Chichilnisky & Rieke, 2005; Borghuis et al., 2008, 2009). Fisher LDA optimally separates two arbitrary noise distributions in the projected single dimension, and is optimal for multidimensional Gaussian distributions of equal covariance. Therefore it is nearly optimal for discriminating retinal responses, because their noise distributions typically comprise a single mode near the mean, and even with substantial nonlinearities, their noise distributions change little with a small change in the stimulus (Murphy & Rieke, 2008), e.g. when measuring the increment threshold. However, as with any analysis method, the Fisher LDA template may be inaccurate when the data do not adequately sample the noise distributions (see Appendix, A.2; Victor, 2005a).

In our example of the ideal observer, the template coefficients represent the weight given to each bin, i.e. the relative sensitivity of each bin for the stimulus discrimination task. Neurons or bins that contain more signal and/or less noise are weighted with a larger coefficient, and those that contain only noise are ignored. The template defined in this manner is a candidate for the neural code, because it represents the optimum spatio-temporal pattern for a noiseless set of downstream neurons or an observer to measure the SNR of a response evoked by a specific discrimination task (Johnson, 1980b). Although this code measured in a sensory neuron may not be precisely the one employed by the organism, it is of interest to the investigator because it is objectively derived from the neural response and conveys maximal SNR about the stimulus discrimination task. The neural code actually employed by the organism to generate its behavior may differ from the neural code measured in a sensory neuron or array because the spatio-temporal extent of the response and its divergence and noise properties vary along a pathway. But if the neural code for the decision-making neurons involved in a visual task could be measured using a Bayesian method similar to the one described here, we argue that this would approach the neural code for the organism (Chen et al., 2006).

5.3. Intuition from ideal observer measurements

One can derive valuable intuition about the functional role of circuit mechanisms by comparing loss of performance with known synaptic release rates. The losses determined by Borghuis et al. (2009), ~4-fold from photon absorption to photoreceptor output, and ~4-fold from photoreceptor output to ganglion cell spikes, raise the question of how the loss occurs and what trade-offs it implies about retinal function (Schellart & Spekreijse, 1973; Levine, 2007). The retinal pathway from cones to a ganglion cell carries the visual signal with a decreasing number of quanta at each stage (Sterling & Freed, 2007). In daylight, a just-noticeable response in a large brisk-transient ganglion cell is carried by thousands of photons, several hundred vesicles released from cones, possibly as few as several dozen vesicles released from bipolar cells, and one ganglion cell spike (Ashmore & Copenhagen, 1983; Berntson & Taylor, 2003; Choi et al., 2005; Sterling & Matthews 2005; Freed, 2000,2005; DeVries et al., 2006; Sheng et al., 2007; Sterling & Freed, 2007). One might wonder how this feat is accomplished. One might imagine that the later stages, e.g. vesicle release by bipolar cells, would dominate the loss, because their lower quantal release rate would, by the root-mean-square rule, carry a less distinguishable signal (Freed, 2000, 2005).

However, the known synaptic parameters suggest that a lower vesicle release rate from bipolar cell ribbons is compatible with the measured losses (Choi et al., 2005; Dunn et al., 2006; Borghuis et al., 2009). Compared to the cone response, the bipolar cell response amplitude is greater, typically by 2–5-fold (Belgum & Copenhagen, 1988; Wu, 1994; Pang et al., 2007). If both cone and off-bipolar cell ribbon synapses release vesicles with a similar gain (vesicles released/mV of evoked response), the bipolar cell’s evoked release of vesicles will be larger than the cone’s, and the modulation of its vesicle release rate will be greater. This suggests the hypothesis that the evoked signal can be carried by fewer quanta in successive stages because at each stage it modulates a larger fraction of the maintained rate. If correct, this would imply that for each sequential synaptic stage along the visual pathway, fewer quanta carry the signal, but less performance is lost. The exact balance between amplification and noise, which sets how much performance is lost at each stage, is likely to be constrained as described below by evolutionary pressure to minimize the total loss.

This design, in which the first stage of a signal processing system generates most of the noise, is a widely employed system engineering principle (Pelli, 1990; Sarpeshkar, 1998; Dobkin, 2005). The rationale is that the first stage carries the smallest signals, and therefore is the one most challenged by its own intrinsic noise limitations. However the amplification of the first stage improves the ratio of the signal to intrinsic noise for later stages, which can then be constructed with noisier components. This hypothesis was tested with the ideal observer by comparing the sensitivity of an ideal model to the sensitivity of the cone synaptic output (in horizontal cells) and to the ganglion cell’s spike output (Borghuis et al., 2009). It could be further tested by ideal observer measurements of sensitivity in photoreceptors and bipolar cells.

Because many noise sources along the pathway from photoreceptors to ganglion cell are thought to be independent in the absence of an evoked response, noise may accumulate along the sequential pathway as the root-mean-square rule that applies to Poisson and Gaussian distributions (Hemila et al., 1998; Hopfner & Brodda, 2006). This would imply that the larger noise sources of a pathway tend to dominate. However, evolutionary pressure to maximize sensitivity of a sensory system would be expected to reduce the largest noise sources in line with all the others as found between 2 retinal layers (Figure 19; Borghuis et al., 2009). Therefore the apparent domination of synaptic noise suggests that either it cannot be reduced or there is some other reason for maintaining relatively low rates of vesicle release.

This raises a related question, why has neural circuitry evolved to depend on vesicle release for synaptic transmission, when less-noisy alternatives for release of neurotransmitter, such as transporters, are commonly present at synapses (Schwartz, 2002; Lukasiewicz, 2005; Heidelberger et al., 2005). One possibility is that vesicle release by synaptic ribbons is not independent but can be temporally correlated within or between presynaptic terminals (Schein & Ahmad, 2005). This might be the case if, for example, release at bipolar cell ribbon synapses is reliably synchronized by voltage transients (Freed, 2005; Sterling & Freed, 2007). This and similar possibilities could be tested with the ideal observer by comparing performance of presynaptic and postsynaptic signals. Another possibility is that noise in ganglion cells is maintained to desynchronize spike trains between neighboring cells, allowing greater coding accuracy in cortical processing (Perkel et al., 1967; Knight, 1972; van Rossum et al., 2002; Levine, 2007; Ermentrout et al., 2008). Finally, the noisiness of exocytotic vesicle release might be the cost for a presumed higher gain and greater speed, or a higher metabolic efficiency (Attwell & Laughlin, 2001; Schreiber et al., 2002; Vincent & Baddely, 2003; Niven & Laughlin, 2008). Constraints such as metabolic costs can be included in the ideal observer (Geisler, 2004). Resourceful use of the ideal observer can play an important role in exploring these issues.

5.4. Conclusions and Future Directions

Using an objective method for measuring signal quality, the neurophysiologist can discover how signals are processed and transmitted in the retina and other neural circuits in the brain. In one paradigm, the ideal observer tracks performance for a specific stimulus between neurons or arrays in a pathway to discover the loss of performance from the pathway’s signal processing mechanisms (Figure 11). The loss can then be linked with the specific amplification and noise properties of the pathway, e.g. synaptic processing (Figure 13). The performance of a real neuron or array can be compared with the performance of a model, either to validate the model or to provide intuition or constraints about the real circuit’s function (Figure 19).

The function of an array of neurons, e.g. ganglion cells, can be explored using a multi-electrode array to measure the performance of the individual cells’ spike trains, their collective performance, and their spatio-temporal neural code for a stimulus discrimination task. In a similar way, measurement of calcium concentration in a compartment of a specific cell type, for example, the presynaptic axon terminals of a transgenically labeled bipolar cell type, will allow the ideal observer to analyze a different metric of the array’s synaptic release. This could provide, for example, a measurement of synaptic performance across the array of bipolar cell ribbon synapses onto the ganglion cell array. Imaging the activity of cortical circuits with voltage-sensitive dyes has already accomplished a similar measurement of performance (Chen et al., 2006). An essential point is that to discover the spatial extent of the neural code and how performance extends from one layer to the next, a measurement of the evoked signal in the arrays extending just beyond the divergence from the stimulus is sufficient (Figures 11, 13).

A model that includes noise allows the ideal observer to link a measurement of performance to the underlying neural circuit. Many models of the ganglion cell have been derived that generate noisy spike trains. In the simplest models, consisting of a temporal receptive field filter followed by a compressive nonlinearity modulating a noisy spiking mechanism, the spike train approaches realism (Passaglia & Troy, 2004; Carandini et al., 2005; Pillow et al., 2005, 2008; Zhong et al., 2005; Greschner et al., 2006). When parameters for the noise sources are determined from biophysical properties and a second noise mechanism is added before the nonlinearity, the model simulates a realistic ganglion cell graded potential, and its performance measured by the ideal observer can be compared with real recordings to provide intuition about mechanisms.

Further intuition is provided by an explicit link from phototransduction through synaptic release to spike initiation. As more mechanisms are included, their effect on performance will provide intuition about their function in the real circuit. For example, when realistic synaptic gains and noise properties are included, the level of performance measured in a bipolar or ganglion cell can be linked deterministically to the synaptic release rates and signal processing in the presynaptic circuit (Figure 19; Dunn et al., 2006; Appendix of Borghuis et al., 2009; Jackman et al., 2009). Spatial receptive field components may extend the performance of the circuit. For example, we hypothesize a specific role of the surround in the cone and bipolar cells’ local circuits. The feedback from horizontal cell to cone and from amacrine cell to bipolar cell may maximize SNR of the synaptic input signal to the ganglion cell over a wider range of background illuminance (Figure 22). Therefore to explore the rationale for local circuit properties such as electrical coupling and the surround, one must develop more realistic models that link synaptic gains, nonlinearities, and noise sources over different background levels (Levine, 2007), evaluated by ideal observer measurements of performance.

Figure 22.

Hypothesis: adaptational components extend performance (contrast sensitivity) over a wide range of background at the cost of lower optimal performance. (A) Ganglion cell circuit with adaptation and inhibitory feedback. Performance of a ganglion cell in a contrast discrimination task extends over a wide range of backgrounds. At low backgrounds, performance is low, but relatively high compared to ideal. At high backgrounds, performance drops relative to ideal. (B) Performance of ganglion cell in a circuit without adaptation or feedback will be limited to a narrow range because it thresholds at low backgrounds and saturates at high backgrounds. Adaptation and surround antagonism reduce performance at optimal background. Ideal performance (dashed line) is defined by square root law.

In another paradigm, the ideal observer can compare the performance of intact and modified circuits (Figure 23). This allows determining the function of circuit mechanisms such as anatomical divergence and convergence, gap junction coupling, center-surround subtraction, and nonlinear effects such as adaptation in feedforward and feedback pathways. These can be tested with experimental protocols that vary the the state of the preparation, e.g. the amount of center vs. surround stimulation or the state of adaptation. These mechanisms can also be tested by ideal observer measurement of the performance of animal models with pharmacological block, or deletions of neuron types or specific mechanisms, e.g. connexins or synaptic proteins (Soucy et al., 1998; Strettoi et al., 2002; Shelley et al., 2006; Pang et al., 2007; Wang et al., 2007; Dedek et al., 2008; Kerschensteiner et al., 2008; Kim et al., 2008; Umino et al., 2008; Fadool & Dowling, 2008), or knock-ins of novel mechanisms (Bi et al., 2006). The ideal observer can explore models that include different noise sources, can determine the effect of each noise source on performance, and can compare their effects with a variety of circuits and stimuli.

Figure 23.

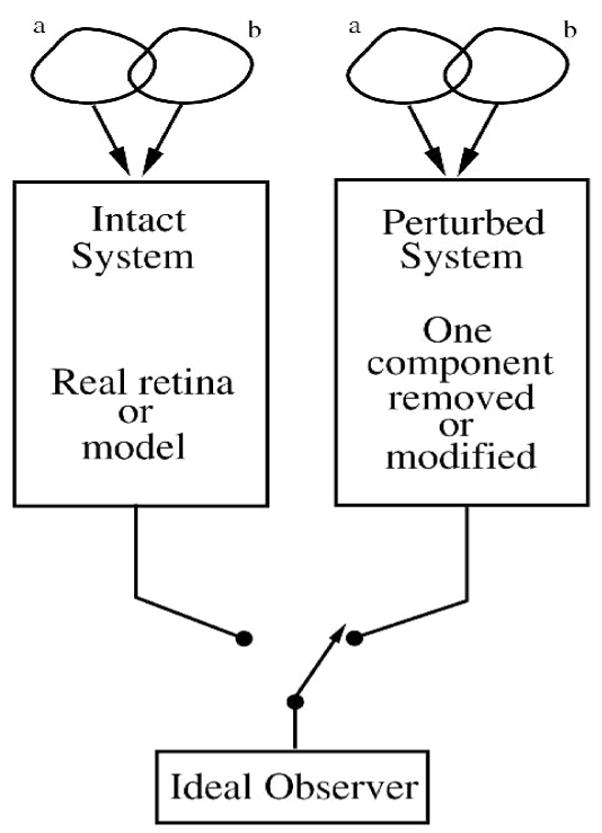
Identify the specific role of components in the circuit. Use pairs of stimuli that vary in one parameter to measure the system’s performance. Then perturb the system, measure its performance, and compare to the original to find the role of the perturbed component in signal quality of the system’s output. This paradigm can probe the performance of a single neuron or an array.

The ideal observer can determine the neural code for a variety of stimuli and test dimensions and can explore how signal processing mechanisms such as feedback, adaptation, and noise sources modulate the neural code. Because these mechanisms are unique for each type of neuron along a pathway and in parallel pathways, each has a different receptive field containing a unique proportion of signal and noise. Therefore the ideal observer will determine for each neuron type a different optimal stimulus and a different neural code. That the optimal stimulus and neural code differ for neurons along a pathway suggests that each neuron’s local circuit is uniquely designed to maximize its signal quality. The signal collection and weighting of synaptic inputs performed by each neuron represents a template to optimize its function over a range of stimuli (Tsukamoto et al., 1990). This suggests the hypothesis that the characteristic shape of a neuron’s specific loss (Figures 15–17, 21) selects signal components optimal for the neuron’s function in the local circuit. However, what is good for a cone is good for a bipolar cell, and what is good for bipolar cell is good for the ganglion cell. If this hypothesis is correct, it implies that the classic center-surround receptive field organization of retinal neurons is driven by the need for the local circuitry to optimize the quality of the visual signal at each stage.

Appendix: Comparison to other methods

Many methods exist for measuring signal quality. The example ideal observer presented above is an excellent choice for most retinal signals because it is simple, powerful, and can be directly compared with behavioral performance. However, it is not necessarily the best choice for measuring signal quality, and for some purposes other methods could be substituted. The ideal observer was originally developed from signal detection theory, which is similar but has slightly different assumptions. Both are derived from Bayes’ theorem which defines for a specific task the probability of a stimulus given a particular response (Gold & Shadlen, 2007). An alternative to Bayesian methods is Shannon mutual information, which is widely used as a measure of signal quality and offers some advantages. These comparisons provide background on the fundamental nature of the ideal observer and the visual discrimination task.

The form of the ideal observer is based on the properties of the noise distributions it is given. When given a theoretical model which precisely defines the noise distributions in advance, the observer can be very simple. For example, when given Poisson noise distributions from an ideal model, the ideal observer can be based on the “square root rule”: the distributions are discriminable if they differ by more than the square root of their mean (1 standard deviation). When the properties of the noise distributions are not known in advance, but the observations consist of a single dimension, the observer can still be very simple because the discrimination consists of a simple comparison between 2 probability values.

A.1. Signal detection methods

Ideal observer methods were originally derived from signal detection theory and receiver operating characteristic (ROC) analysis (Rose, 1942; DeVries, 1943; Barlow, 1957, 1962; Barlow et al., 1971; Johnson, 1980a,b; Green & Swets, 1988; Parker & Newsome, 1998; Levick et al., 1983; Duda et al., 2001; Gold & Shadlen, 2007). Signal detection implies a “yes-no” decision based on an observation in one dimension, which can be stated as a ROC detection task, and can be converted to an equivalent ideal observer discrimination task (Parker & Newsome, 1998). ROC analysis defines performance of a sensory detection task as the relation between the true positive rate (or “hits”) vs. the false positive rate (or “false alarms”), where the detection criterion is varied over the range of possible responses (Barlow et al., 1971; Parker & Newsome, 1998). The area under the resulting ROC curve is a measure of the detectability of the stimulus (Barlow et al., 1971; Green & Swets, 1988; Parker & Newsome, 1998). The equivalent ideal observer sums the total correct choices without reporting separate false positive and false negative rates (Green & Swets, 1988). The parameter d′ (criterion SNR) used in signal detection and ROC analysis is a measure of the detectability of the signal: d′ = difference between the means/standard deviation. Another common method is to measure, sometimes in combination with spectral analysis, the standard deviation of the response, setting threshold at 2 standard deviations (Barlow & Levick, 1969; Derrington & Lennie, 1982; Troy, 1983). This is more stringent than the ideal observer method presented here (d′ = 1), and has lower false positive and higher false negative rates.

A.2. Other likelihood methods

When the noise distributions of a neural response comprise several dimensions, to compute the likelihood ratio the ideal observer must utilize a method for dimensional reduction, which is known in a more general context as “categorization” or “classification” of distinct populations (Duda et al., 2001; Victor, 2005a). The critical concept is that multiple dimensions can provide more discriminability than one if they are reduced to one using an appropriate method.

The most straightforward method, a multiple-dimension probability density function (PDF), is the easiest to grasp and free from assumptions: each response is summed into a multi-dimensional frequency histogram, and when enough points to define smooth distributions have been collected, the histogram is normalized into a PDF, then directly evaluated with the test set (Geisler et al., 1991; Dhingra et al., 2003; Victor, 2005a). However to be accurate this method requires a very large sample size, so for most studies it is impractical. To improve the method, the noise distributions can be approximated by fitting to a Gaussian, and the bias from an inadequate sample size can be approximated (Victor, 2006).

The best method for dimensional reduction and classification to include in the ideal observer depends on the nature of the noise distributions, which may vary according to the neural circuit and recording mode. Some methods, e.g. Fisher LDA, reduce the dimensions before the discrimination, and others classify in the original multi-dimensional space or in a higher-dimensional space (Duda et al., 2001; Victor, 2005a). They all share the problem that to classify populations defined in many dimensions requires some simplifying assumptions and a large sample size (Friedman, 1989; Foffani & Moxon, 2004). Fisher LDA sets the template weights and projection angles to optimally separate two populations by simultaneously maximizing the difference between the means and minimizing the variances of the distributions in the final projection to one dimension (Figure 5C,5D)(Duda et al., 2001). For Gaussian distributed noise distributions with equal covariance Fisher LDA is optimal, and for typical noise distributions recorded from retinal neurons, Fisher LDA in combination with the likelihood decision rule is near optimal (Dhingra & Smith, 2004; Chichilnisky & Rieke, 2005; see Victor, 2005a).

For some types of neural response other methods may be more appropriate. An alternate simplified method that obviates a template can be used if the response variability is known to be uncorrelated. For example, when analyzing spike train responses where the response noise is uncorrelated beyond one bin, the simplified method generates a pair of PDFs for each bin. Then, to test a trial, for each stimulus the probabilities for all the bins are multiplied and the most likely stimulus is determined from the ratio of the products (Geisler et al., 1991; Dhingra et al., 2003; Geisler, 2004).

An ideal observer can calculate performance from an ideal model by constructing and evaluating the PDFs analytically. Alternately, it can evaluate theoretical performance from empirical PDFs without a test set (Appendix A in Geisler et al., 1991). However, in this case the limited sample size (number of trials) in the empirical data set upwardly biases the performance obtained. This is due to the limited size of the data set which generates a noisy PDF that does not correctly represent the original noise distribution (Duda et al., 2001). This issue is partially corrected by the use of separate likelihood and test sets, because in this case the performance bias from a limited sample size is conservative, i.e. downwards biased.

Another possibility, useful when the number of dimensions is high and noise distributions are correlated between bins, is to perform principal components analysis (PCA) on the binned responses (Duda et al., 2001; Chichilnisky & Rieke, 2005; Victor, 2005a; Thakur et al., 2007), reducing the number of dimensions to generate a smaller set of PCA components that are uncorrelated. To further reduce to one dimension, one possibility is to employ a template to generate PDFs and test as described above. Alternately, the PCA components can be reduced with the “alternate simplified method” described above to directly estimate the probability ratio defining the most likely stimulus (Geisler et al., 1991). PCA may thus allow the separation of the two populations by a discriminant template to be more accurate (Duda et al., 2001; Chichilnisky & Rieke, 2005).

When analyzing highly nonlinear systems, in which responses to a pair of stimuli cannot be distinguished when projected onto a line, a higher-order discriminant method to classify noise distributions over multiple dimensions may be more accurate. There are many higher-dimensional nonlinear methods which can be more accurate than LDA methods for discriminating some types of neural response, but they require more data and are generally more complex than one-dimensional methods (Foffani & Moxon, 2004; Friedman, 1989). For example, more complex discrimination methods can distinguish highly nonlinear responses that cannot be separated by projection into one dimension because their noise distributions are non-monotonic or concave in N-space (Friedman, 1989; Duda et al., 2001; Meyer et al., 2003; Victor 2005a,b, 2006; Murphy & Rieke, 2006). However, in comparison to higher-dimensional methods, the dimensional reduction by Fisher LDA is an advantage when the sample size is limited by recording time, because one-dimensional PDFs are more easily filled, allowing them to be more complete and therefore more accurate (Wahl & Kronmal, 1977; Dhingra & Smith, 2004; Victor, 2005a). Therefore, in typical retinal recordings where the number of trials is adequate, Fisher LDA is often simpler and close to optimal.

To correctly compute the Fisher LDA template the number of trials should exceed the number of dimensions, for best accuracy by several-fold (Duda et al., 2001). The reason is due to a limitation on solving the inverse matrix for Fisher LDA, and also to “overfitting” which gives incorrect results when the Fisher LDA template attempts to fit spurious correlations that occur with a limited number of trials (Duda et al., 2001). This will not usually be a problem for recordings from single neurons or pairs, but when recording from an array, with some combinations of multiple time (t) and space bins (s), the Fisher LDA discriminant may require a prohibitively large (s*t) number of trials, depending on the noise distributions and the correlations between them. Thus for some experimental studies the spatial and temporal resolution may require a trade-off.

A.3. Other ideal observer methods

An advantage of the ideal observer presented above, a single-interval two-alternative task, is that it allows a direct comparison between neural and behavioral performance (Geisler, 1989; Geisler et al., 1991; Dhingra et al., 2003; Kiorpes et al., 2003). However, when a human observer is presented a stimulus which is visible on some presentations but not on others (i.e. one stimulus of the pair is zero contrast), typically there is psychological bias either for or against reporting detection, originating in the decision criterion (Green & Swets, 1988; Klein, 2001). To reduce this type of bias, an equivalent “two-interval” forced choice paradigm is commonly used in which each observation consists of both stimuli, randomly ordered either side-by-side in space or sequentially in time (Green & Swets, 1988; Klein, 2001). Compared to a “single-interval” task, such a “two-interval” task is inherently more symmetrical because for each observation both stimuli are visible (Johnson, 1980a; Green & Swets, 1988; Klein, 2001; Kiorpes et al., 2003). This reduces psychophysical detection bias because the decision is comparative. Two-interval paradigms have also been utilized with a computer-based decision algorithm similar to the likelihood method described above (Kiorpes et al., 2003). Threshold criterion for two-interval tasks is usually set at 75% (Kiorpes et al., 2003; Green & Swets, 1988), which is equivalent to 68% for a single-interval task (Green & Swets, 1988; Geisler et al, 1991) because the two-interval likelihood distributions (PDFs), being the result of 2 signals, are narrower. Multiple-alternative paradigms are possible and are typically applied to measure performance of cortical neurons that are highly selective over a small region of parameter space (Geisler & Albrecht, 1997; Geisler, 1989, 2004; Klein, 2001). However, when testing discriminations along one dimension the two-alternative paradigm is often preferable because of its simplicity.

A further complication is that human observers have an innate uncertainty about the spatial location and time of the stimulus, which reduces behavioral performance. Uncertainty can be readily added to the ideal observer, and the performance reduction depends on the stimulus extent and envelope of the uncertainty window (spatial and temporal duty cycle) (Geisler et al., 1991; Dhingra et al., 2003). For measurement of neural performance without the need for a direct comparison to behavioral performance, this type of uncertainty is usually disregarded. A variety of ideal models have been constructed for use with analytical ideal observers, for example to compare with psychophysical results (Williams et al., 1993; Geisler, 2004; Brainard et al., 2006; Knill, 1998, 2007). Another form of the ideal observer calculates Fisher information, a measure of performance approximately equivalent to the likelihood method described above (Abbott & Dayan, 1999; Xu & Abshire, 2005; Durant et al., 2007).

A.4. Comparison to information theory

The method of information theoretic analysis is widely used to characterize the signal quality of neural systems (Shannon, 1948; Cover & Thomas, 1991; Rieke et al., 1997; Brenner et al., 2000). Shannon information is a measure of the reduction in uncertainty (entropy) about the stimulus. It bears some resemblance to performance for a Bayesian ideal observer (Thomson & Kristan, 2005; Victor, 2006; Victor & Nirenberg, 2008). Shannon information represents an average performance over a sequence of stimuli, and in this respect is analogous to the average performance of a Bayesian observer. Information theory computes the mutual Shannon information between the stimulus and response, which quantifies how closely the response corresponds to the stimulus (Schneidman et al., 2003; Thomson & Kristan, 2005; Shlens et al., 2007). The Bayesian ideal observer in a multiple-alternative paradigm can also quantify how closely the response corresponds to the stimulus. However, the methods differ because of how they convert the measured stimulus-response joint probabilities into a single number that measures performance (Victor & Nirenberg, 2008). The Shannon mutual information is calculated as the entropy of the response minus the entropy of the response given the stimulus: I(X;Y) = H(Y) − H(Y|X), where X is the stimulus and Y the response, and thus is computed as a function of all the probabilities in a multi-level response. In contrast, Bayesian methods use a decision rule which depends only on the most likely probabilities. Thus for the same set of stimulus-response joint probabilities, the Bayesian and Shannon measures will differ (Victor & Nirenberg, 2008). The ideal observer distinguishes distributions hit-or-miss on the basis of the likelihood, whereas Shannon information takes into account near misses and different levels of uncertainty (Victor & Nirenberg, 2008).

With identical stimulus paradigms and Gaussian response noise distributions, the two methods are equivalent, but for different stimulus paradigms or more complex response noise distributions the performances may diverge substantially (Thomson & Kristan, 2005; Victor & Nirenberg, 2008). Although the Bayesian ideal observer is commonly preferred for a sensory discrimination task because of its simplicity and correspondence to typical behavioral discrimination tasks, its reduction of the neural response to a binary decision represents a potential loss of Shannon information available to the brain that could be used for other sensory tasks (Victor & Nirenberg, 2008). The analogous ideal observer measure to Shannon information is the number of gray levels, estimated as the dynamic range divided by the noise level (see Figure 7), which is a fundamental measure of discriminability for the specific stimulus that generated the measurement. However, the measure of gray levels need not correspond to the potential mutual Shannon information available because each gray level is discriminated with a binary decision and is dependent on an arbitrary level for the threshold criterion (d′). Shannon information can readily be calculated with the same stimulus pairs used by the ideal observer, and in that case, the mutual information I = H(both stimuli) − [H(A) + H(B)]/2, where H(x) means the entropy of the response given stimulus × (Victor & Nirenberg, 2008). Both methods have the disadvantage that in practice it is difficult to present a stimulus sequence long enough to fully populate the stimulus-response probability histogram, but in some cases the resulting bias can be partially corrected (Victor, 2006).