An Expanded Theoretical Treatment of Iteration-Dependent Majorize-Minimize Algorithms

Abstract

The Majorize-Minimize (MM) optimization technique has received considerable attention in signal and image processing applications, as well as in the statistics literature. At each iteration of an MM algorithm, one constructs a tangent majorant function that majorizes the given cost function and is equal to it at the current iterate. The next iterate is obtained by minimizing this tangent majorant function, resulting in a sequence of iterates that reduces the cost function monotonically. A well-known special case of MM methods are Expectation-Maximization (EM) algorithms. In this paper, we expand on previous analyses of MM, due to [14, 15], that allowed the tangent majorants to be constructed in iteration-dependent ways. Also, in [15], there was an error in one of the steps of the convergence proof that this paper overcomes.

There are three main aspects in which our analysis builds upon previous work. Firstly, our treatment relaxes many assumptions related to the structure of the cost function, feasible set, and tangent majorants. For example, the cost function can be non-convex and the feasible set for the problem can be any convex set. Secondly, we propose convergence conditions, based on upper curvature bounds, that can be easier to verify than more standard continuity conditions. Furthermore, these conditions allow for considerable design freedom in the iteration-dependent behavior of the algorithm. Finally, we give an original characterization of the local region of convergence of MM algorithms based on connected (e.g., convex) tangent majorants. For such algorithms, cost function minimizers will locally attract the iterates over larger neighborhoods than is guaranteed typically with other methods. This expanded treatment widens the scope of MM algorithm designs that can be considered for signal and image processing applications, allows us to verify the convergent behavior of previously published algorithms, and gives a fuller understanding overall of how these algorithms behave.

1 Introduction

This paper pertains to the Majorize-Minimize (MM) optimization technique¹ as applied to minimization problems of the form

$$\mathrm{min.}\mathrm{\Psi }(\mathit{x})\mathrm{s.t.}\mathit{x}\in X\subset {ℝ}^p.$$ (1)

Here Ψ is a continuously differentiable, but possibly non-convex cost function, and X is a convex feasible subset of ℝ^p, the space of real, length p column vectors.

The MM technique has a long history in a range of fields. In the statistics literature, a prominent example is the Expectation Maximization (EM) methodology [10] which is an application of MM to maximum likelihood estimation. Further examples can be found in in [16, 17, 22, 24]). The interest in maximum likelihood estimation for tomographic image reconstruction subsequently led to many examples of EM, and more general MM algorithms, in image processing (e.g., [34, 23, 7, 8, 9, 38, 36]). MM has also received considerable attention in the signal processing literature, including [28, 4, 21, 26, 5].

An MM algorithm reduces Ψ monotonically by minimizing a succession of approximations to Ψ, each of which majorizes Ψ in a certain sense. An MM algorithm uses what we call a majorant generator ϕ_[·](·) to associate a given expansion point xⁱ with a tangent majorant ϕ_xⁱ (·). In the simplest case, illustrated for a 1D cost function in Figure 1, a tangent majorant satisfies Ψ(x) ≤ ϕ_xⁱ (x) for all x ∈ X and Ψ(xⁱ) = ϕ_xⁱ (xⁱ). That is, ϕ_xⁱ (·) majorizes Ψ with equality at xⁱ. The constrained minimizer xⁱ⁺¹ ∈ X of ϕ_xⁱ (·) satisfies Ψ (xⁱ⁺¹) ≤ Ψ(xⁱ). Repeating these steps iteratively, one obtains a sequence of feasible vectors {xⁱ} such that {Ψ (xⁱ)} is monotone non-increasing.

Figure 1.

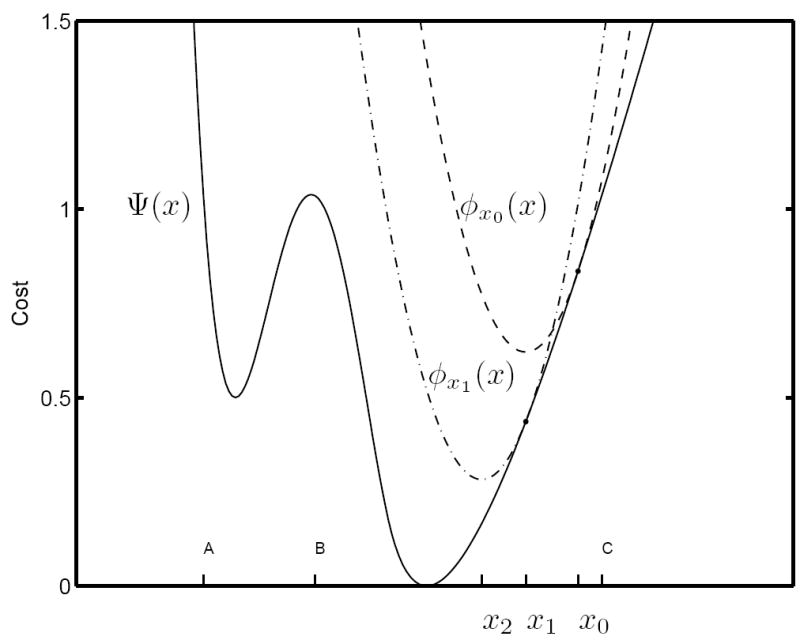
One-dimensional illustration of an MM algorithm.

A more elaborate form of MM was introduced in [14] that allows an iteration-dependent sequence $\{{\varphi }_{[·]}^i(·)\}$ of majorant generators to be used, rather than just a single ϕ_[·](·). This generalization allows considerable freedom in choosing the form of the majorant generator at a given iteration. For example, its form can be adaptively determined based on the observed progress of the algorithm over previous iterations. In addition, one can allow the tangent majorants $\{{\varphi }_{{\mathit{x}}^i}^i(·)\}$ to be functions of i-dependent subsets of the components of x. The latter results in iterative steps that, similar to coordinate descent, reduce Ψ(x) as a function of subsets of the optimization variables. This technique, called block alternation, can simplify algorithm design, because the majorization requirement need be satisfied only with respect to the variables being updated. Furthermore, because the majorization requirement is easier to satisfy, there is empirical evidence that tangent majorants obtained this way may approximate Ψ better (leading to faster convergence) than non-block alternating alternatives. An example of where block alternation led to faster convergence was presented in [14]. Block alternating MM has also seen subsequent use in [28, 30, 12, 4, 21, 26, 5].

The reasons why the MM technique has been attractive to algorithm designers are mixed, and some of the work in this paper may motivate some new reasons. Historically, the main appeal of MM is perhaps that it often leads to algorithms in which the iteration updates are given by simple closed-form formulas (e.g., [34, 7, 8, 11]) and hence, in these cases, tend to be easy to implement. This is in contrast to standard gradient descent methods that employ numerical line searches to ensure global convergence. For large-scale problems, the efficient implementation of line search operations can require complicated customized software implementation, as well as special hardware resources. For example, consider the minimization of the Poisson loglikelihood function encountered in fully 3D Positron Emission Tomography (PET) image reconstruction, e.g., [30]. There, efficiency demands that line searches be implemented in sinogram space. Doing so in turn necessitates considerable RAM, such as would be available on a parallel computing platform. It is likely that, for this reason, investigators in the field of 3D PET have looked to MM alternatives such as [34, 8]. A related reason why MM is attractive is that, when the tangent majorants are computationally simple to manipulate, one might hope for reduced overall CPU time. This benefit is harder to guarantee, because it demands not only that the tangent majorants have a simple form, but also that they provide accurate approximations to Ψ, and these two design requirements can conflict. Hence, one sometimes sees examples of MM in the literature that, although easy to implement, converge quite slowly (e.g., [34]). Conversely, a successful instance of MM acceleration was presented in a logisitic regression example in [24, Example 11]. There, the MM algorithm was found to compare favorably, in terms of convergence rate, with Newton’s method. In this paper (see Section 6), we suggest what might be a third benefit of MM. Namely, we discuss how the unusual local convergence properties of MM might be harnessed by certain non-convex minimization strategies.

The overall endeavour of this paper is to revisit and expand the MM convergence analysis of [15]. The scope of [15] is the only one that we know of that includes simultaneously the case where the majorant generator sequence $\{{\varphi }_{[·]}^i(·)\}$ can vary non-trivially with i and, furthermore, where minima may lie at constraint boundaries. Our treatment makes three principal contributions to the work begun there. (In the course of our analysis, we also remedy an error in [15], see Remark 4.5).

Our first contribution is to rework the analysis of iteration-dependent MM while relaxing many specific structural assumptions made in [15] on the form of the constraints, the cost function Ψ, and the tangent majorants. For example, in [15], only non-negativity constraints were considered, whereas in this paper, X can be any convex set or, in the case of block alternating MM, any convex set appropriately decomposable into a Cartesian product. Furthermore, in [15], Ψ and the tangent majorants were both assumed to be strictly convex. Here, we consider cases in which neither of the two are even convex. Flexibility is also introduced in the domain over which the tangent majorants are defined. In [15], the tangent majorant domains were assumed to be all of X, whereas here, the domains can be strict subsets of X. It is not uncommmon for tangent majorants to have smaller domains than Ψ. It is true, for example of the ML-EM algorithm of [34] (see Section 5) and also for the algorithm designs that we proposed (see [19] and [18, Section 6.6]) for a motion-corrected PET image reconstruction application. Lastly, in [15], the tangent majorants were assumed twice-differentiable, whereas in our analysis, only once-differentiability is assumed. These generalizations widen the range of applications to which [15] is applicable and provide a more flexible framework for algorithm design. Moreover, they allow us to verify the convergence (or at least the asymptotic stationarity) of some previously published block alternating MM algorithms not encompassed by the convergence analysis in [15]. Among these are the algorithm proposed in [12, Section 6] and those in [19] and [18, Section 6.6]. The convergence analysis in [15] does not apply to these examples at minimum because they involve non-convex Ψ. The line of proof used in [15] depended critically on the strict convexity of the cost function. Also, as discussed above, some of these algorithms use tangent majorants having domains that are not the entire set X. Further motivating examples for these generalizations are discussed in [20, Section 6].

Our second contribution is an alternative set of convergence conditions requiring local upper curvature bounds. In the MM literature involving iteration-independent majorant generators (e.g., [35, 23, 29]), convergence proofs usually invoke an assumption that the $\{{\varphi }_{[·]}^i(·)\}$ are continuous (jointly in both arguments). This continuity assumption admits an analysis using Zangwill’s convergence theorem [37, p. 91]. In [15], this line of analysis was generalized to iteration-dependent majorant generators under certain additional conditions, and the present paper continues to study these. In addition, however, we show that the continuity condition can be relaxed in favor of a requirement that the tangent majorant curvatures are uniformly locally upper bounded in the region of the expansion points. This latter condition is sometimes more easily verifiable than the standard continuity-based ones. Furthermore, this alternative condition admits considerable freedom in the iteration-dependent behavior of the algorithm (see Remark 4.6).

Our third contribution is an original characterization of the local region of convergence of MM algorithms to local minima. This branch of our analysis is restricted to tangent majorants that are connected (e.g., convex), which is a common practical case. Usually, algorithm developers design tangent majorants that are convex to facilitate their minimization. Our results show that the associated MM algorithm will be attracted to a strict local minima from essentially any point within a basin-like region surrounding that minimum. The same is not generally true of standard gradient algorithms. This property has important implications for the tendency of common kinds of MM designs to become trapped at local minima in non-convex minimization problems. However, we also discuss how this property might be harnessed by some established non-convex minimization strategies.

The rest of the paper is organized as follows. In Section 2, we formalize the class of MM algorithms considered in this paper. Next, in Section 3, we give a few additional mathematical preliminaries and describe various conditions imposed in the subsequent analysis. Our analysis begins in Section 4, where we study the global convergence of both block alternating and nonblock alternating MM. In this section, the principal step is showing the stationarity of MM limit points under conditions alluded to above. (This asymptotic stationarity property is often used as a definition for “convergence” in the nonlinear optimization literature.) Once asymptotic stationarity is established, convergence of MM in norm can be proved (Theorem 4.4) in a standard way by imposing discreteness assumptions² on the set of stationary points of (1). In Section 5, we discuss EM algorithms as a special case of MM algorithms and how certain EM algorithms from the tomographic imaging literature relate to our framework. Finally, Section 6 gives our analysis of the local region of convergence for MM, and its relation to capture basins. A concluding summary follows in Section 7.

2 Mathematical Description of MM Algorithms

In this section, we describe the class of MM algorithms considered in this paper. With no loss of generality, we assume that the feasible set X is a Cartesian product of M ≤ p convex sets, i.e.,

$$X=X_1\times X_2\times \dots \times X_M,$$ (2)

where X_m ⊂ ℝ^p_m, m = 1, …, M and ${\sum }_{m=1}^M{p}_m=p$. Since X is assumed convex, such a representation is always at least trivially accomplishable with M = 1.

To facilitate discussion, we first introduce some indexing conventions. Given x = (x₁, …, x_p) ∈ X, we can represent x as a vertical concatenation³ of vector partitions x = (x₁, x₂, …, x_M) where x_m ∈ X_m, m = 1, …, M. We shall refer to any subsequence S = (m₁, m₂, …, m_q) of (1, …, M) as a block index, and use the notation

$$\begin{array}{lll}{\mathit{x}}_S& =& ({\mathit{x}}_{m_1},{\mathit{x}}_{m_2},\dots ,{\mathit{x}}_{m_q})\\ X_S& =& X_{m_1}\times X_{m_2}\times \dots \times X_{m_q}\\ {ℝ}_S& =& {ℝ}^{p_{m_1}+p_{m_2}+\dots +p_{m_q}}\end{array}$$

to indicate certain Cartesian sub-products and their elements. Thus, one has x_S ∈ X_S ⊂ ℝ_S. The block index formed from the complement of S in (1, …, M) shall be denoted S͂. It will be necessary at times to view Ψ(x) as a function of x_S only with the components of x_S͂ held fixed. We use the notation

$${\mathrm{\Psi }}_S^{\mathit{y}}(\mathit{z})\triangleq \mathrm{\Psi }(\mathit{x}){\mid }_{\begin{array}{l}{\mathit{x}}_s=\mathit{z},\\ {\mathit{x}}_{\overline{s}}={\mathit{y}}_{\overline{s}}\end{array}}$$

for this purpose, where z ∈ X_S and y ∈ X.

Given a block index S and a point-to-set mapping D(·) such that y_S ∈ D(y) ⊂ X_S for all y ∈ X, we define a majorant generator ϕ_[·] (·) as a function mapping each y ∈ X to what we call a tangent majorant, a function ϕ_y(·) : D(y) ⊂ X_S → ℝ satisfying

$$\begin{array}{ll}{\mathrm{\Psi }}_S^{\mathit{y}}(\mathit{z})& -\mathrm{\Psi }(\mathit{y})\\ & \le {\varphi }_{\mathit{y}}(\mathit{z})-{\varphi }_{\mathit{y}}({\mathit{y}}_S),\forall \mathit{z}\in D(\mathit{y}).\end{array}$$ (3)

We call y the expansion point of the tangent majorant. We then also have ϕ_[·](·) : D → ℝ, in which

$$D=\left\{(\mathit{z},\mathit{y}):\mathit{z}\in D(\mathit{y})\subset X_S,\mathit{y}\in X\right\}$$

denotes the domain of the majorant generator. The simplest case is when D = X_S and D = X_S × X.

To design an MM algorithm, one selects an initial point x⁰ ∈ X, a sequence of block indices ${\left\{S^i\right\}}_{i=0}^{\infty }$, and a sequence of majorant generators ${\left\{{\varphi }_{[·]}^i(·):D^i\to ℝ\right\}}_{i=0}^{\infty }$ with domains

$$D^i=\left\{(\mathit{z},\mathit{y}):\mathit{z}\in D^i(\mathit{y})\subset X_{S^i},\mathit{y}\in X\right\}.$$

where the Dⁱ(·) ⊂ X_Sⁱ are point-to-set mappings of the type described above. Once the majorant generators are chosen, the MM algorithm is implemented by generating an iteration sequence ${\left\{{\mathit{x}}^i\in X\right\}}_{i=0}^{\infty }$ satisfying,

$${\mathit{x}}_{S^i}^{i+1}\in \underset{\mathit{z}\in D^i({\mathit{x}}^i)}{\mathrm{argmin}}{\varphi }_{{\mathit{x}}^i}^i(\mathit{z})$$ (4)

$${\mathit{x}}_{{\stackrel{\sim }{S}}^i}^{i+1}={\mathit{x}}_{{\stackrel{\sim }{S}}^i}^i.$$ (5)

Here, we assume that the set of minimizers in (4) is non-empty. We shall refer to the sequence ${\left\{{\mathit{x}}^i\right\}}_{i=0}^{\infty }$ produced this way as an MM sequence. In the simplest case, in which one chooses ${\varphi }_{\mathit{y}}^i({\mathit{x}}_{S^i})={\mathrm{\Psi }}_{S^i}^{\mathit{y}}({\mathit{x}}_{S^i})$ for all i, (4) and (5) become a generalization of block coordinate descent (e.g., [1, p. 267]), in which the coordinate blocks are not necessarily disjoint. By virtue of (3) and (4), {Ψ(xⁱ)} is monotonically non-increasing.

When the block indices Sⁱ are not all equal to (1, …, M), we say that the algorithm is block alternating (cf. [14, 15]). When the algorithm is not block alternating, i.e., if all Sⁱ = (1, …, M), then (3) simplifies to

$$\begin{array}{ll}\mathrm{\Psi }(\mathit{z})& -\mathrm{\Psi }(\mathit{y})\\ & \le {\varphi }_{\mathit{y}}(\mathit{z})-{\varphi }_{\mathit{y}}(\mathit{y}),\forall \mathit{z}\in D(\mathit{y}),\end{array}$$ (6)

while (4) and (5) reduce to

$${\mathit{x}}^{i+1}\in \underset{\mathit{x}\in D^i({\mathit{x}}^i)}{\mathrm{argmin}}{\varphi }_{{\mathit{x}}^i}^i(\mathit{x}).$$ (7)

Observe in (6) that when Ψ(y) = ϕ_y(y) (something we could always ensure by adding a y-dependent constant to ϕ_y(·)), one has ϕ_y(z) ≥ Ψ(z) with equality at z = y. That is, ϕ_y(·) majorizes Ψ and is tangent to it at y. This is the reason for our choice of the terminology tangent majorant.

The technique of block alternation can be advantageous because it can be simpler to derive and minimize tangent majorants satisfying (3), which involve functions of fewer variables, than tangent majorants satisfying (6). Block alternation can also provide faster alternatives to certain non-block alternating algorithm designs [14]. To apply block alternation, X must be decomposable into the Cartesian product form (2) with M > 1.

3 Mathematical Preliminaries and Assumptions

In this section, we overview mathematical ideas and assumptions that will arise in the analysis to follow.

3.1 General Mathematical Background

A closed d-dimensional ball of radius r and centered at u ∈ ℝ^d is denoted

$$B^d(r,\mathit{u})\stackrel{\mathrm{\Delta }}{=}\left\{{\mathit{u}}^{\prime }\in {ℝ}^d:\Vert {\mathit{u}}^{\prime }-\mathit{u}\Vert \le r\right\}.$$

where ∥ · ∥ is the standard Euclidean norm. For the minimization problem (1), we shall also use the notation

$$B_S(r,\mathit{z})\stackrel{\mathrm{\Delta }}{=}{X}_S\cap \left\{{\mathit{z}}^{\prime }\in {ℝ}_S:\Vert {\mathit{z}}^{\prime }-\mathit{z}\Vert \le r\right\}.$$

to denote certain constrained balls. Given a set G ⊂ ℝ^d, the notation cl(G), ri(G), and aff(G) shall denote the closure, relative interior, and affine hull of G, respectively. For a more leisurely discussion of these concepts, see [1, 33]. The notation ∂G will denote the relative boundary, cl(G) \ ri(G).

A function f : D ⊂ ℝ^d → ℝ is said to be connected on a set D₀ ⊂ D if (see [31, p. 98]), given any u, v ∈ D₀, there exists a continuous function g : [0, 1] → D₀ such that g(0) = u, g(1) = v, and

$$f(g(\alpha ))\le \max \{f(\mathit{u}),f(\mathit{v})\}$$

for all α ∈ (0, 1). A set C ⊂ ℝ^d is said to be path-connected if, given any u, v ∈ C there exists a continuous function g : [0, 1] → C such that g(0) = u and g(1) = v. Convex and quasi-convex functions are simple examples of connected functions with g(α) = αv + (1 − α)u. Also, it has been shown (e.g., Theorem 4.2.4 in [31, p. 99]) that a function is connected if and only if its sublevel sets are path-connected.

A key question in the analysis to follow is whether the limit points of an MM algorithm (i.e., the limits of subsequences of {xⁱ}) are stationary points of (1). By a stationary point of (1), we mean a feasible point x* that satisfies the first order necessary optimality condition,

$$\langle \nabla \mathrm{\Psi }({\mathit{x}}^{\ast }),\mathit{x}-{\mathit{x}}^{\ast }\rangle \ge 0\forall \mathit{x}\in X.$$ (8)

Here 〈·, ·〉 is the usual Euclidean inner product. If an algorithm produces a sequence {xⁱ} whose limit points (if any exist) are stationary points of (1), we say that the algorithm and the sequence {xⁱ} are asymptotically stationary.

3.2 Assumptions on MM Algorithms

Throughout the article, we consider cost functions Ψ and tangent majorants ϕ_y(·) that are continuously differentiable throughout open supersets of X and D(y) respectively. For every y, the domain D(y) is assumed convex. In addition, for a given MM algorithm and corresponding sequence $\{{\varphi }_{{\mathit{x}}^i}^i(·)\}$, we impose conditions that fall into one of two categories. Conditions in the first category, listed next, are what we think of as regularity conditions. In this list, a condition enumerated (Ri.j) denotes a stronger condition than (Ri), i.e., (Ri.j) implies (Ri). Typical MM algorithms will satisfy these conditions to preclude certain degenerate behavior that could otherwise be exhibited.

• (R1)
  Feasibility of the algorithm. We assume that the sequence {xⁱ} lies in a closed subset of X. Thus, any limit point of {xⁱ} is feasible. There are a variety of standard conditions under which (R1) will hold. The simplest case is if X is itself closed. Alternatively, (R1) will hold if one can show that the sublevel sets ${\mathrm{sublev}}_{\tau }\mathrm{\Psi }\stackrel{\mathrm{\Delta }}{=}\left\{\mathit{x}\in X:\mathrm{\Psi }(\mathit{x})\le \tau \right\}$ of Ψ are closed, which is often a straightforward exercise. For example, the closure of sublevel sets often follows if Ψ is coercive, i.e., tends to infinity at the boundary of X and at infinity. In such cases then, with τ₀ = Ψ(x⁰), the sublevel set sublev_τ0 Ψ is closed, and because {Ψ(xⁱ)} is montonically non-increasing, it follows that the entire sequence {xⁱ} is contained in this set.

  • (R1.1)
    Feasibility/boundedness of the algorithm. The sequence {xⁱ} is contained in a compact subset of X. Similar to (R1), if X (or just sublev_τ0 Ψ) is compact, then (R1.1) holds. This again is often the case when Ψ is coercive.
• (R2)Agreement and continuity of first derivatives. The gradient of every tangent majorant agrees with that of Ψ at its expansion point. Formally, for every i and y ∈ X,
  $$\nabla {\varphi }_{\mathit{y}}^i({\mathit{y}}_{S^i})=\nabla {\mathrm{\Psi }}_{S^i}^{\mathit{y}}({\mathit{y}}_{S^i}).$$ (9)

• Because Ψ is continuously differentiable, it follows from (9) that ∇ϕ_yⁱ(y_Sⁱ) is continuous with respect to y.

• (R3)Minimum size of tangent majorant domains. Each tangent majorant is defined on a feasible neighborhood of some minimum size around its expansion point. Formally, there exists an r > 0 such that $B_{S^i}(r,{\mathit{x}}_{S^i}^i)\subset D^i({\mathit{x}}^i)$ for all i. The simplest scenario is when Dⁱ(x) = X_Sⁱ for all i and x ∈ X, in which case (R3) holds with any r > 0.

Remark 3.1 Equation (9) is, in fact, implied by (3) whenever aff(Dⁱ(y)) = aff(X_Sⁱ) and y_Sⁱ ∈ ri(Dⁱ(y)). For details, see [20, Note A.2].

Remark 3.2 As discussed in [20, Note A.3], Condition (R2) can be weakened when X_Sⁱ is of measure zero in ℝ_Sⁱ.

Aside from the above regularity conditions, most results will require specific combinations of the following technical conditions. Similar to before, a condition denoted (Ci.j) implies (Ci).

• (C1)Connected tangent majorants. Each tangent majorant ${\varphi }_{{\mathit{x}}^i}^i(·)$ is connected on its respective domain Dⁱ(xⁱ). The typical case is when the tangent majorants are convex.
• (C2)Finite collection of majorant generators. The elements of the sequence $\{{\varphi }_{[·]}^i(·)\}$ are chosen from a finite set of majorant generators.
• (C3)Continuity of majorant generators in both arguments. For each i, the majorant generator ${\varphi }_{[·]}^i(·)$ is continuous on its domain Dⁱ. In addition, for any closed subset Ƶ of X, there exists an r_Ƶⁱ > 0 such that the set $\left\{(\mathit{z},\mathit{x}):\mathit{z}\in B_{S^i}(r_{Ƶ}^i,{\mathit{x}}_{S^i}^i),\mathit{x}\in Ƶ\right\}$ lies in a closed subset of Dⁱ. This is a generalization of the joint continuity condition for EM proposed in [35].
• (C4)Regular updating of coordinate blocks. Every sub-vector x_m ∈ X_m, m = 1 … M of x is updated by the algorithm at least once in every sequence of J iterations. Formally, for each m, there exists a block index S^(m) containing m, so that the set I_m = {i : Sⁱ = S^(m)} satisfies,
  $$\forall n\ge 0,\exists i\in \left[n,n+J\right]\mathrm{s.t.}i\in I_m.$$

  A simple case is when the block indices simply cycle over (1, …, M) according to Sⁱ = i mod M + 1.

• (C5)
  Diminishing differences. The sequence xⁱ satisfies $\underset{i\to \infty }{\lim }\Vert {\mathit{x}}^{i+1}-{\mathit{x}}^i\Vert =0$. This condition has frequently been encountered in the study of feasible direction methods (e.g., [31, p. 474]). In the MM context, this condition is implied by the following, often readily verifiable condition,

  • (C5.1)
    Uniform strong convexity. The sequence {xⁱ} has at least one feasible limit point. Also, there exists a γ⁻ > 0, such that for all i and z, w ∈ Dⁱ (xⁱ),
    $$\begin{array}{c}\langle \nabla {\varphi }_{{\mathit{x}}^i}^i(\mathit{z})-\nabla {\varphi }_{{\mathit{x}}^i}^i(w),\mathit{z}-w\rangle \\ \ge {\mathrm{\gamma }}^{-}{\Vert \mathit{z}-w\Vert }^2.\end{array}$$
    In other words, the $\{{\varphi }_{{\mathit{x}}^i}^i(·)\}$ are strongly convex with curvatures that are uniformly lower bounded in i. The fact that (C5.1) implies (C5) is proved in [20, Section 6.3.3]. Essentially, the proof is done by using Lemma 3.3(b) in this paper with u = xⁱ⁺¹, v = xⁱ, and f = ϕ_xⁱ(·). Condition (C5.1) generalizes [15, Condition 5].
• (C6)Uniform upper curvature bound. In addition to (R3), there exists a γ⁺ ≥ 0, such that for all i and $\mathit{z}\in B_{S^i}(r,{\mathit{x}}_{S^i}^i)$ (here r is as in (R3)),
  $$\begin{array}{c}\langle \nabla {\varphi }_{{\mathit{x}}^i}^i(\mathit{z})-\nabla {\varphi }_{{\mathit{x}}^i}^i({\mathit{x}}_{S^i}^i),\mathit{z}-{\mathit{x}}_{S^i}^i\rangle \\ \le {\mathrm{\gamma }}^{+}{\Vert \mathit{z}-{\mathit{x}}_{S^i}^i\Vert }^2.\end{array}$$

  In other words, the curvatures of the tangent majorants are uniformly upper bounded along line segments emanating from their expansion points. The line segments must extend to the boundary of a feasible neighborhood of size r around the expansion points. When the tangent majorants are twice differentiable, this is equivalent to saying that the second derivatives are locally bounded by γ⁺.

3.3 Lemmas

We now give several lemmas that facilitate the analysis in this paper. Most of these lemmas are slight generalizations of existing results. Their proofs are straightforward and are given in [20, Section 6.3.3].

Lemma 3.3 (Functions with curvature bounds) Suppose f : D ⊂ ℝ^d → ℝ is a continuously differentiable function on a convex set D and fix v ∈ D.

1. If 〈∇f(u) − ∇f(v), u−v〉 ≤ γ⁺∥u − v∥² for some γ⁺ > 0 and ∀u ∈ D, then likewise

   $$f(\mathit{u})-f(\mathit{v})\le \langle \nabla f(v),\mathit{u}-\mathit{v}\rangle +\frac{1}{2}{\mathrm{\gamma }}^{+}{\Vert \mathit{u}-\mathit{v}\Vert }^2.$$

2. If 〈∇f(u) − ∇f(v), u−v〉 ≥ γ⁻∥u − v∥² for some γ⁻ > 0 and ∀u ∈ D, then likewise

   $$f(\mathit{u})-f(\mathit{v})\ge \langle \nabla f(\mathit{v}),\mathit{u}-\mathit{v}\rangle +\frac{1}{2}{\mathrm{\gamma }}^{-}{\Vert \mathit{u}-\mathit{v}\Vert }^2.$$

Lemma 3.4 (Implications of limit points) Suppose that {xⁱ} is an MM sequence with a limit point x* ∈ X. Then

1. {Ψ(xⁱ)} ↘ Ψ(x*).

2. If x** ∈ X is another limit point of {xⁱ}, then Ψ(x**) = Ψ(x*).

3. If (C5.1) also holds then, $\underset{i\to \infty }{\lim }\Vert {\mathit{x}}^i-{\mathit{x}}^{i+1}\Vert =0$.

Lemma 3.5 (Convergence to isolated stationary points) Suppose {xⁱ} is a sequence in a compact set K ⊂ X and whose limit points S ⊂ K are stationary points of (1). Let C denote the set of all stationary points of (1) in K. If either of the following is true,

1. C is a singleton, or

2. Condition (C5) holds and C is a discrete set,

then {xⁱ} in fact converges to a point in C.

4 Asymptotic Stationarity and Convergence to Isolated Stationary Points

In this section, we establish conditions under which MM algorithms are asymptotically stationary. Convergence in norm is then proved under standard supplementary assumptions that the stationary points are isolated (see Theorem 4.4). Theorem 4.1, our first result, establishes that non-block alternating MM sequences are asymptotically stationary under quite mild assumptions. Two sets of assumptions are considered. One set involves (C3), a continuity condition similar to that used in previous MM literature (e.g., [35, 15, 29]). The continuity condition is motivated by early work due to Zangwill [37, p. 91], which established a broadly applicable theory for monotonic algorithms.

In the second set, the central condition is (C6), which requires a uniform local upper bound on the tangent majorant curvatures. To our knowledge, we are the first to consider such a condition in the context of MM methods.⁴ Condition (C6) can be easier to verify than (C3). For example, the algorithm of [11] is an example of MM based on separable quadratic tangent majorants. The optimal choice of curvatures for these quadratics is derived in [11], and is given by a complicated formula. It is much easier to show that these curvatures are uniformly bounded than to show that they are continuous.

Theorem 4.1 (Stationarity without block alternation) Suppose that all Sⁱ = (1,…, M), that {xⁱ} is an MM sequence generated by (7), and that the regularity conditions (R1), (R2), and (R3) hold. Suppose further that either (C6) or the pair of conditions {(C2), (C3)} holds. Then any limit point of {xⁱ} is a stationary point of (1).

Proof. Suppose x* ∈X is a limit point of {xⁱ} (it must lie in X due to (R1)) and, aiming for a contradiction, let us assume that it is not a stationary point. Then there exists x′ ≠ x* ∈ X such that

$$\langle \nabla \mathrm{\Psi }(\mathit{x}\ast ),\frac{{\mathit{x}}^{\prime }-\mathit{x}\ast }{\Vert {\mathit{x}}^{\prime }-\mathit{x}\ast \Vert }\rangle <0.$$ (10)

Since ∇Ψ is continuous, then, with (R2) and (R3), it follows that there exists a constant c < 0 and a subsequence {x^i_k} satisfying, for all k,

$$\Vert {\mathit{x}}^{\prime }-{\mathit{x}}^{i_k}\Vert \ge \min (r,\Vert {\mathit{x}}^{\prime }-\mathit{x}\ast \Vert /2)\stackrel{\mathrm{\Delta }}{=}\overline{t},$$ (11)

where r is as in (R3), and

$$\langle \nabla {\varphi }_{{\mathit{x}}^{i_k}}^{i_k}({\mathit{x}}^{i_k}),\frac{{\mathit{x}}^{\prime }-{\mathit{x}}^{i_k}}{\Vert {\mathit{x}}^{\prime }-{\mathit{x}}^{i_k}\Vert }\rangle \le c.$$ (12)

Define the unit-length direction vectors

$${\mathrm{s}}^k\stackrel{\mathrm{\Delta }}{=}\frac{{\mathit{x}}^{\prime }-{\mathit{x}}^{i_k}}{\Vert {\mathit{x}}^{\prime }-{\mathit{x}}^{i_k}\Vert },\mathrm{s}\ast \stackrel{\mathrm{\Delta }}{=}\frac{{\mathit{x}}^{\prime }-\mathit{x}\ast }{\Vert {\mathit{x}}^{\prime }-\mathit{x}\ast \Vert }$$

and, for t ∈ [0, t̄], the scalar functions

$$\begin{array}{lll}{h}_k(t)& \stackrel{\mathrm{\Delta }}{=}& {\varphi }_{{\mathit{x}}^{i_k}}^{i_k}({\mathit{x}}^{i_k}+t{\mathrm{s}}^k)\\ & & -\left[{\varphi }_{{\mathit{x}}^{i_k}}^{i_k}({\mathit{x}}^{i_k})-\mathrm{\Psi }({\mathit{x}}^{i_k})\right].\end{array}$$ (13)

Due to (R3) and (11), all h_k are well-defined on this common interval. The next several inequalities follow from (7), (6), and Lemma 3.4(a), respectively,

$$\begin{array}{lll}{h}_k(t)& \ge & {\varphi }_{{\mathit{x}}^{i_k}}^{i_k}({\mathit{x}}^{i_k+1})-[{\varphi }_{{\mathit{x}}^{i_k}}^{i_k}({\mathit{x}}^{i_k})-\mathrm{\Psi }({\mathit{x}}^{i_k})]\\ & \ge & \mathrm{\Psi }({\mathit{x}}^{i_k+1})\end{array}$$ (14)

$$\ge \mathrm{\Psi }(\mathit{x}\ast ).$$ (15)

The remainder of the proof addresses separately the cases where {(C6)} and {(C2), (C3)} hold.

First, assume that (C6) holds. This, together with Lemma 3.3(a), implies that for t ∈ [0, t̄],

$$h_k(t)-h_k(0)\le {\dot{h}}_k(0)t+\frac{{\mathrm{\gamma }}^{+}}{2}{t}^2.$$

However, h_k(0) = Ψ(x^i_k), while ḣ_k(0) ≤ c due to (12). These observations, together with (15), leads to

$$\mathrm{\Psi }(\mathit{x}\ast )-\mathrm{\Psi }({\mathit{x}}^{i_k})\le \mathit{ct}+\frac{{\mathrm{\gamma }}^{+}}{2}{t}^{2}t\in \left[0,\overline{t}\right].$$

Passing to the limit in k,

$$\mathit{ct}+\frac{{\mathrm{\gamma }}^{+}}{2}{t}^2\ge 0,t\in \left[0,\overline{t}\right].$$

Finally, dividing this relation through by t and letting t ↘ 0 yields c ≥ 0, contradicting the assumption that c < 0, and completing the proof for this case.

Now, assume {(C2), (C3)}. In light of (C2), we can redefine our subsequence {x^i_k} so that, in addition to (11) and (12), ${\varphi }_{·}^{i_k}([·])$ equals some fixed function ϕ̂_·([·]) for all k. That and (14) give, for t ∈ [0, t̄],

$$h_k(t)={\widehat{\varphi }}_{{\mathit{x}}^{i_k}}({\mathit{x}}^{i_k}+t{\mathrm{s}}^k)-\left[{\widehat{\varphi }}_{{\mathit{x}}^{i_k}}({\mathit{x}}^{i_k})-\mathrm{\Psi }({\mathit{x}}^{i_k})\right]$$ (16)

$$\ge \mathrm{\Psi }({\mathit{x}}^{i_k+1}).$$ (17)

From (R1), we know that {x^i_k} lies in a closed subset Ƶ of X. With (C3), there therefore exists a positive r_Ƶ ≤ t̄ such that h_k(t) as given in (16), converges as k → ∞ to $h\ast (t)\stackrel{\mathrm{\Delta }}{=}{\widehat{\varphi }}_{\mathit{x}\ast }(\mathit{x}\ast +t\mathrm{s}\ast )-\left[{\widehat{\varphi }}_{\mathit{x}\ast }(\mathit{x}\ast )-\mathrm{\Psi }(\mathit{x}\ast )\right]$ for all t ∈ [0, r_Ƶ]. Letting k → ∞ in (17) therefore yields,

$$h\ast (t)\ge \mathrm{\Psi }(\mathit{x}\ast )\forall t\in [0,r_{Ƶ}].$$ (18)

The function h*(t) is differentiable at t = 0 due to (R2). Now, h_k(0) = Ψ(x^i_k), so that in the limit, h*(0) = Ψ(x*). Thus, we have that (18) holds with equality at t = 0, from which it follows that

$${\dot{h}}^{\ast }(0)\ge 0.$$ (19)

However, ḣ_k(0) ≤ c due to (12). Furthermore, since ∇ϕ_yⁱ(y_Sⁱ) is continuous in y due to (R2), we have that ḣ_k(0) converges to ḣ*(0) as k → ∞. With (19), these observations lead to c ≥ lim inf_k ḣ_k(0) ≥ 0, contradicting again the assumption that c < 0.

The following example provides a simple illustration of how an MM algorithm can be non-asymptotically stationary when the assumptions of Theorem 4.1 are not met.

Example 4.2 Consider the 1D problem X = [0, 1.5], and Ψ(x) = 2 − x. Take x⁰ = 0 and let {xⁱ} be the sequence generated via (7) with majorant generator

$${\varphi }_y^i(x)={\varphi }_y(x)\stackrel{\mathrm{\Delta }}{=}c(y){(x-y)}^2+\mathrm{\Psi }(x)$$

$$c(y)\stackrel{\mathrm{\Delta }}{=}\{\begin{array}{ll}1& y=1\\ \frac{1}{\mid y-1\mid }& y\ne 1\end{array}$$

The resulting sequence of iterates {xⁱ} and tangent majorants ϕ_xⁱ(·) are depicted for several iterations in Figure 2. By induction, one can show that xⁱ = 1 − 2⁻ⁱ. Hence, {xⁱ} converges to 1 which is not a stationary point. This presents no conflict with Theorem 4.1, however. The tangent majorants do not satisfy condition (C6), since the tangent majorant curvatures {c(xⁱ) = 2ⁱ} tend to infinity. Also, ϕ_y(x) is discontinuous at y = 1, so (C3) is not satisfied. Consequently, the hypothesis of Theorem 4.1 does not hold.

Figure 2.

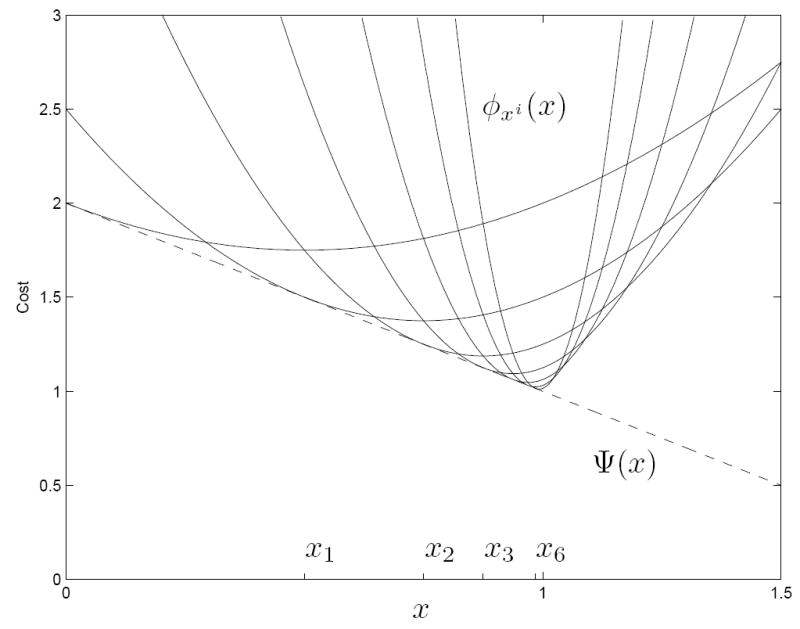
Illustration of Example 4.2. The MM sequence {xⁱ} converges to a non-stationary point. This is possible since the conditions of Theorem 4.1 are not satisfied.

The next result addresses the block alternating case, but requires additional conditions, namely (C4) and (C5). (Although, Condition (C2) is no longer required.) These conditions, however, are no stronger than those invoked previously in [15]. Condition (C4) is a generalization of [15, Condition 6]. Condition (C5) is an implied condition in [15], as shown in Lemma 3 in that paper.

Theorem 4.3 (Stationarity with block alternation) Suppose that {xⁱ} is an MM sequence generated by (4) and (5). As in Theorem 4.1, assume that (R1), (R2), (R3), and either (C6) or the pair of conditions {(C2), (C3)} hold. In addition, suppose that (C4) and (C5) hold. Then any limit point of{xⁱ} is a stationary point of (1).

Proof. Suppose x* ∈ X is a limit point of {xⁱ} (it must lie in X due to (R1)) and, aiming for a contradiction, let us assume that it is not a stationary point. In light of (2), there therefore exists x′ ≠ x* ∈ X and m ∈ {1, …, M}, such that

$$\langle \nabla {\mathrm{\Psi }}_m^{\mathit{x}\ast }({\mathit{x}}_m^{\ast }),{{\mathit{x}}^{\prime }}_m-{\mathit{x}}_m^{\ast }\rangle <0$$ (20)

and such that ${{\mathit{x}}^{\prime }}_{\stackrel{\sim }{m}}={\mathit{x}}_{\stackrel{\sim }{m}}^{\ast }$, ∀m̃ ≠ m. Then, with S^(m) as in (C4), it follows from (20) that,

$$\langle \nabla {\mathrm{\Psi }}_{S^{(m)}}^{\mathit{x}\ast }(\mathit{x}\ast ),\frac{{{\mathit{x}}^{\prime }}_{S^{(m)}}-{\mathit{x}}_{S^{(m)}}^{\ast }}{\Vert {{\mathit{x}}^{\prime }}_{S^{(m)}}-{\mathit{x}}_{S^{(m)}}^{\ast }\Vert }\rangle <0.$$ (21)

Now, consider a subsequence {x^i_k} converging to x*. We can assume that S^i_k = S^(m), for otherwise, in light of (C4), we could construct an alternative subsequence {x^i_k+J_k}, J_k ≤ J which does have this property. Furthermore, this alternative subsequence would also converge to x* due to (C5).

Similar to the proof of Theorem 4.1, we can also choose {x^i_k} so that,

$$\Vert {\mathit{x}}^{\prime }-{\mathit{x}}^{i_k}\Vert \ge \min (r,\Vert {\mathit{x}}^{\prime }-\mathit{x}\ast \Vert /2)\stackrel{\mathrm{\Delta }}{=}\overline{t}.$$

and, in light of (21) and (R2), so that

$$\langle \nabla {\varphi }_{{\mathit{x}}^{i_k}}^{i_k}({\mathit{x}}_{S^{(m)}}^{i_k}),\frac{{{\mathit{x}}^{\prime }}_{S^{(m)}-}{\mathit{x}}_{S^{(m)}}^{i_k}}{\Vert {{\mathit{x}}^{\prime }}_{S^{(m)}-}{\mathit{x}}_{S^{(m)}}^{i_k}\Vert }\rangle \le c.$$

for some c < 0. Now define

$${\mathrm{s}}^k\stackrel{\mathrm{\Delta }}{=}\frac{{{\mathit{x}}^{\prime }}_{S^{(m)}}-{\mathit{x}}_{S^{(m)}}^{i_k}}{\Vert {{\mathit{x}}^{\prime }}_{S^{(m)}}-{\mathit{x}}_{S^{(m)}}^{i_k}\Vert }$$

and, for t∈ [0, t̄]

$$\begin{array}{lll}{h}_k(t)& \stackrel{\mathrm{\Delta }}{=}& {\varphi }_{{\mathit{x}}^{i_k}}^{i_k}({\mathit{x}}_{S^{(m)}}^{i_k}+t{\mathrm{s}}^k)\\ & & -[{\varphi }_{{\mathit{x}}^{i_k}}^{i_k}({\mathit{x}}_{S^{(m)}}^{i_k})-\mathrm{\Psi }({\mathit{x}}^{i_k})].\end{array}$$

Manipulations of this h_k(t) verbatim to those in the proof of Theorem 4.1 lead to the contradiction c ≥ 0, and complete the proof of this theorem, as well.

The following theorem establishes convergence in norm by adding discreteness assumptions on the stationary points of (1).

Theorem 4.4 (Convergence in norm) Suppose {xⁱ} is an MM sequence satisfying (R1.1) and the conditions of either Theorem 4.1 or Theorem 4.3. Suppose, in addition, that either of the following is true.

1. The problem (1) has a unique solution as its sole stationary point, or

2. Condition (C5) holds and (1) has a discrete set of stationary points.

Then {xⁱ} converges to a stationary point. Moreover, in case (a), the limit is the unique solution of (1).

Proof. Under (R1.1), {xⁱ} lies in a compact subset of X. Moreover, the limit points of {xⁱ} are all guaranteed to be stationary by either Theorem 4.1 or Theorem 4.3. The result then follows from Lemma 3.5.

Remark 4.5 (An error remedied) The analysis in [15] of MM convergence is less general than stated there due to an error in the proof of Lemma 6 in that paper. The error occurs where it is argued “if ${\nabla }_k{\varphi }^{(k)}({\mathit{x}}_{S^{(k)}}^i;{\mathit{x}}^i)>0$ then ${\mathit{x}}_k^{i+1}>{\mathit{x}}_k^i$”. This argument would be valid only if, in addition to what was already assumed, ϕ^(k)(·; xⁱ) were a function of a single variable. Due to the analysis in the present paper, however, we can claim that the conclusions of [15] are indeed valid, even if the arguments are not. This follows from Theorem 4.4(a) above, which implies convergence under conditions no stronger than those assumed in [15].

Remark 4.6 (Curvature and iteration-dependence) In Theorems 4.1 and 4.3, when the curvature upper bound (C6) holds, there is very little restriction on how $\{{\varphi }_{[·]}^i(·)\}$ can depend on i, as compared to when {(C2), (C3)} are invoked.

This is useful, for example, if one wishes to use majorant generators that change adaptively based on several previous iterations of the algorithm sequence {xⁱ}. For example, one strategy that can be helpful for certain cost functions is to use a block alternating MM algorithm that monitors the gradient sequence {∇Ψ(xⁱ)}. When certain gradient components are persistently larger than others over several iterations, one switches to a majorant generator that updates only the variables corresponding to those components, thereby conserving computation. Such majorant generator sequences $\{{\varphi }_{[·]}^i(·)\}$ will not generally satisfy Condition (C2), and so one could not invoke Theorem 4.3 with {(C2), (C3)}. However, $\{{\varphi }_{[·]}^i(·)\}$ could well be made to satisfy (C6).

5 EM as a Special Case of MM

As discussed in Section 1, the family of Expectation Maximization (EM) algorithms is a prominent special case of MM algorithms for minimizing the negative loglikelihood Ψ(x) = − logp_x(u) of a random measurement vector U. In the classical set-up, one develops an EM algorithm by devising a so-called complete data random vector V whose joint distribution with U is of the form⁵

$$p_{\mathit{x}}(u,v)=p(u|v)p_{\mathit{x}}(v),$$ (22)

i.e., the conditional distribution of U given V is independent of the unknown parameter vector x. An EM algorithm is then just an MM algorithm based on the majorant generator,

$${\varphi }_{\mathit{y}}(\mathit{x})=\mathrm{\Psi }(\mathit{x})+\mathrm{KL}[p_{\mathit{y}}(v|u)\Vert p_{\mathit{x}}(v|u)],$$ (23)

where KL [f ∥ g] is the Kullback-Leibler (KL) divergence between two probability distributions f and g. For discrete U and V, this is

$$\mathrm{KL}[f\Vert g]\stackrel{\mathrm{\Delta }}{=}\sum _{z}f(\mathit{z})\left(-\log \frac{g(z)}{f(z)}\right).$$ (24)

For continuous random variables, the sum is to be replaced by an integral. A straightforward consequence of Jensen’s inequality is that KL [f ∥ g] ≥ 0 with equality iff f = g. It follows that (23) satisfies the majorization property (6), which in turn ensures the monotonicity of the algorithm.

The term “Expectation Maximization” comes from the fact that

$$\begin{array}{lll}{\varphi }_{\mathit{y}}(\mathit{x})& =& -\sum _z\log p_{\mathit{x}}(v)p_{\mathit{y}}(v|u)+\mathrm{const.}\\ & =& -{\mathrm{E}}_{\mathit{y}}(\log p_{\mathit{x}}(V)|U=u)+\mathrm{const.},\end{array}$$

which one can readily show by combining (23) with (22). Thus, processing the tangent majorant in each iteration is equivalent to taking a conditional expectation and maximizing the result.

A well established convergence condition for EM is the joint continuity assumption proposed in [ 35], a forerunner to our Condition (C3). A hazard in the design of MM algorithms can arise due to the singularity in the integrand in (24) at f = g = 0. Thus, unless p_x(u |v) is bounded away from zero as a function of x, this singularity may translate into singularities in the tangent majorant(23), so that Condition (C3) is violated. Algorithms such as these therefore do not satisfy standard regularity conditions for EM (or MM) convergence. Such algorithms would also violate Condition (C6), since curvatures in the neighbourhood of a singularity are unbounded.

Examples of these pathological cases are to be seen in certain EM algorithms that have been proposed for emission tomographic imaging. A widely considered statistical model for emission tomography projection measurements is

$$U_i~\mathrm{Poiss}\{\sum _j{a}_{\mathit{ij}}{\mathit{x}}_j+r_i\}.$$

where x_j ≥ 0 denote unknown image voxel values, a_ij ≥ 0 are system matrix elements, and r_i ≥ 0 are mean background radiation measurements. An EM algorithm investigated in [32] was based on the complete data choice,

$$\begin{array}{l}{V}_{ij}^{(1)}=\mathrm{Poiss}\{a_{\mathit{ij}}{x}_j\},V_i^{(2)}=\mathrm{Poiss}\{r_i\},\\ U_i=\sum _j{V}_{ij}^{(1)}+V_i^{(2)}\end{array}$$

for which (23) becomes,

$${\mathit{e}}_j(\mathit{y})\stackrel{\mathrm{\Delta }}{=}\left(\sum _i\frac{u_i}{{\sum }_j{a}_{\mathit{ij}}{y}_j+r_i}\right)$$ (25)

$${\varphi }_{\mathit{y}}(\mathit{x})=\sum _i{a}_{\mathit{ij}}{x}_j-{\mathit{e}}_j(\mathit{y})y_j\log x_j+\mathrm{const.}$$ (26)

In the particular case r_i = 0, this algorithm reduces to the ML-EM algorithm of algorithm of [34]. Clearly this ϕ_[·](·) can approach singularities as (x_j, y_j) → (0, 0), and hence (C3) and (C6) are violated. Although the algorithm has been proven to converge for r_i = 0, existing analyses (e.g., [3]) are difficult and very specific to the structures of Ψ and ϕ. The algorithm has not, to our knowledge, been shown to converge for the more general case r_i ≥ 0, although some relevant analysis was done in [13].

Another consequence of the singularities in KL is that, when all y_j > 0, the domain D(y) of the tangent majorant(26) is the interior of the non-negative orthant, which is normally a strict subset of the feasible set X. Normally, there are feasible images x in which some of the voxel values are zero (e.g., when for all i, the mean background radiation terms r_i > 0) and such images are excluded from the domain of (26). From similar considerations, one can also see that the tangent majorant fails to satisfy Condition (R3) at y near the boundary of the non-negative orthant.

A modification called ML-EM-3 was proposed in [15] that remedies the singularity issue in most practical cases. ML-EM-3 is based on complete data,

$$\begin{array}{l}{V}_{\mathit{ij}}^{(1)}=\mathrm{Poiss}\{a_{\mathit{ij}}(x_j+m_j)\},\\ V_i^{(2)}=\mathrm{Poiss}\{r_i-\sum _j{a}_{\mathit{ij}}{m}_j\},\\ U_i=\sum _j{V}_{\mathit{ij}}^{(1)}+V_i^{(2)}\end{array}$$

where m_j ≥ 0 are parameters chosen to satisfy Σ_j m_j ≤ r_i. With this complete data, (23) becomes,

$${\varphi }_{\mathit{y}}(\mathit{x})=\sum _i{a}_{\mathit{ij}}{x}_j-{\mathit{e}}_j(\mathit{y})(y_j+m_j)\log (x_j+m_j)+\mathrm{const.}$$

In practice, one generally has r_i > 0 for all i, and hence can choose m_j > 0 for all j. In this case, ϕ_[·](·) satisfies both (C3) and (C6). Moreover, the domain of these tangent majorants is the entire non-negative orthant. So, by Theorem 4.1, we can conclude that ML-EM-3 is asymptotically stationary.

In summary, although EM algorithms are special cases of MM, the applicability of the MM theory of this paper and its forerunners (e.g., [35]) depends on the choice of complete data.

6 Region of Local Convergence for Connected Tangent Majorants

In the study of minimization algorithms, one often wishes to know over what surrounding region of a strict local minimizer an algorithm is guaranteed to converge to that minimizer. In this section, we characterize regions of capture and convergence for MM algorithms that use connected (e.g., convex) tangent majorants. It is a prevalent design choice to make the tangent majorants convex, since this facilitates their minimization. We show in Theorem 6.4 that such algorithms are captured in any basin-shaped region in the graph of Ψ. If the basin contains a minimizer, then with suitable additional conditions (see Theorem 6.5), the entire basin is a region of convergence to that minimizer.

This is to be contrasted with the standard theory of gradient methods (e.g., steepest descent, Newton’s, Levenberg-Marquardt). General gradient methods are driven by the minimization of quadratic approximations to Ψ. These approximations may not majorize Ψ as tangent majorants do. Standard analyses of regions of capture for gradient methods (e.g., [1, p. 51, Proposition 1.2.5] and [1, p. 90, Proposition 1.4.1(a)]) guarantee capture only in a neighbourhood where the derivatives of Ψ are sufficiently similar to the derivatives at the minimum. In Example 6.6, we illustrate how this region of capture can be a strict subset of a basin-shaped region around the minimizer. Thus, our findings suggest that connected tangent majorants lead to larger regions of capture/convergence for MM than for (non-MM) gradient methods. This property has various practical implications that we shall discuss.

To proceed with our analysis, we require a formal mathematical definition of a “basin”. The following definition generalizes usual notions of a basin-shaped region.

Definition 6.1 We say that a set G ⊂ X is a generalized basin (with respect to the minimization problem (1)) if, for some x ∈ G, the following is never violated

$$\mathrm{\Psi }(\mathit{x})<\mathrm{\Psi }(\stackrel{\sim }{\mathit{x}}),\stackrel{\sim }{\mathit{x}}\in \mathrm{cl}(G)\cap \mathrm{cl}(X\backslash G).$$ (27)

Moreover, we say that x is well-contained in G.

Thus, a point is well-contained in G if it has lower cost than any point x̃ in the common boundary cl(G) ⋂ cl(X \ G) between G and its complement.

Remark 6.2 (Special Cases of Basins) Definition 6.1 is worded so that cl(G) ⋂ cl(X \ G) can be empty. Thus, for example, the whole feasible set X always constitutes a generalized basin, provided that it contains some x. This is because cl(X) ⋂ cl(X \ X) is empty, implying that (27) can never be violated by any x.

Any sublevel set G = {x ∈ X : Ψ (x) ≤ τ} is a generalized basin so long as τ is not the global minimum value of Ψ over X. Moreover, any global minimizer x* is well-contained in G. For further discussion of the basic properties of generalized basins, see [18, pp. 104-5,136-7].

The following proposition lays the foundation for the results of this section. It asserts that, if the expansion point of a connected tangent majorant is well-contained in a generalized basin G, then any point that decreases the cost value of that tangent majorant (relative to the expansion point) is likewise well-contained in G.

Proposition 6.3 Suppose that ϕ_y(·) is a tangent majorant that is connected on its domain D(y) ⊂ X_S and whose expansion point y ∈ X is well-contained in a generalized basin G. Suppose, further, that x ∈ X satisfies

$$\begin{array}{c}{\mathit{x}}_s\in D(\mathit{y}),{\mathit{x}}_{\stackrel{\sim }{S}}={\mathit{y}}_{\stackrel{\sim }{S}},\\ {\varphi }_{\mathit{y}}({\mathit{x}}_S)\le {\varphi }_{\mathit{y}}({\mathit{y}}_S),\end{array}$$ (28)

Then x is likewise well-contained in G.

Proof. It is sufficient to show that x ∈ G. For taking any x̃ ∈ cl(G) ⋂ cl(X \ G), and then combining (28), (3), and the fact that y is well-contained in G,

$$\mathrm{\Psi }(\mathit{x})\le \mathrm{\Psi }(\mathit{y})<\mathrm{\Psi }(\stackrel{\sim }{\mathit{x}}),$$ (29)

implying that x is also well-contained in G. Aiming for a contradiction, suppose that x ∈ X \ G. Since ϕ_y(·) is connected on D (y), there exists a continuous function g : [0, 1] → X with g(0) = y, g(1) = x, and such that, for all α ∈ (0, 1), one has

$$\begin{array}{lll}{[\mathbf{g}(\alpha )]}_S& \in & D(\mathit{y}),\\ {[\mathbf{g}(\alpha )]}_{\stackrel{\sim }{S}}& =& {\mathit{y}}_{\stackrel{\sim }{S}},\\ {\varphi }_{\mathit{y}}({[\mathbf{g}(\alpha )]}_S)& \le & \max \{{\varphi }_{\mathit{y}}({\mathit{y}}_S),{\varphi }_{\mathit{y}}(x_S)\}\\ & =& {\varphi }_{\mathit{y}}({\mathit{y}}_S),\end{array}$$ (30)

where the equality in (30) is due to (28). Also, since g(0) = y ∈ G,

$$\alpha \ast \stackrel{\mathrm{\Delta }}{=}\sup \left\{\alpha \in \left[0,1\right]:\mathbf{g}(\alpha )\in G\right\}$$

is well-defined. Finally, let w = g(α*). Combining the definitions of g() and α*, the continuity of g(), and the fact that x ∈ X \ G, one can readily show that w ∈ cl(G) ⋂ cl(X \ G).

Therefore, from the rightmost inequality in (29), we have, with x̃ = w,¡

$$\mathrm{\Psi }(\mathit{y})<\mathrm{\Psi }(\mathit{w})={\mathrm{\Psi }}_S^{\mathit{y}}({[\mathbf{g}(\alpha \ast )]}_S).$$ (31)

With (3), this implies that ϕ_y([g(α*)]_S) > ϕ_y(y_S), contradicting (30).

The following consequence of Proposition 6.3 articulates a capture property for MM sequences.

Theorem 6.4 (Capture property of MM) Suppose that {xⁱ} is an MM sequence generated by (4) and (5). In addition, suppose that some iterate xⁿ is well-contained in a generalized basin G and that the tangent majorant sequence ${\{{\varphi }_{{\mathit{x}}^i}^i(·)\}}_{i=n}^{\infty }$ satisfies (C1). Then likewise xⁱ is well-contained in G for all i > n.

Proof. The result follows from Proposition 6.3 and an obvious induction argument.

Finally, we obtain the principal result of this section.

Theorem 6.5 (Region of Convergence) In addition to the assumptions of Theorem 6.4, suppose that the conditions of either Theorem 4.1 or Theorem 4.3 are satisfied. Suppose further that G is bounded and cl(G) contains a single stationary point x*. Then {xⁱ} converges to x*.

Proof. Since G is bounded, it follows from Theorem 6.4 that the sequence ${\left\{{\mathit{x}}^i\right\}}_{i=1}^{\infty }$ lies in the compact set K = cl(G). Moreover, all limit points of {xⁱ} are stationary, as assured by either Theorem 4.1 or Theorem 4.3. The conclusions of the theorem then follow from Lemma 3.5(a).

Example 6.6 (Gradient Methods with Ad Hoc Steps) Here we illustrate how gradient algorithms with ad hoc step size choices may have a radius of capture that does not cover the entire basin surrounding a minimum. Consider the following 1D cost function, also depicted in Figure 3,

Figure 3.

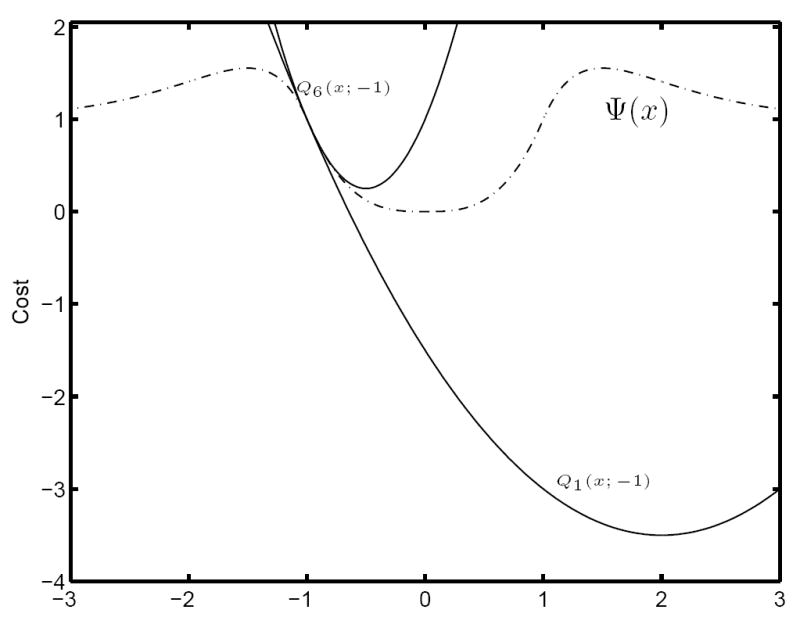
Comparing the capture properties of MM with gradient methods.

$$\mathrm{\Psi }(x)=\{\begin{array}{ll}{\mid x\mid }^3,& \mid x\mid \le 1\\ 3(\mid x\mid -1)e^{-2(\mid x\mid -1)}+1,& \mid x\mid >1.\end{array}$$

From Figure 3, one can see that the open interval (−1.5, 1.5) is a generalized basin in which all points are well-contained. It will be useful to note also that

$$\mid \frac{d\mathrm{\Psi }(x)}{\mathit{dx}}\mid \le 2\mid x\mid ,x\frac{d\mathrm{\Psi }(x)}{\mathit{dx}}\ge 0,\forall \mid x\mid \le 2/3.$$ (32)

Consider now the family of quadratic expansions,

$$\begin{array}{lll}{Q}_{s^k}(x;x^k)& =& \mathrm{\Psi }(x^k)\\ & & +\frac{d\mathrm{\Psi }(x^k)}{dx}(x-x^k)+\frac{1}{2S^k}{(x-x^k)}^2.\end{array}$$ (33)

The minimizer x^k+1 of Q_s^k(·; x^k) is given by the gradient algorithm step,

$$x^{k+1}=x^k-s^k\frac{d\mathrm{\Psi }(x^k)}{\mathit{dx}}.$$ (34)

Suppose we choose an arbitrary and constant step size parameter s^k = 1. From (32), it then follows that if x^k lies in the interval |x| ≤ 2/3, the gradient step (34) cannot cross the origin to a point more distant from the origin than x^k. Consequently, all subsequent iterations of (34) remain trapped in the region |x| ≤ 2/3 and hence also in the larger basin-like interval (−1.5, 1.5). (One can also show that the algorithm converges monotonically to the minimum when initialized in |x| < 2/3, but this is tangential to the point of this example.)

This capture property does not hold, however, for all starting points in (−1.5, 1.5). In particular, if |x^k| = 1, then $\mid \frac{d\mathrm{\Psi }(x)}{\mathit{dx}}\mid =3$. With s^k = 1, this means that the gradient step (34) will be large enough to put x^k+1 in the region |x| > 1.5. Not only does this step escape from the basin (−1.5, 1.5), but the gradient algorithm will also never return there. For, once |x^k+1| > 1.5 the direction of the gradient will carry all subsequent iterations of (34) off toward infinity.

This example is to be contrasted with the choice s^k = 6. The iterations are then driven by the minimizations of the functions Q₆(·; x^k) which are not only convex, but are also tangent majorants. The latter can be verified, for instance, using Lemma 3.3(a) with γ⁺ = 6 and f = Ψ. Theorem 6.4 therefore applies and shows that if x^k lies in (−1.5, 1.5), then all subsequent iterations of the algorithm will as well.

The distinction between these two cases is also illustrated graphically in Figure 3 with x^k = −1. There, we see that, since Q₆(·; −1) majorizes Ψ, its minimum is constrained by the graph of Ψ to lie in (−1.5, 1.5). Conversely, since Q₁(·; −1) does not majorize Ψ, its minimum is not constrained in this way.

The above example illustrates how non-MM gradient methods with constant step sizes can escape from a basin. However, it is also easy to see how this would be true even when conventional line search algorithms are used. Generally, line search methods can find any 1D stationary point along the search line and different 1D stationary points can lie in different generalized basins. For example, in Figure 1, the stationary points in the intervals [A, B] and [B, C] clearly lie in different generalized basins. The MM steps in Figure 1 respect the basin boundaries, consistent with Theorem 6.4, whereas a line search algorithm would not be expected to.

There are both positive and negative practical implications to Theorem 6.5. Since it is common to use convex (and hence connected) tangent majorants, it is essential for MM algorithm designers to be aware of these implications. A positive consequence is that global minimizers will, as a special case, attract the iterates over larger distances. Thus, if a moderately good initial guess of the solution is available, the chances of getting pulled toward the global solution may be higher. A negative consequence is that sub-optimal local minimizers will also attract the iterates over larger distances. Thus, if not even a moderately good initial guess is available, the chances of becoming trapped at a sub-optimal local minimum can be high, depending on the preponderance of different minima in the graph of Ψ.

A potential application of Theorem 6.5 is to non-convex optimization strategies that decompose the problem into a sequence of local minimization steps. These include a method due to [2] called Graduated Non-Convexity (GNC), in which a parametric family of approximations to the cost function Ψ are locally minimized at successive increments of the parameter. Another example is the strategy of selecting a mesh of initial points and locally minimizing Ψ around each point so as to probe for the global minimum. In these strategies, MM with connected tangent majorants seem an appropriate tool for implementing the local minimization steps since, of course, local minimization tasks benefit from a wide region of convergence.

7 Summary

In this paper, we have revised the analysis of [15] in an expanded framework, introduced alternative convergence conditions, and provided original insights into the locally convergent behavior of iteration-dependent MM. In the course of doing so, we also remedied an error in the previous convergence proof (see Remark 4.5). The core results of our global convergence analysis were Theorems 4.1 and 4.3, which proved asymptotic stationarity for non-block alternating and block alternating MM respectively. The core result of our local convergence analysis was Proposition 6.3, which proved a fundamental property of MM algorithms employing connected tangent majorants, namely that they remain in basin-like regions of the cost function. Our treatment here, we believe, provides enhanced insight into the behavior of MM, as well as a highly broad and flexible framework for MM algorithm design. The results have been useful in verifying the convergence of previously proposed algorithms for different PET imaging applications [12, 19, 18].

An unresolved theoretical question is whether MM will converge in norm when the stationary points of the optimization problem are non-isolated. It is rare to be able to prove this behavior for iterative optimization algorithms in general. However, it has been proven for the EM algorithm of Shepp and Vardi [34], a prominent example of MM in the field of emission tomography. Thus, it is tempting to think that this behavior may be provable in wider generality within the class of MM algorithms. Our preliminary work on this question in [20] may be a starting point for future analysis.