Structural analysis of protein dynamics by MD simulations and NMR spin-relaxation

Abstract

Molecular dynamics (MD) simulations and nuclear magnetic resonance spin-relaxation measurements provide detailed insights into ps-ns structural dynamics of proteins. An analysis of discrepancies between the two methods is presented for the B3 immunoglobulin-binding domain of streptococcal protein G. MD simulations using three MD force fields (OPLS-AA, AMBER ff99SB, and AMBER ff03) overestimate the flexibility of backbone N—H vectors at the borders of secondary structure and in loops when compared with experimentally determined backbone amide generalized order parameters (Hall and Fushman, J Am Chem Soc 2006; 12:7855–7870). Comparison with a previous study of residual dipolar coupling constants (Bouvignies et al., Proc Natl Acad Sci USA 2005;102:13885–13890) indicates that slower timescale motions do not account for the discrepancies. Structural analysis reveals that relative imbalance between the description of hydrogen bonding and other terms of modern force fields may be responsible for disagreement.

INTRODUCTION

Biological processes, including folding and assembly, ligand binding and molecular recognition, allostery and cooperativity, and catalysis, ultimately rely on conformational changes in proteins and other macromolecules. Nuclear magnetic resonance (NMR) spectroscopy is a powerful experimental technique for elucidating protein dynamics that yields site-specific information about internal motions spanning many timescales.¹ The focus of the present work is laboratory frame NMR spin-relaxation of backbone amide moieties, which allows the determination of amplitudes and correlation times of N—H bond vector motions on the ps-ns timescale.²

The amplitudes are described by the square of the generalized order parameter, S².³ Order parameters have been reported for hundreds of proteins from a wide range of structural and functional families.⁴ A number of these studies have noted significant changes in protein backbone flexibility between biologically relevant conformations. These observations pose the hypothesis that ps-ns protein dynamics could make significant thermodynamic contributions to biological function via changes in conformational entropy.⁵ Coupling of motions between atomic sites complicates quantitative conversion of changes in order parameters into differences in entropy between protein conformations. Coupled internal motions in proteins also could provide a microscopic mechanism for allostery and cooperativity, and thus have independent biological relevance.⁴ Conventional NMR spin-relaxation parameters provide limited mechanistic details about coupled motions between atomic sites.

The interpretation of entropic changes in proteins also is complicated by the limited timescales of motions, typically less than or similar to the timescale of overall rotational tumbling, that contribute to relaxation-derived order parameters. Order parameters can also be derived from residual dipolar couplings (RDCs)⁶ and are sensitive to a much wider range of time scales than order parameters derived from NMR spin-relaxation. However, a number of assumptions are made in the determination of order parameters from RDCs that can strongly affect the results, and the optimal approach for the analysis has not been established.

Order parameters for the B3 immunoglobulin-binding domain of streptococcal protein G (GB3), a 56 amino acid α/β protein, derived from NMR spin-relaxation have been reported by Hall and Fushman.⁷ Order parameters from an analysis of RDCs for GB3 by Bouvignies et al.⁸ show sites of increased disorder, lower order parameters, compared with the relaxation-derived order parameters. A separate analysis of the same set of RDCs by Clore and Schwieters,⁹ however, yielded order parameters indicating no additional flexibility compared with the motions captured by NMR spin-relaxation for GB3.⁷ These two analyses reflect different approaches toward interpretation of RDC data and highlight the current need for caution.

Molecular dynamics (MD) simulation is the only method capable of describing atomistic details of protein dynamics.¹⁰ Since the first protein MD study¹¹ force fields,^12–17 solvation models¹⁸ and procedures for overcoming the problem of limited sampling¹⁹ have undergone constant improvement. For the last decade, efforts to improve classical MD force fields have focused in particular on reparameterization of torsion angle terms, after newly available high-level ab initio quantum mechanical (QM) calculations had been established as a benchmark for force field comparison and development.²⁰ This approach was pursued initially for the OPLS-AA force field,¹⁵ followed by similar studies yielding the CHARMM22 CMAP correction¹² and the AMBER ff99SB force field.¹⁴ In an alternate approach AMBER partial charges were reparameterized by direct incorporation of a low-dielectric continuum model into QM calculations, resulting in the AMBER ff03 force field.²¹ Despite the impressive improvements achieved by such efforts the description of macromolecular dynamics is however still imperfect. Hydrogen bonds are prominent in protein structures and the treatment of hydrogen-bonding interactions is an area of active research.^22–24 In current MD force fields, hydrogen bonding is treated as a purely electrostatic effect between fixed atom-centered partial charges, which implies the linearity of hydrogen bonds.²³ Recent QM studies, however, indicate a slight preference for bent conformations. ²⁵ Two approaches are currently being pursued to address this problem: introduction of a directionality term for hydrogen bonds in classical fixed charge force fields²⁵ and development of polarizable force fields.¹³

NMR relaxation measurements have long been recognized as a benchmark crucial to establishing confidence in the accuracy of the simplified classical mechanical description of intramolecular forces used in MD simulation.¹¹ An atomistic interpretation of NMR relaxation data, which is in principle only possible in terms of an MD trajectory, is in turn necessary for drawing conclusions about the functional relevance of detected motions.⁴ Accurate detailed descriptions of internal motions by MD simulations will, for example, allow reliable detection of coupled motions to quantify the conformational entropy of a protein from NMR spin-relaxation. The two methods thus benefit reciprocally from quantitative comparison. To date, however, agreement between the two techniques remains semi-quantitative,^12,14,26 severely limiting attempts to investigate changes in protein dynamics upon biologically relevant transitions through a combination of the two techniques.^27,28 Few detailed investigations of the discrepancies have been attempted, in part because the absolute accuracy of experimental order parameters is difficult to establish. ²⁹ In particular, nanosecond timescale motions with relatively small amplitude are difficult to detect and if undetected lead to elevated values of order parameters.³⁰

In a recent study,³¹ order parameters derived from the analysis of RDCs for GB3 by Bouvignies et al.⁸ were used to tune accelerated molecular dynamics (AMD) simulations. Starting structures for classical MD simulations were selected from the structural ensemble resulting from the AMD simulations. The authors obtained increased agreement with NMR spin-relaxation order parameters compared with classical MD simulations starting from the crystal structure. These findings emphasize the importance of the timescale limitation of NMR spin-relaxation order parameters.

In the present study, a structural analysis of the discrepancies between NMR spin-relaxation order parameters⁷ and order parameters calculated from MD simulations for GB3 is used to identify potential deficiencies in MD force fields. RDC-derived order parameters are used only as a qualitative indicator of slow-timescale motions. In contrast to the previous AMD study, however, the discrepancies between MD simulations and NMR spin-relaxation data observed are not explained entirely by slow-timescale motions. Because of computational limitations, insufficient sampling of protein conformational space can never be excluded as a source of disagreement between simulation and experiment. Nevertheless, the analysis presented here suggests that an inaccurate description of hydrogen bonding relative to other terms of the force fields studied may contribute to the observed discrepancies. The present work does not intend to distinguish in quality between force fields. The motivation in choosing several force fields for the analysis lies rather in the similarity of the functional forms of modern classical MD force fields and the general relevance of the issue of hydrogen-bonding description.

MATERIALS AND METHODS

Molecular dynamics simulations

The N-terminus of the 1.1 Å resolution crystal structure of GB3 (PDB code 1IGD)³² was altered using VMD³³ to conform to the construct used for the NMR spin-relaxation studies⁷ (Δ1–5, T6M, T7Q). The mutated structure was energy minimized and side chain conformations optimized using PLOP.³⁴ The resulting structure was solvated with 5080 TIP4P³⁵ water molecules in a 56 Å cubic box to accommodate a minimum thickness of 1 nm for the water shell. Two sodium ions were added to the system to maintain electric neutrality. They were placed close to negatively charged residues. OPLS-AA¹⁵ simulations were conducted with the MD simulation software SIM.³⁶ Particle–Mesh–Ewald periodic boundary conditions with a 0.8 nm cutoff were used for electrostatic interactions and a 1-nm cutoff for Lennard–Jones interactions. The RATTLE³⁷ and SHAKE³⁸ algorithms were applied for constraining vibrations of bonds involving hydrogen atoms in OPLS-AA and AMBER simulations, respectively, and a time step of 2 fs was used. A 1-ns equilibration simulation was conducted at a constant temperature of 297 K (corresponding to the NMR spin-relaxation study) and a constant pressure of 1 atm (NPT). Thirty structures were extracted at equal intervals from this NPT simulation and used as starting structures for thirty 2.4 ns constant energy (NVE) production simulations.

AMBER simulations were conducted with the sander module in the AMBER 9.0 MD package with all simulation parameters and the solvent model identical to the OPLS-AA simulations. Thirteen of the 30 starting structures generated for OPLS-AA simulations were randomly chosen as starting structures for the 13 ff03²¹ simulations. The same 13 structures plus one more OPLS-AA starting structure were used as starting structures for the 14 ff99SB¹⁴ simulations. Each starting structure was solvated with 5080 TIP4P solvent molecules and energy minimized. The solvent was equilibrated subsequently in a 100-ps NPT simulation with the protein atom positions constrained. Thirteen and 14 2.4-ns NVE simulations were conducted with ff03 and ff99SB, respectively.

Coordinate sets were saved every 1 ps in all simulations. Analysis of simulations was conducted with an in-house MD analysis package.

Internal correlation functions

The effects of overall tumbling during the simulations were removed by superposition of backbone heavy atoms for each coordinate set using the energy-minimized mutated crystal structure as the reference structure. Internal correlation functions were then calculated for each trajectory according to

$$C_{\mathrm{I}}(\mathrm{\tau })=\langle P_2[\mathrm{\mu }(t)\times \mathrm{\mu }(t+\mathrm{\tau })]\rangle$$ (1)

where P₂[x] is the second Legendre polynomial, μ is the N—H bond vector scaled to unit magnitude and angular brackets indicate averaging over time t.² The resulting set of correlation functions was averaged to give one correlation function per set of simulations.

Order parameters

Order parameters were calculated as ensemble averages according to

$$S^2=\frac{\mathrm{\zeta }}{2}\left(3{\displaystyle \sum _{i=1}^3{\displaystyle \sum _{j=1}^3{\langle {\mathrm{\mu }}_i{\mathrm{\mu }}_j\rangle }^2-1}}\right)$$ (2)

where μ₁, μ₂ and μ₃ are the x, y, and z components of μ, respectively.³⁹ Angular brackets indicate averaging over all snapshots in all trajectories of the respective set. Scaling by ζ = (1.02/1.04)⁶ ≈ 0.89 accounts for zero point vibrational motions of the bond vectors not captured by MD simulations utilizing SHAKE and a 2-fs time step.⁴⁰

Hydrogen bonding

A hydrogen bond was considered to be formed between a donor hydrogen atom (hydrogen attached to a nitrogen, sulfur, or oxygen atom) and an acceptor atom (nitrogen, sulfur or oxygen atom) when the distance between donor hydrogen and acceptor was less than 3.0 Å, and simultaneously the angle between donor, donor hydrogen, and acceptor as well as the angle between donor hydrogen, acceptor, and the acceptor bound atom were both larger than 100°.⁴¹

RESULTS

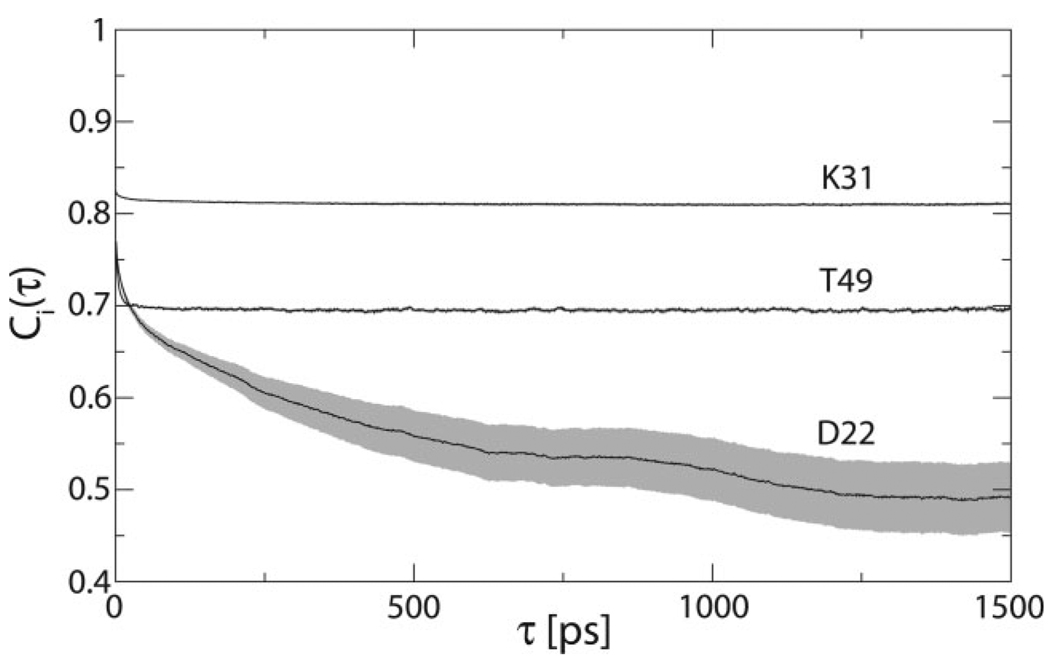
Thirty 2.4 ns simulations of GB3 were conducted with the OPLS-AA force field,¹⁵ fourteen 2.4 ns simulations with the AMBER ff99SB force field,¹⁴ and thirteen 2.4 ns simulations with the AMBER ff03 force field.²¹ All simulations used the TIP4P explicit solvent model.³⁵ Internal correlation functions of backbone N—H vectors were averaged over all simulations for each force field. Three cases representative of the full spectrum of motional amplitudes observed in the OPLS-AA simulations are shown in Figure 1. The internal correlation functions converge for all backbone amides except the most flexible sites in the protein.

Figure 1.

Three representative internal correlation functions from OPLS-AA simulations. The standard error of the mean is shown in gray.

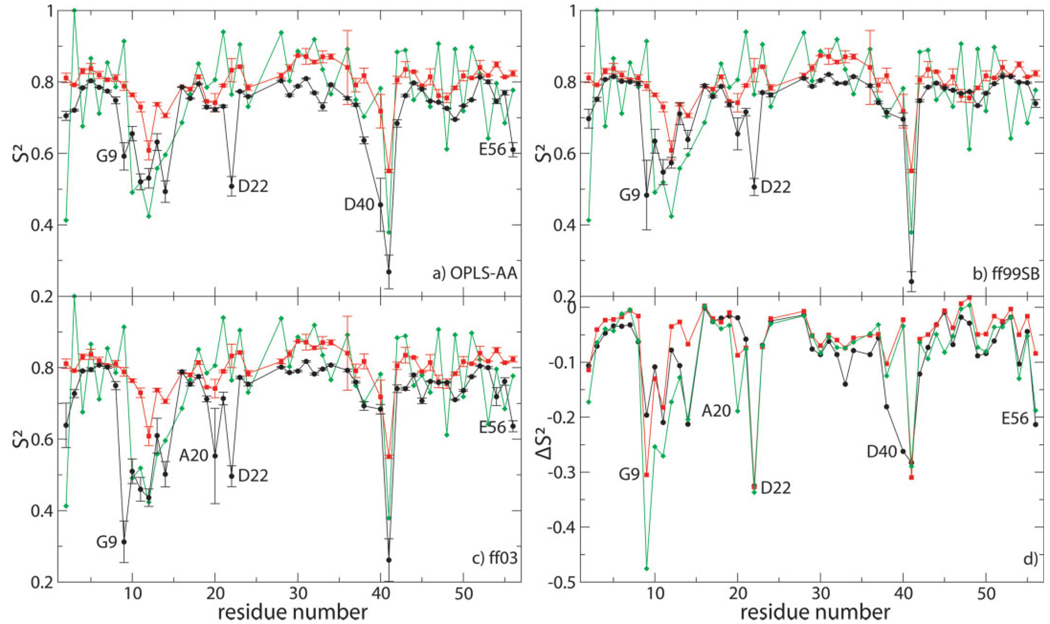
Order parameters calculated as ensemble averages (S²_MD) are shown in Figure 2(a–c) for all three force fields compared with experimental order parameters derived from NMR spin-relaxation measured at 14.1 T⁷ using the Lipari–Szabo model-free approach³ (S²_LS) and to experimental order parameters derived from RDCs⁸ $\left(S_{\text{RDC}}^2\right)$. The NMR spin-relaxation order parameters displayed in Figure 2 were derived assuming a uniform chemical shift anisotropy (CSA) of −174.2 ppm for all backbone amides in the protein [these values are identical to the values shown as a green trace in Fig. 6(b) of Ref. 7]. Comparison with order parameters derived from NMR spin-relaxation measured at different magnetic field strengths or assuming site-specific CSA values⁷ is not qualitatively different (data not shown). Despite a general trend of underestimating the experimental order parameters in all three sets of simulations, S²_MD values are in good agreement with S²_LS values for most residues, especially those that reside in elements of secondary structure [Fig. 2(d)]. For each force field, however, MD order parameters of several residues are significantly lower than NMR spin-relaxation order parameters $\left({S^2}_{\text{MD}}-S_{\text{LS}}^2<-0.15\right)$, indicating that these residues are overly flexible in silico. G9, T11, D22, and G41 are overly flexible in all three sets of simulations, while G14 and the C-terminal E56 are overly flexible in OPLS-AA and ff03 simulations; Q2, K10, L12, and A20 are overly flexible only in ff03 simulations; and G38 and D40 are overly flexible only in OPLS-AA simulations. None of the internal correlation functions of these outliers are converged, indicating slow-timescale motions in silico. The effective correlation times of nonconverged correlation functions are difficult to estimate. The question whether these slower dynamic processes are detectable experimentally by NMR spin-relaxation and consequently also the question whether they might occur in vitro can therefore not be addressed by comparison with NMR spin-relaxation order parameters alone. According to the dynamic interpretation by Bouvignies et al.,⁸ RDCs contain evidence of slow timescale motions $\left(S_{\text{RDC}}^2-S_{\text{LS}}^2<-0.1\right)$ for Q2, residues 10–14, G38 and G41, not, however, for G9, A20, D22, D40, or E56. These latter residues are henceforth termed the primary outliers for their respective force field(s). G9 resides at the beginning of the turn between β1 and β2, A20 at the end of β2, D22 at the end of the turn between β2 and the helix, D40 in the loop between the helix and β3, and E56 at the end of β4. The set of primary outliers is conservatively chosen. The RDC-derived order parameters reported by Clore and Schwieters⁹ would predict additional primary outliers.

Figure 2.

(a–c) Order parameters calculated from simulations (black) compared with NMR spin-relaxation⁷ (red) and RDC-derived order parameters⁸ (green). Errors in MD order parameters are obtained by jackknife calculations in which one of the trajectories was omitted at a time.⁴² The primary outliers of each force field are labeled. (d) Difference between simulated (black: OPLS-AA; red: ff99SB; green: ff03) and NMR spin-relaxation order parameters. All primary outliers are labeled.

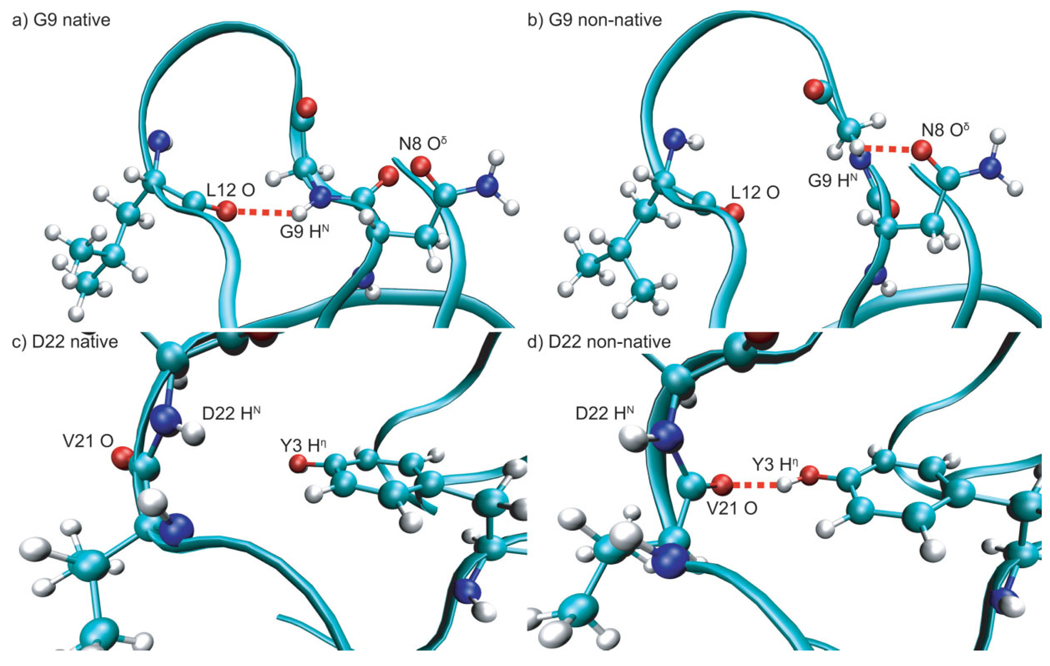
Figure 6.

Structures representative of alternate conformations for G9 and D22. Red dashed lines indicate hydrogen bonds. (a) Native conformation of G9 from ff99SB simulations with G9 H^N hydrogen-bonded to L12 O; (b) nonnative conformation of G9 from ff99SB simulations with G9 H^N hydrogen-bonded to N8 O^δ; (c) native conformation of D22 from OPLS-AA simulations with D22 H^N not hydrogen bonded and V21 O solvent exposed; and (d) nonnative conformation of D22 from OPLS-AA simulations with D22 H^N solvent exposed and V21 O hydrogen bonded to the side chain hydroxyl hydrogen of Y3.

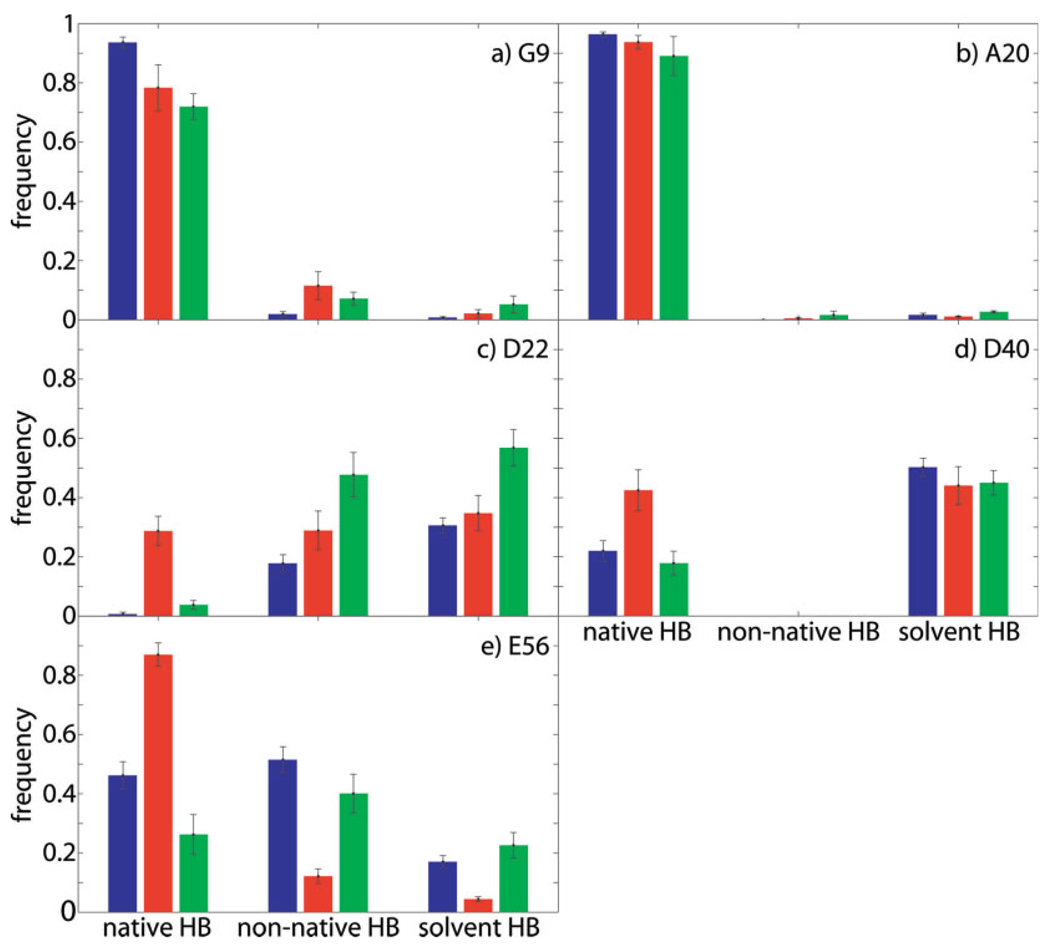
All primary outliers show, during simulation trajectories, decreased frequency of formation of hydrogen bonds that are formed in the crystal structure³² and observed experimentally by scalar couplings⁴³ (henceforth termed native hydrogen bonds) and/or increased frequency of formation of alternative, in some cases compensatory hydrogen bonds that are neither formed in the crystal structure nor detectable by scalar couplings (henceforth termed nonnative hydrogen bonds), as depicted in Figure 3.

Figure 3.

Hydrogen bonding behavior of primary outliers with error bars indicating the standard error of the mean calculated over the respective set of trajectories; blue: OPLS-AA, red: ff99SB, green: ff03. For D22 H^N, which has no native hydrogen-bonding partner, the “native HB” bars indicate the frequency of formation of the nonnative hydrogen bond between D22 H^N and T25 O^δ, which stabilizes the native conformation [see Fig. 4(g–i) and Fig 5(d–f)].

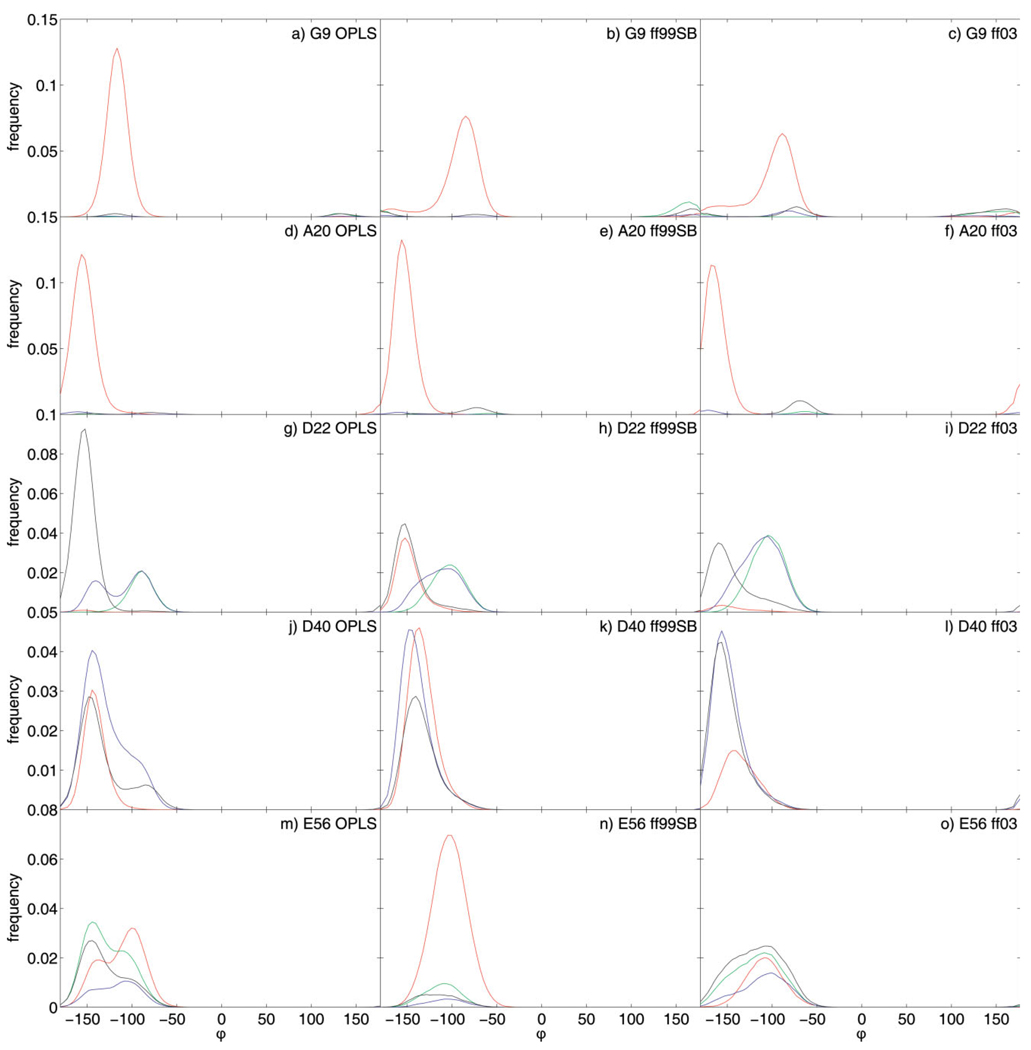
Structural analysis of MD trajectories reveals that all primary outliers populate at least two distinct conformations. These conformations can be distinguished by the backbone dihedral angle φ, as shown in Figure 4. In all cases, alternate conformations are also characterized by patterns of hydrogen bonding. The native conformation is predominantly populated when the native hydrogen bond is formed, while nonnative conformations are populated in the case of nonnative hydrogen bonding, including hydrogen bonding to solvent and absence of hydrogen bonds.

Figure 4.

Distributions of dihedral angle φ for primary outliers calculated using angular bins of 4° and subsequently smoothed with a five-point weighted moving average. Red distributions were calculated from natively hydrogen-bonded conformations, green distributions from nonnatively hydrogen-bonded conformations (other than solvent exposed), blue distributions from conformations hydrogen-bonded to solvent and black distributions from not hydrogen-bonded conformations. For D22 H^N, which has no native hydrogen bonding partner, the red distribution is calculated for conformations forming the nonnative hydrogen bond between D22 H^N and T25 O^δ, which stabilizes the native conformation [see also Fig. 5(d–f)].

G9 H^N populates two conformations in OPLS-AA and ff99SB simulations and three conformations in ff03 simulations [Fig. 4 (a–c)]. The native conformation (centered around a φ-value of −110° in OPLS-AA simulations and −80° in AMBER simulations; φ = −93° in crystal structure) displays native hydrogen bonding to L12 O. The native hydrogen bond between G9 H^N and L12 O is formed 94% of the time in OPLS-AA simulations, 83% of the time in ff99SB simulations, and 77% of the time in ff03 simulations [Fig. 3(a)]. The main nonnative conformation (centered around a φ-value of 130° in OPLS-AA simulations and 160° in AMBER simulations) displays mainly hydrogen bonding to the side chain carboxamide oxygen of N8 or absence of hydrogen bonding. The nonnative hydrogen bond between G9 H^N and the side chain carboxamide oxygen of N8 is formed 2% of the time in OPLS-AA simulations, 12% in ff99SB simulations, and 7% in ff03 simulations. The nonnative hydrogen bonds to solvent are formed 0.8% of the time in OPLS-AA simulations, 2.2% of the time in ff99SB simulations, and 5.2% of the time in ff03 simulations.

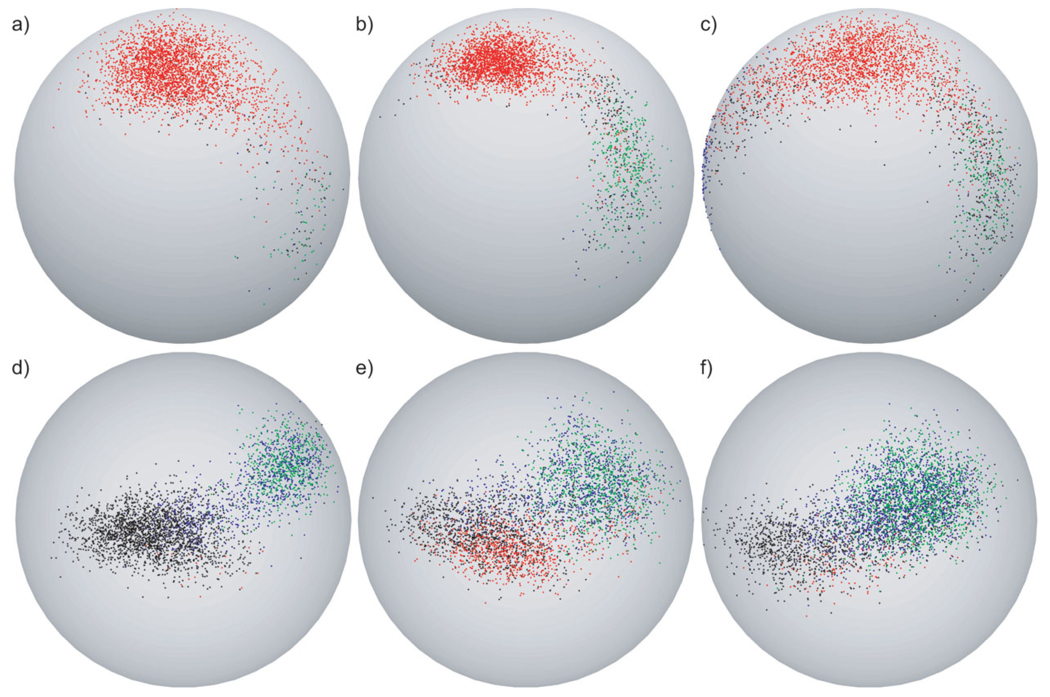
Spherical plots showing the three-dimensional orientations of the N—H bond vector of G9 over all simulations in each of the three sets reveal that an additional third conformation is populated in ff03 simulations [Fig. 5(a–c)]. This third conformation is not immediately recognizable in the φ-distribution plots, because its φ-value is close to the φ-value of the native conformation. This third conformation can be recognized by its distinct hydrogen bonding behavior with G9 H^N either hydrogen bonded to solvent or not hydrogen bonded. The large angular difference between the average N—H bond vector orientation in this third conformation and the other two conformations explains the additional decrease in order parameter in ff03 simulations despite the similarity in φ-value to the native conformation. A better view of the third conformation, which resides on the side of the sphere facing toward the back in Figure 5(c), is shown in supplementary Figure S1. Snapshots representative of the two conformations populated in all force fields are shown in Figure 6(a,b).

Figure 5.

Spherical plots for G9 and D22. In the case of G9 (a–c), red dots indicate natively hydrogen-bonded conformations, green dots indicate nonnatively hydrogen-bonded conformations (other than solvent exposed), blue dots indicate conformations hydrogen-bonded to solvent and black dots indicate not hydrogen-bonded conformations. In the case of D22 (d–f), red dots indicate conformations forming the nonnative hydrogen bond between D22 H^N and T25 O^δ, which stabilizes the native conformation, green dots indicate conformations forming the nonnative hydrogen bond between V21 O and Y3 O^η, blue dots indicate conformations hydrogen bonded to solvent and black dots indicate not hydrogen-bonded conformations. To reduce the amount of data and display equal numbers of conformations for each set of simulations every 23rd conformation was selected from OPLS-AA simulations (a,d), every 11th from ff99SB simulations (b,e), and every 10th from ff03 simulations (c,f).

In concordance with the hydrogen-bonding behavior depicted in Figure 3(a), the nonnatively hydrogen-bonded conformation is populated more in the two sets of AMBER simulations than in the OPLS-AA simulations. Therefore, hydrogen-bonding propensities of G9 H^N in the three force fields mirror the extent to which the three force fields overestimate the flexibility of G9 H^N.

The behaviors of A20, D40, and E56 H^N are similar to that of G9 H^N [Fig. 3(b,d,e) and Fig 4(d–f,j–o)]. In all cases, population of the nonnative conformation requires the breaking of a native hydrogen bond, although it is substantially more prominent in the cases of D40 and E56. For A20 and E56, the native hydrogen bond is a backbone–backbone hydrogen bond, while for D40 it involves a side-chain carboxyl oxygen. Although the nonnative conformations of D40 and E56 display compensatory hydrogen bonding to solvent, the nonnative conformation of A20 H^N is not hydrogen bonded. The nonnative conformation of E56 is additionally stabilized by a nonnative hydrogen bond between the side chain hydroxyl hydrogen of T55 and N8 O, the native hydrogen-bonding partner of E56 H^N.

D22 H^N presents a special case in that it has no native intramolecular hydrogen-bonding partner. It also, however, populates two conformations in all simulations [Fig. 4(g–i)]. The native conformation (centered around a φ-value of −155° in all simulations; φ = −153° in crystal structure) displays no intramolecular hydrogen bonding in OPLS-AA simulations and is stabilized by a nonnative hydrogen bond to the side chain hydroxyl oxygen of T25 in ff99SB simulations and to a lesser extent in ff03 simulations [labeled “native HB” in Fig. 3(c)]. In all simulations this conformation displays limited solvent accessibility. The nonnative conformation (centered around a φ-value of −90° in all simulations) is solvent exposed. Population of this alternate conformation correlates with the formation of a nonnative hydrogen bond between the natively solvent exposed V21O and the side chain hydroxyl hydrogen of Y3 [labeled “non-native HB” in Fig. 3(c) and represented by green distribution in Fig. 4(g–i)]. This nonnative hydrogen bond is formed 18% of the time in OPLS-AA simulations, 29% of the time in ff99SB simulations, and 48% of the time in ff03 simulations. Spherical plots showing the three-dimensional orientations of the N—H bond vector of D22 over all simulations of each of the three sets demonstrate their correlation with hydrogen-bonding behavior [Fig. 5(d–f)]. Snapshots representative of the two conformations are shown in Figure 6(c,d).

Despite quantitative differences in the extent of nonnative hydrogen bonding and associated population of the alternate conformation, all three force fields overestimate the flexibility of D22 H^N equally, indicating that order parameters are quantitatively sensitive only to relatively small populations of alternate conformations, as in the case of G9 H^N.

Spherical plots for the other primary outliers (Fig. S2) and representative snapshots (Fig. S3) can be found in the supplementary materials.

DISCUSSION

The results presented herein indicate a correlation between nonnative hydrogen bonding (breaking of native hydrogen bonds and/or forming of alternative nonnative hydrogen bonds) and increased flexibility in silico in the three sets of MD simulations. All primary outliers populate nonnative conformations, which requires the breaking of a native hydrogen bond with intramolecular hydrogen-bonding partners. The frequency of formation of native hydrogen bonds for G9, A20, and E56 across force fields and the associated population of nonnative conformations correlate with the extent of underestimation of the respective order parameters by the three force fields (Fig. 3 and Fig 4). Although the frequency of formation of the native hydrogen bond for A20 is equal within errors for all three sets of simulations, the mean values correlate with the disagreement between S²_MD and S²_LS for each force field. In spite of A20 being considered a primary outlier only in ff03 simulations and the large error in its ff03 order parameter, the slightly decreased order parameter for this residue in ff99SB simulations can also be attributed to breaking of the native hydrogen bond. D22 exhibits extensive nonnative hydrogen-bonding behavior correlated with population of a nonnative conformation in all three sets of simulations, mirroring the equal underestimation of its order parameter by all three force fields. In contrast to the two primary outliers identified in ff99sb simulations here (G9 and D22), 60 2-ns ff99sb simulations of GB3, using the TIP3P water model, conducted previously by Markwick et al.³¹ show increased flexibility for G9, but not for D22. To investigate whether the water model is the source of this difference, 14 ff99sb simulations were conducted using the TIP3P water model. The resulting simulated order parameters are identical to the TIP4P results presented here within errors and also identify D22 as a primary outlier (data not shown). Further investigation of this issue, which must arise from differences in starting structures or details of the simulation protocols, requires an explicit comparison of the output of the two sets of simulations and lies beyond the scope of the present work.

For all primary outliers, nonnative hydrogen bonding is accompanied by population of nonnative conformations that leads to decreased order parameters in silico (Fig. 4). In the case of D40 in AMBER simulations, especially ff03, decreased frequency of formation of the native hydrogen bond does not, however, lead to population of the nonnative conformation, indicating that breaking of the native hydrogen bond is not sufficient for population of the alternative conformation in this case [Fig. 3(d) and Fig 4(j–l)]. One possible explanation is that the dihedral terms of the AMBER force fields are sufficient to keep this site rigid. Besides D40, which resides in a loop, a number of residues within elements of secondary structure also show close agreement between S²_MD and S²_LS values in spite of decreased frequencies of formation of their native hydrogen bonds (data not shown). Rigidity of the amide moieties of these residues is however not assured by dihedral energies, but rather by the formation of two native hydrogen bonds by each peptide plane in elements of secondary structure.

Order parameters calculated from natively hydrogen-bonded sub-ensembles (S²_HB) are higher than overall order parameters or order parameters calculated from nonnatively hydrogen-bonded sub-ensembles (S²_NHB) and in better agreement with experimental values for all primary outliers (Table I). This suggests that nonnative hydrogen bonding and associated population of alternate conformations are responsible for increased flexibility in silico. In addition, the overall MD order parameter S²_MD is always lower than the population average of the order parameters calculated from hydrogen-bonding sub-ensembles S²_HB and S²_NHB. In some cases, both S²_HB and S²_NHB are higher than S²_MD. Thus, angular differences in the average bond vector orientation between states, rather than increased flexibility in any one of the states, are primarily responsible for decreased MD order parameters.

Table I.

Order Parameters Calculated From MD Simulations for All Primary Outliers

	OPLS-AA			ff99SB			ff03
Res.	$S_{\text{MD}}^2$ a	$S_{\text{HB}}^2$ b	$S_{\text{NHB}}^2$ c	$S_{\text{MD}}^2$	$S_{\text{HB}}^2$	$S_{\text{NHB}}^2$	$S_{\text{MD}}^2$	$S_{\text{HB}}^2$	$S_{\text{NHB}}^2$
G9	0.60	0.66	0.30	0.48	0.68	0.61	0.31	0.52	0.26
A20	0.72	0.75	0.26	0.66	0.76	0.48	0.55	0.76	0.59
D22d	0.51	0.75	0.69	0.51	0.70	0.68	0.50	0.70	0.60
D40	0.45	0.76	0.44	0.69	0.77	0.68	0.69	0.74	0.69
E56	0.61	0.73	0.57	0.74	0.77	0.65	0.63	0.74	0.63

^aOrder parameters calculated from full MD ensembles.

^bOrder parameters calculated from natively hydrogen-bonded sub-ensembles.

^cOrder parameters calculated from not natively hydrogen-bonded sub-ensembles.

^dThe native conformation of D22 is not hydrogen-bonded. $S_{\text{HB}}^2$ was calculated from the ensemble forming the nonnative hydrogen bond that stabilizes the native conformation in this case.

These results suggest that increased mobility in silico of all primary outliers with the exception of D40 points to specific inaccuracies of the treatment of hydrogen bonding in the respective force field. The precise causality is however difficult to determine from the present data set. Whether the breaking of the native hydrogen bond is necessary and sufficient for population of alternative conformations, or improper dihedral energies contribute to breaking of native hydrogen bonds, cannot be answered definitively. Clearly, however, breaking of native hydrogen bonds is at least necessary for increased flexibility in simulations compared with experiment. Therefore, a better treatment of hydrogen bonds relative to the other terms of the force field that could reproduce a more native-like difference in potential energy between natively and non-natively hydrogen-bonded conformations would result in better agreement with experimental order parameters.

This work was restricted to significant outliers for which even the most dynamic interpretation of RDCs contains no evidence of slow timescale motions. Considering that the length of MD simulations was shorter than the rotational correlation time of GB3 (2.4 vs. 3.4 ns) the increased flexibility of the other significant outliers (Q2, residues 10–14, G38 and G41) must be considered an inaccurate description of dynamics in silico regardless of the possibility of slow timescale motions in vitro. This inaccuracy can be interpreted in two ways, depending on which analysis of RDCs is assumed to be accurate. Assuming the more rigid interpretation of RDCs that results in similar order parameters derived from spin relaxation and RDC measurements,⁹ the decreased order parameters of these outliers in MD simulations would indicate that the force fields overestimate the population of alternative conformations, as for the five primary outliers analyzed here. For residues with native hydrogen-bonding partners (K10 and G14) this could analogously point to inaccuracies in hydrogen-bonding description. Assuming the more dynamic interpretation of RDCs that results in lower order parameters compared with spin relaxation,⁸ the decreased order parameters in MD simulations compared with spin relaxation, but improved agreement with RDCs, would indicate underestimation of the timescales of motions, rather than overestimation of the amplitudes. This would suggest that energy barriers rather than differences in potential energy between native and nonnative conformations are underestimated by the respective force fields.

CONCLUSION

This study has shown that specific deficiencies in MD simulations can be identified by comparison with NMR spin-relaxation data for the case of GB3. The results provide evidence for a specific link between force field deficiencies and disagreement between experimental and MD order parameters. For all five sites of disagreement studied here breaking of native hydrogen bonds is necessary and, except for D40 in AMBER simulations, sufficient for increased flexibility in silico. The analysis suggests that inaccuracies in the relative balance between hydrogen bonding and other terms in all three force fields studied may lead to an inaccurate description of backbone N—H vector flexibility in GB3. Whether this shortcoming should be addressed by increasing the relative weight of hydrogen-bonding energies in the functional form of the force field, or by decreasing the relative weight of other terms, for example dihedral energies, cannot be decided based on these results and will be investigated in future studies. Another possibility is that no simple reweighting of terms in the current functional form of MD force fields is sufficient to eliminate the discrepancies between simulation and experiment, and thus new functional forms that more accurately describe hydrogen bonding are necessary. For example, it may be that explicit polarization effects preferentially stabilize the native-like hydrogen bond conformation when compared with alternatives. If this is in fact the explanation, comparison with NMR data may prove to be an effective approach in validating polarizable force fields, and quantitatively demonstrating their superiority when compared with fixed charge models. However, any such assertion awaits explicit simulations with polarizable models as well as assessment of a considerably larger body of experimental and simulation data.