Gesturing Gives Children New Ideas About Math

Abstract

How does gesturing help children learn? Gesturing might encourage children to extract meaning implicit in their hand movements. If so, children should be sensitive to the particular movements they produce and learn accordingly. Alternatively, all that may matter is that children move their hands. If so, they should learn regardless of which movements they produce. To investigate these alternatives, we manipulated gesturing during a math lesson. We found that children required to produce correct gestures learned more than children required to produce partially correct gestures, who learned more than children required to produce no gestures. This effect was mediated by whether children took information conveyed solely in their gestures and added it to their speech. The findings suggest that body movements are involved not only in processing old ideas, but also in creating new ones. We may be able to lay foundations for new knowledge simply by telling learners how to move their hands.

Why do people gesture when they talk? Perhaps people gesture for their listeners. After all, listeners can glean information from the gestures speakers produce (McNeill, Cassell, & McCullough, 1994). However, people also gesture when no one is watching (Alibali, Heath, & Myers, 2001; Krauss, Dushay, Chen, & Rauscher, 1995) and even when talking to blind individuals (Iverson & Goldin-Meadow, 1998). So, perhaps people gesture for themselves. Indeed, children who produce gestures modeled by the teacher during a lesson are more likely to profit from the lesson than children who do not produce the gestures (Cook & Goldin-Meadow, 2006). Gesturing may not only identify children as ready to learn (Goldin-Meadow, Alibali, & Church, 1993), it may actually help them learn.

However, to distinguish causation from correlation, researchers need to manipulate children’s gesturing. Gesturing has been manipulated in studies of memory––children told to gesture when trying to recall an event do, in fact, remember more about the event than children prevented from gesturing (Stevanoni & Salmon, 2005). Gesturing has also been manipulated in studies of learning––children told to gesture when explaining how they solved a math problem learn more when later given instruction in the problem than children told not to gesture (Broaders, Cook, Mitchell, & Goldin-Meadow, 2007). These studies suggest that gesturing can play a role in memory and learning, but they do not specify a mechanism. The goal of this study was to explore the mechanism by which gesturing plays a role in learning.

One possibility is that the act of producing particular movements helps children focus on the information displayed in these movements. When children produce potentially meaningful movements in the right context, these movements may begin to take on meaning and, in this way, facilitate learning. If so, children should be sensitive to the specific information represented in the hand movements they produce and should learn when those movements highlight correct information. Alternatively, the particular movements children produce in their hands may be irrelevant to learning––all that may matter is that they move their hands (indeed, tapping in a rhythmic but meaningless pattern has been shown to facilitate lexical access; Ravizza, 2003). If so, children should learn regardless of the particular hand movements they produce. To distinguish between these possible mechanisms, we manipulated not only whether children gestured during a math lesson, but also the particular gestures they produced.

METHOD

Pretest

Children in the third and fourth grades (ages 9–10) were given a pretest containing six problems of the following type: 3 + 2 + 8 = __ + 8. Only children who solved none of the pretest problems correctly (n = 128; 81 girls, 47 boys) were included in the study. Children were also asked to explain how they solved each problem. The pretest, and indeed the entire session, was videotaped, and children’s explanations were coded for gesture and speech according to a previously established system (Perry, Church, & Goldin-Meadow, 1988). There were no differences across the three conditions in numbers or types of strategies produced at pretest.

Prelesson Instructions

Children were randomly assigned to one of three conditions (see Fig. 1).

Fig. 1.

Examples of the gestures children were taught prior to the math lesson. During the lesson, children produced these gestures before and after each problem they solved. The pictures in the top row show a child in the correct-gesture condition; the child indicated with a V-hand the two numbers whose sum is the correct solution to the problem and then pointed at the blank (a correct rendition of the grouping strategy), while saying, “I want to make one side equal to the other side” (the equivalence strategy). The pictures in the middle row show a child in the partially-correct-gesture condition; the child indicated with a V-hand the two numbers whose sum is not the correct solution and then pointed at the blank (a partially correct rendition of the grouping strategy), while verbalizing the equivalence strategy. The pictures in the bottom row show a child in the no-gesture condition; the child produced no hand movements while verbalizing the equivalence strategy.

Children in the no-gesture condition (n = 42) were shown a new problem without an answer, 6 + 3 + 4 = __ +4, and taught the words “I want to make one side equal to the other side,” a correct equivalence problem-solving strategy that children who succeed on problems of this type often produce (Perry et al., 1988).

Children in the correct-gesture condition (n = 43) were shown the same problem, 6 + 3 + 4 = __ + 4, and were taught the same words plus the following gestures: point with V-hand to 6 + 3, point with index finger to the blank. Note that if these two numbers are grouped together and summed, they generate the number that belongs in the blank. This grouping strategy is one that is also often spontaneously produced by children who succeed on problems of this type (Perry et al., 1988).

Children in the partially-correct-gesture condition (n = 43) were shown the same problem and were taught the same words but different gestures: V-hand pointing at 3 + 4, index finger pointing at the blank. The V-hand indicates numbers whose sum is not the correct answer. However, the V-hand does highlight the fact that two numbers can be grouped, and, in conjunction with the point at the blank, the gesture emphasizes the fact that the equation has two sides—two aspects of the problem children find difficult. These gestures thus highlight the grouping operation, which can be applied to two numbers in the problem to solve it correctly, but they indicate the wrong numbers. In this sense, the gestures are only partially correct.

All children then practiced the words or words and gestures they had been taught by repeating them in reference to two additional problems, 9 + 2 + 3 =__ +3 and 8 + 4 + 6 = __ + 6, neither of which was solved by the children or the experimenter.

Math Lesson

Next, all children were given the same math lesson. The experimenter wrote one new problem on the board (e.g., 5 + 6 + 3 = __ + 3), filled in the correct answer, and then explained how he solved the problem by verbalizing the equivalence strategy in speech, tailoring it to the particular problem; he said, for example, “I want to make one side equal to the other side; 5 plus 6 plus 3 equals 14, and 11 plus 3 equals 14, so one side is equal to the other side.” The experimenter produced no gestures during the lesson. Children were then given one new problem of their own and asked to first repeat the words or words and gestures they had practiced, to then write an answer in the blank, and finally to repeat the words or words and gestures again. They were given no feedback on their answers. This alternating procedure was repeated for 12 problems; 6 problems were solved by the experimenter, and 6 problems were solved by the child.

Posttest

After the lesson, children were given a posttest consisting of six problems comparable to those on the pretest, and asked to explain how they solved each problem. The number of problems solved correctly was calculated for each child. Each child’s explanations were coded to identify children who added grouping to their spoken repertoires after the lesson (e.g., a child who had not mentioned grouping on the pretest said, “I added the 6 and 7 and put 13 in the blank,” for the problem 6 + 7 + 4 = __ + 4 on the posttest).

Math Computation Speed

To account for possible differences in computational skills, we gave the children a sheet of paper with 20 problems of the form 4 + 5 = __ and asked them to solve the problems as quickly as possible. Time taken to solve the problems was used as a measure of computation speed (M = 65.4 s, SD = 30.1; children solved almost all of the 20 problems correctly, M = 19.4, SD = 2.5).

RESULTS

We first verified that children followed our instructions during the lesson. All of the children in the two gesture conditions moved their hands on each of the 12 opportunities (two times on each of the six problems), whereas no children in the no-gesture condition did. Moreover, children in the correct-gesture condition correctly copied the gesture model they were shown before the lesson on 91% of the 12 opportunities, and children in the partially-correct gesture condition correctly copied the gesture model on 96% of the 12 opportunities.

We hypothesized that children told to produce correct gestures would extract the grouping strategy from those gestures and, as a result, do better on the posttest than children told to produce partially correct gestures who, in turn, would do better than children told to produce no gestures––in other words, we predicted that the effect of gesture condition on posttest performance would be mediated by whether or not children added the grouping strategy to their spoken repertoires. To test this hypothesis, we computed a series of regression equations, as prescribed by Baron and Kenny (1986). According to this approach, three relations must hold to test for mediation.

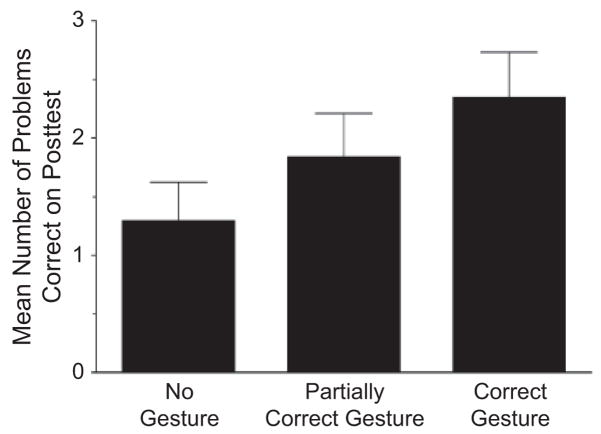
First, the independent variable (gesture condition) must predict the dependent variable (posttest performance). To test this prediction, we rank-ordered conditions from no gesture (−1) to partially correct gesture (0) to correct gesture (+1) and regressed the rank ordering on posttest performance (number of problems correct), using computation speed as a covariate; recall that none of the children solved any of the problems correctly on the pretest. The more correct their gestures during the lesson, the better children performed on the posttest, controlling for differences in computation speed, β =.19, t(125) = 2.23, p <.03 (Fig. 2).

Fig. 2.

Mean number of posttest problems solved correctly in each gesture condition. Error bars represent standard errors.

Second, the independent variable (gesture condition) must predict the mediator variable (adding grouping in speech). We again regressed the rank ordering of conditions but this time on the mediator variable (number of children who added grouping to their spoken repertoires after the lesson). As predicted, the more correctly children’s hand movements simulated grouping during the lesson, the more likely they were to add grouping in speech after the lesson, β =.20, t(125) = 2.25, p <.03, controlling for differences in computation speed (only 1 child produced grouping in speech at pretest; this child was in the no-gesture condition and did not produce grouping at posttest). Importantly, the experimenter did not mention grouping in either speech or gesture during the lesson. Grouping was thus evident during the lesson only in the gestures that the children themselves produced. The grouping operation was instantiated in the hand movements produced by both gesture groups. Children in the correct-gesture group indicated the correct numbers to which the operation should be applied; children in the partially-correct-gesture group indicated one correct and one incorrect number.

Third, the mediator variable (adding grouping in speech) must predict the dependent variable (posttest performance). We regressed the mediator variable on posttest performance and found that children who added grouping in speech solved more posttest problems correctly than children who did not add grouping, β =.35, t(125) = 4.21, p <.0001, controlling for differences in computation speed.

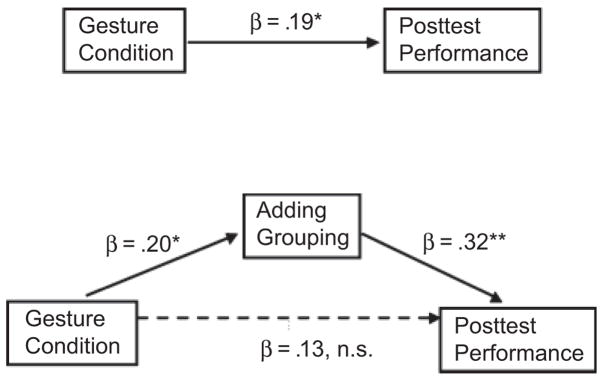
The mediation hypothesis is supported if the effect of the independent variable (gesture condition) on the dependent variable (posttest performance) is significantly reduced when accounting for the effect of the hypothesized mediator (adding grouping in speech). This prediction was confirmed: When the hypothesized mediator was added to the analysis, the effect of gesture condition on posttest performance was reduced and no longer significant, β =.13, t(124) = 1.54, n.s., controlling for differences in computation speed. Importantly, the mediator (adding grouping in speech) continued to predict posttest performance, β =.32, t(124) = 3.85, p <.0002. A Sobel test (Preacher & Hayes, 2004) of the reduction in the direct effect of gesture condition on posttest performance was significant, z = 1.93, p =.05, providing support for the hypothesis that gesturing improves posttest performance by helping children add the grouping strategy to their spoken repertoires. The results of the regression analyses are displayed in Figure 3.

Fig. 3.

Results of the regression analyses testing the hypothesis that the effect of gesture condition on children’s posttest performance was mediated by adding the grouping strategy to the spoken repertoire. The top panel shows the direct effect of gesture condition on posttest performance; the bottom panel includes the mediator and shows that the effect is indirect. Asterisks indicate significant coefficients, ^*p <.03, ^**p <.001.

DISCUSSION

Previous studies have shown that gesturing improves learning. The question we ask here is how. We found that children told to move their hands in a fully correct rendition of a particular problem-solving strategy (grouping) during a math lesson solved more math problems correctly after the lesson than children told to move their hands in a partially correct rendition of the strategy, who, in turn, solved more problems correctly than children told not to move their hands at all. This effect was mediated by whether children added the grouping strategy to their postlesson spoken repertoires, thus suggesting a mechanism by which gesture may influence learning. Because the grouping strategy was never expressed in speech during the lesson by either child or experimenter, nor was it expressed in gesture by the experimenter, the information that children incorporated into their postlesson speech must have come from their own gestures. The data thus suggest that gesturing can facilitate learning by helping children extract information from their own hand movements.

An alternative possibility, however, is that the children’s gestures merely helped them focus their attention on the particular numbers that needed to be manipulated. However, note that the gestures children produced in the partially-correct-gesture condition focused their attention on the wrong numbers. Nevertheless, children in this condition improved on the posttest more than children who did not gesture, making it unlikely that gesture’s sole function was to regulate attention. Rather, the gestures that the children produced appeared to help them learn the grouping operation, as evidenced by the fact that children who were told to gesture added grouping to their spoken repertoires after the lesson. In this regard, it is important to note that all three groups were given a math lesson that has been shown to be effective in teaching children how to solve problems of this type, even when presented without gesture (Cook & Goldin-Meadow, 2006). Thus, the gestures that the children were told to produce were not compensating for an inadequate math lesson; they were instead providing information about grouping that increased the effectiveness of the lesson.

Can the children’s hand movements really be considered gestures? Gestures tend to be meaningful movements produced along with speech (Goldin-Meadow, 2003; McNeill, 1992). The movements that the children in our study produced were taught to them in rotelike fashion; that is, without any explanation and along with words that conveyed a different, albeit related, problem-solving strategy (equivalence). However, the movements that we asked children to produce were modeled after gestures that children who know how to solve problems of this type typically produce. In this sense, the children’s movements were gestures. The movements were atypical only in that they were initially produced by rote (we told the children what movements to make). The striking result is that these movements, which were likely to be meaningless to the children initially, began to take on meaning when produced in a supportive learning context (the math lesson). We suggest that this progression may be a general one––when children first learn a task, the gestures they produce may not be fully imbued with meaning. It may be only in the continued doing that these gestures take on their full meaning.

Does gesture’s effectiveness as a learning tool stem from the fact that it is performed by the body (cf. Barsalou, 1999; Beilock & Holt, 2007; Glenberg & Robertson, 2000)? Previous work has shown that motor representations of the body are involved in processing known ideas. For example, when comprehending an action word that is semantically related to a body part (e.g., lick, pick, kick), the motor area in the brain that is associated with that part (the face, hand, or leg area, respectively) is routinely activated (Pulvermuller, 2005; see also Pulvermuller, Hauk, Nikulin, & Ilmoniemi, 2005; Pulvermuller, Shtyrov, Ilmoniemi, 2005). Also, people are particularly likely to remember an action that they have used their bodies to perform (Cohen, 1981; Engelkamp & Krumnacker, 1980; Saltz & Donnenwerth-Nolan, 1981), and are particularly likely to remember an event that they have used speech-accompanying hand gestures to describe (Cook, Yip, & Goldin-Meadow, 2008). These studies all demonstrate that movements of the body are involved in retrieving one’s knowledge about the world.

The present study takes the phenomenon one important step further by suggesting that body movements are also part of how people learn––they are involved not only in processing old ideas, but also in creating new ones. The study thus highlights the importance of motor learning even in nonmotor tasks, and suggests that we may be able to lay the foundation for new knowledge just by telling learners how to move their hands.