Protein Structure Refinement Using ¹³Cα Chemical Shift Tensors

Abstract

We have obtained the ¹³Cα chemical shift tensors for each amino acid in the protein GB1. We then developed a CST force field and incorporated this into the Xplor-NIH structure determination program. GB1 structures obtained by using CST restraints had improved precision over those obtained in the absence of CST restraints, and were also more accurate. When combined with isotropic chemical shifts, distance and vector angle restraints, the root-mean squared error with respect to existing x-ray structures was better than ~1.0 Å. These results are of broad general interest since they show that chemical shift tensors can be used in protein structure refinement, improving both structural accuracy and precision, opening up the way to accurate de novo structure determination.

Introduction

Folding a protein into its native conformation generates a large range of chemical shifts.^1–3 For ¹H, the shift range is ~2–3 ppm, for ¹³C about 10 ppm, and for ¹⁵N, about 35 ppm. These shifts are often diagnostic of the type of secondary structure present; for example, Cα chemical shifts for residues in α-helices are downfield from those in β-sheet regions.⁴ There was, however, a gap of ~20 years between the first observation of folding-induced nonequivalence and the ability to actually predict ¹³C NMR shifts in proteins, using quantum chemistry.^5–9 Now such calculations are more routine and open up the possibility of using quantum chemically derived chemical shift surfaces—how, e.g., the ¹³Cα shift varies with backbone torsion φ and ψ—in structure determination and refinement. In early work, it was shown that ¹³C isotropic chemical shifts could be used in protein structure refinement.^10–12 Much more recently, Cavalli et al.¹³ have shown that complete three dimensional protein structures (having root mean squared deviation (RMSD) values of <2 Å from corresponding x-ray structures) can be determined by using solely isotropic ¹³C and ¹⁵N NMR chemical shifts (and empirical correlations with known structures) as experimentally determined properties. However, if there are N isotropic chemical shifts, there are 3N associated chemical shift tensor elements (as well as 3N orientations), so it should, at least in principle, be possible to obtain structures having improved accuracy and precision by using chemical shift tensor (CST) information.^12,14–18

In this work, we report the structures of a solid protein, the β1-immunoglobulin binding domain of protein G (GB1), refined to high resolution through the use of Cα CST data. We first present complete measurements of the backbone Cα CST values in GB1 by combining our previous pulse sequence methods^19,20 with isotopic labeling schemes that provide enhanced resolution.^21–23 We then use Cα CST data to refine the structure of GB1 using theoretical C^α shielding surfaces incorporated into the Xplor-NIH program. The resulting structures have high precision (~0.2–0.3 Å backbone RMSD) and accuracy (~1.0 Å in comparison with the closest crystal structure, pdb entry 2QMT), opening up the way to using both isotropic¹³ as well as anisotropic chemical shift results in the de novo determination of high accuracy, solid-state protein structures.

Experimental and Computational Methods

Samples of GB1 were prepared using 1,3-¹³C-glycerol or 2-¹³C-glycerol as the primary carbon sources in the growth media.^21–24 Hydrated nanocrystals (~18 mg) of each labeled sample were packed into the central 80% of limited speed, 36 μL, 3.2 mm Varian rotors (Varian, Inc., Palo Alto, California and Fort Collins, Colorado). NMR spectra were acquired using a 500 MHz Varian InfinityPlus spectrometer equipped with a 3.2 mm T3 Balun^™ probe optimized for triple resonance ¹H-¹³C-¹⁵N experiments. Pulse widths (π/2) for ¹H, ¹³C, and ¹⁵N were 1.9 μs, 2.5 μs, and 5.0 μs, respectively. Spinning was maintained at 11.111 ± 0.002 kHz via a Varian MAS controller.

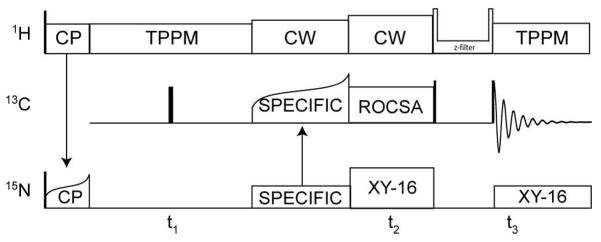
The ROCSA recoupling sequence²⁵ was incorporated into a 3D experiment in a manner similar to that reported previously, but with a slightly modified set of isotropic (¹⁵N and ¹³C) and anisotropic (¹³C) dimensions. We refer to this pulse sequence as ¹⁵N-[¹³C CSA]-¹³C (Figure 1). Optimal resolution and sensitivity for the ¹⁵N-¹³C 2D planes were achieved as described,²⁶ using the SPECIFIC CP²⁷ condition near ω_N = 5/2 ω_r and ω_C = 3/2 ω_r. TPPM decoupling was utilized during acquisition,²⁸ with a nutation frequency of ~75 kHz, a 14° total phase shift and 6.3 μs pulse width. SPECIFIC CP efficiency was approximately 55%, when comparing the ¹⁵N-filtered ¹³C spectrum to the 1D ¹³C spectrum based on ¹H-¹³C CP.²⁶ The direct ¹³C dimension was digitized as 3072 complex points with a 10 μs dwell time. The indirect ¹⁵N dimension (t₁) was digitized as 160 real points, with an increment of 180 μs. The ROCSA dimension was digitized with 14 hypercomplex points using States-TPPI sampling²⁹ and an increment of 180 μs (two rotor periods). The pulse delay was 3 s, resulting in a total measurement time of ~20 h per experiment. The experiment was repeated twice, to confirm that the measurements were stable to within the signal-to-noise ratio. The C4₄¹ element was used for ROCSA, sampling two complex points per ROCSA cycle.

Figure 1.

¹⁵N-[¹³C CSA]-¹³C 3D ROCSA pulse sequence. Transverse ¹⁵N coherence is created by adiabatic CP from ¹H, followed by isotropic chemical shift evolution period (t₁) and selective polarization transfer to ¹³Cα with SPECIFIC-CP.²⁷ ROCSA²⁵ recoupling is applied to the ¹³C spins, with a coherence filter (including States-TPPI hypercomplex sampling) prior to acquisition. During ¹³C ROCSA, ¹H was decoupled with a CW field (~125 kHz nutation frequency) and ¹⁵N with rotor-synchronized π-pulses of 10 μs with XY-16 supercycling.

Spectra were processed using NMRPipe.³⁰ The ¹⁵N interferogram was doubled by linear prediction (to 320 points) prior to Fourier transformation. Lorentzian-to-Gaussian apodization functions were applied in the two isotropic chemical shift dimensions, with a net line broadening matched to the typical linewidths observed (30 Hz for ¹³C and 15 Hz for ¹⁵N). Peak intensities in each ¹⁵N-¹³C (F1-F3) plane were determined and trajectories of the ROCSA time domain (t₂) extracted using the autoFit.tcl package in NMRPipe.

The ROCSA trajectories were fit (without apodization) to exact spin simulations in the time domain, using in-house FORTRAN-77 code that combines external MINUIT minimization libraries³¹ with the SPINEVOLUTION³² simulation package. For lineshape fitting, we used the notational convention described by Haeberlen,³³ which is standard in simulation packages such as SPINEVOLUTION. In this convention, the three axes in the Principal Axis System (PAS) are defined as δ_xx, δ_yy, and δ_zz, and are ordered as:

$$\mid {\delta }_{zz}-{\delta }_{\mathit{iso}}\mid \ge \mid {\delta }_{xx}-{\delta }_{\mathit{iso}}\mid \ge \mid {\delta }_{yy}-{\delta }_{\mathit{iso}}\mid$$ (1)

Two other quantities are required in order to convert from Cartesian to polar coordinates: the reduced anisotropy (δ = δ_zz − δ_iso), and the asymmetry parameter (η = (δ_yy − δ_xx)/δ). Four parameters were fit iteratively using MINUIT minimization: δ, η, a phenomenological single exponential relaxation rate, Γ₁, and an amplitude scaling factor. Standard errors were determined from the error matrix calculated by MINUIT during fitting. The measured values of δ and η were then converted into the Herzfeld-Berger convention,^34,35 in which tensor elements are ordered from downfield (δ₁₁) to upfield (δ₃₃), with δ₂₂ in the center. The tensor rhombicity is given by two parameters, the span (Ω = δ₁₁ − δ₃₃) and the skew (κ = 3(δ₂₂ − δ_iso)/Ω).

The fitted tensor parameters were compared to ab initio chemical shielding surfaces^12,15–18 which are available for all 20 common amino acids (http://feh.scs.uiuc.edu/amino_acid.php). As described previously,^12,15–18 these surfaces were computed with Hartree-Fock (HF) theory and gauge-including atomic orbitals (GIAO) methodology as implemented in the Gaussian-98 program. Coupled Hartree-Fock shielding calculations used dense 6-311++G(2d,2p) basis sets on sites of interest with 6-311G basis sets used on neighboring atoms. Ab initio CST calculations provide shielding values referenced relative to the bare nucleus, which need to be re-referenced relative to DSS, for comparison with experimentally determined chemical shifts. This procedure has been performed in previous studies by regression analysis versus experimental data from samples of known geometry, such as tripeptides with highly resolved x-ray or neutron diffraction structures. ^12,15–18 This fitting protocol produces two additional parameters: a scaling factor (least squares slope) and an offset (y-intercept). Ideally, the scaling factors should be −1.0, but in practice range from −0.7 to 1.1 for different amino acid residue types, due presumably to basis set deficiencies, and of course these scaling factors need to be taken into account by the structure calculation protocol, as described below. It is possible that discrepancies between x-ray and actual geometry make small contributions to these scaling factors; however, as illustrated below, scaling factors are in absolute terms uncertain, and therefore must be considered variable parameters in order to determine molecular geometry directly. Structure calculations were performed using a customized version of Xplor-NIH³⁶ that includes a CST potential term.

Given a molecular structure, the three theoretical CST values δ_nn (n=1, 2, 3) can be determined for each Cα atom using chemical shielding surfaces, and the associated backbone torsion angle values ϕ and ψ, according to the linear equation:

$${\delta }_{nn}=p_{\text{ofsett}}+p_{\text{scale}}{\sigma }_{nn}^o(\phi ,\psi ),$$ (2)

where p_scale and p_offset are the scaling factor and offset, respectively, and are unique for each residue type; ${\sigma }_{nn}^o(\phi ,\psi )$ is a 2D cubic spline representation³⁷ of the ab initio values implemented with derivatives continuous with respect to ϕ and ψ. To restrain calculated CST values to the experimental values ( ${\delta }_{nn}^{\mathit{obs}}$), the following pseudo-energy was used during simulated-annealing structure determination:

$$E_{\text{CST}}=k_{\text{CST}}\sum {({\delta }_{nn}-{\delta }_{nn}^{\mathit{obs}})}^2,$$ (3)

where the force constant k_CST, is varied during the course of the simulated annealing, and the sum is over all tensor orientations of all Cα atoms of a given type. If p_scale and p_offset are known, they can be held constant during the structure calculation. However, because these parameters are generally not known with high precision, we determined them self-consistently within the structure calculation itself. To do this, a subroutine (to be included in a new Xplor-NIH release) was developed to compute p_scale and p_offset for each residue type. This routine uses singular value decomposition, which is computationally inexpensive and can thus be performed at each annealing temperature during the structure calculation.

The force constant k_CST was chosen to be ~0.005 kcal/ppm² at the beginning of structure calculation, so that the CST energy term made a negligible contribution. Then, during the course of annealing, k_CST was increased geometrically, to a final value of ~0.5 kcal/ppm². This value was calibrated by monitoring convergence of the structure calculations over a range of final k_CST values, from 0.1 to 1.25 kcal/ppm². The CST potential does not take experimental error into account, so even an error of 1 ppm between shift and shielding, (within the experimental error for most sites), can create a significant energy penalty. Because of this relatively stiff force field, and the variable reference between theory and experiment, setting the CST potential too high impedes convergence. This effect arises because each CST site produces three potential surfaces, which are relatively rough over the Ramachandran space; thus, if the CST energy is too high early in the annealing process, structures possibly will be trapped within local minima, with insufficient energy to traverse the barriers and arrive at the global minimum energy value. A subset of structures (or regions of the protein) may converge to high structure quality, but the overall convergence properties of the ensemble may be greatly compromised. These problems are especially pronounced in cases where p_scale and p_offset are allowed to vary. These issues are mitigated by the use of a small force constant value early in the annealing process, as detailed above.

For each set of parameters, ensembles of 200 structures were calculated by performing molecular dynamics at 3000 K for 40 ps, followed by slow cooling from 3000 K to 25 K in 25 K increments, with 2.5 ps of dynamics at each temperature, using a soft square NOE potential. Each structure was then refined by repeating the annealing protocol with only 15 ps of initial annealing using a hard square NOE potential with the k_NOE force constant held constant at 30 kcal. Although no NOE restraints are used in SSNMR structure determinations, SSNMR distances (¹³C-¹³C, ¹⁵N-¹⁵N and ¹H-¹H) are included using the NOE potential function within Xplor-NIH. In calculations where pseudobond angles were used, the energy of bond and improper angles was reduced by an order of magnitude.

Results and Discussion

Chemical shift tensor determinations

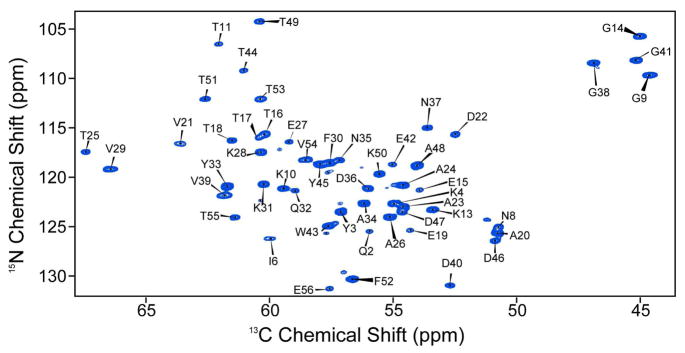
We first determined experimentally the ¹³Cα shift tensor elements δ₁₁, δ₂₂ and δ₃₃, for all 56 residues in GB1, to provide a complete data set for CST backbone structure refinement. In earlier work²⁰ we reported the Cα CSTs for 39 of these residues, but 17 were unresolved in the isotropic shift dimension, due to the relatively limited resolution in some regions of the ¹³C-¹³C correlation spectra. This is a consequence of using a uniformly ¹³C,¹⁵N-labelled GB1 sample in which homonuclear J-couplings and off rotational-resonance effects^38–40 increased the effective line widths in the directly detected dimension. To remedy this, we used here a modified version of our 3D pulse sequence, together with sparse ¹³C labeling as derived from [2-¹³C]- or [1,3-¹³C]-glycerol. When using a [2-¹³C]-glycerol-[U-¹⁵N]-labeled GB1 sample, essentially all ¹⁵N-¹³C^α peaks can be resolved and assigned in the first 2D ¹⁵N-¹³C plane of the 3D ROCSA experiment (Figure 2). The exception is that Leu residues are not ¹³Cα-labeled in this sample, so we also acquired data on a sample prepared from [1,3-¹³C]-glycerol (and ¹⁵N ammonium chloride). The amino acids for which the Cα sites are fractionally labeled in both preparations (e.g., Thr, Asp, Lys, Ile) also provide an internal control in the data fitting, and we found agreement between the two data sets to be within experimental error (±1 ppm, see below).

Figure 2.

First ¹⁵N-¹³Cα plane from the ¹⁵N-[¹³C CSA]-¹³C 3D experiment. Spectra was acquired and processed with parameters discussed in the Experimental Section. Resonance assignments are based upon published values.²⁴

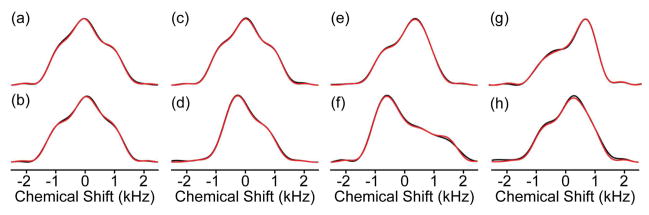
Spectra were then assigned,²⁴ the 2D planes integrated, and recoupled CSA trajectories fit as discussed above. The experimental spectra have high sensitivity and the best fit simulations are in excellent agreement (Figure 3), with RMSD values for each fitted spectrum of 3%, typically <2%. The resulting CSA tensor parameters (Table 1) are presented in both the Haeberlen and Herzeld-Berger conventions. Within amino acid type, variations in tensor parameters are characteristic of secondary structures. For example, Cα tensors of α-helical residues are systematically narrower than those of β-sheet residues. This trend has a common origin to previously observed isotropic secondary chemical shifts,⁴ yet the overall dependence of the CST on molecular geometry captures additional subtleties within secondary structure type, as the tensor elements can be measured with sufficient precision to identify changes of ~5° in dihedral angles.

Figure 3.

ROCSA experimental and simulated lineshapes. Experimental ROCSA pseudostatic powder patterns (black) are overlaid with the best-fit simulations (red). Sites presented are: (a) A26, (b) A48, (c) D36, (d) D47, (e) K28, (f) K50, (g) T25, (h) T51. Fit values and experimental errors for each site are provided in Table 1.

Table 1.

Experimental chemical shift tensor (CST) values for protein GB1.

Res	δ (ppm)	σδa (ppm)	η	σηa	δ11 (ppm)	σδ11a (ppm)	δ22 (ppm)	σδ22a (ppm)	δ33a (ppm)	σδ33 (ppm)
Q2	15.80	1.45	0.90	0.06	71.70	1.45	55.14	1.36	40.86	1.54
Y3	−21.34	1.20	0.78	0.02	76.03	1.20	59.31	1.17	35.66	1.22
K4	18.20	0.90	0.74	0.01	73.10	0.90	52.51	0.89	39.09	0.90
L5	19.55	1.48	0.93	0.07	72.55	1.48	52.30	1.38	34.15	1.59
I6	15.23	1.14	0.99	0.14	75.23	1.14	59.96	0.98	44.81	1.30
L7	−20.32	1.48	0.52	0.07	70.14	1.48	59.59	1.38	34.38	1.59
N8	21.35	1.25	0.76	0.10	72.05	1.25	48.12	1.12	31.93	1.38
G9	26.44	1.82	0.94	0.09	71.04	1.82	43.85	1.65	18.91	1.98
K10	−17.24	0.49	0.69	0.01	73.83	0.49	62.01	0.49	42.06	0.49
T11	−21.02	2.31	0.48	0.06	77.47	2.31	67.35	2.17	40.88	2.44
L12	17.44	1.03	0.82	0.03	71.84	1.03	52.79	1.00	38.57	1.06
K13	20.02	3.04	0.84	0.13	73.32	3.04	51.70	2.63	34.88	3.45
G14	−19.26	1.55	0.73	0.01	61.58	1.55	47.47	1.54	25.64	1.56
E15	17.81	1.82	0.73	0.08	71.71	1.82	51.52	1.68	38.48	1.96
T16	16.89	0.54	0.30	0.07	76.99	0.54	54.19	0.50	49.12	0.57
T17	17.83	1.73	0.65	0.13	78.13	1.73	57.18	1.51	45.59	1.95
T18	16.40	1.42	0.22	0.19	77.70	1.42	54.89	1.15	51.31	1.69
E19	16.95	1.64	0.87	0.07	71.25	1.64	53.23	1.52	38.41	1.75
A20	−22.54	0.51	0.86	0.09	71.69	0.51	52.25	0.47	28.16	0.56
V21	−13.42	1.01	0.58	0.04	74.08	1.01	66.34	0.97	50.08	1.05
D22	21.39	1.00	0.81	0.04	73.89	1.00	50.51	0.96	33.09	1.04
A23	−20.75	1.19	0.91	0.20	74.37	1.19	55.57	0.95	33.85	1.42
A24	18.59	1.72	0.85	0.16	73.09	1.72	53.07	1.45	37.34	1.99
T25	−18.68	0.87	0.37	0.04	80.02	0.87	73.06	0.84	48.52	0.91
A26	19.45	0.61	0.90	0.03	74.45	0.61	54.00	0.59	36.55	0.63
E27	−15.26	1.34	0.95	0.13	73.97	1.34	59.49	1.17	43.84	1.51
K28	−17.79	1.78	0.63	0.03	74.72	1.78	63.47	1.73	42.41	1.83
V29	−15.87	0.95	0.29	0.04	76.53	0.95	71.94	0.92	50.43	0.99
F30	−19.09	0.38	0.93	0.04	75.88	0.38	58.22	0.36	38.41	0.39
K31	−19.54	0.97	0.54	0.07	75.12	0.97	64.61	0.90	40.56	1.04
Q32	15.11	0.90	0.95	0.11	74.01	0.90	58.53	0.80	44.16	1.00
Y33	13.94	3.14	0.80	0.06	75.54	3.14	60.21	2.93	49.05	3.34
A34	19.07	0.85	0.96	0.05	75.17	0.85	55.74	0.81	37.39	0.89
N35	17.70	1.01	0.77	0.07	74.70	1.01	54.96	0.94	41.34	1.08
D36	18.65	0.27	0.97	0.05	74.55	0.27	55.64	0.25	37.51	0.28
N37	22.99	1.48	0.74	0.11	76.49	1.48	50.49	1.33	33.52	1.64
G38	26.18	0.85	0.68	0.00	72.98	0.85	42.65	0.85	24.77	0.86
V39	−15.08	2.10	0.82	0.11	75.41	2.10	63.06	1.87	46.62	2.33
D40	16.18	1.46	0.69	0.07	68.98	1.46	50.26	1.36	39.16	1.56
G41	22.20	0.44	1.00	0.07	67.30	0.44	45.10	0.41	22.90	0.47
E42	18.52	0.35	1.00	0.08	73.62	0.35	55.10	0.32	36.58	0.38
W43	19.51	2.34	1.00	0.09	77.01	2.34	57.50	2.13	37.99	2.55
T44	19.54	2.57	0.79	0.02	80.44	2.57	58.83	2.51	43.44	2.63
Y45	14.79	1.11	0.68	0.13	72.59	1.11	55.47	0.97	45.34	1.25
D46	17.62	0.36	0.66	0.07	68.52	0.36	47.94	0.34	36.25	0.39
D47	16.04	0.89	0.57	0.02	70.64	0.89	51.16	0.87	42.00	0.90
A48	−19.95	1.48	0.95	0.10	73.41	1.48	54.53	1.34	34.05	1.62
T49	−19.94	1.08	0.75	0.10	77.75	1.08	62.80	0.97	40.36	1.19
K50	26.69	1.21	0.35	0.04	82.29	1.21	46.98	1.16	37.53	1.26
T51	−18.09	1.03	0.74	0.03	78.20	1.03	64.89	0.99	44.41	1.06
F52	18.43	1.29	1.00	0.10	75.03	1.29	56.60	1.17	38.17	1.42
T53	18.60	1.29	0.77	0.12	79.00	1.29	58.30	1.13	43.90	1.45
V54	19.19	2.71	0.53	0.18	77.69	2.71	53.95	2.22	43.86	3.20
T55	−17.81	1.52	0.86	0.12	77.89	1.52	62.53	1.33	43.49	1.70
E56	18.39	1.33	0.97	0.06	75.99	1.33	57.35	1.26	39.46	1.41

^aEstimated standard deviation for each subscripted quantity.

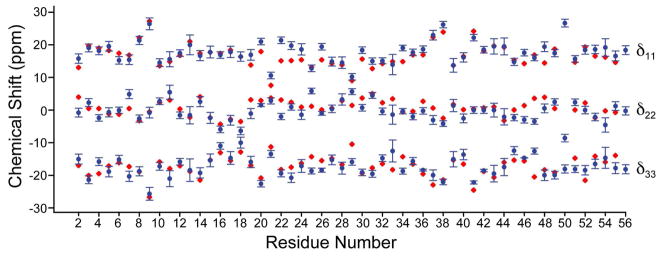
These results are of interest since they represent the first determination of the principal components of the ¹³Cα shift tensor for each residue in a protein. As can be seen in Figure 3 (and Figure S2 in the Supporting Information) there is a very broad range of lineshapes seen experimentally, reflecting the strong influence of φ, ψ (and χ₁) on electronic structure and hence, the shift (or shielding) tensor. There is, however, good overall accord between the experimental and computed shift tensor elements. This is illustrated in Figure 4, where we show δ₁₁, δ₂₂ and δ₃₃ for each residue in GB1 (as a function of residue number, in blue), together with the shift tensor elements predicted by using ab initio shielding surfaces (red, Figure 4). For shift predictions, we used backbone dihedral angles (φ, ψ) from the highest resolution (1.04 Å) crystal structure available for this mutant of GB1 (pdb entry 2QMT), a structure that is also the most closely related polymorph to the microcrystalline form used here.⁴¹ For convenience, the chemical shielding tensor elements were converted to shifts, and are shown in the traceless representation. Overall statistical agreement between theory and experimental δ_ii is very good, with R² = 0.99 over all residues and a RMSD of 2.27 ppm (see Figure 4).

Figure 4.

Plot of chemical shift tensor principal elements compared with ab initio chemical shielding values. Values are presented in the traceless representation, with experimental values in blue (with error bars) and theoretical values in red. An ideal scaling between experimental chemical shift and theoretical shielding of −1.0 is assumed.

This good agreement might at first seem surprising, given that the amino-acid models used to construct the shielding surfaces were all simply N-formyl-amino acid amides, such as N-formyl valine amide in which the most populous side-chain confirmations (in the Protein Data Bank) were chosen. Also, there are likely to be small conformational differences between the 2QMT crystals and our nanocrystals, and protein x-ray structures do have their own associated φ,ψ errors. Moreover, the correlations we see here – especially when the shift tensor elements are compared for each individual amino-acid in GB1 (Figure S3, Supporting Information) are really no worse than those seen in tripeptides or even pure amino-acids^{12,14–18,42–44} – but of course the reason for the excellent results on GB1 is that there are (in general) no strong electrostatic interactions with nearly terminal CO₂⁻ or NH₃⁺ groups, which greatly complicate shift calculations in the smaller molecules. There are, however, small differences in the slopes (p_scale) and intercepts (p_offset) for each amino-acid (Table 2), but as in previous work16 and as described in Equation 2 in the Experimental and Computational Methods section, these can be readily taken into account by a linear fitting procedure.

Table 2.

Statistical agreement of experimental CST data and ab initio chemical shielding surfaces.

Residue Type	R2	pscale	poffset (ppm)	RMSD (ppm)
Alanine	0.99	−1.18	222.8	1.64
Asparagine	0.99	−0.97	196.8	1.59
Aspartic Acid	0.92	−0.95	193.1	4.25
Glutamine	0.95	−0.96	195.7	3.01
Glutamic Acid	0.93	−1.00	202.3	3.64
Glycine	0.99	−0.96	194.3	1.80
Leucine	0.98	−1.04	207.6	1.89
Lysine	0.98	−1.01	201.6	1.95
Phenylalanine	0.97	−0.95	186.3	2.65
Threonine	0.97	−1.06	212.4	2.39
Tyrosine	0.96	−0.91	185.6	2.17
Valine	0.94	−1.12	217.5	2.62

We now consider how shift tensor elements can be incorporated into solid-state protein structure refinement. To investigate to what extent it might be possible to refine solid-state NMR-derived protein structures, we first performed a series of structure determinations using previously reported distance restraints,^45–47 together with the new CST restraints, as discussed in the Experimental Section. Important statistics for each structure are given in Table 3. Each structure is assigned a number and name defined by the information used during refinement. In this nomenclature “N” refers to distance information (from the NOE potential used), “T” refers to semi-empirical dihedral angles from TALOS, “C” refers to CST restraints, “V” refers to Vector Angles, and “semi-empirical” indicates that RAMA and HBDB potentials were included in the calculation. We first computed two “control” structures, incorporating either (a) distance or (b) both distance and semi-empirical torsion angles, deduced from the TALOS program,⁴⁸ as reported previously.⁴⁷ The family of ten lowest energy structures, derived with distances only (N, structure 1 in Table 3), had good precision (a backbone RMSD of 0.59 ± 0.08 Å) and accuracy (1.30 ± 0.08 Å), but the addition of TALOS dihedral angles (NT, structure 2 in Table 3) improved significantly in terms of both precision (0.29 ± 0.06 Å) and accuracy (1.15 ± 0.03 Å vs. 2QMT) (Supporting Figure 3).

Table 3.

Internal backbone RMSD values (ten lowest energy structures) and backbone RMSD values versus the x-ray crystal structure PDB entry 2QMT as a function of refinement method and statistical agreement with chemical shielding surfaces and isotropic chemical shifts predicted by SPARTA.

Structurea		bbRMSDb (Å)	RMSD vs. c 2QMT (Å)	Most Favored d Regions	R2 e CST	σ CSTf (ppm)	σ Cα δisog (ppm)
1	N	0.59 ± 0.08	1.30 ± 0.08	56.0%	0.92	4.38	1.28
2	NT	0.29 ± 0.06	1.15 ± 0.03	92.0%	0.96	3.03	1.08
3	NC (uncalibrated)	0.38 ± 0.08	1.13 ± 0.04	82.0%	0.99	1.56	1.12
4	NCT	0.23 ± 0.03	1.01 ± 0.04	93.8%	0.99	1.66	1.08
5	NCTV	0.19 ± 0.04	1.01 ± 0.03	95.6%	0.99	1.69	1.03
6	NCTV (semi-empirical)	0.19 ± 0.04	0.98 ± 0.04	96.0%	0.99	1.81	1.08
7	NTV (semi-empirical)	0.27 ± 0.03	1.04 ± 0.03	98.4%	0.97	2.52	1.18
8	NC (calibrated)	0.27 ± 0.06	1.09 ± 0.04	88.0%	0.99	1.56	1.09
9	2QMT			96.0%	0.97	2.52	0.93
10	2JSV	0.31 ± 0.06	1.43 ± 0.08	92.0%	0.97	2.91	1.06
	Solid vs. Solution δiso						0.59

^aAcronyms here indicate: N = distances, T = TALOS dihedral angles, C = Cα CST constraints, V = Vector Angles, and “semi-empirical” refers to calculations using RAMA and HBDB potentials.

^bRMSD of ten lowest energy structures.

^cRMSD between ten lowest energy structures and the 2QMT crystal structure.

^dThe percentage of residues occupying most favored regions of Ramachandran space.

^eCorrelation coefficient between experimental chemical shift tensor elements and theoretical chemical shielding.

^fRMSD between experimental anisotropic shifts and theoretical shieldings.

^gRMSD between experimental isotropic chemical shifts and chemical shifts predicted by SPARTA.

We next investigated the effects of incorporating CST restraints in structure refinement, using the new potential for Xplor-NIH described above in the Experimental and Computational Methods sections. In a first set of calculations (NC (uncalibrated), structure 3 in Table 3), we allowed p_offset and p_scale to vary during the annealing and cooling process. The inclusion of this CST constraint again improved both the precision (0.38 ± 0.08 Å) and accuracy (1.13 ± 0.04 Å vs. 2QMT) of the structure ensemble compared to that obtained by using distances restraints alone, with the precision being slightly worse than that obtained with the TALOS dihedral angle restraints, while the accuracy (versus 2QMT) was statistically equivalent. We then solved the structure of GB1 by combining CST constraints with TALOS dihedral angles (NCT, structure 4 in Table 3), while allowing p_scale and p_offset to vary. Combining Cα CST restraints with TALOS resulted in a substantial improvement in both the precision of the ensemble (RMSD = 0.23 ± 0.03 Å) as well as accuracy (a 1.01 Å ± 0.04 Å RMSD versus 2QMT). This ensemble exhibited comparable accuracy, but slightly worse precision compared to the ensemble including Cα CST, TALOS, and vector angle restraints (NCTV, structure 5 in Table 3; 0.19 ± 0.04 and 1.01 ± 0.03 Å). Based upon these results, we decided to calibrate p_scale and p_offset to a structural ensemble combining Cα CSTs, TALOS, vector angles, and empirical database potentials which improve Ramachandran quality (RAMA)^49,50 and hydrogen bonding networks (HBDB).⁵¹ When these potentials were included in the calculation the precision (NCTV (semi-empirical), structure 6 in Table 3) remained at 0.19 ± 0.04 Å, while the RMSD relative to 2QMT improved by one standard deviation, to 0.98 ± 0.04. As a control, CST restraints were then removed (NTV (semi-empirical), structure 7 in Table 3): precision decreased to 0.27 ± 0.03, and the RMSD relative to 2QMT increased nearly two standard deviations, to 1.04 ± 0.03 Å. In the final structure solved, p_scale and p_offset were set to the values provided in Table 4, which correspond to the structure with the lowest total CST energy in the structure 6 ensemble. In this final structure (NC (calibrated), structure 8 in Table 3) the precision and accuracy are comparable to the structure solved using TALOS dihedral angles (bbRMSD = 0.27 ± 0.6 Å, 1.09 ± 0.04 Å vs. 2QMT).

Table 4.

p_scale and p_offset determined from structure determinations using distance, CST, TALOS, and VEAN data sets.

Residue Type	pscale	poffset (ppm)
Alanine	−1.21	226.5
Asparagine	−0.98	198.0
Aspartic Acid	−1.09	212.9
Glutamine	−0.89	186.0
Glutamic Acid	−1.00	201.3
Glycine	−1.00	200.2
Isoleucine	−0.81	173.4
Leucine	−1.05	208.7
Lysine	−1.09	211.9
Phenylalanine	−1.04	198.8
Threonine	−1.08	215.2
Tryptophan	−0.98	199.4
Tyrosine	−0.87	181.2
Valine	−1.12	217.7

When each of the eight structures shown in Table 3 are used to back-calculate experimental isotropic (using the SPARTA program)⁵² and anisotropic shifts (from the shielding surfaces), we find that agreement between experimental and computational isotropic as well as anisotropic shifts improves with the addition of Cα CST information, as shown in Table 3. The worst results are all found with the distance-only structure (structure 1), where, the RMSD between experimental isotropic Cα (1.28 ppm) and anisotropic shifts (4.38 ppm) are significantly worse than the results obtained by using all of the other structures. Likewise, the structure solved with distances and TALOS (structure 2) had only a fair agreement with anisotropic constraints (R² = 0.96, RMSD = 3.03 ppm). Overall, structures which included Cα CST information exhibited RMSDs between experimental and predicted anisotropic chemical shifts of 1.56–1.81 ppm and R² values of 0.99, with the best agreement being in structures solved with only distance and CST constraints, as expected. The agreement between CST values predicted from 2QMT were slightly worse vs. experiment (R² = 0.97, RMSD = 2.52 ppm), and equivalent to values predicted from structure 7, where CST restraints were removed. Likewise, the isotropic shifts exhibited clear trends depending upon constraints used. The agreement between predicted Cα isotropic chemical shifts and experiment for structures solved using CST constraints range from 1.03 to 1.12 ppm, slightly worse than shifts predicted using the x-ray structure where the RMSD between predicted and experimental shifts is 0.93 ppm. It should be noted that all reported deviations for the isotropic Cα shifts are within the reported reliability of the SPARTA program and the agreement between shifts measured in solid vs. solution for comparable samples of GB1 (Table 3, last row).

These results are of course not wholly unexpected since the structures were based at least in part of isotropic and anisotropic shift information. However, it is not unreasonable to believe that a significant part of the ~1Å RMSD found between the NMR and x-ray structures arises from uncertainties in the x-ray coordinates themselves. How big are these errors? As noted by Blundell,⁵³ “The accuracy of atomic positions in x-ray crystal structures remains an open and contentious question, with quoted errors ranging form 0.1–0.3 Å to around 0.5 Å to 0.6–1.0 Å.” The errors would have major effects on shift and shift tensor calculations, since bond length and bond angle shielding derivatives are large, as are φ,ψ effects on shielding. The origins of the ~1.0 Å RMSD between the x-ray and NMR determined structures is, therefore, an open question. However, as more shift and shift tensors elements are determined, for both backbone and side-chain atoms, it may soon be possible to deduce which structures are indeed the most accurate, in much the same way that the combination of solid-state ¹³C and ¹⁷N NMR, ⁵⁷Fe NMR, Mössbauer and infra-red spectroscopies, combined with quantum chemistry, enabled the first accurate prediction of the CO ligand geometry in carbonmonoxy-myoglobin,⁵⁴ in advance of its revised crystallographic structures.^53,55–57

At present, the major outliers we find in our chemical shift predictions are those for aspartic acid residues. We attribute this observation to the fact these residues may have ionized sidechains (in GB1), creating a complex dependence of the shielding tensors on local electrostatics. The shifts are hard to compute precisely, since the dielectric constant and solvation state are not precisely known, and so, interpretation of shielding tensors for readily ionized residues should be utilized with caution, and such uncertainties are therefore included in the structure calculations. We anticipate the same effects for Lys and Arg, but in GB1 (which has no Arg residues) the Lys residues fit quite well with theory, due most likely to the fact that the location of the sidechain charge is more distal to Cα than it is in Asp. As noted above in Table 2, Asp residues exhibit the greatest deviation from the theoretical prediction, due to the high likelihood of the ionized carboxylate and its proximity to the backbone. Nevertheless, the overall agreement throughout GB1 is better than 3 ppm in comparison to the theoretically computed tensor parameters, in the case of all the available high-resolution structures. Indeed, as shown in Figure 6, tensor parameters calculated from the high-resolution structures (even those lacking CST information in refinement) demonstrated superior agreement with the experimentally demonstrated CST values, illustrating the self-consistency of the CST method and a rigorous cross-validation with other structure refinement techniques.

Figure 6.

Comparison between experimental and theoretical CST elements, obtained by using different backbone geometries. In all cases, theoretical chemical shielding tensor principal components were converted to chemical shift tensor elements using regression analysis. Backbone geometries represented, and R² and RMSD between theory and experiment are: (a) Structure calculated with distance only (structure 1, Table 3), R² = 0.92, RMSD = 4.4 ppm. (b) 2QMT crystal structure, R² = 0.97, RMSD = 2.5. (c) Previously published SSNMR structure of GB1 (structure 10, Table 3. pdb cod 2JSV), R² = 0.97, RMSD = 2.9 ppm. (d) Structure solved with calibrated CST data (structure 8) R² = 0.99, RMSD = 1.6 ppm.

Conclusions

The results we have presented above are of interest for several reasons. First, they represent the first experimental determination of the ¹³Cα shift tensor elements for all amino acids in a protein, GB1. Second, we find that the experimentally determined shielding tensor elements are in good accord with those obtained by using quantum chemistry. Third, we have incorporated these shielding tensor restraints into the Xplor-NIH program and used them, together with additional restraints (distances, TALOS-derived torsion angles and vector angles) to produce refined solid-state NMR structures of the GB1 protein. Both isotropic chemical shifts as well as the ¹³Cα shift tensor elements improve the agreement between the NMR and x-ray deduced structures, and vector angles improve the agreement even further. Fourth, we find that both back-calculated isotropic, as well as anisotropic, shift predictions improve considerably using the refined structures, which themselves have no major distance or other violations. Fifth, the data acquired in this study required less than 48 hours of experiment time, suggesting comparable results might be acquired on larger systems using 4D spectroscopy in less than a week. In the future, it seems likely that CST restraints will prove most informative in unusual geometric situations, since these are by definition, under-represented in isotropic shift data bases. Properly constraining these residues, which often occur in turns and loops, may be of particular use in larger systems, such as membrane proteins, where turn residues between α-helices are difficult to constrain. In such cases, knowledge of backbone ¹⁵N and ¹³C′ tensors or sidechain resonances where already, γ-gauche effects are known to dominate isotropic chemical shifts,^44,58 would complement Cα information. It has been shown previously that Cα tensor orientation is also a powerful indicator of molecular geometry, and it should also be possible to use shift tensor element orientations in structure refinement¹⁴ of high-resolution SSNMR structures.

The importance of CST constraints extends beyond MAS SSNMR. Spectra of samples in aligned bilayers or other aligned media are strongly dependent upon both tensor magnitude and orientation relative to the magnetic field.^59–65 SSNMR techniques for aligned membrane protein samples exploit knowledge of the orientation and magnitudes of ¹H-¹⁵N dipole, ¹⁵N CST,^{59,60 13}C′ CST^64,65 and other tensors. Therefore improved knowledge of tensor magnitude and orientations in peptides and proteins has the potential to enhance structure quality derived from such oriented sample experiments, as well as in the MAS techniques shown here.

Figure 5.

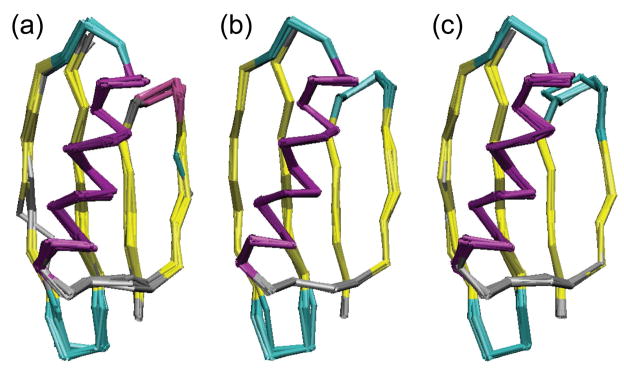
Ensembles of ten lowest energy structures of GB1 computed with CST restraints: (a) using distances and CST data and variable p_offset and p_scale; (b) using distances, CST, TALOS, and VEAN restraints and variable p_offset and p_scale; (c) using distances and CST with p_scale and p_offset fixed to values from the lowest energy structure in (b). The coloring is according to secondary structure (helix in purple, strands in yellow, turns in cyan, and coils in grey).