Using visual noise to characterize amblyopic letter identification

Abstract

Amblyopia is a much-studied but poorly understood developmental visual disorder that reduces acuity, profoundly reducing contrast sensitivity for small targets. Here we use visual noise to probe the letter identification process and characterize its impairment by amblyopia. We apply five levels of analysis — threshold, threshold in noise, equivalent noise, optical MTF, and noise modeling — to obtain a two-factor model of the amblyopic deficit: substantially reduced efficiency for small letters and negligibly increased cortical noise. Cortical noise, expressed as an equivalent input noise, varies among amblyopes but is roughly 1.4× normal, as though only 1/1.4 the normal number of cortical spikes are devoted to the amblyopic eye. This raises threshold contrast for large letters by a factor of √1.4 = 1.2×, a negligible effect. All 16 amblyopic observers showed near-normal efficiency for large letters (> 4× acuity) and greatly reduced efficiency for small letters: 1/4 normal at 2× acuity and approaching 1/16 normal at acuity. Finding that the acuity loss represents a loss of efficiency rules out all models of amblyopia except those that predict the same sensitivity loss on blank and noisy backgrounds. One such model is the last-channel hypothesis, which supposes that the highest-spatial-frequency channels are missing, leaving the remaining highest-frequency channel struggling to identify the smallest letters. However, this hypothesis is rejected by critical band masking of letter identification, which shows that the channels used by the amblyopic eye have normal tuning for even the smallest letters. Finally, based on these results, we introduce a new “Dual Acuity” chart that promises to be a quick diagnostic test for amblyopia.

Introduction

Amblyopia is a developmental disorder of spatial vision, usually affecting only one eye, that impairs visual acuity, reducing contrast sensitivity for small targets (Gstalder & Green, 1971; Hess & Howell, 1977; Levi & Harwerth, 1977; Bradley & Freeman, 1981; for a review, see Levi, 1991). While the loss can be profound, the nature of the deficit is still mysterious. To better characterize it, we measured identification thresholds in visual noise for letters of all sizes, 0.2 to 4.5 deg.

Contrast sensitivity is usually studied by measuring threshold on a blank background. By also measuring threshold on a background of visual noise, it is possible to factor the observer’s visual sensitivity into two useful components: equivalent noise N_eq and efficiency η⁺ (Pelli & Farell, 1999). Efficiency rates the observer’s computational performance (ability to identify faint letters) on an absolute scale. The equivalent noise represents the amount of visual noise added to the display that would account for the observer’s threshold on a blank screen.

Figure 1 is a new eye chart, based on the results of this work, that is designed to diagnose amblyopia. This “Dual Acuity” chart measures letter acuity with and without noise. We discuss it, below, in Clinical Application.

Figure 1.

Pelli-Levi Dual Acuity Chart. Ask the observer to read all six letters on each line, continuing down the chart until the observer gets all three no-noise letters wrong. Give credit (1/3 line) for each letter right in the last triplet in which any letters were correctly read. The chart is scale-invariant and may be used at any distance. The score of interest is the difference in log acuities (i.e., lines) between the two sides. So far, we have found no difference in six normals and a 1 or 2 line difference in the five amblyopes tested. The chart is available at http://psych.nyu.edu/pelli/dualacuity/. Copyright © 2004 Denis Pelli & Dennis Levi.

Factoring sensitivity into efficiency and equivalent noise allows one to distinguish differing explanations for the sensitivity. While there are many independent sources of noise in the visual system, usually one will dominate, making the others negligible. Reduced gain early in the visual pathway (optical or neural), before the dominant noise source, would increase the equivalent input noise level. Also, one could imagine that fewer cortical spikes are devoted to the amblyopic eye, because the neurons are sparser or less responsive (Kiorpes, Kiper, O’Keefe, Cavanaugh, & Movshon, 1998). Changes in channel tuning, making the channel less well matched to the signal, would reduce efficiency. For example, if the channel normally used for letter identification is missing or impaired, the amblyope might have to use a less optimal channel, and thus operate less efficiently.

It is not clear whether the loss of contrast sensitivity in amblyopes represents a loss of efficiency, an increase in equivalent noise, or both. While the characteristic loss of contrast sensitivity on a blank screen has been well documented (Gstalder & Green, 1971; Hess & Howell, 1977; Levi & Harwerth, 1977; Bradley & Freeman, 1981), it has been suggested that the loss occurs only at threshold, and that vision is normal at high contrasts (Hess & Bradley, 1980; Loshin & Levi, 1983). This would be consistent with increased equivalent noise. Grating contrast sensitivity in noise has been reported for amblyopic humans (Nordmann, Freeman & Casanova, 1992; Kersten, Hess & Plant, 1988) and monkeys (Kiorpes & Movshon, 1998). In one human study (Kersten et al., 1988), two of the three amblyopes showed substantial losses of contrast sensitivity in noise, indicating that most of the deficit was due to reduced efficiency, and the third showed only a small loss of sensitivity in noise, indicating that most of the deficit was due to increased equivalent noise.

In many respects, the vision of amblyopes is comparable to that of infants (Kiorpes, 1992; Levi & Carkeet, 1993). Both amblyopes and infants have reduced acuity and contrast sensitivity, and several studies suggest that the infant visual system has both increased equivalent noise and reduced efficiency (Brown, 1994; Kiorpes & Movshon, 1998; Skoczenski & Norcia, 1998).

Our first goal was to factor the loss of contrast sensitivity into its two components: reduced efficiency and increased equivalent noise. We measured amblyopes’ threshold contrasts for identifying letters on blank and on noisy backgrounds. We chose letters (rather than gratings) as targets in our experiments because (1) letters are used to measure acuity clinically; (2) contrast sensitivity for small letters is severely reduced in amblyopia (Lawwill & Burian, 1966) and amblyopia impairs letter acuity more than grating acuity (Gstalder & Green, 1971; Levi & Klein 1982); and (3) we have learned something about the factors determining letter identification in normal vision (Chung, Legge, & Tjan, 2002a; Pelli, Burns, Farell, & Moore, in press; Pelli, Farell, and Moore, 2003; Majaj, Pelli, Kurshan, & Palomares, 2002).

As noted above, a loss of efficiency in amblyopia could be due to the use of a less optimal channel by the amblyopic visual system, because the mechanisms normally used to identify small letters are impaired or absent. A similar loss of efficiency occurs in normal peripheral vision, and has been similarly attributed to the use of a last channel (Pelli et al., in press). In its simplest form, this last-channel hypothesis makes two predictions: (1) For the amblyopic eye, the channel spatial frequency should increase as the letter frequency increases, and then remain fixed (at the last channel). Thus, the amblyopic and non-amblyopic eyes will use different channels to analyze the same small letter. Selection of a lower spatial frequency channel does occur when viewing a broadband line Vernier target with the amblyopic eye (Levi, Waugh, & Beard, 1994). (2) Efficiency will drop precipitously when the letter frequency exceeds that best-served by the last channel. To test the last-channel hypothesis, we conducted a second experiment using critical band masking (Solomon & Pelli, 1994; Majaj et al., 2002).

Experiment 1: Effect of white noise

Methods

Letter size and frequency

We specify letter size using the typographer’s measure, x-height, the height of the lowercase letter x. Majaj et al. (2002) have shown that normal observers use a channel tuned to spatial frequency f =3/s ^2/3 to identify Bookman letters of size s. This frequency is the bottom scale in most of our graphs.

General

In most of the experiments, the signals were letters (Bookman font) presented briefly (200 ms) on either a uniform background or on a background of dynamic white noise of the same mean luminance (45 cd/m²). The noise began 496 ms before the signal and ended 496 ms after the end of the signal, and covered an area approximately twice as wide and twice as high as the average letter width and height. The noise consisted of independently generated square checks. The noise check duration was 45 ms. The power spectral density N of the noise is the product of contrast power $c_{\text{rms}}^2$, area, and duration of a check. The noise checks and letters were displayed at a fixed physical size. To create letters smaller than 1 deg, we increased viewing distance, with a fixed letter size (typographic x-height) of 0.94 cm at the display. For larger letters we increased the letter size on the screen, with a fixed viewing distance of 0.6 m. The noise check size scaled with the letter size so that there were always 14.5 checks per letter size, as in Figure 1. The letters and noise were generated by a Macintosh IIci or a PowerMac 6100, and displayed on a 12-in monochrome display screen using a video attenuator (Pelli & Zhang, 1991) and TextInNoise, a stand-alone C application that we wrote, which was a predecessor to the Psychophysics Toolbox extensions to MATLAB (Brainard, 1997; Pelli, 1997; http://psychtoolbox.org/).

Each trial was initiated by the observer clicking the mouse, and consisted of a brief presentation of a faint letter on either a uniform (N = 0) or noisy (N > 0) background. The stimulus was then replaced by a response screen consisting of the 26 letters of the alphabet displayed at a high contrast. The observer responded by using the mouse to place the cursor on the matching letter, and clicking, which initiated feedback and a new trial. We used an extra large cursor, so that all the observers could see it. Each correct response was rewarded by a beep. In each run of 40 trials, the signal size and noise contrast were fixed. The signal contrast was controlled by an efficient staircase (improved QUEST – Watson & Pelli, 1983; King-Smith, Grigsby, Vingrys, Benes, & Supowit, 1994), which estimates the contrast required for 64% correct identification. We varied the letter size and noise contrast (usually 0 or 25%) between runs. Each threshold reported here is the geometric mean of 3 to 6 threshold estimates.

Observers

We tested 19 observers: 3 with normal vision (including two authors, DL and SC), and 16 amblyopes with anisometropia (7), strabismus (6), or both (3). All observers were experienced in making psychophysical judgments, having done thousands to millions of trials. Details are provided in Table 1.

Table 1.

Visual characteristics of amblyopic observers. The observers are color-coded by spatial frequency acuity (Table 2), which is a handy index of the severity of amblyopic deficit: green for the mildest (spatial frequency acuity 14 to 15 c/deg), blue for moderate (9.5 to 13 c/deg), and red for severe (6 to 9 c/deg).

Observer	Age	Sex	Eye	Rx.	Acuity1	Fixation2	Strabismus	Cortical noise re normal3
7 Anisometropic4
RJ	53	M	O.D.	+0.50/−0.25 × 95	20/14	central	none
			O.S.	+2.50/−0.75 × 125	20/57	central		0.7
AA	27	M	O.D.	pl/−0.25 × 180	20/12	central	none
			O.S.	+3.75/−1.50 × 20	20/52	central		2.0
EW	26	F	O.D.	+1.50/−0.75 × 95	20/80	central	none	1.4
			O.S.	plano	20/16	central
RM	27	M	O.D.	−2.00	20/15	central
			O.S.	−12.50	20/70	central	occasional l. xt.	3.1
CT	24	M	O.D.	−0.25	20/15	central
			O.S.	+4.00	20/50	central	none	1.5
DT	26	M	O.D.	+7.00/1.25 × 160	20/200	central	none	0.7
			O.S.	+0.50	20/10	central
DN	22	M	O.D.	−1.75	20/20	central
			O.S.	+3.25/−0.25 × 180	20/100	central	none	2.2
6 Strabismic
RH	32	M	O.D.	−1.00/−0.50 × 170	20/15	central
			O.S.	−1.50/−1.50 × 10	20/59	unsteady	microtropia l. et., 2Δ	1.7
JB	39	M	O.D.	+1.75/−0.50 × 142	20/49	0.25° nasal	constant r. et., 6Δ	2.3
			O.S.	+1.25/−1.0 × 025	20/20	central
JV	33	M	O.D.	−3.75/−0.50 × 025	20/15	central
			O.S.	−0.75/−0.75 × 155	20/33	1° temp	constant l. et., 5Δ	1.2
LM	25	F	O.D.	−0.25/−1.25 × 112	20/20	central
			O.S.	+0.50/−1.75 × 24	20/104	0.50° nasal	constant l. xt., 45Δ	0.7
LH	21	F	O.D.	−0.25/	20/60		constant r. et., 5Δ	2.4
			O.S.	pl/−0.75 × 95	20/20		& hyper 4Δ
JC	22	F	O.D.	+1.00/−0.75 × 100	20/20	central
			O.S.	+0.50/−100 × 107	20/60	0.25° nasal & superior	constant l. xt., 16Δ	2.6
3 Anisometropic & Strabismic
DS	22	M	O.D.	+0.25/−0.25 × 90	20/15	central
			O.S.	+7.25/−0.50 × 120	20/101	unsteady (0.25° sup)	constant l. xt., 6Δ	0.5
CB	37	M	O.D.	+4.25	20/15	central
			O.S.	−9.75/−0.75 × 140	20/200	0.75–1° nasal	constant l. et., 4Δ	1.7
AJ	27	F	O.D.	+5.50/−2.50 × 20	20/60	1.5° temporal	constant r. xt., 4Δ	1.1
			O.S.	+2.5	20/15	central

¹Notes: 75% correct on Davidson-Eskridge charts. Note that “acuity” in the text always refers to the acuity values reported in Table 2, not this.

²Fixation determined with Haidinger’s brushes and visuoscopy.

³From Figure 6.

⁴¹No constant strabismus, and hyperopic anisometropia >+1.5D or myopic anisometropia > 4D.

Ideal observer

The ideal observer threshold contrast c_ideal is measured independently of the human thresholds, by running the same tests on a computer program implementation of the ideal observer. The ideal observer knows the noisy stimulus and chooses the most likely signal (i.e., the one most similar to the stimulus) (Pelli, 1985; Geisler, 1989).

Analysis

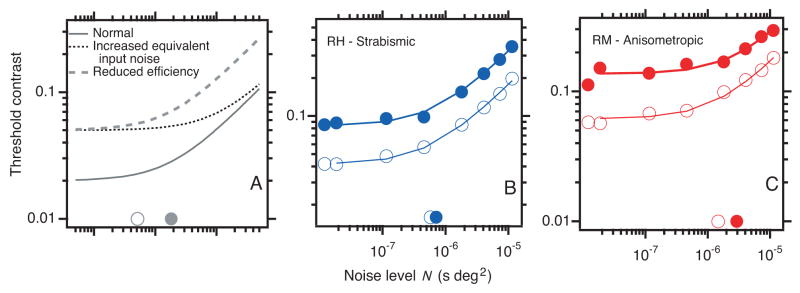
The general approach is illustrated schematically in Figure 2A, which plots threshold contrast for letter identification as a function of noise level. The solid gray line represents a normal eye. When the noise level is less than the observer’s equivalent input noise (open gray circle on the horizontal axis), it has little effect on the threshold. When the noise level exceeds the equivalent noise, threshold contrast increases asymptotically in proportion to the square root of noise level. The dotted line has increased equivalent noise (solid gray circle near the abscissa), while the dashed line has reduced efficiency. Figures 2B and 2C plot threshold contrast for letters as a function of noise level for a strabismic (B) and an anisometropic (C) amblyope. Both amblyopes show a marked loss of efficiency, accompanied by little (C) or no (B) increase in equivalent noise. This previews our main result: amblyopes show a consistent loss of efficiency and a small variable increase in equivalent noise.

Figure 2.

A. Effects of noise and amblyopia. Threshold contrast for letter identification as a function of noise level (power spectral density). The open gray circle on the horizontal axis indicates the equivalent input noise level of a normal observer. The solid gray line represents normal threshold. Each curve represents linear dependence of squared threshold contrast on noise level, c² ∝ N + N_eq, which produces a bent line in the log-log coordinates of Figure 2. When the noise level is less than (to the left of) the equivalent noise, it has little effect on threshold; when the noise exceeds the equivalent noise, threshold contrast increases in proportion to the square root of noise level. The dashed line has reduced efficiency, and the dotted line has increased equivalent noise (solid circle on the horizontal axis). B and C. Letter threshold contrast as a function of noise level for a strabismic (B) and an anisometropic (C) amblyope. Open symbols are the nonamblyopic eyes; solid symbols are the amblyopic eyes. Both amblyopes show a marked loss of efficiency (vertical shift), accompanied by little (C) or no (B) increase in equivalent noise (diagonal shift). Letter size 0.5 deg.

To estimate the equivalent noise and efficiency, it is only necessary to measure two threshold contrasts – one without noise c₀, and one with a high noise c.

Equivalent noise is $N_{\text{eq}}={Nc}_0^2/(c^2-c_0^2)$, where N is the spectral density of the noise. $N=c_{\text{rms}}^2{A}_{\text{check}}{T}_{\text{check}}$, where c_rms is the root mean square noise contrast, A_check is the area of a noise check, and T_check is its duration. Efficiency is ${\eta }^{+}=c_{\text{ideal}}^2/(c^2-c_0^2)$ where c_ideal is the ideal observer’s threshold contrast in noise. Pelli and Farell (1999) call this high-noise efficiency η* ≡ η⁺.

Results

Table 2 reports our results. For each observer, for each letter size, we measured the threshold contrast c₀ (without noise) and c (with noise) for identification. The other quantities (E₀, E, η, N_eq, etc.) are all derived from these two measurements and the stimulus parameters. Each measure gives a slightly different view of the results, as we will now see.

Table 2.

Thresholds for letter identification by 16 amblyopic observers.

Observer facuity	s	f	log N	log c0	log c	log E0	log E+	log Eideal	logη+	log Neq	log H	log Neqr	log Ncortical	log Nphoton	log F1
Normal 16.9 c/deg	3.63	1 3	−3.54	−1 79	−0 53	−3.40	−0.88	−2.51	−1.63	−6.06	−0.03	−6.13	−6.06	−7.23	−2.83
	2.90	1.5	−3.74	−1.75	−0.56	−3.50	−1.13	−2.71	−1.58	−6.11	−0.04	−6.19	−6.19	−7.23	−2.77
	1.45	2.3	−4.34	−1.61	−0.64	−3.84	−1.89	−3.31	−1.42	−6.29	−0.06	−6.41	−6.59	−7.23	−2.54
	0.72	3.7	−4.94	−1.46	−0.67	−4.13	−2.57	−3.91	−1.34	−6.50	−0.11	−6.71	−7.00	−7.23	−2.25
	0.48	4.9	−5.29	−1.39	−0.71	−4.34	−3.00	−4.26	−1.26	−6.63	−0.14	−6.92	−7.23	−7.23	−2.04
	0.36	5.9	−5.55	−1.25	−0.70	−4.32	−3.24	−4.52	−1.28	−6.63	−0.18	−6.99	−7.40	−7.23	−1.96
	0.24	7.8	−5.89	−1.08	−0.69	−4.32	−3.62	−4.86	−1.24	−6.59	−0.25	−7.10	−7.64	−7.23	−1.86
	0.18	9.4	−6.15	−0.89	−0.63	−4.20	−3.82	−5.12	−1.30	−6.53	−0.33	−7.18	−7.80	−7.23	−1.77
	0.14	11.4	−6.53	−0.61	−0.50	−4.01	−4.22	−5.50	−1.28	−6.32	−0.43	−7.18	−7.97	−7.23	−1.77
	0.10	14.1	−6.80	−0.37	−0.30	−3.81	−4.24	−5.77	−1.53	−6.37	−0.62	−7.60	−8.15	−7.23	−1.35
EW—Aniso. 15.0 c/deg	0.72	3.7	−4.94	−1.40	−0.55	−4.01	−2.31	−3.91	−1.60	−6.63	−0.12	−6.87	−7.00	−13.75	−2.08
	0.48	4.9	−5.29	−1.30	−0.58	−4.19	−2.75	−4.26	−1.51	−6.73	−0.16	−7.06	−7.23	−13.75	−1.89
	0.36	5.9	−5.55	−1.21	−0.55	−4.23	−2.94	−4.52	−1.58	−6.84	−0.21	−7.26	−7.40	−13.75	−1.70
	0.24	7.8	−5.89	−1.06	−0.49	−4.30	−3.18	−4.86	−1.68	−7.01	−0.29	−7.60	−7.64	−13.75	−1.36
	0.18	9.4	−6.15	−0.78	−0.39	−3.97	−3.27	−5.12	−1.85	−6.85	−0.39	−7.62	−7.80	−13.75	−1.34
JV—Strab. 14.7 c/deg	1.45	2.3	−4.34	−1.62	−0.63	−3.84	−1.88	−3.31	−1.43	−6.31	−0.07	−6.45	−6.59	−15.33	−2.50
	0.72	3.7	−4.94	−1.43	−0.69	−4.08	−2.62	−3.91	−1.29	−6.40	−0.12	−6.64	−7.00	−15.33	−2.31
	0.48	4.9	−5.29	−1.42	−0.59	−4.40	−2.76	−4.26	−1.50	−6.93	−0.17	−7.27	−7.23	−15.33	−1.69
	0.36	5.9	−5.55	−1.32	−0.57	−4.44	−2.97	−4.52	−1.55	−7.03	−0.21	−7.45	−7.40	−15.33	−1.50
	0.24	7.8	−5.89	−1.13	−0.52	−4.43	−3.24	−4.86	−1.62	−7.08	−0.30	−7.69	−7.64	−15.33	−1.26
	0.18	9.4	−6.15	−0.81	−0.37	−4.04	−3.21	−5.12	−1.91	−6.98	−0.40	−7.78	−7.80	−15.33	−1.17
AA—Aniso. 14.4 c/deg	1.45	2.3	−4.34	−1.53	−0.63	−3.68	−1.86	−3.31	−1.45	−6.16	−0.08	−6.31	−6.59	−14.99	−2.65
	0.72	3.7	−4.94	−1.38	−0.66	−3.98	−2.56	−3.91	−1.35	−6.37	−0.13	−6.62	−7.00	−14.99	−2.34
	0.48	4.9	−5.29	−1.25	−0.66	−4.06	−2.91	−4.26	−1.35	−6.44	−0.17	−6.79	−7.23	−14.99	−2.17
	0.36	5.9	−5.55	−1.18	−0.62	−4.18	−3.07	−4.52	−1.45	−6.66	−0.22	−7.10	−7.40	−14.99	−1.85
	0.24	7.8	−5.89	−0.94	−0.48	−4.04	−3.17	−4.86	−1.69	−6.76	−0.31	−7.39	−7.64	−14.99	−1.57
	0.18	9.4	−6.15	−0.79	−0.38	−3.99	−3.27	−5.12	−1.85	−6.86	−0.41	−7.69	−7.80	−14.99	−1.27
LH—Strab. 12.9 c/deg	1.45	2.3	−4.34	−1.39	−0.55	−3.38	−1.71	−3.31	−1.60	−6.01	−0.08	−6.18	−6.59	−15.30	−2.78
	0.72	3.7	−4.94	−1.27	−0.60	−3.75	−2.43	−3.91	−1.48	−6.26	−0.14	−6.55	−7.00	−15.30	−2.41
	0.48	4.9	−5.29	−1.14	−0.56	−3.84	−2.71	−4.26	−1.55	−6.42	−0.20	−6.81	−7.23	−15.30	−2.14
	0.36	5.9	−5.55	−1.11	−0.54	−4.04	−2.93	−4.52	−1.59	−6.66	−0.25	−7.17	−7.40	−15.30	−1.79
	0.24	7.8	−5.89	−0.78	−0.41	−3.72	−3.06	−4.86	−1.80	−6.55	−0.36	−7.28	−7.64	−15.30	−1.68
JB—Strab. 12.7 c/deg	1.45	2.3	−4.34	−1.51	−0.57	−3.64	−1.76	−3.31	−1.55	−6.22	−0.09	−6.39	−6.59	−14.10	−2.57
	0.72	3.7	−4.94	−1.21	−0.55	−3.64	−2.34	−3.91	−1.57	−6.24	−0.15	−6.53	−7.00	−14.10	−2.43
	0.48	4.9	−5.29	−1.12	−0.52	−3.81	−2.62	−4.26	−1.64	−6.47	−0.20	−6.87	−7.23	−14.10	−2.08
	0.36	5.9	−5.55	−0.97	−0.49	−3.76	−2.84	−4.52	−1.68	−6.46	−0.26	−6.98	−7.40	−14.10	−1.98
	0.24	7.8	−5.89	−0.74	−0.41	−3.65	−3.08	−4.86	−1.78	−6.47	−0.37	−7.21	−7.64	−14.10	−1.75
	0.18	9.4	−6.15	−0.63	−0.35	−3.67	−3.26	−5.12	−1.86	−6.56	−0.50	−7.56	−7.80	−14.10	−1.40
RJ—Aniso. 11.5 c/deg	0.36	5.9	−5.55	−1.04	−0.34	−3.90	−2.50	−4.52	−2.02	−6.95	−0.29	−7.54	−7.40	−9.01	−1.42
AJ—S&A 11.25 c/deg	1.45	2.3	−4.34	−1.52	−0.49	−3.66	−1.61	−3.31	−1.70	−6.39	−0.10	−6.59	−6.59	−15.80	−2.37
	0.72	3.7	−4.94	−1.31	−0.51	−3.84	−2.25	−3.91	−1.66	−6.53	−0.17	−6.87	−7.00	−15.80	−2.09
	0.48	4.9	−5.29	−1.20	−0.54	−3.97	−2.66	−4.26	−1.60	−6.60	−0.23	−7.07	−7.23	−15.80	−1.88
	0.36	5.9	−5.55	−1.11	−0.48	−4.04	−2.80	−4.52	−1.72	−6.78	−0.30	−7.39	−7.40	−15.80	−1.57
	0.24	7.8	−5.89	−0.86	−0.33	−3.87	−2.88	−4.86	−1.98	−6.88	−0.45	−7.78	−7.64	−15.80	−1.18
RH—Strab. 11.1 c/deg	1.45	2.3	−4.34	−1.35	−0.57	−3.30	−1.78	−3.31	−1.53	−5.86	−0.10	−6.06	−6.59	−13.77	−2.89
	0.72	3.7	−4.94	−1.17	−0.59	−3.53	−2.41	−3.91	−1.50	−6.06	−0.17	−6.40	−7.00	−13.77	−2.55
	0.48	4.9	−5.29	−1.06	−0.41	−3.68	−2.42	−4.26	−1.84	−6.55	−0.24	−7.03	−7.23	−13.77	−1.93
	0.36	5.9	−5.55	−0.92	−0.31	−3.66	−2.45	−4.52	−2.07	−6.76	−0.31	−7.37	−7.40	−13.77	−1.58
	0.24	7.8	−5.89	−0.61	−0.14	−3.39	−2.49	−4.86	−2.37	−6.79	−0.46	−7.71	−7.64	−13.77	−1.25
	0.18	9.4	−6.15	−0.35	−0.10	−3.12	−2.79	−5.12	−2.33	−6.48	−0.64	−7.76	−7.80	−13.77	−1.20
CT—Aniso. 9.5 c/deg	1.45	2.3	−4.34	−1.44	−0.53	−3.48	−1.67	−3.31	−1.64	−6.15	−0.12	−6.39	−6.59	−7.96	−2.56
	0.72	3.7	−4.94	−1.23	−0.52	−3.68	−2.26	−3.91	−1.65	−6.36	−0.21	−6.78	−7.00	−7.96	−2.18
LM—Strab. 8.8 c/deg	1.45	2.3	−4.34	−1.52	−0.47	−3.65	−1.55	−3.31	−1.76	−6.44	−0.13	−6.70	−6.59	−7.41	−2.25
	0.72	3.7	−4.94	−1.19	−0.45	−3.60	−2.12	−3.91	−1.79	−6.41	−0.23	−6.87	−7.00	−7.41	−2.09
	0.48	4.9	−5.29	−0.98	−0.35	−3.52	−2.28	−4.26	−1.98	−6.53	−0.32	−7.18	−7.23	−7.41	−1.78
	0.36	5.9	−5.55	−0.73	−0.31	−3.27	−2.50	−4.52	−2.02	−6.32	−0.43	−7.17	−7.40	−7.41	−1.78
	0.24	7.8	−5.89	−0.33	−0.18	−2.83	−2.81	−4.86	−2.05	−5.90	−0.68	−7.26	−7.64	−7.41	−1.70
JC—Strab. 8.5 c/deg	1.45	2.3	−4.34	−1.43	−0.65	−3.47	−1.91	−3.31	−1.40	−5.89	−0.13	−6.16	−6.59	−14.40	−2.79
	0.72	3.7	−4.94	−1.13	−0.53	−3.47	−2.30	−3.91	−1.61	−6.11	−0.24	−6.58	−7.00	−14.40	−2.38
	0.48	4.9	−5.29	−0.85	−0.43	−3.27	−2.49	−4.26	−1.77	−6.07	−0.34	−6.74	−7.23	−14.40	−2.21
	0.36	5.9	−5.55	−0.59	−0.29	−2.98	−2.52	−4.52	−2.00	−6.01	−0.45	−6.91	−7.40	−14.40	−2.05
	0.24	7.8	−5.89	−0.28	−0.11	−2.72	−2.64	−4.86	−2.22	−5.98	−0.72	−7.43	−7.64	−14.40	−1.53
DS—S&A 7.5 c/deg	3.63	1.3	−3.54	−1.64	−0.47	−3.08	−0.75	−2.51	−1.76	−5.87	−0.08	−6.03	−6.06	−14.56	−2.52
	2.90	1.5	−3.74	−1.65	−0.39	−3.30	−0.79	−2.71	−1.92	−6.25	−0.09	−6.44	−6.19	−14.56	−2.52
	1.45	2.3	−4.34	−1.47	−0.30	−3.56	−1.21	−3.31	−2.10	−6.69	−0.16	−7.00	−6.59	−14.56	−1.95
	0.72	3.7	−4.94	−1.07	−0.04	−3.36	−1.30	−3.91	−2.61	−6.99	−0.28	−7.56	−7.00	−14.56	−1.40
DT—Aniso. 6.7 c/deg	1.45	2.3	−4.34	−1.34	−0.36	−3.30	−1.33	−3.31	−1.98	−6.31	−0.18	−6.66	−6.59	−14.11	−2.29
	0.72	3.7	−4.94	−1.09	−0.28	−3.40	−1.78	−3.91	−2.13	−6.55	−0.32	−7.20	−7.00	−14.11	−1.75
	0.48	4.9	−5.29	−0.62		−2.80		−4.26
RM—Aniso. 6.66 c/deg	1.45	2.3	−4.34	−1.19	−0.57	−2.98	−1.77	−3.31	−1.54	−5.56	−0.18	−5.92	−6.59	−13.89	−3.04
	0.72	3.7	−4.94	−0.92	−0.49	−3.06	−2.29	−3.91	−1.62	−5.71	−0.33	−6.37	−7.00	−13.89	−2.59
	0.48	4.9	−5.29	−0.76	−0.34	−3.11	−2.31	−4.26	−1.95	−6.09	−0.49	−7.07	−7.23	−13.89	−1.88
DN—Aniso. 6.5 c/deg	2.90	1.5	−3.74	−1.24	−0.42	−2.49	−0.86	−2.71	−1.85	−5.37	−0.11	−5.5 9	−6.19	−14.65	−3.37
	1.45	2.3	−4.34	−1.13	−0.43	−2.87	−1.49	−3.31	−1.82	−5.72	−0.19	−6.09	−6.59	−14.65	−2.86
	0.72	3.7	−4.94	−0.98	−0.39	−3.18	−2.02	−3.91	−1.89	−6.10	−0.34	−6.78	−7.00	−14.65	−2.18
	0.48	4.9	−5.29	−0.68	−0.23	−2.91	−2.07	−4.26	−2.19	−6.13	−0.51	−7.16	−7.23	−14.65	−1.80
CB—S&A 6.3 c/deg	3.63	1.3	−3.54	−1.57	−0.49	−2.94	−0.80	−2.51	−1.71	−5.68	−0.10	−5.87	−6.66	−6.61	−3.08
	2.90	1.5	−3.74	−1.50	−0.60	−3.00	−1.21	−2.71	−1.50	−5.52	−0.11	−5.75	−6.19	−6.61	−3.21
	1.45	2.3	−4.34	−1.25	−0.51	−3.11	−1.64	−3.31	−1.67	−5.81	−0.19	−6.20	−6.59	−6.61	−2.76

Our results:

Observer = name and (extrapolated) channel spatial frequency acuity f_acuity.

s = letter size (typographic x-height) in deg.

f = 3/s^2/3 = channel spatial frequency of letter in c/deg (Majaj et al., 2002).

$N=c_{\text{rms}}^2{A}_{\text{check}}{T}_{\text{check}}$ = power spectral density of the noise.

c₀ = threshold contrast in zero noise (i.e., no noise).

c = threshold contrast in noise.

E₀ = threshold energy in zero noise (i.e., no noise).

E⁺ = E−E₀, where E is threshold in noise.

E_ideal = threshold energy of the ideal observer for this task.

η⁺ = E_ideal/E⁺.

N_eq =equivalent input noise at display.

$H=\left(\frac{2}{\pi }arccos(f^{\prime })-f^{\prime }\sqrt{1-{f^{\prime }}^2}\right)$ =estimated MTF of the optics of the eye (i.e., ratio of contrast at retina to contrast at visual field), where f′ = f/(r_acuity f_acuity) and r_acuity = 1.3.

N_eqr = H²N_eq =equivalent input noise at retina.

$F_1=Q^{-1}{N}_{\text{eqr}}^{-1}$ =transduction efficiency, where Q is the photon flux (i.e., retinal illuminance expressed as 555 nm quanta s⁻¹ deg⁻²), which is the product of luminance and pupil area.

Notes. All data are monocular. Most of the data were collected under the same conditions for all observers, natural pupil, 45 cd/m². SC’s natural pupil diameter is 4.5 mm under these conditions, and we use that value for all the natural pupils to calculate retinal illuminance. Most of the normal thresholds, at the top of the table, are the average of three normal observers (including SC and DL). However, years later, we extended the domain of the normal curve by adding two new points for letter sizes 0.1 and 0.14 deg for SC. These new points were measured with a new CRT, with slightly lower luminance, 35 vs. 45 cd/m², and bigger noise checks, 4/29 vs. 2/29 of the letter size, which quadrupled the noise level. When we added these two new SC points to the normal curve, we used our estimate of what the in-noise threshold c would have been had we used the smaller check size used for the rest of the normal data, $c^{\prime }=\sqrt{c_0^2+c_{+}^2/4}$.

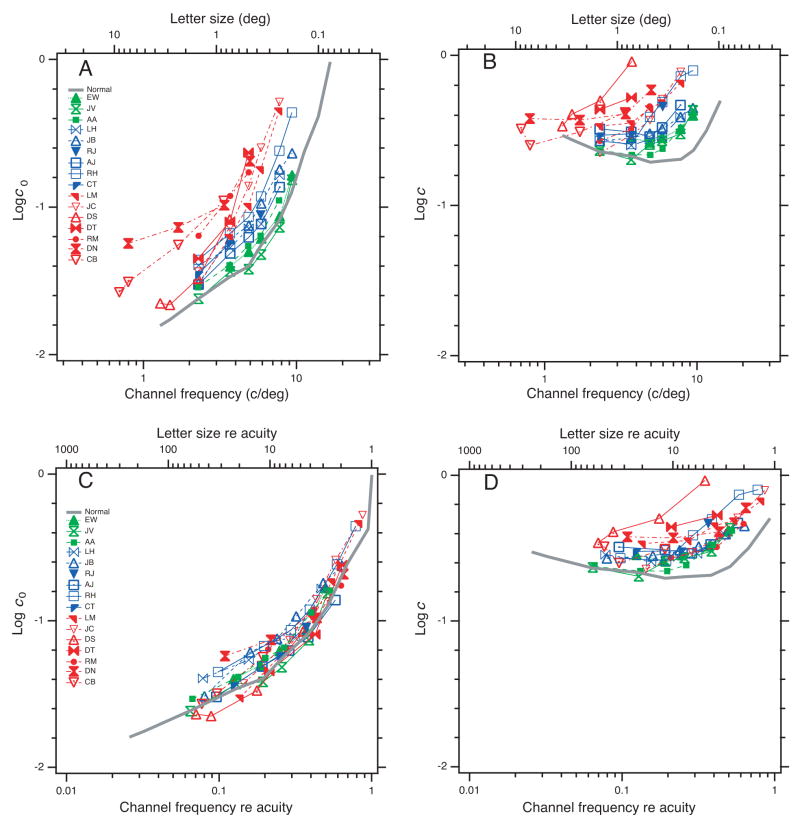
Although we have ordinary letter-chart measurements of acuity (Table 1), we also wanted to know the acuity (letter size at which c₀ = 1) under the precise test conditions of this experiment: isolated letter, brief presentation, etc. We estimated the acuity for each observer directly from the data in Figure 3A by finding the horizontal shift of the normal curve that best fits each observer’s data, taking the extrapolation of the normal curve to c₀ = 1 as the acuity estimate. We shall call this “acuity.” We call the channel spatial frequency 3/s^2/3 corresponding to this letter size s the “spatial frequency acuity” f_acuity. The observers in Table 2 are ordered and color-coded by acuity, which is a handy index of the severity of amblyopic deficit: green for the mildest (spatial frequency acuity 14 to 15 c/deg), blue for moderate (9.5 to 13 c/deg), and red for severe (6 to 9 c/deg). Gray is the average of three normal observers, tested monocularly (acuity 17 c/deg).

Figure 3.

Threshold contrast for identifying letters, with and without noise, as a function of letter size. A. Without noise. B. With noise. C and D. Without and with noise, as a function of letter size re acuity. The gray curve is the average threshold for three normal observers. The coloring is based on acuity, as in Table 2. All panels use the same symbols.

These derived measures – efficiency and equivalent noise – have fancy names yet bear an easily understood relation to the original thresholds. Efficiency can be expressed as ${\eta }^{+}=c_{\text{ideal}}^2/c_{+}^2$, where $c_{+}=\sqrt{c^2-c_0^2}$ is negligibly different from c when the noise level is high (i.e., c ≫ c₀), as in our experiments. Equivalent noise can be expressed as $N_{\text{eq}}={Nc}_0^2/c_{+}^2$. Thus efficiency is inversely proportional to the threshold in noise, ${\eta }^{+}\propto c_{+}^{-2}$, and the equivalent noise is proportional to the ratio of thresholds without and with noise, $N_{\text{eq}}\propto c_0^2/c_{+}^2$.

We find it helpful to calculate efficiency because it is a meaningful scale, comparable across a wide range of conditions.

Threshold

We find that amblyopic eyes have increased thresholds for small letters both on blank and noisy backgrounds. Figures 3A (without noise) and 3B (with noise) show threshold contrast as a function of letter size (top scale) or channel spatial frequency (i.e., 3/s^2/3) (bottom scale). Threshold goes up as the letter gets smaller. The colored curves are amblyopes. The gray curve, for comparison, is the average of thresholds from three normal observers.

Figure 3 plots threshold contrast with and without noise, as a function of spatial frequency. The data are orderly and seem to tell a story, or rather, two stories, as the results with noise are quite different from those without. Two stories is one too many, and it will take us the remaining pages of this section to wrestle these data into the confines of a single account.

Our results without noise confirm the well known loss of contrast sensitivity in amblyopic eyes for high spatial frequency gratings (Gstalder & Green, 1971; Hess & Howell, 1977; Levi & Harwerth, 1977; Bradley & Freeman, 1981) and small letters (Lawwill & Burian, 1966) presented on a blank field. Our finding of similar frequency-dependent loss in noise is new.

Figure 3A shows threshold without noise. The curves are color-coded by acuity, and we see an orderly progression. Amblyopia shifts the curve to the left along the log frequency axis: the poorer the acuity, the greater the shift. The mild amblyopes’ thresholds (green) are very nearly normal (gray). The blue and red curves are also similar to normal, but shifted left. This is confirmed in Figure 3C, where the horizontal axis is now relative to each observer’s acuity and the curves all superimpose. Thus, for all the amblyopes and normals, threshold depends solely on the letter size re acuity. If the letter is acuity-scaled, amblyopes and normals are all alike.

Note that most of the normal curve is the average of three normal observers and was collected under the same conditions as that for the amblyopes. As noted in Table 2, the normal curve was subsequently extended by adding thresholds for SC (one of the normal observers) at two smaller letter sizes (channel frequencies 11.4 and 14.1 c/deg).

Figure 3B shows threshold in noise. Again the curves are orderly, similarly shaped, progressing from gray (normal) to green, blue, and red. However, even the mildest amblyopes (green) have higher thresholds than normal at spatial frequencies greater than 3 c/deg. Recall that without noise (Figure 3A) the mild amblyopes hug the normal curve up to 10 c/deg, the highest frequency (smallest letter) we tested. Figure 3D shows that scaling by acuity does not succeed in superimposing the with-noise curves. In this case, the amblyopic thresholds are well above normal, and the color banding in the figure shows that more severe amblyopes have higher thresholds. The simple acuity scaling that aligned all the no-noise data in Figure 3C fails to align the with-noise data in Figure 3D. Note the color banding as threshold rises from gray to green to blue to red.

That’s as far as we got by looking at just the raw thresholds. Without noise, amblyopic and normal thresholds depend only on size re acuity (Figure 3C). With noise, the parallel curves in Figure 3B suggest that threshold elevation (re normal) depends only on size re acuity.

Efficiency

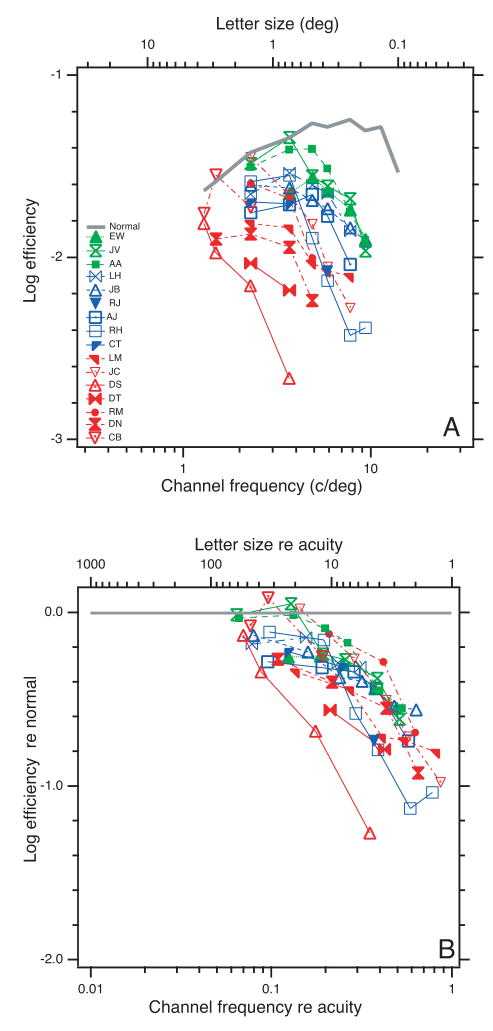
Having measured thresholds with and without noise, we follow the recommendation of Pelli and Farell (1999), and convert these two numbers into two new numbers that are easier to interpret: efficiency η⁺ and equivalent noise N_eq. Figure 4A shows efficiency as a function of letter size. Recall that efficiency is inversely proportional to the threshold in noise, ${\eta }^{+}\propto 1/c_{+}^2$, so it is essentially an upside-down version of the threshold in noise graph (Figure 3B), showing a family of curves that are flat and near normal at large letter size and which fall off in a similar way for small letters, with more severe amblyopes (red) falling off sooner (at a larger letter size). Dividing by the normal efficiency (gray curve) and replotting the data as a function of normalized letter size (Figure 4B) reveals that, as we anticipated, normalizing by acuity shifts the curves into horizontal alignment. All but one of the amblyopes have similar efficiency deficit (re normal) as a function of acuity-scaled letter size. DS is the exception, lying about a factor of 3 to the left of the rest. Each observer’s efficiency re normal is low-pass: unimpaired for large letter sizes and dropping steeply for small letters approaching the acuity limit. All amblyopic observers showed near-normal efficiencies for large letters (> 4× acuity), and a marked loss of efficiency at small letter sizes, 1/4 at 2×, and approaching a factor of 1/16 as we near the acuity limit.

Figure 4.

A. Efficiency η⁺ = E_ideal/E⁺ as a function of letter size. B. Efficiency re normal as a function of letter size re acuity. Both panels use the same symbols.

Equivalent noise

The amblyopes’ loss of efficiency near the acuity limit accounts for the thresholds in noise, but to account for the thresholds without noise, which are proportional to the ratio of equivalent noise and efficiency $c_0^2\propto N_{\text{eq}}/{\eta }^{+}$, we must also examine their equivalent noise.

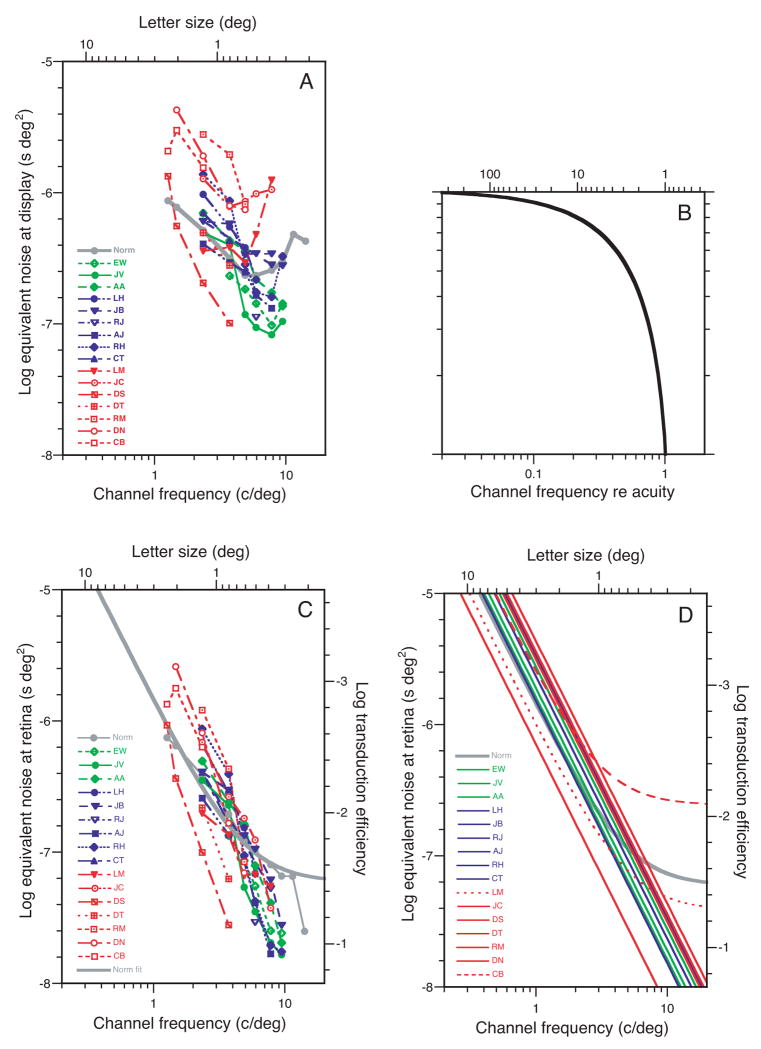
Figure 5A shows the equivalent noise of our observers as a function of letter size. It is a complicated graph that took us some time to unravel. The curves are roughly parallel to each other. Except for the ever-different DS, the curves show a more or less orderly progression. As acuity worsens (green to blue to red) the curves rise, indicating that equivalent noise tends to be higher when amblyopia is more severe. The vertical range, among observers, is a factor of 10, like the range of efficiency among observers (Figure 4A). At low spatial frequency (2.3 c/deg) all the observer groups (green, blue, and red) are roughly centered on the normal (gray). But at high spatial frequency (7.8 c/deg) the groups splay out to show their colors. At 7.8 c/deg all mild amblyopes have less than normal equivalent noise – quite surprising! – and each higher degree of amblyopia has a higher equivalent noise level. We are surprised because we presume that the normal visual system is optimized and that a disease state would be worse, not better.

Figure 5.

Equivalent noise N_eq as a function of letter size. A. Measured equivalent noise (at display) for each observer as a function of letter size. B. Estimated optical MTF (H in Table 2) as a function of spatial frequency re acuity. C. Estimated equivalent noise at retina N_eqr = H² N_eq. D. Fits of the Raghavan and Pelli equation N_eq = N_photon + k_cortical s²T to each observer’s data, where N_photon and k_cortical are fitted constants, s is letter size, and T is duration (0.2 s).

Raghavan and Pelli (2004) have made extensive equivalent noise measurements like these, but with normal observers, and showed that the equivalent noise N_eq is well described as the sum of cortical and photon noises (Pelli, 1990; Raghavan, 1995). At the retina, the cortical noise spectrum is f⁻², and the photon noise spectrum is frequency independent f⁰, where f is spatial frequency. Figure 5A is the observer’s equivalent input noise at the display. To apply their analysis we must estimate the equivalent input noise at the retina. To convert, we multiply by the contrast power of the eye’s optics H²(f). The optical MTF H(f) is the ratio of image contrast at the retina to the object contrast in the visual field.

We did not measure the optical MTF of our observers’ eyes, but we can estimate it. We expect amblyopes with lower acuity to focus less accurately (Ciuffreda, Levi, & Selenow, 1991) and thus to have a broader optical point spread function. It is known that myopes have reduced sensitivity to blur (Rosenfield & Abraham-Cohen, 1999). Noting that the contrast sensitivity functions of amblyopic and normal eyes all scale with acuity (Figure 3C), we assume that the optical point-spread function does too. Needing a functional form for the MTF, we somewhat arbitrarily use that of a diffraction-limited lens (Goodman, 1968), but without reference to the (unknown) actual pupil size. We allowed ourselves one degree of freedom r_acuity for the whole pool of observers: the ratio of the cut-off frequency of the MTF (for incoherent light) to the spatial frequency acuity of the observer’s eye. After trying several values, we set r_acuity to 1.3, but it is not critical: Results are very similar for values of 1.1 and 1.5. This estimated MTF is shown in Figure 5B. Note that the MTF affects our calculations only at frequencies at which we have data (i.e., up to about half the acuity in c/deg).

Figure 5C shows the equivalent input noise at the retina. It is much simpler than Figure 5A. Now the curves for each observer are approximately straight. The splaying is gone. Green, blue, and red are equally commingled at all spatial frequencies.

Raghavan and Pelli (2004) find that the equivalent noise at the retina is well described as the sum of two noises: photon noise N_photon corresponding to 2% transduction efficiency at 555 nm, and an f⁻² cortical noise N_cortical = k_corticalAT with a power spectral density independent of luminance but proportional to letter area A = (3/f)² and duration T. Under most conditions, either one noise or the other dominates, and that is true for most of our observers. However, for a few of our observers, our letters (45 cd/m², duration T = 0.2 s, size s = 0.3 to 4 deg) straddle both domains. For larger letters the cortical noise dominates; for a few observers, for smaller letters, the photon noise dominates. We fit the Raghavan and Pelli model to our data,

$$N_{\text{eq}}=N_{\text{photon}}+N_{\text{cortical}}$$ (1)

$$=N_{\text{photon}}+k_{\text{cortical}}{(3/f)}^{2}T$$ (2)

taking N_photon and k_cortical as degrees of freedom.

Figure 5D shows the fit of the Raghavan and Pelli model to the N_eq data in Figure 5C. This reveals order that was hard to discern in the raw N_eq data of Figure 5A. Returning to Figure 5D, on the left of the plot, N_eq has a log-log slope of −2, because it is dominated by cortical noise f⁻², and on the right, for the normals and two amblyopes, N_eq has a log-log slope of zero, because it is dominated by photon noise f⁰. At low spatial frequencies, where the slope is −2, the amblyopes are all near or above normal, indicating that they have higher-than-normal cortical noise. The low-frequency portion of the curve is very little affected by our admittedly crude MTF correction. Using a different approach, Levi and Klein (2003) reached a similar conclusion. At high spatial frequency, all but one of the amblyopes are below normal, indicating that their photon noise is below normal. All but 2 of the levels of cortical noise (i.e., on the left) are above normal. They span a range of 0.8 log units, and do not seem to be correlated with acuity (i.e., the different color-coded acuities are all jumbled up). The next figure offers a closer look.

The Raghavan and Pelli model has two degrees of freedom, which we may conveniently take to be N_cortical and N_photon re normal. The scatter diagram in Figure 6 plots N_cortical re normal, one point per observer, as a function of the observer’s acuity. There is quite a bit of scatter across observers, especially among the most severe amblyopes, but the regression line through the data has nearly zero slope, indicating practically no correlation between log N_cortical and log acuity.

Figure 6.

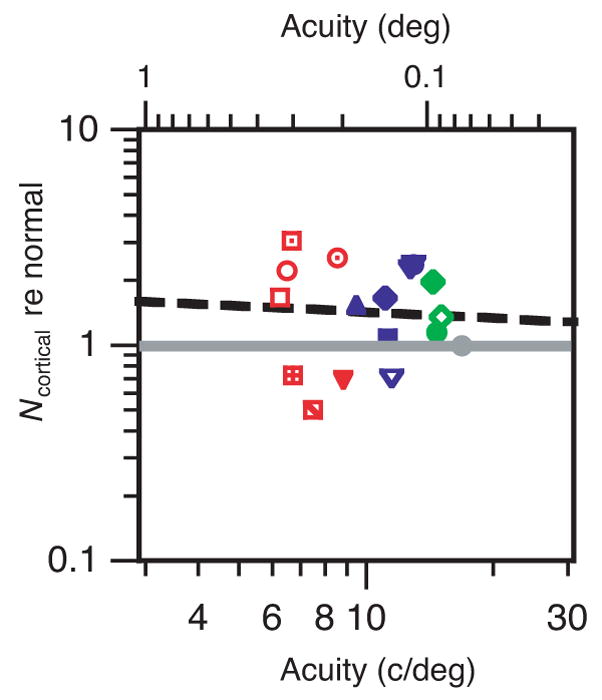
Cortical noise relative to normal versus acuity. Same symbols as in Figure 5. The solid gray line is normal; the dashed black line is a regression line with slope −0.096 and R²=0.004. The geometric mean of N_cortical re normal is 1.33 for the severe (red), 1.48 for the moderate (blue), and 1.45 for the mild (green) amblyopes. The geometric mean is 1.41 across all the amblyopes.

The estimates of N_cortical and N_photon are made after applying our estimate of the MTF (Figure 5B). However, the MTF is nearly 1 at low and mid spatial frequencies, varying significantly only at the high spatial frequencies. The estimate of N_cortical depends primarily on the low and mid frequencies, and thus is insensitive to the MTF, and the estimate of N_photon depends primarily on the high spatial frequencies and is thus extremely sensitive to the assumed MTF.

The right vertical scale in Figures 5C and 5D, $F_1=Q^{-1}{N}_{\text{eqr}}^{-1}$, where Q is the photon flux (i.e., retinal illuminance expressed as 555 nm quanta s⁻¹ deg⁻²), which is the product of luminance and pupil area. Raghavan and Pelli used an artificial pupil and found that the transduction efficiency is about 2% (at 555 nm in the fovea). The transduction efficiency estimate for our normal observers is 0.7%. We use the pupil size of 4.5 mm, measured on SC’s eye, but note that every observer will have a different pupil size and that this variation in retinal illuminance would explain the variance in N_photon and transduction efficiency.

The highest-spatial-frequency data in Figure 5 indicate that the amblyopes nearly all have lower photon noise than the normal observers. We think this is an artifact of underestimating the pupil size or MTF – our optical assumptions. It is hard to imagine how amblyopes could transduce a larger-than-normal fraction of light incident on the retina, but it is easy to suppose that they have a larger-than-normal pupil under monocular testing conditions. Relative to normal control observers, Barbur, Hess, and Pinney (1994) report that both eyes of amblyopes show a reduced amplitude of the pupil light reflex. For patterned stimuli, the amblyopic eye’s pupil response amplitude is, on average, about 1.8× smaller than normal. That is in the right direction, but pupil response amplitude is a nonlinear function of luminance, so we could not calculate, from the Barbur et al. results, how much bigger than normal our amblyopes’ pupils were. Photon noise that is 0.4× normal would result from a pupil area 1/0.4 = 2.5× normal, or a pupil size √2.5 = 1.6× normal. We checked the plausibility of this increased-pupil-size explanation by measuring the pupil size of four normal and five amblyopic observers under the conditions of our experiment. The means are 4.9 mm (normal), 4.3 mm (amblyopic), and 3.9 mm (non-amblyopic) with a SE of 0.4 mm. To account for the low photon noise estimate, the amblyopic pupil should have been much larger than normal, but in fact is insignificantly smaller. More precisely, the difference in log pupil size should have been 0.23, but the measured difference (mean ± SE) in log pupil size between amblyopic and normal eyes is −0.05 ± 0.06. Having ruled out a sufficiently large increase in pupil size, we tentatively ascribe our low photon-noise estimate to underestimating the optical MTF at high spatial frequencies (Figure 5B). Using a small artificial pupil (with a correspondingly brighter display) would eliminate this uncertainty. Our assumed value for the MTF (Figure 5B) has a large effect on the estimated photon noise, but has little or no effect on the estimated cortical noise, which depends only on the low- and mid-frequency results, where the MTF is nearly 1.

Based on the literature, we have made what we feel are reasonable optical assumptions about pupil size, defocus, and MTF. Both optical assumptions could be eliminated by doing all testing with a 1-mm pupil (and a correspondingly brighter display). These assumptions have no effect on efficiency. They only affect equivalent noise. In fact they affect our estimates of photon noise, introducing uncertainty into our transduction efficiency estimates, but have little or no effect on our estimates of cortical noise. Thus our main conclusions are unaffected by any doubts about the optics.

As a check, suggested by a reviewer, we tested one normal (SC) and one amblyope (DM) with a 1-mm artificial pupil and confirmed the amblyopic efficiency loss at high spatial frequencies (−0.66 log unit re normal at 3.7 c/deg; i.e., 0.7 deg x-height) and slightly increased cortical noise. These results are not included with those of the other observers because the artificial pupil resulted in a much lower retinal illuminance.

Thus we identify four distinct factors in accounting for amblyopic letter identification thresholds with and without noise.

1. Efficiency. All but one of our 16 amblyopic observers show the same low-pass loss of efficiency re normal as a function of spatial frequency re acuity, dropping to 0.5 at half acuity. Thus even our mildest amblyopes, with near-normal acuity, are qualitatively different from normal. Threshold for a small letter in noise is diagnostic.

2. Cortical noise. On average, the amblyopes have 1.4× higher than normal cortical noise, suggesting that, on average, only 1/1.4 the normal number of neural spikes are devoted to that eye, but there are large individual differences and some severe amblyopes have normal cortical noise. This is a very small effect, raising threshold contrast by a negligible factor of √1.4 = 1.2×.

3. MTF. Noting that the contrast sensitivity functions of amblyopes and normals are alike once scaled by acuity, we suppose that the optical point spread is proportional to acuity. This provides a one-parameter account for the splaying of N_eq for different degrees of amblyopia, and allows us to estimate the equivalent noise spectrum at the retina, which is much simpler than at the display.

4. Photon noise. The estimated photon noise for amblyopes is 2.5× below normal, but is relevant only at the highest spatial frequencies. It seems unlikely that amblyopes transduce a larger-than-normal fraction of the photons incident on the retina, and we ruled out larger-than-normal pupils, so we tentatively ascribe our low photon-noise estimate to underestimating the optical MTF (Figure 5B) at the highest spatial frequency by a factor of √2.5 = 1.6×. This has no effect on the estimation of efficiency or cortical noise.

Only the first factor, efficiency, is required to account for the thresholds in high noise. All four factors are required to account for the measured thresholds without noise. The large loss of efficiency for near-acuity letters and the slightly increased cortical noise are fundamental neural deficits. The acuity-dependent defocus is an optical effect, probably secondary to the neural impairments.

The key result of Experiment 1 is a substantial loss of efficiency in the amblyopic eye for small near-acuity letters and negligible increase in equivalent noise. A particularly appealing explanation would be that the amblyopic eye lacks sensitive letter channels operating at high spatial frequencies, and, therefore, uses a less optimal channel. The following experiment was designed to evaluate this last-channel hypothesis.

Experiment 2: Critical band masking

To test the last-channel hypothesis, we used critical band masking to characterize the channel used to identify letters by our amblyopic observers.

Methods

We identify the channel by measuring threshold contrast energy (i.e., the integrated squared contrast) for letter identification as a function of the cut-off frequency of high- and low-pass noise. The methods here are essentially identical to those described by Solomon and Pelli (1994) with the simplified fitting procedure of Majaj et al. (2002). In the present experiments, the letters were again Bookman, and the root mean square noise contrast was 20% before filtering. Five of the amblyopes who participated in Experiment 1 were also tested in Experiment 2.

Results

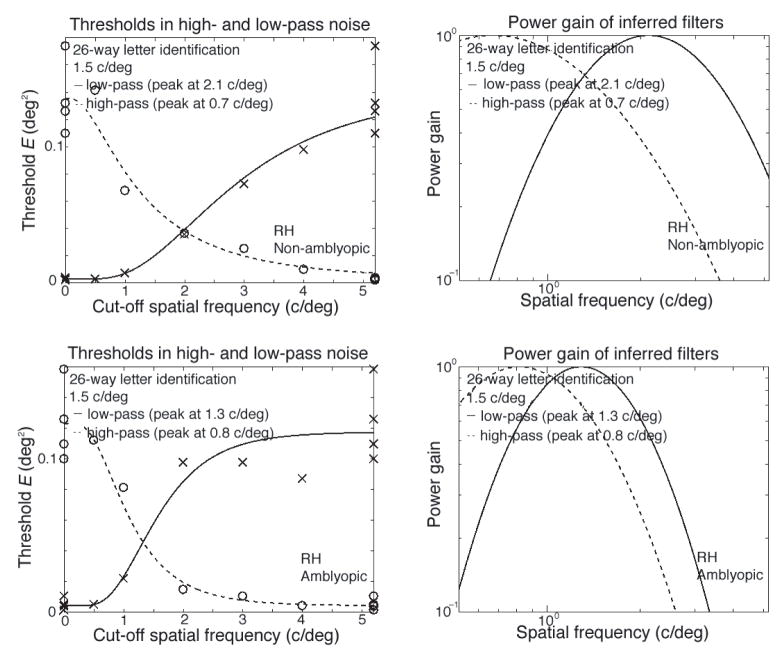
As an example, Figure 7 shows RH’s thresholds in noise (left) and the derived filters (right) for his non-amblyopic (top) and amblyopic eye (bottom) at one letter size (2 deg). Following Solomon and Pelli (1994), we use the geometric mean of the center frequencies of the inferred low- and high-pass filters to summarize the peak spatial frequency of the filter selected for letter identification. Our critical band masking results are summarized graphically in Figure 8A, which plots the estimated filter frequency (the geometric mean of the high- and low-pass estimates) against the predicted channel frequency 3/s^2/3 of the letter. The measured channel frequency follows the predicted channel frequency increases as nominal letter spatial frequency in both the non-amblyopic and amblyopic eyes (Figure 8A). This agrees with the relationship (gray line) found in normal observers (Majaj et al., 2002). While there are fairly large individual differences, the channel used by an amblyopic eye appears to have the same center frequency as that used in normal eyes.

Figure 7.

Examples of thresholds in noise (left), and the derived filters (right) are shown for each eye of a single amblyopic observer (RH), for a single letter size (2 deg). The top row is for the non-amblyopic eye; the bottom row is for the amblyopic eye.

Figure 8.

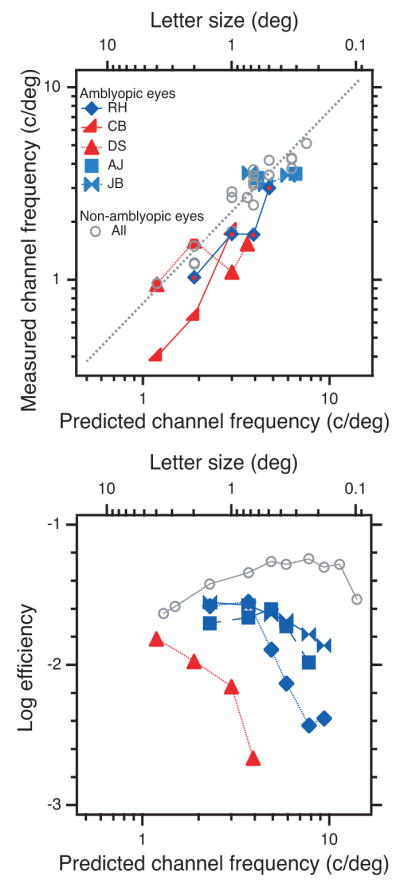
Channel frequency and efficiency. A. The measured channel frequency (geometric mean of the high- and low-pass estimates) as a function of letter size (top scale) and the predicted (i.e., normal) channel frequency f = 3/s^2/3(bottom scale). The measured channel frequency of non-amblyopic eyes (gray circles) agrees with the normal result (dotted line) of Majaj et al. (2002). B. Efficiency as a function of letter size. For RH and DS, efficiency drops precipitously while their channel frequency (in A) is still rising. For JB and AJ, efficiency is about half normal despite the fact that channel frequency is approximately normal. Thus the less-than-normal efficiency for small letters cannot be a direct result of using a channel with lower-than-normal frequency. This rejects the last-channel hypothesis.

The last-channel hypothesis supposes that when the letter spatial frequency is high the amblyopic and non-amblyopic eyes use different channels to analyze a letter of the same physical size, and amblyopic efficiency will fall precipitously. Such a shift in the spatial scale of analysis does occur when viewing a broadband line Vernier target with the amblyopic eye (Levi et al., 1994). However, the last-channel hypothesis cannot explain the present data. Figure 8 plots measured channel frequency (Figure 8A) and efficiency (Figure 8B) as a function of letter size. At first sight these graphs seem to support the last-channel hypothesis for the several observers whose channel frequency saturates and efficiency drops. However, closer examination rejects the hypothesis.

In normal eyes, channel frequency can be predicted from letter size f = 3/s^2/3, and this predicted (i.e., normal) channel frequency is displayed as the bottom scale of each graph. Figure 8A plots channel frequency. For non-amblyopic eyes (gray circles) the channel frequency is normal, within measurement error of the dotted line. For two of the five amblyopic eyes, RH and CB, the channel frequency is less than normal, but increases over the measured range, with no hint of saturating. For the other three, DS, AJ, and JB, the channel frequency does seem to hit a ceiling, as predicted by the last-channel hypothesis. However, the hypothesis predicts that the less-than-normal efficiency is a direct result of less-than-normal channel frequency. For RH and DS, efficiency (Figure 8B) drops precipitously while channel frequency (Figure 8A) continues to increase in parallel with the normal dotted line. For JB and AJ, efficiency is about half normal despite the fact that channel frequency is approximately normal. Thus, we cannot attribute the low efficiency for small letters of any of our observers to abnormally low channel frequency. Two recent studies have reached similar conclusions, for letters close to the acuity limit (Hess, Dakin, Tewfik, & Brown, 2001) and for letters up to about 20 times the acuity limit (Chung, Levi, Legge, & Tjan, 2002b).

General discussion

Delving into amblyopic letter identification, we passed through five levels of analysis. Each level explained a part, and passed on the unexplained remainder to the next level. The five steps are:

1. Measure threshold without noise (Figure 3A). As was already known, amblyopic and normal thresholds are equal for letters that are the same multiple of acuity. That is, by this measure, all observers are alike when scaled for acuity (Lawwill & Burian, 1966).

2. Measure threshold in noise (Figure 3B). Unlike 1., above, simple acuity scaling fails. Compute efficiency (Figure 4). Efficiency re normal does scale (i.e., is the same low-pass function of letter size re acuity) among amblyopes, though there is a difference between amblyopes and normals (Figure 4B).

3. Compute the equivalent input noise (Figure 5A). This exposes what is left unaccounted for in the no-noise thresholds after factoring out the efficiency loss. This graph is bewilderingly complicated: the curves tend to hook upward and splay out at high spatial frequencies.

4. Estimate the optical MTF (Figure 5B) and apply this contrast gain to the equivalent input noise at the display to estimate the equivalent input noise at the retina (Figure 5C). This straightens out the hooking and splaying, greatly simplifying the graph.

5. Fit the Raghavan and Pelli two-component noise model to the equivalent noise spectrum (Figure 5D). For each observer we estimate the amount of cortical noise and photon noise (Figure 6).

From this five-level analysis we learn that we may account for amblyopic thresholds by the following efficiency and noise model:

• Efficiency re normal of amblyopes is a low-pass function of letter size re acuity, 1 for large letters (> 4× acuity), dropping to 1/4 at 2× acuity, and approaching 1/16 at acuity.

• Cortical noise is roughly 1.4× normal (Figure 6B). This raises threshold contrast without noise by roughly $\sqrt{1.4}=1.2\times$ at all frequencies at which cortical noise dominates. Cortical noise dominates at low spatial frequencies; photon noise dominates at high spatial frequencies.

Our key finding, that the acuity loss represents a loss of efficiency, has important theoretical and clinical implications. Our results show that amblyopia is not restricted to the most sensitive neurons that are active at threshold on a blank background (Hess & Bradley, 1980), and narrow the range of possible models for amblyopia by ruling out all models that do not predict equal losses on a blank field and in noise. We tested one appealing model that correctly predicts equal losses, the last channel hypothesis. This model is rejected by our critical band experiments, which show that the loss of efficiency is not a consequence of a channel mismatch – amblyopes’ letter channels have normal spatial frequency tuning.

We did our experiments with natural pupils, and neglected to measure pupil size, so we struggled to estimate optical MTF and pupil area. Future experiments would be enhanced by using a 1-mm artificial pupil to eliminate our uncertainty about optical MTF and pupil area, if the experimenters can align the pinhole and natural pupil despite the unsteady fixation and low acuity of the amblyopic eye. As noted above, these optical effects affect our estimates of photon noise, introducing uncertainty into our transduction efficiency estimates, but have little or no effect on our estimates of efficiency or cortical noise. Thus our main conclusions are unaffected by any doubts about the pupil size and defocus.

Relation to previous work

Kersten et al. (1988) tested three amblyopes, measuring grating detection thresholds with and without dynamic 1-D noise. Their results are much more diverse than ours. Only one of their 3 amblyopes conforms to the pattern we found for all 16 of ours: reduced efficiency solely at high spatial frequencies. Their second amblyope had 1/30 normal efficiency at all frequencies tested (0.06 to 1 c/deg), and their third amblyope had normal efficiency at all frequencies tested (1 to 7 c/deg). Our testing conditions are different (letter identification vs. grating detection, 2-D vs. 1-D dynamic noise, rectangular vs. gaussian temporal signal envelope, and 45 vs. 380 cd/m² luminance), but, even so, we do not understand why their amblyopes should differ so much more than ours. Note that 2 of their 3 amblyopes had extremely poor acuity (1/60 and 2/60), well outside the range of our observers and the range of acuities that are typical of amblyopia (Ciuffreda et al., 1991).

In many respects, amblyopic vision is considered to be immature (e.g., see Levi & Carkeet, 1993), so it is informative to look at developmental studies. Three studies have estimated equivalent noise in infants (human and macaque: Brown, 1994; Kiorpes & Movshon, 1998; Skoczenski & Norcia, 1998), finding that infants have a much higher than adult level of equivalent noise, which falls as threshold contrast decreases with age. Threshold contrast on noisy backgrounds is also elevated in infants (Kiorpes & Movshon, 1998; Skoczenski & Norcia, 1998), suggesting that infants, like amblyopes, also have reduced efficiency. There are hints in the Kiorpes and Movshon data that, at high spatial frequencies, efficiency may be more important in limiting performance than equivalent noise, presaging what we report here.

Though our two-parameter account for amblyopia is progress, one would like to understand more precisely how to account for these changes at the level of the neural computation.

In the Raghavan and Pelli model, cortical noise, expressed as an equivalent input noise, is inversely proportional to the spike flux (i.e., the number of cortical spikes per second devoted to a square degree of visual field). Our estimate, varying among observers, of roughly 1.4× normal noise implies 1/1.4 the normal spike flux. Recording from V1 cortical cells in monkey with experimentally induced amblyopia, Kiorpes et al. (1998) report less than a factor of 2 reduction in the proportion of cells that respond to stimulation of the amblyopic eye: strabismic/normal 57–67%/84%, anisometropic/normal 40–59%/84%. That is in good agreement with what we report here. However, they note that severity of amblyopia is a continuum, that they excluded severe cases to be able to run all their tests, and that more severe deprivation leads to greater loss, whereas our estimates of cortical noise were practically independent of severity of amblyopia.

Our masking result is consistent with that of Chung et al. (2002b), using filtered letters. They found that the spatial-frequency characteristics of letter identification are similar between the amblyopic and the non-amblyopic eyes, differing only by a scale factor – the acuity – and concluded that the visual deficits in amblyopes do not have an impact on the spatial-frequency properties associated with letter identification.

All together, these results bear out the suggestion by Pelli and Farell (1999) that, having measured the no-noise threshold, it can be very helpful to also measure threshold in noise, even if one’s only goal is to explain the threshold without noise. The pristine acuity scaling of threshold without noise is awe inspiring, but reveals little to us about the underlying neural deficit. In particular, the no-noise thresholds (Figure 3C) suggest a continuum from normal through mild to severe amblyopia, indexed by acuity, but the in-noise thresholds show that all amblyopes are a tight group, distinct from normals (Figure 4B).

Clinical application

Clinically, amblyopia is diagnosed by exclusion (of uncorrected refractive error, disease, etc.) and circumstantial evidence (e.g., the presence of strabismus, anisometropia, etc.). It would be better to have a positive diagnostic test for amblyopia, and our results point to one approach to this (i.e., using letters in noise).

In noise, mild amblyopes with near normal acuity have twice normal threshold contrast at 9.4 c/deg. Thus, at least for the observers we tested, a pass/fail test at 33% contrast at 9.4 c/deg (i.e., a 0.18-deg letter) in noise would distinguish amblyopes from normals. This test is relatively immune to optical errors because both the signal and noise are similarly affected, leaving the signal-to-noise ratio unchanged. (This principle is also the basis of the grating-in-noise demonstration by Kersten et al., 1988, and the letters-in-noise chart of Pelli & Hoepner, 1989. [Chart]) That test, using one letter size at one contrast in noise, would quickly screen for amblyopia in a mostly normal population.

Within a clinical population, where one would like to distinguish amblyopia from all other visual impairments, our results suggest that it might be helpful to supplement ordinary acuity by a second acuity measured in noise (Figure 1). The stereotyped efficiency loss in Figure 4B suggests that the ratio of acuities with and without noise will vary little across amblyopes, yet be very different from normal. Optical defocus and most retinal diseases impair vision by raising equivalent noise, not reducing efficiency, so such patients will have the same acuity with and without noise.

Figure 1 is a new “Dual Acuity” eye chart – based on the results of this work – that is designed to be diagnostic of amblyopia. It measures threshold with and without noise to make inferences about internal processing. All letters on the chart are at the same contrast. The left half is essentially an ordinary acuity chart (Snellen, 1866). The right half is the same, but with the addition of white noise. The noise is made up of checks, and there are always 14.5 checks per letter size (typographic x-height). All the letters in noise are at the same signal-to-noise ratio. The ideal observer has the same error rate on all of them, independent of letter size. On this chart, most visual impairments (e.g., optical blur) will result in equal acuity with and without noise. Based on our results, we expect amblyopic eyes to have much poorer acuity (1 or 2 lines) when viewing targets with noise than without. Preliminary tests of six normal (no difference) and five amblyopic observers (all 1 or 2 lines worse with noise) suggest that this may be a useful approach.

Theory of Pelli-Levi Dual Acuity Chart

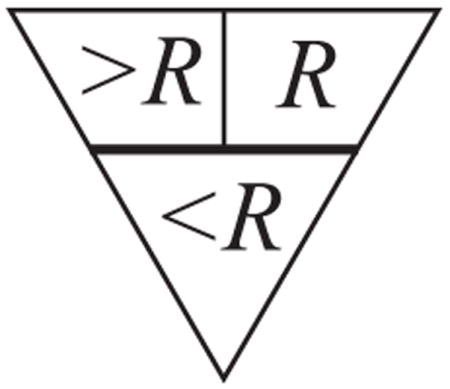
The goal is to detect observers with lower-than-normal efficiency for small letters. The right side of the chart is at a fixed signal-to-noise ratio E/N = R that was chosen to be just above normal threshold, just barely readable by an observer with normal efficiency. It is below threshold (i.e., unreadable) for an observer whose efficiency is much lower than normal. In general, the observer’s efficiency and equivalent noise are both letter-size-dependent. The chart noise is high at the top and drops from line to line. For optical reasons discussed in the text, the observer’s equivalent noise increases for the smallest letters. The observer’s equivalent noise adds to the chart, and at some line is equal, in effect, to the noise on the chart. That dividing line is the key to understanding this chart. The triangular diagram above shows this horizontal dividing line and specifies the chart’s effective signal-to-noise ratio above and below it. Our analysis is all relative to the location of this dividing line, whose location on the chart depends on the observer and viewing distance, but the observer’s final score does not depend on where the dividing line is because, in the end, we consider only the difference between left and right acuities. In the upper part of the chart, above the dividing line, the chart noise is absent on the left and dominates on the right, producing an effective signal-to-noise ratio of R on the right, and greater than R on the left; in the lower part, below that line, the observer’s equivalent noise dominates both left and right sides, producing practically the same effective signal-to-noise ratio, less than R, on both sides. Thus the left and right sides are functionally different in the upper part and functionally identical in the lower part. One measures acuity by finding the smallest letter size at which the letters can be read (i.e., at which the chart’s effective signal-to-noise ratio is above the observer’s threshold). Any observer with normal efficiency for large letters will be able to read the top line, and thus will have a measurable acuity on both sides of the chart. Observers with normal efficiency for small letters will progress further down in noise (right side) than less efficient observers. If the in-noise acuity is below the line, then the no-noise acuity will be the same, because there’s effectively the same noise level on left and right. If the observer’s in-noise (right side) acuity is above the dividing line, then the no-noise (left side) acuity will be better, because there is less noise on the left. Thus the chart noise (right side) worsens the acuity of observers with low efficiency for small letters, but has no effect on the acuity of observers with normal efficiency for small letters. This acuity difference, occurring only for observers with low efficiency for small letters, is proposed as a diagnostic test for amblyopia. The acuity difference is relatively immune to optical blur, as increasing the blur simply increases the equivalent noise, shifting the dividing line up, with little effect on the left-right acuity difference.

The Dual-Acuity Chart (Figure 1) promises to provide quick screening for amblyopia. It is available, free, at http://psych.nyu.edu/pelli/dualacuity/. By design, it is relatively immune to the typical variations in printing.

Conclusion

Our measurements and analysis show that the acuity deficit in amblyopia is a substantial efficiency loss at high spatial frequencies, accompanied by a negligible increase in cortical noise at low spatial frequencies. In principle, a loss of sensitivity could be due to either (or both) loss of efficiency or increase in equivalent noise (e.g., see Pelli & Farell, 1999). Showing that it is an efficiency loss greatly restricts the possible explanations. Some explanations of amblyopic acuity loss would predict an effect only on a blank field, whereas others would predict the same loss on blank and noise fields. Our results rule out the former, and strongly support the latter. The high-frequency efficiency loss suggests that testing acuity in noise may provide a sensitive diagnostic test for amblyopia. A suitable test chart is now available.

In normals, identification of letters at each size is mediated by a corresponding spatial frequency channel. We supposed that amblyopes might have lost their highest frequency channels, and that the measured drop in efficiency represented the poorer performance of their last channel, as it struggles to process letters smaller than the size it would normally identify. We tested the last-channel hypothesis directly, using critical band masking to measure channel tuning for each letter size, and found near-normal results. Thus, our results rule out one class of explanation for the efficiency loss and show that the amblyopes’ letter channels have normal spatial frequency tuning, yet have low efficiency for near-acuity letters for as yet unknown reasons.