An anisotropic scale-invariant unstructured mesh generator suitable for volumetric imaging data

Abstract

We present a boundary-fitted, scale-invariant unstructured tetrahedral mesh generation algorithm that enables registration of element size to local feature size. Given an input triangulated surface mesh, a feature size field is determined by casting rays normal to the surface and into the geometry and then performing gradient-limiting operations to enforce continuity of the resulting field. Surface mesh density is adjusted to be proportional to the feature size field and then a layered anisotropic volume mesh is generated. This mesh is “scale-invariant” in that roughly the same number of layers of mesh exist in mesh cross-sections, between a minimum scale size L_min and a maximum scale size L_max. We illustrate how this field can be used to produce quality grids for computational fluid dynamics based simulations of challenging, topologically complex biological surfaces derived from magnetic resonance images. The algorithm is implemented in the Pacific Northwest National Laboratory (PNNL) version of the Los Alamos grid toolbox LaGriT[14]. Research funded by the National Heart and Blood Institute Award 1RO1HL073598-01A1.

1 Introduction

Computational continuum physics is fast becoming an important part of biomedical research. Typically, the geometries for biomedical problems are derived from medical imaging modalities such as magnetic resonance imaging (MRI), and are geometrically complex compared to many engineering problems. Efficient unstructured mesh generation of these geometries is especially challenging because no ‘true’ reference geometry exists, due to the finite resolution of the imaging data. In this presentation, we propose a novel approach to this problem, based on a fast estimation of the local feature size. Due to the inherent uncertainty in the imaging-derived geometries, we formally restrict our attention to problems wherein there is a definite lower bound on the local feature size (i.e., on the order of a voxel) and to situations where, given that uncertainty, we have the latitude to alter the envelope of the prescribed surface mesh (i.e., on order a fraction of a voxel) to make the mesh suitable for computational fluid dynamics (CFD) or other numerical simulations.

Excellent isotropic unstructured tetrahedral grid generation algorithms exist for creating finite-element or finite-volume grids from closed triangulated manifolds [3,17]. Isotropic algorithms, i.e. approaches that attempt to construct tetrahedral elements with nearly equal internal angles and approximately equal edge lengths, may be well suited to a large class of biomedical problems. However, for certain classes of problems such as computational fluid dynamics, isotropic elements may be neither necessary nor particularly appropriate. In boundary layer regions of the flow field, for example, derivatives normal to the wall can be much greater than they are parallel to the flow. Anisotropic grids can better resolve these features of the flow [11,22] by concentrating computational grid at the wall while keeping the overall computational cost of the problem tractable. That efficiency applies to problems beyond CFD as well. An excellent reference on anisotropic mesh generation is [9].

Achieving a pre-determined number of elements or a minimum number of elements through the smallest features of a geometry, is important for correctly resolving gradients [8] or to capture physical variations such as laminae. An example of the latter is the musculature of the heart which has three distinct layers of fiber orientations. A layered anisotropic approach — whether advancing front or Delaunay — has the advantages of creating elements that are mostly orthogonal to the wall while essentially decoupling the grid density in the normal and tangential directions. That decoupling raises the issue of what criterion to adopt for the tangential density. With surfaces derived from imaging data, the organization and density of the original surface triangles are functions of the resolution of the digital data rather than the numerical problem to be solved. Simply generating a volume grid from the original surface spacing could result in grossly under-resolving the computed field where the surface density is close to that of the local feature size or conversely over-resolving the computed field where the surface density is much finer than that of the local feature size. These observations lead to a consideration of the local feature size as an important criterion for sizing and gradation control of the surface that is complimentary to criteria that attempt to preserve surface features, topology and curvature.

In large part, previous attempts to base grid density on a concept of local feature size or scale have either been based on the definition of “throw-away” background grids onto which a local feature size field was computed [20,31,29,21], or have been based on point-insertion techniques to locally refine — but not derefine — coarse tetrahedral grids [16], or have been based on advancing fronts [10,20]. An earlier related approach was based on Dijkstra’s algorithm and element subdivison [8]. As an example of an approach based on a pre-computed feature size field, Persson [21] recently defined a local feature size field on a background grid. The feature field was defined locally as the sum of the distance of a given point to the boundary and to the medial axis. Element sizes were determined by gradient-limiting competing local element size fields based on the feature field and the curvature field. The disadvantages of this and related approaches are twofold. First, the medial axis of a triangulated manifold is inherently unstable in the sense that small perturbations in the surface triangulation can lead to large perturbations in the medial axis and thus also in the definition of local feature size. Second, the construction and computation of a feature size field on a “throw-away” background grid is computationally expensive.

In this paper, we define a feature size field on an input triangulated surface mesh without a background grid and without referencing the medial axis. Thus, determination of the feature size field is not only computationally efficient, but also robust in the sense that it is continuous and does not change unreasonably under perturbation of the surface mesh. Field values at a point on the surface are generated by shooting a ray from the point in the direction of an inwards “synthetic” normal that is well-defined even where the surface is not smooth and measuring the distance until the surface is re-intersected by the ray. We then perform a gradient-limiting operation on the field to enforce continuity. Layered, conforming, anisotropic volume mesh generation is accomplished directly with this surface field. Prior to volume mesh generation, we modify the surface mesh so that edge lengths are proportional to the feature size field, with the constraint that refinement/de-refinement preserves topology and geometry. Surface modification is iterated with a volume-conserving smoothing, with the result that surface triangles are well-shaped, well-organized and graded. Following surface modification, layers of points are strategically placed along the rays normal to the surface and connected into orthogonal layers with a Delaunay algorithm.

Because we employ Delaunay meshing, the degree of anisotropy is effectively limited by the consideration that sampling frequency on the boundary must be greater than some multiple of the local feature size in order for the topology of the input surface to be known rigorously to be recoverable from the Delaunay volume mesh [1]. We note, however, that in practice surface point densities may be lower than the rigorous result and still lead to successful boundary recovery. Point densities in [2] as well as in this work are significantly lower. These point densities translate into modest degrees of anisotropy that can still bring significant savings in terms of overall element count.

We show the results of our algorithm on three complex geometries derived from medical imaging data: a rat nose phantom (genus 1), a rat lung (genus 0)and a human heart (genus 12). The resulting meshes are deemed scale-invariant in that it is possible to obtain a desired number of layers across cross-sections in the domain, independent of scale. For each of these cases, we give aspect-ratio statistics that indicate the high quality of tetrahedra that the approach is able to produce.

2 Approach

Let S be an oriented closed unstructured surface mesh consisting of planar triangles. It is desired that we produce a volume mesh V consisting of tetrahedra that is bounded by S. Herein we focus on a surface derived from imaging data. Thus, S is a volumetric constraint or isosurface produced by the Marching Cubes algorithm [15,19], rather than a surface of known geometry. As such, it has finite resolution and a minimum resolveable feature size of a single voxel. In order to produce a mesh that is useful for numerical analysis, we perform the operations of smoothing, refinement and de-refinement to S, subject to that volumetric constraint by limiting perturbations to S to a small fraction of a voxel. In practice, this assures that the geometry is unchanged within experimental uncertainty and that the topology is respected.

We begin this remeshing of the isosurface with several iterations of volume-conserving smoothing ([13] Algorithm 4) which sweeps through nodes of the surface mesh, and for each node performs a Laplacian smoothing followed by node repositioning to exactly maintain the volume enclosed by the surface mesh. In Figure 1, we see both the the jagged features of a Marching-Cubes-generated isosurface derived from magnetic-resonance data (A,B), followed by the result of applying volume-conserving smoothing (C,D). The volume of the smoothed object has been conserved to round-off error and the motion of the surface is a fraction of a voxel.

Fig. 1.

Marching Cubes derived isosurface, before and after volume-conserving smoothing.

We allow S to consist of one large enclosing closed surface S₀ and possibly any number S₁, … S_n of closed surface “holes” inside of S₀. Any of the surfaces S₀, S₁, … S_n may have “handles” (have nonzero genus). In the biomedical applications of interest to us, we desire each cross section of V to have a certain number M of layers of elements across. (See Figure 2.) We thus desire a “scale-invariant” meshing algorithm where a cross-section with diameter d will be filled by M layers of mesh, independent of d, as long as d is within a range of feature sizes that is bracketed away from zero:

$$0<L_{\text{min}}\le d\le L_{\text{max}}.$$ (1)

Fig. 2.

M layers across cross-sections.

If d < L_min, we allow a mesh cross-section to receive less than M layers; if d > L_max, we allow a mesh cross-section to receive more than M layers. (1) thus defines our “zone of invariance”. We assume L_min > 0, because the resolution of our data is one voxel; L_min is usually a specified fraction of a voxel width.

We now make (1) more precise, by specify how d, the “feature size” is to be defined and evaluated.

2.1 Definition of Local Diameter

Usually the feature size at a point x on a surface S is defined as the distance from x to the closest point of the medial axis of the volume V bounded by S [1,21]. Here the medial axis is the set of points in V defined by

$$\mathbf{y}\in \text{medial axis of}V\iff \mathbf{y}\text{has more than one closest point}\mathbf{z}\in S.$$ (2)

Figure 3 shows the pitfalls of this definition. If S is the surface of a sphere, the medial axis of V, the solid sphere bounded by S, is the single point at the center of V. The feature size at any point x ∈ S would thus be equal to the radius of the sphere. However, if the surface S is instead represented as a triangular faceted surface (e.g., make S the largest icosahedron that fits inside the original sphere), then the medial axis of the solid bounded by S consists of points on the planes that bisect the solid angles between adjacent pairs of facets. Then points x on S will be deemed to have feature sizes ranging from zero (if x is on a boundary edge of S) to r_ins, where r_ins is the largest inscribed radius of any facet in S. Thus, the mere act of discretizing the geometry by representation by piecewise linear facets has caused a violent change in the definition of “feature size”.

Fig. 3.

Difficulty with medial-axis based definition of feature size. A small alteration in a figure changes a one-point medial axis (center of circle on left figure) to a complex medial axis (angle bisectors on right figure). This causes a great change in feature size if feature size at x is defined to be distance from x to the nearest point on the medial axis (y).

In contrast, we wish to define a feature size field that is more robust with respect to perturbations of the geometry and which does not require construction of the medial axis. Our feature size will be roughly twice that computed using the previous definition, in the case that the geometry is smooth and free of low amplitude undulations. In addition, it will be robust to perturbations.

For any point x ∈ S, we define the “raw feature size” or “local diameter” D(x) as the length of the line segment formed by shooting a ray from x in the direction of n̂(x), the inward normal at x, and truncating the ray at the first new intersection with S. That is

$$D(\mathbf{x})\equiv \text{min}\{\mathrm{\lambda }>0|\mathbf{x}+\mathrm{\lambda }\widehat{\mathbf{n}}(\mathbf{x})\in S\}.$$ (3)

See Figure 4(a). In the case that S is differentiable at x, and thus the classical normal exists, we have that points on the segment x + λn̂(x) for very small λ > 0 have a single closest point on the boundary, namely x. When $\mathrm{\lambda }=\frac{D(\mathbf{x})}{2}$, x + λn̂(x) has equal distance to x and the boundary point x + D(x)n̂(x). If the ray does not intersect the medial axis at a point before $\mathbf{x}+\frac{D(\mathbf{x})}{2}\widehat{\mathbf{n}}(\mathbf{x})$, we would have to conclude that $\mathbf{x}+\frac{D(\mathbf{x})}{2}\widehat{\mathbf{n}}(\mathbf{x})$ is on the medial axis. We thus conclude that the distance from x to the medial axis is bounded above by $\frac{D(\mathbf{x})}{2}$.

Fig. 4.

(a) Definition of “local diameter” D(x) is length to first re-intersection with surface of a ray normally cast inwards from x. (b) Gradient-limiting of D(x) field yields d(x) field which removes effect of “lucky rays” that travel far further than twice the distance to the medial axis.

In the case that S is differentiable at x, the classical normal exists and so the choice of n̂ is unambiguous. The usual case, however, is that S is piecewise linear, and that in fact x is a vertex where the normal is not classically defined. In this case, we define a “synthetic normal” at x as follows. Consider the neighborhood

$${\mathcal{N}}_{ϵ}(\mathbf{x})\equiv B_{ϵ}(\mathbf{x})\cap S,$$ (4)

where B_ϵ(x) is the solid ball of radius ϵ centered at x. We note that in the case that x is a vertex in the piecewise linear geometry of S, that the classical normal is defined everywhere in 𝒩_ϵ(x) except for a set of surface measure zero. That is because 𝒩_ϵ(x) is a piece of surface near x, while the only points y ϵ S that the classical normal n̂ (y) is not defined on are those points that reside on a set of surface edges incident upon x. With this in mind we define the “synthetic” normal as

$${\widehat{\mathbf{n}}}_{\text{synth}}(\mathbf{x})\equiv \begin{array}{c}\text{lim}\\ ϵ\to 0\end{array}\frac{{\int }_{\mathbf{y}\in {\mathcal{N}}_{ϵ}(\mathbf{x})}\widehat{\mathbf{n}}(\mathbf{y})dS}{\Vert {\int }_{\mathbf{y}\in {\mathcal{N}}_{ϵ}(\mathbf{x})}\widehat{\mathbf{n}}(\mathbf{y})dS\Vert }.$$ (5)

The integral in the numerator of the right-hand side is well-defined (since the integrand is defined almost everywhere) and indeed the limit exists when the patches of surface incident upon x are smooth. We note trivially that if the normal is classically defined at x, then n̂_synth is equal to the classical normal and if x is a vertex of a piecewise linear surface, then

$${\widehat{\mathbf{n}}}_{\text{synth}}=\frac{{\displaystyle {\mathrm{\sum }}_i}{\theta }_i{\widehat{\mathbf{n}}}_i}{\parallel {\displaystyle {\mathrm{\sum }}_i}{\theta }_i{\widehat{\mathbf{n}}}_i\parallel },$$ (6)

where the sum is over the triangles T_i sharing x, the n̂_i are the normals of the T_i, and θ_i are the vertex angles at x for each of the T_i. We can thus say that for piecewise linear surfaces, the “synthetic normal” is an “angle-weighted” normal [27]. (Figure 5.) Since (5) indicates the synthetic normal is actually an intrinsic property of the surface independent of triangulation, we have that it won’t change much if surface deformation due to refinement/derefinement is sufficiently small. Although this normal is very robust [4], we doublecheck n̂_synth actually points “into” the geometry by checking it makes a positive dot product with all the n̂_i. (In the highly unlikely case it does not, a value D(x) = L_max is assigned which will be reduced to a value comparable with the feature size at neighboring nodes by the gradient-limiting operation to be described.)

Fig. 5.

The synthetic normal at a vertex i of a piecewise linear surface is the angle-weighted normal.

So, choosing n̂ to be the synthetic normal, the ray proceeding from x in the direction n̂_synth will again intersect S at least once (since S is assumed closed) and D(x) is well-defined.

Note: We also perform an “outwards” interrogation of the geometry by computing another D(x) at x using (3) using n̂ = −n̂_synth. This outwards value (which we call D_out(x)) is only finite in some areas at most (e.g., where S is concave) and is used to ensure the topology of the final volume mesh agrees with the topology of the input surface mesh S in those regions. Use of D_out(x) is discussed in Section 2.3.

Having defined the raw feature size by interrogation of the geometry (3), we then enforce the restriction (1) by performing ‘max’ and ‘min’ operations with L_min and L_max, respectively. To be clear, we restate that L_min and L_max are user parameters, bounded below by a fraction of a voxel and bounded above by the largest dimension of the geometry. The last step in computing a local feature size is now to modify D(x) so that we obtain a smooth function of x and S — so that feature size won’t change much if the surface point x or if the surface S itself is perturbed slightly. This is accomplished by performing a gradient-limiting procedure similar to that in [21].

In [21], the author defines a feature size function over a surface mesh, extends the definition to the entire volume enclosed by the surface, and then performs gradient-limiting on the function. Given a desired bound G on the gradient of a feature size function d defined on a volume V, d is limited by the following update:

$$d(\mathbf{x})\leftarrow \underset{\mathbf{y}}{\text{min}}(d(\mathbf{y})+G\cdot \text{dist}(\mathbf{x},\mathbf{y})).$$ (7)

Here dist (x, y) = ‖x − y‖ is the Euclidean distance in IR³. The update (7) is performed repeatedly on a discrete Cartesian grid until convergence occurs. Clearly the gradient-limited d is less than or equal to the original non-gradient-limited d and it obeys

$$|d(\mathbf{x})-d(\mathbf{y})|\le G\parallel \mathbf{x}-\mathbf{y}\parallel \text{,}$$ (8)

which means that d is Lipschitz continuous, with Lipschitz constant G. Since we are on a discrete mesh, this essentially amounts to delivering the desired bound ‖∇d‖ ≤ G.

In contrast, we perform the gradient-limiting operation (7) on d(x) which is initialized with the values of D(x) on the surface and is not extended to the volume. Instead dist (x, y) is to be interpreted as the distance between x and y measured on the surface of S — the geodesic distance. Our algorithm (Algorithm 1) is performed on the unstructured surface mesh, rather than a Cartesian volume mesh. The algorithm involves placing directed surface edges $\overrightarrow{{\mathbf{x}}_1{\mathbf{x}}_2}$ of S into a priority queue [5] ranked by

$$d({\mathbf{x}}_1)-(d({\mathbf{x}}_2)+G\parallel {\mathbf{x}}_1-{\mathbf{x}}_2\parallel ),$$

which is how much the gradient over the directed edge of d violates the gradient limit. (Only directed edges for which this quantity is positive are placed in the queue.) The directed edge is then relaxed to satisfy the gradient limit and then all directed edges in the neighborhood are added, deleted, or re-ranked in the priority queue as necessary. The process continues until the queue is empty and hence the field d(x) is gradient-limited.

One question is what is a good value for G? In fact, it can be argued that a natural bound on G is O(1). That is because our “feature size” is the length of a normal ray traversing a geometry, and for smooth geometries this is essentially double the distance from the boundary point x to the medial axis — and a natural bound on the gradient of this distance is 1. This latter assertion can be seen as follows. Let d_MA(x) be the distance from x ∈ S to the closest point on the medial axis of V. That is

$$d_{\text{MA}}(\mathbf{x})=\parallel \mathbf{x}-{\mathbf{P}}_{\text{MA}}(\mathbf{x})\parallel ,$$ (9)

where P_MA(x) is the closest point on the medial axis to x. Let Δ be an arbitrary change in x such that x + Δ is also on S. Then

$$\begin{array}{cc}{d}_{\text{MA}}(\mathbf{x}+\mathrm{\Delta })& =\parallel \mathbf{x}+\mathrm{\Delta }-{\mathbf{P}}_{\text{MA}}(\mathbf{x}+\mathrm{\Delta })\parallel \\ & \le \parallel \mathbf{x}+\mathrm{\Delta }-{\mathbf{P}}_{\text{MA}}(\mathbf{x})\parallel \\ & \le d_{\text{MA}}(\mathbf{x})+\parallel \mathrm{\Delta }\parallel .\end{array}$$

Similarly,

$$d_{\text{MA}}(\mathbf{x})\le d_{\text{MA}}(\mathbf{x}+\mathrm{\Delta })+\parallel \mathrm{\Delta }\parallel .$$

So

$$|d_{\text{MA}}(\mathbf{x}+\mathrm{\Delta })-d_{\text{MA}}(\mathbf{x})|\le 1\cdot \parallel \mathrm{\Delta }\parallel .$$

So d_MA (x) is Lipschitz continuous with Lipschitz constant no larger than 1. It is quite easy to construct a geometry where the Lipschitz constant of d_MA (x) is arbitrarily close to 1. Thus, d_MA (x) is Lipschitz continuous over all geometries with uniform Lipschitz constant 1. Since our function d(x), the “local diameter” at x typically behaves like 2d_MA(x) (in the case of smooth geometries), we have that “2” would be a natural Lipschitz constant to enforce for d(x). In practice, we have found increasing the amount of gradient-limiting further is desirable for producing tighter, more disciplined layers of volume mesh parallel to the surface mesh in the volume mesh generation phase. For our runs, we have used G = 0.85 which is a value that has worked well over all geometries.

Our resulting gradient-limited feature size or “local diameter” function d(x) defined over surfaces is now a continuous function of x. (Figure 4(b).) If S is perturbed slightly, a ray shot from a vertex x_i on the surface might transition from being clipped to not being clipped by an interceding piece of geometry (as in Figure 6), but the fact that d(x) is gradient-limited will limit the jump in d(x_i) to being bounded by G‖x_i − x_j‖ where x_j is a neighbor of x_i that already “sees” the interceding geometry. (Note: this argument breaks down if x_i possesses no neighbor x_j that sees the interceding geometry, but this is unlikely if the surface reasonably resolves the geometry. In the following sections we show how a good discretization of S by a surface grid is found and then a final “stable” d(x) can be computed on this improved surface discretization if necessary.) Since the jump in d(x) is usually bounded by a small multiple of the surface discretization edge length, it is reasonable to say that d(x) behaves “smoothly” with respect to perturbations in the geometry S.

Fig. 6.

Without gradient-limiting D(x_i) can discontinuously jump with a small perturbation in the surface S due to borderline clipping of local diameter ray. With gradient-limiting, this jump in d(x_i) is limited to G‖x_i − x_j‖, where x_j is a neighbor whose local diameter ray is robustly clipped.

Although it would appear that it is a daunting task to construct D(x) by shooting rays from all surface vertices and detecting all subsequent first intersections of these rays with S, it is in fact a rapid process. For this we employ an axis-aligned bounding box (AABB) tree [25,12] that contains at its leaf nodes bounding boxes for each of the N_surf triangles discretizing S. This is a balanced binary tree where each node is assigned the smallest Cartesian axis-aligned bounding box that contains the bounding boxes of its two children; this structure can be constructed in O(N_surf log N_surf) time. The root node is thus assigned a bounding box for the whole geometry. When we seek intersections of a ray with S, we thus intersect the ray with the root bounding box and refine the query by asking which of the child boxes intersect the ray. We then query the child boxes of only those boxes that are found to intersect the ray. (The ray-box intersection test is quickly done.) We continue on in this way until in O(log N_surf) operations we obtain the leaf boxes of all surface triangles that could possibly intersect the ray. We then simply compute the exact distance along the ray with the closest of the candidate triangles so found to intersect the ray. The operation for computing D(x) thus has complexity O(N_surf log N_surf).

Algorithm 1: Processing of Raw Local Diameter Field

[Process local diameter field to be within limits and be gradient-limited so that it is an acceptable feature size field]

[Copy raw local diameter field to d]

For each surface node i

• $$d({\mathbf{x}}_i)\leftarrow D({\mathbf{x}}_i)$$

[Force d(x) to lie between L_min and L_max]

For each surface node i

• $$d({\mathbf{x}}_i)\leftarrow \text{min}(L_{\text{max}},d({\mathbf{x}}_i))$$
• $$d({\mathbf{x}}_i)\leftarrow \text{max}(L_{\text{min}},d({\mathbf{x}}_i))$$

[Reduce d(x) in tight concave areas (See Section 2.3)]

For each surface node i

• $$d({\mathbf{x}}_i)\leftarrow \text{min}\left(d({\mathbf{x}}_i),2\frac{M}{K}{D}_{\text{out}}({\mathbf{x}}_i)\right)$$

[Decrease d(x) to ensure gradient of d along edges is less than G]

For each node i

• For each node neighbor j

  • excess(i, j) ← d(x_i) − (d(x_j) + G‖x_i − x_j‖)
    If excess(i, j) > 0 Then
• [Priority queue P will contain directed edges with positive excess values]

  • Place directed edge $\overrightarrow{{\mathbf{x}}_i{\mathbf{x}}_j}$ in priority queue P

While P nonempty do

• Pop $\overrightarrow{{\mathbf{x}}_i{\mathbf{x}}_j}$ with maximal excess(i, j) from P

• [Decrease d(x_i) to conform to gradient limit]

• d(x_i) ← (d(x_j) + G‖x_i − x_j‖)

• For all directed edges $\overrightarrow{{\mathbf{x}}_i{\mathbf{x}}_k}$ emanating from i

• Recompute excess(i, k) ← d(x_i) − (d(x_k) + G‖x_i − x_k‖)

• Add, delete, or rerank $\overrightarrow{{\mathbf{x}}_i{\mathbf{x}}_k}$ in P as appropriate

• For all directed edges $\overrightarrow{{\mathbf{x}}_k{\mathbf{x}}_i}$ incident on i

• Recompute excess(k, i) ← d(x_k) − (d(x_i) + G‖x_i − x_k‖)

• Add, delete, or rerank $\overrightarrow{{\mathbf{x}}_k{\mathbf{x}}_i}$ in P as appropriate

2.2 Generation of a surface mesh discretization commensurate with d(x)

Let K be the desired anisotropy of layers that we wish to generate near the boundary of S. That is, we wish the average surface triangle edge length at a point x on S to be K times the normal thickness of tetrahedra in layers parallel to the surface. At the same time, we wish to establish M layers across the cross-section of the geometry. The resolution of these two requirements is to make the edge length of the discretization of S at x be proportional to the feature size d(x) at x. Indeed, if we generate M layers of mesh across the “local diameter” d(x), and the surface edge length in the neighborhood of x is $\frac{K}{M}d(\mathbf{x})$, then the ratio of the base triangle edge length to the altitude of tetrahedra generated at x will be $\frac{K}{M}d(\mathbf{x})/\frac{1}{M}d(\mathbf{x})=K$ (assuming equal spacing of the M layers). This means that the tetrahedra generated on the surface layers will have constant anisotropy K independent of x.

Surface modification as a function of local diameter consists of (1) Rivara edge bisection operations to establish a maximum edge length $\frac{K}{M}d(\mathbf{x})$ over the whole surface mesh, (2) node merge operations, and (3) edge swap operations.

In regions where the edges are longer than $\frac{K}{M}d(\mathbf{x})$, we bisect edges (see Figure 7), doubling the number of triangles incident on the refined edge. We use the principle due to Rivara [23] that restricts edge bisection to those edges that are the longest edges in their neighborhood which consists of all of the edges in all the elements that share the edge in question. If an edge is not the longest edge in its neighborhood, we consider refining the edge that is the longest edge in the neighborhood as a precondition for refining the desired edge. Continuing recursively in this fashion, a “Rivara” chain is constructed which ends in a terminal edge that is in fact the longest edge in its neighborhood and which can be bisected. Continued attempts to refine an edge will result in the refinement of a certain number of terminal edges until the original edge is eventually refined. The effect of the refinement of the additional edges is a stable refinement that tends not to degrade element quality. The edge bisection algorithm is given in Algorithm 2. bisection_length as stated in the algorithm is $\frac{K}{M}d(\mathbf{x})$.

Fig. 7.

Refinement of edge. (a) Two triangles that share an edge. (b) Two triangles have become four after bisection of edge.

The node merging algorithm is given in Algorithm 3. We sweep through the mesh, considering nodes i and whether it is advisable to merge them into their neighbors j. (See Figure 8.) If a merge x_i → x_j would take place, the triangles {T_k} containing node i would be replaced by a new set of triangles $\{T_k^{\text{new}}\}$ all containing node j. After a sufficient number of passes, the surface mesh will be derefined where needed. Nodes are attempted to be merged if edge lengths are less than one-half the local target edge length in the neighborhood of node i. That is, merge_length is set to $\frac{K}{2M}d({\mathbf{x}}_i)$. Setting merge_length equal to a fraction significantly less than the desired length prevents “thrashing” where node merge and edge bisection operations pointlessly alternate in the same region. This has the effect that observed anisotropies of elements will actually be in a range between $\frac{K}{2}$ and K. (Layer thickness $\frac{d(\mathbf{x})}{M}$ will however vary smoothly as d(x) is a smooth function of x.)

Fig. 8.

Merging of node i at x_i to neighboring node j at x_j.

The “damage” of the merge x_i → x_j is a measure of the deformation of the surface caused by the merge. Our estimate of surface deformation (the “damage” function) is given in the Appendix. If the damage of a merge is anticipated to cause a damage exceeding one-thirtieth of the bisection length $(\frac{K}{30M}d({\mathbf{x}}_i))$, the damage is considered unacceptable and the merge operation x_i → x_j is rejected. For a given node i, there may be one or more neighboring nodes j that produce an acceptable damage estimate, even if some neighboring nodes j would result in unacceptable damage. The new triangulation $T_k^{\text{new}}$ produced by an x_i → x_j merge depends on which neighbor j is chosen and we only accept a new triangulation if the minimum inscribed radius in $\{T_k^{\text{new}}\}$ would be at least one-half as big as the minimum inscribed radius of the original triangulation {T_k}. (If the minimum inscribed radius of the original triangulation is especially small, this requirement is tightened further.)

Note that our node merge operation differs from the standard procedure presented in [6]. The standard algorithm greedily contracts edges in ascending order of damage on a priority queue. Here we aspire for a target minimum edge length $\frac{K}{2M}d({\mathbf{x}}_i)$ and greedily contract the shortest edges less than this length, stopping only if the damage caused by the single contraction or the resulting grid quality is unacceptable.

Edge swap operations (Figure 9) attempt to maximize the minimum vertex angle of a candidate pair of adjacent surface triangles. We repeatedly sweep through candidates in the mesh and perform swaps if the minimum of the six vertex angles is increased by swapping their common edge, provided that the damage to the surface by such a swap is deemed acceptable. (As in the case of node merging, the damage should not exceed $(\frac{K}{30M}d({\mathbf{x}}_i))$ and the damage is similarly estimated.)

Fig. 9.

Surface edge swap: swapping mutual edge of two adjacent surface triangles.

Refinement and de-refinement of the surface alternates node merging with edge swapping until neither operation changes the mesh, and then ends with edge refinement. This modification of the surface is repeatedly called and alternated with volume-conserving smoothing.

After several such cyles, the surface mesh has been suitably processed so that the edge length at a node x_i on the surface is roughly $\frac{K}{M}d({\mathbf{x}}_i)$.

Algorithm 2: Edge_Bisection

[Algorithm refines mesh by bisecting edges exceeding a variable node-based bisection length tolerance]

Find set of edges $E=\{e=\overline{{\mathbf{x}}_1{\mathbf{x}}_2}|$ length(e) > min(bisection_length(x₁), bisection_length(x₂))}

While E ≠ ∅ do

• Sort E in decreasing order of (Euclidean) length

• For each e ∈ E do

  • Refine terminal member of Rivara chain spawned by e

• Recompute E

Algorithm 3: Node Merging

[Algorithm derefines mesh by merging nodes to neighboring nodes where appropriate]

Do until nothing changes

• For each node i

  • Order node neighbors j by increasing distance from i
    For each neigbor j of i

    • If ‖x_i − x_j‖ < merge_length Then

      • If damage(x_i → x_j) < toldamage Then

        • If minimum inscribed radius $(\{T_k^{\text{new}}\})\ge \frac{1}{2}$. minimum inscribed radius({T_k}) Then merge(x_i → x_j) break out of inner For loop

Algorithm 4: Offset Points

[Algorithm computes layers of points in volume V offset from the surface points of S]

For each node i ∈ S

• [Surface points become ‘layer 0’ volume points]

• $${\mathbf{x}}_i^0\leftarrow {\mathbf{x}}_i$$

• dist ← 0

• [Add points along normal ray from surface out to half raw local diameter. For uniform spacing, fractional distance between points ${\mathrm{\lambda }}_m=\frac{1}{M}$, and approximately $\frac{M}{2}$ points will be layed down]

• Do while m = 1, 2, …

  • If $m\le \lfloor \frac{M}{2}\rfloor )$ then

    • $$\text{dist}\leftarrow \text{dist}+{\mathrm{\lambda }}_{m}d({\mathbf{x}}_i)$$
  • Else

    • $$\text{dist}\leftarrow \text{dist}+\frac{1}{M}\text{min}(D({\mathbf{x}}_i),L_{\text{max}})$$
  • If $\text{dist}\le \frac{D({\mathbf{x}}_i)}{2}$ then

    • $${\mathbf{x}}_i^m\leftarrow {\mathbf{x}}_i+\text{dist}{\widehat{\mathbf{n}}}_{\text{synth}}({\mathbf{x}}_i)$$
  • Else

    • Exit Do loop on m

2.3 Generation of a volume mesh from the processed surface mesh

Once a suitable surface mesh has been obtained with edge length on the surface of order $\frac{K}{M}d({\mathbf{x}}_i)$ at point i, we cast m_i points in the direction n̂_synth (x_i) (Algorithm 4) forming the point set

$$\{{\mathbf{x}}_i^m|1\le i\le N_{\text{surf}},0\le m\le m_i\},$$ (10)

where here we have defined ${\mathbf{x}}_i^0\equiv {\mathbf{x}}_i$ to be the surface points in S.

To explain the rationale of Algorithm 4, we provide the following argument. If we distribute $\lfloor \frac{M}{2}\rfloor$ points normally from x_i to ${\mathbf{x}}_i+\frac{1}{2}d({\mathbf{x}}_i){\widehat{\mathbf{n}}}_{\text{synth}}({\mathbf{x}}_i)$, spacing them out equally (that is using spacing $\frac{d({\mathbf{x}}_i)}{M}$ between points on the normal ray), they will naturally form layers. Indeed, for two points x_i, x_j on the surface that are close together and connected by an edge in S, we have d(x_i) ≈ d(x_j) due to gradient-limiting. Thus for small m, points ${\mathbf{x}}_i^m$ and ${\mathbf{x}}_j^m$ will be approximately the same distance normal from the surface and will therefore have a high probability of being connected by an edge as well. We call these points between x_i and ${\mathbf{x}}_i+\frac{1}{2}d({\mathbf{x}}_i)\widehat{\mathbf{n}}({\mathbf{x}}_i)$ “layer-making” interior points. (More generally, we can choose the distance between ${\mathbf{x}}_i^{m-1}$ and ${\mathbf{x}}_i^m$ to be some fraction λ_md(x_i) with ${\displaystyle {\mathrm{\sum }}_{m=1}^{\frac{M}{2}}{\mathrm{\lambda }}_m=\frac{1}{2}}$, with λ_m monotonically increasing to create layers with closer spacing at the boundary.)

However, due to gradient-limiting, d(x_i) may be quite reduced from the raw local diameter D(x_i) defined in Equation (3). Thus more points based on D(x_i) rather than d(x_i) may have to be laid down in places. These points will be termed “filler” interior points.

Consider

$$L(\mathbf{x})=\{\mathbf{y}|\mathbf{y}=\mathbf{x}+\mathrm{\lambda }\widehat{\mathbf{n}}(\mathbf{x}),0\le \mathrm{\lambda }\le \frac{1}{2}D(\mathbf{x})\}.$$

We call L(x) a semi-diameter segment associated with the surface point x.

Lemma

Coverage by Semi-diameter segments. If S is closed and C² and thus possesses a classical normal at each point, then V (the volume bounded by S) is covered by all the semi-diameter segments associated with all points of S. That is

$$V={\cup }_{\mathbf{x}\in S}L(\mathbf{x}).$$

Proof

learly for each x, L(x) ⊆ V, so V ⊇ ∪_x∈S L(x). Clearly S ⊆ ∪_x∈S L(x). Now let y be any point in the interior of V. Let x be the closest point on S to y. That is, choose some x_c such that ‖y − x_c‖ = min_x∈S ‖y − x‖. Then we claim y ∈ L(x_c). First, it must be true that (y − x_c) ‖ n̂ (x_c). For otherwise, one could choose a point on S in the neighborhood of x_c closer to y, contradicting our assumption that x_c is a closest point to Y. Suppose the ray starting from x_c in the direction n̂(x_c) has a first re-intersection with S at ${\mathbf{x}}_c^{\text{opp}}$. Then $\parallel {\mathbf{x}}_c^{\text{opp}}- {\mathbf{x}}_c\parallel =D({\mathbf{x}}_c)$ by (3). We have that x_c, y, and ${\mathbf{x}}_c^{\text{opp}}$ are collinear and since x_c is a closest point to y,

$$\parallel \mathbf{y}-{\mathbf{x}}_c\parallel \le \frac{1}{2}D({\mathbf{x}}_c).$$

Hence, y ∈ L(x_c). Since y is an arbitrary point in the interior of V, we conclude V ⊆ ∪_x∈S L(x). Hence V = ∪_x∈S L(x)

By the lemma, we surmise that if we spread points along all the semi-diameter segments that we would adequately cover V. This is not rigorously true if the conditions of the lemma are violated. That is, if S has a sharp corner where it has no classical normal, there could be a gap in the coverage of the interior. Strictly speaking, there is no classical normal at any vertex of the piecewise linear S, but if the number of nodes on S provide sufficient angular resolution, the idea of the lemma is effectively applicable to S.

However we had previously determined that we want to distribute points between x_i and ${\mathbf{x}}_i+{\widehat{\mathbf{n}}}_{\text{synth}}({\mathbf{x}}_i)\frac{d({\mathbf{x}}_i)}{2}$ at equal intervals in order to form layers. Due to gradient-limiting, we could have d(x_i) < D(x_i). Also we may have adjusted d(x_i) so that L_min ≤ d(x_i) ≤ L_max. Thus it is quite possible that d(x_i) = D(x_i). In this case, what is the best resolution for these contradictory criteria?

In a very tight space where D(x_i) < L_min, we have that the minimum spacing between nodes should be $\frac{L_{\text{min}}}{M}$. Thus we cover the distance from x_i to ${\mathbf{x}}_i{+\widehat{\mathbf{n}}}_{\text{synth}}({\mathbf{x}}_i)\frac{D({\mathbf{x}}_i)}{2}$ with points spaced uniformly $\frac{d({\mathbf{x}}_i)}{M}=\frac{L_{\text{min}}}{M}$ starting from the boundary. Potentially less than $\lfloor \frac{M}{2}\rfloor$ points will be laid down (making less than M layers across) but that is a necessary consequence of our limiting the feature size to a lower bound of L_min.

If d(x_i) < D(x_i), we must place $\lfloor \frac{M}{2}\rfloor$ points between x_i and ${\mathbf{x}}_i+{\widehat{\mathbf{n}}}_{\text{synth}}({\mathbf{x}}_i)\frac{d({\mathbf{x}}_i)}{2}$ because the gradient-limited d(x) field varies smoothly along the surface; placing them instead from x_i to ${\mathbf{x}}_i+{\widehat{\mathbf{n}}}_{\text{synth}}({\mathbf{x}}_i)\frac{D({\mathbf{x}}_i)}{2}$ would cause significant jumps in the distances from boundary points to corresponding interior points at some adjacent boundary nodes. However to guarantee filling out of the interior, we must add additional points between ${\mathbf{x}}_i+{\widehat{\mathbf{n}}}_{\text{synth}}({\mathbf{x}}_i)\frac{d({\mathbf{x}}_i)}{2}$ and ${\mathbf{x}}_i+{\widehat{\mathbf{n}}}_{\text{synth}}({\mathbf{x}}_i)\frac{D({\mathbf{x}}_i)}{2}$. In this interior region, we consider the feature size to be min(D(x_i), L_max) and add these “filler” interior points with spacing $\frac{1}{M}$ min(D(x_i), L_max) to fill out the semi-diameter segment.

The points generated in Algorithm 4 are handed off to the Delaunay mesh generator described in Algorithm 5. A “big tet” is made which encloses the region to be meshed in IR³ and the points $\{{\mathbf{x}}_i^m\}$ are inserted layer by layer using the incremental point insertion algorithm of Watson [28]. In the Watson algorithm, the insertion of a new point ${\mathbf{x}}_i^m$ leads to removal of all tetrahedra whose circumspheres contain the point. (When the tetrahedra are removed a simply connected “insertion cavity” is formed and each of the triangular bounding facets of the cavity are visible to the new point.) In the standard Watson algorithm, ${\mathbf{x}}_i^m$ is connected to each of the facets bounding the cavity to form a set of tetrahedra that fill the cavity and the procedure continues with insertion of the next point in the insertion list. In our version of the insertion algorithm, we abort the insertion of ${\mathbf{x}}_i^m$ if $m>\lfloor \frac{M}{2}\rfloor$ —that is, if ${\mathbf{x}}_i^m$ is a “filler” interior point greater than a distance $\frac{d({\mathbf{x}}_i)}{2}$ but less than a distance $\frac{D({\mathbf{x}}_i)}{2}$ from x_i—if it would result in the formation of a tetrahedron containing an edge that would connect ${\mathbf{x}}_i^m$ to a boundary point ${\mathbf{x}}_j^0$ on S. The reason is that filler interior points can be on “lucky” rays that travel far from the originating surface point (recall Figure 4(a)) and in particular they might pass very close to the surface of S in a totally unexpected location and consequently degrade the quality of or even ruin the triangulation near the boundary. Indeed the purpose of filler interior points is to fill gaps in the interior and they should not connect to the boundary. After running through the list once, we run through it a couple of more times to be sure previously rejected points can’t be eventually inserted.

The final step of Algorithm 5 is rejection of tetrahedra that fall outside of the bounding surface S. We simply delete all tetrahedra that do not have an internal point (i.e. a point ${\mathbf{x}}_i^m$, m ≥ 1). It is however possible that a tetrahedron could be formed that connects an internal point to a “layer 0” point across a small gap where boundary points are misaligned. We prevent this by increasing the surface node density in such problem areas. This is accomplished as follows. The field D_out computed in Section 2.1 is computed at the same time as the inwards pointing rays are computed. The purpose of D_out is not to influence the size of elements, but to only prevent “connect-across” situations like in Figure 10 occurring. We have found that in these kinds of regions where separate pieces of geometry lie close together, it is necessary to have the surface edge length less than 2D_out(x) in order to prevent these situations. Since we create a mesh with characteristic edge length $\frac{K}{M}d({\mathbf{x}}_i)$ using the refinement, de-refinement and swap operations previously mentioned, we thus desire

$$\frac{K}{M}d({\mathbf{x}}_i)\le 2D_{\text{out}}(\mathbf{x})$$ (11)

Fig. 10.

Connect-across phenomenon where separate pieces of the mesh region lie close together. In the figure, the circumcircle of external triangle b, c, d formed with ‘layer 0’ points barely excludes the ‘layer 1’ points a, e. If the two meshed regions approach any closer, triangle b, c, d will not be part of a Delaunay mesh and undesirable connection between the meshed regions occurs. Similar phenomena occur in 3-D. This is prevented by enforcing (11).

To force this, in Algorithm 1, we accordingly reduce d(x_i) where necessary so that (11) holds with equality before the final gradient-limiting operation of the feature size field d. This can in principle lead to spots where d(x_i) < L_min, but in this case it is more important to prevent incorrect grid topology at the expense of having some small cells.

We note that this increase in surface density to recover surface topology under Delaunay triangulation is an issue addressed by Amenta et al. [1,2]. In [1] a high surface point sampling density is required for a rigorous proof that correct surface topology will be recovered under 3-D Delaunay triangulation. In [2] a much lower density is shown to work in practice. Our required point density (as forced by (11)) is also much lower and we attribute this to the fact that our point sets are isotropically distributed on the surface and then stacked along the normals in the volume. This is a highly advantageous configuration for avoiding the “connect-across” phenomenon. Thus, we enjoy significant decreases in surface point density required to avoid incorrect topology. We note however that our suggested point density necessary to prevent incorrect topology for our normally-distributed point distributions is simply based on experience and that we always perform a topology check to ensure a clean boundary. We sweep through all surface nodes in the 3D mesh and check that the incident tetrahedra on each surface node form a single face-connected component. If not, the problem is re-run with a higher surface density in the problem region.

2.4 3-D mesh improvement operations

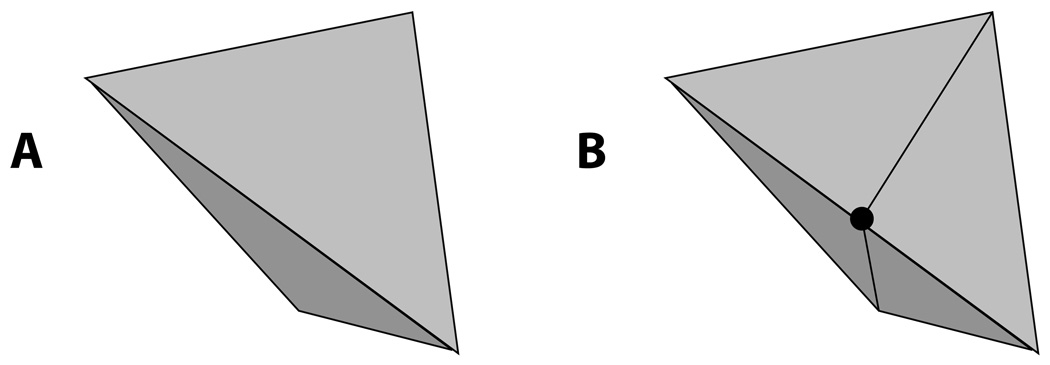
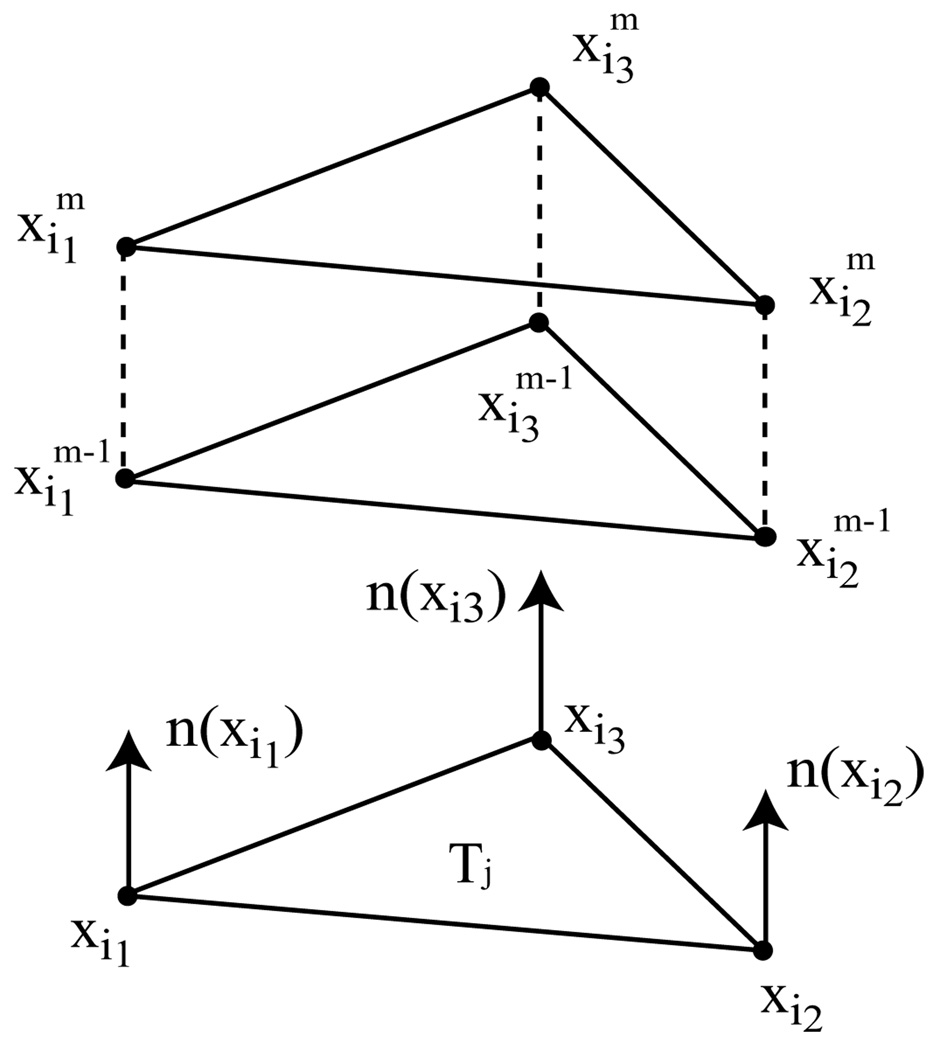
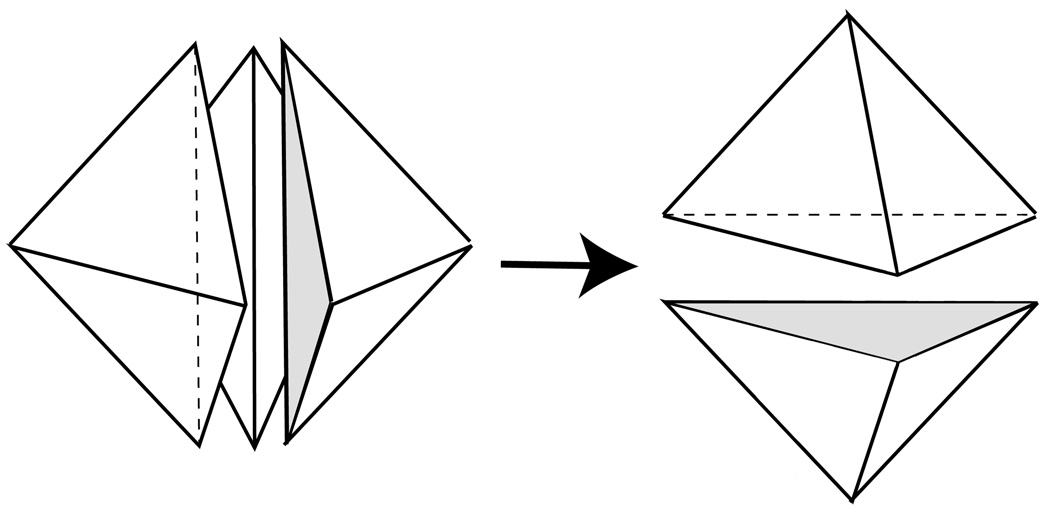
After the 3-D mesh has been generated by Algorithm 5, adjacent layers of volume points generated from the vertices of a surface triangles will tend to form prisms. (See Figure 11.) Many adjacent prisms in the same layer will have inconsistent triangulations, resulting in a thin sliver element between them. (See Figure 12.) These slivers can in many cases be flipped away using a 3 → 2 swap operation. (See Figure 13.) It has been our experience that the following heuristic volume criterion eliminates slivers so that over 99% of the elements are not slivers and the swaps do not significantly disrupt the layer structure of the mesh. We perform a 3 → 2 swap operation if the minimum tetrahedral volume in the new set of (2) tetrahedra yielded by the operation is greater than 3 times the minimum tetrahedral volume in the old set of (3) tetrahedra eliminated by the operation. We use minimum tetrahedral volume instead of a worst aspect ratio criterion, because worst aspect ratio might improve if perfectly good anisotropic layers are destroyed and this is not our intent. We intend to rid ourselves of slivers within an anisotropic layer while preserving the layer. Nevertheless, tetrahedra with aspect ratio much higher than K (the anisotropy of the point distribution) will generally be flipped away when the volume flipping criterion is employed. (Note: although the vast majority of flips are 3 → 2, we find that a very small number of potential 2 → 3 flips and 4 → 4 flips also satisfy the volume criterion and are flipped as well. Topologically, the 2 → 3 flip is the opposite of the 3 → 2 flip, while a diagram showing a 4 → 4 flip is given in [9, page 225].)

Fig. 11.

Layer m − 1 and layer m nodes generated from vertices of a surface triangle T_j form vertices of a prism.

Fig. 12.

Adjacent prisms with inconsistent (opposing diagonal) triangulations on their shared quad face force the Delaunay mesh to have a sliver.

Fig. 13.

Three to two flip: replacing a set of three tets with two new tets that occupy the same volume.

Finally, we have developed a ‘tet crushing algorithm’ that inserts nodes on the opposed diagonals of the slivers and then merges the nodes together, eliminating the slivers. The results from this heuristic algorithm as gauged by its performance on the examples in Section 3 are good: all tetrahedra with very small aspect ratio are eliminated. Since we are given latitude to make small finite deformations in the mesh, it is not surprising that results may exceed those of algorithms where connectivity changes are allowed but node displacements are not performed. An example of the latter is sliver exudation [7]. Our tet crushing algorithm will be presented elsewhere.

Algorithm 5: Conforming Delaunay 3-D Triangulation

[Take point set of Algorithm 4 and form layered Delaunay mesh that respects boundaries]

Create an initial mesh consisting of a single “big tetrahedron” containing all points in $\{{\mathbf{x}}_i^m\}$ in its interior.

[Process all points from one layer before moving onto next layer]

Do m = 1, 2, …, $\frac{M}{2}$, …

• For each node i ∈ S

  • If ${\mathbf{x}}_i^m$ exists and has not been inserted into mesh Then

    • Compute insertion cavity $\mathcal{C}({\mathbf{x}}_i^m)$ consisting of the space occupied by all tetrahedra whose circumspheres contain ${\mathbf{x}}_i^m$.
    • Insert ${\mathbf{x}}_i^m$ iff connecting ${\mathbf{x}}_i^m$ to triangular boundary facets of $\mathcal{C}({\mathbf{x}}_i^m)$

      1. does not create extremely small tetrahedra and
      2. does not connect a filler point ${\mathbf{x}}_i^m$ with $m>\frac{M}{2}$ to a previously inserted boundary node ${\mathbf{x}}_{i\prime }^0$,

Repeat above Do Loop a couple of times to see if previously rejected ${\mathbf{x}}_i^m$ can be subsequently inserted.

[Delete tetrahedra exterior to S]

Delete all tetrahedra containing a point from the “big tet”

Delete all tetrahedra not containing an internal point ${\mathbf{x}}_i^m$ with m ≥ 1

2.5 Overall tet mesh generation algorithm

The overall algorithm for producing tet meshes from an initial triangulated surface S is given in Algorithm 6. This algorithm will produce a mesh where the typical cross-section has M equally spaced layers and the tet anisotropy is generally between $\frac{K}{2}$ and K near the surface S.

Clearly one can alter the parameter settings given in Algorithm 6, but these standard settings produce satisfactory meshes for a wide variety of input surfaces.

3 Examples

We give three examples of the use of the mesh generation algorithm.

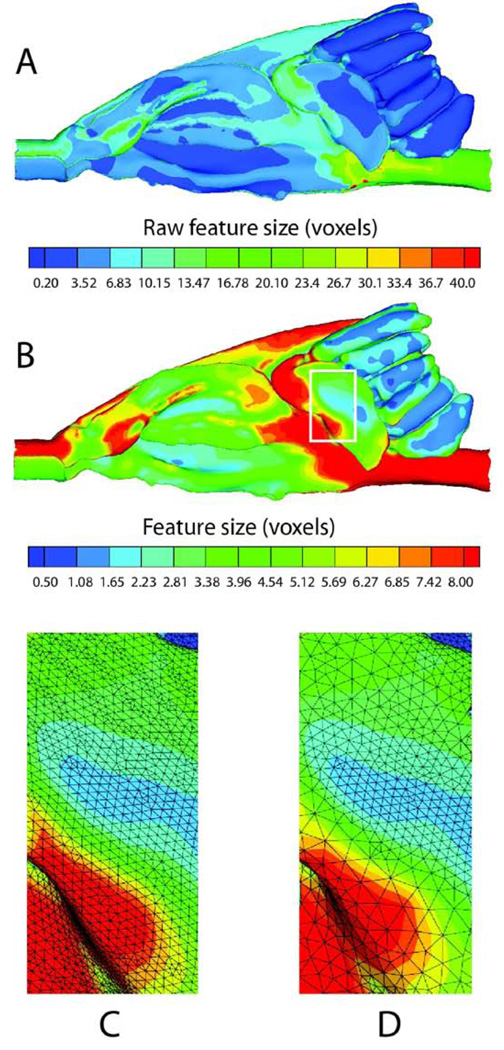
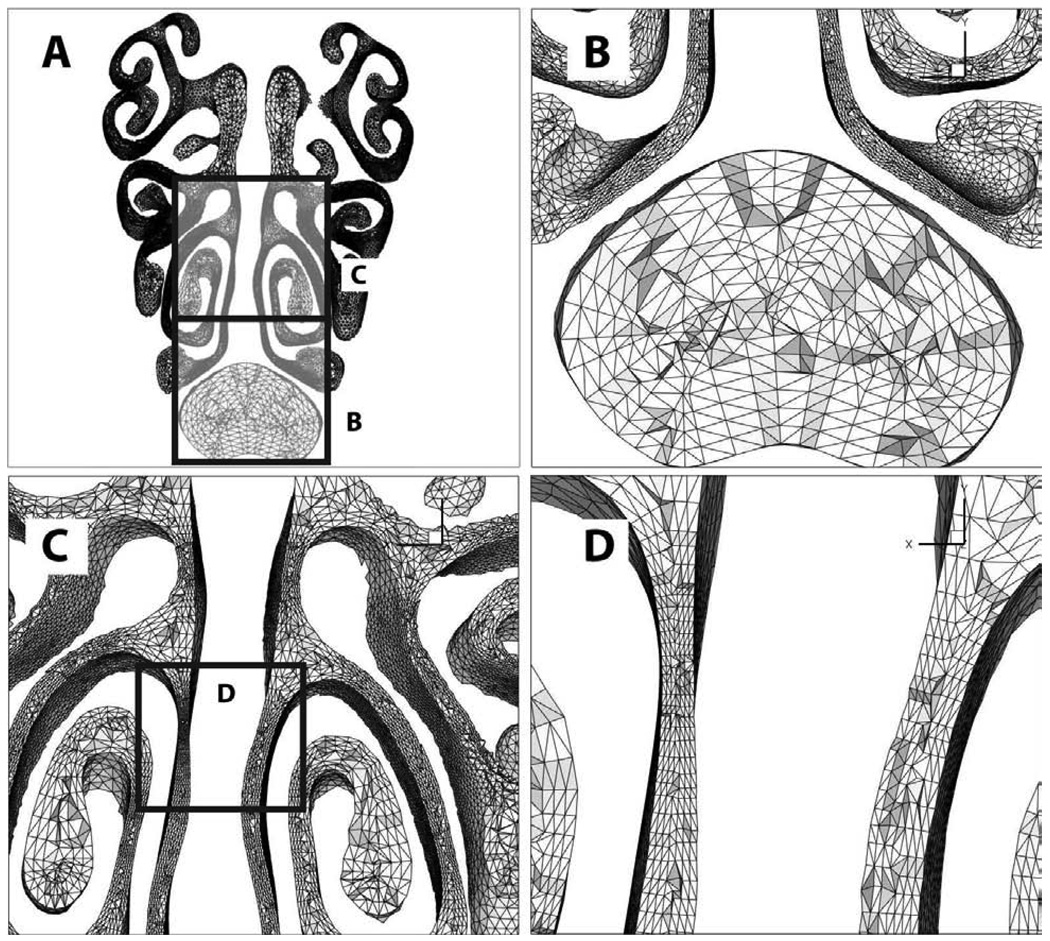
Our first example geometry is the upper respiratory tract of a rat (genus 1). The geometry goes from nostrils (left hand side of Figure 14A) to trachea (right hand side of Figure 14A). The data is obtained from magnetic resonance imaging and the length scale is in voxel widths. The raw feature size exceeds 40 voxels at two isolated points where a few rays penetrate down rather than across an airway. The largest feature, the trachea, is correctly estimated to be in the 20–23 voxel range. Above the trachea are some folds that are in blue, meaning that they are the boundaries of smaller airways. These airways are in fact called the “turbinates” and they are intricate, convoluted airways used by the olfactory system. The smallest raw feature size is 0.2 voxels. In Panel B, we clip and gradient-limit the feature size field below at L_min =0.5 voxel widths (eliminating dubious subvoxel features) and above at L_max =8 voxel widths (eventually forcing more layers in the trachea). Panels C and D show close-up pictures of the same piece of surface mesh before and after surface refinement, respectively. Edge-bisection, node-merge, and edge-swap operations establish edge length between $\frac{K}{2M}d(\mathbf{x})$ and $\frac{K}{M}d(\mathbf{x})$, where here we have chosen meshing parameters K = 4.2 and M = 7.

Fig. 14.

Surface mesh of rat upper respiratory tract. A Raw feature size function depicted. B Clipped, gradient-limited feature size function. C Close-up of surface mesh at original density. D Close-up of surface mesh with revised density as determined by feature size function.

In Figure 15 we see vertical cutaway sections through the resulting volume mesh and in Figure 16 we see a horizontal cutaway section through the volume mesh. We note that we do indeed have 6 or 7 intact layers across airways as desired.

Fig. 15.

Vertical slices from volume mesh of rat upper respiratory tract produced using Algorithm 6 with K = 4.2 and M = 7.

Fig. 16.

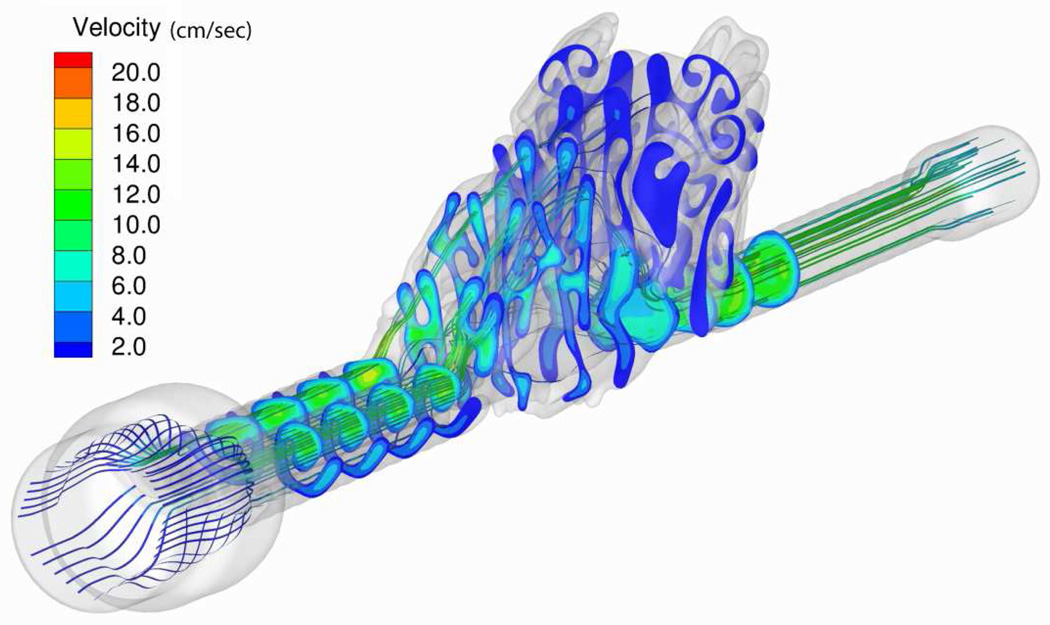
Cutplanes along flow in CFD computation using volume mesh in rat upper respiratory tract. Nasal inlets are extruded forward and trachea outlet is extruded backward to match experimental setup.

In Figure 16 we see a converged computation on the rat nose mesh using the commercial STAR-CD computional fluid dynamics code [26]. Nasal inlets are extruded forward and trachea outlet is extruded backward to match the experimental setup where prescribed flow is applied at beginning of an inlet tube and zero pressure boundary conditions are prescribed at outlet of exit tube. (Inlet and outlet tubes respectively intersect extruded nostril and trachea sections.) A description of our efforts at modeling airflow for purposes of particulate dosimetry estimation is given in [18].

Our second example (Figure 17) is a rat lung (genus 0). Meshing parameters were again set to K = 4.2 and M = 7. Magnetic imaging data was acquired using silicone casts of pulmonary airways in a 9-wk-old, male, Sprague-Dawley rat. Panel A shows the feature size field on the lung surface, as well as the locations of the cutaway sections B, C & D. Panel B shows the interior tetrahedra in a large airway, with D(x) greater than L_max, transitioning to a smaller airway with L_min < D(x) < L_max. Panels C & D show sections through the trachea and a through a pair of airways downstream of the bifurcation, respectively Panels E & F show both the external boundary and the tetrahedra in the neighborhood of several outlets. The outlet surfaces visible in panels E & F are not physical tissue surfaces but are cross-sectional surfaces at which outflow boundary conditions are applied. As such, M layers go across the outlet rather than into the outlet. This is accomplished by constraining the physical tissue normals adjacent to each outlet to lie in the plane of that outlet.

Fig. 17.

Vertical slices from volume mesh of rat lung produced using Algorithm 6 with K = 4.2 and M = 7. Panel A shows the feature size field on the lung surface, as well as the locations of the cutaway sections B, C & D. Panel B shows the interior tetrahedra in a large airway, with D(x) greater than L_max, transitioning to a smaller airway with L_min < D(x) < L_max. Panels C & D show sections through the trachea and a through a pair of airways downstream of the bifurcation, respectively. Panels E & F show both the external boundary and the tetrahedra in the neighborhood of several outlets.

Our third example (Figure 18) is a human heart (genus 12): Meshing parameters were again set to K = 4.2 and M = 7. Panel A shows the feature size field on the surface of the heart, as well as the locations of sections B & C. Panel B is a vertical cutaway through the heart, revealing the interior tetrahedra in the thick myocardium as well as the inter-atrial septum (detail in D). Panel C shows a diagonal cutaway through the heart, revealing myocardium, arterial lumen (top left) and the edge of the mitral valve. A magnified cross-section of the mitral valve is shown in Panel E. These cutaways demonstrate that we were able to achieve nearly orthogonal layering at both top and bottom scales.

Fig. 18.

Vertical slices from volume mesh of human heart produced using Algorithm 6 with K = 4.2 and M = 7. Panel A shows the feature size field on the surface of the heart, as well as the locations of sections B & C. Panel B is a vertical cutaway through the heart, revealing the interior tetrahedra in the thick myocardium as well as the inter-atrial septum (detail in D). Panel C shows a diagonal cutaway through the heart, revealing myocardium, arterial lumen (top left) and the edge of the mitral valve. A magnified cross-section of the mitral valve is shown in Panel E.

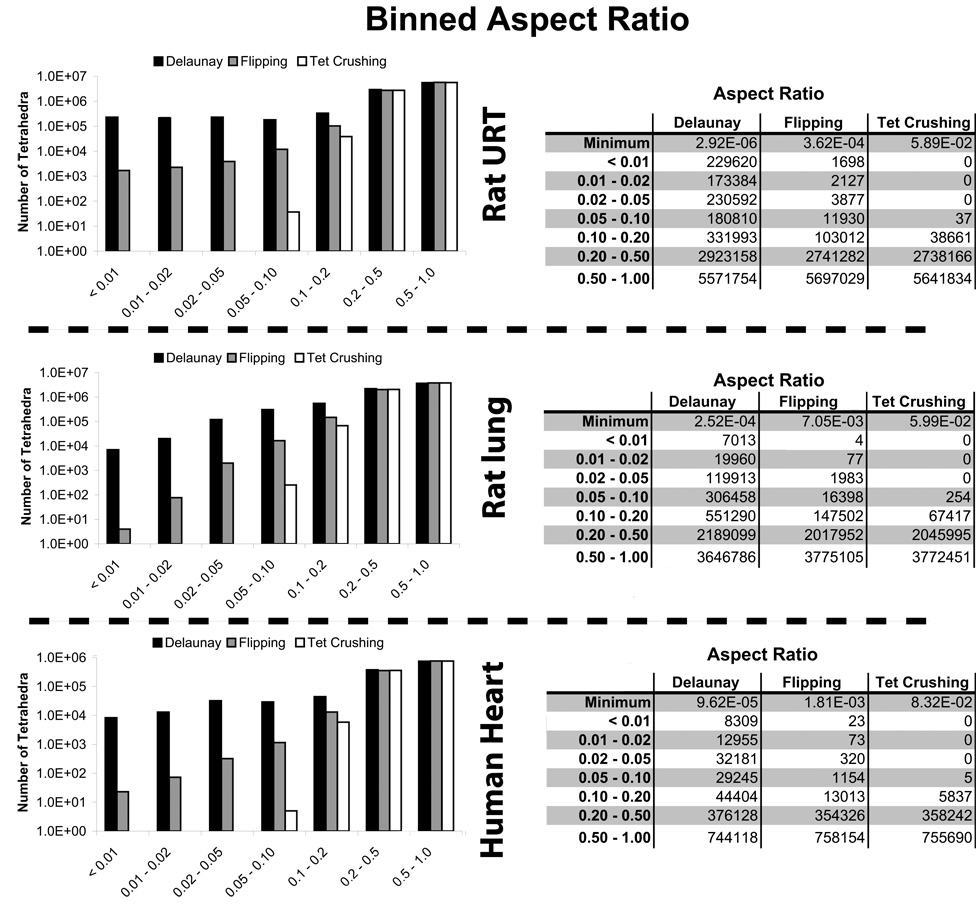
Finally, we present mesh quality statistics in Figure 19 for the meshes produced in these three examples. Here we present aspect ratio improvement, where for tetrahedra, we have defined:

$$\text{aspect ratio}\equiv 2\sqrt{6}\frac{\text{inscribed radius}}{\text{length of longest edge}},$$

which has maximum value 1 for a regular tetrahedron. The cumulative aspect ratio improvement is critical in allowing us to perform numerical computations on these challanging biomedical geometries.

Fig. 19.

Mesh quality improvement by flipping and then tet crushing for one human and two rat geometries.

Algorithm 6: Overall Mesh Generation Algorithm

[Smooth initial marching cubes triangulation]

Perform Volume Conserving Smoothing (Algorithm 4 in [13]) for 10 sweeps with underrelaxation coefficient ω = 1.

[Improve surface mesh S]

Determine raw feature size D(x) using (3) and (6)

Gradient-limit D(x) to yield feature size d(x) using Algorithm 1

[Change S to have edge length between $\frac{K}{2M}d(\mathbf{x})$ and $\frac{K}{M}d(\mathbf{x})$]

For i = 1, 3

• Do until nothing changes

  • Merge nodes using Algorithm 3 with merge_length = $\frac{K}{2M}d(\mathbf{x})$ and toldamage = $\frac{K}{30M}d(\mathbf{x})$
  • Swap surface edges (as in Figure 9) with toldamage = $\frac{K}{30M}d(\mathbf{x})$

• Refine edges with Algorithm 2 with bisection_length = $\frac{K}{M}d(\mathbf{x})$

• Perform Volume Conserving Smoothing (Algorithm 4 in [13]) for 10 sweeps with underrelaxation coefficient ω = 0.1.

[Create Volume Mesh]

Create volume points using Algorithm 4 with ${\mathrm{\lambda }}_m=\frac{1}{M}$

Create volume tet mesh using Algorithm 5

Use 3 → 2 swaps and other mesh improvement operations (Section 2.4) to eliminate slivers

4 Limitations and Areas for Future Improvement

This algorithm deposits nodes along rays to the raw local half-diameter. For smooth geometries, this produces coverage of the interior. However when there is a jump in the surface normal due to “man-made” non-biological features, such as a machined edge, there may be incomplete coverage. In this case, at surface points where the neighborhood has a jump in the surface normal, we must cast multiple rays of interior points at various angles to the surface. For the smooth geometries shown, this is not necessary.

Highly curved concave boundaries, such as encountered when meshing the complement of a tubular region are likely to result in incomplete coverage of the interior region as in the case just mentioned. In this case the most straightforward approach is to let the feature size also contain a term for curvature:

$$D(\mathbf{x})=\text{min}(D_{\text{ray}–\text{shoot}},2*R_{\text{curvature}}),$$ (12)

where R_curvature is the principal radius of curvature of smallest magnitude. This result is then gradient-limited as before. A numerically stable algorithm for computing principal curvatures is given in [24]. Our experience with airway geometries has been that this is not required, but we have found that meshing of the tissue space around the coronary arteries of the heart necessitates this term.

The scheme of depositing points along rays to half the local diameter can also cause significant overlap with some kinds of geometries. Clearly, for a perfect sphere or torus there is no overlap, but for e.g. a (rounded) brick, there is significant overlap. The biological geometries we deal with here are tubular or crevasse-like and there is usually little overlap. Extra points in the interior region are usually acceptable. It is advisable to filter the set of interior points before Delaunay connection so that if two interior points (generated from two different surface points) are by chance a small fraction of a voxel apart, the one which is further from its surface generator point is deleted. (This filtration is rapidly done with a AABB tree.)

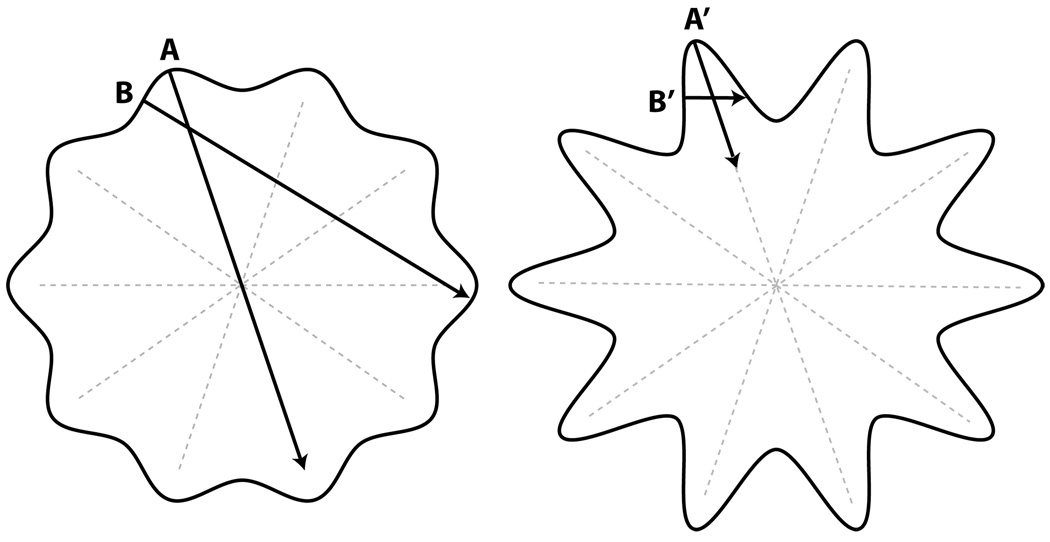
Our algorithm makes an automatic choice of when small-scale features should be ignored. In Figure 20 in the left-side illustration, the surface undulations are so gentle they do not figure into the feature size computed by the algorithm. Indeed rays cast from points A and B miss neighboring features. The result is that the medial axis (dotted gray lines) is effectively ignored and the feature size reflects only the larger scale size of the geometry. On the right-side illustration, the amplitude of the undulations is large enough to be detected by the algorithm. Here, a ray cast normally from the inflection point between a peak and a trough (point B′) intersects a neighboring feature, causing the feature size to be lessened to the scale of the undulations. (The feature size at the point A′ is also reduced as indicated, due to gradient-limiting of the feature size field.) Hence, the medial axis (dotted lines) is effectively recognized. We have found this automatic behavior to be desirable for meshing our biological geometries. However, the user may demand some control over what is or is not an “ignorable” undulation on the surface. One solution that would cause the algorithm to recognize smaller undulations would be adding a curvature correction to the feature size computation as in (12).

Fig. 20.

Perturbation from circular shape in left-hand figure is too small to affect feature size. Larger perturbations in right-hand figure are not ignored. Smaller feature size detected at B′ forces smaller feature size at A′ due to gradient-limiting.

5 Conclusions

We have implemented in the PNNL version of the LaGriT grid management toolbox an algorithm for the generation of anisotropic meshes that are scale-invariant over a prescribed range. The algorithm relies on a concept of feature size that is obtained by considering the lengths of rays that are shot normally from the surface into the volume and reintersect the surface. This approach is especially suited to rapid, quality meshing of biological structures where CFD calculations require a definite number of intact mesh layers in regions of great geometric complexity.

A Damage Estimate for Node Merging

If we merge node i into merge j in the neighborhood Ω_i of x_i, we create a new patch Ω_new of piecewise linear triangles as in Figure A.1. Here, the triangles T_k in Ω_i that contain the edge $\overline{{\mathbf{x}}_i{\mathbf{x}}_j}$ are eliminated (since the edge is contracted to a point) and all other triangles T_k yield a new triangle $T_k^{\text{new}}$ by replacement of node i with node j and keeping the other two nodes the same.

Fig. A.1.

Merging of node i at x_i to neighboring node j at x_j. A Appearance before merge where neighborhood Ω_i of x_i consists of N surface triangles T_k. B Appearance after merge where replacement neighborhood Ω_new consists of N − 2 new surface triangles $T_k^{\text{new}}$. C Deformation of surface by this merge sweeps out a volume that can be decomposed into N − 2 tetrahedra 𝛵_k.

Thus the action of merging node i to node j deforms the neighborhood Ω_i into Ω_new; the thickness of the volume between these two surface patches is thus a good measure of the damage of the merge operation. Note that in fact the volume between Ω_i and Ω_new is tetrahedralized by the set of tetrahedra {𝛵_k} formed by adjoining the point x_i to each of the triangles in Ω_new. The altitude of 𝛵_k above its base $T_k^{\text{new}}$ is |(x_i − x_j) · ${\widehat{\mathbf{n}}}_k^{\text{new}}$|, where ${\widehat{\mathbf{n}}}_k^{\text{new}}$ is the unit vector normal to $T_k^{\text{new}}$. So the volume swept out by merging i to j is formed by the union of tetrahedra sitting atop Ω_new, none of which has altitude exceeding

$$\text{height bound}\equiv \underset{k}{\text{max}}|({\mathbf{x}}_i-{\mathbf{x}}_j)\cdot {\widehat{\mathbf{n}}}_k^{\text{new}}|.$$ (A.1)

We thus naturally define damage(x_i → x_j) to be this height bound.

Note that this damage estimate discriminates among possible merge neighbors in neighborhoods with creases, such as depicted in Figure A.2. Here the merge i → j has a damage estimate of zero, while, e.g., the merge i → k has a positive damage estimate. For a sufficiently small damage tolerance, the merge i → k will not be performed.

Fig. A.2.

Merging along crease (x_i → x_j) incurs far less damage than merging down the crease (x_i → x_k).

We also perform an orientation check to make sure that merge i → j does not introduce a fold into the mesh. We define a “patch normal” x_Ωi, similar to (6) but instead each triangle is weighted by triangle area:

$${\widehat{\mathbf{n}}}_{{\mathrm{\Omega }}_i}\equiv \frac{{{\displaystyle {\mathrm{\sum }}_k{A}_k\widehat{\mathbf{n}}}}_k}{\parallel {{\displaystyle {\mathrm{\sum }}_k{A}_k\widehat{\mathbf{n}}}}_k\parallel },$$ (A.2)

where the sum is over the triangles T_k incident on node i and then A_k and n̂_k are the areas and normals of the triangles. This normal is more representative than n̂_synth of the average normal direction of the whole patch Ω_i and in fact it is easy to prove that it is independent of the position x_i and is only determined by the geometry of the line segments comprising the patch boundary ∂Ω_i.

To check that the merge i →j does not introduce a fold into the mesh, we check that if ${\widehat{\mathbf{n}}}_k^{\text{new}}$ are the normals for the new triangles in Ω_new, that

$${\widehat{\mathbf{n}}}_{{\mathrm{\Omega }}_i}\cdot {\widehat{\mathbf{n}}}_k^{\text{new}}>0\forall k.$$ (A.3)

If this condition is not obeyed, we surmise that merge i → j will introduce a fold into surface and we do not perform the operation.

B Damage estimate for surface edge swapping

The swap of the mutual diagonal of adjacent triangles (Figure 9) also introduces damage. However, this operation can be viewed as the merging of a hypothetical node x_i on the midpoint of the initial diagonal to one of the vertices x_j not on the diagonal. Accordingly, the damage estimate damage(x_i → x_j) from the previous section is employed. Also, to prevent introduction of creases into the surface mesh, we use the orientation check (A.3) from the previous section.