MULTISCALE MODELS OF TAXIS-DRIVEN PATTERNING IN BACTERIAL POPULATIONS

Abstract

Spatially-distributed populations of various types of bacteria often display intricate spatial patterns that are thought to result from the cellular response to gradients of nutrients or other attractants. In the past decade a great deal has been learned about signal transduction, metabolism and movement in E. coli and other bacteria, but translating the individual-level behavior into population-level dynamics is still a challenging problem. However, this is a necessary step because it is computationally impractical to use a strictly cell-based model to understand patterning in growing populations, since the total number of cells may reach 10¹² - 10¹⁴ in some experiments. In the past phenomenological equations such as the Patlak-Keller-Segel equations have been used in modeling the cell movement that is involved in the formation of such patterns, but the question remains as to how the microscopic behavior can be correctly described by a macroscopic equation. Significant progress has been made for bacterial species that employ a “run-and-tumble” strategy of movement, in that macroscopic equations based on simplified schemes for signal transduction and turning behavior have been derived [14, 15]. Here we extend previous work in a number of directions: (i) we allow for time-dependent signals, which extends the applicability of the equations to natural environments, (ii) we use a more general turning rate function that better describes the biological behavior, and (iii) we incorporate the effect of hydrodynamic forces that arise when cells swim in close proximity to a surface. We also develop a new approach to solving the moment equations derived from the transport equation that does not involve closure assumptions. Numerical examples show that the solution of the lowest-order macroscopic equation agrees well with the solution obtained from a Monte Carlo simulation of cell movement under a variety of temporal protocols for the signal. We also apply the method to derive equations of chemotactic movement that are governed by multiple chemotactic signals.

1. Introduction

New techniques in cell and molecular biology have produced huge advances in our understanding of signal transduction and cellular response in many systems, and this has led to better cell-level models for problems ranging from biofilm formation to embryonic development. However, many problems involve large numbers of cells $\left(\mathcal{O}({10}^{12}-{10}^{14})\right)$, and detailed cell-based descriptions are computationally prohibitive at present. Thus rational techniques for incorporating cell-level knowledge into macroscopic equations are needed for these problems. One such problem arises when large numbers of individuals collectively organize into spatial patterns, as for instance in bacterial pattern formation and biofilms. In these systems the collective organization involves response to spatial gradients of attractants or repellents. When cells move toward (away from) favorable (unfavorable) conditions, the movement is called positive (negative) taxis if they adjust the direction of movement in response to the signal, and kinesis if the frequency of directional changes or the speed of movement is changed. If the active movement is in response to the gradient of a chemical we call it chemotaxis or chemokinesis. In this paper we focus on bacterial chemokinesis, which has been studied extensively in the bacterium Escherichia coli. Despite the clear difference in the type of response, both taxis and kinesis are lumped together in the literature, and we do not distinguish between them here.

Escherichia coli is a cylindrical enteric bacterium ~ 1-2 μm long, that swims using a run-and-tumble strategy [4, 5, 38]. Each cell has 5-8 helical flagella that are several body lengths long, and each flagellum is rotated by a basal rotary motor embedded in the cell membrane. When all are rotated counterclockwise (CCW) the flagella form a bundle and propel the cell forward in a smooth “run” at a speed s = 10-30 μm/s; when rotated clockwise (CW) the bundle flies apart, the cell stops essentially instantaneously because of its low Reynolds number, and it begins to “tumble” in place. After a random time the cell picks a new run direction with a slight bias in the direction of the previous run [6]. The alternation of runs and tumbles comprises the “run-and-tumble” random movement of the cell. In the absence of a signal gradient the run and tumble times are exponentially distributed with means of 1 s and 0.1 s, respectively, but when exposed to a signal gradient, the run time is extended when the cell moves up (down) a chemoattractant (chemorepellent) gradient [6]. The molecular basis of signal transduction and motor control will be described in Section 2.

Under certain conditions, the collective population-level response to attractants produces intricate spatial patterns, even though each individual executes the simple run-and-tumble strategy. For instance, in Adler's capillary assay E. coli cells move up the gradient of a nutrient (an attractant), and the population forms moving bands or rings [1]. More recently, Budrene and Berg found that when E. coli move up the gradient of a nutrient, they can also release another stronger chemoattractant. They studied the patterns in two experimental configurations, one in which a small inoculant of cells is introduced at the center of a semi-solid agar layer containing a single carbon source, such as succinate or other highly-oxidized intermediates of the TCA cycle. In this case the colony grows as it consumes the nutrients, cells secret the chemoattractant aspartate, and a variety of spatial patterns of cell density develops during a two-day period, including outward-moving concentric rings, and symmetric arrays of spots and stripes. In the second type of experiment, wherein cells are grown in a thin layer of liquid medium with the same carbon source, a network-like pattern of high cell density forms from the uniform cell density, but this subsequently breaks into aggregates in 5-15 minutes. The formation of these patterns involves intercellular communication between millions of cells through the secreted chemoattractant aspartate, and thus detailed cell-based models of signal transduction, attractant release, and cell movement would be computationally expensive.

Heretofore, models of these and similar patterns have employed the classical Patlak-Keller-Segel (PKS) description of chemotactic movement [2, 35, 37, 36, 31]. Additional mechanisms assumed in these models include nonlinearity in the chemotactic coefficient, loss of motility under starvation conditions, or a second repellent or waste field. To understand the patterns formed in the soft agar, Brenner et al. [8] coupled the PKS chemotaxis equation with reaction-diffusion equations for both the attractant and nutrient, and proposed a minimal mechanism for the swarm ring and aggregate formation. They suggest that the motion of the swarm ring is driven by local nutrient depletion, with the integrity resulting from the high concentration of the attractant at the location of the ring; in contrast, the aggregates formed in the ring results from fluctuations near the unstable uniform cell density. However, the question of how to justify the chemotaxis equation from a microscopic description is not addressed in any of the foregoing analyses. In [12] it was assumed ab initio that the cell density satisfies the chemotaxis equation, and a formula for the sensitivity was obtained, but the use of the chemotaxis equation was not justified, nor were any of the known biochemical steps in signal transduction and response incorporated.

Recently significant progress has been made toward incorporating characteristics of the cell-level behavior into the classical description of chemotaxis [14, 15]. Using a simplified description of signal transduction, these authors studied the parabolic limit of a velocity-jump process that models the run-and-tumble behavior of bacteria, and showed that the cell density n evolves according to the parabolic equation

$$\frac{\partial n}{\partial t}=\nabla \cdot \left(\frac{s^2}{N{\lambda }_0}\nabla n-\frac{b{s}^2{t}_a{G}^{\prime }\left(S\right)}{N{\lambda }_0(1+t_a{\lambda }_0)(1+t_e{\lambda }_0)}n\nabla S\right).$$ (1.1)

Here S is the attractant concentration; N is the space dimension, s is the speed of the cells, λ₀ is the reciprocal of the mean run time in the absence of a signal, b reflects the sensitivity of the motor, t_e and t_a are the excitation and adaptation time scales, and G(S) models the signal detection and transduction via receptors. The authors assumed that (a) the signal function G(S(x)) is time-independent, (b) the gradient of the signal as measured by $G^{\prime }\left(S\right)\nabla S\cdot \mathbf{v}\sim \mathcal{O}\left(\epsilon \right){\sec }^{-1}$ is shallow, (c) the turning rate depends linearly on the internal state of the cell (λ = λ₀ - by₁), and (d) the quasi-steady-state approximation for intracellular dynamics is valid in estimating the higher order moments in the moment closure step. However, assumption (a) is often unrealistic in the context of bacterial pattern formation, and assumption (c) imposes additional restrictions on $y_1,i.e.,y_1<\frac{{\lambda }_0}{b}$, in order to guarantee the positivity of the turning rate. Assumption (b) was used to justify the neglect of the higher order moments, and while analysis showed that (b) can alternatively be replaced by (d) in order to allow larger signal gradients, (b) is implicitly required in the perturbation analysis on the diffusion time and space scales, as will be shown in Section 3.

In this paper we remove some of these restrictions. In Section 3 we relax the assumptions (a) and (c) in order to allow time-dependent signals and a general dependence of the turning frequency on the internal state of the cells, and show that when (b) is violated, diffusion time and space scales are inapplicable. There we also develop a new method for solving the infinite system of the moment equations, which allows elimination of (d). The method involves systematic application of a solvability theorem to a perturbation expansion of the solution. In Section 4 we compare the solution of the macroscopic chemotaxis equation and a stochastic simulation of chemotactic cell movement under a variety of temporal dynamics of the signal. In Section 5 we extend the method to allow for external force terms in the transport equation. We illustrate the use of the resulting equation with an application to the model of spiral stream formation in Proteus mirabilis colonies [39], where a biasing force is generated during cell movement. Finally, we explore macroscopic chemotaxis equations for bacterial populations when exposed to several chemosignals in Section 6. Before introducing the details of the analysis, we describe the cell-based model of bacterial pattern formation used in [39], which is based on a cartoon description of signal transduction introduced in [28]. The equations we derive incorporate measurable characteristics of signal transduction and thus are amenable to experimental verification.

2. The cell-based model

Bacterial cells are small; the swimmers we study here are typically 1-2 μm long. Therefore, we characterize their movement by their position $\mathbf{x}\in {\mathbb{R}}^N$ and velocity $\mathbf{v}\in V\subseteq {\mathbb{R}}^N$ as functions of time t. In the experiments of Budrene and Berg [9], the cell density is $\mathcal{O}\left({10}^8\right){\mathrm{ml}}^{-1}$, thus the average volume fraction of the cell population in the substrate is $\mathcal{O}\left({10}^{-4}\right)$. Even if in an aggregate cells are 100 times more crowded than average, the volume fraction would still be as small as $\mathcal{O}\left({10}^{-2}\right)$. Therefore, it is plausible to assume that cells are well separated, and there is no mechanical interaction between them. This means that we can treat the movement of different cells as independent processes. In E. coli the cell speed is more or less constant throughout the movement, so we assume that only the direction of the velocity changes during a tumble. In addition, since the mean tumbling time (~ 0.1 s) is much shorter than the run time (~ 1 s), we here neglect the tumbling time and assume that cells reorient immediately. In addition, we neglect the rotational diffusion of cells during a run. Therefore, movement of cells can be characterized by independent velocity-jump processes of the type introduced in [26] and later used in [18, 27, 14, 15].

The velocity-jump process is determined by a turning rate λ, and a turning kernel T(v, v′,…) which gives the probability density of turning from v′ to v after making the decision to turn. The dots indicate that T may depend on the signal or intracellular variables which are independent of cell velocity v. Since T is a probability density it must satisfy

$${\int }_{V}T(\mathrm{v},{\mathrm{v}}^{\prime },\dots )d\mathrm{v}=1,$$

which means that no cells are lost during the reorientation. A generalization can be made to include the tumbling of cells as a separate resting phase [26]. In that case, the stochastic process would be determined by three parameters: the transition rate from the moving phase to the resting phase λ, the transition rate from the resting phase to the next moving phase denoted as μ, and the turning kernel T. It has been shown, in the absence of internal dynamics, that inclusion of a resting phase results in a re-scaling of the diffusion rate and the chemotactic sensitivity in the resulting macroscopic equation, which is essentially a re-scaling of time [27].

When there is no signal gradient, the turning rate λ is a constant, while in the presence of a signal gradient, λ depends on the current state of the flagella motor, which in turn is determined as the output of the underlying signal transduction network that transduces the extracellular signal into a change in rotational state.

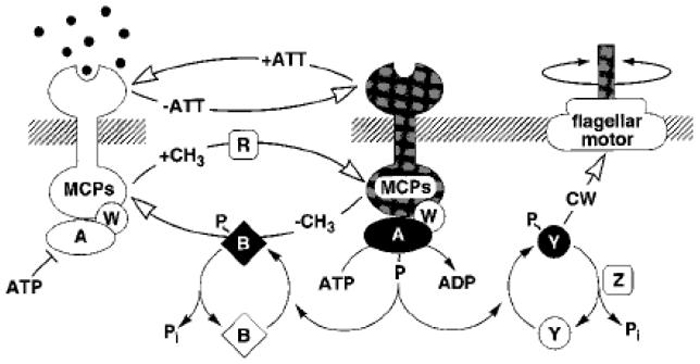
Signal transduction in E. coli is a very complicated input-output process (Figure 2.1). Attractant binding to a receptor reduces the autokinase activity of the associated CheA, and therefore reduces the level of phosphorylated CheY_p, which is the output of the transduction network, on a fast time scale (~ 0.1 s). This constitutes the excitation component. Changes in the methylation level of the receptor by CheR and CheB restores the activity of the receptor complex to its pre-stimulus level on a slow time scale (seconds to minutes), which is called adaptation. Adaptation allows the cell to respond to further signals. The output CheY_p in turn changes the rotational bias of the flagellar motors, and thus changes the run-and-tumble behavior [22, 38, 7].

Fig. 2.1.

The signal transduction pathway for E. coli chemotaxis. Chemoreceptors (MCPs) span the cytoplasmic membrane (hatched lines), with a ligand-binding domain on the periplasmic side and a signaling domain on the cytoplasmic side. The cytoplasmic signaling proteins are represented by single letters, e.g., A = CheA. (From [34] with permission.)

Several detailed mathematical models have been proposed to model the entire signal transduction network [34, 33, 24, 32]. In the deterministic models, the state of a cell can be described by a set of intracellular variables $\mathbf{y}=(y_1,y_2,\cdots ,y_q)\in {\mathbb{R}}^q$, and different models can be described by systems of the form

$$\frac{d\mathrm{y}}{dt}=\mathrm{f}(S(\mathrm{x}\left(t\right),t),\mathrm{y})$$ (2.1)

with different f, where S(x(t), t) is the extracellular signal and x(t) is the position of the cell at time t. In this article we adopt a simplified cartoon description, which is minimal (q = 2) yet captures the essential excitation and adaptation components:

$$\frac{d{y}_1}{dt}=\frac{G\left(S\right)-(y_1+y_2)}{t_e},$$ (2.2)

$$\frac{d{y}_2}{dt}=\frac{G\left(S\right)-y_2}{t_a}.$$ (2.3)

Here t_e and t_a with t_e << t_a are the excitation and adaptation time scales, x is the current spatial position of the cell, and G(S) is a functional of the signal detected by the receptors. If we assume that there is no cooperative binding and the binding reaction

$$S+R\underset{k^{-}}{\overset{k^{+}}{\rightleftarrows }}\stackrel{‒}{SR}$$

equilibrates rapidly, then G is given by

$$G\left(S\right)=G_0\left(\frac{S}{K_D+S}\right)$$ (2.4)

with the binding coefficient K_D = k^-/k⁺. Here R denotes the unbound receptor and $\stackrel{‒}{SR}$ denotes the receptor-signal complex. G(S) is bounded by G₀ since the receptors will be saturated at large concentrations of the attractant. The cartoon model has been shown to predict the input-output behavior of the full model [34] in response to step changes in the signal [14].

We may identify y₁ as the negative of the deviation of CheY_p from its steady state, and therefore, we assume the turning rate of each cell depends only on y₁, i.e.,

$$\lambda =\lambda \left(y_1\right).$$

In addition, we assume that the turning kernel T has no explicit space dependence and is independent of the internal state y: therefore

$$T=T(\mathrm{v},{\mathrm{v}}^{\prime }).$$

It has been shown experimentally that after a tumble, a cell has slight tendency to continue its previous direction of movement [4], and this will be included later.

Finally, the above description of cell movement can be coupled with components of cell metabolism and cell division, and with reaction-diffusion equations for the nutrient and attractant. We note that the description of cell movement used here comes directly from the biological observations, and by using reaction-diffusion equations for the chemicals, as in Section 4, convection of the chemicals in the fluid flow is implicitly neglected. This approximation is valid here because the flow is very slow as a result of the small Reynolds number and low volume fraction of the cell population.

A Monte Carlo scheme can be used to simulate the model, but stochastic simulation can become extremely expensive because of cell division. Suppose that cells double in 2 hours, and that the entire experimental process can last 2 days. Assuming that 10⁵-10⁷ cells are introduced into the petri dish initially, there would be 2²⁴×(10⁵-10⁷) ≃ 10¹² - 10¹⁴ cells after two days; thus we need a higher level description. In the next section we introduce a new method to embed the cell-level behavior in the population-level description, so as to derive an evolution equation for the cell density n(x, t) from the transport equation.

3. The transport equation and its diffusion limit absent external forces

Let p(x, v, y, t) be the density of cells having position $\mathbf{x}\in \Omega \subset {\mathbb{R}}^N$, velocity $\mathbf{v}\in V\subset {\mathbb{R}}^N$, and internal states $\mathbf{y}\in {\mathbb{R}}^q$ at time t ≥ 0, where V is a compact subset of ${\mathbb{R}}^N$ and symmetric about the origin. Then the velocity-jump process used previously [26, 14, 15] leads to the following transport equation when there is no cell growth

$$\frac{{\partial }_p}{{\partial }_t}+{\nabla }_{\mathrm{x}}\cdot \left(\mathrm{v}p\right)+{\nabla }_{\mathrm{y}}\cdot \left(\mathrm{f}p\right)=-\lambda \left(\mathrm{y}\right)p+{\int }_V\lambda \left(\mathrm{y}\right)T(\mathrm{v},{\mathrm{v}}^{\prime },\mathrm{y})p(\mathrm{x},{\mathrm{v}}^{\prime },\mathrm{y},t)d{\mathrm{v}}^{\prime }.$$ (3.1)

Here the left hand side of the equation describes the change of the population density due to the cell runs and the evolution of internal states, while the right hand side models the reorientation during the tumbles. The backward equation corresponding to the transport equation without internal variables was derived from the underlying stochastic process in [30]. A fundamental assumption in using a velocity-jump process to model the run-and-tumble movement is that jumps occur instantaneously, and therefore the forces are Dirac functions. This approximation is appropriate for swimming bacteria since the Reynolds number is so small that inertial effects are negligible.

In [27], a resting phase has been introduced to incorporate cell birth and death. While in some organisms it is true that cells stop to divide or give birth, the swimming bacterium E. coli has been observed to divide while swimming smoothly [3]. Thus the resting phase introduced is not necessary here. Therefore, by assuming that the growth rate r is a function of the local nutrient level c(x, t), the transport equation with cell growth reads

$$\frac{{\partial }_p}{{\partial }_t}+{\nabla }_{\mathrm{x}}\cdot \left(\mathrm{v}p\right)+{\nabla }_{\mathrm{y}}\cdot \left(\mathrm{f}p\right)=-\lambda \left(\mathrm{y}\right)p+{\int }_V\lambda \left(\mathrm{y}\right)T(\mathrm{v},{\mathrm{v}}^{\prime },\mathrm{y})p(\mathrm{x},{\mathrm{v}}^{\prime },\mathrm{y},t)d{\mathrm{v}}^{\prime }+r\left(c\right)p.$$ (3.2)

When cells grow in the exponential phase in a rich medium, r is a constant. By defining $p=\stackrel{‒}{p}{e}^{rt}$ and observing that $\stackrel{‒}{p}$ satisfies equation (3.1), we can derive the equation for $\stackrel{‒}{n}=\int \stackrel{‒}{p}dx$ and therefore $n=\stackrel{‒}{n}{e}^{rt}$. For this reason we begin with the transport equation (3.1) in the following derivation.

Define

$$z_1=y_1,z_2=y_2-G\left(S\right),$$

then from the equations (2.2, 2.3) for y₁, y₂, we obtain the system

$$\{\begin{array}{cc}\frac{d{z}_1}{dt}\hfill & =\frac{-z_1-z_2}{t_e},\hfill \\ \frac{d{z}_2}{dt}\hfill & =-\frac{z_2}{t_a}-G^{\prime }\left(S(x\left(t\right),t)\right)\left(\nabla S\cdot \mathrm{v}+\frac{\partial S}{\partial t}\right)\hfill \end{array}\phantom{\}}$$ (3.3)

and the turning rate becomes λ(z₁) = λ(y₁). The transport equation in the new internal variables (z₁, z₂) reads

$$\begin{array}{c}\frac{\partial p}{\partial t}+{\nabla }_{\mathrm{x}}\cdot \left(\mathrm{v}p\right)+\frac{\partial }{\partial z_1}\left[\left(\frac{-z_1-z_2}{t_e}\right)p\right]\hfill \\ \hfill +\frac{\partial }{\partial z_2}\left[\left(-\frac{z_2}{t_a}-G^{\prime }\left(S\right)(\nabla S\cdot \mathrm{v}+\frac{\partial S}{\partial t})\right)p\right]\hfill \\ \hfill =-\lambda \left(z_1\right)p+\lambda \left(z_1\right){\int }_{V}T(\mathrm{v},{\mathrm{v}}^{\prime })p\left({\mathrm{v}}^{\prime }\right)d{\mathrm{v}}^{\prime }.\end{array}$$ (3.4)

This change of variables for the internal state makes the following analysis much simpler.

In the remainder of this section we relax a number of assumptions used in [14, 15] and present a new method to derive the chemotaxis equation in the diffusion limit of the transport equation (3.4). We first list the assumptions on the turning kernel and turning rate.

3.1. Assumptions on the turning kernel and turning rate

In our analysis we adopt the assumptions of the turning kernel T in [18, 27, 15]. The notation used here coincides with that in [27, 15].

Define operator $\mathcal{T}$ and its adjoint $\mathcal{T}\ast$ : L²(V) → L²(V) as follows:

$$\left(\mathcal{T}g\right)\left(\mathrm{v}\right)={\int }_{V}T(\mathrm{v},{\mathrm{v}}^{\prime })g\left({\mathrm{v}}^{\prime }\right)d{\mathrm{v}}^{\prime },\left({\mathcal{T}}^{\ast }g\right)\left(\mathrm{v}\right)={\int }_{V}T({\mathrm{v}}^{\prime },\mathrm{v})g\left({\mathrm{v}}^{\prime }\right)d{\mathrm{v}}^{\prime }.$$ (3.5)

Denote by $\mathcal{K}$ to be the non-negative cone of $L^2\left(V\right),\mathcal{K}=\{g\in L^2\left(V\right)\mid g\ge 0\}$. The assumptions on the turning kernel T ∈ L²(V × V) are

A1

$T(\mathbf{v},{\mathbf{v}}^{\prime })\ge 0,{\int }_{V}T(\mathbf{v},{\mathbf{v}}^{\prime })d\mathbf{v}={\int }_{V}T({\mathbf{v}}^{\prime },\mathbf{v})d\mathbf{v}=1$.

A2

There are functions $u_0,\varphi ,\psi \in \mathcal{K}$ with the property u₀, ϕ > 0 a.e. such that $u_0\left(\mathbf{v}\right)\varphi \left({\mathbf{v}}^{\prime }\right)\le T(\mathbf{v},{\mathbf{v}}^{\prime })\le u_0\left(\mathbf{v}\right)\psi \left({\mathbf{v}}^{\prime }\right)$.

A3

$\parallel \mathcal{T}{\parallel }_{{\langle 1\rangle }^{\perp }}<1$.

From these assumptions, one can prove [18] that (a) $\mathcal{T}$ is a compact operator on L²(V), with spectral radius 1; (b) 1 is a simple eigenvalue with normalized eigenfunction g(v) ≡ 1.

Next define the operators

$$\mathcal{A}=-I+\mathcal{T},{\mathcal{A}}^{\ast }=-I+{\mathcal{T}}^{\ast }.$$ (3.6)

Note that the operator $\mathcal{L}$ defined in [27] is $\lambda \mathcal{A}$ here; in our derivation we use $\mathcal{A}$ instead of $\mathcal{L}$ because $\mathcal{A}$ is independent of y. One can easily prove that $\mathcal{A}$ has the following properties:

1. $\parallel \mathcal{A}\parallel \le 2$.

2. $\mathcal{N}\left(\mathcal{A}\right)=\mathcal{N}(\mathcal{A}\ast )=\langle 1\rangle$, $\mathcal{R}\left(\mathcal{A}\right)=\mathcal{R}(\mathcal{A}\ast )=\langle 1{\rangle }^{\perp }=\{g\in L^2\left(V\right)\mid {\int }_{V}g\left(\mathbf{v}\right)d\mathbf{v}=0\}$

3. $\forall \gamma$ with positive real part, $\gamma I-\mathcal{A}$ is invertible.

For the turning rate, we introduce a more general form than used in [14, 15]. We assume λ can be expanded to a Taylor series

$$\lambda ={\lambda }_0-a_1{z}_1+a_2{z}_1^2-a_3{z}_1^3+\cdots$$

with a radius of convergence at least max{G₀, 1}, which implies that

$$\sum _{k=1}^{\infty }\mid a_k\mid <\infty .$$ (3.7)

The negative signs in the expansion of λ are introduced for the convenience of later analysis. The form λ = λ₀ - by₁ used in [14, 15] is a special case of this general form with a₁ = b positive and a_k = 0 for all k > 1.

3.2. The parabolic scaling

To simplify the exposition we assume at first that excitation is much faster than other processes, that is, t_e = 0, z₁ = -z₂. The general result is simply stated later. Therefore the transport equation becomes

$$\begin{array}{c}\frac{\partial p}{\partial t}+{\nabla }_{\mathrm{x}}\cdot \left(\mathrm{v}p\right)+\frac{\partial }{\partial z_2}\left(-\frac{z_2}{t_a}-G^{\prime }\left(S\right)(\nabla S\cdot \mathrm{v}+\frac{\partial S}{\partial t})p\right)\hfill \\ \hfill =({\lambda }_0+a_1{z}_2+a_2{z}_2^2+\cdots )(-p+{\int }_{V}T(\mathrm{v},{\mathrm{v}}^{\prime })p\left({\mathrm{v}}^{\prime }\right)d{\mathrm{v}}^{\prime }).\end{array}$$ (3.8)

Since the total cell mass is conserved, we denote

$$N_0={\int }_{\Omega }{\int }_V{\int }_{\mathbb{R}}pd{z}_{2}d\mathrm{v}d\mathrm{x},$$ (3.9)

and scale p by setting,

$$\widehat{p}=\frac{p}{N_0}.$$ (3.10)

The mean run time of E. coli is T ≃ 1 s, the speed is 10 ~ 30 μm/s [4], and a self-organized aggregate of cells has spatial dimension of 150-250 μm [25]. Thus, let s₀ = 10 μm/s, L = 1 mm, and re-scale the variables by setting,

$$\begin{array}{c}\hfill \widehat{\mathrm{v}}=\frac{\mathrm{v}}{s_0},\widehat{x}=\frac{x}{L},\widehat{t}=\frac{t}{T_p},\widehat{V}=\frac{V}{s_0},\hfill \\ \hfill {\widehat{\lambda }}_0={\lambda }_{0}T,{\widehat{a}}_k=a_{k}T,{\widehat{t}}_a=\frac{t_a}{T},ϵ=\frac{T{s}_0}{L}=0.01,T_p=\frac{T}{{ϵ}^2}.\hfill \end{array}$$

Therefore, $\widehat{\mathbf{v}},\widehat{\mathbf{x}},{\widehat{t}}_a,{\widehat{\lambda }}_0,{\widehat{a}}_k\sim \mathcal{O}\left(1\right)$. We also re-scale

$$\widehat{S}=\frac{S}{K_D},\widehat{G}\left(\widehat{S}\right)=G\left(\widehat{S}{K}_D\right),\widehat{T}(\widehat{\mathrm{v}},{\widehat{\mathrm{v}}}^{\prime })=s_0^{N-1}T(\mathrm{v},{\mathrm{v}}^{\prime }),$$ (3.11)

where K_D is the binding constant defined earlier.

In these variables equation (3.8) becomes, after dropping the hats,

$$\begin{array}{c}\hfill {ϵ}^2\frac{\partial p}{\partial t}+ϵ{\nabla }_{\mathrm{x}}\cdot \left(\mathrm{v}p\right)+\frac{\partial }{\partial z_2}\left(-\frac{z_2}{t_a}-G^{\prime }\left(S\right)(ϵ\nabla S\cdot \mathrm{v}+{ϵ}^2\frac{\partial S}{\partial t})p\right)\hfill \\ \hfill =({\lambda }_0+a_1{z}_2+a_2{z}_2^2+\cdots )(-p+{\int }_{V}T(\mathrm{v},{\mathrm{v}}^{\prime })p\left({\mathrm{v}}^{\prime }\right)d{\mathrm{v}}^{\prime }).\hfill \end{array}$$ (3.12)

Here the space and time variation of S enters at $\mathcal{O}\left(ϵ\right)$ and $\mathcal{O}\left({ϵ}^2\right)$ respectively.

The goal of the moment closure method is to derive an approximating evolution equation for the cell density n(x,t) from the transport equation (3.12). To do that, we have to integrate (3.12) with respect to both z₂ and v ¹. There are two places that one can apply the perturbation expansion: (a) to the partial moments, viz, the z₂-moments or v-moments; or (b) to the complete moments which are obtained by integrating with respect to both z₂ and v. The latter will be used in Section 5 where there are external forces acting on the cells . However, in this section, we show that because the z₂-moment $M_0^0$ is independent of v, applying the perturbation method to the z₂-moments directly can lead to the approximating equation for n(x, t) with minimal assumptions.

3.3. The z₂-moment equations

Define the moments of z₂ as follows:

$$M_j=\int z_2^{j}pd{z}_2,\forall j=0,1,2,3,\dots ,\mathrm{M}={(M_0,M_1,M_2,\dots )}^t.$$ (3.13)

By multiplying equation (3.12) by 1, $z_2^j∕j$ for j ≥ 1 and integrating, we obtain the moment equations in the following compact form:

$${ϵ}^2\frac{\partial }{\partial t}\Lambda \mathrm{M}+ϵ\mathrm{v}\cdot {\nabla }_x\Lambda \mathrm{M}={ϵ}^2\mathrm{BM}+ϵ\mathrm{CM}+\mathrm{DM}.$$ (3.14)

Here

$$\mathrm{B}=-G^{\prime }\left(S\right)\frac{\partial S}{\partial t}{\mathbf{J}}^t,$$ (3.15)

$$\mathrm{C}=-G^{\prime }\left(S\right)(\nabla S\cdot \mathrm{v}){\mathbf{J}}^t,$$ (3.16)

and

$$\mathrm{D}=-\frac{1}{t_a}\text{diag}\{0,1,1,\cdots \}+\mathcal{A}\Lambda ({\lambda }_0\mathbf{I}+a_1\mathbf{J}+a_2{\mathbf{J}}^2+\cdots ),$$ (3.17)

where $\mathcal{A}$ is the operator defined in (3.6), $\Lambda :l^{\infty }\left(L^2\left(V\right)\right)\to l^{\infty }\left(L^2\left(V\right)\right)$ is a diagonal scaling operator $\Lambda =\mathrm{diag}\{1,1,\frac{1}{2},\frac{1}{3},\cdots \}$, and $\mathbf{J}:l^{\infty }\left(L^2\left(V\right)\right)\to l^{\infty }\left(L^2\left(V\right)\right)$ is the shift operator that has ones on the upper diagonal entries:

$$\mathbf{J}=\left[\begin{array}{cccc}\hfill 0\hfill & \hfill 1\hfill & \hfill 0\hfill & \hfill \dots \hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 1\hfill & \hfill \dots \hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill \dots \hfill \\ \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill \ddots \hfill \end{array}\right].$$ (3.18)

One can easily prove that J has the following properties:

$${\parallel \mathbf{J}\parallel }_{l^{\infty }\left(L^2\left(V\right)\right)}=1,\text{ker}\left(\mathbf{J}\right)=<{(1,0,0,0,\cdots )}^t>,$$ (3.19)

$$\left\{0\right\}\subset \text{ker}\left(\mathbf{J}\right)\subset \text{ker}\left({\mathbf{J}}^2\right)\subset \cdots \subset \text{ker}\left({\mathbf{J}}^k\right)\subset \cdots \subset l^{\infty }\left(L^2\left(V\right)\right),$$ (3.20)

$$\bigcup _{k=1}^{\infty }\text{ker}\left({\mathbf{J}}^k\right)⫋l^{\infty }\left(L^2\left(V\right)\right).$$ (3.21)

Therefore, B and C are bounded linear operators on l^∞(L²(V)). One can also easily prove that D is a bounded linear operator on l^∞(L²(V)) under the assumptions on the turning kernel and turning rate introduced in Section 3.1.

Since we are interested in the long-time dynamics, we will apply the regular perturbation method to solve the system (3.14). We explore two sets of assumptions. In the first, we assume that ${\widehat{G}}^{\prime }\left(\widehat{S}\right)\frac{\partial \widehat{S}}{\partial \widehat{t}}$ and ${\widehat{G}}^{\prime }\left(\widehat{S}\right)\nabla \widehat{S}\cdot \widehat{\mathbf{v}}$ are of $\mathcal{O}\left(1\right)$ on the parabolic scale, which corresponds to $G^{\prime }\left(S\right)\frac{\partial S}{\partial t}\sim \mathcal{O}\left({ϵ}^2\right){\sec }^{-1}$ and $G^{\prime }\left(S\right)\nabla S\cdot \mathbf{v}\sim \mathcal{O}\left(ϵ\right){\sec }^{-1}$ in the original variables. We show in Section 3.5 that this assumption leads to the same chemotaxis equation as in [15]. In the second, we relax the first set of assumptions to allow ${\widehat{G}}^{\prime }\left(\widehat{S}\right)\frac{\partial \widehat{S}}{\partial \widehat{t}}$ to be $\mathcal{O}\left(\frac{1}{ϵ}\right)$, or $G^{\prime }\left(S\right)\frac{\partial S}{\partial t}\sim \mathcal{O}\left(ϵ\right){\sec }^{-1}$. This assumption means that a cell doesn't experience a significant change in the fraction of receptors bound during an average run time. If the gradient is very large, this assumption may be violated and the characteristic space and time scale may be very different from those of the diffusion process. Therefore, the solution of the diffusion-limit chemotaxis equation may not be a good approximation of the underlying velocity-jump process at the location where sharp spikes of the attractant arise. For this set of assumptions, we show in Section 3.7 that the equation for the first order approximation n⁰ of the cell density remains the same, but the equation for higher order terms n^j depends on $\frac{\partial S}{\partial t}$. First however we prove a solvability theorem that will be used in the asymptotic analysis.

3.4. A solvability theorem

For k ≥ 1, we introduce sub-matrix operators of D defined by partitioning D as follows

$$\mathbf{D}=\left[\begin{array}{cc}\hfill {\mathbf{E}}_k\hfill & \hfill {\mathbf{F}}_k\hfill \\ \hfill 0\hfill & \hfill {\mathbf{G}}_k\hfill \end{array}\right].$$

Here E_k is the upper-left k×k submatrix of D, F_k is the upper-right k × ∞ submatrix, and G_k is the lower-right remainder. Written out,

$${\mathbf{E}}_1=\left[{\lambda }_0\mathcal{A}\right],{\mathbf{F}}_1=\mathcal{A}[a_1,a_2,\cdots ],$$

and for k > 1,

$${\mathbf{E}}_k=\left[\begin{array}{cccc}\hfill {\lambda }_0\mathcal{A}\hfill & \hfill a_1\mathcal{A}\hfill & \hfill \dots \hfill & \hfill a_{k-1}\mathcal{A}\hfill \\ \hfill 0\hfill & \hfill {\lambda }_0\mathcal{A}-\frac{1}{t_a}\hfill & \hfill \dots \hfill & \hfill a_{k-2}\mathcal{A}\hfill \\ \hfill \dots \hfill & \hfill \dots \hfill & \hfill \dots \hfill & \hfill \dots \hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill \dots \hfill & \hfill \frac{{\lambda }_0}{k-1}\mathcal{A}-\frac{1}{t_a}\hfill \end{array}\right],{\mathbf{F}}_k=\mathcal{A}\left[\begin{array}{cccc}\hfill a_k\hfill & \hfill a_{k+1}\hfill & \hfill a_{k+2}\hfill & \hfill \dots \hfill \\ \hfill a_{k-1}\hfill & \hfill a_k\hfill & \hfill a_{k+1}\hfill & \hfill \dots \hfill \\ \hfill \dots \hfill & \hfill \dots \hfill & \hfill \dots \hfill & \hfill \dots \hfill \\ \hfill \frac{a_1}{k-1}\hfill & \hfill \frac{a_2}{k-1}\hfill & \hfill \frac{a_3}{k-1}\hfill & \hfill \dots \hfill \end{array}\right],$$

for any k ≥ 1,

$${\mathbf{G}}_k=-\frac{1}{t_a}\mathbf{I}+\mathcal{A}\mathrm{diag}\left\{\frac{1}{k},\frac{1}{k+1},\frac{1}{k+2},\cdots \right\}({\lambda }_0\mathbf{I}+a_1\mathbf{J}+a_2{\mathbf{J}}^2+\cdots )=-\frac{1}{t_a}\mathbf{I}+\mathcal{A}{\Lambda }_k\Phi ,$$

with ${\Lambda }_k:=\mathrm{diag}\{\frac{1}{k},\frac{1}{k+1},\frac{1}{k+2},\cdots \}$ and $\Phi ≔{\lambda }_0\mathbf{I}+a_1\mathbf{J}+a_2{\mathbf{J}}^2+\cdots$.

Since components of D are operators on the space L²(V), E_k is an operator on (L²(V))^k. Also by the assumption on the turning rate (3.7), F_k : l^∞(L²(V)) → (L²(V))^k, G_k : l^∞ (L²(V)) → l^∞(L²(V)). In the following theorem we prove that for any k, the operators G_k are bounded and invertible. We denote the l^∞(L²(V)) norm by $\parallel \cdot \parallel$ and the corresponding operator norm by $\parallel \mid \cdot \mid \parallel$.

Theorem 3.1. For any k ≥ 1, we have that

1. G_k is bounded with $\parallel \mid {\mathbf{G}}_k\mid \parallel \le \frac{1}{t_a}+\frac{1}{k}\parallel \mathcal{A}{\parallel }_{L^2\left(V\right)}({\lambda }_0+{\sum }_{j=1}^{\infty }\mid a_j\mid )$;

2. G_k is invertible, i.e.,${\mathbf{G}}_k\mathbf{W}=0,\mathbf{W}\in l^{\infty }\left(L^2\left(V\right)\right)\Rightarrow \mathbf{W}=0$.

Proof. (i) $\forall \mathbf{W}\in l^{\infty }\left(L^2\left(V\right)\right)$, we have

$$\begin{array}{c}\hfill \parallel \Phi \mathbf{W}\parallel =\underset{i=1}{\overset{\infty }{\max }}\parallel {\lambda }_0{W}_i+\sum _{j=1}^{\infty }{a}_j{W}_{i+j}\parallel \le \parallel \mathbf{W}\parallel \cdot (\mid {\lambda }_0\mid +\sum _{j=1}^{\infty }\mid a_j\mid ),\hfill \\ \hfill \parallel {\Lambda }_k\mathbf{W}\parallel =\underset{i=1}{\overset{\infty }{\max }}\mid \frac{1}{k+i-1}{W}_i\mid \le \frac{1}{k}\parallel \mathbf{W}\parallel ,\hfill \\ \hfill \parallel \mathcal{A}\mathbf{W}\parallel \le {\parallel \mathcal{A}\parallel }_{L^2\left(V\right)}\cdot \parallel \mathbf{W}\parallel .\hfill \end{array}$$

Therefore, Φ, Λ_k and $\mathcal{A}$ are bounded operators on l^∞(L²(V)). Since ${\mathbf{G}}_k=-\frac{1}{t_a}\mathbf{I}+\mathcal{A}{\Lambda }_k\Phi$, we have

$$\parallel \mid {\mathbf{G}}_k\mid \parallel \le \frac{1}{t_a}+{\parallel \mathcal{A}\parallel }_{L^2\left(V\right)}\parallel \mid {\Lambda }_k\mid \parallel \parallel \mid \Phi \mid \parallel \le \frac{1}{t_a}+\frac{1}{k}{\parallel \mathcal{A}\parallel }_{L^2\left(V\right)}({\lambda }_0+\sum _{j=1}^{\infty }\mid a_j\mid ).$$

(ii) For $k>t_a\parallel \mathcal{A}{\parallel }_{L^{2}V}\parallel \mid \Phi \mid \parallel$, we have $\parallel \mid t_a\mathcal{A}{\Lambda }_k\Phi \mid \parallel <1$. Therefore G_k is invertible with ${\mathbf{G}}_k^{-1}=-\frac{1}{t_a}{\sum }_{i=0}^{\infty }(t_a\mathcal{A}{\Lambda }_k\Phi {)}^i,i.e.,{\mathbf{G}}_k\mathbf{W}=0\Rightarrow \mathbf{W}=0$.

For $k\le t_a\parallel \mathcal{A}{\parallel }_{L^{2}V}\parallel \mid \Phi \mid \parallel$, find $m>0s.t.k+m>t_a\parallel \mathcal{A}\parallel \parallel \Phi \parallel$. Since G_k is upper triangular, we get $W_j=0,\forall j\ge m$ by observing G_k+m is invertible; we then apply Gaussian elimination to the first m - 1 equations in G_kW = 0 from the (m - 1)th row back to the 1st row to get W_j = 0, j < m. Property (iii) of the operator $\mathcal{A}$ guarantees that Gaussian elimination applies. This completes the proof.

3.5. The asymptotic analysis of (3.14)

Write M as an expansion in powers of ϵ as

$$\mathrm{M}={\mathrm{M}}^0+ϵ{\mathrm{M}}^1+{ϵ}^2{\mathrm{M}}^2+\cdots$$ (3.22)

or

$$\left(\begin{array}{c}\hfill M_0\hfill \\ \hfill M_1\hfill \\ \hfill M_2\hfill \\ \hfill M_3\hfill \\ \hfill ⋮\hfill \end{array}\right)=\left(\begin{array}{c}\hfill M_0^0\hfill \\ \hfill M_1^0\hfill \\ \hfill M_2^0\hfill \\ \hfill M_3^0\hfill \\ \hfill ⋮\hfill \end{array}\right)+ϵ\left(\begin{array}{c}\hfill M_0^1\hfill \\ \hfill M_1^1\hfill \\ \hfill M_2^1\hfill \\ \hfill M_3^1\hfill \\ \hfill ⋮\hfill \end{array}\right)+{ϵ}^2\left(\begin{array}{c}\hfill M_0^2\hfill \\ \hfill M_1^2\hfill \\ \hfill M_2^2\hfill \\ \hfill M_3^2\hfill \\ \hfill ⋮\hfill \end{array}\right)+\cdots .$$ (3.23)

The subscript indicates the order of the z₂-moment and the superscript indicates the order of the term in the expansion.

After substituting (3.22) into the evolution equation (3.14) and comparing terms we find that $\mathcal{O}\left({ϵ}^0\right)$:

$${\mathbf{DM}}^0=0.$$

By Theorem 3.1, we have

$$\mathcal{A}{M}_0^0=0\&M_j^0=0,\forall j>0.$$ (3.24)

By property (ii) of $\mathcal{A}$, we have $M_0^0$ independent of v, i.e., $M_0^0=M_0^0(\mathbf{x},t)$. Then at $\mathcal{O}\left({ϵ}^1\right)$:

$$\mathbf{v}\cdot {\nabla }_{\mathbf{x}}\Lambda {\mathbf{M}}^0={\mathbf{CM}}^0+{\mathbf{DM}}^1,$$

or by using (3.24)

$$\left[\begin{array}{c}\hfill \mathbf{v}\cdot {\nabla }_{\mathbf{x}}{M}_0^0\hfill \\ \hfill G\prime \left(S\right)\nabla S\cdot \mathbf{v}{M}_0^0\hfill \\ \hfill 0\hfill \\ \hfill 0\hfill \\ \hfill ⋮\hfill \end{array}\right]={\mathbf{DM}}^1=\left[\begin{array}{cc}\hfill {\mathbf{E}}_2\hfill & \hfill {\mathbf{F}}_2\hfill \\ \hfill 0\hfill & \hfill {\mathbf{G}}_2\hfill \end{array}\right]{\mathbf{M}}^1.$$

Again, by Theorem 3.1, we have $M_j^1=0,\forall j>1$, and the problem reduces to solving

$$\begin{array}{cc}\hfill \mathbf{v}\cdot {\nabla }_{\mathbf{x}}{M}_0^0& ={\lambda }_0\mathcal{A}{M}_0^1+a_1\mathcal{A}{M}_1^1,\hfill \\ \hfill G\prime \left(S\right)\nabla S\cdot \mathbf{v}{M}_0^0& =({\lambda }_0\mathcal{A}-\frac{1}{t_a})M_1^1.\hfill \end{array}$$

By property (iii) of $\mathcal{A},{\lambda }_0\mathcal{A}-\frac{1}{t_a}$ is invertible, and thus,

$$\begin{array}{c}\hfill M_1^1={({\lambda }_0\mathcal{A}-\frac{1}{t_a})}^{-1}G\prime \left(S\right)\nabla S\cdot \mathbf{v}{M}_0^0,\hfill \\ \hfill \mathcal{A}{M}_0^1=\frac{1}{{\lambda }_0}\mathbf{v}\cdot {\nabla }_{\mathbf{x}}{M}_0^0-\frac{a_1{t}_a}{{\lambda }_0}\mathcal{A}{(t_a{\lambda }_0\mathcal{A}-1)}^{-1}G\prime \left(S\right)\nabla S\cdot \mathbf{v}{M}_0^0.\hfill \end{array}$$

By property (ii) of $\mathcal{A}$, 0 is a simple eigenvalue, and we can define a pseudo-inverse operator of $\mathcal{A}$ as $\mathcal{B}={\left(\mathcal{A}{{\mid }_{\langle 1\rangle }}^{\perp }\right)}^{-1}$. Therefore, we obtain the representation,

$$M_0^1=\mathcal{B}\frac{1}{{\lambda }_0}\mathbf{v}\cdot {\nabla }_{\mathbf{x}}{M}_0^0-\frac{a_1{t}_a}{{\lambda }_0}{(t_a{\lambda }_0\mathcal{A}-1)}^{-1}G\prime \left(S\right)\nabla S\cdot \mathbf{v}{M}_0^0+P_1,$$ (3.25)

where $P_1\in \langle 1\rangle$, i.e.,P₁ = P₁(x, t), is arbitrary. Notice that $n^1={\int }_V{M}_0^{1}d\mathbf{v}=P_1\mid V\mid$; thus n¹ can be determined once P₁ is known. At $\mathcal{O}\left({ϵ}^2\right)$:

$$\frac{\partial }{\partial t}\Lambda {\mathbf{M}}^0+\mathbf{v}\cdot {\nabla }_{\mathbf{x}}\Lambda {\mathbf{M}}^1={\mathbf{BM}}^0+{\mathbf{CM}}^1+{\mathbf{DM}}^2.$$

The first equation of the system implies that

$$\frac{\partial }{\partial t}{M}_0^0+{\nabla }_{\mathbf{x}}\cdot \mathbf{v}{M}_0^1\in \mathcal{R}\left(\mathcal{A}\right).$$

By property (ii) of $\mathcal{A}$,

$${\int }_V\left(\frac{\partial }{\partial t}{M}_0^0+\mathbf{v}\cdot {\nabla }_{\mathbf{x}}{M}_0^1\right)d\mathbf{v}=0.$$

Using (3.25), we get an equation for $M_0^0$

$$\begin{array}{cc}\hfill \mid V\mid \frac{\partial }{\partial t}{M}_0^0+& \frac{1}{{\lambda }_0}{\nabla }_{\mathbf{x}}\cdot {\int }_V\mathbf{v}\mathcal{B}\mathbf{v}\cdot {\nabla }_{\mathbf{x}}{M}_0^{0}d\mathbf{v}\hfill \\ \hfill & -\frac{a_1{t}_a}{{\lambda }_0}{\nabla }_{\mathbf{x}}\cdot {\int }_V(\mathbf{v}{(t_a{\lambda }_0\mathcal{A}-1)}^{-1}G\prime \left(S\right)\nabla S\cdot \mathbf{v}{M}_0^0)d\mathbf{v}=0.\hfill \end{array}$$ (3.26)

By defining

$$D_n=-\frac{1}{\mid V\mid {\lambda }_0}{\int }_V\mathbf{v}\otimes \mathcal{B}\mathbf{v}d\mathbf{v}$$ (3.27)

and

$$\chi \left(S\right)=-\frac{a_1{t}_a}{\mid V\mid {\lambda }_0}G\prime \left(S\right){\int }_V\mathbf{v}\otimes {(t_a{\lambda }_0\mathcal{A}-1)}^{-1}\mathbf{v}d\mathbf{v},$$ (3.28)

we can rewrite equation (3.26) as

$$\frac{\partial }{\partial t}{M}_0^0={\nabla }_{\mathbf{x}}\cdot (D_n{\nabla }_{\mathbf{x}}{M}_0^0-\chi \left(S\right)M_0^0{\nabla }_{\mathbf{x}}S).$$ (3.29)

The cell density n(x, t) is defined as

$$\begin{array}{cc}\hfill n& ={\int }_V{\int }_{Z}p(x,v,z_2,t)d{z}_{2}d\mathbf{v}={\int }_V{M}_0(x,v,t)d\mathbf{v}\hfill \\ \hfill & ={\int }_V(M_0^0+ϵM_0^1+{ϵ}^2{M}_0^2+\cdots )d\mathbf{v}.\hfill \end{array}$$

By expanding $n=n^0+ϵn^1+{ϵ}^2{n}^2+\cdots$, we find that

$$n^i={\int }_V{M}_0^{i}d\mathbf{v},\forall i\ge 0.$$

In particular, $n^0=\mid V\mid M_0^0$, thus $n=\mid V\mid M_0^0+\mathcal{O}\left(ϵ\right)$, and therefore we obtain the chemotaxis equation

$$\frac{\partial }{\partial t}{n}^0={\nabla }_{\mathbf{x}}\cdot (D_n{\nabla }_{\mathbf{x}}{n}^0-\chi \left(S\right)n^0{\nabla }_{\mathbf{x}}S)$$ (3.30)

with a general tensor form of the diffusion rate (3.27) and the chemotaxis sensitivity (3.28).

Our standing assumption is that the cell speed is constant, and thus V is the sphere of radius $s=\sqrt{\mathbf{v}\cdot \mathbf{v}}$ in 3-D. In the case that cells change direction of movement purely randomly, the turning kernel is given by the uniform density

$$T(v,v\prime )=\frac{1}{\mid V\mid }.$$ (3.31)

In this case, the tensors D_n and $\chi \left(S\right)$ can be reduced to diagonal matrices, and thus scalars,

$$D_n=\frac{s^2}{N{\lambda }_0}I,\chi \left(S\right)=G^{\prime }\left(S\right)\frac{a_1{s}^2{t}_a}{N{\lambda }_0(1+t_a{\lambda }_0)}.$$ (3.32)

As a result, we obtain the classical chemotaxis equation for n⁰

$$\frac{\partial }{\partial t}{n}^0={\nabla }_{\mathrm{x}}\cdot \left(\frac{s^2}{N{\lambda }_0}{\nabla }_{\mathrm{x}}{n}^0-G^{\prime }\left(S\right)\frac{a_1{s}^2{t}_a}{N{\lambda }_0(1+t_a{\lambda }_0)}{n}^0{\nabla }_{\mathrm{x}}S\right).$$ (3.33)

It is observed experimentally that the movement of E. coli shows directional persistence, and the turning kernel only depends on the angle θ between the old direction v^′ and the new direction v [6, 23], i.e.,

$$T(\mathbf{v},{\mathbf{v}}^{\prime })=h\left(\theta \right).$$ (3.34)

In this case, $\mathcal{T}$ is a symmetric operator, the average velocity $\stackrel{‒}{\mathbf{v}}$ after reorientation

$$\stackrel{‒}{\mathbf{v}}={\int }_{V}T(\mathbf{v},{\mathbf{v}}^{\prime })\mathbf{v}d\mathbf{v}$$

is parallel to the previous velocity v, and thus the diffusion rate and the chemotaxis sensitivity are isotropic tensors (cf. [18], Theorem 3.5). As a result, one finds that $\mathcal{A}\mathbf{v}=-(1-{\psi }_d)\mathbf{v}$ and

$$D_n=\frac{s^2}{N(1-{\psi }_d){\lambda }_0}I,\chi \left(S\right)=G^{\prime }\left(S\right)\frac{a_1{s}^2{t}_a}{N{\lambda }_0(1+(1-{\psi }_d)t_a{\lambda }_0)},$$ (3.35)

where

$${\psi }_d=\frac{\stackrel{‒}{\mathbf{v}}\cdot {\mathbf{v}}^{\prime }}{s^2}\in [-1,1]$$ (3.36)

is the index of directional persistence introduced in [26]. We note that ψ_d can not be 1 in order to satisfy Assumption 2 on the turning kernel, andψ_d has been reported to be about 0.33 in the wild-type E. coli [4]. From (3.35), we can see that the larger ψ_d is, the larger D_n and χ are, and therefore the larger the macroscopic chemotaxis velocity ${\mathbf{u}}_S=\chi \left(S\right)\nabla S$. The increase of u_S to the persistence has also been analyzed in [21], where weak chemotaxis coupled with rotational diffusion was analyzed.

3.6. Macroscopic equations for higher order terms and a finite excitation rate

In order to obtain equations for higher order approximations of the cell density n(x, t), we can repeat the above calculation. The full equation system at $\mathcal{O}\left({ϵ}^2\right)$ is

$$\left[\begin{array}{c}\hfill \frac{\partial }{\partial t}{M}_0^0+\mathbf{v}\cdot {\nabla }_{\mathrm{x}}{M}_0^1\hfill \\ \hfill \mathbf{v}\cdot {\nabla }_{\mathrm{x}}{M}_1^1+G^{\prime }\left(S\right)(\frac{\partial S}{\partial t}{M}_0^0+(\nabla S\cdot \mathbf{v})M_0^1)\hfill \\ \hfill G^{\prime }\left(S\right)\nabla S\cdot \mathbf{v}{M}_1^1\hfill \\ \hfill 0\hfill \\ \hfill ⋮\hfill \end{array}\right]=\left[\begin{array}{c}\hfill {\lambda }_0\mathcal{A}{M}_0^2+a_1\mathcal{A}{M}_1^2+a_2\mathcal{A}{M}_2^2+\cdots \hfill \\ \hfill ({\lambda }_0\mathcal{A}-\frac{1}{t_a})M_1^2+a_1\mathcal{A}{M}_2^2+\cdots \hfill \\ \hfill (\frac{{\lambda }_0}{2}\mathcal{A}-\frac{1}{t_a})M_2^2+\cdots \hfill \\ \hfill (\frac{{\lambda }_0}{3}\mathcal{A}-\frac{1}{t_a})M_3^2+\cdots \hfill \\ \hfill ⋮\hfill \end{array}\right].$$

By reasoning as before, we find that $M_j^2=0,\forall j\ge 3$ and

$$M_2^2=2{({\lambda }_0\mathcal{A}-\frac{2}{t_a})}^{-1}{G}^{\prime }\left(S\right)(\nabla S\cdot \mathbf{v})M_1^1,$$

$$M_1^2={({\lambda }_0\mathcal{A}-\frac{1}{t_a})}^{-1}(\mathbf{v}\cdot {\nabla }_{\mathrm{x}}{M}_1^1+G^{\prime }\left(S\right)\frac{\partial S}{\partial t}{M}_0^0+G^{\prime }\left(S\right)(\nabla S\cdot \mathbf{v})M_0^1-a_1\mathcal{A}{M}_2^2),$$

$$M_0^2=\frac{\mathcal{B}}{{\lambda }_0}\mathbf{v}\cdot {\nabla }_{\mathrm{x}}{M}^1-\frac{a_1}{{\lambda }_0}{M}_1^2-\frac{a_2}{{\lambda }_0}{M}_2^2+P_2.$$

Here, the term $(\mathcal{B}∕{\lambda }_0)(\partial ∕\partial t{M}_0^0)$ in $M_0^2$ is absorbed into the v-independent term P₂. By considering the solvability condition of equations at the next order of ε, the equation for P₁, and therefore, for $n^1=P_1\mid V\mid$, can be obtained. Calculation reveals that the equation for n¹ is the same as n⁰ in case that v is an eigenfunction of $\mathcal{T}$, in particular for the turning kernel (3.34),

$$\frac{\partial }{\partial t}{n}^1={\nabla }_{\mathrm{x}}\cdot \left(\frac{s^2}{N(1-{\psi }_d){\lambda }_0}{\nabla }_{\mathrm{x}}{n}^1-G^{\prime }\left(S\right)\frac{a_1{s}^2{t}_a}{N{\lambda }_0(1+(1-{\psi }_d)t_a{\lambda }_0)}{n}^1{\nabla }_{\mathrm{x}}S\right).$$

If we force n⁰ to satisfy the initial and boundary conditions of those for the cell density n, the higher order terms n^j, j > 0 should satisfy homogeneous initial and boundary conditions, and the zero mean constraint. Therefore, we conclude that $n^1\equiv 0$, and thus, $n=n^0+\mathcal{O}\left({ϵ}^2\right)$.

By allowing a finite excitation time in the cartoon model, one can show that the chemotaxis sensitivity tensor becomes

$$\chi \left(S\right)=\frac{a_1{t}_a}{\mid V\mid {\lambda }_0}{G}^{\prime }\left(S\right){\int }_V\mathbf{v}\otimes (t_e{\lambda }_0\mathcal{A}-1{)}^{-1}(t_a{\lambda }_0\mathcal{A}-1{)}^{-1}\mathbf{v}d\mathbf{v},$$ (3.37)

as in [15], and using the turning kernel (3.34), the chemotaxis equation becomes

$$\frac{\partial }{\partial t}{n}^0=\nabla \cdot \left(\frac{s^2}{N(1-{\psi }_d){\lambda }_0}\nabla n^0-\frac{a_1{s}^2{t}_a{G}^{\prime }\left(S\right)}{N{\lambda }_0(1+(1-{\psi }_d)t_a{\lambda }_0)(1+(1-{\psi }_d)t_e{\lambda }_0)}{n}^0\nabla S\right).$$ (3.38)

From this equation we can see that: (a) directional persistence increases both the diffusion rate and the macroscopic chemotactic velocity, as analyzed in [21]; (b) inclusion of the non-instantaneous excitation results in re-scaled chemotaxis sensitivity. The only difference by using the full cartoon model is, that instead of using matrix representations of M and operators B, C, D, block matrices should be used. A similar version of Theorem 3.1 can be proved without difficulty. One can also show that inclusion of a resting phase due to tumbling would result in a diffusion rate and chemotaxis sensitivity rescaled by the fraction of time spent running.

3.7. A weaker assumption on the extracellular signal

In the above derivation we assumed that $G^{\prime }\left(S\right)\frac{\partial S}{\partial \widehat{t}}\sim \mathcal{O}\left(1\right)$ on the parabolic (diffusion) time scale. However, when cells contribute to the signal field by secretion (example 4.2), $G^{\prime }\left(S\right)\frac{\partial S}{\partial t}$ can become large when the cell density is large. Here we relax the assumption to allow $G^{\prime }\left(S\right)\frac{\partial S}{\partial t}\sim \mathcal{O}\left(\frac{1}{ϵ}\right)$ on the parabolic time scale, which is $\mathcal{O}\left(ϵ\right){\sec }^{-1}$ in the dimensional variables. Under this assumption, we need to regroup the terms in the z₂-moment equation (3.14). We define ${\stackrel{‒}{S}}_t=ϵ\frac{\partial \widehat{S}}{\partial \widehat{t}}\sim \mathcal{O}\left(1\right),\stackrel{‒}{B}=ϵ\mathbf{B}\sim \mathcal{O}\left(1\right)$, then equation (3.14) can be rewritten as

$${ϵ}^2\frac{\partial }{\partial t}\Lambda \mathbf{M}+ϵ\mathbf{v}\cdot {\nabla }_x\Lambda \mathbf{M}=ϵ(\stackrel{‒}{B}+\mathbf{C})\mathbf{M}+\mathbf{DM}.$$ (3.39)

In this case, the equations at $\mathcal{O}\left(ϵ\right)$ are

$$\mathbf{v}\cdot {\nabla }_{\mathbf{x}}\Lambda {\mathbf{M}}^0=(\stackrel{‒}{B}+\mathbf{C}){\mathbf{M}}^0+{\mathbf{DM}}^1,$$

from which one finds that

$$M_1^1=({\lambda }_0\mathcal{A}-\frac{1}{t_a}{)}^{-1}{G}^{\prime }\left(S\right)({\stackrel{‒}{S}}_t+\nabla S\cdot \mathbf{v})M_0^0,$$ (3.40)

$$M_0^1=\mathcal{B}\frac{1}{{\lambda }_0}\mathbf{v}\cdot {\nabla }_{\mathbf{x}}{M}_0^0-\frac{a_1{t}_a}{{\lambda }_0}(t_a{\lambda }_0\mathcal{A}-1{)}^{-1}{G}^{\prime }\left(S\right)\nabla S\cdot \mathbf{v}{M}_0^0+P_1.$$ (3.41)

In the representation of $M_0^1$ (3.41), the term ${(t_a{\lambda }_0\mathcal{A}-1)}^{-1}{G}^{\prime }\left(S\right){\stackrel{‒}{S}}_t{M}_0^0$ is absorbed by P₁, since it is independent of v. Therefore the equation for n⁰ remains the same, i.e., (3.30). However, if we continue the calculation for higher order terms, we obtain

$$M_2^2=2({\lambda }_0\mathcal{A}-\frac{2}{t_a}{)}^{-1}{G}^{\prime }\left(S\right)({\stackrel{‒}{S}}_t+\nabla S\cdot \mathbf{v})M_1^1,$$

$$M_1^2=({\lambda }_0\mathcal{A}-\frac{1}{t_a}{)}^{-1}(\mathbf{v}\cdot {\nabla }_{\mathbf{x}}{M}_1^1+G^{\prime }\left(S\right)({\stackrel{‒}{S}}_t+\nabla S\cdot \mathbf{v})M_0^1-a_1\mathcal{A}{M}_2^2),$$

$$M_0^2=\frac{\mathcal{B}}{{\lambda }_0}\mathbf{v}\cdot {\nabla }_{\mathbf{x}}{M}_0^1-\frac{a_1}{{\lambda }_0}{M}_1^2-\frac{a_2}{{\lambda }_0}{M}_2^2+P_2.$$

Here a₁, a₂, $\nabla S,{\stackrel{‒}{S}}_t$, n⁰ and $\nabla n^0$ enter the expression of $M_0^2$, and by considering the solvability condition at $\mathcal{O}\left({ϵ}^3\right)$,

$${\int }_V\frac{\partial }{\partial t}{M}_0^1+\mathbf{v}\cdot {\nabla }_{\mathbf{x}}{M}_0^{2}d\mathbf{v}=0,$$

we obtain an equation for n¹,

$$\frac{\partial }{\partial t}{n}^1={\nabla }_{\mathbf{x}}\cdot \left[\frac{s^2}{N{\lambda }_0(1-{\psi }_d)}{\nabla }_{\mathbf{x}}{n}^1-G^{\prime }\left(S\right)\frac{a_1{s}^2{t}_a}{N{\lambda }_0(1+t_a{\lambda }_0(1-{\psi }_d))}{n}^1{\nabla }_{\mathbf{x}}S\right]+h(a_1,a_2,\nabla S,{\stackrel{‒}{S}}_t,n^0,\nabla n^0,\cdots ).$$ (3.42)

The first-order term n⁰ enters into the equation for n¹ through the function h which is linear in n⁰. In particular, for the turning kernel (3.34), h has the form

$$\begin{array}{cc}\hfill h=& \nabla \cdot [\frac{a_1{t}_a^2{s}^2\nabla \left(G^{\prime }\left(S\right){\stackrel{‒}{S}}_t{n}^0\right)}{N{\lambda }_0(1+{\lambda }_0{t}_a(1-{\psi }_d){)}^2}\phantom{]}\hfill \\ \hfill & +\frac{a_1{t}_a{s}^2{G}^{\prime }\left(S\right){\stackrel{‒}{S}}_t}{N{\lambda }_0(1+t_a{\lambda }_0(1-{\psi }_d))}\left(\frac{\nabla n^0}{{\lambda }_0(1-{\psi }_d)}-\frac{a_1{t}_a{n}^0{G}^{\prime }\left(S\right)\nabla S}{{\lambda }_0(1+t_a{\lambda }_0(1-{\psi }_d))}\right)\hfill \\ \hfill & \phantom{[}+\left(\frac{a_1^2{t}_a(1-{\psi }_d)}{{\lambda }_0(1+{\lambda }_0{t}_a(1-{\psi }_d))}+\frac{a_2}{{\lambda }_0}\right)\frac{4t_a^2{s}^2{n}^0{G}^{\prime }\left(S\right){\stackrel{‒}{S}}_t\nabla S}{N(2+{\lambda }_0{t}_a(1-{\psi }_d))(1+{\lambda }_0{t}_a(1-{\psi }_d))}].\hfill \end{array}$$

In this case, the solution of the n¹-equation is generally nonzero, and therefore $n=n^0+ϵn^1+\mathcal{O}\left({ϵ}^2\right)$, in contrast with the previous case.

4. Numerical comparisons

According to the above perturbation analysis, the bacterial cell-based model in Section 2 can be approximated by the solution of the chemotaxis equation (3.38) when coupled with an equation for the signal. In this section we first present two examples in 1-D to illustrate how accurate the approximation is. In both examples, we assume no cell growth and fast excitation, i.e., t_e = 0; thus the equations for the internal dynamics become

$$\frac{d{y}_2}{dt}=\frac{G\left(S(\mathbf{x},t)\right)-y_2}{t_a},$$ (4.1)

$$y_1=G\left(S\right)-y_2.$$ (4.2)

with G(S) defined by (2.4). We also assume no persistence (ψ_d = 0), and the turning rate

$$\lambda ={\lambda }_0-\frac{2{\lambda }_0}{\pi }ta{n}^{-1}\left(\frac{y_1\pi b}{2{\lambda }_0}\right),$$ (4.3)

which has the Taylor expansion,

$$\lambda ={\lambda }_0-b{y}_1+\cdots .$$

In this case, we compare with the stochastic simulation with the solution of

$$\frac{\partial }{\partial t}{n}^0={\nabla }_{\mathbf{x}}\cdot \left(\frac{s^2}{N{\lambda }_0}{\nabla }_{\mathbf{x}}{n}^0-G^{\prime }\left(S\right)\frac{b{s}^2{t}_a}{N{\lambda }_0(1+t_a{\lambda }_0)}{n}^0{\nabla }_{\mathbf{x}}S\right).$$ (4.4)

We then apply the 2-D version of both the continuum model and the cell-based model to the network-aggregate formation in E. coli colonies in Section 4.3. The numerical method used in implementing the cell-based model is described in detail in Appendix A.

4.1. Aggregation and dispersion in one space dimension

In this example we analyze the motion of a bacterial population in response to a diffusing attractant on a periodic domain 4 mm long. The dynamics of the attractant are described by the diffusion equation

$$\frac{\partial S}{\partial t}=D_s\Delta S,$$ (4.5)

with the initial condition

$$S(x,0)=80(1-\mid 1-x\mid ).$$ (4.6)

Here, we use a nondimensional signal S. We suppose that initially the cells are uniformly distributed in the domain at a density n(x,0) = n₀ mm^-1.

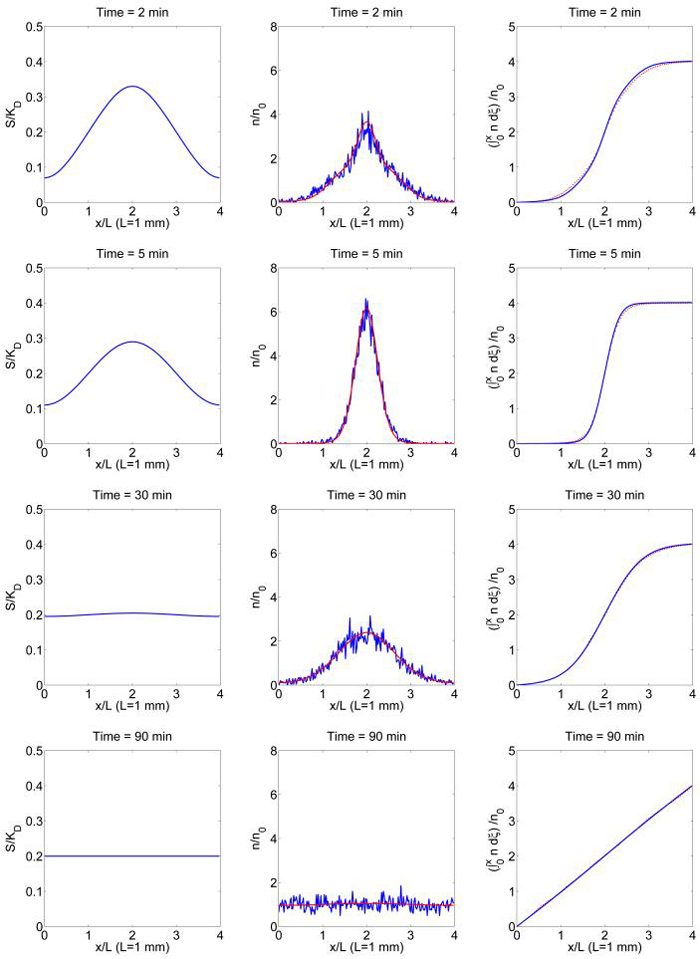
In Figure 4.1 we compare the stochastic simulation of the cell-based model with the solution of the macroscopic equations (4.4, 4.5, 4.6). For the stochastic simulation, cell density is computed as the linear interpolation of the histogram for the positions of the cells. Figure 4.1 shows that in the first few minutes, an aggregate of cells forms because of the initial attractant gradient, but later on the aggregate tends to be dispersed because diffusion smoothes out the attractant gradient. In this regime the attractant concentration, cell density and cumulative cell density agree very well between the two models. We also notice that in this example $G^{\prime }\left(S\right)\nabla S\cdot \mathbf{v}$ becomes as large as 15 ϵ sec^-1, but the solution of the chemotaxis equation (4.4) still provides a good approximation of the results of the cell-based model. This means that the chemotaxis equation may also be a good approximation of the underlying velocity-jump process for a slightly weaker assumption than we used. For this example, equation (3.42) is also solved together with (4.4, 4.5, 4.6) to construct the higher order approximation of n, and both n⁰ and n⁰ + ϵn¹ are plotted in Figure 4.1. However, it turns out that $n^1\le \mathcal{O}\left(ϵ\right)$ and the curves for n⁰ and n⁰+ϵn¹ become indistinguishable.

Fig. 4.1.

Aggregation and dispersion in a time-dependent signal field. First order and second order approximations of the cell density n⁰ and n⁰ + ϵn¹ computed from equation (4.4, 3.42) (smooth line) are compared with stochastic simulation of the cell based model when coupled with the attractant dynamics (4.5, 4.6). The left, center and right columns are the attractant concentration scaled by K_D, the cell density and cumulative cell density scaled by the average cell density n₀ at t = 2, 5, 30 and 90 min. G(S), λ and T(v, v′) are given by equations (2.4, 4.3, 3.31). 4 × 10³ cells are used for the Monte Carlo simulation (n₀ = 10³). Other parameters used are λ₀ = 1 s⁻¹, b = 1 s⁻¹, t_a = 2 s, s = 20 μm/s, K_D = 200, G₀ = 200, D_s = 8 × 10⁻⁴ mm²/s.

4.2. Self-organized aggregation in one dimensional space

In this example we investigate the motion of bacterial cells driven by the attractant that they produce. Thus the attractant dynamics is governed by

$$\frac{\partial S}{\partial t}=D_s\Delta S+\gamma n-\mu S.$$ (4.7)

We assume initially no attractant is added to the domain,

$$S(x,0)=0.$$ (4.8)

Periodic boundary conditions and the same parameters as in the first example are used. We set the initial cell density to be

$$n(x,0)=n_0(1+\xi \left(x\right)){\mathrm{mm}}^{-1},$$ (4.9)

where ξ(x) is a small random term of zero mean.

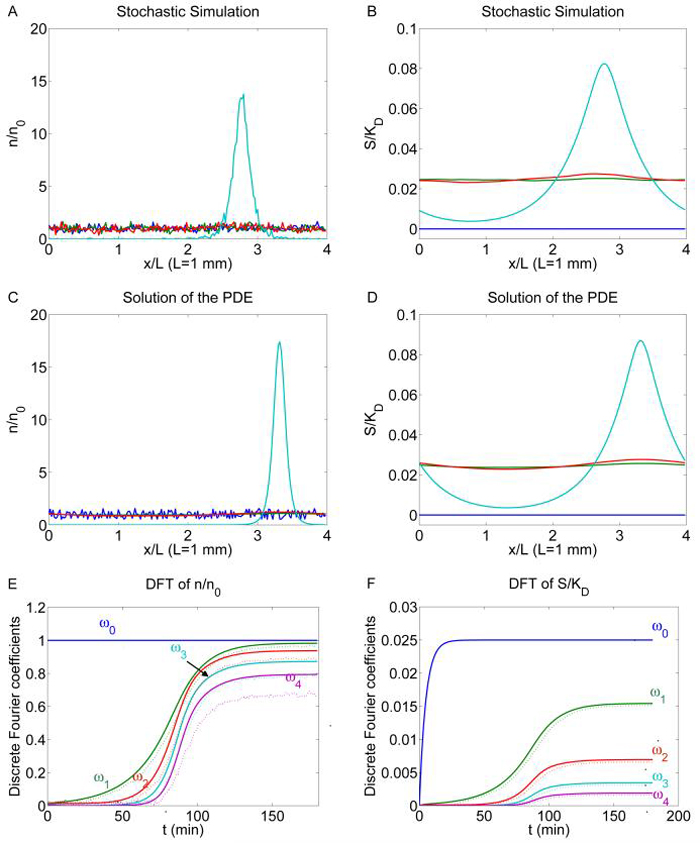
Figure 4.2 compares the stochastic simulation of the cell-based model with the attractant dynamics (4.7, 4.8) and the solution of the continuum model (4.4, 4.9, 4.7, 4.8). There we used $\mu =1∕3\times {10}^{-2}∕\mathrm{s},\gamma =1∕6\times {10}^{-1}∕n_0{\mathrm{s}}^{-1}$ per cell. A linear stability analysis (see Appendix B) of the continuum model around the uniform steady state (USS) (n, S) ≡ (n₀, γn₀/μ) shows that there are three unstable modes ${\psi }_k=e^{ik\frac{2\pi }{L}x}$, k = 1, 2, 3 with exponential growth rates 0.1439, 0.1954, 0.0904. Thus, we expect that instabilities develop around the uniform steady state and nonuniform peaks appear in the cell density profiles. The system (4.4, 4.7) has no solutions that blow up in finite time [10], therefore a nonuniform steady state develops finally.

Fig. 4.2.

Self-organized aggregation in bacterial colonies. (A)-(D): the solution of system (4.4, 4.9, 4.7, 4.8) is compared with one realization of the stochastic simulation of the cell based model coupled with the attractant dynamics given by equation (4.7, 4.8). The blue, green, red and cyan curves represent profiles taken at t = 0, 20, 40, 180 min. (resp.) (E), (F): comparisons of the amplitudes of the first 4 Fourier modes of the solutions. Smooth lines: solution for the PDE system; dotted lines: stochastic simulation. 4 × 10³ cells are used for the Monte Carlo simulation (n₀ = 10³). μ = 1/3 × 10^-2 s^-1, γ = 1/6 × 10^-4 s^-1 per cell. Other parameters used are the same as in Figure 4.1.

Figures 4.2 A - D show that in both models, the state of the system first evolves towards the unstable uniform steady state (green curve), then small perturbations finally lead the system to the stable nonuniform steady state (cyan curve). Because the perturbations in the two models are random and the periodic boundary condition allows for translation of solutions, we cannot expect the peaks to appear at the same x coordinate. Therefore neither averaging over different stochastic simulations of the cell-based model nor a point-wise comparison of the solutions of the two models is appropriate. Instead we compare the Fourier coefficients ω_k of different modes ${\left({\varphi }_k\right)}_j=e^{k\frac{2\pi i}{N_x}j}$, k, j = 0, 1, . . ., N_x − 1 (Figures 4.2 E and F) in single realizations. We see that in both models, the 0th mode amplitude ω₀ of n is constant because of the conservation of the total number of cells, and the 0th mode amplitude ω₀ of S increases to its value at the USS γn₀/μ and remains there. Initially the amplitudes of the linearly-unstable modes ω₁, ω₂ of n increase exponentially, and the amplitudes of the other stable modes decrease exponentially. Thereafter due to the nonlinearity of the system, energy in the stable modes (for both n and S) transfers to other modes, and coefficients ω_k increase until the system reaches the nonuniform steady state.

We observed that in numerical calculations the exact time for the unstable modes to amplify sharply (around t = 70 min~ 100 min in this realization) depends strongly on the spectrum of the initial noise of the continuum model and the intrinsic noise of the cell-based model. Once the Fourier coefficients of the unstable modes exceeds a threshold (about 0.1 in this example), they start to grow faster than exponential. The amplitude of the most rapidly-varying modes of the cell-based model was observed to be much more noisy than that of the continuum model, because of the intrinsic time-dependent noise of the stochastic simulation.

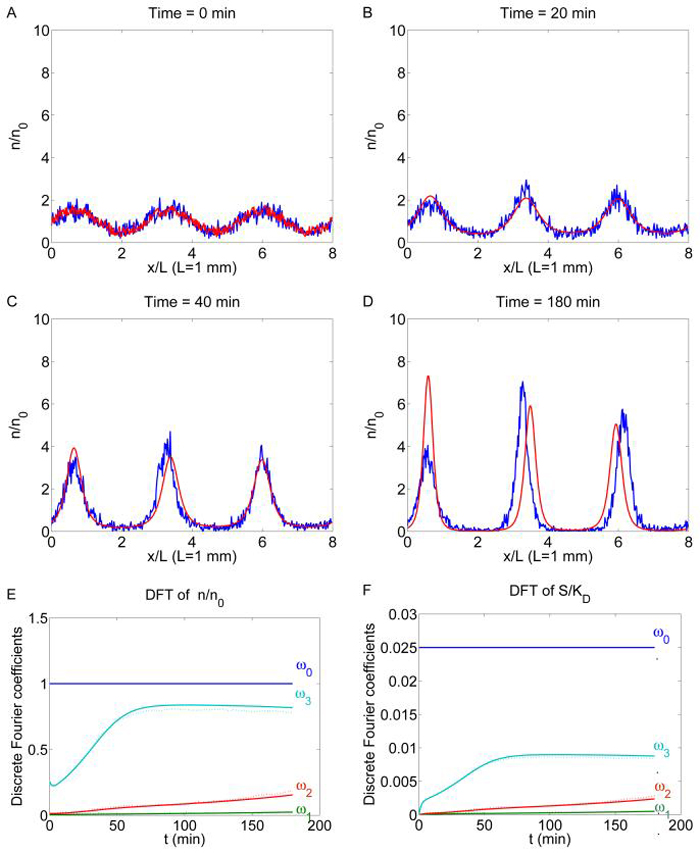
To compare the two models in the case of multi-aggregate formation, we enlarge the domain from 4 mm to 8 mm to allow for more unstable modes. To match the number and location of the peaks in the early dynamics, we choose an initial cell density with a sinusoidal perturbation plus noise

$$n(x,0)=n_0(1+\eta \sin \left(\frac{3\pi }{4}x\right)+\xi \left(x\right)).$$ (4.10)

In order to focus on the development of the instability, we set the signal at the uniform steady state initially

$$S(x,0)=\frac{\gamma }{\mu }.$$ (4.11)

The numerical results for η = 0.5 are shown in Figure 4.3. We observe that aggregates form at the locations with maximum initial cell density (20 min, 40 min). Then, due to the instability of the multi-aggregate steady state, unevenness among different aggregates develops (180 min) and leads to merging of aggregates. Finally the single-aggregate, stable steady state is reached (not shown). At t = 20 min, the different origin of noise in the two models is not significant, and the continuum model agrees well with the cell-based model (Figure 4.3 B). However, at t = 40 min and 180 min, the noise driven instability becomes important (Figures 4.3 C, D), and there one cannot directly compare the exact value of the solution of the two models.

Fig. 4.3.

Multi-aggregate formation in bacterial colonies. In the top four plots, the time-lapse shots of the cell density obtained from the continuum model (red line) is compared with one realization of the stochastic simulation of the cell based model (blue line) with initial conditions (4.10, 4.11). In the bottom two plots, the amplitude of the first 4 Fourier modes of the solutions are compared. Smooth lines: solution of the PDE system; dotted lines: stochastic simulation. 8 × 10³ cells are used for the Monte Carlo simulation (n₀ = 10³). The same parameters are used as in Figure 4.2.

From Figures 4.2 and 4.3 we conclude that the dynamics of both models agree very well except for the location of the peaks which is sensitive to noise, and some difference in the amplitude. This difference in amplitudes is reflective of the fact that the signal gradients exceed the magnitudes assumed in the derivation of the macroscopic equation. In the next section, we apply both models in the context of network and aggregate formation in the E. coli liquid assay.

4.3. Bacterial pattern formation: E. coli network and aggregate formation in liquid culture

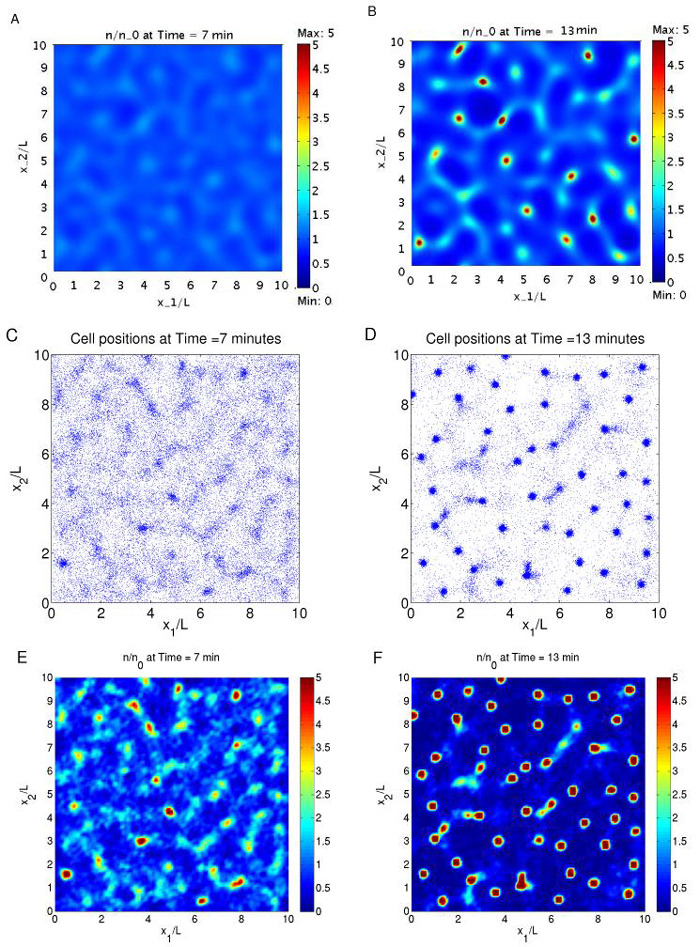
When E. coli cells are suspended in a well-stirred liquid medium with succinate as the nutrient, they secrete the attractant aspartate and initially self-organize into a thread-like network, which quickly breaks into aggregates. The network-aggregate pattern appears on a time scale of 10 min. Since excess succinate is provided, cells grow in the exponential phase, and nutrient depletion is not involved. In this example, we model the above dynamics in 2-D by both the hybrid cell-based approach and the macroscopic PDE approach, and compare the results.

The dynamics of the attractant is governed by the reaction-diffusion equation (4.7). The total cell number in the domain is N₀ and the average cell density n₀. We use no-flux boundary conditions since there is no material exchange of the system with the environment. The uniform steady state of the continuum model (3.33, 4.7) is (n, S) = (n₀, γn₀/μ). A linear analysis (see Appendix B) around the uniform steady state explains the pattern formation as the result of the amplification of the unstable modes of the fluctuations. To focus on the dynamics during pattern formation, we start from the uniform steady state with a small perturbation as the initial values,

$$n=n_0(1+\text{small random noise}){\mathrm{mm}}^{-2},$$ (4.12)

$$S(x,y,0)=\gamma n_0∕\mu .$$ (4.13)

In Figure 4.4, we compare the numerical results of the continuum model (4.4, 4.7, 4.12, 4.13) with one realization of the stochastic simulation of the cell-based model. We used COMSOL Multiphysics to solve the 2-D continuum model (with 15648 triangles, using Lagrange elements), and the numerical algorithm given by Appendix A to simulate the cell-based model. The initial values for the continuum model are obtained by interpolating from the initial values of the cell-based model. Although the exact details of the transient dynamics can be different because of different noise in the two models, we note that both models predict comparable temporal and spatial features of the dynamical evolution from the network to aggregate formation.

Fig. 4.4.

E. coli network and aggregate formation. (A), (B): the cell density from the continuum model (A: t = 7min, B: t = 13min); (C), (D): the positions of the cells calculated from the cell-based model at the same time points; (E), (F): the interpolated cell density from (C) and (D). Parameters used include λ₀ = 1 s^-1, b = 5 s^-1, t^a = 2 s, s = 20 μm/s, k_d = 40, D_s = 8 × 10^-4 mm²/s, μ = 1/3 × 10^-2 s^-1, γ = 1/6 × 10^-1/n₀ s^-1, n₀ = 400, L = 1mm.

5. Chemotactic movement in external fields

Bacterial cells can swim in more complicated environments with external forces acting on them. For example, when the cell density becomes large, there may be mechanical interactions between cells, which may affect their swimming speed and direction. Another example arises when gravity becomes important. During the formation of bio-convection patterns reported in [11], aerotaxis drives the cells toward the top of the medium, while gravity acts downward. Therefore, the above analysis should be generalized to incorporate both forces between cells and forces due to external fields. The transport equation with external forces has the form

$$\frac{\partial p}{\partial t}+{\nabla }_{\mathbf{x}}\cdot \left(\mathbf{v}p\right)+{\nabla }_{\mathbf{x}}\cdot \left(\mathbf{a}p\right)+{\nabla }_{\mathbf{y}}\cdot \left(\mathbf{f}p\right)=-\lambda \left(\mathbf{y}\right)p+{\int }_V\lambda \left(\mathbf{y}\right)T(\mathbf{v},{\mathbf{v}}^{\prime },\mathbf{y})p(\mathbf{x},{\mathbf{v}}^{\prime },\mathbf{y},t)d{\mathbf{v}}^{\prime }.$$ (5.1)

Previous results have been obtained for crawling cells [16], where the active force generation is incorporated by a simple description, and the velocity jumps model random polarization of cells when no signal gradient is detected. Because the internal state of each cell varies spatially, further dimension reduction is needed in that analysis.

Here we extend the analysis in Section 3 to include external forces and consider a particular case in which bacteria swim close to a surface. In three dimensional space, bacterial cells swim in straight “runs”, but are subject to rotational diffusion. However, when they move near a surface, the “runs” display a consistent clockwise bias when observed from above [17, 13]. The bias can be explained by the interaction between the surface and the cell [20]. During a run, the cell body rotates clockwise while the flagella rotate counterclockwise when observed from behind. Therefore, when a cell swims parallel to a surface a larger viscous force is exerted on the bottom of the cell (closer to the surface) than that on the top of the cell, and thus net forces arise on both the cell body and the flagella. These net forces induce the bias in the motion.

In the patterns formed in P. mirabilis colonies in [39], cells swim in a thin fluid-like slime layer on top of the hard surface, and therefore the runs are biased. By incorporating a constant swimming bias to each cell's right, a two dimensional cell-based model predicts the chirality of spiral stream formation in P. mirabilis colonies [39]. In this section, we derive a corresponding macroscopic chemotaxis equation from the cell-based model with swimming bias. We also incorporate persistence in the motion and thus assume the form of the turning kernel given by (3.34). The resulting equation enables us to see the interplay of chemotaxis and the swimming bias.

Let ω₀ be the constant angular velocity during a run. Then the acceleration has the form a = ω₀v × ν, where ν is the normal vector of the surface pointing to the fluid side, i.e., a = (ω₀v₂, -ω₀v₁). Let p(x, v, z₂, t) be the cell density function. After nondimensionalization, the transport equation reads,

$$\begin{array}{c}{ϵ}^2\frac{\partial p}{\partial t}+ϵ\frac{\partial }{\partial x_1}\left(v_{1}p\right)+ϵ\frac{\partial }{\partial x_2}\left(v_{2}p\right)-{\omega }_0\frac{\partial }{\partial v_1}\left(v_{2}p\right)-{\omega }_0\frac{\partial }{\partial v_2}\left(v_{1}p\right)\hfill \\ \hfill \hfill \\ \hfill +\frac{\partial }{\partial z_2}\left(-\frac{z_2}{t_a}-G^{\prime }\left(S\right)(ϵv_1\frac{\partial S}{\partial x_1}+ϵv_2\frac{\partial S}{\partial x_2}+{ϵ}^2\frac{\partial S}{\partial t})p\right)\hfill \\ \hfill =({\lambda }_0+a_1{z}_2+a_2{z}_2^2+\cdots )(-p+{\int }_{V}T(V,V^{\prime })p\left(v^{\prime }\right)d{v}^{\prime }).\end{array}$$

By multiplying 1, $z_2^j∕j,j\ge 1$, and integrating with respect to z₂, we obtain a system of equations for the z₂-moments M(t, x, v), where M is defined as in (3.13),

$${ϵ}^2\frac{\partial }{\partial t}\Lambda \mathbf{m}+ϵv_1\frac{\partial }{\partial x_1}\Lambda \mathbf{m}+ϵv_2\frac{\partial }{\partial x_2}\Lambda \mathbf{m}+{\omega }_0{v}_2\frac{\partial }{\partial v_1}\Lambda \mathbf{m}-{\omega }_0{v}_1\frac{\partial }{\partial v_2}\Lambda \mathbf{m}={ϵ}^2\mathbf{BM}+ϵ\mathbf{CM}+\mathbf{DM}$$ (5.2)

If we apply the perturbation method directly to equation (5.2), there is no easy way to derive an approximating equation of the cell density, since $M_0^0$ is no longer independent of v, and thus there is no simple relation between the cell density n and $M_0^0$. Instead, we choose to proceed by multiplying (5.2) by 1, v₁ and v₂, and integrating with respect to v to get the complete moment equations.

We define the density moments

$$n(\mathbf{x},t)=\int M_{0}d\mathbf{v},n_j(\mathbf{x},t)=\int M_{j}d\mathbf{v},j=1,2,\cdots ,\mathbf{n}=(n,n_1,n_2,\cdots ,{)}^t,$$

and the velocity flux moments

$$\begin{array}{c}\hfill J_{j,k}(\mathbf{x},t)=\int v_k{M}_{j}d\mathbf{v},j=0,1,2,\cdots ,{\mathbf{J}}_k=(J_{0,k},J_{1,k},J_{2,k},\cdots {)}^t,k=1,2,\hfill \\ \hfill J_{j,kl}(\mathbf{x},t)=\int v_k{v}_l{M}_{j}d\mathbf{v},j=0,1,2,\cdots ,{\mathbf{J}}_{kl}=(J_{0,kl},J_{1,kl},J_{2,kl},\cdots {)}^t,k,l=1,2.\hfill \end{array}$$

The subscript j is the index of the order of the z₂-moment, and subscripts k, l are the indices of the velocity moment. We decompose C defined at (3.16) into C = C₁ + C₂, where

$${\mathbf{C}}_k=-G^{\prime }\left(S\right)\frac{\partial S}{\partial x_k}\mathrm{diag}\{0,1,1,\cdots \}{\mathbf{J}}^t,k=1,2.$$ (5.3)

Here J is the matrix operator defined in (3.18), but now acting on $l^{\infty }\left(\mathbb{R}\right)$. We also define matrix operators

$${\mathbf{D}}_1=-\mathrm{diag}\left\{0,\frac{1}{t_a},\frac{1}{t_a},\frac{1}{t_a},\cdots \right\},{\mathbf{D}}_2=-\Lambda ({\lambda }_0\mathbf{I}+\sum _{i=1}^{\infty }{a}_i{\mathbf{J}}_i)(1-{\psi }_d)+{\mathbf{D}}_1.$$ (5.4)

To obtain the complete moment equations, we have to calculate ∫_V DMdv and ∫_V v_kDMdv. Notice that, by property (ii) of $\mathcal{A}$, for any f(v),

$${\int }_{v}Afd\mathbf{v}={\int }_V\left(\int -I+T(\mathbf{v},{\mathbf{v}}^{\prime })d\mathbf{v}\right)f\left({\mathbf{v}}^{\prime }\right)d{\mathbf{v}}^{\prime }=0,$$

therefore ∫_V DMdv = D₁n. Assuming the turning kernel (3.34) and considering that

$${\int }_V\mathbf{v}Afd\mathbf{v}={\int }_V\left({\int }_V-\mathbf{v}f\left(\mathbf{v}\right)+\mathbf{v}T(\mathbf{v},{\mathbf{v}}^{\prime })d\mathbf{v}\right)f\left({\mathbf{v}}^{\prime }\right)d{\mathbf{v}}^{\prime }=-(1-{\psi }_d)\int \mathbf{v}f\left(\mathbf{v}\right)d\mathbf{v},$$

we obtain

$${\int }_V{v}_k\mathbf{DM}d\mathbf{v}={\int }_V{\mathbf{D}}_2{v}_k^{\prime }\mathbf{M}\left(V^{\prime }\right)d{\mathbf{v}}^{\prime }={\mathbf{D}}_2{\mathbf{J}}_k,k=1,2.$$

Therefore the complete moment equations are

$${ϵ}^2\frac{\partial }{\partial t}\Lambda \mathbf{n}+ϵ\frac{\partial }{\partial x_1}\Lambda {\mathbf{J}}_1+ϵ\frac{\partial }{\partial x_2}\Lambda {\mathbf{J}}_{,2}={ϵ}^2\mathbf{Bn}+ϵ{\mathbf{C}}_1{\mathbf{J}}_1+ϵ{\mathbf{C}}_2{\mathbf{J}}_2+{\mathbf{D}}_1\mathbf{n},$$ (5.5)

$${ϵ}^2\frac{\partial }{\partial t}\Lambda {\mathbf{J}}_1+ϵ\frac{\partial }{\partial x_1}\Lambda {\mathbf{J}}_{11}+ϵ\frac{\partial }{\partial x_2}\Lambda {\mathbf{J}}_{12}-{\omega }_0\Lambda {\mathbf{J}}_2={ϵ}^2{\mathbf{BJ}}_1+ϵ{\mathbf{C}}_1{\mathbf{J}}_{11}+ϵ{\mathbf{C}}_2{\mathbf{J}}_{12}+{\mathbf{D}}_2{\mathbf{J}}_1,$$ (5.6)

$${ϵ}^2\frac{\partial }{\partial t}\Lambda {\mathbf{J}}_2+ϵ\frac{\partial }{\partial x_1}\Lambda {\mathbf{J}}_{12}+ϵ\frac{\partial }{\partial x_2}\Lambda {\mathbf{J}}_{22}+{\omega }_0\Lambda {\mathbf{J}}_1={ϵ}^2{\mathbf{BJ}}_2+ϵ{\mathbf{C}}_1{\mathbf{J}}_{12}+ϵ{\mathbf{C}}_2{\mathbf{J}}_{22}+{\mathbf{D}}_2{\mathbf{J}}_2.$$ (5.7)

Here B is defined by (3.15). To close the moment equations, we follow [15] and assume the second velocity moments are isotropic, which is exact in 1-D:

$$J_{0,kl}=\frac{s^2}{2}n{\delta }_{kl},J_{j,kl}=\frac{s^2}{2}{n}_j{\delta }_{kl},k,l=1,2.$$ (5.8)

Then the moment equations reduce to

$${ϵ}^2\frac{\partial }{\partial t}\Lambda \mathbf{n}+ϵ\frac{\partial }{\partial x_1}\Lambda {\mathbf{J}}_1+ϵ\frac{\partial }{\partial x_2}\Lambda {\mathbf{J}}_2={ϵ}^2\mathbf{Bn}+ϵ{\mathbf{C}}_1{\mathbf{J}}_1+ϵ{\mathbf{C}}_2{\mathbf{J}}_2+{\mathbf{D}}_1\mathbf{n},$$ (5.9)

$${ϵ}^2\frac{\partial }{\partial t}\Lambda {\mathbf{J}}_1+ϵ\frac{\partial }{\partial x_1}\left(\frac{s^2}{2}\Lambda \mathbf{n}\right)-{\omega }_0\Lambda {\mathbf{J}}_2={ϵ}^2{\mathbf{BJ}}_1+ϵ{\mathbf{C}}_1\left(\frac{s^2}{2}\mathbf{n}\right)+{\mathbf{D}}_2{\mathbf{J}}_1,$$ (5.10)

$${ϵ}^2\frac{\partial }{\partial t}\Lambda {\mathbf{J}}_2+ϵ\frac{\partial }{\partial x_1}\left(\frac{s^2}{2}\Lambda \mathbf{n}\right)-{\omega }_0\Lambda {\mathbf{J}}_1={ϵ}^2{\mathbf{BJ}}_2+ϵ{\mathbf{C}}_2\left(\frac{s^2}{2}\mathbf{n}\right)+{\mathbf{D}}_2{\mathbf{J}}_2.$$ (5.11)

Assuming the regular perturbation expansions, with superscript indicating the order of expansion,

$$\mathbf{n}={\mathbf{n}}^0+ϵ{\mathbf{n}}^1+{ϵ}^2{\mathbf{n}}^2+\cdots ,{\mathbf{J}}_k={\mathbf{J}}_k^0+ϵ{\mathbf{J}}_k^1+{ϵ}^2{\mathbf{J}}_k^2+\cdots ,k=1,2,$$

substituting into the moment equations (5.9-5.11), and comparing terms of equal orders of ε, we obtain, $\mathcal{O}\left({ϵ}^0\right)$:

$${\mathbf{D}}_1{\mathbf{n}}^0=0,$$ (5.12)

$${\mathbf{D}}_2{\mathbf{J}}_1^0=-{\omega }_0\Lambda {\mathbf{J}}_2^0,$$ (5.13)

$${\mathbf{D}}_2{\mathbf{J}}_2^0={\omega }_0\Lambda {\mathbf{J}}_1^0,$$ (5.14)

$\mathcal{O}\left({ϵ}^1\right)$:

$$\frac{\partial }{\partial x_1}\Lambda {\mathbf{J}}_1^0+\frac{\partial }{\partial x_2}\Lambda {\mathbf{J}}_2^0={\mathbf{C}}_1{\mathbf{J}}_1^0+{\mathbf{C}}_2{\mathbf{J}}_2^0+{\mathbf{D}}_1{\mathbf{n}}^1,$$ (5.15)

$$\frac{s^2}{2}\frac{\partial }{\partial x_1}\Lambda {\mathbf{n}}^0-{\omega }_0\Lambda {\mathbf{J}}_2^1=\frac{s^2}{2}{\mathbf{C}}_1{\mathbf{n}}^0+{\mathbf{D}}_2{\mathbf{J}}_1^1,$$ (5.16)

$$\frac{s^2}{2}\frac{\partial }{\partial x_2}\Lambda {\mathbf{n}}^0+{\omega }_0\Lambda {\mathbf{J}}_1^1=\frac{s^2}{2}{\mathbf{C}}_2{\mathbf{n}}^0+{\mathbf{D}}_2{\mathbf{J}}_2^1,$$ (5.17)

$\mathcal{O}\left({ϵ}^2\right)$:

$$\frac{\partial }{\partial t}\Lambda {\mathbf{n}}^0+\frac{\partial }{\partial x_1}\Lambda {\mathbf{J}}_1^1+\frac{\partial }{\partial x_2}\Lambda {\mathbf{J}}_2^1={\mathbf{B}}_1{\mathbf{n}}^0+{\mathbf{C}}_1{\mathbf{J}}_1^1+{\mathbf{C}}_2{\mathbf{J}}_2^1+{\mathbf{D}}_1{\mathbf{n}}^2.$$ (5.18)

From equation (5.12) we get ${\mathit{n}}_j^0=0$, ${\forall }_j\ge 1$, or n⁰ = (n⁰, 0, 0, ⋯)^t. From equations (5.13, 5.14), we see that ${\left({\Lambda }^{-1}{\mathbf{D}}_2\right)}^2{\mathbf{J}}_1^0=-{\omega }_0^2{\mathbf{J}}_1^0$, ${\left({\Lambda }^{-1}{\mathbf{D}}_2\right)}^2{\mathbf{J}}_2^0=-{\omega }_0^2{\mathbf{J}}_2^0$. Since all the eigenvalues of ${\left({\Lambda }^{-1}{\mathbf{D}}_2\right)}^2$ are positive, it follows that ${\mathbf{J}}_1^0={\mathbf{J}}_2^0=0$.

Therefore equation (5.15) reduces to ${\mathbf{D}}_1{\mathbf{n}}^1=0$, which means that $n_j^1=0,j\ge 1$, or n¹ = (n¹, 0, 0, ⋯)^t. Applying a similar argument to the 3rd and higher components of the equations (5.16, 5.17) gives $J_{j,1}^1=J_{j,2}^1=0,\forall j\ge 2$. Thus the first two components of (5.16, 5.17) become

$$\frac{s^2}{2}\frac{\partial }{\partial x_1}{n}^0-{\omega }_0{J}_{0,2}^1=-{\lambda }_0(1-{\psi }_d)J_{0,1}^1-a_1(1-{\psi }_d)J_{1,1}^1,$$ (5.19)

$$-{\omega }_0{J}_{1,2}^1=-\frac{s^2}{2}{G}^{\prime }\left(S\right)\frac{\partial S}{\partial x_1}{n}^0-[{\lambda }_0(1-{\psi }_d)+\frac{1}{t_a}]J_{1,1}^1,$$ (5.20)

$$\frac{s^2}{2}\frac{\partial }{\partial x_2}{n}^0+{\omega }_0{J}_{0,1}^1=-{\lambda }_0(1-{\psi }_d)J_{0,2}^1-a_1(1-{\psi }_d)J_{1,2}^1,$$ (5.21)

$${\omega }_0{J}_{1,1}^1=-\frac{s^2}{2}{G}^{\prime }\left(S\right)\frac{\partial S}{\partial x_2}{n}^0-[{\lambda }_0(1-{\psi }_d)+\frac{1}{t_a}]J_{1,2}^1.$$ (5.22)

From equations (5.20, 5.22), we find that

$$\left(\underset{J_{1,2}^1}{\overset{J_{1,1}^1}{}}\right)=-\frac{s^2{G}^{\prime }\left(S\right)n^0}{2({\lambda }_0(1-{\psi }_d)+\frac{1}{t_a}{)}^2+2{\omega }_0^2}\left[\begin{array}{cc}\hfill {\lambda }_0(1-{\psi }_d)+\frac{1}{t_a}\hfill & \hfill {\omega }_0\hfill \\ \hfill -{\omega }_0\hfill & \hfill {\lambda }_0(1-{\psi }_d)+\frac{1}{t_a}\hfill \end{array}\right]\nabla S.$$ (5.23)

From equations (5.19, 5.21), we obtain

$$\left(\underset{J_{0,2}^1}{\overset{J_{0,1}^1}{}}\right)=-\frac{1}{{\lambda }_0^2(1-{\psi }_d{)}^2+{\omega }_0^2}\left[\begin{array}{cc}\hfill {\lambda }_0(1-{\psi }_d)\hfill & \hfill {\omega }_0\hfill \\ \hfill -{\omega }_0\hfill & \hfill {\lambda }_0(1-{\psi }_d)\hfill \end{array}\right]\left(\frac{s^2}{2}\nabla n^0+a_1(1-{\psi }_d)\left(\underset{J_{1,2}^1}{\overset{J_{1,1}^1}{}}\right)\right).$$ (5.24)

The first component of equation (5.18) is

$$\frac{\partial }{\partial t}{n}^0+\frac{\partial }{\partial x_1}{J}_{0,1}^1+\frac{\partial }{\partial x_2}{J}_{0,2}^1=0.$$ (5.25)

Substituting $J_{0,1}^1$, $J_{0,2}^1$ by equations (5.24) gives the final chemotaxis equation,

$$\frac{\partial }{\partial t}{n}^0=D_n\Delta n^0-\nabla \cdot \left[G^{\prime }\left(S\right)n^0({\chi }_0\nabla S+{\beta }_0(\nabla S{)}^{\perp })\right],$$ (5.26)

where

$$D_n=\frac{s^2}{2{\lambda }_0(1-{\psi }_d)+\frac{2{\omega }_0^2}{{\lambda }_0(1-{\psi }_d)}},$$ (5.27)

$${\chi }_0=\frac{a_1{s}^2(1-{\psi }_d)[{\lambda }_0(1-{\psi }_d)({\lambda }_0(1-{\psi }_d)+\frac{1}{t_a})-{\omega }_0^2]}{2(({\lambda }_0(1-{\psi }_d)+\frac{1}{t_a}{)}^2+{\omega }_0^2)({\lambda }_0^2(1-{\psi }_d{)}^2+{\omega }_0^2)},$$ (5.28)

$${\beta }_0=\frac{{\omega }_0{a}_1{s}^2(1-{\psi }_d)(2{\lambda }_0(1-{\psi }_d)+\frac{1}{t_a})}{2(({\lambda }_0(1-{\psi }_d)+\frac{1}{t_a}{)}^2+{\omega }_0^2)({\lambda }_0^2(1-{\psi }_d{)}^2+{\omega }_0^2)},$$ (5.29)

and

$$\nabla S=\left(\underset{\frac{\partial S}{\partial x_2}}{\overset{\frac{\partial S}{\partial x_1}}{}}\right),(\nabla S{)}^{\perp }=\left[\begin{array}{cc}\hfill 0\hfill & \hfill 1\hfill \\ \hfill -1\hfill & \hfill 0\hfill \end{array}\right]\nabla S.$$

From the forms of D_n, χ₀ and β₀, we notice that when ω₀ = 0, (5.26) reduces to the chemotaxis equation we derived in Section 3.5 in a two-dimensional space. (5.26) can also be derived by using the assumptions in Section 3.7. The macroscopic chemotactic velocity in (5.26) is given by

$${\mathbf{u}}_S=G^{\prime }\left(S\right)({\chi }_0\nabla S+{\beta }_0(\nabla S{)}^{\perp }).$$ (5.30)

The magnitude of u_S is

$$\begin{array}{cc}\hfill \parallel {\mathbf{u}}_S\parallel & =\parallel G^{\prime }\left(S\right)\nabla S\parallel \sqrt{{\chi }_0^2+{\beta }_0^2}\hfill \\ \hfill & =\parallel G^{\prime }\left(S\right)\nabla S\parallel \cdot \frac{a_1{s}^2(1-{\psi }_d)}{2\sqrt{({({\lambda }_0(1-{\psi }_d)+\frac{1}{t_a})}^2+{\omega }_0^2)({\lambda }_0^2(1-{\psi }_d{)}^2+{\omega }_0^2)}}\hfill \\ \hfill & =\parallel G^{\prime }\left(S\right)\nabla S\parallel \cdot \frac{a_1{s}^2{t}_a}{2{\lambda }_0(1+(1-{\psi }_d){\lambda }_0{t}_a)}\cdot \frac{1}{\sqrt{(1+\frac{{\omega }_0^2}{({\lambda }_0(1-{\psi }_d)+\frac{1}{t_a}{)}^2})(1+\frac{{\omega }_0^2}{{\lambda }_0^2(1-{\psi }_d{)}^2})}}.\hfill \end{array}$$ (5.31)

The angle between u_S and ∇S is

$${\theta }_{\mathbf{u}S,\nabla S}={\tan }^{-1}\frac{{\omega }_0(2{\lambda }_0(1-{\psi }_d)+\frac{1}{t_a})}{{\lambda }_0(1-{\psi }_d)({\lambda }_0(1-{\psi }_d)+\frac{1}{t_a})-{\omega }_0^2},$$ (5.32)

which, surprisingly, is independent of ∇S and a₁.

5.1. Numerical comparison of the macroscopic chemotaxis velocity

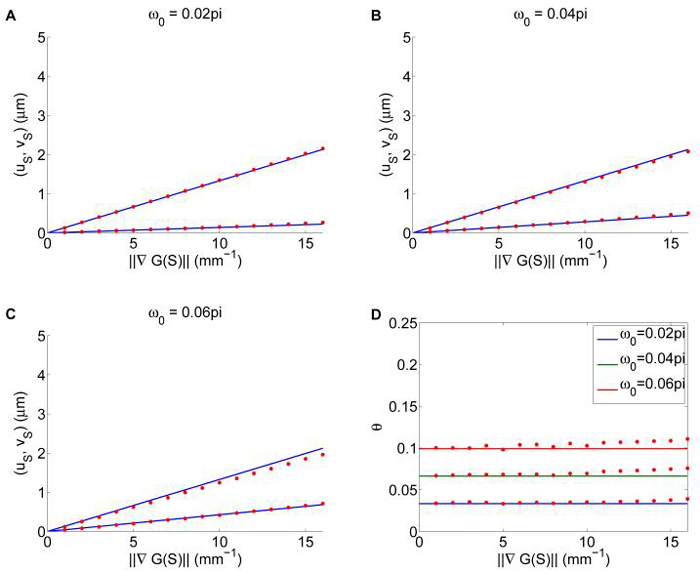
The analytical prediction of the macroscopic chemotaxis velocity (5.30) is shown to agree very well with statistics from the cell-based model at different signal gradients and bias levels ω₀ in Figure 5.1. Even for the large signal gradient $\parallel \nabla G\left(S\right)\parallel =15$ (i.e., $G^{\prime }\left(S\right)\nabla S\cdot \mathbf{v}=30ϵ{\mathrm{s}}^{-1}$), the difference is still within 10%.

Fig. 5.1.

Comparison of the macroscopic velocity from equation (5.30, 5.32) with statistics from the cell-based model. In the first three plots, we compare (u_S, v_S) = (u_S ⋅ ∇S u_S ⋅ (∇S)^⊥) as a function of ∇G(S) for ώ₀ = 0.02π, 0.04π, 0.06π. Solid lines are computed from equation (5.30), dots are computed from the cell-based model; upper lines and dots are for u_S , lower lines and dots are for v_S. The fourth plot is a comparison of the predicted angle θ_uS,∇S by equation (5.32) with simulation at different parameters. All other parameters are the same as the previous examples.

In Figure 5.1, the macroscopic chemotaxis velocity from the cell-based model is computed in the following way. For a given combination of ∇G(S) and ω₀, we used G(S) = S, and a time-independent signal S = Rx₂ in order to guarantee ∇G(S) to be constant R in the whole path of a cell. Other parameters used remain the same as in previous examples. For each parameter combination, 6 × 10³ cells are put at the same location x = 0 with random initial velocity and zero initial y₂. The positions of each cell are recorded every 1 min for a 30 min period. The position vector xⁱ at time t_i = i min is computed by averaging all the cell positions. Then the macroscopic velocity vector is computed by applying the least square method to the averaged position, i.e., by finding v that minimizes ${\sum }_i{(x_j^i-v_j{t}_i)}^2$, where j = 1, 2 is the index of the space direction.

6. Chemotaxis induced by multiple signals

Single chemical induced chemotactic movement has been studied experimentally for various types of cells and modeled mathematically both microscopically and macroscopically [22, 38, 19]. However, many cell types are known to have multiple receptor types and thus can respond to many different chemicals. For instance, E. coli has five major types of receptors for various nutrients, oxygen, etc. [38]. How these signals are integrated inside the cell is not generally known and may depend on the cell type. Macroscopic phenomenological chemotaxis equations have been proposed in [29]. In this section, we derive chemotaxis equations from a modified cell-based model by allowing multiple chemosignals.

In the case of E. coli, the signalling pathways for different chemicals share the same downstream phosphorl-relaying network (including reactions of CheA, CheW, CheY, CheB, CheR, CheZ etc.), the only difference is the upstream transmembrane receptor. In the cell-based model in Section 2, G(S) describes detection of the signal, and y describes the state of proteins within the cell. When there are multiple signals, G is generally a function of all possible signals, G = G(S₁, S₂, ⋯, S_m). By performing the standard procedure in Section 3, a chemotaxis equation for multiple signals can be derived that has the following form

$$\frac{\partial }{\partial t}n=\nabla \cdot \left[D_n{\nabla }_n-{\chi }_{0}n\left(\frac{\partial G}{\partial S_1}\nabla S_1+\cdots +\frac{\partial G}{\partial S_m}\nabla S_m\right)\right],$$ (6.1)

where

$${\chi }_0=\frac{a_1{s}^2{t}_a}{N{\lambda }_0(1+(1-{\psi }_d)t_a{\lambda }_0)(1+(1-{\psi }_d)t_e{\lambda }_0)}.$$ (6.2)

The functional form of G depends on the binding of the signal molecules to the receptors. Consider for example, the case of two attractants, and assume that all the binding is non-cooperative, and the two attractants S₁, S₂ competitively bind to the same receptor R as follows

$$S_1+R\underset{k_1^{-}}{\overset{k_1^{+}}{\rightleftarrows }}\stackrel{‒}{S_{1}R},S_2+R\underset{k_2^{-}}{\overset{k_2^{+}}{\rightleftarrows }}\stackrel{‒}{S_{2}R}.$$ (6.3)

Then according to the law of mass action, we have

$$\{\begin{array}{c}\frac{\stackrel{‒}{d{S}_1}}{dt}=-k_1^{+}{S}_{1}R+k_1^{-}\stackrel{‒}{S_{1}R},\hfill \\ \frac{\stackrel{‒}{d{S}_{1}R}}{dt}=+k_1^{+}{S}_{1}R-k_1^{-}\stackrel{‒}{S_{1}R},\hfill \\ \frac{\stackrel{‒}{d{S}_2}}{dt}=-k_2^{+}{S}_{2}R+k_2^{-}\stackrel{‒}{S_{2}R},\hfill \\ \frac{\stackrel{‒}{d{S}_{2}R}}{dt}=+k_2^{+}{S}_{2}R-k_2^{-}\stackrel{‒}{S_{2}R},\hfill \\ \frac{dR}{dt}=-k_1^{+}{S}_{1}R+k_1^{-}\stackrel{‒}{S_{1}R}-k_2^{+}{S}_{2}R+k_2^{-}\stackrel{‒}{S_{2}R}.\hfill \end{array}\phantom{\}}$$ (6.4)

If we further assume that the total number of receptors R₀ is conserved, then

$$R+\stackrel{‒}{S_{1}R}+\stackrel{‒}{S_{2}R}=R_0$$

Since the time scale of ligand binding is typically $\sim \mathcal{O}\left({10}^{-2}\right)S$, which is small compared to the excitation and adaptation time, we may approximate the number of bound receptors by the quasi-steady state value,

$$\stackrel{‒}{S_{1}R}=\frac{R_0{K}_2{S}_1}{K_1{K}_2+K_2{S}_1+K_1{S}_2},\stackrel{‒}{S_{2}R}=\frac{R_0{K}_1{S}_2}{K_1{K}_2+K_2{S}_1+K_1{S}_2},$$

and G can be written as

$$G=g(\stackrel{‒}{S_{1}R}+\stackrel{‒}{S_{2}R})=g\left(\frac{R_0(K_2{S}_1+K_1{S}_2)}{K_1{K}_2+K_2{S}_1+K_1{S}_2}\right).$$

If the two signals bind to different receptors, then a similar argument leads to the form,

$$G=g(\stackrel{‒}{S_1{R}_1}+\stackrel{‒}{S_2{R}_2})=g\left(\frac{R_{10}{S}_1}{K_1+S_1}+\frac{R_{20}{S}_1}{K_2+S_2}\right).$$

In E. coli, the functioning units of chemoreceptors are observed to be trimers of dimers, and different types of receptors can form hetero-trimers in vivo; thus the form of the function of G actually can be even more complicated.

7. Discussion

In this paper we developed a new method for deriving macroscopic equations for the evolution of cell density from cell-level descriptions of chemotactic movement in bacterial pattern formation. The method involves solving the infinite y-moment equations systematically by applying regular perturbation methods. It allows us to treat more general signal fields and cell-level descriptions than those used earlier [14, 15]. These generalizations include, allowing (a) time-dependent signal functions, (b) nonlinear turning frequency λ(y₁) and (c) external force fields acting on cells. We also note that although we adopted the cartoon description of excitation and adaptation in their paper, the method proposed can manage autonomous ODE models with polynomial right-hand-sides, as long as the time scales of intracellular reactions can be separated from the diffusion time scale of cells. Another advantage of the method is that it doesn't require unnecessary quasi-steady-state assumptions on the internal dynamics for closing the moments. The work is focused on studying run-and-tumble chemotactic movement because it is the most understood biological system. However, the derivation method can also be applied to other systems with minor change, but the limiting macroscopic equation may be different depending on the details of the specific internal dynamics.

In the derivation of equation 3.33 we assumed that the signal detected by the cell in one “run” doesn't change significantly. This assumption is satisfied in most cases, but it may be violated in self-organized aggregates. In this case, using a diffusion time and space scale may not be appropriate, and therefore a chemotaxis equation is not guaranteed to be a good approximation. However, in the numerical examples, we showed that the chemotaxis equation still captures the main dynamics of the cell-based model, although it seems to over-predict the amplitude and sharpness of the aggregates.

To derive macroscopic equations applicable for large signal gradients, a more detailed description of the internal dynamics is needed. The adaptation time t_a can range from a few seconds for small signals to minutes for large signals [34]. To handle the case of a large signal one must incorporate the dependence of the adaptation time on the signal strength, and this can be done by incorporating the fact that chemoreceptors have multiple methylation sites into the cartoon description used here. When the adaptation time is large the time scale for the intracellular response may be comparable to macroscopic time scales, and different balances of the component processes may arise. To treat such cases new moment closure techniques may be needed, and this may lead to other types of macroscopic equations than the classical chemotaxis equation. Finally, in the cell-based model we assumed that cell density is low enough so that there is no mechanical interaction between cells. However, in some cases, the cell density can be high, and direct interaction between cells through the fluid, or more directly, through their flagella, can not be neglected.

Appendix A. Numerical algorithm of the cell-based model

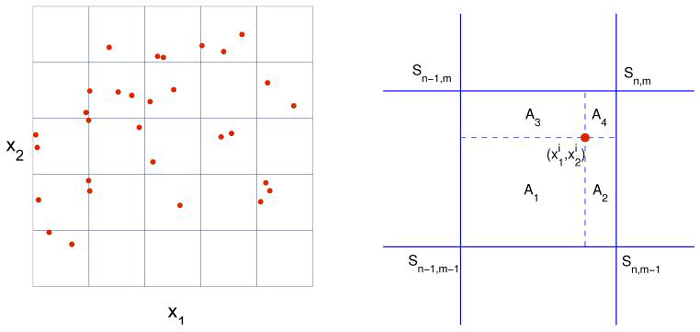
In the implementation of the cell-based model, cell motion is simulated by a standard Monte Carlo method in the whole domain, while the equations for extracellular chemicals are solved by an alternating direction method (Crank-Nicolson in 1-D) on a set of rectangular grid points (Figure A.1, left). In this appendix, we present the numerical algorithm in a two-dimensional domain with only one chemical - the attractant - involved (as in Section 4.3). Each cell is described by its position $(x_1^i,x_2^i)$, internal variables $(y_1^i,y_2^i)$, direction of movement θⁱ and age Tⁱ (the superscript i is the index of the cell). Concentration of the attractant is described by a discrete function defined on the grid for the finite difference method (Figure A.1, left). We denote the time step by k, the space steps by h₁ and h₂. Since two components of the model live in different spaces, two interpolating operators are needed in the algorithm. ${\mathcal{T}}_{gc}$ is used to evaluate the attractant concentration that a cell senses. For a cell at $(x_1^i,x_2^i)$, inside the square with vertex indices (n - 1, m - 1), (n, m - 1), (n - 1, m) and (n, m), ${\mathcal{T}}_{gc}(x_1^i,x_2^i)$ is defined by the bi-linear function:

$${\mathcal{T}}_{gc}(x_1^i,x_2^i)=\frac{A_4}{A}{S}_{n-1,m-1}+\frac{A_3}{A}{S}_{n,m-1}+\frac{A_2}{A}{S}_{n-1,m}+\frac{A_1}{A}{S}_{n,m}$$ (A.1)

where A = h₁h₂ and A_j, j = 1, 2, 3, 4 are the area fractions (Figure A.1, right). On the other hand, the attractant secreted by cells is interpolated as increments at the grid points by ${\mathcal{T}}_{cg}$. Suppose during one time step k, a cell staying at $(x_1^i,x_2^i)$ secretes Δ amount of attractant, we then interpolate the increment of the attractant concentration at the neighboring grid points as follows:

$${\mathcal{T}}_{cg}({\mathbf{x}}^i;p,q)=\{\begin{array}{c}\frac{A_4\Delta }{A^2},(p,q)=(n-1,m-1),\hfill \\ \frac{A_3\Delta }{A^2},(p,q)=(n,m-1),\hfill \\ \frac{A_2\Delta }{A^2},(p,q)=(n-1,m),\hfill \\ \frac{A_1\Delta }{A^2},(p,q)=(n,m),\hfill \\ 0,\text{otherwise}.\hfill \end{array}\phantom{\}}$$ (A.2)

We consider here a periodic boundary condition. The detailed computing procedure is summarized as follows.

Fig. A.1.

Left: a schematic figure of the domains. The reaction-diffusion equations are solved on the grid, while the cells can move around the whole domain. Right: the area fractions used in defining the interpolators (A.1, A.2).

S1 Initialization.

1. Initialize the chemical fields.

2. Initialize the list of swimmer cells. Each cell is put in the domain with random position, moving direction and age. yⁱ is set to be 0.

S2 For time step l (= 1 initially), update the data of each cell.

1. Determine the direction of movement θⁱ by equation (3.34).

   1. Generate a random number r ∈ U[0, 1];
   2. If $r<1-e^{-{\lambda }^{i}k}$, update θⁱ with a new random direction.

2. ${(x_1^i,x_2^i)}_l\leftarrow {(x_1^i,x_2^i)}_{l-1}+(sk\cos {\theta }^i,sk\sin {\theta }^i)$. Apply periodic boundary condition to make sure $(x_1^i,x_2^i)$ inside the domain,

3. ${\left(T^i\right)}_l\leftarrow {\left(T^i\right)}_{l-1}+k$. IF ${\left(T^i\right)}_l\ge$ 2 hours, then divide the cell into two daughter cells. This step is only considered when cell growth is considered.

4. Update $(y_1^i,y_2^i)$ by equations (4.1, 4.2).

   1. Determine the attractant concentration before the cell moves ${\left(S^i\right)}_{l-1}$ and after the cell moves (Sⁱ)_l by using the interpolating operator ${\mathcal{T}}_{gc}$.
   2. Estimate the attractant level during the movement by $S^i\left(t\right)={\left(S^i\right)}_{l-1}\frac{t-lk}{k}+{\left(S^i\right)}_l\frac{lk+k-t}{k}$ and integrate equation (4.1) to get ${\left(y_2^i\right)}_l$.
   3. ${\left(y_1^i\right)}_l\leftarrow G\left(S\right)-{\left(y_2^i\right)}_l$.

S3 Compute the source term of the attractant $f^{l-\frac{1}{2}}$ due to the secretion by the cells using the interpolator ${\mathcal{T}}_{cg}$,

$$f_{p,q}^{l-\frac{1}{2}}=\sum _i\left({\mathcal{T}}_{cg}(({\mathbf{x}}^i{)}_{l-\frac{1}{2}};p,q)\right),$$

where Δ = γk.

S4 Apply the alternating direction implicit method to the equation of the attractant (4.5):

$$\begin{array}{cc}\hfill \frac{S_{p,q}^{l-1∕2}-S_{p,q}^{l-1}}{k∕2}=D_s& \frac{S_{p+1,q}^{l-1∕2}-2S_{p,q}^{l-1∕2}+S_{p-1,q}^{l-1∕2}}{h_x^2}\hfill \\ \hfill & +D_s\frac{S_{p,q+1}^{l-1}-2S_{p,q}^{l-1}+S_{p,q-1}^{l-1}}{h_x^2}-\gamma \frac{S_{p,q}^{l-1}+S_{p,q}^{l-1∕2}}{2}+f_{p,q}^{l-\frac{1}{2}},\hfill \\ \hfill \frac{S_{p,q}^l-S_{p,q}^{l-1∕2}}{k∕2}=D_s& \frac{S_{p+1,q}^{l-1∕2}-2S_{p,q}^{l-1∕2}+S_{p-1,q}^{l-1∕2}}{h_x^2}\hfill \\ \hfill & +D_s\frac{S_{p,q+1}^l-2S_{p,q}^l+S_{p,q-1}^l}{h_x^2}-\gamma \frac{S_{p,q}^{l-1∕2}+S_{p,q}^l}{2}+f_{p,q}^{l-\frac{1}{2}}.\hfill \end{array}$$

For the boundary grid points, use the periodic scheme.

S5 $l\leftarrow l+1$. If lk ≤ T₀, repeat S2-S4; otherwise, return.

Appendix B. linear analysis on the stability of the uniform steady state of the continuum model

Linear analysis of the classical chemotaxis equation system has been done in the literature. For readers' convenience, we include it here. Consider the system

$$\{\begin{array}{c}\frac{\partial n}{\partial t}=\nabla \cdot (D_n{\nabla }_n-\chi \left(S\right)n\nabla S),\hfill \\ \frac{\partial S}{\partial t}=D_s\Delta S+\gamma n-\mu S.\hfill \end{array}\phantom{\}}$$ (B.1)

The uniform steady state is $(n,S)=(n_0,\frac{\gamma }{\mu }{n}_0)$, where n₀ is the averaged cell density. Without loss of generality, we assume a one-dimensional domain [0, L] with periodic boundary conditions, as in the example 4.1 and 4.2. The analysis can be extended without difficulty in the two dimensional case of example 4.3.

Let u = n - n₀, v = S - S₀ with $S_0=\frac{\gamma }{\mu }{n}_0$ By linearizing around the uniform steady state, we get the system

$$\{\begin{array}{c}\frac{\partial u}{\partial t}=D_n\Delta u-\chi \left(S_0\right)n_0\Delta v,\hfill \\ \frac{\partial v}{\partial t}=D_s{\Delta }_v+\gamma u-\mu v.\hfill \end{array}\phantom{\}}$$ (B.2)

Assume

$$u=\sum _{q\ne 0}{\phi }_q\left(t\right)e^{i{\omega }_{q}x},v=\sum _{q\ne 0}{\psi }_q\left(t\right)e^{i{\omega }_{q}x}$$

with ${\omega }_q=2q\pi ∕L$. The system can thus be reduced to

$${\left(\underset{{\psi }_q}{\overset{{\phi }_q}{}}\right)}_t=A_q\left(\underset{{\psi }_q}{\overset{{\phi }_q}{}}\right)\text{with}{A}_q=\left(\begin{array}{cc}\hfill -D_n{\omega }_q^2\hfill & \hfill \chi \left(S_0\right)n_0{\omega }_q^2\hfill \\ \hfill \gamma \hfill & \hfill -D_s{\omega }_q^2-\mu \hfill \end{array}\right)$$ (B.3)

for any $q\in \mathbb{Z},q\ne 0$. The uniform steady state of the nonlinear system is unstable if the linearized system (B.2) has exponentially growing non-homogeneous modes, which means that there exists a wave number q such that A_q has a positive eigenvalue.

Simple calculation leads to

• $T_r\left(A_q\right)=-(D_n+D_s){\omega }_q^2-\mu <0$

• $Det\left(A_q\right)={\omega }_q^2(D_n{D}_s{\omega }_q^2+\mu D_n-\gamma \chi \left(S_0\right)n_0)$

• $Tr{\left(A_q\right)}^2-4Det\left(A_q\right)={[(D_s-D_n){\omega }_q^2+\mu ]}^2+4\gamma {\omega }_q^2\chi \left(S_0\right)n_0>0$.

Therefore A_q is simple with eigenvalues

$${\lambda }_q^{\pm }=\frac{Tr\left(A_q\right)\pm \sqrt{Tr(A_q{)}^2-4Det\left(A_q\right)}}{2}.$$ (B.4)

${\lambda }_q^{-}$ is always negative and approaches -∞ as $n,m\to \infty ,{\lambda }_q^{+}$ can be positive when $Det\left(A_q\right)={\lambda }_q^{-}{\lambda }_q^{+}<0$. Thus, the instability condition→of∞the uniform steady state is,

$${\exists }_q\ne 0,s.t.Det\left(A_q\right)<0\iff {\omega }_q^2(D_n{D}_s{\omega }_q^2+\mu D_n-\gamma \chi \left(S_0{n}_0\right)<0,$$

which is equivalent to

$$4{\pi }^2{D}_s+L^2(\mu -\frac{\gamma \chi (\gamma ∕\mu n_0)n_0}{D_n})<0.$$ (B.5)

. The growth rate of an unstable mode in the linear system is given by ${\lambda }_q^{+}$.

From the instability analysis, we can also see that if the qth mode is unstable, the lower modes are always unstable. This leads to multiple nonuniform steady states of the nonlinear system (B.1), but only the one with a single high peak is stable.