Analysis of the kinetics of folding of proteins and peptides using circular dichroism

Abstract

Circular dichroism (CD) is a useful spectroscopic technique for studying the secondary structure, folding and binding properties of proteins. This protocol covers how to use the intrinsic circular dichroic properties of proteins to follow their folding and unfolding as a function of time. Included will be methods of obtaining data and how to analyze the folding and unfolding data to determine the rate constants and the order of the folding/unfolding reactions. The protocol focuses on the use of CD to follow folding when it is relatively slow, on the order of minutes to days. The methods for analyzing the data, however, can also be applied to data collected with a CD machine equipped with stopped-flow accessories in the millisecond to second range and folding analyzed by other spectroscopic methods including changes in absorption or fluorescence spectra as a function of time.

INTRODUCTION

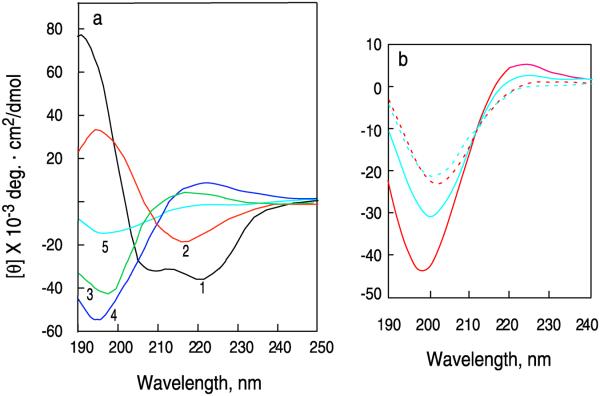
Circular dichroism is a useful spectroscopic method for studying conformational changes that occur during the folding and unfolding of proteins. The wavelengths and magnitudes of the ellipticity bands of the amide backbones of proteins are dependent on their conformation making them a useful index of protein folding. In general, proteins with a high degree of order, such as those with a high helical content, have large distinctive CD bands which are not present in unfolded proteins. Figure 1a shows CD curves of some representative secondary structures commonly found in proteins. Changes in ellipticity can be used to follow the folding or unfolding of proteins as a function of temperature, denaturants or stabilizing agents, ligands or time. This protocol is the fourth in a series of protocols on how to apply CD spectroscopy to study the folding and interactions of proteins. The first protocol covers the technique of CD in general, i.e. how to set up CD spectrometers, how to prepare protein samples, buffers and cells to obtain high quality CD data and how to use CD to estimate the secondary structure of proteins¹. The second and third protocols cover how to use changes in the spectra of proteins collected as a function of temperature² or perturbants³ to determine their enthalpies and free energies of unfolding. The effects of ligand binding and protein-protein interactions on protein folding are also described in these protocols.

Figure 1. Circular dichroism (CD) spectra of proteins and peptides with representative secondary structures.

a, CD spectra of poly-L-lysine in the 1, α-helical (black), 2 antiparallel β-sheet (red), and 3 extended disordered conformations (green)⁵⁵ and placental collagen in its 4, native triple-helical (blue) and 5, denatured (cyan) forms⁵⁶. The α-helical and β-forms of poly-L-lysine are observed at pH 11, while the extended form is observed pH 5.1 where the molecule is charged⁵⁵. The spectrum of poly-L-lysine at this pH is similar that of poly-L-Proline II⁵⁴,⁵⁷-⁶⁰, which is a left handed extended helix with 3 residues per turn and the amide backbone bonds are trans to each other. b, A 33-residue peptide fragment of human type-I α-collagen (residues 1162-1194) with the sequence: IGPPGPRGRTGDAGPVGPP_OHGPP_OHGPP_OHGPP_OHGPP_OHSA (WT) where P_OH is hydroxyproline and a peptide containing the mutation G14A at 2 °C and 60 °C° in water at pH 5.1. The concentration of peptide chains were 0.04 mM. (solid red line) WT at 2 °C; (dashed red line) WT at 60 °C; (solid cyan line) G14A at 2 °C; (dashed cyan line) G14A at 60.

This current protocol is a basic introduction to the use of CD to study protein folding as a function of time and includes some simple methods to estimate the rate constants and reaction orders of folding and unfolding from the analysis of CD data. It is not intended as a comprehensive guide to the use of spectroscopy to follow kinetics as there is extensive literature on this subject (e.g. see reviews^4-11). The protocol specifically addresses the case of using CD to follow folding when it is relatively slow, on the order of minutes to days, but the methods of data analysis can also be applied to data collected with a CD machine equipped with stopped-flow accessories in the millisecond to second range. The same equations used to analyze CD data can be used to fit data collected by other spectroscopic methods including changes in absorption, IR, or fluorescence spectra. It should be emphasized that the kinetic analysis of folding data can in some cases disprove a proposed folding pathway, but it can never prove that one is correct. Data analysis only shows whether data can be fit to a model. Before fitting data to a model it is important to determine the oligomeric state of the folded and unfolded proteins and peptides by some independent method such as equilibrium ultracentrifugation or light scattering¹². In addition, CD does not give residue specific information about the kinetics of folding. Recently, detailed characterization of folding pathways have been obtained using rapid hydrogen exchange techniques in conjunction with structural analysis using NMR and/or mass spectroscopy (see reviews^11,13-17).

Circular dichroism can be used to follow the folding or unfolding of proteins and peptides utilizing the fact that the spectra of folded and unfolded proteins and peptides usually have very different spectra (Figures 1a, 1b). In the simplest case a molecule undergoes a folding transition between two states: folded, F, and unfolded, U. For a molecule with identical subunits, at any temperature, T, the constant of folding, K_F, is:

$${\mathrm{K}}_{\mathrm{F}}=\left[\mathrm{F}\right]∕{\left[\mathrm{U}\right]}^{\mathrm{n}}$$ (1)

Where [F] and [U] are the molar concentrations of folded and unfolded protein, respectively and n denotes how many chains associate when the protein is folded. At a given temperature the rate of folding equals k₁[U]ⁿ and the rate of unfolding equals k₋₁[F], where k₁ and k₋₁ are the rate constants for folding and unfolding, respectively. At equilibrium the rates of folding and unfolding are equal, i.e., k₁[U]ⁿ =k₋₁[F]. Since K_F=[F]/[U]ⁿ it follows that K_F=k₁/k₋₁.

The free energy of folding is ΔG.

$$\Delta \mathrm{G}=-{\mathrm{RTlnK}}_{\mathrm{F}}$$ (2)

Where R is the Gas constant =1.98 cal/mol, and T is the absolute temperature (Kelvin). The fraction folded, α_i can be evaluated from the ellipticity under any condition, i, using the formula:

$${\alpha }_l=({\left[\theta \right]}_{\mathrm{i}}-{\left[\theta \right]}_{\mathrm{U}})∕({\left[\theta \right]}_{\mathrm{F}}-{\left[\theta \right]}_{\mathrm{U}})$$ (3)

Where [θ]_i is the ellipticity at any time, temperature or concentration of perturbant, [θ]_F is the ellipticity when the molecule is fully folded and [θ]_U is the ellipticity of the fully unfolded molecule. In all of the equations given below, unless otherwise stated, [θ] is the mean residue ellipticity of a protein is expressed in deg. · cm²/dmol so that data obtained at different protein concentrations can be directly compared. Mean residue CD data can also be expressed in units of the difference between the absorption of left handed and right handed circularly polarized light, Δε_L–R, which is equal to [θ] divided by 3298. Methods to calculate the mean residue ellipticity from raw data are given in the first protocol in this series¹.

The folding constant for a monomeric protein is:

$${\mathrm{K}}_{\mathrm{F}}=\alpha ∕(1-\alpha )$$ (4)

For a homodimer the equation is:

$${\mathrm{K}}_{\mathrm{F}}=\alpha ∕{\left(2{\mathrm{P}}_{\mathrm{t}}(1-\alpha )\right)}^2$$ (5)

and for a homotrimer the equation is:

$${\mathrm{K}}_{\mathrm{F}}=\alpha ∕{\left(3{\mathrm{P}}_{\mathrm{t}}(1-\alpha )\right)}^3$$ (6)

where P_t is the concentration of the protein when it is fully folded. The total concentration of protein chains, c, are equal to n[F] plus [U], i.e., c = nP_t. If the equilibrium of a solution of a peptide or protein is disturbed by changing the temperature or concentration, or by adding or diluting out a denaturant, the ellipticity will change until a new equilibrium is reached. The rate of change for a molecule with identical subunits is given by:

$$\delta {\left[\theta \right]}_{\mathrm{t}}∕\delta \mathrm{t}={\mathrm{nk}}_1\{{({\left[\theta \right]}_{\mathrm{F}}-{\left[\theta \right]}_{\mathrm{t}})}^{\mathrm{n}}∕({{\left[\theta \right]}_{\mathrm{F}}-{\left[\theta \right]}_{\mathrm{U}})}^{\mathrm{n}-1}\}{\mathrm{c}}^{\mathrm{n}-1}-{\mathrm{k}}_{-1}(\left[\theta \right]-{\left[\theta \right]}_{\mathrm{U}})$$ (7)

where δ[θ]_t/δt is the rate of change of ellipticity at any time, t; [θ]_t is the ellipticity at time t; n is the number of chains in the folded protein; k₁ is the rate of folding; k₋₁ is the rate of unfolding; [θ]_F is the ellipticity when fully folded and [θ]_U is the ellipticity when fully unfolded¹⁸.

The initial change in ellipticity of the unfolded form, v₀, equals δ[θ]_t/δt at t=0. v₀ can be estimated by fitting the earliest points of the curve of ellipticity as a function of time by a straight line. At time zero, [θ]_t=[θ]_U Equation (7) simplifies to give:

$${\mathrm{v}}_0={\mathrm{nk}}_1({\left[\theta \right]}_{\mathrm{F}}-{\left[\theta \right]}_{\mathrm{U}}){\mathrm{c}}^{n-1}$$ (8)

The value of the order of the reaction, n, can be calculated from the slope of a plot of ln(v₀) versus ln(c)¹⁸. Alternatively the order, n, can be determined for 0 to 3^rd order reactions as described by Wilkinson¹⁹ using equation (9) by plotting the time divided by the fraction folded as a function of time:

$$\mathrm{t}∕\alpha =1∕{(k}_1{\mathrm{c}}_0)+\mathrm{nt}∕2$$ (9)

Here k₁ is the rate constant of folding and c₀ is the initial concentration of unfolded protein chains, t is the time and the slope is equal to the order of the reaction divided by two. The slope of the line is one half the reaction order, and the rate constant can be calculated from the intercept.

The rate constants for folding and unfolding can be determined from the change in ellipticity as a function of time. Table 3 has the equations for determining the rate constants from CD data for 0 to 3^rd order reactions. Simple scripts for fitting changes in CD data to equations describing first, second and third order reactions are in SUPPLEMENTARY MATERIALS in SigmaPlot format in the file kinetics.doc.

In a more complete treatment on the rate of change of ellipticity¹⁸, the initial rate data includes the temperature dependence of the rate constant of folding. For example, in the case of protein folding, the initial velocity of the folding reaction, v₀, is dependent on the rate constant of folding, k₁, which is defined by the Arrhenius equation:

$${\mathrm{k}}_1={\mathrm{k}}_0{e}^{-\Delta \mathrm{H}{1}^{\ast }}∕\mathrm{RT}$$ (10)

where ΔH_l* is the heat of activation for formation of the folded protein, T is the absolute temperature (Kelvin), R is the Gas constant= 1.98 cal/mol and k₀ is a statistical factor. When the equations (8) and (10) are combined, the rate of folding is described by the relationship:

$$\ln \left({\mathrm{v}}_0\right)=(-\Delta {{\mathrm{H}}_1}^{\ast }∕\mathrm{R})(1∕\mathrm{T})+\ln \left({\mathrm{nk}}_0\right)+(\mathrm{n}-1)\ln \left(\mathrm{c}\right)+\ln ({\left[\theta \right]}_{\mathrm{F}}-{\left[\theta \right]}_{\mathrm{U}})$$ (11)

Plots of the natural logarithm of the initial rates of change of the ellipticity versus 1/T at various protein concentrations can be fit globally to equation 11 to yield the values of ΔH₁*, n, and k₀ using non-linear least squares curve fitting procedures²⁰ implemented in many graphics programs (see software) and k_l can then be obtained from equation (10) as described by Sherman and Piez¹⁸.

A strategy to determine the kinetic constants of folding over a large temperature range is to take advantage of the relationship between the equilibrium constant of folding, K_F, and the rate constants of folding, k₁ and unfolding k₋₁¹⁸. The folding constant K_F, can be determined at any temperature using equations 1-6 as described previously². If there are linear changes in ellipticity preceding or following the unfolding transition, the ellipticity of the fully folded and unfolded forms at any temperature can be evaluated by extrapolation of the linear parts of the unfolding curve^21,22 (see Figure 2a). The 1st order unfolding constants can be evaluated at temperatures where the protein readily unfolds. The rate constants at low temperatures, where the rate of unfolding is low, can be determined using the Arrhenius relationship given in equation 10. For any given temperature, the rate constant of folding, k₁ equals the product of K_F multiplied by k₋₁ at the same temperature.

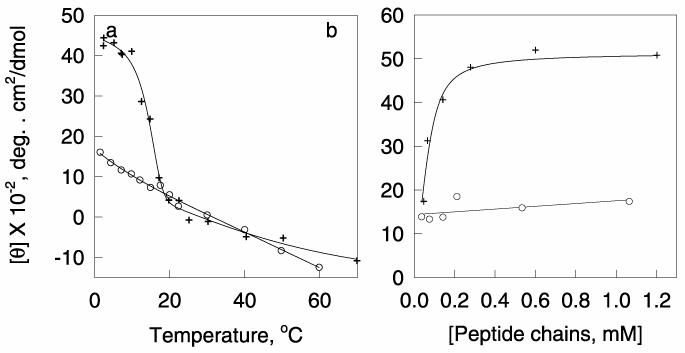
Figure 2. Circular dichroism of the WT and G14 Mutant collagen peptides as a function of temperature and peptide concentration.

(+) WT, (o) G14A. a, The mean residue ellipticity at 223 nm of the (+) WT and (o) G14A collagen peptides as a function of temperature. The total peptide chain concentration was 0.4 mM at pH 5.1 in H₂O. b, The mean residue ellipticity at 223 nm of the (+) WT and (o) G14A mutant peptides as a function of concentration at 2 °C in water at pH 7.0.

The collection of kinetic data using CD is relatively simple, but analysis of the data can be very complicated if there are multiple folding reactions. The equations described above assume that the transitions are two-state, between the folded and unfolded forms. Jackson and Fersht²³ have described the requirement for the folding of a protein to be considered to be “two-state”. (1) The unfolding and refolding data as a function of temperature, denaturant or osmolyte must be able to be fit to a single transition. This means the values of the ellipticity as a function of temperature or denaturant must be identical whether one starts with the unfolded protein and decreases the temperature or concentration of denaturant, or starts with the folded protein and increases the temperature or concentration of denaturant. (2) The unfolding data must be independent of the probe used to determine the state of the protein, e.g. CD, fluorescence, absorbance, c NMR, etc. (3) The van't Hoff enthalpy of denaturation (determined using spectroscopic methods) and the calorimetric enthalpy of denaturation must be identical. (4) The kinetics of unfolding and refolding must be monophasic processes (with the exception that there may be heterogeneity of the unfolded form due to proline isomerization). (5) When the folding is examined as a function of denaturants, the logarithms of the equilibrium constants for unfolding and those of the rate constants for both folding and unfolding must be linearly dependent on the concentration of denaturant. (6) The value for the slope, m, of the change in the folding constant, K_F, as a function of denaturant, calculated from equilibrium unfolding transitions, must be the same as that calculated from the effect of denaturants on the kinetic constants of folding and unfolding. If the reaction is two-state the rate constant of both unfolding (equation 12) and folding (equation 13) are linearly dependent on the concentration of denaturant.

$$\ln \left({\mathrm{k}}_{-1}\right)=\ln \left({\mathrm{k}}_{-1\left(0\right)}\right)+{\mathrm{m}}_{-1}\left[\mathrm{D}\right]$$ (12)

$$\ln \left({\mathrm{k}}_1\right)=\ln \left({\mathrm{k}}_{1\left(0\right)}\right)+{\mathrm{m}}_1\left[\mathrm{D}\right]$$ (13)

where k₋₁ and k₁ the observed unfolding and folding constants at any concentration of denaturant, [D], k₁₍₀₎ and k−1(0) are the values in the absence of denaturant, and m₋₁ and m₁ are the slopes of the line when one plots the logarithms of the folding constants as a function of denaturant. The slope m, from the equilibrium unfolding studies must equal m₁ + m₋₁ from the kinetic studies and the extrapolated equilibrium constant of folding in the absence of denaturant, KF(0) , must equal k₁₍₀₎/k₋₁₍₀₎.

Most often when proteins fold or unfold, however, there are intermediate partially folded states. The kinetics of unfolding and refolding can sometimes detect folding intermediates which are not stable enough to be observed under equilibrium conditions. Experiments to detect the kinetic folding intermediates are usually performed by following the rate of unfolding when a protein is diluted into a denaturant or folding when the protein is diluted from a concentrated solution containing a denaturant into one without denaturant. Such experiments are usually performed using rapid mixing techniques to detect fast reactions. Most often the folding is followed using changes in fluorescence rather than CD because fluorescence is much more sensitive than CD and measurements can be made at wavelengths where solutions containing urea and guanidine-HCl have low absorbance. The most accurate analyses of the kinetics of folding are obtained when the CD data are combined with other methods to evaluate folding such as NMR and fluorescence^11,24.

One method to determine whether there are kinetic folding intermediates is to employ the use of “chevron plots” Equations (12) and (13) can be combined to give an expression that describes the unfolding or folding rates, k, at any concentration of denaturant²³:

$$\ln \left(\mathrm{k}\right)=\ln \left\{\right({\mathrm{k}}_{1\left(0\right)}\exp (-{\mathrm{m}}_1\left[\mathrm{D}\right])+{\mathrm{k}}_{-1\left(0\right)}\exp \left({\mathrm{m}}_{-1}\left[\mathrm{D}\right]\right\}$$

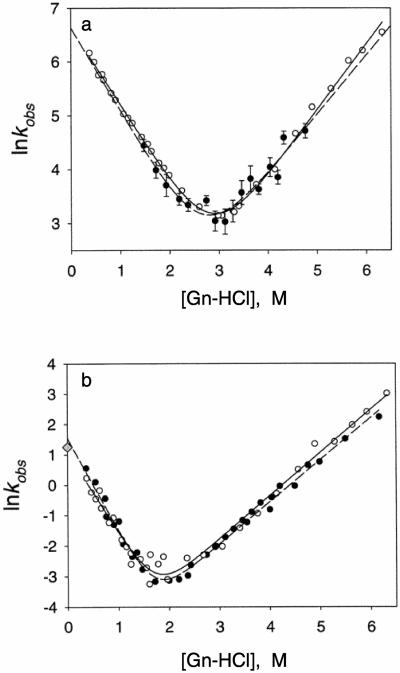
When the reaction is two state one will have a plot of two intersecting straight lines, one for the change in the unfolding rate constant and the other for the folding rate constant. When the folding is not two-state, one or more of the lines will be curved. Figure 3 illustrates a chevron plot obtained from stopped-flow CD measurements of the folding of two isolated domains of a ribosomal protein, L9²⁵. Data obtained from stopped-flow CD and fluorescence measurements are compared. Two intersecting straight lines are obtained from a plot of ln(k) versus guanidine-HCl, suggesting that the folding of the isolated domains occur in two-state transitions.

Figure 3. Chevron plots of the rate constants of folding and unfolding of two isolated domains of a ribosomal protein, L9, as a function of the concentration of a denaturant.

Plots of the natural logarithm of the observed rate constants of the folding and unfolding of two domains of the multidomain ribosomal protein L9 from Bacillus stearothermophilus versus the concentration of guanidine-HCl. Open circles and solid lines are from stopped-flow fluorescence experiments⁶¹. Closed circles and broken lines are from stopped-flow CD experiments²⁵. a, The N-terminal domain. The solid and broken lines are the data obtained from CD and fluorescence measurements, respectively. b, The C-terminal domain. The solid and broken lines are the best fits of fluorescence and CD data, respectively. The shaded diamond represents the results from the pH jump experiments using CD and fluorescence detection. The same rate was obtained using the CD and fluorescence measurements. Reprinted from Sato et al.²⁵ with permission from the American Chemical Society.

Description of methods

In this protocol two types of folding experiments will be described: Slow temperature jump and dilution from denaturant. These can be adapted to study protein unfolding. Also included are the methods for analyzing the data.

Slow temperature jump experiments

In this method a solution of a protein is equilibrated at a temperature where it is unfolded. The protein can be equilibrated in a cuvette with a short pathlength (e.g. 0.1 cm) with a large surface area, or a concentrated stock solution of the protein can be prepared. The cuvette containing the protein is plunged into a cell holder that is pre-equilibrated at a temperature where the protein is folded and data collection is started immediately. (Note that a 0.1 cm cell takes ∼ 1 minute to equilibrate from 25 to 2 degrees under these conditions). Alternatively, a large volume of buffer is equilibrated at the folding temperature in a temperature controlled cell holder that has a motor to stir a magnetic stirring bar. The control on the CD spectrometer is set so that the solution is stirred during data collection. Data collection is started and a small aliquot of the protein is added to the equilibrated buffer. The dead time in this case is about 10 seconds, including adding the protein and closing the cover to the CD machine.

Dilution from denaturant

A concentrated solution of protein is dissolved in a denaturant such as 8M urea or 6M guanidine-HCl is pre-incubated at a temperature where the protein is folded in the absence of denaturant. The buffer is equilibrated at the same temperature and stirred with a magnetic stirring bar and data collection is started while stirring. A small aliquot of the protein in the denaturant is added and the folding data is collected. The dead time between adding the sample and closing the cover to the CD machine is ∼10 sec. Note that the dilution methods will only work if the solutions can be rapidly mixed and work best if the CD machine has a built in motor which can spin a magnetic stirring bar that fits into the cuvette containing the folding buffer.

Unfolding Experiments

Essentially the method is the same as the folding experiments, but one starts by equilibrating a protein at a low temperature under conditions where it is folded. The sample can be equilibrated directly in a CD cuvette or equilibrated at higher concentrations in a small test tube. The sample may then either be placed directly into the cell holder in the CD machine, which has been pre- equilibrated at a temperature at which the protein unfolds, or the folded protein may be diluted into a solution equilibrated in a 1 cm cuvette (3 ml volume) at a higher temperature where it unfolds. Note, this method cannot be used to study the kinetics of unfolding into high concentration of guanidine-HCl or urea because they both absorb strongly in the far UV region. When examining unfolding or folding reactions using concentrations of urea or guanidine > 0.5 M it is necessary to run the experiments in cells with path lengths of 0.1 cm or less. Ideally the final protein concentrations would be 0.1 to 0.2 mg/ml with the highest concentration of guanidine-HCl or urea equaling ∼ 4 and 6 M, respectively. One quickly adds an aliquot of protein with a syringe or pipette to the solution containing the denaturant and seals the cell with a Teflon stopper or paraffin film, and inverts the cell 4 to 5 times to disperse the protein and then plunges the cell into the holder and starts collecting data. The dead time for this is approximately 20 sec.

Data Analysis

For simple analysis of data, it is possible to linearize the equations describing the folding and unfolding of proteins (See Table 1). These methods have the advantage that it is easy to determine whether there are multiple folding steps and whether the data fits the proposed kinetic models by visual inspection of the graphs. For more sophisticated analyses, the folding and unfolding curves can be analyzed by direct fitting of the data using general graphics software, mathematics packages including MatLab and Mathematica or specialized programs developed for the analysis of kinetics (see Software). When kinetic data are fit using either linear or non-linear least squares analyses, for the fitted curves to be a good match to the raw data, the residuals of the dependent variable plotted as a function of the independent variable must be uniformly distributed around a straight line whose slope and intercept are zero. Having a good fit of folding data to a kinetic model, however, doesn't insure that the model is correct. Most commercial curve fitting programs will output the estimates of the standard errors of the fits of the parameters in the equations used to fit the data. The errors in the curve-fitting parameters are better estimated, however, by using the average values and standard deviations of the parameters obtained from replicate experiments.

Table 1.

Equations for Calculating Rate Constants of Folding from Changes in Ellipiticity as a Function of Time^*.

Reaction Order	Rate Equation	Integrated Rate Equation	Linear Plot	Slope	Units of Rate Constant
0	− δ[U] / δτ = k	[U]= [U]0 − kt	[U] vs t	−k	mol L−1 s−1
1st	− δ[U]/ δτ = k [U]	[U]= [U]0e −kt	ln[U] vs t	−k	s−1
2nd	− δ[U] / δτ = k [U]2	1/[U]= 1/[U]0 + kt	1/ [U] vs t	K	L mol−1 s−1
3rd	− δ[U] / δτ = k [U]3	1/[U]2 = 1/[U]02 + 2kt	1/ [U]2 vs t	2k	L2 mol−2 s−1

^*In all of the equations in Table 1, k is the folding constant and t is the time in seconds. [U] is the concentration of unfolded protein at any time t. [U₀] is the concentration when all of the protein is unfolded. [U]= [U]₀(1-α), where α is the fraction folded, which equals ([θ]_t – [θ]_U) / ([θ]_F – [θ]_U). [θ]_t is the ellipticity at any time, t, [θ]_F is the ellipticity of the fully folded protein and [θ]_U is the ellipticity of the fully unfolded protein.

Applications

Many diseases are caused by mutations in proteins and biological peptides, which affect their rates of folding^26-28. CD is an excellent method to determine the structural changes caused by mutations and to determine how the mutations affect the rates of folding. Many folding diseases involve relatively slow conformational changes that can easily be followed using CD. One example of such a disease is osteogenesis imperfecta, which is primarily caused by mutations of glycines in collagen, which slow the rate of formation of the collagen triple helix²⁴. Another large class of diseases is caused by mutations in proteins and peptides that lead to the formation of amyloids²⁸. These diseases include Alzheimer's disease and related dementias²⁹, prion diseases such as “mad cow disease”²⁷, and diseases caused by the aggregation of proteins containing repeat sequences of poly-L-glutamine, such as found in Huntington's disease³⁰. The amyloid diseases all involve slow conformational transitions between non-aggregated states where the proteins or peptides are soluble, with conformations that are partially helical, to a state with a high proportion of β-structure. The formation of intermolecular β-sheets is often followed by aggregation and precipitation. These conformational transitions are easily characterized by CD^31-40. The conformational changes due to amyloid formation often follow kinetics where there is a slow initiation step followed by a propagation step. The curves of the kinetics of the conformational changes are often sigmoidal; a lag phase is followed by an exponential growth phase^41,42.

In addition to its use for studying conformational transitions leading to diseases, kinetic studies using CD spectroscopy often give insight into the fundamentals underlying the folding of proteins and the linkage between protein folding and function^8,43,44

MATERIALS

Reagent Setup

The preparation of protein samples and buffers suitable for CD have been discussed previously¹. For the best characterization of the folding of proteins, data should be collected on protein samples with concentrations ranging over 2 orders of magnitude. If one is studying the folding of proteins with a high α-helical content, and following the folding at 222 nm, a practical concentration range is 0.02 to 2 mg/ml in a 0.1 cm cell, as the concentration is limited by the ellipticity range of the spectrometer (generally −500 to 500 millidegrees) and the absorption of the samples. The concentrations of collagen-like proteins can be increased to 15-20 mg/ml if the folding is followed at 223 nm since they have lower mean residue ellipticity at this wavelength than globular or coiled-coil α-helical proteins. The higher concentrations may also be used if one is following changes in the aromatic region of the protein as a function of time.

Equipment

Sources of CD instruments and cuvettes and preparation have been previously described¹.

Equipment Setup

Software

General graphics packages such as GraphPad, http://www.graphpad.com/; Psi-Plot, http://www.polysoftware.com/aboutpsi.htm; Origin, http://www.originlab.com; and SigmaPlot, http://www.systat.com; general mathematical software such as Matlab http://www.mathworks.com/ or Mathematica http://www.wolfram.com/products/mathematica/index.html or specialized software developed for the analysis of kinetics. Examples include Kinteksim http://www.kintek-corp.com and FAST http://www.edinst.com/fast.htm.

Procedures for starting CD instruments have been previously described¹.

Caution!

Make sure that the instrument is flushed with nitrogen before firing the lamp and that circulating water baths if they are needed for cooling the lamp or acting as a heat trap for the temperature controllers are turned on before the CD software is started.

Preliminary Experiments

Obtain full CD spectra at selected temperatures to determine the conditions at which the protein is fully folded and fully unfolded and to determine the optimum wavelengths for following the structural transition as described previously^1-3.

Protocol

Timing 30 minutes to overnight

1 Equilibrate protein solutions at a temperature where they are unfolded, e.g. 70 °C for globular proteins, 25 °C for unstable peptides or protein fragments, in a temperature block or heating bath for folding experiments or where they are fully folded (e.g. on ice) for unfolding experiments. (Details on how to insure that a protein is fully folded have been described previously^1,2). For slow temperature jump experiments, preincubate the protein at the desired concentration in 0.1 cm cuvettes. For dilution from denaturant experiments, preincubate a concentrated stock of native or denatured protein in a small test tube.

2 Pre-cool or pre-heat the cell holder to the desired temperature, e.g. 25 °C for globular proteins or 0-4 °C for peptides or protein fragments for folding experiments; 10 to 70 °C for unfolding experiments.

3 Set the CD machine to collect kinetic data at a single wavelength. Suggested parameters would be to collect points every second with an averaging time of 1.0 sec and a pen response time of 0.1 sec. Suggested wavelengths are 222 nm for peptides and proteins with high helical contents, 218 nm for proteins with high contents of β-structure, and 225 or 200 nm for proteins with a collagen-like triple helical structure.

4 Start the collection program and begin to acquire data. For slow temperature jump experiments, quickly plunge the CD cell into the sample compartment and close the machine cover. For dilution from denaturant experiments, equilibrate 3 ml of the desired buffer at low temperature in a 1 cm cell while stirring with a magnetic bar. Start collecting data as a function of time (stirring during the measurement) and add a small aliquot of protein in a denaturant (e.g. 10 μl of 6M guanidine-HCl or 8M urea containing 0.1 to 10 mg/ml protein) or protein pre-equilibrated at a temperature where it is unfolded and close the machine cover.

CRITICAL STEP When using the dilution technique make sure that the solution is being stirred while the concentrated sample is added so that it quickly disperses.

TROUBLESHOOTING

TROUBLESHOOTING

4	The CD machine does not have a stirring motor	Rapidly add the sample and stir the sample using the pipette tip or stopper the cell with a Teflon stopper or Parafilm and invert several times to mix the solution thoroughly.
5	The signal is still changing after 30 minutes to one hour.	Try to transfer the sample to a water bath or temperature controlled block and equilibrate it overnight or several days. Then run CD spectra to determine the endpoint of the folding or unfolding reaction.
7	The change in CD as a function of time can't be fit by any of the equations in table 1.	Make sure that the ellipticity values of the fully folded and unfolded proteins were obtained under equilibrium conditions. Plot the data on a log scale as shown in Figures 3 and 5a to determine how many folding transitions are observed using CD and try to use the sum of several folding equations to fit the data. Alternatively, try to analyze the folding by kinetics of nucleation followed by propagation as described for amyloid formation42.

5 Collect data until the ellipticity change as a function of time levels off.

TROUBLESHOOTING

6 Save the data for each sample as individual files of ellipticity (y) as a function of time (x).

7 Analyze the data to determine the order of the folding/unfolding reactions and the time constants of folding.

TROUBLESHOOTING

ANTICIPATED RESULTS

If the folding of a protein is slow and there is at least a 10 millidegree change between the ellipticities of the folded and unfolded form, it is relatively easy to obtain kinetic data with high signal to noise. If the protein folds and unfolds in a two-state transition between folded and unfolded forms, data analysis is relatively simple (e.g. see a study on the folding of the coiled coil domain of the yeast transcription factor determined using stopped-flow CD⁴⁵). However, data analysis is much more complicated when there are multiple folding transitions. For example, the determination of equilibrium folding constants, orders of the folding reactions and the rate constants of folding and unfolding from global analysis of data collected for several collagen-like peptides as a function of temperature and time, have been described in several papers in detail^18,22,46. These types of peptides form triple helices when folded and have complicated folding paths. When these peptides are rapidly cooled they often exhibit a fast CD change as a function of time followed by a much slower change.

Figures 1,2 and 4-6 illustrate an example of the use of CD to determine folding orders and rate constants of folding and unfolding of a fragment of human type I α-collagen containing 33 residues from a region near the C terminus⁴⁷, which forms a collagen-like triple helix, and the same peptide containing a mutation, G14A, which greatly inhibits the ability of the peptide to form a trimer. The circular dichroism spectra of the WT peptide are similar to those observed for other collagen fragments, which contain high percentages of proline and hydroxyproline (P_OH) with glycine at every third position^18,48-50 and polypeptide collagen mimetics such as poly(PPG)₁₀ and poly(PP_OHG)₁₀^22,51-53. For the study illustrated here ∼ 0.004 to 1.2 mM of the collagen peptides were preincubated at 25 °C, where they were unfolded in a 0.1 cm cuvette and quickly plunged into a chamber equilibrated at 2 °C and data were collected at 223 nm at one second intervals to study the folding reaction. Alternatively, the samples were preincubated on ice for several days to fold them, and then rapidly plunged into a cell holder at 17 °C to study unfolding.

Figure 4. Unfolding of the WT and G14 mutant collagen peptides as a function of time.

Unfolding of the WT (+) and G14A (o) when the temperature is rapidly raised from 2 to 17 °C. The peptide chains were 0.25 mM in water at pH 7.0. The first order rate constants of unfolding are 3.6 ± 1.2 x 10⁻³ s⁻¹ for the triple helical WT peptide and 2.9 ± 0.7 × 10⁻² s⁻¹ for the single stranded peptide containing the mutation, respectively.

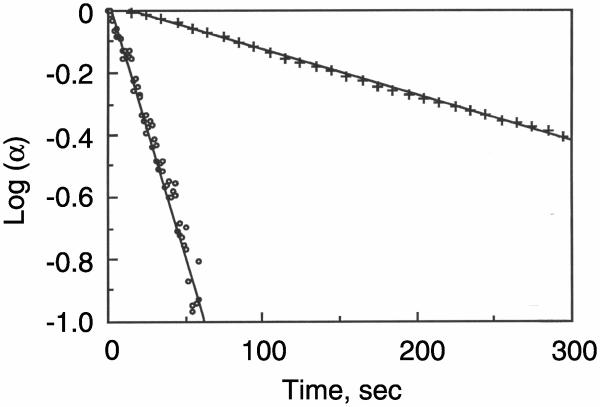
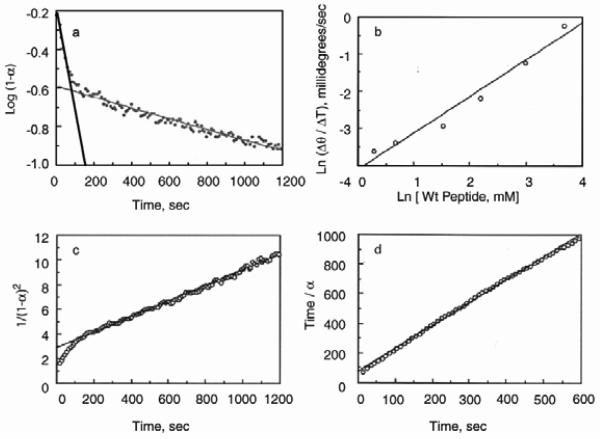
Figure 6. Linear analyses of the kinetics of folding of the WT collagen peptide at 2 °C.

a, A solution of the peptide was rapidly cooled from 25 to 2 °C. Shown is the plot of the log of the fraction unfolded of the WT peptide as a function of time. The peptide chain concentration was 0.6 mM in water at pH 5.1. The folding is biphasic. When fit by two straight lines, the first phase is linear for ∼ 100 seconds, suggesting that the initial folding reaction is first order, but the second phase deviates from linearity. b, Plot of the initial rate of folding (0 to 60 sec) of the wild-type peptide as a function of peptide concentration at 2 °C in water at pH 5.1. The rates are a linear function of peptide concentration also suggesting that the initial folding reaction is 1^st order. c, plot of 1/(fraction unfolded)² against time. The curve is linear between 2 and 10 minutes following the change in temperature, consistent with 3^rd order folding kinetics. f, The reaction order, determined by the method of Wilkinson¹⁹, is also consistent with third order folding kinetics for the slow step and equals 3.1 ± 0.2.

Figure 1b shows the spectra of the wild-type and G14A peptides at 2 and 70 °C. At the lower temperature the mean residue ellipticity of the wild-type peptide resembles that of triple stranded collagen while the mutant has a spectrum similar to that of monomeric poly-L-proline II⁵⁴, while at 70 °C, both peptides have a spectrum similar to unfolded collagen (Figure 1a).

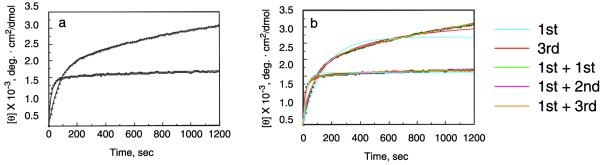
Figure 2a shows the folding of the peptide as a function of temperature at 223 nm, and Figure 2b shows the concentration dependence of the equilibrium value of the ellipticity. The ellipticity of the wild-type peptide has a large dependence on the peptide concentration, showing that it is a multimer (Figure 2b). The wild-type peptide (WT) shows a major unfolding transition (Figure 2a), in which the T_M is concentration dependent (data not shown), followed by a linear change in ellipticity of the dissociated peptide chains above 20 °C as a function of temperature. The ellipticity of the mutant is almost independent of peptide concentration (Figure 2a) suggesting that it is almost all in the monomeric state, even at 2 °C, and also shows a linear change in ellipticity as a function of temperature (Figure 2b) above 20 °C. The folded form of the wild-type peptide has a much higher molecular weight than the unfolded form and the folded and unfolded forms can be separated by size-exclusion chromatography at 4 °C and 14 °C (data not shown). At 25 °C only the lower molecular weight unfolded peptide is observed. The mutant peptide shows only one chromatography peak between 4-25 °C with the same molecular weight as the unfolded wild-type peptide showing that the mutation greatly inhibits the ability of the peptide to form a stable triple helix. A similar replacement of a single glycine in the middle of the polypeptide (PP_OHG)₁₀ with an alanine, greatly decreases the stability of the peptide and the rate of folding of the triple helix, but does not destroy the ability to form a triple helix⁵³.

Figure 4 is a plot of the log of the fraction folded versus time for the unfolding of the WT and mutant peptides when they are transferred from an ice bath to 17 °C. The plots are linear, showing that both peptides unfold via first order reactions, but the unfolding of the mutant is considerably faster than the wild-type.

Figure 5a shows the folding of the peptides when they are rapidly cooled from 25 to 2 °C. The wild-type and mutant peptides both exhibit biphasic folding curves. Both appear to quickly refold (within the first 200 seconds) to form a structure that resembles the conformation of poly-L-proline II. The initial rate of folding of the mutant peptide is faster than that of the WT peptide and is limited by the rate of cooling of the cuvette. After the initial rapid change in ellipticity, the wild-type peptide exhibits a much slower increase in folding that is not completed in 20 minutes, which is highly dependent on the concentration of peptide. The ellipticity of the mutant peptide also increases but at a much slower rate than that of the wild-type peptide.

Figure 5. Folding of the wild-type and G14A mutant collagen model peptides as a function of time.

a, The change in mean residue ellipticity at 223 nm as a function of time (+) WT, (o) G14A. The peptide chains were 0.6 mM in water at pH 5.1. b. the data in panel a fit by integrated rate equations (see Table 1) using the Levenberg-Marquardt algorithm²⁰: (cyan) a single 1^st order reaction; (red) a single third order reaction; (green) the sum of two first order reactions; (pink) the sum of a 1^st order and 2^nd order reaction and (orange) the sum of a first order and 3^rd order reaction.

The raw data for the folding of the WT and G14A mutant peptides were fit in Figure 5b by the integrated equations in Table 1 for first order (cyan) and third order (red) folding reactions. The fits were poor, showing that a single folding reaction is inadequate to fit the data, and the residual when plotted showed a large slope (data not shown). The folding curves were better fit by the sum of a 1st order reaction, followed by a second folding reaction. The data for both the wild-type and mutant peptides in Figure 5b are almost equally well fit by an initial 1^st order reaction, followed by a second, 1^st order (green) , 2^nd order (pink) or 3^rd order reaction (orange), with the best fits obtained for the sum of two 1st order reactions. However, this simple model is not adequate to describe the folding reactions. First, the rate constant for the second reaction for the wild-type peptide is highly dependent on the initial concentration of the unfolded peptide showing that the second folding reaction can not be first order. Second, it is difficult to deconvolute the folding reactions to determine the correct extinction coefficients for the first and second folding reactions because the parameters of the fits are highly dependent on one another. Finally, the simple model assumes that the first reaction is independent of the second, and there is no way to determine from these CD experiments whether the initial folding to a peptide with a poly-L-proline-like conformation represents the formation of an obligate intermediate before chains begin to associate.

While in theory, the most accurate rate constants are obtained by direct fitting of raw data to integrated rate equations, it is easier to visualize the folding reactions if the data is transformed to linear equations as described in Table 1. Figure 6a, shows a plot of the log of the fraction folded of the WT peptide as a function of time. This plot is linear for first order reactions. The folding is clearly biphasic. The first reaction is well fit by a first order folding equation, but the second is not. The initial rate of folding for the WT and the G14 peptide (data not shown) both followed first order kinetics with rate constants of 2.3 ± 0.6 × 10⁻² s⁻¹ and 2.8 ± 0.8 × 10⁻² s⁻¹, respectively. A plot of the initial rate of folding of the WT peptide as a function of initial peptide concentration is also almost linear (Figure 6b) suggesting that the first reaction is indeed first order, but plotting the rate obtained between 200 and 1200 seconds shows a large dependence on concentration (data not shown), indicating that a simple model of two first order reactions is not correct. Figure 6c shows the folding of the wild-type peptide, 0.6 mM, plotted as a third order reaction. The data collected between 200 and 1200 are better fit by a plot of 1/[A]2 vs t (3^rd order reaction) than 1/[A] vs t (2^nd order reaction, data not shown), suggesting that the folding follows 3^rd order kinetics, consistent with the formation of a triple helix. Plotting the time divided by the fraction folded against time by the method of Wilkinson¹⁹ gives slope of 1.54 (Figure 6d), which is also consistent with the second phase being 3^rd order. Similar results were obtained at the highest concentration studies, 1.2 mM.

If the ellipticity changes were only due to a single third order reaction, the folding constant would equal the slope of the plot of 1/(1-α)² versus t divided by 2c² where c is the starting concentration of the unfolded protein chains. However, the data analysis is complicated in this example, because the change in ellipticity has two components, making it difficult to determine the concentration of the triple-helical peptide from the ellipticity change seen upon folding, because about one third of the change at 2 °C is due to the change in the ellipticity of the monomeric peptide as a function of temperature preceding formation of the triple helix.