Atypical mechanism of conduction in potassium channels

Abstract

Potassium channels can conduct passively K⁺ ions with rates of up to ≈10⁸ ions per second at physiological conditions, and they are selective to these species by a factor of 10⁴ over Na⁺ ions. Ion conduction has been proposed to involve transitions between 2 main states, with 2 or 3 K⁺ ions occupying the selectivity filter separated by an intervening water molecule. The largest free energy barrier of such a process was reported to be of the order of 2–3 kcal mol⁻¹. Here, we present an alternative mechanism for conduction of K⁺ in potassium channels where site vacancies are involved, and we propose that coexistence of several ion permeation mechanisms is energetically possible. Conduction can be described as a more anarchic phenomenon than previously characterized by the concerted translocations of K⁺–water–K⁺.

K⁺ channels are perhaps the most extensively studied family of ion channels, both experimentally and computationally. In 1955, Hodgkin and Keynes proposed (1) that K⁺ ions would move through the membrane in narrow channels and that the ions would be constrained to move in single file with, on average, several ions in a channel at any moment. In their description of the so-called “knock-on” mechanism, they suggested that occasional vacancies should arise when K⁺ ions dissociate from the ends of the chains and that these vacancies would be transferred through the membrane in a random manner by being filled in from adjacent sites (1). Subsequently, laborious crystallographic experiments characterized the selectivity filter (SF) of K⁺ channels as the structural element essential to the permeation and the selectivity mechanisms (2). At present, it is well known that thousands of millions of K⁺ ions per second can diffuse in single file down their electrochemical gradient across the membrane at physiological conditions, and the largest free energy barrier of the process is of the order of 2–3 kcal mol⁻¹ (3, 4).

Four identical subunits are symmetrically disposed around the central pore of potassium channels. Each subunit contributes to the SF with a conserved signature peptide, namely TVGYG in most of the channels. Alignment of the channel sequences shows that the pore region, which includes a short helix and the SF, is the most conserved part of the channel (5). The carbonyl oxygens of the backbone of the SF point toward the lumen orchestrating the movements of ions in and out of the channel. These key carbonyl oxygens together with the side-chain hydroxyl oxygen of the threonine residue define 4 equally spaced potential ion-binding sites, designated S1–S4 starting at the extracellular side (6). In addition, 1 ion can bind in the central water-filled cavity and two alternate positions of a single K⁺ ion are observed at the extracellular side (6), here denoted S0 and S_ext (a point external to the S0 binding site). The SF is too narrow to fit an ion with its solvation shell; thus ions must be dehydrated to enter this region of the channel and must replace the solvation shell by the carbonyl oxygens of the protein. Each of these protein sites binds the permeant cation with a tight-fitting cage of 8 carbonyl oxygen atoms that resembles the solvation shell of hydrated K⁺ ions. The ions' mutual repulsion is balanced by their interactions with these carbonyl residues of the protein.

Crystallographic studies of the bacterial potassium channel KcsA revealed fundamental atomic details to describe ion conduction and showed that the SF adopts at least 2 different conformations in response to concentration of K⁺ ions (6, 7). At low K⁺ concentrations, the SF adopts a collapsed conformation and only 2 ions can be observed at both ends of the filter, in sites S1 and S4. At high K⁺ concentrations the SF is in a conductive state, where 2 additional K⁺ ions populate it. Crystallographic structures are averages over many molecules and reveal only where K⁺ ions bind. They do not reveal how many ions bind at once and due to experimental difficulties absolute occupancies are difficult to determine (8). Although K⁺ ions may in principle occupy adjacent sites in the SF, it was expected that most often they are separated by an intervening water molecule (7). How many water molecules move across the pore with K⁺ ions is not well established. Electrophysiologists have estimated (9, 10) that 1.0–1.5 water molecules per K⁺ ion cross the SF. Computational studies have confirmed that the configuration space for ion translocation includes local minima corresponding to discrete ion occupancy states of the SF. The conduction mechanism involves the concerted transitions of K⁺ ions between 2 equally doubly occupied states S1/S3 or S2/S4 separated by a water molecule. A third ion in the cavity or at the extracellular side (S0) is also involved.

Results and Discussion

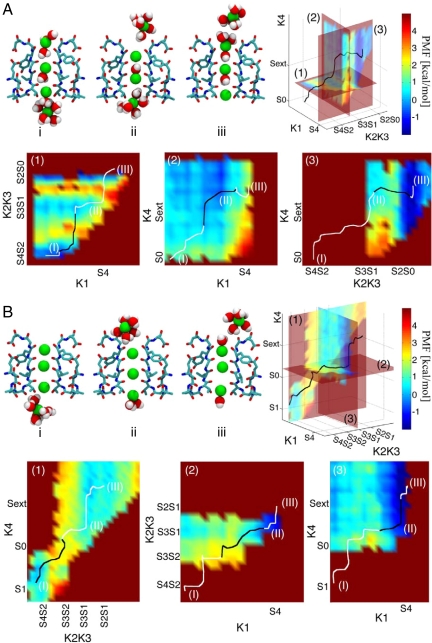
We have computed the energetics of ion conduction along 2 different pathways, using the umbrella sampling technique. The first pathway, K⁺–water–K⁺ (KWK), originally proposed by crystallographers (6, 7) and computational work (3, 4), features 2 K⁺ ions separated by a water molecule (Fig. 1A). The second pathway studied, KK, has ions at adjacent binding sites (Fig. 1B). This alternative pathway allows the possible presence of vacancies, that is, neither K⁺ ions nor water molecules in certain sites. Classical molecular dynamics simulations of 20-ns length were also performed with different arrangements of ions in the SF of KcsA and KirBac to validate the integrity of the crystal structures and to validate some of the snapshots describing the KK conduction mechanism.

Fig. 1.

(A) KWK conduction mechanism in KcsA: different snapshots of the SF of KcsA along the KWK conduction pathway. Two opposite subunits of the SF region are shown in licorice representation, colored by atom type (Glu-71-Asp-80); K⁺ ions (green) and water molecules are depicted in Van der Waals (VDW) representation. The potential of mean force and the minimum energy path (MEP) are shown in the 3D plot and reported in 2D maps (1–3). In the 2D maps a black line is used for the fraction of the MEP lying on the plane, while a white line is used for the remaining part of the path. Labels I–III highlight the position along the MEP of the SF structures shown in the snapshots. Outward conduction is initiated by the ions in S4 and S2 moving toward S3 and S1 sites; the cavity ion is attracted toward S4 (map 1, snapshots I–II). This movement in turn destabilizes the ion in S0, which moves toward the extracellular milieu (map 2). Finally, ions in S3 and S1 move to S2 and S0, causing the outermost ion to travel/advance toward the lumen (map 3, snapshot III). The reverse mechanism describes the inward permeation process. (B) KK conduction mechanism in KcsA. Snapshots I–III show the SF of KcsA in different states along the KK conduction pathway. The same notation as in A is adopted. Outward conduction is initiated by the ion in S1 moving toward S0 (map 1). After that, ions in S4 and S2 move to S3 and S1 (map 2). Configuration II is the most stable one along the minimum energy path in the KK conduction mechanism. When the innermost ion reaches S4, upward movements of the ion in S3 to S2 and of the outermost ion to the extracellular milieu conclude the conduction event (map 3, snapshot III). The reverse mechanism describes the inward permeation process.

Energy barriers for the conduction processes are listed in Table 1. Three-dimensional and 2-dimensional maps of the free energy landscape governing the ion conduction through the SF of both processes in KcsA and KirBac are presented in Fig. 1 and Fig. S1 in supporting information (SI) Text. In the conventional mechanism, where K⁺–water–K⁺ transitions take place, moving ions from Cavity/S4/S2/S0 to S4/S2/S0/external requires 2.81 ± 0.56 kcal/mol in KirBac and 2.40 ± 0.48 kcal/mol in KcsA, while the reverse transition requires 2.72 ± 0.30 kcal/mol in KirBac and 3.75 ± 0.67 kcal/mol in KcsA. These values agree with the energy barriers computed for an analogous conduction mechanism in KcsA (4). The KK mechanism, where vacancies are involved in the permeation process, displays similar energy barriers (Table 1).

Table 1.

Energetic barriers for ion conduction in KcsA and KirBac

Conduction mechanism	Conduction direction	KcsA, kcal/mol	KirBac, kcal/mol
KWK	Outward	2.40 ± 0.48	2.81 ± 0.56
	Inward	3.75 ± 0.67	2.72 ± 0.30
KK	Outward	2.53 ± 0.20	2.10 ± 0.78
	Inward	2.24 ± 0.40	2.60 ± 0.20

To test if the KK mechanism can be conceived as a plausible alternative conduction mechanism to the long-accepted KWK, the free energy of configurations along the KK and the KWK permeation pathways was compared using the free energy perturbation technique. It was found that the energy cost to arrive at a given configuration of the KK mechanism from the analogous configuration of the KWK mechanism was 1.45 ± 0.33 kcal/mol in KcsA and 0.82 ± 0.77 kcal/mol in KirBac. These are values comparable with the energetic barriers observed along the 2 permeation pathways.

In both mechanisms, movement of one ion tends to assist the others to travel in the same direction. Energetic analysis of the 2 permeation mechanisms, KK and KWK, demonstrates that alternative pathways for ion conduction to the one already described in the literature are possible. The presence of a water molecule separating the ions inside the SF does not seem to be as compulsory as previously thought. According to our results, the 2 conduction mechanisms are equally likely in both channels.

It was pointed out from analysis of crystallographic data (8, 11) that some deviations from strictly S1/S3 and S2/S4 configurations undoubtedly occur because the ion occupancy at S1 does not exactly equal the occupancy at S3, and S2 and S4 are also not exactly equal either. It was also observed that S1 and S4 sites systematically had a higher occupancy than S2 and S3. This was attributed to the possible presence of some channels with an S1/S4 configuration and water in S2/S3. However, this can now be also understood in view of the current alternative mechanism where gaps can be found in S2 and S3 sites. It is less likely that S1 and S4 sites are empty at some point as they are easily accessible by K⁺ ions and water molecules. This mechanism is also in agreement with the observations described on the distribution of ions in the SF and the conduction of ions through it when Thr is mutated to Cys (11). Experimentally it is observed that this mutation reduces the total occupancy of the filter to 2 ions on average; the occupancy of S2/S4 sites is lowered while that of S1/S3 sites is unmodified. In this scenario, when a single site is altered by the mutation, the mechanism KK would imply the existence of just 3 sites S1/S2/S3 and the possibility of a gap in S2 during conduction. That is, the occupancy of S1/S3 would be left unaltered and that of S2 would be reduced as proposed in ref. 11.

The KK mechanism described here is likely to be just 1 example among the plethora of alternative configurations and conduction pathways that ions and water may adopt during permeation. The appearance of these vacancies or empty sites is not likely to be related to the appearance of those proposed by Roth et al. (12), whereby bubbles are produced through dewetting by capillary evaporation, because the SF is the hydrophilic region of the channel and only hydrophobic surfaces would allow the cohesive forces of water to pull the fluid away from the wall. The mechanism presented here can be viewed as a perturbation of the long-accepted mechanism involving neatly organized ion–water fluxes.

The equilibrium binding constants for different ion occupancies of the SF of KcsA have been obtained by fitting experimental conductance data (13). The average number of K⁺ ions in the SF was correctly predicted in agreement with the experimental value. In view of the results presented here, it would be interesting to revisit many of the kinetic models proposed in the literature that aimed at describing ion conduction in low- and high-conductance ion channels and that did not successfully achieve an agreement between experimental data for conductance and ion occupancies. Crystallographers are also likely to assume in their refinements that if a site is not occupied by an ion, the site is likely to be occupied by a water molecule, and in light of the present study, this might not always be the case.

Materials and Methods

Model Definitions.

The SF of K⁺ channels is the structural element essential to the permeation and the selectivity mechanisms. The sequence T-x-x-T/S-x-G-Y/F-G forms an extended strand where the carbonyl oxygens of the backbone point toward the lumen orchestrating the movements of ions in and out of the channel. KcsA and KirBac1.1 share the same SF sequence. In contrast to the KcsA and KirBac1.1 channels, both of which have a valine at positions 76 and 111, respectively, KirBac1.3 has an isoleucine in this position (97 in its sequence). Thus, to validate the permeation mechanism in at least 2 different potassium channels, we decided to choose the KirBac1.1 structure rather than the KirBac3.1 even if it is in the crystal structure of KirBac3.1 where an empty site is observed (S3). Atomic structures of KcsA and KirBac were based on the protein data bank entries 1K4C (6) and 1P7B (14), respectively. Only the pore regions were included in the channel models, i.e., amino acids Ala-23-Gly-123 for KcsA and amino acids Ala-40-Arg-151 for KirBac. N termini were acetylated and an N-methylamide group was added to the C termini. The amino acid Glu-71 of KcsA was modeled in the protonated state, to form a diacid hydrogen bond with Asp-80. The analogous amino acid in KirBac (Glu-106) was also modeled in the protonated state. Default ionization states were used for the remaining amino acids. Three starting structures were defined, characterized by different configurations of K⁺ ions and water molecules inside the SF: (I) K⁺ ions in S3, S1, and S_ext and water molecules in S4, S2, and S0; (II) K⁺ ions in S3, S2, and S0 and a water molecule in S4; and (III) K⁺ ions in S4, S2, and S0. Neither a K⁺ ion nor water molecules occupy S1 in configuration II. In configuration III both S3 and S1 sites were empty. A K⁺ ion occupies the cavity in all of the models. Four water molecules were placed at the back of the SF, in agreement with crystallographic data and previous molecular dynamics (MD) simulations. The channels were embedded in a preequilibrated lipid bilayer of 256 1-Palmitoyl,2-oleoyl-sn-Glycero-3-phosphocholine (POPC) molecules. The channel axis was aligned to the bilayer normal, and the extracellular aromatic belt (amino acids Tyr-45 in KcsA and amino acids Tyr-82 in KirBac) was aligned to the bilayer surface. Lipid molecules closer than 1.0 Å to protein atoms were removed. The atomic systems were solvated by the Solvate plug-in of VMD (15), and then water molecules within 1.2 Å of protein and lipid atoms were removed. Potassium and chloride ions, corresponding to a concentration of 150 mM, were added to neutralize the systems.

Molecular Dynamics Simulations.

The KcsA and KirBac system models were validated by MD simulations. The same protocol was used for all of the models. Harmonic restraints with a force constant of 20 kcal mol⁻¹Å⁻² were applied to the protein backbone atoms in the first 500 ps. Then 20 ns of unrestrained dynamics were performed. The CHARMM27 force field with CMAP correction (16, 17) was used for lipid and protein, together with the TIP3P model for water molecules (18). Parameters for K⁺ ions inside the SF were selected according to ref. 19. Default CHARMM parameters were used for potassium ions in bulk solution and chloride ions. A particle mesh Ewald algorithm was used to treat the electrostatic interactions (20). Van der Waals forces were smoothly switched off at 10–12 Å. Bonds with hydrogen atoms were restrained by the SETTLE algorithm (21), to use a 2-fs time step. The multi-time-step algorithm r-RESPA (22) was used to integrate the equation of motion. Nonbonded short-range forces were computed every time step, while electrostatic forces were updated every 2 time steps. MD simulations were performed in the NPT ensemble. Pressure was kept at 1 atm by the Nose–Hoover Langevin piston method (23, 24), with a damping time constant of 100 ps and a period of 200 ps. Temperature was kept at 300 K by coupling to a Langevin thermostat, with a damping coefficient of 5 ps⁻¹. Calculations were performed using version 2.6 of NAMD (25, 26).

Umbrella Sampling and Potential of Mean Force.

The potential of mean force (PMF) for K⁺ conduction through the SF was computed by a procedure based on umbrella sampling (27). The 4 ions involved in the conduction process were named K1 (outermost ion, extracellular side) to K4 (innermost ion, intracellular side). Biasing potentials controlled the positions along the channel axis of ions K1 and K4. The position along the axis of K2 and K3 was controlled by a harmonic potential acting on the center of mass of the pair. The center of the biasing potential acting on K4 moved from the intracellular cavity to the binding site S4, while the biasing potential acting on K1 moved from the binding site S0 to the extracellular milieu. The energetics of ion conduction along 2 different pathways were analyzed (Fig. 1). The first pathway, KWK, resembled the one originally proposed by computational studies (4), with 2 ions separated by a water molecule (Fig. 1A). To calculate the PMF for this conduction pathway, the center of the biasing potential acting on K2 and K3 moved from a situation with ions at the binding sites S4 and S2 to a situation with ions at binding sites S2 and S0. Compared to the strategy used in ref. 4, the present approach provides the PMF for a conduction event including 4 ions. The absence of the fourth ion caused a sensibly higher energy barrier for ion translocation in our computations. A second conduction pathway, KK, with ions at adjacent binding sites, was also tested (Fig. 1B). To calculate the PMF the center of the biasing potentials action on K2 and K3 moved from a situation with ions at binding sites S4 and S2, and a vacancy at S3, to a situation with ions at binding sites S1 and S2. Harmonic potentials were updated in 0.5-Å steps; intermediate steps were also calculated where this was necessary to obtain better sampling. The force constant of the harmonic potentials was set to 20 kcal mol⁻¹Å⁻². Starting configurations were generated manually, moving the 4 ions to the center of the biasing potentials and translating the water molecules accordingly. Simulations of 120 ps were performed for each configuration of the biasing potentials. The first 20 ps were discarded as an equilibration period. In total, 400 windows were run per system. Data were unbiased by the weighted histogram analysis method (28) to obtain the 3-dimensional PMF maps. The minimum energy path between the extreme ion configurations, that is, the energy barriers for the permeation process, was then computed on the 3-dimensional maps by the string method (29). Errors in the free energy barriers were estimated by dividing the MD trajectories into 3 data sets and repeating the analysis separately on each set.

It is important to point out that these PMF profiles are representative of complete conduction events under the assumption that the entrance/exit of a K⁺ ion to/from the intracellular cavity is not associated with large energetic barriers. In agreement with this hypothesis, the difference in solvation energy for a K⁺ ion in the cavity or S_ext, defined by the free energy difference between configuration I and III, is ≈1 kcal/mol in both mechanisms. Structural data (30) as well as electrostatics calculations (31, 32) also support this hypothesis. The cavity reduces the dielectric barrier when a monovalent cation travels toward the intracellular side of the selectivity filter, and the energy for transferring a K⁺ ion from water to different locations along the pore axis between −4 Å and 4 Å, relative to zero at the cavity center, was shown to be similar. In other words, the ion is focused along the pore axis, but the “energy well” is broad (6, 33). Therefore, the decisive length of the permeation pathway can be restricted exclusively to the SF, and the translocation of K⁺ ions in single file through the narrowest region of the pore is the rate limiting step in the conduction mechanism (4).

Free Energy Perturbation Calculations.

Free energy differences between configurations from the KK and KWK conduction pathways were calculated using the free energy perturbation (FEP) technique (34) under the dual-topology paradigm, using version 2.7 of NAMD. In a typical FEP calculation involving the transformation of 2 chemical species in the course of a simulation, the atoms in the molecular topology can be classified into 3 groups: (i) a group of atoms that do not change during the simulation, e.g., the environment, (ii) the atoms of the reference or initial state, and (iii) the atoms of the final state. In the dual topology paradigm (ref. 35 and references therein), the changes are specified in terms of a system where 2 complete versions of the initial and final states, that is, the group of atoms that are changing, coexist. Atoms of the initial state should not interact with those of the final state throughout the simulation, although they interact with the rest of the system. Starting points were representative snapshots of configurations I, II, and III of Fig. 1A, which were alchemically transformed to configurations I, II, and III of Fig. 1B, respectively, or vice versa (see Fig. S2 in SI Text). The alchemical transformation was realized, changing the coupling parameter λ in 34 steps. Soft-core potentials were used with a shifting coefficient for the van der Waals radii of 2.0. Each window was simulated for 65 ps, and the first 15 ps were discarded as an equilibration period. Each FEP simulation had a total aggregate simulation time of ≈1.1 ns. Six different FEP values were averaged for each of the systems, KcsA or KirBac.