Abstract
Recent experiments have demonstrated that plastic strains in nanocrystalline aluminum and gold films with grain sizes on the order of 50 nm are partially recoverable. To reveal the mechanisms behind such strain recovery, we perform large scale molecular dynamics simulations of plastic deformation in nanocrystalline aluminum with mean grain sizes of 10, 20, and 30 nm. Our results indicate that the inhomogeneous deformation in a polycrystalline environment results in significant residual stresses in the nanocrystals. Upon unloading, these internal residual stresses cause strain recovery via competitive deformation mechanisms including dislocation reverse motion/annihilation and grain-boundary sliding/diffusion. By tracking the evolution of each individual deformation mechanism during strain recovery, we quantify the fractional contributions by grain-boundary and dislocation deformation mechanisms to the overall recovered strain. Our analysis shows that, even under strain rates as high as those in molecular dynamics simulations, grain-boundary-mediated processes play important roles in the deformation of nanocrystalline aluminum.
Keywords: grain-boundary diffusion, grain-boundary sliding, molecular dynamics simulation
Despite a number of controversial viewpoints about deformation mechanisms in nanocrystalline (nc) materials, it is increasingly recognized that plastic deformation mediated by grain boundaries (GBs) should play a crucial role in truly nc materials (1–7). To ensure geometrical compatibility, GB sliding or GB diffusion cannot occur alone in a polycrystalline material in the absence of some other deformation mechanisms (8–14). In other words, a coupling of no less than two deformation mechanisms is necessary, among possibilities such as GB sliding, GB diffusion, dislocation glide, intragranular dislocation climb, and elastic deformation in grains. The overall deformation behavior of nc materials can be attributed to two or more of these competing deformation mechanisms, the details of which could be influenced by both microstructures and testing conditions, such as strain rates and temperatures.
Recent experimental studies on deformation in freestanding nc fcc aluminum (Al) and gold thin films (15) have shown: (a) that plastic deformation in these materials is partially recoverable; (b) that elevated temperatures expedite the recovery process; and (c) that longer time results in more recovered strain. Similar phenomena have also been observed in nc copper thin film (16, 17), as well as in bulk nc-ultrafine Al with bimodal grain size distribution under compression (18). So far, several explanations have been proposed to interpret the observed strain recovery. One viewpoint (15) is that the plastic strain recovery is due to pinning of dislocations during loading and depinning of them during unloading. An alternative viewpoint is that heterogeneous GB diffusion and sliding can also account for the recoverable plastic strain (14, 17, 19). The present work is aimed to clarify some of the controversial issues by conducting a quantitative analysis of plastic strain recovery in nc Al at different grain sizes and temperatures via massively parallel molecular dynamics (MD) simulations. By tracking the evolutions of individual deformation mechanisms separately, we intend to identify the mechanisms accounting for plastic strain recovery and to quantify the fractional contributions to strain recovery due to GB and dislocation deformation mechanisms.
Results and Discussion
To mimic the loading-unloading-annealing procedure used in the experiment (15), we load a sample at 300 K to a total strain of 9.3%, and unload it to a macroscopically stress-free state. The sample is subsequently allowed to undergo free structural relaxation at a fixed annealing temperature. After unloading, the sample reaches zero “macroscopic stress,” but may have high internal residual stresses (local stress). Fig. 1A shows the atomic configuration* of a nc sample with mean grain size d = 20 nm after unloading. Plenty of dislocation debris and stacking faults can be observed in this snapshot. The same unloaded sample is then “annealed” at three different temperatures of 300, 500, and 700 K. By measuring the change of the sample size in the loading direction, we found that the annealing process results in strain recovery by 1.26%, 1.41%, and 1.55% at 300, 500, and 700 K, respectively. Corresponding atomic configurations after “annealing” are shown in Fig. 1 B–D. In contrast to the sample right after unloading (see Fig. 1A), there is a dramatic reduction of dislocations and stacking faults in the sample after “annealing” (see Figs. 1 B–D), which indicates that annihilation of dislocations and stacking faults have contributed to the recovered plastic strain. In contrast to samples annealed at low temperatures, those annealed at high temperatures exhibit higher vacancy concentration and lower dislocation density. Corresponding energy profiles of these configurations can be found in Fig. S1. For comparison, configurations of samples with grain sizes of d = 10 nm and 30 nm after unloading and “annealing” are shown in Fig. S2 and S3, respectively.
Fig. 1.
Snapshots of initial and final configurations of an nc Al sample with a mean grain size d = 20 nm. (A) Initial configuration at 300 K before strain recovery. (B–D) Final configurations after strain recovery at 300, 500, and 700 K, respectively. Some grains change their shape during annealing. Dynamic recrystallization is observed at 700 K, as evidenced by the formation of some small grains such as those labeled by “a” and “b.” (Scale bar, 5 nm.)
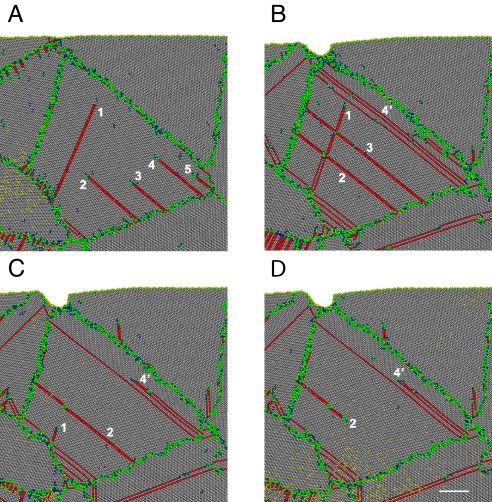
Throughout the simulation, we record the stress along the loading direction (σ11) and potential energy as a function of strain (ε11), as shown in Fig. 2A. The sample is subject to a total strain of 9.3%. During unloading, about 2.0% of elastic stain is reversed; the subsequent “annealing” at 300 K leads to a recovery of 1.26% plastic strain. After the sample is loaded to macroscopic yielding, some grains with favorable crystal orientations and sizes start to deform plastically by means of dislocations nucleating at GBs and propagating across grain interiors, while other grains remain “elastic” without apparent dislocation activities [see Movies S1–S9]. As illustrated in Fig. 2B, such heterogeneous deformation gives rise to nonuniform stress distribution in the sample, especially in GBs and triple junctions. After we unload the sample to a macroscopically stress-free state, the nonuniform deformation leaves a distribution of residual stresses, which is seen in Fig. 2C. During annealing, the stored elastic strain energy associated with these residual stresses serves as a driving force for the strain recovery, which can be implied by the continuous decrease of potential energy after unloading in Fig. 2A. Microscopically, thermally assisted dislocation activities and GB deformation may be activated at longer time scales and/or higher temperatures, leading to the attenuation of residual stresses, as shown in Fig. 2D. Snapshots in Fig. 3 capture in detail the underlying dislocation activities in the periods of both loading and strain recovery. At the loading stage, dislocations nucleated at GBs (see Fig. 3A) can traverse whole grains and reach neighboring GBs (see Fig. 3B). Stacking faults left behind by partial dislocations may remain in the interior of a grain and impede the generation or motion of other dislocations. During annealing, we observe retraction of dislocations, e.g., partial dislocation labeled “3” is completely retracted while partials “1” and “4′” are still in the process of moving back (see Fig. 3C). Partial “1” eventually moves back to the GB where it was nucleated, while partial “2” is still moving backwards (see Fig. 3D). Such dislocation retraction during “annealing” is commonly observed in our simulations. Such processes can reduce dislocation density and lower residual stresses, as shown in Fig. 2 B–D.
Fig. 2.
Representative behaviors of plastic deformation in an nc Al sample with a mean grain size of d = 20 nm at 300 K. (A) Stress-strain curve and relevant energy evolution. (B–D) Stress contours (σ11) at points “A,” “B,” and “C” marked in Fig. 2A, respectively. (Scale bar, 5 nm.)
Fig. 3.
Successive snapshots of reverse motion of partial dislocations inside a large gain in the d = 20 nm sample at 300 K. (A) At 0.50 ns, partial dislocations are nucleated from GBs. (B) At 0.96 ns, partial dislocations glide through the grain, leaving behind some stacking faults. Dislocations “4” and “5” interact by emission of partials at the neighboring slip plane, generating a dislocation ‘4′“ and a twin boundary, and twin boundary hinders the further motion of dislocation ”1.“ (C) At 1.78 ns, dislocations ”1“ and ”4′“ move in reverse, while partial ”3“ disappears after complete retraction. (D) At 1.86 ns, partials ”2“ and ”4′“ moves backwards, and partial ”1“ completely disappears. (Scale bar, 5 nm.)
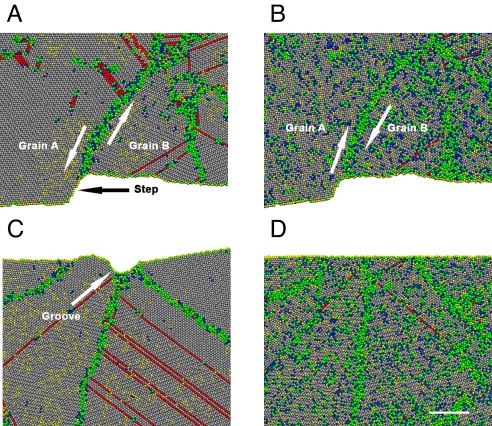
In addition to dislocation activities, GB sliding and diffusion are also observed in our simulations. The snapshots in Figs. 4 A–B show that GB sliding occurs in one GB inclined to the free surface of the sample with a mean grain size of d = 30 nm. During loading, adjacent grains slide over each other, resulting in displacement jumps across the GB and formation of a surface step. The offset of this step gradually decreases during “annealing,” as seen in Fig. 4B. Similar sliding events are also found in our simulations with different grain sizes (see Movies S1–S9). These observations confirm that GB sliding is an operative mechanism for strain recovery even under strain rates as high as those applied in MD simulations. After the sample undergoes loading, unloading and “annealing,” the majority of grains retain their original shapes, suggesting that GB sliding at room temperature (RT) is of the Rachinger type (13), and is accommodated by the motion of dislocations. Indeed, such low temperature GB sliding in nc metals has been reported (1, 4, 22, 23). During high temperature structural relaxation, the Lifshitz type (13) of GB sliding, which is accompanied by significant shape changes in grains and facilitated by GB diffusion through vacancy flow, should become more important. This can be seen in Movies S1–S9, where vacancies (surrounded by blue atoms) migrate and diffuse along GBs during relaxation. Fig. 4 C and D show that a GB groove forms (a direct consequence of GB diffusion) on the surface during loading and is subsequently filled up during annealing. Interestingly, two GBs near the groove are observed to migrate via vacancy flow and separate from each other, suggesting significant bulk diffusion. Generally, both GB diffusion and bulk diffusion involve rather complex atomistic mechanisms, such as long distance jump of vacancies (24) and cyclic exchange of atoms (25), which is beyond the scope of this report. Furthermore, we note that some small grains, such as those labeled by “a” and “b” in Fig. 1D, emerge at elevated temperatures. This is a manifestation of dynamic recrystallization process (26) associated with collective collaboration of dislocation activities and GB deformation behaviors.
Fig. 4.
Successive snapshots of a surface step and groove in the d = 30 nm sample at 700 K, showing evidences of GB sliding and GB diffusion. (A) A step forms during loading. (B) The step gradually diminishes during annealing. (C) A groove forms due to vacancy diffusion along GB during loading. (D) The groove diminishes during annealing. (Scale bar, 5 nm.)
To quantitatively study the relative contributions of different deformation mechanisms to the overall plastic strain recovery at different temperatures, we calculate the fractional strains from dislocation activities, GB sliding, and GB diffusion during “annealing” as follows. We identify all dislocations occurring in the MD simulations by the neighbor analysis and Burgers circuit technique, and determine the dislocation mediated plastic strain as
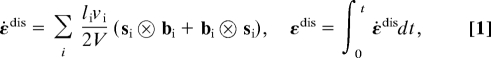 |
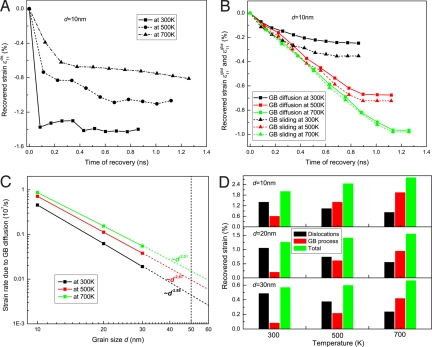
where li is the length of the i-th dislocation, vi its velocity, si the unit normal of the slip plane, bi the Burger vector, and V the volume of the system. Fig. 5A shows the fractional strain ε11dis due to dislocation motion in the sample with a grain size of d = 10 nm. The strain evolutions at different temperatures suggest the existence of two dislocation mechanisms in the process of strain recovery. At the beginning of recovery, some initially nucleated dislocations move backward through thermally assisted depinning (15, 27), driven by internal residual stresses. Such a mechanism leads to rapid strain recovery, corresponding to the portion with larger slope in each curve in Fig. 5A. As the recovery process proceeds, dislocations originally located in GBs can move or rearrange into lower energy configurations to relieve internal strain energy. Most of dislocations are eventually annihilated by climbing along GBs. This process depends strongly on dislocation structures and vacancy concentration at GBs, leading to the slow strain recovery in Fig. 5A.
Fig. 5.
Contributions of GB- and dislocation-mediated deformation mechanisms to total plastic strain recovery. (A) Recovered strain due to dislocation mechanisms as a function of time in the d = 10 nm sample. (B) Recovered strains due to GB sliding and GB diffusion as a function of time in the d = 10 nm sample. (C) Grain size dependence of strain rate due to GB diffusion. The values of strain rate corresponding to grain size of d = 50 nm are estimated by a linear extrapolation. (D) Fractional strains due to GB and dislocation processes at different grain sizes and temperatures.
For the quasi three-dimensional configuration, the plastic strain rate and corresponding fractional strains due to GB sliding and GB diffusion can be calculated from (19)
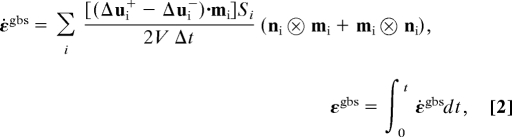 |
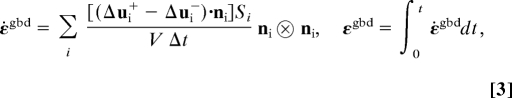 |
where Δui+ and Δui− denote the displacements of the two sides of the i-th GB during a time interval of Δt; mi, ni and Si are, respectively, the tangential, normal and area of the i-th GB. The detailed calculation procedures are given in Methods. Fig. 5B shows the time evolution of the recovered strain due to GB mediated processes. At the initial stage, the recovered strain is nearly proportional to time. As the recovery continues, GB mediated processes are gradually weakened due to the reduction of internal stress, which finally leads to the saturation of recovered strain. By fitting the linear parts of the curves in Fig. 5B, we obtain the recovered strain rate due to GB diffusion as a function of grain size, as shown in Fig. 5C. At lower temperatures, the exponent of the grain size dependence of GB diffusion induced strain rate is close to −3, which is consistent with Coble creep. However, significant deviation of this exponent is observed as temperature rises, which is likely caused by bulk diffusion. The high strain rate contributed by GB diffusion here is mainly due to high local stresses (GPa-level) and high-angle GBs in the sample. Notably, when comparing the results in Fig. 5 A and B (also Fig. S4 A–D), we found that the fractional strains due to dislocation activities, GB sliding, and GB diffusion are nearly identical at 700 K, suggesting certain coupling between these three mechanisms (28).
Fig. 5D shows the fractional strains recovered by GB and dislocation mechanisms at different temperatures for samples with grain sizes of d = 10, 20, and 30 nm. As the temperature increases, the contribution from dislocation mechanism decreases, whereas those by GB-mediated processes increase. At low temperatures, dislocation activities dominate plastic deformation, while GB-mediated mechanisms make relatively small contributions to the strain recovery. At high temperatures, vacancy diffusion is activated and further promotes Lifshitz type of GB sliding and dislocation annihilation. In this situation, GB-mediated processes make more significant contributions to the strain recovery, although dislocation activities can also assist vacancy diffusion. It is found that GB-mediated processes contribute more to plastic strain recovery in samples with smaller grain sizes. This is consistent with our expectation that small grain size facilitates GB-mediated mechanisms, and explains why the total recovered strains increase with decreasing grain sizes. We found that the sum of fractional stains from dislocation activities, GB sliding, and GB diffusion is slightly less than the total measured stain, with a discrepancy of up to 0.2% strain at high temperatures (see Fig. 5D). This difference may be attributed to other deformation mechanisms, e.g., bulk diffusion and dynamic recrystallization. Aside from the grain size effect, the sample size should also affect the plastic strain recovery to the extent that there may be strong coupling between free surfaces and GBs. The surface steps/grooves in Fig. 1 indicate strong interactions between GBs and free surfaces. On the other hand, we do not expect that the phenomenon of plastic strain recovery would be qualitatively affected by the size of the sample, as evidenced by experimentally reported plastic strain recovery in both bulk nc Al (18) and nc Al thin films (15).
In MD simulations discussed above, the samples have been prepared using randomly oriented Voronoi grains. Such a procedure may result in quite unrealistic GB character. To verify the generality of our results, we have also performed MD simulations with a more realistic sample that resembles a “real” scanning electron microscope image of a polycrystalline metal with an average grain size of d = 20 nm. The details about the procedure used to generate such a sample can be described in Methods. Fig. S5 A–D shows the atomic configurations of the sample after annealing under different temperatures. It is observed that the strain recovery still occurs in the “real” sample. A quantitative comparison of recovered strains induced by GB and dislocation mechanisms in the “Voronoi” and “real” samples is shown in Fig. S6. The “real” sample exhibits slightly smaller recovered strain than the “Voronoi” sample with the same mean grain size of d = 20 nm, which may be attributed to differences in the GB structures. The “Voronoi” GB structure is expected to have higher energy than the “real” sample, hence slightly stronger recovery. The basic phenomenon of plastic strain recovery remains essentially similar for the two kinds of samples.
In summary, we have performed massively parallel MD simulations to investigate the atomic-scale deformation mechanisms related to the plastic strain recovery in nc Al with different grain sizes of d = 10, 20, and 30 nm. The simulations show that the plastic strain recovery results from a combination of dislocation activities and GB-mediated processes driven by residual stresses in the sample due to nonuniform deformation in the constituent grains. The contributions of dislocation activities and GB-mediated processes to the overall recovered plastic strain are quantitatively analyzed. At lower temperatures and larger grain sizes, reverse glide, and annihilation of dislocations dominate the plastic strain recovery. At higher temperatures and smaller grain sizes, GB sliding, and GB diffusion tend to dominate. Although GB-mediated mechanisms are expected to become less important at higher strain rates, it is interesting that, even under strain rates as high as those applied in MD simulations, GB-mediated processes still play such an important role in the plastic strain recovery. Although our study captures the essential roles and relationships of different mechanisms in the plastic strain recovery, we note that the simulations are performed under much higher strain rates than those accessible in laboratory. Nevertheless, the coupled mechanisms revealed in our study can provide insightful guidance for modeling efforts at the continuum level, whereby time and length scales comparable to experiments can be achieved.
Methods
The simulations are performed on quasi three-dimensional columnar polycrystals with the column axis orientated in the ξ direction. Two kinds of samples are constructed: one is the “Voronoi” sample, which is produced from the usual Voronoi construction (1), and the other is the so-called “real” sample, which is prepared based on the microstructure of a real polycrystal. The “Voronoi” sample contains randomly orientated grains with a random distribution of GB misorientations, resulting in a majority of high-angle GBs with highly disordered atomic structures. The “Voronoi” samples all have the same grain configurations consisting of 28 columnar grains and 50 distinct GBs, with grain sizes varying between 10 nm and 30 nm. Each sample has an aspect ratio of 2:1. The maximal system size is 183.2 nm × 91.6 nm × 1.92 nm, which amounts to a total of 2,250,000 atoms. The “real” sample is composed of 21 grains, most of which have a size around 20 nm. The dimension of this sample is 92.1 nm × 73.4 nm × 1.92 nm.
Before starting a simulation, we perform a relaxation of the simulated system for 200 ps at RT. This ensures the system with high-energy GBs and randomly oriented grains to reach an equilibrium configuration. In the simulations, we use the embedded-atom method potential (29) for Al to describe the interatomic interactions. We impose periodic boundary condition in the direction of sample thickness. According to the local crystalline order method (20, 21), we paint gray for atoms in perfect fcc lattice, red for atoms in stacking faults, green for atoms in GBs or dislocation cores, blue for atoms in the vicinity of vacancies, and yellow for fully disordered atoms.
During a simulation, the sample is loaded along the direction of sample length, which is denoted as the 1-axis, with the 2- and 3-axes along the direction of sample width and thickness, respectively. To mimic the loading, unloading, and annealing stages in the experiment (15), we initially impose a constant tensile strain rate of 108/s to the constructed sample along the 1-axis for a duration of 0.9 ns, and then unload at a strain rate of −4 × 107/s. During unloading, we monitor the average normal stress along the loading direction (σ11) and stop unloading as soon as σ11 approaches zero. Subsequently, the two ends of the sample along the 1-axis are set free to allow relaxation (annealing) at an elevated temperature, while the total potential energy of the system is monitored. The process is terminated when the energy of the system converges to the equilibrium value at a given temperature.
To achieve uniaxial tensile loading and unloading at a constant temperature, we use the stepwise loading technique (30) combined with a Nose-Hoover thermostat (31, 32). In each loading step, we displace all atoms according to a prescribed uniform strain of 0.05% along the loading direction while fixing the atoms at two ends of the system, and then dynamically relax the system at RT for 5 ps. In the same manner, the unloading process is implemented with a strain increment of −0.02%. After loading and unloading, the system is subjected to annealing at an elevated temperature, during which the constrained atoms at both ends are set free. To improve the efficiency and accuracy of calculations, we adopt a multiple-time-step algorithm (33) in which a shorter integration time step of 1.0 fs and a longer time step of 3.0 fs are used.
When calculating the fractional strains associated with GB sliding and diffusion, we focus on the evolution and motion of every GB. Firstly, we record positions of atoms located in the GBs at different times via a combination of geometry and energy identifications. Subsequently, we split each GB into two parts along their midlines based on the coordinates of atoms. Thus, we obtain the displacement vectors of two parts in adjacent grains by subtraction between different configurations at different times. Finally, we sum over each GB and integrate over time using Eqs. 2 and 3. All macroscopic parameters are calculated from the statistical average over all GBs. We include all GBs marked in the initial configurations but exclude the influence of new GBs formed during recrystallization at high temperatures.
Supplementary Material
Acknowledgments.
This work was supported by National Science Foundation Grant CMMI-0758535; MRSEC program Award DMR-0520651 at Brown University; and the National Science Foundation of China Grant 50890174 and the 973 Projects of China (W.Y.).
Footnotes
The authors declare no conflict of interest.
This article is a PNAS Direct Submission. I.P. is a guest editor invited by the Editorial Board.
This article contains supporting information online at www.pnas.org/cgi/content/full/0901765106/DCSupplemental.
References
- 1.Schiøtz J, Di Tolla FD, Jacobsen KW. Softening of nanocrystalline metals at very small grain sizes. Nature. 1998;391:561–563. [Google Scholar]
- 2.Lu L, Sui ML, Lu K. Superplastic extensibility of nanocrystalline copper at room temperature. Science. 2000;287:1463–1466. doi: 10.1126/science.287.5457.1463. [DOI] [PubMed] [Google Scholar]
- 3.Yamakov V, Wolf D, Phillpot SR, Gleiter H. Grain-boundary diffusion creep in nanocrystalline palladium by molecular-dynamics simulation. Acta Mater. 2002;50:61–73. [Google Scholar]
- 4.Schiøtz J, Jacobsen KW. A maximum in the strength of nanocrystalline copper. Science. 2003;301:1357–1359. doi: 10.1126/science.1086636. [DOI] [PubMed] [Google Scholar]
- 5.Yamakov V, Wolf D, Phillpot SR, Mukherjee AK, Gleiter H. Deformation-mechanism map for nanocrystalline metals by molecular-dynamics simulation. Nat Mater. 2004;3:43–47. doi: 10.1038/nmat1035. [DOI] [PubMed] [Google Scholar]
- 6.Yip S. Nanocrystalline metals: Mapping plasticity. Nat Mater. 2004;3:11–12. doi: 10.1038/nmat1053. [DOI] [PubMed] [Google Scholar]
- 7.Wolf D, Yamakov V, Phillpot SR, Mukherjee A, Gleiter H. Deformation of nanocrystalline materials by molecular-dynamics simulation: Relationship to experiments? Acta Mater. 2005;53:1–40. [Google Scholar]
- 8.Ashby MF. Interface-reaction control of Nabarro-Herring creep and sintering. Scr Metall. 1969;3:837–842. [Google Scholar]
- 9.Ashby MF. Boundary defects, and atomistic aspects of boundary sliding and diffusional creep. Surf Sci. 1972;31:498–542. [Google Scholar]
- 10.Arzt E, Ashby MF, Verrall RA. Interface controlled diffusional creep. Acta Metall. 1983;31:1977–1789. [Google Scholar]
- 11.Cocks ACF. Interface reaction controlled creep. Mech Mater. 1992;13:165–174. [Google Scholar]
- 12.Yang W, Wang HT. Mechanics modeling for deformation of nano-grained metals. J Mech Phys Solids. 2004;52:875–889. [Google Scholar]
- 13.Langdon TG. Grain boundary sliding revisited: Developments in sliding over four decades. J Mater Sci. 2006;41:597–609. [Google Scholar]
- 14.Wei YJ, Bower AF, Gao HJ. Recoverable creep deformation due to heterogeneous grain-boundary diffusion and sliding. Scrip Mater. 2007;57:933–936. [Google Scholar]
- 15.Rajagopalan J, Han JH, Saif MTA. Plastic deformation recovery in freestanding nanocrystalline aluminum and gold thin film. Science. 2007;315:1831–1834. doi: 10.1126/science.1137580. [DOI] [PubMed] [Google Scholar]
- 16.Wei XD, Kysar JW. Plastic strain recovery of free-standing nanocrystalline Cu films. 2008 Spring Meeting of MRS, Symposium U3.7.2008. [Google Scholar]
- 17.Wei XD, Kysar JW. Strain recovery driven by grain-boundary diffusion for nanocrystalline thin films. 2008 Fall Meeting of MRS, Symposium EE2.8.2008. [Google Scholar]
- 18.Lonardelli I, Almer J, Ischia G, Menaoace C, Molinar A. Deformation behavior in bulk nanocrystalline-ultrafine aluminum: In situ evidence of plastic strain recovery. Scrip Mater. 2008;60:520–523. [Google Scholar]
- 19.Wei YJ, Bower AF, Gao HJ. Recoverable creep deformation and transient local stress concentration due to heterogeneous grain-boundary diffusion and sliding in polycrystalline solids. J Mech Phys Solids. 2008;56:1460–1483. [Google Scholar]
- 20.Van Swygenhoven H, Farkas D, Caro A. Grain boundary structures in polycrystalline metals at the nanoscale. Phys Rev B. 2000;62:831–838. [Google Scholar]
- 21.Li XY, Yang W. Atomistic simulations for the evolution of a U-shaped dislocation in fcc Al. Phys Rev B. 2006;74:144108. [Google Scholar]
- 22.Van Swygenhoven H, Spaczer M, Caro A, Farkas D. Competing plastic deformation mechanisms in nanophase metal. Phys Rev B. 1999;60:22–25. [Google Scholar]
- 23.Schiøtz J, Vegge T, Di Tolla FD, Jacobsen KW. Atomic-scale simulations of the mechanical deformation of nanocrystalline metals. Phys Rev B. 1999;60:11971–11983. [Google Scholar]
- 24.Kwok T, Ho PS, Yip S, Balluffi RW, Bristowe PD, Brokamn A. Evidence for vacancy mechanism in grain boundary diffusion in bcc iron: A molecular dynamics study. Phys Rev Lett. 1981;47:1148–1151. [Google Scholar]
- 25.Rakitin RY, Poletaev GM, Aksenove MS, Starostenkov MD. Mechanisms of grain-boundary diffusion in two-dimensional metals. Tech Phys Lett. 2005;31:650–652. [Google Scholar]
- 26.Humphreys FJ, Hatherly M. Recrystallization and related annealing phenomena. Oxford: Pergamon Press; 1996. pp. 363–392. [Google Scholar]
- 27.Van Swygenhoven H, Derlet PM, Frøseth AG. Nucleation and propagation of dislocations in nanocrystalline fcc metal. Acta Mater. 2006;54:1975–1983. [Google Scholar]
- 28.Wei YJ, Bower AF, Gao HJ. Enhanced strain-rate sensitivity in fcc nanocrystals due to grain-boundary diffusion and sliding. Acta Mater. 2008;56:1741–1752. [Google Scholar]
- 29.Mishin M, Farkas D, Mehl MJ, Papaconstantopoulos DA. Interatomic potential for monoatomic metals from experimental data and ab initio calculations. Phys Rev B. 1999;59:3393–3407. [Google Scholar]
- 30.Gall K, Diao JK, Dunn ML. The strength of gold nanowires. Nano Lett. 2004;4:2431–2436. [Google Scholar]
- 31.Nose SA. A unified formulation of the constant temperature molecular dynamics methods. J Chem Phys. 1984;81:511–519. [Google Scholar]
- 32.Hoover WG. Canonical dynamics: Equilibrium phase-space distributions. Phys Rev A. 1985;31:1695–1697. doi: 10.1103/physreva.31.1695. [DOI] [PubMed] [Google Scholar]
- 33.Tuckerman M, Berne BJ, Mantyna GJ. Reversible multiple time scale molecular dynamics. J Chem Phys. 1992;97:1990–2001. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.