Setting cumulative emissions targets to reduce the risk of dangerous climate change

Abstract

Avoiding “dangerous anthropogenic interference with the climate system” requires stabilization of atmospheric greenhouse gas concentrations and substantial reductions in anthropogenic emissions. Here, we present an inverse approach to coupled climate-carbon cycle modeling, which allows us to estimate the probability that any given level of carbon dioxide (CO₂) emissions will exceed specified long-term global mean temperature targets for “dangerous anthropogenic interference,” taking into consideration uncertainties in climate sensitivity and the carbon cycle response to climate change. We show that to stabilize global mean temperature increase at 2 °C above preindustrial levels with a probability of at least 0.66, cumulative CO₂ emissions from 2000 to 2500 must not exceed a median estimate of 590 petagrams of carbon (PgC) (range, 200 to 950 PgC). If the 2 °C temperature stabilization target is to be met with a probability of at least 0.9, median total allowable CO₂ emissions are 170 PgC (range, −220 to 700 PgC). Furthermore, these estimates of cumulative CO₂ emissions, compatible with a specified temperature stabilization target, are independent of the path taken to stabilization. Our analysis therefore supports an international policy framework aimed at avoiding dangerous anthropogenic interference formulated on the basis of total allowable greenhouse gas emissions.

The ultimate goal of climate policies is to reduce the amount of anthropogenic greenhouse gas (GHG) emissions to achieve “stabilization of greenhouse gas concentrations in the atmosphere at a level that would prevent dangerous anthropogenic interference with the climate system” (United Nations Framework Convention on Climate Change, Article 2). Commonly, dangerous anthropogenic interference (DAI) is characterized in terms of the impacts of climate change. For instance, the Intergovernmental Panel on Climate Change (IPCC) developed a framework that relates different categories of impacts, ranging from impacts on unique and vulnerable systems to large-scale geophysical discontinuities, to the level of temperature change at which they are likely to occur (1, 2). Despite increasing evidence about the consequences of climate change, there can be no objective scientific definition of what constitutes DAI, because such a definition is ultimately a normative decision, influenced by value judgments. In recent years, international climate policy discussions have been framed around limiting the global mean temperature increase to 2 °C relative to preindustrial times, a number that some have argued represents a threshold beyond which climate impacts become “dangerous”. For example, in 1996 the European Council adopted the target to limit global mean warming to 2 °C. This target has since been reaffirmed by the European Union on a number of occasions, such as March 2005 (3) and January 2007 (4).

In this study we derive allowable CO₂ emissions levels that are compatible with a set of long-term temperature targets to avoid DAI. Our study differs from earlier attempts to derive “safe” emissions levels (5, 6, 7, 8, 9, 10, 11) in that we (i) use an inverse approach, whereby we work backwards from a specified temperature target to CO₂ emissions (12, 13); (ii) extend the cause-effect chain to include the linkage between CO₂ emissions and concentrations (through an explicit representation of the carbon cycle); and (iii) use a state-of-the-art coupled climate-carbon cycle model. This approach allows us to gain new insights into the transient evolution of the coupled climate-carbon cycle system toward temperature stabilization and to consistently derive cumulative CO₂ emissions levels to reduce the risk of DAI.

We adopt a risk management approach, whereby key uncertainties in the coupled system are described in terms of probability density functions (PDFs). Major uncertainties in the long-term climate system response to specified emissions trajectories include uncertainties in the climate sensitivity and the response of the marine and terrestrial carbon sinks to climate change (14). The climate sensitivity summarizes the feedbacks in the response of the physical climate system to radiative forcing and is here defined as the expected equilibrium global mean surface temperature response to a doubling of the preindustrial atmospheric CO₂ concentration. In recent years, a growing number of studies have attempted to constrain climate sensitivity from present-day climatology (15, 16, 17, 18), the historical temperature evolution (19, 20, 21, 22, 23, 24), and paleo-climatic records (25). However, climate sensitivity is only weakly constrained by any of these observations, so that large uncertainty remains as to its value. Here, we use several of the published PDFs for climate sensitivity to derive the likelihood that a given temperature target is exceeded for a specific CO₂ emissions level.

Unlike climate sensitivity, no probabilistic measure has been derived for the uncertainty in the carbon cycle response. The modification of the marine and terrestrial carbon sinks because of climate change is usually quantified in terms of the climate-carbon cycle feedback (26). Although varying widely in magnitude, this feedback is positive in most models (14), implying faster accumulation of CO₂ in the atmosphere. Accordingly, climate-carbon cycle feedbacks reduce the amount of emissions compatible with a given CO₂ concentration or global mean temperature target (27, 28). In our analysis, we incorporate carbon cycle uncertainty by exploring the sensitivity of the resulting allowable CO₂ emissions to the strength of the climate-carbon cycle feedback.*

We use the University of Victoria Earth System Climate Model (UVic ESCM) version 2.8 (29) (see Methods). The model was integrated over the historical period (1800–2000) by using known natural and anthropogenic forcings (including forcing-from-greenhouse gases such as CO₂, CH₄, NO₂, and halocarbons, sulfate aerosols, land-use change, solar irradiance, volcanoes and orbital changes). The resulting change in global mean temperature in the year 2000 is 0.68 °C relative to preindustrial times. Following an inverse approach, we then performed an ensemble of model simulations spanning the 2000–2500 period, whereby we diagnosed CO₂ emissions compatible with prescribed temperature trajectories. These simulations differed in the prescribed temperature stabilization profile and the value of the climate sensitivity (see Methods).

Results and Discussion

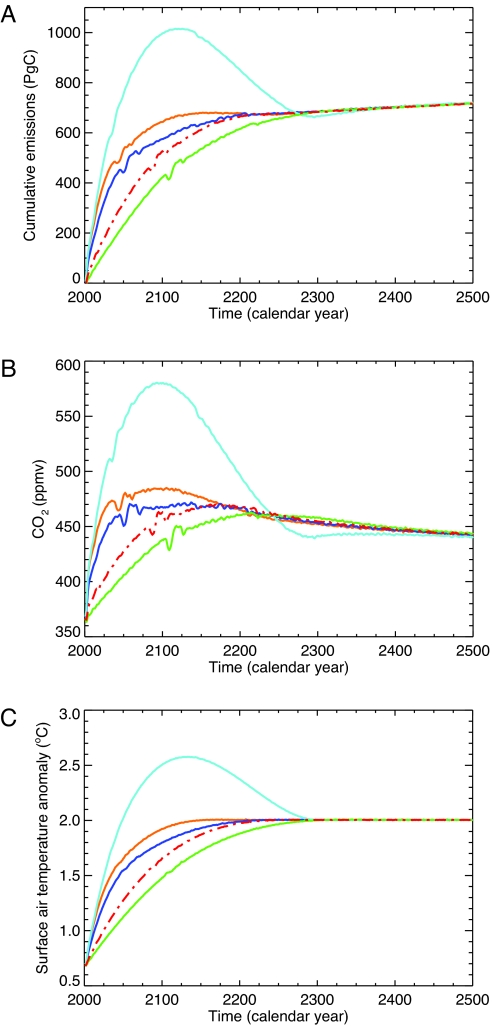
Our results indicate that the cumulative CO₂ emissions compatible with a given global mean temperature target are independent of the path taken to stabilization. Fig. 1 illustrates this path independency for trajectories stabilizing at 2 °C (relative to preindustrial): No matter whether temperature is stabilized in 2150, 2200, or 2300, or the target is temporarily exceeded (“overshoot” scenario), admissible cumulative CO₂ emissions converge to the same value at about 2350. In 2500, cumulative emissions (computed from the beginning of 2001) are 716 PgC^† for all temperature trajectories. For all profiles, stabilization at 2 °C requires atmospheric CO₂ to peak and decline afterward to compensate for the ocean's thermal inertia. In the long-term, atmospheric CO₂ must be <450 parts per million by volume (ppmv), given the standard value for climate sensitivity of the UVic ESCM (3.6 °C). Note that in the case of the overshoot scenario (light blue curve in Fig. 1), the 2 °C stabilization target can only be met if CO₂ is artificially removed from the atmosphere, resulting in negative emissions.

Fig. 1.

Path independency of cumulative CO₂ emissions. (A) Cumulative CO₂ emissions and (B) CO₂ concentrations compatible with a global mean temperature increase of 2 °C relative to preindustrial times. The different curves refer to experiments with different prescribed temperature change trajectories (C). The red-dashed trajectory is the standard trajectory used throughout the analysis. Cumulative emissions are computed from the year 2001 onwards.

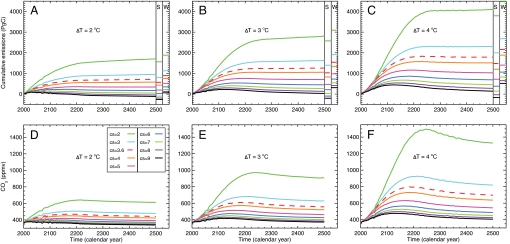
The above finding has important implications as it allows one to relate CO₂ cumulative emissions to the temperature target independently of the specific trajectory taken to stabilization. If global mean temperature thresholds for DAI of 3 °C and 4 °C are assumed, allowable cumulative emissions from 2001 to 2500 are found to be 1,260 PgC and 1,790 PgC, respectively. In terms of long-term atmospheric CO₂ concentrations, the above targets imply levels of <550 ppmv and <700 ppmv (red-dashed lines in Fig. 2).

Fig. 2.

Dependence of cumulative CO₂ emissions on climate sensitivity. Cumulative CO₂ emissions (A–C) and CO₂ concentrations (D–F) compatible with a long-term global mean temperature increase, (ΔT), of 2 °C (A and D), 3 °C (B and E) and 4 °C (C and F) relative to preindustrial times (the prescribed temperature trajectories are displayed in Fig. S3). The different curves refer to experiments with climate sensitivities (cs) in the range 2–9 °C (the curves for cs = 1 °C are not shown for clarity). The standard climate sensitivity of the UVic ESCM is 3.6 °C (red-dashed curves). (A–C Right) Cumulative emissions in 2500 under assumption of weak (W) and strong (S) climate-carbon cycle feedbacks are shown.

These figures are highly sensitive to the value of climate sensitivity. Using an uncertainty range for climate sensitivity (CS) of 1 °C to 9 °C, which encompasses the 5–95% range of most published PDFs for climate sensitivity (Box 10.2 in ref. 34), we find that the admissible cumulative emissions from 2001 to 2500 vary widely (Fig. 2). The range is −110 to 4,230 PgC for the 2 °C temperature stabilization target, 30 to 8,080 PgC for the 3 °C target, and 140 to 15,940 PgC for the 4 °C target. Fig. 2 indicates that the sensitivity is largest at low values of CS and decreases with increasing values of CS.^‡ Interestingly, for all three targets long-term temperature stabilization results in near-constant cumulative emissions, implying that annual emissions must decrease to ≈zero (35). However, this result is less true for very low CS, which allows small positive CO₂ emissions far into the future, or for very high CS, which requires negative future emissions.

As discussed above, the sensitivity of allowable cumulative emissions to the assumed CS value is large, with lower limits of the computed ranges being rather ambitious and upper limits exceeding the estimate of carbon bound in known fossil fuel reserves (≈5,000 PgC) (36). In terms of climate policy, such a large range implies responses ranging from very stringent CO₂ mitigation policies to virtually no mitigation at all (“business-as-usual”). Clearly, to be of any value for climate decision-making, the above estimates of cumulative emissions need to be weighted by their associated probabilities. To obtain such a weighting, we used several published PDFs for climate sensitivity (16–20, 22, 23). For each value of CS used in this study (1–9 °C), we then computed the cumulative probability that the actual value of CS is larger then the assumed value, for one specific PDF. For each simulation with a specific CS, we can then relate this probability to the probability that the associated allowable CO₂ emissions would lead to exceeding the specified temperature-stabilization target. Assume, for instance, a CS of 3 °C. For the PDF of Forest et al. (22), there is a 0.67 cumulative probability that the actual CS value is larger than 3 °C. It follows that the probability that the allowable cumulative emissions computed with a CS of 3 °C will exceed the intended target in 2500 is also 0.67.

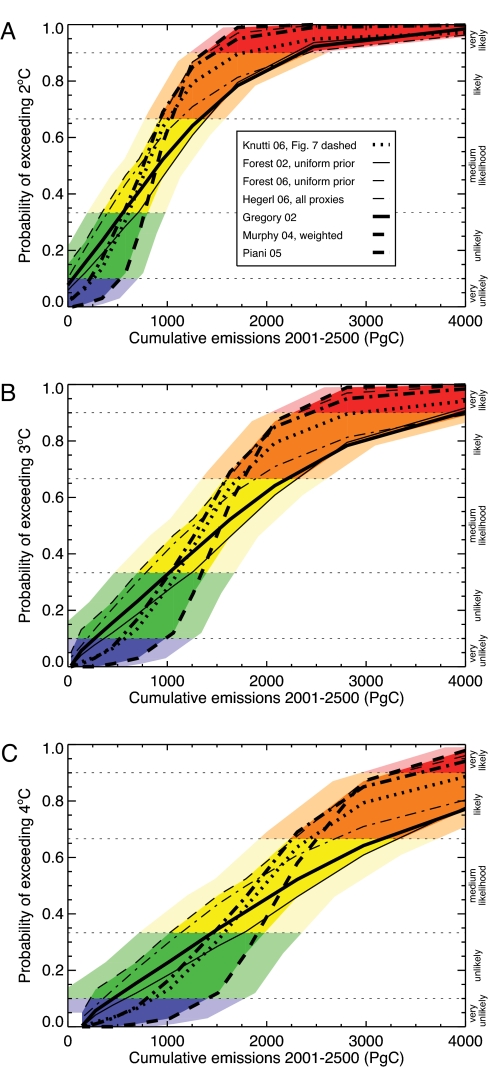
Fig. 3 displays the probabilities of exceeding temperature stabilization targets of 2–4 °C for a range of cumulative emissions and seven published PDFs for climate sensitivity. For a specific temperature target, the probability of exceeding that target increases with higher cumulative emissions. Conversely, lower acceptable probabilities of exceeding require lower emissions levels. We find that for the 2 °C target, cumulative CO₂ emissions after 2000 need to be limited to a median value of 550 PgC (with a range of 300–770 PgC depending on the climate sensitivity PDF), if the probability of exceeding that target is to be kept within the “unlikely” domain (corresponding to a probability between 0.1 and 0.33 in the IPCC terminology) (37). If the acceptable probability of exceeding the 2 °C target is taken to be <0.1, allowable CO₂ emissions must not exceed a median of 120 PgC (with a range of −100 to 500 PgC). Assuming a threshold for DAI of 3 °C and an acceptable probability of exceeding that target of <0.33, allowable cumulative emissions need to be <1,020 PgC (range, 700–1,300 PgC). The associated median value for the 4 °C target is 1,450 PgC (range, 1,000 to 1,900 PgC).

Fig. 3.

Probability of exceeding specified global mean temperature targets for different CO₂ emissions levels. (A) 2 °C target. (B) 3 °C target. (C) 4 °C target. The brighter colors denote the range in emissions spanned by the different climate sensitivity PDFs, and the weaker colors denote the range spanned by additional uncertainty in the strength of the climate-carbon cycle feedback. Using the nomenclature suggested by the IPCC (37), we have divided the probability range into “very unlikely” (0.01 < P < 0.1), “unlikely” (0.1 < P < 0.33), “medium likelihood” (0.33 < P < 0.66), “likely” (0.66 < P < 0.9), and “very likely” (0.9 < P < 0.99).

It can be expected that these figures are sensitive to the strength of the climate-carbon cycle feedback. According to the Coupled Carbon Cycle Climate Model Intercomparison Project (C⁴MIP) (14), the UVic ESCM simulates a climate-carbon cycle feedback that lies approximately in the middle of the range spanned by state-of-the-art climate-carbon cycle models. If the feedback simulated by the UVic ESCM was stronger, allowable emissions under a specific temperature threshold for DAI would be lower, and vice versa. To estimate the range of permissible emissions under consideration of different strengths of the climate-carbon cycle feedback, we reconstructed the allowable emissions that would be simulated by the C⁴MIP models with the strongest (HadCM3LC) and the weakest (IPSL-CM4-LOOP) feedback under the same temperature trajectory. This reconstruction was achieved by scaling the reduction in allowable emissions because of the feedback as simulated by the UVic ESCM based on the respective normalized gain factor (see Methods). Fig. 2 A–C Right displays allowable CO₂ emissions in 2500 under assumption of weak (IPSL-CM4-LOOP) and strong (HadCM3LC) climate-carbon cycle feedbacks. Taking this additional uncertainty into account, the total range in year-2500 cumulative emissions for the 2 °C target is −260 to 4,410 PgC (compared with −110 to 4,230 PgC, taking into account uncertainty in climate sensitivity alone). Note that for a specific temperature target the range in allowable emissions because of uncertainty in the climate-carbon cycle feedback is independent of the CS value, because the strength of the feedback depends only on the global mean temperature change and not on the atmospheric CO₂ level. Accordingly, the relative uncertainty range because of climate-carbon cycle feedbacks is smaller at lower CS.

Fig. 3 displays the effect of different assumptions regarding the climate-carbon cycle feedback on the probability of exceeding specified temperature targets. Generally, the probability that any given emissions level will exceed the specified temperature target decreases (increases) under assumption of a weak (strong) climate-carbon cycle feedback. If the acceptable probability of exceeding the 2 °C target is taken to be 0.33 (keeping it in the unlikely domain), median allowable CO₂ emissions, under inclusion of the uncertainty in both climate sensitivity and the climate-carbon cycle feedback, are 590 PgC^¶ (range, 200 to 950 PgC). If the acceptable probability of exceeding the 2 °C target is taken to be <0.1 (very unlikely), allowable CO₂ emissions must not exceed a median of 170 PgC (range, −220 to 700 PgC).

We emphasize that the allowable emissions estimates presented in this study refer purely to CO₂ and are only valid more generally if the radiative forcing of other greenhouse gases continues to be approximately compensated by that of sulfate aerosols, as has been approximately true in the past.

Although the probabilities of exceeding given in this article have been derived for the long-term (year-2500) temperature response, they also apply, with some approximation,^§ to the instantaneous temperature response. Fig. S1 demonstrates that even if the total allowable emissions compatible with the 2 °C target are emitted very quickly, the resulting temperature anomaly exceeds the target transiently by only a very small amount (SI Text).

It is notable that the range of allowable CO₂ emissions for 2 °C warming derived from transient climate-carbon model simulations (38), albeit over a more limited range of climate sensitivities, are nevertheless consistent with the results we report here. Our estimate of allowable emissions compatible with the 2 °C target is not directly comparable to that of Meinshausen et al. (39), who consider emissions budgets for the 2000–2050 period.

In view of climate policy, an interesting question regards the least-cost allocation of allowable CO₂ emissions over time. The cumulative emissions estimates presented in this article, which have been derived by using a three-dimensional, state-of-the-art climate model, can be used as a constraint for the derivation of “economically optimal” emissions paths by using a model of the energy-technology sector and the world economy. Because in such a cost-effectiveness framework no additional specification of climate parameters is required, the resulting optimal emissions trajectory would be entirely consistent with the temperature targets initially prescribed to the UVic ESCM.^‖

The independence of the amount of total allowable emissions on the emissions trajectory found in this study supports an international policy framework aimed at avoiding DAI, which is formulated on the basis of total allowable GHG emissions. Such a framework could avoid some of the complications arising from getting all major GHG emitting nations to agree to a common timetable for emissions reductions. Given the large uncertainties associated with total emissions compatible with long-term temperature targets, interim revision of the allowable emissions in light of the latest scientific evidence should be warranted under such a framework. Also, by focusing on absolute temperature targets, such an approach would neglect the role of path-dependencies in causing DAI. In fact, if the intended temperature target is reached earlier, implying faster rates of climate change, or temporarily exceeded, dangerous climate impact thresholds are more likely to be crossed (7, 40).

Materials and Methods

Model Description.

The UVic ESCM version 2.8 consists of a 19-layer ocean general circulation model with isopycnal mixing and a Gent and McWilliams (41) parameterization of the effect of eddy-induced tracer transport. For diapycnal mixing, it uses a horizontally constant profile of diffusivity with values of ≈0.3 × 10⁻⁴ m²s⁻¹ in the pycnocline. The ocean model is coupled to a dynamic-thermodynamic sea-ice model and an energy-moisture balance model of the atmosphere (29). Atmospheric heat and moisture transports are parameterized through Fickian diffusion. All experiments presented here are computed with advection of heat and specific humidity. The atmospheric model includes a parameterization of water vapor/planetary long-wave feedbacks, and the radiative forcing associated with changes in atmospheric CO₂ is included as a modification of planetary long-wave flux. The land surface and terrestrial vegetation are represented by a simplified version of the Hadley Centre's MOSES land-surface scheme coupled to the dynamic vegetation model TRIFFID (42). Ocean carbon is simulated by means of a OCMIP-type inorganic carbon-cycle model (J. Orr, R. Najjar, C. Sabine, and F. Joos, Abiotic how-to document, 2000, available at http://www.ipsl.jussieu.fr/OCMIP) and a marine ecosystem model solving prognostic equations for nutrients, phytoplankton, zooplankton, and detritus (43). Sediment processes are represented using an oxic-only model of sediment respiration (44). The coupled model has a resolution of 3.6° in longitude and 1.8° in latitude and conserves energy, water, and carbon to machine precision without the use of flux adjustment. The model has participated in a number of model intercomparison projects including the C⁴MIP (14), the Paleoclimate Modeling Intercomparison Project (PMIP) (45), and the coordinated thermohaline circulation experiments (46, 47). In addition, the model was used as an assessment tool in the 4th Assessment Report of the IPCC (34).

Historical Simulations.

The model was spun up for 10,000 years under year-1800 radiative forcing (prescribed atmospheric CO₂ concentration of 284 ppm). Afterward, the model was integrated in the fully coupled mode for another 5,000 years. Over the last 4,000 years of simulation, the model did not exhibit any discernible drift. The model was then integrated forward to the end of year 2000 by prescribing the observed atmospheric CO₂ profile (with 2000 having an average concentration of 368 ppm). The climatic effect of land-use change over the 20th century was accounted for by changing specified surface albedo in regions of croplands (48). Other forcings varying over the historical period included non-CO₂ greenhouse gases (CH₄, N₂O, halocarbons), sulfate aerosols (direct effect), solar irradiance, volcanoes, and orbital changes. The resulting temperature change in 2000 was 0.68 °C. Fig. S2 displays the temperature trajectory for 1800–2000 as compared with observational data (49). To ensure a smooth transition for future projections, we performed a second simulation over the historical period (1800–2000) by using the temperature trajectory from the experiment described above to diagnose CO₂ emissions compatible with that trajectory (with all non-CO₂ forcings specified as above). The procedure used to “track” a specified temperature profile is described below. The year-2000 state of the coupled climate-carbon cycle system as computed by this historical run was used to initialize the model simulations spanning the 2000–2500 period.

Future Simulations.

For the future simulations we diagnosed CO₂ emissions compatible with prescribed temperature trajectories. These temperature profiles were synthetically constructed by specifying an initial rate of temperature change (which was taken to be the rate of temperature change averaged over the last 10 years of the historical simulation), a target temperature, and a year of temperature stabilization. The standard profiles used in this study for stabilization at 2 °C, 3 °C, and 4 °C (relative to preindustrial) are shown in Fig. S3. The “temperature tracking” was implemented through a simple proportional control equation, of the form

where E(t) are CO₂ emissions, and ΔT^DATA(t) − ΔT(t) is the error between prescribed and simulated temperature change at a specific time, t. The proportionality constant pk includes factors converting temperature to CO₂ concentrations (CO₂ concentration divided by climate sensitivity) and CO₂ concentrations to emissions. Also, pk is taken to be inversely proportional to the response time scale of the system. This time scale was tuned so as to optimize the tracking, by making sure that the control parameter, E(t), would not react too quickly nor too slowly to the diagnosed temperature error. Fig. S4 Top demonstrates the accuracy of this procedure. The future temperature tracking runs were integrated from a common year-2000 state to the year 2500 by holding all non-CO₂ forcings (except orbital forcing) fixed at year-2000 levels.

Climate Sensitivity Uncertainty.

We constructed an ensemble of 13 model versions for which the equilibrium climate sensitivity varies from 1 °C to 9 °C. To alter the equilibrium temperature response to a doubling of the atmospheric CO₂ concentration, we included an adjustable temperature-longwave radiation feedback (50):

where L_out is the unmodified outgoing longwave radiation and L_out* is the new outgoing longwave radiation. The feedback term is proportional to the difference between global mean surface air temperature and the year-1800 temperature, T(t) − T₀. The chosen parameterization serves to increase the net climate feedback by damping the increase in outgoing longwave radiation with increased surface temperature (mimicking, for example, a strong positive cloud feedback). The proportionality constants, c, corresponding to specific equilibrium climate sensitivities, were determined from a set of prior model simulations. For those runs (seven in total), we specified values of the constant that we guessed would give rise to climate sensitivities in the chosen range (1–9 °C). We then forced the model with an instantaneous doubling of the preindustrial CO₂ concentration and diagnosed the equilibrium global mean temperature response. For chosen climate sensitivities lying between diagnosed values, we derived the respective constant by interpolation. To reproduce the observed historical temperature trajectory for model versions with climate sensitivities different from the standard value of the UVic ESCM (3.6 °C), we compensated the feedback associated with different climate sensitivities [i.e., the term −c(T(t) − T₀)] by adjusting poorly known transient radiative forcings (mainly from sulfate aerosols) through the historical period. This procedure ensures that all future simulations are initialized from a common year-2000 state of the model. After 2000, the forcing anomalies (relative to the standard case) are taken to vary proportionally to CO₂ emissions, eventually declining to near zero. The motivation for this choice is that emissions of sulfate aerosol precursors, such as SO₂, are tightly linked to CO₂ emissions. Note that the rate of ocean heat uptake is the same for all model versions. The reason is that in a complex three-dimensional coupled climate-carbon cycle model such as the UVic ESCM it is a difficult task to generate different model versions with different mixing parameterizations and a reasonable preindustrial state and transient response over the historical period. In such a model (as opposed to two-dimensional physical climate models such as those used in refs. 15 and 20), varying the mixing parameterization would not only alter the ocean heat uptake, but would also degrade the spatial distribution of physical and biogeochemical tracers, such as salinity, temperature, dissolved inorganic carbon, alkalinity, etc.

Climate-Carbon Cycle Feedback Uncertainty.

A common procedure to diagnose the climate-carbon cycle feedback is to compute the difference in atmospheric CO₂ between the fully coupled experiment and an experiment where the additional CO₂ is treated as a radiatively inactive gas (referred to as the “uncoupled” experiment) (14, 26). When forced by historical CO₂ emissions for 1800–2000 and the Special Report on Emission Scenarios (SRES) A2 scenario thereafter, the climate-carbon cycle feedback simulated by the UVic ESCM is 110 ppm in 2100. The associated feedback gain factor is 0.18, lying approximately in the middle of the range simulated by the climate-carbon cycle models that participated in the C⁴MIP model intercomparison (14). In the case of the inverse modeling framework used here, an alternative method to compute the feedback has to be applied, because the uncoupled experiment described above is not meaningful (if the modeled atmosphere does not “feel” the climatic effects of additional CO₂, the allowable cumulative emissions compatible with a given temperature profile would be infinitely large). We proceed as for the standard temperature tracking experiments described above, but prescribe preindustrial atmospheric CO₂ levels to the ocean and the terrestrial biosphere. From these experiments we can then derive the reduction in allowable emissions because of climate-carbon cycle feedbacks by diagnosing the effect of climate change on ocean and land carbon inventories. We find that the reductions in allowable emissions are 247 gigatons of carbon (GtC), 392 GtC, and 522 GtC in 2500 for climate targets of 2 °C, 3 °C, and 4 °C, respectively. These numbers are independent of the value of climate sensitivity, because the feedback depends only on the change in global mean temperature (which is the same given one stabilization target) and not on the atmospheric CO₂ level. Fig. S5 displays allowable emissions with and without climate-carbon cycle feedbacks for the three chosen temperature targets. Given the uncertainty in the strength of the climate-carbon cycle feedback, the curves without feedback can be interpreted as upper bounds on the allowable emissions. To estimate the range of permissible emissions considering different strengths of the climate-carbon cycle feedback, we drew on results of the C⁴MIP model intercomparison (14). The feedback simulated by the participating models varies widely, with the feedback gain factor (g) ranging from 0.04 to 0.31. Because these gain factors are dependent on the respective model's climate sensitivity, we normalized them to the climate sensitivity of the UVic ESCM, using the year-2100 surface-air temperature change per unit CO₂ concentration change (α) listed in ref. 14. This procedure gives a range in normalized gain factors of 0.05 (for the IPSL-CM4-LOOP model) to 0.26 (HadCM3LC). We then reconstructed the range in allowable emissions that would be simulated by the C⁴MIP models by scaling the reduction in allowable emissions computed with the UVic ESCM based on the ratio of the respective model's normalized gain factor to that of the UVic model (28). Note that here we use a g value for the UVic ESCM of 0.18 and an α value of 0.0055 °C ppm⁻¹ that are lower than the values indicated in the C⁴MIP study (14), which were calculated based on an earlier version of the model. Note also that in our procedure we assume that the relation between the models' gain factors remains constant through time and across emissions scenarios, which is not entirely accurate (14).