Skip to main content
NCBI home page
Bioinformatics logoLink to Bioinformatics
. 2009 Jul 14;25(19):2595–6602. doi: 10.1093/bioinformatics/btp428

A multi-dimensional evidence-based candidate gene prioritization approach for complex diseases–schizophrenia as a case

Jingchun Sun 1,2,†, Peilin Jia 1,2,†, Ayman H Fanous 2,3, Bradley T Webb 4, Edwin JCG van den Oord 2,4, Xiangning Chen 2,5, Jozsef Bukszar 4, Kenneth S Kendler 2,5, Zhongming Zhao 1,2,5,*
PMCID: PMC2752609  PMID: 19602527

Abstract

Motivation: During the past decade, we have seen an exponential growth of vast amounts of genetic data generated for complex disease studies. Currently, across a variety of complex biological problems, there is a strong trend towards the integration of data from multiple sources. So far, candidate gene prioritization approaches have been designed for specific purposes, by utilizing only some of the available sources of genetic studies, or by using a simple weight scheme. Specifically to psychiatric disorders, there has been no prioritization approach that fully utilizes all major sources of experimental data.

Results: Here we present a multi-dimensional evidence-based candidate gene prioritization approach for complex diseases and demonstrate it in schizophrenia. In this approach, we first collect and curate genetic studies for schizophrenia from four major categories: association studies, linkage analyses, gene expression and literature search. Genes in these data sets are initially scored by category-specific scoring methods. Then, an optimal weight matrix is searched by a two-step procedure (core genes and unbiased P-values in independent genome-wide association studies). Finally, genes are prioritized by their combined scores using the optimal weight matrix. Our evaluation suggests this approach generates prioritized candidate genes that are promising for further analysis or replication. The approach can be applied to other complex diseases.

Availability: The collected data, prioritized candidate genes, and gene prioritization tools are freely available at http://bioinfo.mc.vanderbilt.edu/SZGR/.

Contact: zhongming.zhao@vanderbilt.edu

Supplementary information:Supplementary data are available at Bioinformatics online.

1 INTRODUCTION

It is now commonly accepted that many complex illnesses are not inherited in a Mendelian fashion and that they are polygenic/multifactorial (Schork, 1997). Identifying causal genetic factors including genes and genetic markers is an essential step in our understanding and subsequent prevention and treatment of these complex diseases. During the past decade, we have seen an exponential growth of vast amounts of biological data generated by the revolutionary high throughput technologies of genomics, transcriptomes and proteomics (Leung and Pang, 2002). A variety of strategies for the selection of candidate genes for the follow up studies of complex diseases are available, including but not limited to, positional cloning, functional candidates, and the use of microarray and pathway data (Sullivan et al., 2004). For each of these strategies, even though the number of genes to consider has been greatly reduced, a large number still remains and secondary selection procedures are necessary. However, most procedures are not conducted with an a priori strategy. Rather, information is weighed and ranked intuitively by the investigator. Specifically in psychiatric genetics, most of the studies thus far have been limited to functional candidates suggested by neurotransmitter psychopharmacology, falling under the heading referred to as ‘the usual suspects’ (Sun et al., 2008). Currently, across a variety of complex biological problems, there is a strong tendency towards the integration of data from multiple sources, including gene sequence information, gene expression, protein–protein interactions, Gene Ontology (GO) annotations, and the use of this integrated data to select a list of ‘prioritized’ candidate genes (Aerts et al., 2006; Le-Niculescu et al., 2007; Ma et al., 2007; Rossi et al., 2006; Xu and Li, 2006). Such selections of prioritized candidate genes are much needed for follow-up studies and also for systems biology approaches such as network or pathway analysis (Goh et al., 2007; Guo et al., 2009). So far, these candidate gene approaches have been designed for specific purposes (e.g. gene network and pathway analysis) or for utilizing only some of possible sources of genetic studies (e.g. gene expression) (Franke et al., 2006; Le-Niculescu et al., 2007). For many complex diseases or disorders, massive multiple-dimensional genetic datasets have been available. These include thousands association studies, many genome-wide linkage scans and gene expression studies as well as cross species gene information. This provides us an opportunity but also a great challenge to develop effective approach for data collection, curation and integration so that candidate genes can be selected based on all available genetic evidence, weighed and then prioritized.

Schizophrenia is a major complex and debilitating psychiatric disorder with a lifetime prevalence of ∼1% in the world (Gottesman, 1991). The disease originates from a complex combination of genetic effect and environmental factors, which has been strongly supported by family, twin and adoption studies (Ross et al., 2006; Sullivan et al., 2003). Because of the severe effects of this illness, researchers and clinicians have been working together for decades to identify susceptibility genes or genetic markers. So far, thousands of reports have declared or refuted association to genes or linkage to genomic regions in schizophrenia, as well as numerous gene expression studies. Frustratingly, the traditional approach of trying to find the causative variation in the genomic regions that are associated with the disease has not, to date, proven very successful, and for some disease-susceptibility genes or regions, their genomic structures, functional regulations and evolutionary patterns appear complicated. This calls for alternative approaches to study genetic effects on complex diseases such as complicated gene regulation (i.e. gene–gene interactions) and gene–environment interactions. A list of candidate genes is needed for such purpose.

In this study, we propose a multi-dimensional evidence-based candidate gene prioritization approach. In this approach, we collected and curated all the available genetic studies of schizophrenia including more than two thousand association studies, genome-wide linkage scans, and gene expression studies. By developing a weight scheme, genes were ranked by weighted evidence from different studies. We evaluated these prioritized candidate genes using independent unbiased genome-wide association studies (GWAS) and also gene expression data in human tissues. This multi-dimensional evidence-based approach and framework can be applied to many other complex diseases such as alcohol dependence, depression, anxiety, nicotine dependence and Alzheimer's disease.

2 CANDIDATE GENE SELECTION AND PRIORITIZATION

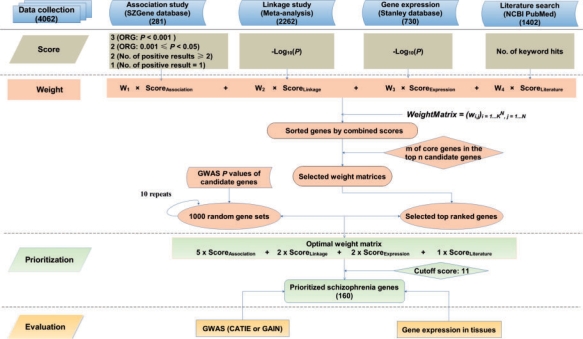
We introduce a comprehensive scoring and weighting scheme that can be applied to prioritize candidate genes for complex diseases based on their multiple sources of genetic data. The design is shown in Figure 1. The framework includes five steps: data collection and curation, scoring, weighting, prioritization, and evaluation. First, we collected all the data with experimental evidence including association studies, linkage scans, gene expression and high throughput literature search. To address the great variety of data and its unequal amount of information, and to further increase user flexibility, we categorized the data into different groups such as ‘association’, ‘linkage’, ‘gene expression’, and ‘literature search’. Second, we assigned scores for the genes in each data category by category-specific scoring method. Third, we developed a weight scheme to weigh the evidence from different categories of data. An optimal weight scheme was found from weight matrix pool by using (i) a small set of genes that have been well considered as candidate genes by experts or by recent meta-analysis of association studies, and (ii) random selected data (P-values) from independent GWA studies. Fourth, these genes were assigned an integrated score by using the optimal weight scheme and then prioritized based on the integrated scores. Fifth, the prioritized genes were evaluated by cross-using independent GWAS information, independent gene expression in human tissues, or follow up experimental verification. The approach was illustrated by using schizophrenia as a case (Fig. 1).

Fig. 1.

Fig. 1.

Open in a new tab

Framework for prioritization of candidate genes. ORG represents genes selected based on combined odds ratio method (see text). m is the proportion (%) of core genes and n is the proportion of all available candidate genes. A parameter set of m and n is used to search the optimal weight scheme (see text). GWAS information used in searching optimal weight matrix (random P-values from GWAS P value pool, either CATIE or GAIN) is different from that in evaluation step (only P-values in the selected genes are used). For a non-redundant use of GWAS information, when CATIE dataset is used in randomness step, GAIN dataset would be used in evaluation step, and vice versa.

2.1 Four categories of data for gene ranking

2.1.1 Association study

The recently established SchizophreniaGene database collected and curated association studies for schizophrenia in about 1400 publications (Allen et al., 2008). We extracted all association studies published in peer-reviewed journals from the SchizophreniaGene database. The extracted information included gene annotations, study information (e.g. ethnic groups), statistical analysis methods in association studies and their results, number of cases and controls, number of families (number of affected and unaffected family members), and genotypes of each polymorphism.

In our previous study (Sun et al., 2008), we developed a combined odds ratio (OR) method to combine the ORs from multiple association studies of each gene. For each gene, we first performed an extensive evaluation of risk allele of each marker based on its ORs, confidence intervals (CIs) and P-values in multiple studies. We then calculated ORs using the risk alleles that we evaluated. The largest OR among the markers surveyed in each study was selected to represent its effect size in that association study. These OR values were next combined by using R package ‘meta’ and a P-value was obtained by a Z-test. Thus, this P-value suggests a rough proxy of the magnitude of positive association evidence. Because the smaller P-value indicates stronger evidence, we assigned a score 3 to a gene whose P-value <0.001, 2 whose P-value is [0.001–0.05), and 0 otherwise. These genes were annotated as ORG (genes selected by the combined OR method) in Figure 1.

The combined OR method requires at least two representative markers in each study and at least two association studies to combine their representative OR values (Sun et al., 2008). Some genes having at least two positive association studies might have been excluded in the procedure. Moreover, more association studies and genes have been published since then (as of August, 2007). When we prepared the data for this gene ranking, the number of genes has increased from 539 to 693 (as of April, 2008), but most of these new genes (91.6%) had only one study report. The number of genes with at least two positive association results increased from 115 to 124. Because replication is still a great challenge in schizophrenia research, we assigned a score 2 to those genes with at least two positive results and a score 1 to those with only one positive result to reflect different extent of association. We applied this combinatory strategy (i.e. P-value from combined OR method and scores based on the number of positive association studies) to all genes that had association report. Theoretically, the largest score of a gene would be 3. As a result, we had 281 genes with the assigned scores ranging from 1 to 3.

2.1.2 Linkage study

More than 32 genome-wide linkage scans and fine mapping studies for schizophrenia have suggested multiple regions that harbor genes influencing susceptibility to schizophrenia (Fanous et al., 2007; Lewis et al., 2003; Ng et al., 2009), but no region has shown strong consistent support for these linkage analyses. We used the results in a recent meta-analysis of 20 complete genome scans of schizophrenia (Lewis et al., 2003). The results suggested 12 consecutive bins that met two aggregate criteria for linkage (PAvgRnk and Pord <0.05). Those bins located in the following regions: 2q, 5q, 3p, 11q, 6p, 1q, 22q, 8p, 20q and 14p. The two aggregate criteria P-values were calculated based on permutation test. PAvgRnk is the probability of observing, by chance, each bin's average rank, and Pord is the probability of observing it for a bin with the same place in the order of average ranks in each permutation. We used those 12 consecutive bins, identified their corresponding physical locations on chromosomes, and extracted genes within these regions. This resulted in a total of 2262 genes with official gene symbols. We assigned score to each gene by its -log10(PAvgRnk).

During our preparation of the manuscript, Ng et al. (2009) published a new meta-analysis of 32 genome-wide linkage studies for schizophrenia. We did a similar gene prioritization analysis by using the genes extracted from the 10 bins with nominally significance evidence. We prioritized 173 genes, 119 of which overlapped with the 160 prioritized genes based on Lewis et al. (2003) (see Section 3.3). The analysis based on Ng et al. data is available at http://bioinfo.mc.vanderbilt.edu/SZGR/.

2.1.3 Gene expression data

The Stanley Medical Research Institute (SMRI) has assembled a large number of microarrays for schizophrenia and bipolar studies. Thus, we used Stanley Array collection data, which provided meta-analysis of 12 individual gene expression datasets involved in 988 arrays (https://www.stanleygenomics.org/, November 2007) (Higgs et al., 2006). For schizophrenia only, we downloaded the overall P-values for the genes from the database and extracted those genes whose P-values were <0.05. This resulted in 730 genes with gene symbols. We assigned score to each gene by its -log10P, where P is based on the t-statistic for the weighted fold change and combined standard error of the fold change.

2.1.4 Literature search

Co-occurrence of two entries in a document has often been applied to identify relationship (Roberts, 2006). We used NCBI PubMed automatic term mapping strategy to examine whether a gene and a schizophrenia-related keyword co-occur in the same document. Such a relationship suggests that the gene might have been studied for schizophrenia, and likely the gene is associated with schizophrenia because positive results have often been selected for publication. We evaluated different terms that are related to schizophrenia and selected six of them: ‘schizophrenia’, ‘schizophrenias’, ‘schizophrenic’, ‘schizophrenics’, ‘schizotypy’ and ‘schizotypal’. We extracted 25 759 human protein-coding genes from the file “Homo_sapiens.gene_info” downloaded from the NCBI FTP Gene (ftp://ftp.ncbi.nlm.nih.gov/gene/). Next, we used NCBI Entrez Programming Utilities ESearch to search NCBI PubMed. If a gene and a keyword co-occur in the same publication, a hit would be assigned. For example, the keyword ‘schizophrenia’ and gene ‘DTNBP1’ co-occurred in 113 publications and 113 hits were assigned to DTNBP1 and schizophrenia. Because the number of hits does not provide quantitative measurement of evidence, we assigned score 1 for a gene that has any hit(s) with a keyword. For the six keywords that we used, a gene might have score ranging from 0 (no hit with any keyword) to 6 (hits with all six keywords). After manual checking the results of special gene symbols (e.g. gene symbols containing a hyphen), we had 1402 genes whose scores were >0. It is worth noting that there is some duplication of information with association studies, but literature search provides additional information.

2.2 Data for evaluation: core genes and random sets from GWAS

To find an optimal weight scheme for all the genes (4062) we collected in the above four categories, we prepared for a small gene set which includes genes that have been commonly considered candidate genes in expert review or had significant results in the meta-analysis of association studies. Ross et al. (2006) reviewed the evidence in four domains (association with schizophrenia, linkage to gene locus, biological plausibility and altered expression in schizophrenia) and suggested 19 genes being candidates. We also included 27 genes with significant meta-analysis results performed by the SchizophreniaGene team (as of November 5, 2008). The genes were selected by having a nominally significant summary OR in all ethnic groups or Caucasian samples. When we combined the genes from these two sources, we had a total of 37 non-redundant genes. Among these genes, 33 appeared in our list of 4062 genes. We considered these 33 genes as a core gene set and used it to evaluate weight matrices.

We used GWAS data to evaluate whether the top genes ranked by a weight scheme have enriched markers with small P-values in the GWAS. So far, there have been two published GWA studies for schizophrenia: Clinical Antipsychotic Trials of Intervention Effectiveness [CATIE (Sullivan et al., 2008)] and Genetic Association Information Network [GAIN (Manolio et al., 2007)]. CATIE is a multi-phase randomized controlled trial of antipsychotic medications involving 1460 persons with schizophrenia. CATIE GWAS included 492 900 SNPs genotyped in a total of 738 cases and 733 group-matched controls (Sullivan et al., 2008). GAIN is a public–private partnership and includes many phenotypes. We used GAIN data for schizophrenia based on European Americans (1440 cases and 1469 controls), which genotyped 727 600 SNPs. The data was extracted from the NCBI dbGaP (http://www.ncbi.nlm.nih.gov/entrez/query.fcgi?DB=gap). We used these two GWAS datasets in our search of optimal weight matrix and evaluation on the prioritized genes. For each gene, we first identified all the markers genotyped in GWAS that were mapped to the gene. Then, the marker whose P-value was the smallest in a gene was chosen to represent the significance level of that gene.

2.3 Search for optimal weight matrix

2.3.1 Combined scores and weight matrix pool

A simple weight scheme such as the same or similar weight assigned to each of the collected multiple datasets has often been applied to rank candidate genes (Adie et al., 2006; Saccone et al., 2008). Considering the great variety of the datasets and thir genetic information, it is necessary to assign different weights to those datasets. However, such a task is challenging because in many cases we do not exactly know which data contains more useful information. Here we describe a weight vector to assign weight to each data source and then combine them to calculate the score for each gene. Given the number of datasets or sources of information being N (e.g. 4), the original score from each dataset or source could be weighted specifically and then a combined score could be calculated by the following function:

graphic file with name btp428m1.jpg (1)

For N datasets, there are possible K (e.g. N+1) different weights, thus, it forms a KN weight matrix pool.

2.3.2 Step one: weight matrix selection by core gene dataset

The core genes that we prepared in Section 2.2 represent the best reviewed or evaluated candidate genes at present, though it is a small list of genes. We used them to evaluate all possible weight matrices and selected those matrices that could rank the core genes in the top positions in all the available candidate gene pool that we collected from all sources. Here, we introduce two parameters to require the majority of the core genes being included in the top gene list by a weight matrix: proportion of core genes (m, %) and proportion of all candidate genes as considered top ranked genes (n, %). The m and n values can be flexibly set by specific gene ranking procedure; however, a combination of a larger m and a smaller n indicates a better performance. For example, a weight matrix produces 95% of core genes in the top 5% ranked genes of the candidate gene pool shows an ideal performance. The following iterative procedure selects the weight matrices that satisfy the threshold values m and n.

  1. For each weight matrix in the matrix pool, a combined score is calculated for each gene by function 1.

  2. All genes collected from all sources and the core genes are sorted by their combined scores, respectively.

  3. In these two sorting lists, a vector is generated to record the ranking positions of core genes in the ranked candidate gene list.

  4. Select the matrix if m of the core genes is ranked in the top n of the candidate genes. The position (j) where the m-th gene locates in the candidate gene list is recorded for the evaluation in step two.

  5. Repeat the above steps until all weight matrices are analyzed.

2.3.3 Step two: selection of weight matrix by GWAS markers

The weight matrices selected in step one are further selected by using one independent GWAS dataset (CATIE or GAIN) to find which matrix can identify a top list of genes that enrich markers with small P-value in GWAS. In this process, we use the best (i.e. smallest) P-value of each gene without taking into account the number of available GWAS markers in the gene. For each matrix, we select the number of top genes by position j in step one. Similarly, we randomly select 1000 subsets of genes from GWAS dataset with subset size j. For each random set, we compare whether its P-value distribution is statistically different from the selected top ranked gene (Wilcoxon rank-sum test, P <0.05). We repeat this randomization 10 times to estimate the confidence of this approach.

2.4 Prioritization of candidate genes

The weight matrix with the best performance is applied to calculate the combined scores for core genes and candidate genes. The score distribution is examined for the core and candidate genes and a cutoff value is set for approximate maximization of combined scores for core genes.

2.5 Evaluation on prioritized candidate genes

2.5.1 Evaluation using GWAS data

We used CATIE or GAIN GWAS data to evaluate whether the prioritized genes are more likely to enrich markers with small P-values than all the candidate genes. For a non-redundant use of GWAS information, when CATIE dataset is used in randomness step in Section 2.3.3, GAIN dataset would be used in evaluation step, and vice versa.

2.5.2 Gene expression

We evaluated expression of the prioritized candidate genes by comparing with non-disease genes. We compiled non-disease genes using protein coding genes downloaded from the NCBI Gene database and disease genes downloaded from the NCBI OMIM database (ftp://ftp.ncbi.nlm.nih.gov/repository/OMIM/). There were 23 430 genes that had not been annotated with any disease yet. These genes were considered non-disease genes. Next, we extracted gene expression data from WebGestalt (http://bioinfo.vanderbilt.edu/webgestalt/) (Zhang et al., 2005), which included expression data in 47 human tissues originally from the CGAP-expressed sequence tag (EST) project (Strausberg, 2001). We used the WebGestalt Tissue Expression Bar Chart to obtain the number of genes expressed in each tissue. The proportion of genes in a gene list expressed in a tissue was calculated by the count of genes expressed in the tissue divided by the total number of genes. The difference in gene expression distribution between the schizophrenia prioritized candidate genes and non-disease genes was performed by Wilcoxon signed-rank test.

3 RESULTS AND EVALUATION

3.1 Comparison of candidate genes in four data categories

We performed an extensive data collection and annotations to identify candidate genes from four major sources of information: association studies, linkage analysis, gene expression, and high throughput literature search. Table 1 summarizes the collected data, which represents the largest collection and curation of candidate genes from schizophrenia genetic studies. The number of genes varies among data categories, reflecting the different resolution of genomic regions in different studies or technologies.

Table 1.

Schizophrenia candidate genes in four categories

Category Number of genes Number of genes overlapped
Association Linkage Expression
Association 281
Linkage 2262 83
Expression 730 15 86
Literature 1402 239 225 58
Open in a new tab

After removing the redundancy, we had a total of 4062 genes. These genes are considered candidate gene pool and our task is to prioritize them by their combined evidence. There were 239 genes found in both the association studies and literature search. This represents 85% of the genes from association studies and 17% of the genes from literature search, reflecting that literature search is an effective approach (e.g. in terms of coverage) to identify possible candidate genes. Interestingly, 225 genes (10%) from linkage dataset were also found in literature search, suggesting that many genes under linkage peaks (i.e. large genomic regions) have been under extensive follow up investigations. There were only 85 genes shared by at least three categories and five shared by all four sources. The distribution of genes among different categories reflects the complex nature (e.g. low rate of replications) of the causal genetic factors in schizophrenia.

3.2 Search for optimal weight matrix

3.2.1 Selection of effective weight matrices by core gene evaluation

We collected four categories of candidate genes, i.e. genes with four major lines of evidence. The score was assigned for each gene in each data category (Fig. 1, see Section 2.1). In an initial phase, information from each data category was treated equally. In this study, we arbitrarily assigned weight to each data category from 1 to 5. A higher weight for a category leads to a higher score and helps the gene in that category rank better. In an exhaustive search, we have possible 54=625 weight matrices. Considering a total of 33 core genes in the 4062 candidate genes, we set threshold value m to be 95% (31 genes) or 90% (30 genes) and n to be 3% (top 122 genes), 4% (top 162 genes) or 5% (top 203 genes). For example, parameter set (m=95%, n=5%) requires at least 95% of the core genes located in the top 5% of the ranked 4062 candidate genes. Our analysis indicated that it is impractical to set n to be 1 or 2% (see Table 2). Therefore, we had six parameter sets to search for optimal weight matrix.

Table 2.

Search for optimal weight matrix by core genes and GWAS P-values

Parameter seta
 No. of weight matrices Step 1: selection by core genes
 Step 2: selection by GWAS P-values (No. of subsets ± SD)b
m (%) n (%) Weight matrixc Position jd Position le CATIE GAIN
90 5 51 [2, 1, 1, 1] 170 457 663.2 ± 9.4 611.5 ± 17.6
[2, 1, 2, 1] 199 1213 754.2 ± 9.8 526.7 ± 13.5
[3, 1, 1, 1] 168 496 866.5 ± 10.2 762.2 ± 13.2
[3, 1, 1, 2] 186 695 594.6 ± 18.4 470.6 ± 8.7
[3, 1, 2, 1] 179 1247 886.7 ± 10.7 893.4 ± 7.6
⋮ ⋮ ⋮ ⋮
90 4 4 [4, 2, 2, 1] 156 1404 893.0 ± 6.6 678.6 ± 10.2
[5, 2, 2, 1] 157 1419 951.8 ± 6.7 926.3 ± 7.1
[5, 4, 2, 3] 156 634 870.9 ± 10.2 790.6 ± 12.1
[5, 4, 3, 3] 159 652 823.3 ± 11.6 812.0 ± 14.3
90 3 0 NA NA NA NA
95 5 1 [5, 3, 2, 2] 202 715 831.2 ± 8.6 902.4 ± 8.4
95 4 0 NA NA NA NA
95 3 0 NA NA NA NA
Open in a new tab

am and n denote threshold proportion in the core gene set and total candidate gene set (see text).

bNumber of random subsets having significant different P-value distribution from the top ranked candidate genes. SD: standard deviation.

cWeight is ordered by wassociation, wlinkage, wexpression, wliterature. In the parameter set (m=90%, n=5%), only five matrices are listed due to space limitation.

dPosition j is where the m-th core gene locates in the n-th top ranked candidate genes (see Section 2.3.2).

ePosition l is where the last core gene in the ranked candidate gene list.

Only three parameter sets could have weight matrices that satisfied the corresponding criteria (Table 2). There were 51 weight matrices that satisfied parameter set (m=90%, n=5%), suggesting that the criteria in this parameter set are too loose. For other two-parameter sets, we found four weight matrices (m=90%, n=4%) and one matrix (m=95%, n=5%), respectively. These five weight matrices were further analyzed in step two by using GWAS data (see Section 2.3.3).

Using 1000 random sets of genes from the CATIE or GAIN GWAS and repeating this procedure 10 times, we evaluated whether the generated top genes by position j had more chance to have small P-values of GWAS markers than the randomly selected genes. Here j is the position in the ranked candidate genes where the m-th core gene matches. Table 2 shows that all five weight matrices could generate top genes that had high probability of enriched small P-values than the random genes. Among them, the matrix [wassociation=5, wlinkage=2, wexpression=, wliterature=1] stood out by showing the highest probability and confidence. We abbreviated this weight matrix as [5, 2, 2, 1].

3.2.2 Comparison of the five weight matrices

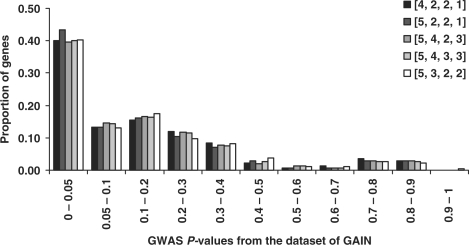
We further examined the distribution of GWAS P-values in the top ranked genes by these five weight matrices. The genes generated by matrix [5, 2, 2, 1] had the highest proportion of small P-values (P <0.05) in GAIN (Fig. 2) or CATIE (Supplementary Fig. 1) dataset, indicating their enrichment of significant markers. This comparison further supports that this matrix had better performance than the other four matrices, which had similar performance. Therefore, we selected weight matrix [5, 2, 2, 1] to calculate the combined scores and to rank genes from the four categories of data.

Fig. 2.

Fig. 2.

Open in a new tab

Distribution of P-values of the GAIN study in the five top gene sets generated by the five weight matrices. On the x-axis, the GWAS P-values were separated into different bins. The weight in the matrix (e.g. [4,2,2,1]) is ordered by , ‘linkage’, ‘expression’ and ‘literature’.

3.3 Prioritization of schizophrenia candidate genes

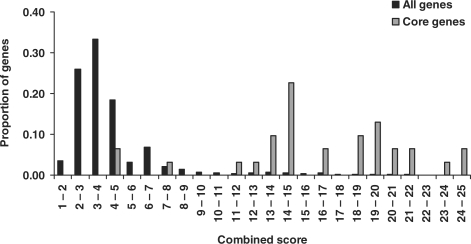
Using the weight matrix [5, 2, 2, 1], we calculated the combined scores for all candidate genes (4062 genes) including the core genes (33 genes). Figure 3 shows the distribution of the combined scores for these two sets of genes. As expected, the core genes tend to have high scores while most of other candidate genes have low scores. A strong difference was observed when we set a cutoff value 11. Most core genes, but only a small portion of the candidate genes, had the score >11. With this cutoff value, we had a total of 160 prioritized genes. Our follow up analysis using GWAS P-values indicated this cutoff value being valid.

Fig. 3.

Fig. 3.

Open in a new tab

Distribution of combined scores in the whole candidate genes and the core genes. In each score bin, proportion was measured by the number of genes having those scores divided by the total number of genes (core genes: 33; all candidate genes: 4062).

3.4 Evaluation of prioritized candidate gene set

3.4.1 Evaluation by GWAS data: P-value distribution of the prioritized genes versus the whole candidate genes

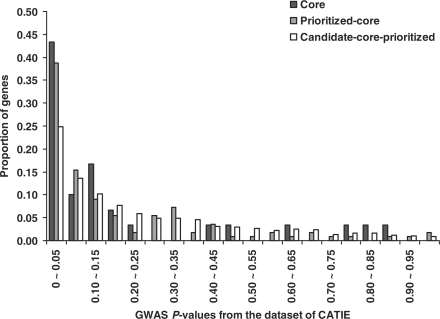
We evaluated the 160 prioritized candidate genes using the P-values of CATIE or GAIN markers. These two studies included genome-wide SNP markers and were independently designed; therefore, an enrichment of small P-values in the prioritized genes implies for its potential utility in follow up studies. Figure 4 displays the distribution of P-values in the core genes, prioritized genes, and all candidate genes using CATIE dataset. 39.9% of the prioritized genes had their P-values smaller than 0.05; this compared to 21.7% of all candidate genes. Similarly, in the GAIN study, we found 42.5% of the prioritized genes had P-values smaller than 0.05, compared to 25.9% of all candidate genes (Supplementary Fig. 2). A Wilcoxon rank-sum test revealed that P-values in the prioritized genes were significantly smaller than those in all candidate genes (CATIE: P=7.50 × 10−5, GAIN: P=3.97 × 10−4). This evaluation suggests it a promising list of candidate genes for further bioinformatics analysis and replication of association studies. It is worthy noting that the information from the GWAS in this evaluation (e.g. P-values in prioritized genes versus all candidate genes) is different from that in our search of optimal weight matrix (random sets from GWAS), and that our cross-use of GWAS dataset (e.g. CATIE in evaluation and GAIN in search of weight matrix, or vice versa) has the same results.

Fig. 4.

Fig. 4.

Open in a new tab

Distribution of P-values of the CATIE study in core genes, prioritized genes excluding core genes, and all candidate genes excluding core and prioritized genes.

3.4.2 Evaluation by GWAS data: P-value distribution among different scores

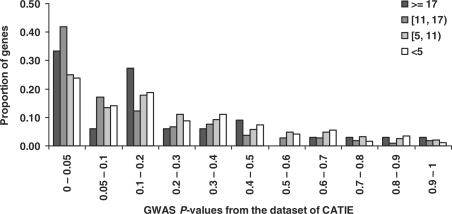
We further examined the distribution of P-values among the candidate genes by their scores. We separated the 4062 candidate genes into four groups: genes whose scores were <5, 5–11, 11–17 and ≥17, respectively. For the genes whose scores ≥17 or 11–17, we observed a higher proportion of small P-values in CATIE (Wilcoxon rank-sum test, P=3.8 × 10−5, Fig. 5) or GAIN (Wilcoxon rank-sum test, P=2.3 × 10−4, Supplementary Fig. 3) than other genes (i.e. score <11). This confirms our cutoff value of 11 used in our prioritization of candidate genes.

Fig. 5.

Fig. 5.

Open in a new tab

Distribution of P-values of the CATIE study in the 4062 candidate genes. The candidate genes were separated into four groups by their scores: <5, 5–11, 11−17 and ≥17.

3.4.3. Evaluation by gene expression in tissues

To further examine whether the prioritized candidate genes support the neurotransmitters and neuroplasticity theories of schizophrenia, we analyzed their gene expression patterns in normal human tissues using gene expression data in 47 tissues from the CGAP-EST project (Strausberg, 2001). We calculated the proportion of the candidate genes and the proportion of non-disease genes expressed in each tissue. We found a statistically significant difference in expression pattern among the 47 tissues between the proportion of the prioritized schizophrenia genes and the proportion of the non-disease genes (Wilcoxon signed-rank test, P=1.32 × 10−24). There are nine tissues related to brain or nerve. When we ranked the expression difference between the prioritized genes and non-disease genes, we found these tissues had their ranks 1st, 2nd, 3rd, 4th, 5th, 6th, 7th, 10th and 16th, respectively. This ranking order is obviously non-random (P = 0). Furthermore, we observed that in six tissues the proportion of the prioritized schizophrenia genes was ∼10% or more than that of non-disease genes. Interestingly, all these six tissues are brain or nerve tissues: cerebrum (proportion difference: +12.7%), brain (+12.3%), nervous (+11.8%), cerebellum (+11.5%), eye (+10.4%) and peripheral nervous system (+9.5%). This evaluation indicates that the prioritized candidate genes are more likely expressed in brain or nerve related tissues.

4. DISCUSSION

We present a multi-dimensional data integration framework by using an optimal weight scheme. This is a comprehensive and effective gene prioritization procedure and fully utilizes the evidence in most genetic studies; thus it differs from the previous ones. We demonstrated this approach by using multiple sources of genetic studies for schizophrenia. We collected and curated the candidate genes from four major sources of genetic data and assigned initial scores to the genes from each source by different scoring methods. For each gene, a combined score, which reflects the effective evidence of the gene, was calculated by optimal weight matrix. The prioritized genes were evaluated by the enriched P-values in two independent GWA studies and also by gene expression pattern in human tissues. Our evaluation suggests that these prioritized genes are promising and may be used for follow up bioinformatics analysis and future replication using other samples. For example, we used the prioritized genes to reconstruct a molecular gene network for schizophrenia based on all the available human protein--protein interactions and found that it had many different network features from the general cancer gene network [Schizophrenia gene networks and implications for psychiatric disorders (Sun et al., in preparation)]. Based on the schizophrenia gene network, we were able to identify several small sub-networks in which eight novel candidate genes (no reports for schizophrenia yet) extensively interact with the genes in our prioritized list. Replication study using our Irish Case-Control Study of Schizophrenia (ICCSS) sample (1021 cases and 626 controls) and Irish Study of High Density Schizophrenia Families (ISHDSF) successfully verified three genes significantly associated with schizophrenia (unpublished data). Furthermore, this approach has been successfully applied to our project, in which 502 genes with different combined weights were selected for follow up replications in our ISHDSF sample using a custom Illumina iSelect chip, which uses the Infinium® assay (unpublished data). Thus, this approach is useful not only for gene prioritization but also for suggesting novel candidate genes for complex disease studies.

The optimal weight matrix (e.g. [5, 2, 2, 1] in this study) depends on the core genes for a specific disease and the independent genome-wide study (e.g. CATIE and GAIN); thus, it is likely different for other complex diseases. Moreover, for control purpose, we used a set of ‘core’ genes recently identified by GWAS for Crohn's disease or randomly selected from the candidate gene pool, no weight matrix could be identified to satisfy parameter set [m, n] by requiring m at least 90% and n at most 5% (e.g. m=95%, n=5%), or even [m=80%, n=50%]. The details are shown in Supplementary data, ‘Crohn's disease and random gene analysis’. This demonstrates that disease-specific core genes are useful in the search of optimal weight matrix.

We collected broadly defined candidate genes based on four lines of evidence, i.e. association, linkage, expression and literature to prioritize them for further analysis. These data were extracted and curated from genetic studies with direct evidence (e.g. experimental data). We may extend this work by including non-experimental data such as GO annotations, gene network/pathway information, genetic markers in the conserved non-coding regions, and regulatory elements (Aerts et al., 2006; van Driel et al., 2005; Wu et al., 2008). This takes advantage of additional biological information generated by computational analysis or the ‘omics’ approach, which is not directly available from the traditional genetic studies. The disadvantages of including such computational or ‘omics’ data are, for example, inconsistent quality across the data set (or low quality), biased approaches in generating such data, and high error rate in some computational analysis. Therefore, data cleaning and development of weight schemes are more complicated.

We performed literature search of candidate genes based on co-occurrence of keywords and genes using the tool developed by the NCBI Entrez team. Our high throughput literature search could find the majority (85%) of genes in association studies that have been collected and carefully curated in the SchizophreniaGene database (Table 1). Text-mining has been extensively applied to biological fields recently due to the exponential growth of biological data (Saccone et al., 2008). Many algorithms and computational tools have been developed (Yu et al., 2008). We may enhance our strategy on searching candidate genes by combining a more efficient algorithm and a better yet more complicated search function such as logical relationship between the keywords and genes.

Supplementary Material

[Supplementary Data]
btp428_index.html (760B, html)

ACKNOWLEDGEMENTS

The authors would like to thank Dr Patrick F. Sullivan for data sharing and Dr Anyuan Guo for assistance. The genotyping of samples was provided through the Genetic Association Information Network (GAIN). The dataset(s) used for the analyses described in this manuscript were obtained from the GAIN Database found at http://view.ncbi.nlm.nih.gov/dbgap-controlled through dbGaP accession number phs000017.v1.p1. Samples and associated phenotype data for the Linking Genome-Wide Association Study of Schizophrenia were provided by P. Gejman.

Funding: NIH grants (AA017437 and LM009598), NARSAD Young Investigator Award, and Thomas F. and Kate Miller Jeffress Memorial Trust grant (to Z.Z.); a grant from the Department of Veterans Affairs Merit Review program (to A.F.).

Conflict of Interest: none declared.

REFERENCES

  1. Adie EA, et al. SUSPECTS: enabling fast and effective prioritization of positional candidates. Bioinformatics. 2006;22:773–774. doi: 10.1093/bioinformatics/btk031. [DOI] [PubMed] [Google Scholar]
  2. Aerts S, et al. Gene prioritization through genomic data fusion. Nat. Biotechnol. 2006;24:537–544. doi: 10.1038/nbt1203. [DOI] [PubMed] [Google Scholar]
  3. Allen NC, et al. Systematic meta-analyses and field synopsis of genetic association studies in schizophrenia: the SzGene database. Nat. Genet. 2008;40:827–834. doi: 10.1038/ng.171. [DOI] [PubMed] [Google Scholar]
  4. Fanous AH, et al. A genome-wide scan for modifier loci in schizophrenia. Am. J. Med. Genet. B Neuropsychiatr. Genet. 2007;144:589–595. doi: 10.1002/ajmg.b.30442. [DOI] [PubMed] [Google Scholar]
  5. Franke L, et al. Reconstruction of a functional human gene network with an application for prioritizing positional candidate genes. Am. J. Hum. Genet. 2006;78:1011–1025. doi: 10.1086/504300. [DOI] [PMC free article] [PubMed] [Google Scholar]
  6. Goh KI, et al. The human disease network. Proc. Natl. Acad. Sci. USA. 2007;104:8685–8690. doi: 10.1073/pnas.0701361104. [DOI] [PMC free article] [PubMed] [Google Scholar]
  7. Gottesman II. In: Schizophrenia Genesis: The Origins of Madness. Freeman WH, editor. New York: 1991. [Google Scholar]
  8. Guo AY, et al. The dystrobrevin binding protein 1 (DTNBP1) gene: features and networks. Mol. Psychiatry. 2009;14:18–29. doi: 10.1038/mp.2008.88. [DOI] [PMC free article] [PubMed] [Google Scholar]
  9. Higgs BW, et al. An online database for brain disease research. BMC Genomics. 2006;7:70. doi: 10.1186/1471-2164-7-70. [DOI] [PMC free article] [PubMed] [Google Scholar]
  10. Le-Niculescu H, et al. Towards understanding the schizophrenia code: an expanded convergent functional genomics approach. Am. J. Med. Genet. B Neuropsychiatr. Genet. 2007;144:129–158. doi: 10.1002/ajmg.b.30481. [DOI] [PubMed] [Google Scholar]
  11. Leung YF, Pang CP. EYE on bioinformatics: dissecting complex disease traits in silico. Appl. Bioinformatics. 2002;1:69–80. [PubMed] [Google Scholar]
  12. Lewis CM, et al. Genome scan meta-analysis of schizophrenia and bipolar disorder, part II: Schizophrenia. Am. J. Hum. Genet. 2003;73:34–48. doi: 10.1086/376549. [DOI] [PMC free article] [PubMed] [Google Scholar]
  13. Ma X, et al. CGI: a new approach for prioritizing genes by combining gene expression and protein-protein interaction data. Bioinformatics. 2007;23:215–221. doi: 10.1093/bioinformatics/btl569. [DOI] [PubMed] [Google Scholar]
  14. Manolio TA, et al. New models of collaboration in genome-wide association studies: the Genetic Association Information Network. Nat. Genet. 2007;39:1045–1051. doi: 10.1038/ng2127. [DOI] [PubMed] [Google Scholar]
  15. Ng M, et al. Meta-analysis of 32 genome-wide linkage studies of schizophrenia. Mol. Psychiatry. 2009;14:774–785. doi: 10.1038/mp.2008.135. [DOI] [PMC free article] [PubMed] [Google Scholar]
  16. Roberts PM. Mining literature for systems biology. Brief Bioinform. 2006;7:399–406. doi: 10.1093/bib/bbl037. [DOI] [PubMed] [Google Scholar]
  17. Ross CA, et al. Neurobiology of schizophrenia. Neuron. 2006;52:139–153. doi: 10.1016/j.neuron.2006.09.015. [DOI] [PubMed] [Google Scholar]
  18. Rossi S, et al. TOM: a web-based integrated approach for identification of candidate disease genes. Nucleic Acids Res. 2006;34:W285–W292. doi: 10.1093/nar/gkl340. [DOI] [PMC free article] [PubMed] [Google Scholar]
  19. Saccone SF, et al. Systematic biological prioritization after a genome-wide association study: an application to nicotine dependence. Bioinformatics. 2008;24:1805–1811. doi: 10.1093/bioinformatics/btn315. [DOI] [PMC free article] [PubMed] [Google Scholar]
  20. Schork NJ. Genetics of complex disease: approaches, problems, and solutions. Am. J. Respir. Crit. Care Med. 1997;156:S103–S109. doi: 10.1164/ajrccm.156.4.12-tac-5. [DOI] [PubMed] [Google Scholar]
  21. Strausberg RL. The Cancer Genome Anatomy Project: new resources for reading the molecular signatures of cancer. J. Pathol. 2001;195:31–40. doi: 10.1002/1096-9896(200109)195:1<31::AID-PATH920>3.0.CO;2-W. [DOI] [PubMed] [Google Scholar]
  22. Sullivan PF, et al. Schizophrenia as a complex trait: evidence from a meta-analysis of twin studies. Arch. Gen. Psychiatry. 2003;60:1187–1192. doi: 10.1001/archpsyc.60.12.1187. [DOI] [PubMed] [Google Scholar]
  23. Sullivan PF, et al. Candidate genes for nicotine dependence via linkage, epistasis, and bioinformatics. Am. J. Med. Genet. B Neuropsychiatr. Genet. 2004;126:23–36. doi: 10.1002/ajmg.b.20138. [DOI] [PubMed] [Google Scholar]
  24. Sullivan PF, et al. Genomewide association for schizophrenia in the CATIE study: results of stage 1. Mol. Psychiatry. 2008;13:570–584. doi: 10.1038/mp.2008.25. [DOI] [PMC free article] [PubMed] [Google Scholar]
  25. Sun J, et al. Candidate genes for schizophrenia: a survey of association studies and gene ranking. Am. J. Med. Genet. B Neuropsychiatr. Genet. 2008;147B:1173–1181. doi: 10.1002/ajmg.b.30743. [DOI] [PubMed] [Google Scholar]
  26. van Driel MA, et al. GeneSeeker: extraction and integration of human disease-related information from web-based genetic databases. Nucleic Acids Res. 2005;33:W758–W761. doi: 10.1093/nar/gki435. [DOI] [PMC free article] [PubMed] [Google Scholar]
  27. Wu X, et al. Network-based global inference of human disease genes. Mol. Syst. Biol. 2008;4:189. doi: 10.1038/msb.2008.27. [DOI] [PMC free article] [PubMed] [Google Scholar]
  28. Xu J, Li Y. Discovering disease-genes by topological features in human protein-protein interaction network. Bioinformatics. 2006;22:2800–2805. doi: 10.1093/bioinformatics/btl467. [DOI] [PubMed] [Google Scholar]
  29. Yu S, et al. Comparison of vocabularies, representations and ranking algorithms for gene prioritization by text mining. Bioinformatics. 2008;24:i119–i125. doi: 10.1093/bioinformatics/btn291. [DOI] [PubMed] [Google Scholar]
  30. Zhang B, et al. WebGestalt: an integrated system for exploring gene sets in various biological contexts. Nucleic Acids Res. 2005;33:W741–W748. doi: 10.1093/nar/gki475. [DOI] [PMC free article] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

[Supplementary Data]
btp428_index.html (760B, html)
btp428_bioinf-2009-0439-File002.doc (37KB, doc)

Articles from Bioinformatics are provided here courtesy of Oxford University Press

RESOURCES