Skip to main content
PMC home page
Bioinformatics logoLink to Bioinformatics
. 2009 Aug 10;25(19):2492–2499. doi: 10.1093/bioinformatics/btp480

Knowledge-guided inference of domain–domain interactions from incomplete protein–protein interaction networks

Mei Liu 1, Xue-wen Chen 1,*, Raja Jothi 2
PMCID: PMC2752622  PMID: 19667081

Abstract

Motivation: Protein-protein interactions (PPIs), though extremely valuable towards a better understanding of protein functions and cellular processes, do not provide any direct information about the regions/domains within the proteins that mediate the interaction. Most often, it is only a fraction of a protein that directly interacts with its biological partners. Thus, understanding interaction at the domain level is a critical step towards (i) thorough understanding of PPI networks; (ii) precise identification of binding sites; (iii) acquisition of insights into the causes of deleterious mutations at interaction sites; and (iv) most importantly, development of drugs to inhibit pathological protein interactions. In addition, knowledge derived from known domain–domain interactions (DDIs) can be used to understand binding interfaces, which in turn can help discover unknown PPIs.

Results: Here, we describe a novel method called K-GIDDI (knowledge-guided inference of DDIs) to narrow down the PPI sites to smaller regions/domains. K-GIDDI constructs an initial DDI network from cross-species PPI networks, and then expands the DDI network by inferring additional DDIs using a divide-and-conquer biclustering algorithm guided by Gene Ontology (GO) information, which identifies partial-complete bipartite sub-networks in the DDI network and makes them complete bipartite sub-networks by adding edges. Our results indicate that K-GIDDI can reliably predict DDIs. Most importantly, K-GIDDI's novel network expansion procedure allows prediction of DDIs that are otherwise not identifiable by methods that rely only on PPI data.

Contact: xwchen@ku.edu

Availability: http://www.ittc.ku.edu/∼xwchen/domainNetwork/ddinet.html

Supplementary information: Supplementary data are available at Bioinformatics online.

1 INTRODUCTION

Recent developments in high-throughput technologies have made it possible to systematically discover physical and functional interactions between proteins (Bork et al., 2004; Chen and Jeong, 2009; Hu et al., 2009; Lin et al. 2009; Parrish et al., 2006; Vidal, 2001). Protein–protein interactions (PPIs), though extremely valuable towards a better understanding of protein functions and cellular processes, do not provide any direct information about the regions/domains, defined as structural or functional sub-units, within the proteins that mediate the interaction (Jothi et al., 2006). Most often, it is only a fraction of a protein that directly interacts with its biological partners. Given that a majority of all proteins are multi-domain proteins (Jothi et al., 2006) and interactions between two proteins are often characterized by interactions between a pair of constituent domains. Thus, understanding interaction at the domain level is a critical step towards (i) thorough understanding of the PPI networks and their evolution; (ii) precise identification of binding sites; (iii) acquisition of insights into the causes of deleterious mutations at interaction sites; and most importantly (iv) development of drugs to inhibit pathological protein interactions (Pawson and Nash, 2003). In addition, information derived from known domain–domain interactions (DDIs) are increasingly used to understand binding interfaces (Akiva et al., 2008; Gong et al., 2005; Shoemaker et al., 2006), which in turn can help discover unrecognized PPIs (Schuster-Bockler and Bateman, 2007).

Many aspects of cell signaling, trafficking and targeting are governed by interactions between globular protein domains and, in some cases, between a globular domain and short peptide segment (Neduva et al., 2005). Interactions between globular domains have drawn increased attention over the last few years. Three-dimensional structures or models are a great aid to understanding the details of how protein or domain interactions are mediated. Recent studies suggest that the limiting factor is no longer the number of protein structures, but the number of 3D templates on which to model interactions (Aloy and Russell, 2004). This has created an urgent need in the community to identify the most comprehensive possible set of interaction templates. Given that it has been estimated that there are about 10 000 interaction types and that it will take more than 20 years before we know a full representative set (Aloy and Russell, 2004), it is important that we expedite the process of identifying all interactions at the domain level to fully understand the structural and evolutionary aspects of protein interactions and complexes (Itzhaki et al., 2006). Understanding interactions at the domain level will move us a step closer towards understanding critical molecular details of how interaction networks are constructed, which in turn will help illuminate cellular processes (Pawson and Nash, 2003).

Although high-throughput techniques used for experimental determination of PPIs can be used to infer interaction between individual domains (Ikeuchi et al., 2003; Sleno and Emili, 2008), to our knowledge, no study has used such approaches to detect DDIs on a genomic scale. One way to infer DDIs is to study 3D structures (Aloy and Russell, 2006; Finn et al., 2005; Littler and Hubbard, 2005; Stein et al., 2005; Russell et al., 2004). Unfortunately, the number of known DDIs is still mostly limited by the availability of 3D structures as the number of PPIs with known structures is far fewer than the number of known interactions. This limits us from uncovering all possible domain level interactions. Moreover, DDIs inferred from structural data could explain no >20% of the PPIs for any of the Escherichea coli, Saccharomyces cerevisiae, Caenorhabditis elegans, Drosophila melanogaster and Homo sapiens organisms (Itzhaki et al., 2006; Schuster-Bockler and Bateman, 2007). To expedite the discovery of DDIs, several computational approaches have been proposed in recent years in an effort to unearth previously unrecognized DDIs on a genome scale.

Attempts have been made to understand DDIs using a hypothesis based on correlated mutations at interaction sites (Jothi et al., 2006; Kann et al., 2007), generally referred to as the co-evolution principle (Pazos and Valencia, 2008). Many other methods rely solely on PPI networks to infer DDIs. One of the first was the Association Method, which seeks domain pairs that co-occur more often in interacting protein pairs than expected by chance (Sprinzak and Margalit, 2001). This idea was later extended using a maximum likelihood estimation approach where domain interaction probability is optimized using an expectation maximization algorithm (Deng et al., 2002; Liu et al., 2005). Other groups have proposed probabilistic network models (Gomez and Rzhetsky, 2002; Nye et al., 2005), machine learning algorithms (Chen and Liu, 2005, 2006), phylogenetic profiling (Pagel et al., 2004) and integrative models (Lee et al., 2006; Ng et al., 2003) to study domain interactions. More recently, a unique class of methods emerged where given a PPI network, the goal is to find an optimal set of DDIs that together could explain or justify the set of all interactions in the PPI network. For instance, the DPEA method (Riley et al., 2005) introduced a new measure for each potentially interacting domain pair, called E-score, which measures the degree of reduction in likelihood of observing the given PPI network when excluding a domain pair. A variant of this method was proposed later (Wang et al., 2007). Similar optimization frameworks were proposed to identify the minimal set of DDIs that could explain the set of all PPIs (Guimaraes et al., 2006; Singhal and Resat, 2007).

In this study, we explore an alternative approach called K-GIDDI (knowledge-guided inference of DDIs) for predicting DDIs from cross-species PPI network data. K-GIDDI begins by constructing an initial DDI network from cross-species PPI networks, which is then expanded by inferring additional DDIs using a divide-and-conquer biclustering algorithm guided by Gene Ontology (GO) information (Ashburner et al., 2000). The expansion of the DDI network is done by identifying partial-complete bipartite sub-networks, guided by GO molecular function terms and adding necessary edges to make them complete bipartite sub-networks. The presumption is that the newly added edges in the DDI network represent missing DDIs, which could be due to the utilization of not-yet-complete PPI networks.

The predicted DDIs are evaluated against a set of known DDIs (Finn et al., 2005; Stein et al., 2005) inferred from PDB structure data (Berman et al., 2000), and predictions from previous approaches stored in the DOMINE database (Raghavachari et al., 2008). Our results indicate that K-GIDDI can reliably predict DDIs, and its performance is better, if not comparable, to that of previous approaches. Most importantly, K-GIDDI's novel network expansion procedure allows prediction of DDIs that are otherwise not identifiable by methods that rely only on PPI data. This is significant because information derived from these novel DDIs could be used to understand binding interfaces, which in turn can help discover unrecognized PPIs.

2 METHODS

2.1 Initial DDI network construction

Most DDI prediction methods are based solely on PPI data. As much as we value the data generated from high-throughput experiments, several independent studies have, however, indicated that their false positive rates could be as high as 50% (Deane et al. 2002; Mrowka et al., 2001; von Mering et al., 2002). Even literature-curated PPI data is of lower quality than commonly assumed (Cusick et al., 2009). Only recently, advances in high-throughput technology have reduced the false positive rates to acceptable levels (Yu et al., 2008). Thus, in order to construct a reliable DDI network from noisy PPI datasets, we designed our approach, K-GIDDI, to take advantage of those PPIs that have been known to occur in many organisms, which, intuitively, are more likely to be true interactions than the ones that have been observed in only one organism. This strategy, which has been used by some of the previous approaches to control noise in the PPI data (Chen et al., 2008; Guimaraes et al., 2006; Riley et al., 2005), has been shown to be effective in minimizing the number of false inferences.

There are cases where a domain from one protein may make direct physical contact with two or more domains from another protein (Pawson and Nash, 2003) that almost always co-occur. In some cases, these co-occurring domains are fused together to form a single domain/protein in some reference organisms (Kamburov et al., 2007). In addition to deducing one-to-one DDI patterns, K-GIDDI was also designed to detect these one-to-many or many-to-many DDI patterns, which may be biologically meaningful interaction templates. In summary, the task at hand was to extract the conserved DDI patterns buried within the noisy PPI datasets derived from diverse organisms.

K-GIDDI accomplishes the task by gathering functionally related PPIs into a ‘group’ from which it derives the most representative and significant interacting domain (DDI) pattern that could explain the set of PPIs within that group. For instance, consider two PPIs between proteins P and Q and between proteins X and Y. The two PPIs (P−Q and X−Y) are defined as functional neighbors and are classified to belong to the same group if and only if proteins P and X, and proteins Q and Y (or P and Y, and Q and X) are functionally ‘similar’ (Fig. 1). Two proteins are considered to be functionally similar if the distance between them, defined as the shortest GO-graph-node distance between their annotated GO molecular function terms, is less than or equal to a threshold t, which is set empirically. Since GO is designed as a directed acyclic graph in which each node represents a term, the GO-graph-node distance is described as the least number of nodes separating the two terms. After obtaining groups of functionally related PPIs, for each group of PPIs, we enumerate all possible DDI patterns. Not only do we consider singular DDIs, in which a domain from one protein interacts with a domain from another protein, but we also consider instances where one domain from one protein interacts with two or more domains from another protein (one-to-many or even many-to-many). To select the most significant DDI patterns occurring within the PPIs in each group, we assess the significance of each DDI pattern in a group by computing its χ2-value using the formula

graphic file with name btp480m1.jpg (1)

where N is the total number of PPIs in the network, A is the number of PPIs in the group that contains the DDI pattern and B is the number of PPIs outside the group that contain the DDI pattern. C and D are the number of PPIs in the group and outside the group, respectively that do not contain the DDI pattern. A DDI pattern occurring more frequently in PPIs inside the group (functionally similar) than those outside the group is expected to have a higher χ2 value, hence is more significant. In our study, only those DDI patterns with the highest χ2 values from each group are retained for DDI network construction.

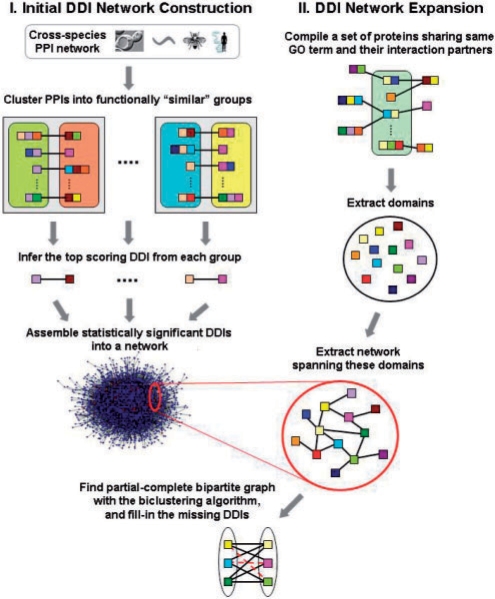
Fig. 1.

Fig. 1.

Open in a new tab

A schematic of the K-GIDDI method to infer DDIs. Colored squares denote protein domains, and proteins are denoted by single or concatenated domains. PPIs and DDIs are denoted by edges/lines connecting proteins or domains, respectively. Colored rounded-rectangles contain proteins sharing the same GO ‘molecular function’ term, and gray squares containing a pair of rounded-rectangles denote groups containing functionally similar PPIs. A representative DDI pattern is derived from each group. Those inferred DDIs that pass the statistical significance thresholds are then assembled to generate the initial DDI network, which is then expanded via a knowledge-guided search to include DDIs that may not be identified otherwise by methods that rely only on PPI data. The network expansion procedure, guided by GO information, identifies proteins sharing the same GO terms and their interaction partners, extracts the network spanning the domains within these proteins, and uses a biclustering algorithm to identify partial-complete bipartite sub-network and fills-in missing edges, denoted as red broken lines, to make them complete bipartite sub-networks.

Our decision to classify PPIs based on GO molecular function rather than GO's ‘cellular component’ or ‘biological process’ terms was based on two reasons: (i) classification of PPIs based on GO cellular component term would be less meaningful as a PPI cannot involve one protein from one cellular compartment and the other from another compartment, and (ii) although classification of PPIs based on GO biological process term could be justifiable, such a classification would result in fewer ‘groups’ (gray squares in Fig. 1) as there are far fewer biological processes in number than molecular functions. Since only the top-scoring DDI from each group is retained for the initial DDI network construction, using GO biological process would effectively result in fewer predicted DDIs during the initial DDI network construction (sparser network), which in turn would affect the subsequent network expansion procedure that searches for dense partial-complete bipartite graphs.

2.2 A knowledge-guided approach for DDI network expansion

Due to incompleteness of the PPI network, DDI prediction methods relying solely on the PPI data may not be able to infer the entire set of DDIs that might exist. Therefore, we propose to expand the above built DDI network by searching for partial-complete bipartite graphs by which novel interactions can be inferred between domains, which may be interacting within the context of one or more PPIs that may not have been discovered yet. The assumption is that few missing interactions between domains in those partial-complete bipartite graphs may be due to the use of incomplete PPI datasets.

Formally, the DDI network determined above can be represented by an undirected graph G=(D, E), where D is the set of domains (vertices), and E is the set of interactions (edges/links). A bipartite graph or bigraph is defined as a graph G=(D=V1∪V2, E), whose vertices can be divided into two disjoint sets V1 and V2 such that every edge connects a vertex in V1 to a vertex in V2. A complete bipartite graph, also called biclique, is a special kind of bipartite graph where every vertex in set V1 is connected to every vertex in set V2. That is, for any two vertices v1 ∈ V1 and v2 ∈ V2, there exists an edge connecting v1 and v2 in graph G, which will contain a total of |V1V2| edges.

Contrary to conventional complete bipartite graphs, the two sets of vertices we look for are not necessarily disjoint to reflect the fact that a domain may interact with itself. Moreover, we aim to find partial-complete instead of complete bipartite graphs. More precisely, the problem to solve here is to identify sub-graphs (or sub-networks) from the DDI network containing two sets of domains DV1 and DV2 such that every domain in DV1 is connected to at least a certain percentage of domains in DV2 and vice versa. Once a partial-complete bipartite graph has been identified, the missing edges (presence of which would otherwise make the partial-complete bipartite graph a complete bipartite graph), representing the additional DDIs, are added to the network.

Instead of blindly searching through the entire DDI network G for partial-complete bipartite graphs, we use GO information to guide the search so that the search space is significantly reduced to only those sub-graphs that contain functionally related domains and their interacting partners. To accomplish this task, for each GO ‘molecular function’ term, we first compile a set of proteins that share that functional annotation, and gather their interaction partners. Let us denote the set of proteins with the annotation term Ti as Pi,1 = {pi,11,pi,12,…} and the set of interaction partners for the proteins in Pi,1 as Pi,2 = {pi,21, pi,22,…}. Then from each set of proteins, the corresponding set of constituent domains are compiled: Di,1 = {di,11, di,12,…, di,1m} from Pi,1, and Di,2 = {di,21, di,22,…, di,2n} from Pi,2. After obtaining the two sets of domains, we extract the subgraph G′ = (Di,1∪Di,2, E′) from the DDI network G = (D, E) such that Di,1⊆D, Di,2 ⊆ D, and (di,1j, di,2k)∈E′ ⊆ E, where j=1–m, and k=1–n.

Once our focus is confined to the subgraph G′=(Di,1 ∪ Di,2, E′), we initiate the search for a partial-complete bipartite graph G* = (DV1∪DV2, E*) such that every domain in DV1 is connected to at least a certain percentage of domains in DV2 and vice versa (Fig. 1). In graph theory, finding complete bipartite sub-graph in a given graph with maximal number of edges is computationally intractable (NP-complete). Thus, the crucial question here is how to search for such graphs. To tackle the challenge, we propose to employ a biclustering algorithm. Biclustering is a simultaneous clustering technique, frequently used in gene expression analysis (Madeira and Oliveira, 2004), applied on both row and column dimensions of a matrix to find sub-matrices in which rows and columns are highly correlated. For the problem at hand, from the sub-graph G′, we can establish an adjacency matrix A where the rows refer to the domains in Di,1 and the columns refer to the domains in Di,2 with dimension m=|Di,1| by n=|Di,2|. Individual elements in the matrix, Aij, is 1 if (di,1j, di,2k)∈E′ and 0 otherwise ∀j and ∀k, and di,1j∈Di,1, di,2k ∈ Di,2. One fundamental difference exists between our problem and the one for gene expression analysis. Instead of having a matrix of real numbers representing expression levels, our adjacency matrix A contains binary values, 1s and 0s, representing whether or not two domains interact. Moreover, the objective in gene expression analysis is to identify correlated expression patterns, which implies that every value is important. In contrast, the 0s in our matrix A are meaningless, and the elements in the resultant sub-matrices will mostly be 1s.

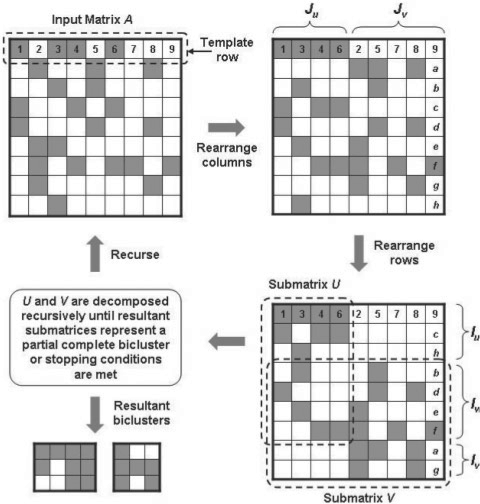
Keeping the above differences in mind, we modify a divide-and-conquer biclustering algorithm called binary inclusion-maximal biclustering algorithm (Bimax) (Prelic et al., 2006) that can be used to identify maximal sub-matrices with all elements equal to 1 (i.e. complete bipartite graphs). However, our objective is to identify partial-complete bipartite graphs and not complete bipartite graphs. To this end, we modify the Bimax algorithm as follows. The divide procedure first partitions the input adjacency matrix A into two smaller, possibly overlapping sub-matrices U and V. This is done by taking an arbitrary row as a template, rearranging the set of columns by separating them into two subsets Ju (containing all 1s) and Jv (containing all 0s) based on the template row (Fig. 2). Then the rows are rearranged as follows: first place the rows Iu with 1s only in the columns corresponding to Ju, then the rows Iw with 1s in the columns corresponding to both Ju and Jv, and finally the rows Iv with 1s only in the columns corresponding to Jv. Iu, Iw and Iv in conjunction with Ju and Jv defines U as the sub-matrix A(Iu ∪ Iw, Ju) and V as the sub-matrix A(Iw ∪ Iv, Ju ∪ Jv). In the conquer procedure, the resulting sub-matrices U and V are then decomposed recursively in the same manner until the resulting sub-matrix (or sub-matrices) represents a bicluster in which each row and column contain a specific percentage, b, of 1s (Fig. 2). The complete Approx-Bimax algorithm is provided as Supplementary Material S1.

Fig. 2.

Fig. 2.

Open in a new tab

A pictorial illustration of the divide-and-conquer biclustering algorithm. An arbitrary row from the input matrix A, containing either 1s or 0s represented as gray and white boxes, is chosen as a template to rearrange the columns such that columns containing 1s in the template row are arranged on the left (Ju) and those containing 0s arranged on the right (Jv). Numbers 1–9 within the template row serves as a guide to the column rearrangement. Next, the rows are rearranged such that submatrices A(Iu, Jv) and A(Iv, Ju) contain only 0s. Letters a–h within right column serves as a guide to the row rearrangement. Matrices U and V are processed recursively until the resultant sub-matrices contain at least a specific percentage of 1s in each column and row.

3 RESULTS AND DISCUSSION

3.1 Data sources

To build the DDI network, we assembled the PPI data for S.cerevisiae, C.elegans, D.melanogaster and H.sapiens from the DIP January, 2008 release (Salwinski et al., 2004), BioGRID 2.0.38 release (Stark et al., 2006) and HPRD September, 2007 release (Peri et al., 2003). The assembled dataset contained 54 987, 3085, 5375 and 30 223 PPIs among 3794, 1609, 2059 and 7167 proteins in S.cerevisiae, C.elegans, D.melanogaster and H.sapiens, respectively.

Domain assignments for each protein were made using the HMM profiles from Pfam 22.0 (Finn et al., 2008). Both the manually curated Pfam-A and the automatically generated Pfam-B profiles were considered for domain assignments. The set of interacting proteins in S.cerevisiae, C.elegans, D.melanogaster and H.sapiens contained a total of 4542, 2346, 3715 and 12 082 unique Pfam domains, respectively. We found a total of 429 Pfam domains that were common among all four organisms. Supplementary Material S2 contains the distribution and overlap of domains across the four organisms. We used GO ‘molecular function’ terms (Ashburner et al., 2000) to assign function for each protein in our dataset. Together, the proteins in our dataset were assigned a total of 2788 unique GO functions.

The DDI network was constructed in two parts. In the first part, an initial DDI network was constructed using K-GIDDI's network construction procedure (Fig. 1; see Section 2 for details). In the second part, this network is then expanded to include additional DDIs via a novel knowledge-guided search for partial-complete bipartite graphs, which in the end are made complete bipartite graphs by adding the missing edges.

3.2 Statistical evaluation of the predicted DDIs

The limited number of gold standard DDIs makes the evaluation of DDI prediction methods a challenging problem. Typically, pairs of domains reported to interact in crystal structures of protein complexes are used as a benchmark for true positives. To evaluate the reliability of DDIs predicted by our algorithm K-GIDDI, we compared them with the set of known DDIs reported in iPfam (Finn et al., 2005). In iPfam, two domains are defined as interacting if and only if they are close enough in at least one PDB complex to form an interaction. However, one must keep in mind that iPfam embodies only a small fraction of all possible DDIs that may exist. According to a recent study (Itzhaki et al., 2006), DDIs in iPfam and 3DID (Stein et al., 2005) databases could explain no > 20% of the PPIs for any of the E.coli, S.cerevisiae, C.elegans, D.melanogaster and H.sapiens organisms. Hence, it must be emphasized that the number of predicted DDIs that can be verified by these two databases of known DDIs is rather small. Just because a predicted DDI cannot be verified using iPfam or 3DID does not necessarily mean that it is a false positive. It is certainly possible that at least a sub-set of unverifiable DDI predictions is true, and that they have not been crystallized yet. For instance, only ∼11.4–17.3% of the DDI predictions by the RCDP approach (Jothi et al., 2006) are known to be true.

Given this backdrop, in order to evaluate the reliability of the DDIs predicted by K-GIDDI, we adopt a statistical approach described by Deng et al. (2002). If K-GIDDI's predictions are reliable, then a DDI predicted by K-GIDDI should be much more likely to be present in the set of known DDIs than an interaction between a random pair of domains. To measure the fold enrichment, we use the following formula, which measures the ratio of the fraction of predicted DDIs known to be true to the fraction of random domain pairs known to interact:

graphic file with name btp480m2.jpg (2)

where n is the number of DDI predictions, k is the number DDI predictions that are known to be true, N is the number of all possible domain pairs and K is the number of all possible domains known to interact.

Recall that K-GIDDI makes DDI predictions in two parts: initial DDI network construction and knowledge-guided expansion of the DDI network. In the first part, an initial DDI network is constructed by mining statistically significant DDI patterns from functionally related PPIs (see Fig. 1 and Section 2 for details). A χ2-value, assessing the significance of each possible DDI pattern, is computed in the process. One would expect that the higher the significance score (high χ2-value), the more likely the predicted DDI is a true interaction. Furthermore, in the second part of K-GIDDI, we expand the DDI network through novel knowledge guided search of partial-complete bipartite sub-networks using the biclustering algorithm Approx-Bimax. Since the emphasis is on partial-complete bipartite sub-networks, one can choose on how partial-complete a bipartite graph needs to be to constitute a desired result. In another words, we can choose the percentage of 1s all rows and columns of a matrix must have in order for it to be classified as a bicluster (or partial-complete sub-network; Fig. 2). Intuitively, one would expect the higher the percentage threshold, the more likely the predicted DDIs are true interactions.

To evaluate the performance of K-GIDDI, we assess the accuracy of the predictions made by the initial DDI network construction procedure and the network expansion procedure separately, and in combination. To this end, predictions were made using various combinations of two parameters: s and b, where s represents the percentage of inferred DDIs with the highest χ2-values that were used to construct the initial DDI network (Fig. 1), and b represents the percentage of 1s all rows and columns of a matrix must have in order for it to be classified as a bicluster (Fig. 2). The fold enrichment [Equation (2)] of DDIs predicted using the network construction and expansion procedures are shown in Tables 1 and 2, respectively.

Table 1.

Evaluation of DDIs predicted from K-GIDDI's network construction procedure alone against the set of known DDIs (Finn et al., 2008)

S (%) Number of predicted DDIs Number of predictions known to be true Fold enrichment over Random
10 298 48 103.4
30 1036 104 64.4
50 1745 141 51.9
70 2548 182 45.8
90 4572 266 37.3
100 5796 319 35.3
Random 2 377 290 3704 1.0
Open in a new tab

Table 2.

Evaluation of DDIs predicted from K-GIDDI's network expansion procedure alone against the set of known DDIs (Finn et al., 2008)

S(%) B (%) Number of predicted DDIs Number of predictions known to be true Fold enrichment over Random
10 50 88 5 36.5
60 47 0 –
30 50 743 27 23.3
60 409 15 23.5
70 101 3 19.1
80 33 0 –
50 50 1579 39 15.9
60 897 29 20.8
70 264 11 26.7
80 72 4 35.7
100 50 5704 66 7.4
60 3411 43 8.1
70 1512 18 7.6
80 643 14 14.0
Random – 2 377 290 3704 1.0
Open in a new tab

As shown in Table 1, the predictions by the K-GIDDI's network construction procedure alone are significantly better than random. The fold enrichment over random decreases as s increases (relaxed) indicating that the higher the χ2-value, the smaller but more reliable the resulting DDI network is. On the other hand, we noticed a drop in fold enrichment values for the DDIs predicted by K-GIDDI's network expansion procedure (Table 2). This drop-off in performance was expected since the goal of the DDI network expansion procedure is to discover those DDIs that may not have been crystallized because of the reasons that the PPIs containing (or mediated by) them may not have been identified yet. These DDIs will be overlooked by prediction methods that rely solely on PPI data.

3.3 Comparison of K-GIDDI's performance with that of other methods

To assess how K-GIDDI stacks against previous approaches, we compared K-GIDDI's performance with that of three sufficiently different approaches: RDFF (Chen and Liu 2005), RCDP (Jothi et al., 2006) and DPEA (Riley et al., 2005). The objective here is to compare the percentages of predictions (by each method) known to be true. It must be emphasized that this is only an indirect comparison as different datasets were utilized in each study, and it would be extremely difficult to test these methods on the same dataset since some of these methods impose unique set of constraints on the input dataset. For example, RCDP (Jothi et al., 2006) considers only those PPIs with both proteins having orthologous hits in 10 or more genomes. As shown in Table 3, the K-GIDDI's performance is better, if not comparable, to that of previous approaches.

Table 3.

Comparison of K-GIDDI's performance with that of previous methods (RDFF (Chen and Liu, 2005), DPEA (Riley et al., 2005), and RCDP (Jothi et al., 2006))

Method Number of predicted DDIs Number of predictions known to be true Percentage of predictions known to be true
RDFF 2475 104 4.2
DPEA 1812 185 10.2
RCDP_SLA50 960 109 11.4
K-GIDDI_10_50a 386 53 13.7
K-GIDDI_10_90a 298 48 16.1
RCDP_SLA75 336 58 17.3
Open in a new tab

aK-GIDDI_X_Y denotes K-GIDDI with parameters s=X and b=Y.

Furthermore, we compared the K-GIDDI's predictions with the set of known and predicted DDIs in the DOMINE database (Raghavachari et al., 2008). DOMINE contains DDIs inferred from PDB entries and those by eight different computational approaches. DOMINE labels the set of known DDIs inferred from PDB crystal structures as ‘PDB’, and those that were predicted by a computational approach as HCP, MCP or LCP representing high-, medium- or low-confidence DDI predictions. High-confidence pairs (HCP) are those that were predicted using multiple sources of information or by at least two sufficiently different computational methods. Medium-confidence pairs (MCP) are predicted by just one approach in which both domains are a part of the same GO biological process. Low-confidence pairs (LCP) are the ones predicted simply by one computational approach. The comparison summary is shown in Table 4. For different choices of parameters, 17–22% of our predictions are confirmed by the set of DDIs in the DOMINE database, and among them 9–13% are known to be true (in PDB) and/or have been predicted using heterogeneous data sources or by multiple approaches.

Table 4.

Fraction of K-GIDDI's DDI predictions confirmed by DOMINE (Raghavachari et al., 2008)

S (%) B (%) Percentage of predictions confirmed by at least one out of eight other methods included in the DOMINE database Percentag of predictions confirmed by PDB + HCP
10 50 21.63 12.77
– 70 20.66 11.98
– 90 20.42 11.89
30 50 19.71 11.02
– 70 19.50 11.25
– 90 18.85 10.72
50 50 16.48 8.37
– 70 17.85 9.53
– 90 17.22 9.26
Open in a new tab

K-GIDDI was designed to take advantage of those PPIs that have been known to occur in many organisms, which intuitively, are more likely to be true interactions compared with the ones that have been observed in only one organism. This strategy, which has been used by some of the previous approaches to control noise in PPI data has been shown to be effective in minimizing the number of false DDI inferences. The method itself does not impose any restriction as to how many genomes should a PPI be conserved for it to be included in the seed set, but those that are conserved in more genomes can be expected to contribute more. Although such a strategy could be a potential limiting factor as well conserved DDIs are more likely to be inferred compared with poorly conserved or lineage specific DDIs, we found that about one-third of our predictions are organism-specific (Supplementary Material S3) demonstrating that K-GIDDI is capable of predicting poorly conserved or lineage-specific DDIs.

3.4 Structure evidence for novel DDIs predicted by K-GIDDI's network expansion procedure

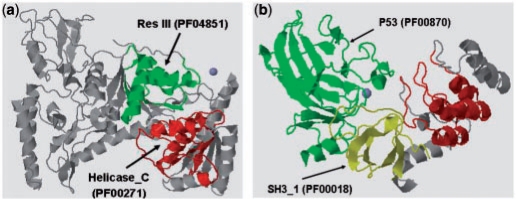
One noteworthy contribution of our study is the novel knowledge-guided approach of DDI network expansion, where possible missing DDI links are inferred from the identified partial-complete bipartite graphs. Some of those novel DDIs may not be directly explainable by observed in current PPI data since none of the interactomes are complete yet. In contrast, other DDI prediction methods that rely solely on PPI data will not be able to infer those DDIs inferred by K-GIDDI's network expansion procedure. For example, domains Res III (PF04851) and Helicase_C (PF00271) were predicted to interact by K-GIDDI's expansion procedure, but was not predicted to interact by any of the eight methods profiled in the DOMINE database (Raghavachari et al., 2008) because the domain pair does neither appear in nor explain any of the PPI in the utilized PPI datasets. Res III domain is the Res sub-unit of the type III restriction enzyme. Type III restriction endonucleases are components of prokaryotic DNA restriction–modification mechanisms that protect the organism against invading foreign DNA. Type III enzymes are composed of two sub-units, Res and Mod. The Mod sub-unit recognizes the DNA sequence specific for the system and is a modification methyltransferase, and the Res sub-unit is required for restriction. The Helicase_C domain is a conserved helicase C-terminal domain. K-GIDDI's prediction of interaction between the Res III and Helicase_C domains is supported by PDB structure (PDB ID: 1d9x), validating the usefulness of K-GIDDI's network expansion procedure.

In addition, if two domains are interacting, they are more likely to exhibit similar functional roles. Res III is found to perform ATP binding (GO:0005524), DNA binding (GO:0003677) and hydrolase activity (GO:0016787). Helicase_C is observed to execute ATP binding (GO:0005524) and nucleic acid binding (GO:0003676), which is a general term for DNA binding (GO:0003677). Furthermore, some interacting domain pairs may have homologs in other genomes that are fused into one protein chain. We have found that Res III and Helicase_C domains co-occur in 1036 protein sequences in the Pfam database. Figure 3a presents an illustration of the PDB structures of the two domains co-occurring within UvrABC system protein B (UniProt: P56981) in Bacillus caldotenax.

Fig. 3.

Fig. 3.

Open in a new tab

(a) PDB structure (PDB ID: 1d9x) showing Res III and Helicase_C domains in UVRBBACCA protein (P56981), highlighted in green and red, respectively. (b) PDB structure (PDB ID: 1ycs) showing the interaction between SH3_1 and P53 domains, highlighted in yellow and green, respectively.

We also found evidences for three other DDIs, predicted by network expansion procedure, which cannot be explained by the current PPI data but are known to be true: SH3_1 (PF00018) and P53 (PF00870) (Fig. 3b), Myosin_head (PF00063) and Dynamin_N (PF00350) and Filament (PF00038) and bZip_1 (PF00170). Table 5 summarizes the fraction of DDIs predicted by the K-GIDDI network expansion procedure that are not observed in current PPI data. Out of the DDIs predicted by network expansion procedure, ∼16.67–51.89% cannot be explained by the currently available PPI datasets, suggesting that there could be PPIs mediated by these novel DDIs that may not been discovered yet. The entire list of DDIs not observed in current PPI data is provided as Supplementary Material S4.

Table 5.

Fraction of DDIs predicted by K-GIDDI's network expansion procedure that are not observed in current PPI data

s (%) b (%) Number of Predictions from network expansion Number of predictions from non-PPI Percentage
10 50 172 34 19.77
– 70 18 3 16.67
30 50 1460 489 33.49
– 70 166 28 16.87
50 50 3426 1364 39.81
– 70 464 111 23.92
100 50 15 048 7808 51.89
– 70 3039 994 32.71
– 90 29 6 20.69
Open in a new tab

3.5 Validation of novel DDIs using shortest GO-graph-node distance

The set of predicted DDIs not in DOMINE were investigated further for supporting evidence. As we know, two domains/proteins interact to enable or perform a certain cellular function. Thus, the interacting domains/proteins are more likely to share similar functional annotations than a random pair of domains. To this end, we examined the closest GO-graph-node distance between each pair of domains predicted to interact, measuring how similar the functional annotations of the two domains are. Although using GO-graph-node distance to benchmark the predicted DDIs may appear to be circular, we wish to emphasize that it is not for the following reason. While PPIs were clustered into groups based on GO molecular function (Fig. 1), the prediction of DDIs itself did not use GO information. Rather, the most significant DDI pattern occurring within each group is inferred based on whether or not this DDI pattern occurs more frequently in PPIs inside the group than those outside the group.

A GO-graph-node distance of 0/1 for a pair of domains indicates that both domains share the same/similar functional annotation. We found that many domain pairs predicted to interact shared the same GO functional annotation or have the smallest GO-graph-node distance of 1, indicating a direct parent–child relationship where the parent is a more general description of a function and the child is more specific description of a function. Using a set of fixed parameters (i.e. s = 10% and b = 90%), there were 569 DDI predictions that were not found in DOMINE (Supplementary Material S5). Among those, 313 DDIs involved pairs of domains for which GO annotations were available for both domains. Of the 313 DDIs, we found 67 DDIs (21.41%) with constituent domains having GO-graph-node distances ≤2. To assess the significance of the percentage, we computed the GO-graph-node distance for all possible domain pairs (2 377 290 in total) to see how many of the random domain pairs would have a distance ≤2. Out of all 2 377 290 domain pairs, 1 408 681 pairs had GO annotations available for both domains. Among the 1 408 681 random domain pairs, 167 309 (11.88%) had GO-graph-node distance ≤2, which is ∼2-fold less than that observed for predicted DDIs (21.41%). Table 6 summarizes the results for various GO-graph-node distances as thresholds.

Table 6.

Comparison between fractions of our predicted DDIs (313 pairs) and random domain pairs (1 408 681 pairs) having certain GO-graph-node distance

Shortest GO-graph-node distance Number of Random domain pairs Percentage of Random domain pairsa Number of Predicted DDIs Percentage of predicted DDIsb
=0 47 150 3.35 19 6.07
≤1 76 648 5.44 30 9.59
≤2 167 309 11.88 67 21.41
≤3 330 705 23.48 97 30.03
≤4 559 503 39.72 134 42.81
Open in a new tab

aCalculation based on a total of 1 408 681 random domain pairs.

bCalculation based on a total of 313 predicted DDIs.

Although the evaluation of DDIs predicted by K-GIDDI's network expansion procedure alone revealed that its performance is lower compared with that for DDIs predicted by K-GIDDI's network construction procedure (Fig. 1; Tables 1 and 2), network expansion procedure is still useful because it is able to infer novel DDIs which would otherwise be not inferred using PPI data alone. From the network expansion procedure, we were able to predict a total of 117 DDIs (Supplementary Material S6), out of which only 88 DDIs had both domains covered by the iPfam domain space. As shown in Table 2, five out of the 88 DDI predictions by the expansion procedure are known to be true, which would not have been predicted by any method that solely relies on PPI data. Of the total 117 DDIs predicted by the expansion procedure, 61 had both domains annotated with GO function, out of which 17 domain pairs (27.87%) shared the exact same GO functional annotation. Most of them were not found among the set of known DDIs, suggesting that these are novel interactions yet to be verified.

4 CONCLUSION

We presented K-GIDDI, a novel knowledge-guided approach for inferring DDIs from incomplete PPI networks. K-GIDDI infers an initial DDI network from cross-species PPI networks, and then expands the DDI network by inferring additional DDIs using a divide-and-conquer biclustering algorithm guided by GO information. Our results indicated that K-GIDDI's performance is better or comparable with previous approaches for predicting DDIs. We found biological evidence supporting some of K-GIDDI's predictions. Most importantly, K-GIDDI's novel network expansion scheme allowed it to predict DDIs that are otherwise not identifiable by methods that rely only on PPI data.

Funding: National Science Foundation (Award IIS-0644366 to X-W.C.); Intramural Research Program of the National Institutes of Health, NIEHS (to R.J.).

Conflict of Interest: none declared.

Supplementary Material

[Supplementary Data]
btp480_index.html (1.3KB, html)

REFERENCES

  1. Akiva E, et al. Built-in loops allow versatility in domain-domain interactions: lessons from self-interacting domains. Proc. Natl Acad. Sci. 2008;105:13292–13297. doi: 10.1073/pnas.0801207105. [DOI] [PMC free article] [PubMed] [Google Scholar]
  2. Aloy P, Russell RB. Ten thousand interactions for the molecular biologist. Nat. Biotechnol. 2004;22:1317–1321. doi: 10.1038/nbt1018. [DOI] [PubMed] [Google Scholar]
  3. Aloy P, Russell RB. Structural systems biology: modeling protein interactions. Nat. Rev. Mol. Cell Biol. 2006;7:188–197. doi: 10.1038/nrm1859. [DOI] [PubMed] [Google Scholar]
  4. Ashburner M, et al. Gene ontology: tool for the unification of biology. The gene ontology consortium. Nat. Genet. 2000;25:25–29. doi: 10.1038/75556. [DOI] [PMC free article] [PubMed] [Google Scholar]
  5. Berman HM, et al. The Protein Data Bank. Nucleic Acids Res. 2000;28:235–242. doi: 10.1093/nar/28.1.235. [DOI] [PMC free article] [PubMed] [Google Scholar]
  6. Bork P, et al. Protein interaction networks from yeast to human. Curr. Opin. Struct. Biol. 2004;14:292–299. doi: 10.1016/j.sbi.2004.05.003. [DOI] [PubMed] [Google Scholar]
  7. Chen XW, Jeong JC. Sequence-based prediction of protein interaction sites with an integrative method. Bioinformatics. 2009;25:585–591. doi: 10.1093/bioinformatics/btp039. [DOI] [PubMed] [Google Scholar]
  8. Chen XW, Liu M. Prediction of protein-protein interactions using random decision forest framework. Bioinformatics. 2005;21:4394–4400. doi: 10.1093/bioinformatics/bti721. [DOI] [PubMed] [Google Scholar]
  9. Chen XW, Liu M. Domain based predictive models for protein-protein interaction prediction. EURASIP J. Appl. Signal Process. 2006;2006 Article ID 32767. [Google Scholar]
  10. Chen XW, et al. Protein function assignment through mining cross-species protein-protein interactions. PLoS ONE. 2008;3:e1562. doi: 10.1371/journal.pone.0001562. [DOI] [PMC free article] [PubMed] [Google Scholar]
  11. Cusick ME, et al. Literature-curated protein interaction datasets. Nat. Methods. 2009;6:39–46. doi: 10.1038/nmeth.1284. [DOI] [PMC free article] [PubMed] [Google Scholar]
  12. Deane CM, et al. Protein interactions: two methods for assessment of the reliability of high throughput observations. Mol. Cell Proteomics. 2002;1:349–356. doi: 10.1074/mcp.m100037-mcp200. [DOI] [PubMed] [Google Scholar]
  13. Deng M, et al. Inferring domain-domain interactions from protein-protein interactions. Genome Res. 2002;12:1540–1548. doi: 10.1101/gr.153002. [DOI] [PMC free article] [PubMed] [Google Scholar]
  14. Finn RD, et al. iPfam: visualization of protein-protein interactions in PDB at domain and amino acid resolutions. Bioinformatics. 2005;21:410–412. doi: 10.1093/bioinformatics/bti011. [DOI] [PubMed] [Google Scholar]
  15. Finn RD, et al. The Pfam protein families database. Nucleic Acids Res. 2008;36:D281–D288. doi: 10.1093/nar/gkm960. [DOI] [PMC free article] [PubMed] [Google Scholar]
  16. Gomez SM, Rzhetsky A. Towards the prediction of complete protein–protein interaction networks. Pac. Symp. Biocomput. 2002:413–424. [PubMed] [Google Scholar]
  17. Gong S, et al. A protein domain interaction interface database: InterPare. BMC Bioinformatics. 2005;6:207. doi: 10.1186/1471-2105-6-207. [DOI] [PMC free article] [PubMed] [Google Scholar]
  18. Guimaraes KS, et al. Predicting domain-domain interactions using a parsimony approach. Genome Biol. 2006;7:R104. doi: 10.1186/gb-2006-7-11-r104. [DOI] [PMC free article] [PubMed] [Google Scholar]
  19. Hu P, et al. Global functional atlas ofEscherichia coliencompassing previously uncharacterized proteins. PLoS Biol. 2009;7:e96. doi: 10.1371/journal.pbio.1000096. [DOI] [PMC free article] [PubMed] [Google Scholar]
  20. Ikeuchi A, et al. Exhaustive identification of interaction domains using a high-throughput method based on two-hybrid screening and PCR-convergence: molecular dissection of a kinetochore subunit Spc34p. Nucleic Acids Res. 2003;31:6953–6962. doi: 10.1093/nar/gkg888. [DOI] [PMC free article] [PubMed] [Google Scholar]
  21. Itzhaki Z, et al. Evolutionary conservation of domain-domain interactions. Genome Biol. 2006;7:R125. doi: 10.1186/gb-2006-7-12-r125. [DOI] [PMC free article] [PubMed] [Google Scholar]
  22. Jothi R, et al. Co-evolutionary analysis of domains in interacting proteins reveals insights into domain-domain interactions mediating protein-protein interactions. J. Mol. Biol. 2006;362:861–875. doi: 10.1016/j.jmb.2006.07.072. [DOI] [PMC free article] [PubMed] [Google Scholar]
  23. Kamburov A, et al. Denoising inferred functional association networks obtained by gene fusion analysis. BMC Genomics. 2007;8:460. doi: 10.1186/1471-2164-8-460. [DOI] [PMC free article] [PubMed] [Google Scholar]
  24. Kann MG, et al. Predicting protein domain interactions from coevolution of conserved regions. Proteins. 2007;67:811–820. doi: 10.1002/prot.21347. [DOI] [PubMed] [Google Scholar]
  25. Lee H, et al. An integrated approach to the prediction of domain-domain interactions. BMC Bioinformatics. 2006;7:269. doi: 10.1186/1471-2105-7-269. [DOI] [PMC free article] [PubMed] [Google Scholar]
  26. Lin XT, et al. Assessing reliability of protein-protein interactions by integrative analysis of data in model organisms. BMC Bioinformatics. 2009;10(Suppl. 4):S5. doi: 10.1186/1471-2105-10-S4-S5. [DOI] [PMC free article] [PubMed] [Google Scholar]
  27. Littler SJ, Hubbard SJ. Conservation of orientation and sequence in protein domain-domain interactions. J. Mol. Biol. 2005;345:1265–1279. doi: 10.1016/j.jmb.2004.11.011. [DOI] [PubMed] [Google Scholar]
  28. Liu Y, et al. Inferring protein-protein interactions through high-throughput interaction data from diverse organisms. Bioinformatics. 2005;21:3279–3285. doi: 10.1093/bioinformatics/bti492. [DOI] [PubMed] [Google Scholar]
  29. Madeira SC, Oliveira A. Biclustering algorithm for biological data analysis: a survey. IEEE/ACM Trans. Comput. Biol. Bioinform. 2004;1:24–45. doi: 10.1109/TCBB.2004.2. [DOI] [PubMed] [Google Scholar]
  30. Mrowka R, et al. Is there a bias in proteome research? Genome Res. 2001;11:1971–1973. doi: 10.1101/gr.206701. [DOI] [PubMed] [Google Scholar]
  31. Neduva V, et al. Systematic discovery of new recognition peptides mediating protein interaction networks. PLoS Biol. 2005;3:e405. doi: 10.1371/journal.pbio.0030405. [DOI] [PMC free article] [PubMed] [Google Scholar]
  32. Ng SK, et al. Integrative approach for computationally inferring protein domain interactions. Bioinformatics. 2003;19:923–929. doi: 10.1093/bioinformatics/btg118. [DOI] [PubMed] [Google Scholar]
  33. Nye TM, et al. Statistical analysis of domains in interacting protein pairs. Bioinformatics. 2005;21:993–1001. doi: 10.1093/bioinformatics/bti086. [DOI] [PubMed] [Google Scholar]
  34. Pagel P, et al. A domain interaction map based on phylogenetic profiling. J. Mol. Biol. 2004;344:1331–1346. doi: 10.1016/j.jmb.2004.10.019. [DOI] [PubMed] [Google Scholar]
  35. Parrish JR, et al. Yeast two-hybrid contributions to interactome mapping. Curr. Opin. Biotechnol. 2006;17:387–393. doi: 10.1016/j.copbio.2006.06.006. [DOI] [PubMed] [Google Scholar]
  36. Pawson T, Nash P. Assembly of cell regulatory systems through protein interaction domains. Science. 2003;300:445–452. doi: 10.1126/science.1083653. [DOI] [PubMed] [Google Scholar]
  37. Pazos F, Valencia A. Protein co-evolution, co-adaptation and interactions. EMBO J. 2008;27:2648–2655. doi: 10.1038/emboj.2008.189. [DOI] [PMC free article] [PubMed] [Google Scholar]
  38. Peri S, et al. Development of human protein reference database as an initial platform for approaching systems biology in humans. Genome Res. 2003;13:2363–2371. doi: 10.1101/gr.1680803. [DOI] [PMC free article] [PubMed] [Google Scholar]
  39. Prelic A, et al. A systematic comparison and evaluation of biclustering methods for gene expression data. Bioinformatics. 2006;22:1122–1129. doi: 10.1093/bioinformatics/btl060. [DOI] [PubMed] [Google Scholar]
  40. Raghavachari B, et al. DOMINE: a database of protein domain interactions. Nucleic Acids Res. 2008;36:D656–D661. doi: 10.1093/nar/gkm761. [DOI] [PMC free article] [PubMed] [Google Scholar]
  41. Riley R, et al. Inferring protein domain interactions from databases of interacting proteins. Genome Biol. 2005;6:R89. doi: 10.1186/gb-2005-6-10-r89. [DOI] [PMC free article] [PubMed] [Google Scholar]
  42. Russell RB, et al. A structural perspective on protein-protein interactions. Curr. Opin. Struct. Biol. 2004;14:313–324. doi: 10.1016/j.sbi.2004.04.006. [DOI] [PubMed] [Google Scholar]
  43. Salwinski L, et al. The Database of Interacting Proteins: 2004 update. Nucleic Acids Res. 2004;32:D449–D451. doi: 10.1093/nar/gkh086. [DOI] [PMC free article] [PubMed] [Google Scholar]
  44. Schuster-Bockler B, Bateman A. Reuse of structural domain-domain interactions in protein networks. BMC Bioinformatics. 2007;8:259. doi: 10.1186/1471-2105-8-259. [DOI] [PMC free article] [PubMed] [Google Scholar]
  45. Shoemaker BA, et al. Finding biologically relevant protein domain interactions: conserved binding mode analysis. Protein Sci. 2006;15:352–361. doi: 10.1110/ps.051760806. [DOI] [PMC free article] [PubMed] [Google Scholar]
  46. Singhal M, Resat H. A domain-based approach to predict protein-protein interactions. BMC Bioinformatics. 2007;8:199. doi: 10.1186/1471-2105-8-199. [DOI] [PMC free article] [PubMed] [Google Scholar]
  47. Sleno L, Emili A. Proteomic methods for drug target discovery. Curr. Opin. Chem. Biol. 2008;12:46–54. doi: 10.1016/j.cbpa.2008.01.022. [DOI] [PubMed] [Google Scholar]
  48. Sprinzak E, Margalit H. Correlated sequence-signatures as markers of protein-protein interaction. J. Mol. Biol. 2001;311:681–692. doi: 10.1006/jmbi.2001.4920. [DOI] [PubMed] [Google Scholar]
  49. Stark C, et al. BioGRID: a general repository for interaction datasets. Nucleic Acids Res. 2006;34:D535–D539. doi: 10.1093/nar/gkj109. [DOI] [PMC free article] [PubMed] [Google Scholar]
  50. Stein A, et al. 3did: interacting protein domains of known three-dimensional structure. Nucleic Acids Res. 2005;33:D413–D417. doi: 10.1093/nar/gki037. [DOI] [PMC free article] [PubMed] [Google Scholar]
  51. Vidal M. A biological atlas of functional maps. Cell. 2001;104:333–339. doi: 10.1016/s0092-8674(01)00221-5. [DOI] [PubMed] [Google Scholar]
  52. von Mering C, et al. Comparative assessment of large-scale data sets of protein-protein interactions. Nature. 2002;417:399–403. doi: 10.1038/nature750. [DOI] [PubMed] [Google Scholar]
  53. Wang H, et al. InSite: a computational method for identifying protein-protein interaction binding sites on a proteome-wide scale. Genome Biol. 2007;8:R192. doi: 10.1186/gb-2007-8-9-r192. [DOI] [PMC free article] [PubMed] [Google Scholar]
  54. Yu H, et al. High-quality binary protein interaction map of the yeast interactome network. Science. 2008;322:104–110. doi: 10.1126/science.1158684. [DOI] [PMC free article] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

[Supplementary Data]
btp480_index.html (1.3KB, html)
btp480_bioinf-2009-0699-File001.doc (25.5KB, doc)
btp480_bioinf-2009-0699-File002.doc (72KB, doc)
btp480_bioinf-2009-0699-File003.doc (32KB, doc)
btp480_bioinf-2009-0699-File004.xls (14KB, xls)
btp480_bioinf-2009-0699-File005.xls (64KB, xls)
btp480_bioinf-2009-0699-File006.xls (40.5KB, xls)

Articles from Bioinformatics are provided here courtesy of Oxford University Press

RESOURCES